Geum.ru

Методические указания к курсовой работе «Алгоритмизация и модификация сае-систем (на примере сае sigma и Nastran)»

Вид материалаМетодические указания

Содержание


2. 2-я часть курсовой работы 8-го семестра
Курсовая работа 8-го семестра
Целью курсовой работы 8-го семестра является
1. 1-ая (обязательная) часть курсовой работы в 8-ом семестре.
П.2. Модифицируя подпрограммы FORMDD
6061-Т651 Al Plate
П.3. (дополнительный, по отдельному заданию преподавателя).
П.4. исследует
4.1. а) проводит
Griddm. getfine
Выбирает вид сетки для дальнейшего выполнения КР.
П.5. а) проводит
П.6. а) осуществляет
П.7. оценивает
П.8. оценивает
П.9. отмечает
1.2. Пояснения к выполнению пунктов задания 1-ой части КР 8-го семестра и требования к оформлению отчета
Московский авиационный институт
Выполнил(а): ст. гр. 06-42 _
Print Screen
...
Полное содержание
Подобный материал:
  1   2   3   4   5





Кафедра 609

Столярчук В.А.

2011


МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КУРСОВОЙ РАБОТЕ

«Алгоритмизация и модификация САЕ-систем

(на примере САЕ Sigma и Nastran) »

по дисциплине «Моделирование физических и технических систем»

8-ой семестр


СОДЕРЖАНИЕ


Курсовая работа 8-го семестра


1. 1-ая (обязательная) часть курсовой работы 8-го семестра

1.1. Содержание 1-ой части КР 8-го семестра

1.2. Пояснения к выполнению пунктов задания 1-ой части КР 8-го семестра и требования к оформлению отчета

2. 2-я часть курсовой работы 8-го семестра

3. Организация работы в 8-ом семестре


Детальное рассмотрение всех аспектов использования программной системы Sigma, вопросы, связанные с алгоритмизацией, а также выполнением курсовых работ приведено в подсистеме «Помощь» комплекса Sigma.

Файл подсистемы «Помощь» включает следующие разделы:
  • Теоретические основы.
  • Программный комплекс Sigma.
  • Работа с программным комплексом
  • Подпрограммы расчетного блока
  • Дополнительные материалы
  • Примеры выполнения отдельных заданий КР в Sigma и Nastran.

Почти каждый раздел делится на главы. Число этих глав 51.

Общее требование по курсовым работам.

Все пункты отчетов по курсовым работам должны заканчиваться выводом или заключением, кратко формулирующим итоги выполнения данного пункта. Все графики, картины напряженно-деформированного состояния и другие графические материалы отчета должны снабжаться анализом, комментариями или выводом.


Курсовая работа 8-го семестра


«Интеллект состоит в том,

чтобы узнавать подобие разных вещей

и разницу подобных»

Шарль Луи де Монтескье, 18 век


«Алгоритмизация и модификация САЕ-систем

(на примере САЕ Sigma и Nastran) »


Прикладная направленность курсовой работы 8-го семестра заключается в решении задачи по расчету напряжённо-деформированного состояния плоской пластины методом конечных элементов в учебной системе Sigma и коммерческой системе Nastran.


Целью курсовой работы 8-го семестра является:

  • углублённое знакомство студентов с САЕ - системами (учебной системой Sigma и коммерческими системами конечно-элементного анализа Nastran и (или) AnSys);
  • исследование работы алгоритма МКЭ в системах Nastran и (или) AnSys на примере реализации учебной САЕ Sigma,
  • получение навыков разработки отдельных подсистем и модулей для системы Sigma на основе других алгоритмов;
  • изучение и применение методов обработки результатов численного эксперимента;
  • приобретение опыта в практических вопросах проектирования математического обеспечения и конструирования соответствующих алгоритмов для САЕ - систем.


Курсовая работа состоит из двух частей. Каждая из частей включает выполнение программного и исследовательского разделов.

1. 1-ая (обязательная) часть курсовой работы в 8-ом семестре.


1.1. Содержание 1-ой части КР 8-го семестра.


Вариант задания совпадает с вариантом КР 7-го семестра, включая геометрию пластины, граничные условия и внешние воздействия. Все изменения в задании, внесенные в процессе работы над КР 7-го семестра, должны быть учтены в КР 8-го семестра. Студент может использовать все наработки КР 7-го семестра, внося необходимые изменения в соответствии с заданием КР 8-го семестра.

В 1-ой части работы студент выполняет 9 обязательных пунктов задания, подкрепляющих лекционный материал и выполняемых по мере прохождения в семестре соответствующих разделов лекционного материала.


П.1. На основе результатов работы КР 7-го семестра изменяет деление пластины на 8-ми-узловые зоны таким образом, чтобы границы некоторых зон приблизительно совпадали с границами подобластей с повышенным уровнем напряжений и с границами подобластей с пониженным уровнем напряжений.

Для границ зон рекомендуется использовать простейшие геометрические линии: прямая, окружность.

Результаты работы необходимо согласовать с преподавателем. Добиться правильного расчета проекта до NRC=12 при толщине пластины = 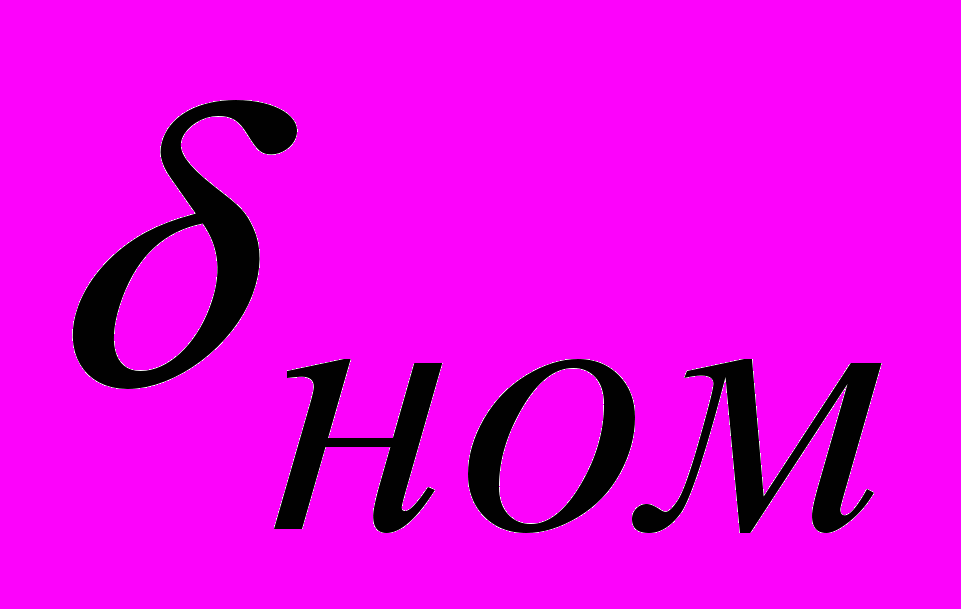, найденной в П.4. КР 7-го семестра и значениях характеристик материала из КР 7-го семестра, рассчитав и установив требуемые размерности массивов для максимального NRC, используя результаты исследования размерностей массивов в КР 7-го семестра.

П.2. Модифицируя подпрограммы FORMDD и (или) GRIDDM (выбрав наиболее рациональный способ), реализует назначение разных свойств КЭ в подобластях с малым, средним и высоким уровнем напряжений.

При этом в подобластях со средним уровнем напряжений использует материал прошлого семестра, с пониженным уровнем напряжений – материал

6061-Т651 Al Plate (из банка материалов FEMAP) толщиной, меньшей 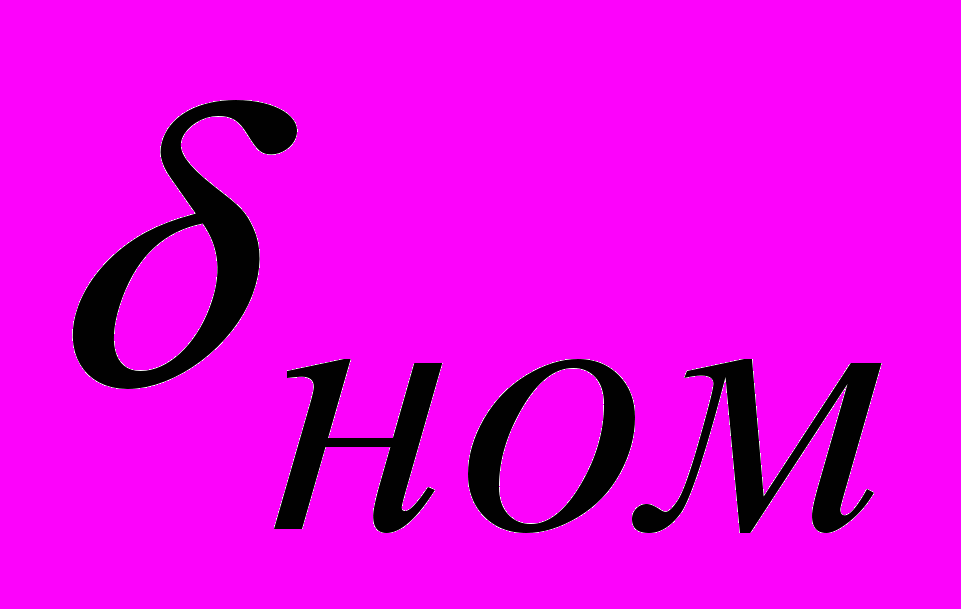, но не меньше технологически допустимой 0.1см, а в областях с повышенным уровнем напряжений – материал 2024-Т351 Al Plate (также из банка материалов

FEMAP) толщиной, большей 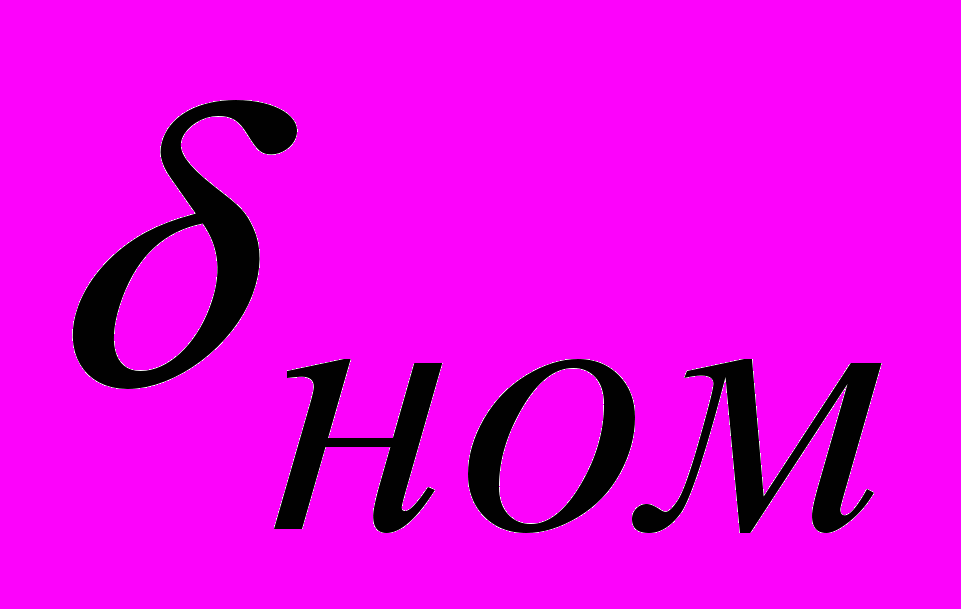. Пример назначения разных свойств КЭ реализован в проекте example3.

Окончательные значения толщин для всех свойств КЭ надо подобрать из условий равнопрочности по напряжениям с максимальными значениями, стараясь вывести хотя бы одно из максимальных значений напряжений примерно на 0.8 от значений допускаемых напряжений. Точность задания толщин не должна превышать 0.01см.

В случае использования только 2-х материалов (обусловленном результатами выполнения КР предыдущего семестра) - подбирает толщины этих 2-х материалов, включая в этом случае и основной, также из условий равнопрочности по напряжениям с максимальными значениями, стараясь вывести хотя бы одно из максимальных значений напряжений примерно на 0.8 от допускаемых напряжений.

Цель – снизить резкие пики, выровнять эти напряжения или добиться плавного перехода от одного значения к другому по всей площади пластины, не превысив, тем не менее, допускаемых напряжений.

Проект должен правильно рассчитывать до NRC=12.


Примечание: Задание номера свойства конечного элемента может быть

осуществлено двумя способами (демонстрация - в Example3):

а) в программе GRIDDM вызовом подпрограммы PROPERTYGRIDDM;

б) в программе FORMDD вызовом подпрограммы PROPERTYFORMDD.

Возможны и другие варианты.

Обе подпрограммы PROPERTYGRIDDM и PROPERTYFORMDD находятся в файле FINDNODD. Подпрограмма PROPERTYGRIDDM назначает номера свойств конечным элементам, находящимся в конкретных зонах, в соответствии с номерами этих зон. Подпрограмма PROPERTYFORMDD назначает номера свойств КЭ исходя из геометрического расположения КЭ. При конкретной реализации необходимо составить алгоритмы, которые наилучшим образом будут назначать номера свойства конкретному элементу тем или иным способом.

В заключение П.2. провести анализ полученного решения при NRC=7, определив области особо опасных напряжений и наибольших перемещений. Дать общую характеристику напряженно-деформированного состояния пластины.

П.3. (дополнительный, по отдельному заданию преподавателя). В подпрограмме force дополняет реализацию распределения сил по узлам от распределённой нагрузки по заданной формуле, осуществлённую в 7-ом семестре, реализацией распределения сил по узлам от распределённой нагрузки по интерполирующему полиному с переключением способа распределения (функция или полином) через панель основных параметров с помощью какого-либо свободного параметра (например, PRM6).

При этом необходимо:
  • выделить наиболее характерные точки функции распределенной нагрузки q (x) и разбить зону приложения q (x) на некоторое число n интервалов, после чего подсчитать по формуле для q (x) значения q в образовавшихся (в том числе характерных и граничных) точках;
  • образовать таблицу значений аргумента х и значений q для n+1 точек;
  • построить интерполирующий полином по любым из этих n+1 значений, включая, прежде всего, характерные и граничные точки q (x) для уменьшения степени интерполирующего полинома. (Для определения коэффициентов полинома, интерполирующего функцию распределённой нагрузки, рекомендуется использовать какую-нибудь распространённую программу, например, SigmaPlot);
  • проверить степень совпадения исходной функции и заменяющего его полинома и отличие суммарной силы от распределённой нагрузки q, подсчитанной по заданной формуле и силы, полученной с помощью интерполирующего полинома. Если отличие будет существенным (более 2%), то увеличить число точек для построения интерполирующего полинома. Тем самым определить необходимую степень интерполирующего полинома;
  • добиться правильного расчета проекта до NRC=11-12.
  • получить окончательное решение с помощью полинома.
  • провести анализ полученного решения при NRC=7, определив области особо опасных напряжений и наибольших перемещений. Дать общую характеристику напряженно-деформированного состояния пластины.

Примечание к п.п. 1-3: требования к формированию зон и КЭ, реализации граничных условий и нагрузки совпадают с требованиями пунктов 1 и 2 курсовой работы 7-го семестра.


П.4. исследует возможности, ограничения и эффективность работы алгоритмов триангуляции и оптимизации сетки КЭ в зависимости от числа конечных элементов, узлов или NRC. При выполнении п.4 границы областей с разными свойствами КЭ при оптимизации не должны изменяться. Неизменность границ свойств КЭ в процессе оптимизации сетки поддерживается подпрограммой findnodd.for, пример реализации которой можно посмотреть в Example 3.

В то же время, для полноты исследования необходимо добиться работы алгоритма во всех зонах. Студент может использовать подпрограммы fs (файл w1calc) и GETFINE (файл w2calc). При необходимости студент модифицирует эти подпрограммы в соответствии с решаемыми задачами.

Целью П.4. является максимально полное заключение об особенностях работы алгоритма оптимизации сетки, эффективности его работы и выполнения функций, для которых он предназначен.

Привести анализ работы алгоритма, указав зоны в которых он работает наиболее интенсивно, и зоны, в которых его работа проявилась наименьшим образом. Попытаться указать причину того и иного явления.


4.1.

а) проводит оптимизацию сетки статическим и динамическим шагом с проверкой сохранение границ свойств КЭ. На основании визуального сравнения устанавливает наибольшее изменение сетки, произведенное тем или иным алгоритмом.

б) выбирает точку для дальнейшего исследования. Исследуемая точка должна иметь целые (желательно) координаты, располагаться в области опасных напряжений, но не находиться в непосредственной близости к местам нагружения пластины и на границах изменения свойств КЭ. При этом, по крайней мере, два вида напряжений должны иметь значения, превышающие уровень 10000Н/см2 при NRC=7. Точка должна находиться в области существенного изменения сетки в результате оптимизации.

Желательно также, чтобы при всех NRC точка находилась как бы внутри одного КЭ, изменяющегося только в размерах. Выполнение всех этих условий облегчит выполнение П. 4, 5. и 6. Выбранную точку согласовать с преподавателем.

в) исследует влияние оптимизации сетки на значения напряжений (без использования алгоритмов сглаживания) и перемещений для выбранной точки и определяет в ней для нескольких NRC относительное изменение значений напряжений в результате использования алгоритма оптимизации. Делает выводы;


4.2. изучает алгоритм оптимизации и исследует эффективность его работы: изменение минимального угла и среднего минимального угла в процессе оптимизации в зависимости от NRC. В случае необходимости строит графики. Делает выводы. При этом, в случае возникновения до оптимизации или после оптимизации одного и того же значения минимального угла при разных NRC (что может быть объяснено спецификой области и её разбиения) или когда значение угла в процессе оптимизации, практически, не меняется, необходимо исключить этот угол из рассмотрения программным методом. Это объясняется необходимостью максимально объективно оценить эффективность данного метода оптимизации сетки.

Значения минимального угла при каждом NRC должны приводиться в текстовом файле результатов расчета пластины.


4.3. изучает теоретические вопросы оценки качества сеток и определяет изменение качества сетки с помощью метода штрафных функций (считая каждый из штрафов равноценным), а также других характеристик сетки до и после оптимизации с помощью программы GETFINE, вызываемой из подпрограммы GRIDDM. GETFINE позволяет оценить качество сетки до оптимизации и после, предварительно воссоздав функцию плотности по исходной сетке. Модифицирует GETFINE и FUNCTION GetShapeFine с целью оценки формы конечных элементов на основе собственных разработок. Для окончательной оценки качества сетки использует не менее трёх функций штрафа.

Оценивает качество сетки до и после оптимизации по критерию Делоне.

Делает окончательные выводы об эффективности реализованного в программе алгоритма оптимизации сетки.

Выбирает вид сетки для дальнейшего выполнения КР.


4.4*. (дополнительный, по заданию преподавателя) определяет, при каком процентном соотношении длины стороны и расстояния от основного узла до промежуточного возможно изменение положения промежуточного узла зоны при разных NRC и сопоставляет с теоретическим материалом, изложенным в лекциях для метода изопараметрических координат. Строит график этой зависимости. Делает выводы по построенной зависимости;


П.5.

а) проводит на выбранном виде сетки расчет в системе Sigma и определяет выходные результаты работы программы - напряжения (и/или перемещения узлов - по отдельному заданию преподавателя) в одной согласованной с преподавателем в П.3. точке пластины, исследуя сходимость результатов в зависимости от степени сгущения сетки КЭ.

б) применяет методы регрессионного анализа и экстраполяции для получения наиболее достоверного результата, используя программу SigmaPlot или какую-либо другую программу обработки результатов численного эксперимента. При построении функций регрессии разрешается игнорировать не более двух из 10 результатов вычислительного эксперимента. Добиваться значения квадратичной регрессии порядка Rsqr = 0.88-1.0.

При определении напряжений учитывает необходимость выполнения соответствия результатов, получаемых в Sigma и Nastran-е (AnSys-е).

Примечание: при определении сходимости перемещений узлов, образующих КЭ с исследуемой точкой, использует только нечетные NRC;

П.6.

а) осуществляет экспорт и расчет модели в Nastran-е (AnSys-е) и определяет выходные результаты работы программы - напряжения (перемещения) в ранее заданной точке пластины, исследуя сходимость результатов в зависимости от степени сгущения сетки КЭ и повторяя последовательность действий п.5. При задании свойства КЭ и характеристик материала предусмотреть цветовое выделение каждого из них.

б) проводит сравнение и анализ значений напряжений и перемещений в системах Sigma и Nastran (AnSys). Делает окончательный вывод по этим значениям на основании расчетов в 2-х системах (чему равны напряжения и с какой точностью определяются эти значения.);

в) при NRC=7 или 8 в конечном элементе, которому принадлежит исследуемая точка, указывает направление координатной оси, относительно которой проводился расчет в Nastran-е. Определяет NRC, при котором направление основных осей в Sigma и Nastrane в конечном элементе, которому принадлежит исследуемая точка, наиболее совпадают.

П.7. оценивает эффективность работы алгоритма упаковки матрицы и исследует запросы к памяти для хранения матрицы в зависимости (на выбор) от числа конечных элементов, числа узлов, а также изменение заполнения массивов, используемых для хранения матрицы в зависимости от количества узлов или числа КЭ. Исследование проводит для упорядоченных и неупорядоченной матриц. Оценивает разреженность матрицы при разных NRC, а также влияние на разреженность работы алгоритма регуляризации сетки.

Пояснение

В задание КР 8-го семестра входит анализ схем хранения и алгоритмов приведения матриц (П.7, П.8), в том числе, при отсутствии подключения алгоритмов упорядочения. В таких случаях запросы программной системы к памяти существенно возрастают. Поэтому при выполнении П.7 и П.8 необходимо задать размерности массивов с учетом максимальных потребностей программы при выполнении КР. Для определения максимальных размерностей массивов необходимо отключить алгоритмы упорядочения (см. панель задания основных параметров), в результате чего в модуле REMNDD отключается вызов подпрограммы GENRCM и выполняются операции группы строк:

DO I=1,NP

PERM(I) = I

ENDDO

При выполнении П.7 и П.8. надо будет объяснить в отчете смысл проводимой операции.

Необходимо также обратить внимание на массивы (например, ENV), используемые программой по разному назначению.


П.8. оценивает работу алгоритмов упорядочения по критерию минимального заполнения множителя L, исследует возможности и ограничения прямого и обратного алгоритма Катхилла-Макки. При этом оценивает эффективность работы ленточного (с отключением обратного упорядочения) и профильного алгоритмов Катхилла-Макки (по ширине ленты, профиля, числу операций при решении системы алгебраических уравнений и т.п.). Сопоставляет ширину ленты и размер профиля исходной матрицы с матрицей, полученной в результате упорядочения.

Исследует эффективность работы алгоритма в зависимости от назначения разных начальных узлов (3-4-х) для начала работы алгоритма Катхилла-Макки, для чего отключает/подключает или изменяет подпрограмму rootls отыскания наиболее оптимального начального узла.

Для доказательства своих выводов изменяет соответствующие подпрограммы, а также вывод числовых данных этих программ с целью получения наиболее наглядного результата.

Внимание! После отключения алгоритмов упорядочения увеличивается размерность массивов, в которых хранится матрица.

П.9. отмечает недостатки системы Sigma и предлагает пути её совершенствования.

П.10*. (дополнительный, по заданию преподавателя) определяет оптимальную комбинацию толщины двух типов конечных элементов для пластины минимальной массы при заданных геометрии, нагрузках и граничных условиях. При этом, следует взять одно NRC, при котором получаются наиболее достоверные результаты по определяющему напряжению, и, меняя толщины, найти такую их комбинацию, при которой масса пластины будет наименьшей;


1.2. Пояснения к выполнению пунктов задания 1-ой части КР 8-го семестра и требования к оформлению отчета



В отчете все разделы должны заканчиваться выводом. Выводы должны сопровождаться графиками и таблицами, число точек которых (число строк) должно обуславливаться степенью точности, установленной исследователем для обоснования своих выводов. Каждая таблица в отчете должна сопровождаться графиком, на основе анализа которого необходимо сделать выводы.

Расположение материала должно быть максимально компактным, но информативным. Большие размеры PreenyScreen-ов рисунков могут свидетельствовать о неумении студента работать с изображениями.


Отчет должен начинаться с титульных строк типа:

---------------------------------------------------------------------------------------------

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(Аэрокосмический факультет, кафедра 609)

Курсовая работа (КР) по дисциплине «Программно-информационные комплексы»

(семестр 8, вариант № ___)

Выполнил(а): ст. гр. 06-42 _ ___________________

(фамилия, инициалы)


ОС Windows _______________

версия программы Sigma 6.1а

---------------------------------------------------------------------------------------------


В отчете должны быть представлены:

П.1 и П.2.:
  • рисунок итогового задания 7-го семестра и рисунок рассчитываемой модели
  • в одной строке Print Screen геометрической модели пластины, полученной при выполнении КР 7-го семестра с указанием номеров зон и Print Screen эквивалентных напряжений на этом разбиении при NRC=7 (со шкалой значений), с выделенными подобластями повышенных и пониженных значений напряжений (из КР 7-го семестра). Указать диапазоны значений напряжений, принятых в качестве нулевых и в качестве повышенных;
  • в одной строке Print Screen геометрической модели пластины с новым разбиением на зоны с указанием номеров зон и Print Screen эквивалентных напряжений на этом разбиении при NRC=7 (со шкалой значений) с использованием одного свойства КЭ. Под рисунком - указать толщину пластины и характеристики материала, а также перечислить номера зон, в которых будет увеличена, уменьшена или оставлена без изменения толщина пластины;
  • в одной строке Print Screen геометрической модели пластины с новым разбиением на зоны с указанием номеров зон и Print Screen эквивалентных напряжений на этом разбиении при NRC=7 (со шкалой значений) с использованием нескольких свойств КЭ. Под Print Screen - значения принятых из условия равнопрочности значений толщины, названия и характеристики использованных материалов;
  • таблица максимальных значений напряжений при старом и новом разбиении (форму таблицы и пример её частичного заполнения см. ниже) с использованием одного и нескольких свойств КЭ (для нового разбиения), завершающаяся краткой характеристикой нового разбиения по сравнению со старым, анализом полученных результатов, а также краткое сравнение уровней напряжений с оценкой плавности перехода от одних напряжений к другим (по картинам эквивалентных напряжений) с одним и несколькими свойствами КЭ;




Разбиение и количество свойств КЭ
Напряжение по Х
Напряжение по Y
Касательное
1-ое главное
2-ое главное
Эквива-лентное

Старое

1

































Новое

1
32800
9200
10000
35100
8100
33300

-21900/32900
21300/31900
-2900/4300
-18300/27400
-23200/34800

Новое

2(3)


































  • краткое описание использованного способа реализации разных свойств

КЭ;
  • для максимального NRC - таблицу размерностей основных массивов

САЕ-Sigma.