Geum.ru

Вестник Брянского государственного технического университета. 2008. №1(17) Технология, инструменты и оборудование машиностроительных производств

Вид материалаДокументы
Подобный материал:

Вестник Брянского государственного технического университета. 2008. № 1(17)


Технология, инструменты и оборудование

машиностроительных производств


УДК 539.1

С.В. Давыдов, Ю.В. Гуляев, В.В.Симочкин


Влияние ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ УГЛЕРОДИСТЫХ СТАЛей

НА ЭВТЕКТОИДНОЕ ПРЕВРАЩЕНИЕ АУСТЕНИТА


Исследовано влияние теплопроводности углеродистых сталей на фазовые превращения в них при разных температурах нагрева.


В настоящее время исследователи не придают должного внимания влиянию теплофизических свойств сталей на процессы структурных превращений, хотя всем известно [1], что процессы теплопередачи играют основную роль в фазовых превращениях и происходящие изменения структуры и свойств определяются температурным режимом. Теплообмен внутри материала происходит всегда, когда есть разность температур, образующаяся при нагреве или охлаждении материала, т.е. движущей силой теплового потока является градиент температур. А так как тепловой поток выражается формулой Фурье: I = – λ·grad T [1], – то, кроме градиента температур, он оказывается в значительной степени зависимым от коэффициента теплопроводности материала λ. Коэффициент теплопроводности для каждой стали является величиной постоянной и зависит от химического состава стали и температуры. Коэффициент теплопроводности характеризует способность тел передавать тепло и численно равен количеству тепла, передаваемому за 1 ч через 1 м² изотермической поверхности (удельному тепловому потоку) при разности температур в 1 °C между поверхностями толщиной 1 м (измеряется в Вт/м ּ°С). структурные составляющие стали отличаются друг от друга по теплопроводности, поэтому и температура их при нагреве или охлаждении будет различной.

Углеродистые стали состоят из двух структурных фаз - феррита и цементита - и их смеси, перлита, поэтому исследовалось влияние теплопроводности этих фаз на структурные превращения. Из литературы [2] известны коэффициенты теплопроводности структурных составляющих при естественных условиях: 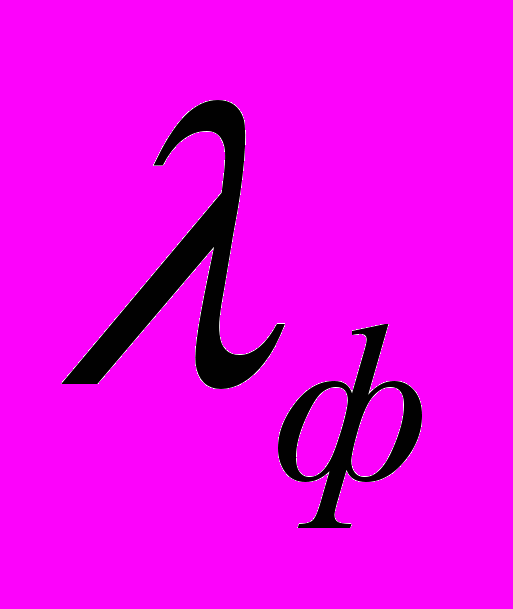=76,8 Вт/мּ°C; λ 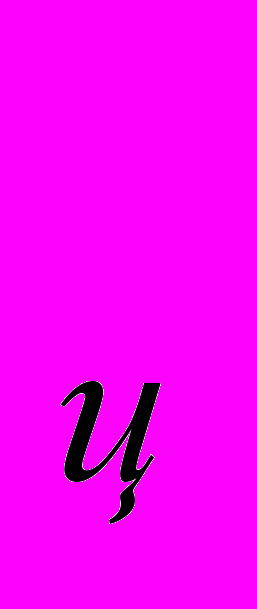=7,1 Вт/мּ°C; λ 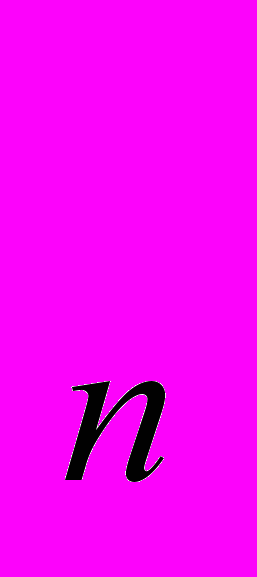=51,9 Вт/мּ°C; λ 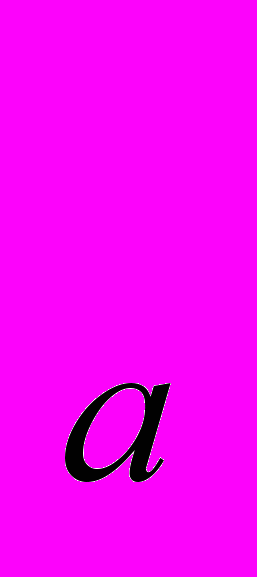=41,9 Вт/мּ°C, где ф – феррит; ц – цементит; п – перлит; а – аустенит.

С повышением содержания примесей и температуры теплопроводность сталей уменьшается. Коэффициент теплопроводности углеродистых сталей в зависимости от содержания примесей и температуры рассчитывается по формуле Б. Е. Неймарка [ 2 ]:

λ =a-bΣ+cΣ²,

где: a = 76, 8-6, 68·10ˉ 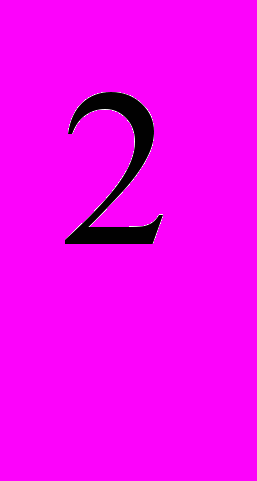t; b = 34, 2-9, 9· 10ˉ 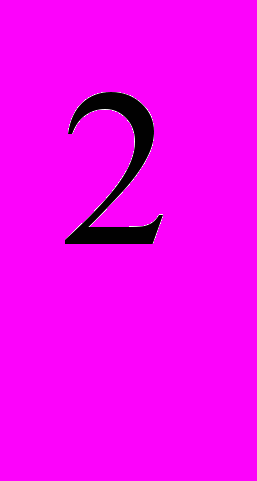t + 0,815·10ˉ t;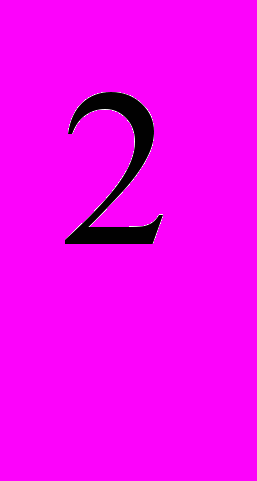

с =9,31-3,96·10ˉ 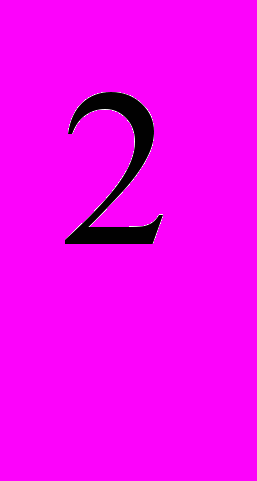t+0,418·10ˉt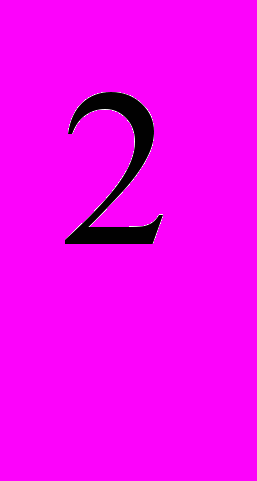; Σ – суммарная добавка остальных элементов (С, Si, Мn, S и др.) к железу, % по массе. Формула действительна для значений Σ от 0,1 до 2,0 и температуры до 500°C .

Коэффициент теплопроводности сталей в зависимости от температуры определяется по формуле [2]

λ 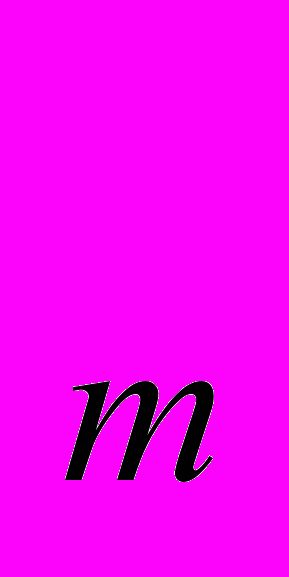= λ ± bt , (1)

где λ – теплопроводность при естественных условиях; t – температура нагрева; b – коэффициент, показывающий изменение λ при изменении t на 1°С, (находится по экспериментальным данным).

Однако формула Б.Е. Неймарка сложна в употреблении и действительна только в узких пределах, а формула (1) неудобна, так как всегда необходимо знать исходную теплопроводность и коэффициент b.

Для практического металловедения наиболее удобны такие закономерности, которые бы определяли теплопроводность стали в зависимости от ее марки, чтобы, зная марку стали (количество структурных составляющих – феррита и цементита) и температуру нагрева, можно было вычислить теплопроводность (вплоть до температур фазовых превращений).

Из литературы [1] известно, что между теплопроводностью и электропроводностью существует прямолинейная зависимость: чем выше электропроводность, тем выше теплопроводность. эта зависимость выражается законом Видемана – Франца – Лоренца:

λ/Н= LT,

где λе – электронная теплопроводность; Н – постоянная, характеризующая отношение теплопроводности к электропроводности; L – коэффициент Лоренца; Т – абсолютная температура.

Между электропроводностью и диффузией также существует определенная зависимость. Формула, полученная в результате прямой замены электрических характеристик их диффузионными аналогами, имеет вид


,


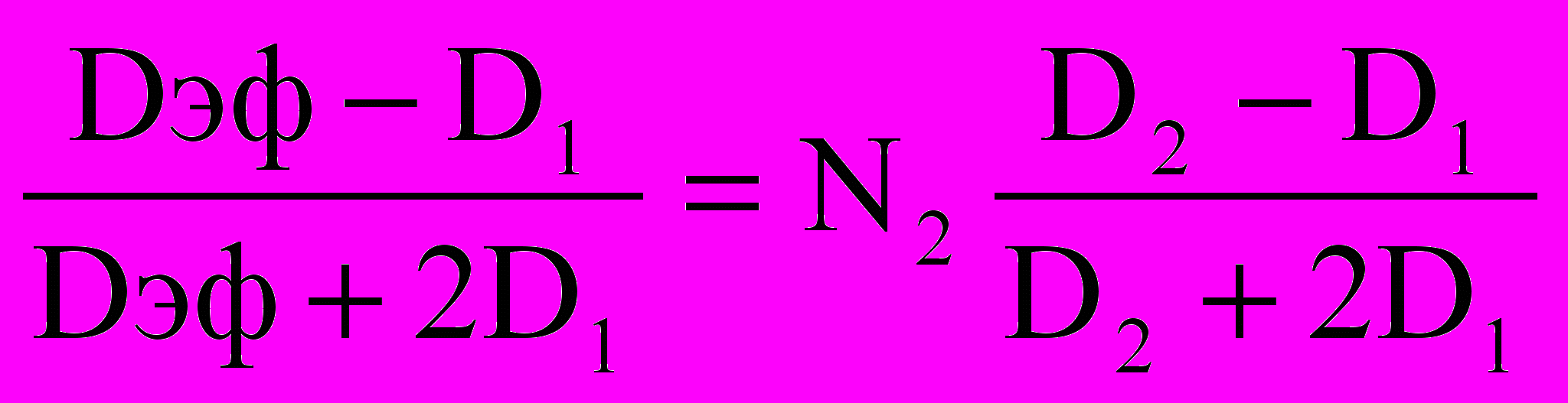где D 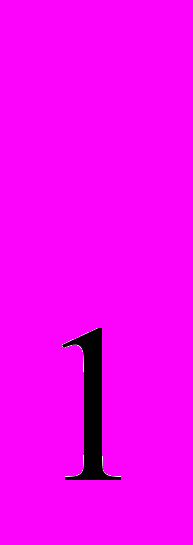– коэффициент диффузии одной фазы; D 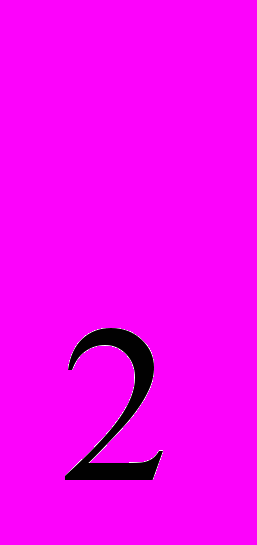– коэффициент диффузии второй фазы; Dэф – эффективный коэффициент диффузии; N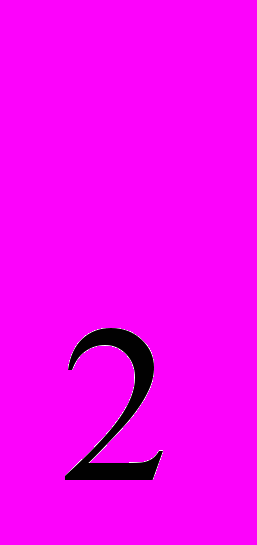- доля второй фазы. Это уравнение наиболее удовлетворительно описывает опытные результаты по диффузии металлов.

На основании изложенного для определения теплопроводности двухфазных сплавов, имеющих в структуре феррит и цементит, можно применить аналогичную формулу, заменив электрические характеристики тепловыми. Формула теплопроводности в данном случае имеет следующий вид:

,


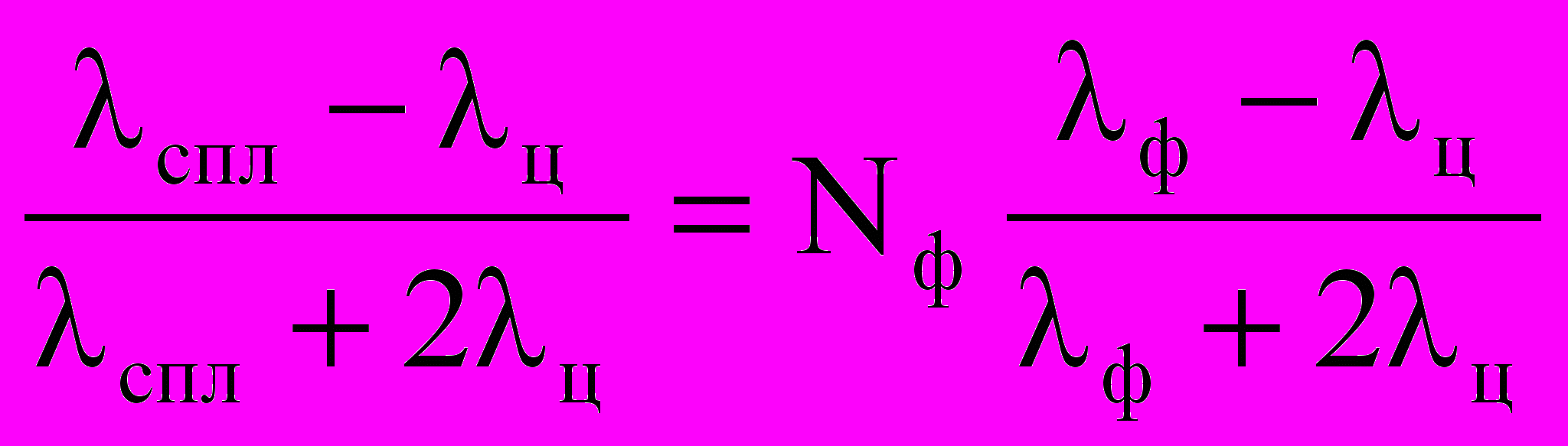где: λ- коэффициент теплопроводности искомого сплава; λф- коэффициент теплопроводности феррита; λ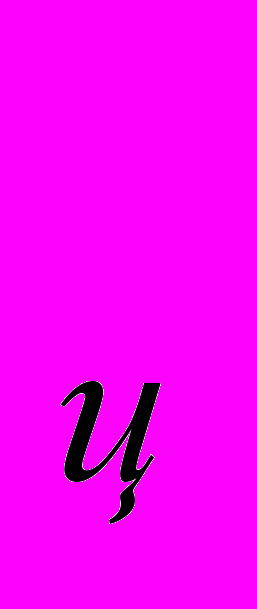 – коэффициент теплопроводности цементита; Nф – доля феррита в сплаве.

Таким образом, зная фазовый состав сплава, теплопроводность феррита и цементита, можно определить теплопроводность сплава при естественных условиях. Экспериментальные результаты исследований [2] подтверждены полученной формулой. Результаты расчетов приведены в табл. 1. Очевидно, что формула показывает хорошую сходимость результатов при погрешности не более 10% для сталей с содержанием углерода свыше 0,8% при комнатной температуре.

Таким образом, данная формула справедлива при определении теплопроводности сталей с содержанием углерода свыше 0,8% при естественных условиях. Упрощая формулу путем математических преобразований, найдем ее наиболее простой и окончательный вид:

λ =. (2)

Таблица 1


Теплопроводность углеродистых сталей при 00С, Вт/м·°С

Марка стали и ее структурные компоненты
Данные

Погрешность, %

Опытные
Расчетные

Сталь 08

(Nф = 0,988;

Nц = 0,012)

59,5

74,55

+25,3

Сталь 20

(Nф = 0,97;

Nц = 0,03)

51,9

69,7

+34,3

Сталь 40

(Nф = 0,94;

Nц = 0,06)

51,9

62,7

+20,8

Сталь У8

(Nф = 0,88;

Nц = 0,12)

49,8

51,7

+3,8

Сталь У12

(Nф = 0,82;

Nц = 0,18)

45,2

43,5

-3,8

Феррит

(Nф = 1,0;

Nц = 0,0)

76,8

78,1

+1,7

Цементит

(Nф = 0,0;

Nц = 1,0)

7,1

7,1

0,0


Анализ экспериментальных данных [2, 3] показал, что теплопроводность стали, ее состав и температура находятся в более сложной зависимости по сравнению с формулой (2). Экспериментально установлено, что зависимость теплопроводности от состава стали выражается уравнением

,

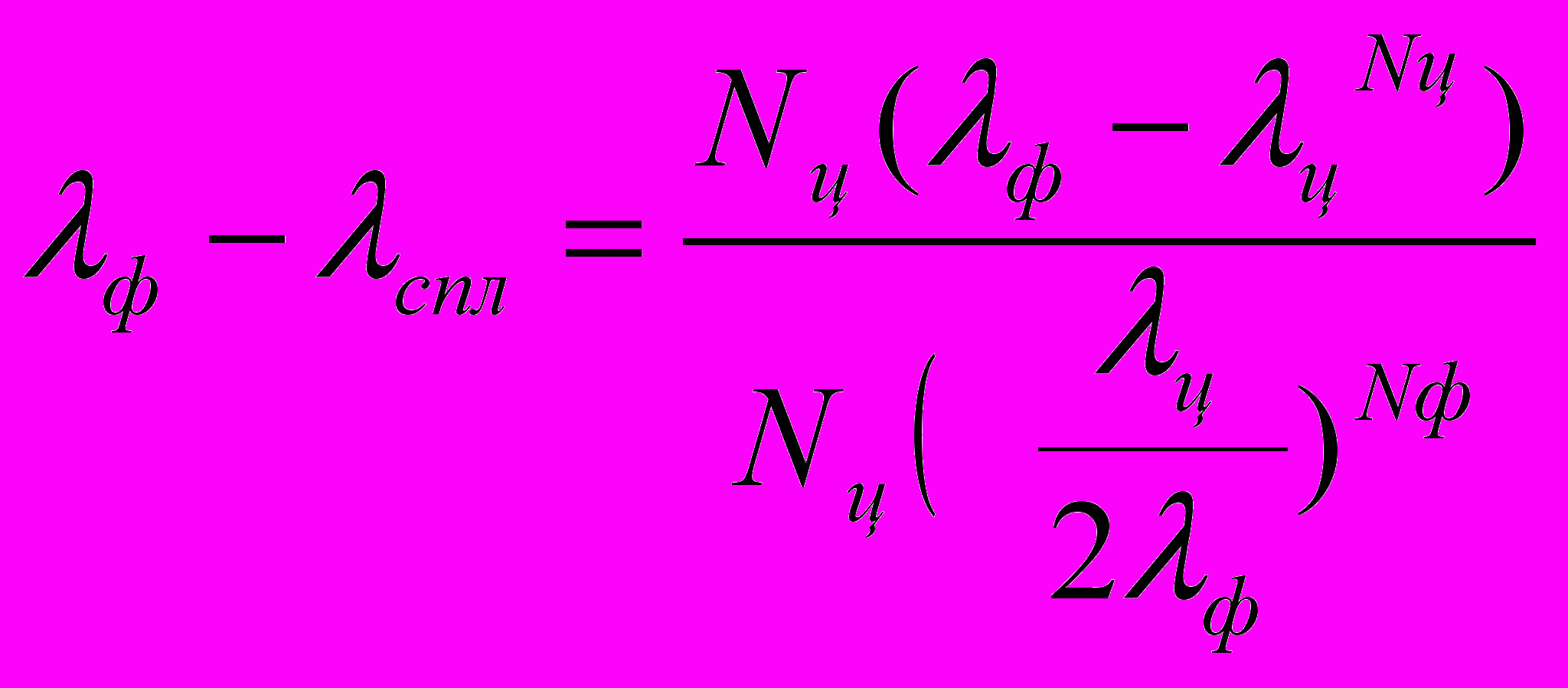а падение теплопроводности от повышения температуры определяется зависимостью

Δ λ= . (3)

Выполнив определенные математические действия и объединив обе формулы, получим следующее уравнение теплопроводности искомого сплава в общем виде:

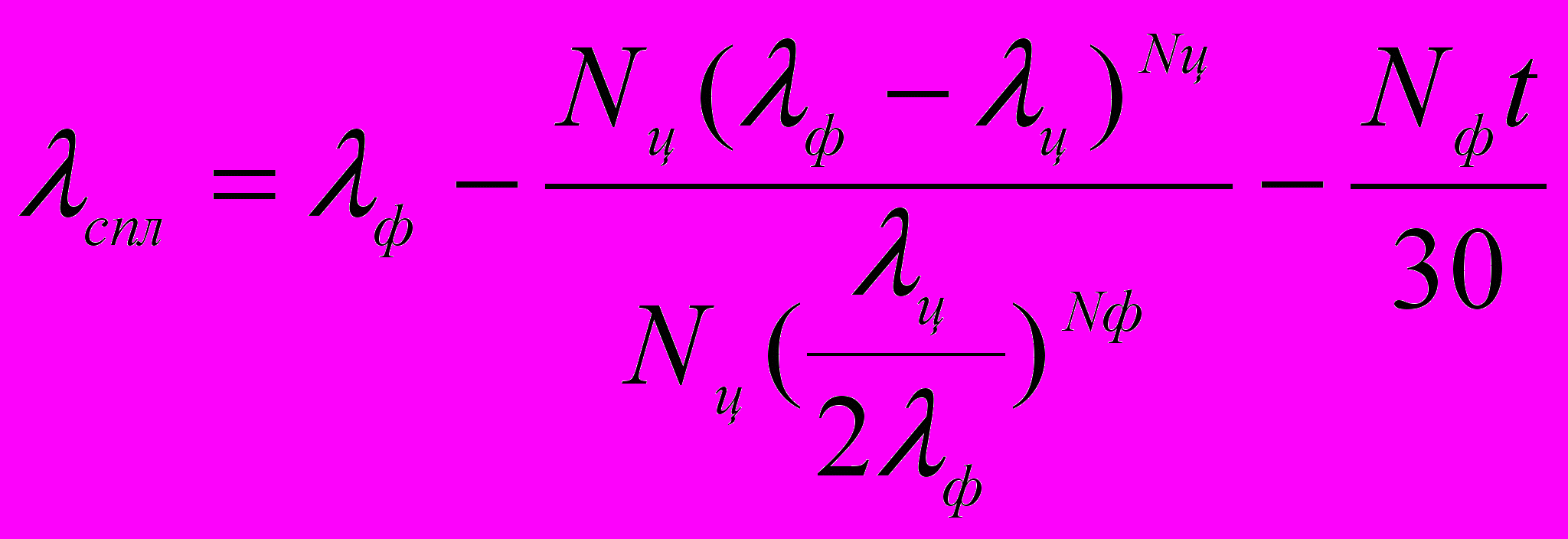, (4)

где λ- коэффициент теплопроводности искомого сплава; λ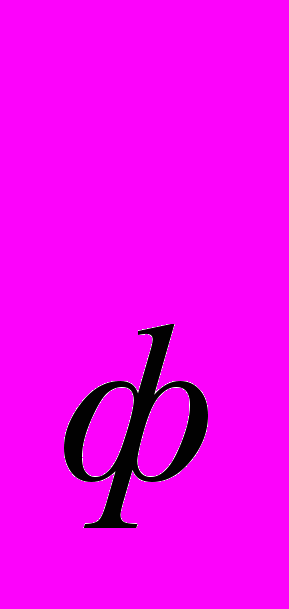 – коэффициент теплопроводности феррита при 0°С (λ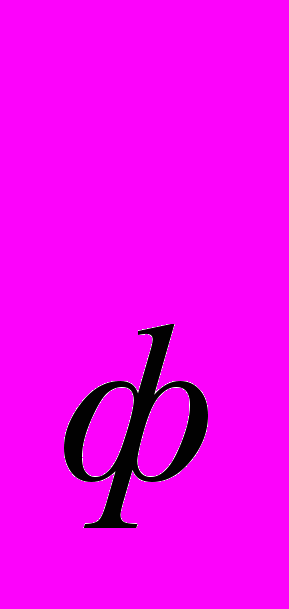=76,8 Вт/м·°С); λ 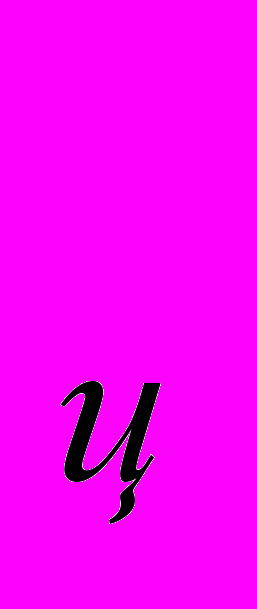– коэффициент теплопроводности цементита (λ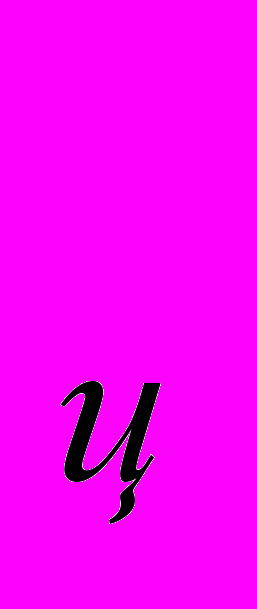=7,1 Вт/м·°С); N 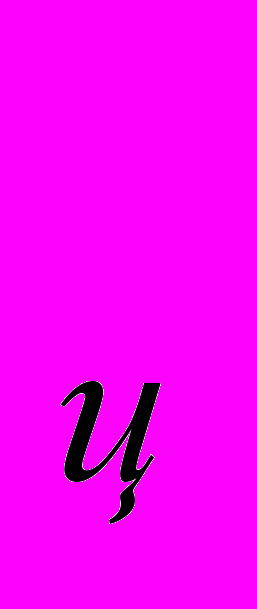– доля цементита в сплаве; N 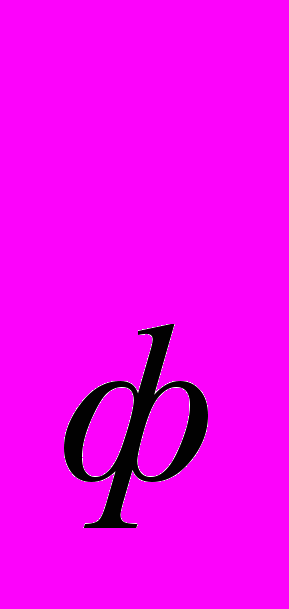– доля феррита в сплаве 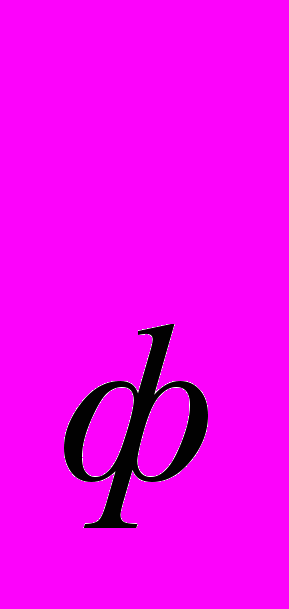(N+ N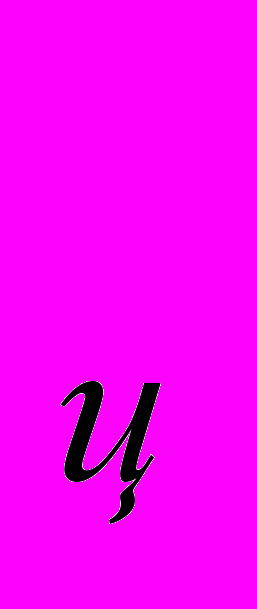=1); t – температура сплава.

Так как в данном случае 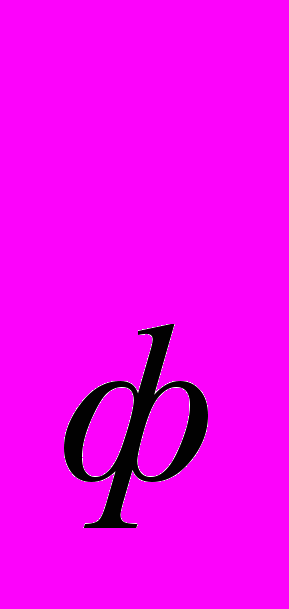λ и λ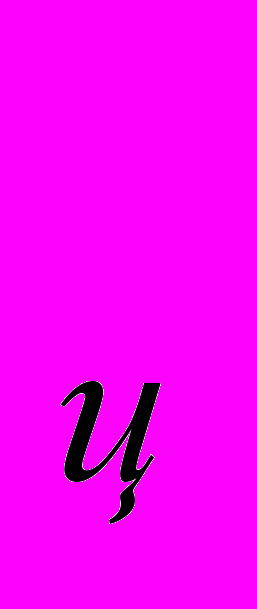 являются постоянными величинами, то после упрощения формула примет окончательный вид:

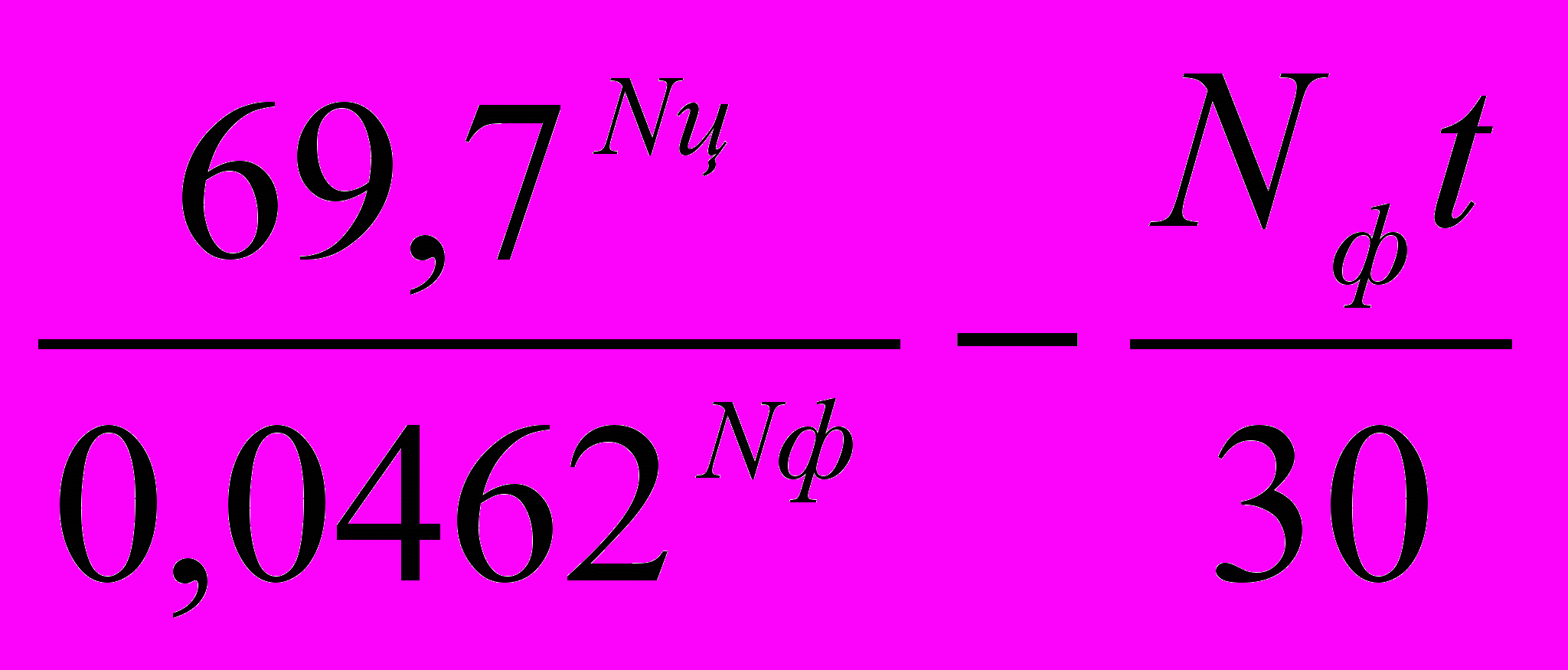λ=76,8- . (5)

Обрабатывая по данной формуле опытные результаты [2, 3], приходим к выводу, что формула (5) применима для всех углеродистых сталей при температуре до 727 °С и дает погрешность в этих условиях не более 10 % (табл. 2).

Таблица 2

Теплопроводность углеродистых сталей в зависимости от температуры, Вт/м·°С

Марка стали и ее структурные компоненты
Данные
Температура, °С

0
100
200
300
400
500
600
700
727

Сталь 08

(Nф =0,988;

Nц = 0,012)
Опытные

Расчетные

Погрешность,%
59,5

55,0

-7,5
57,7

51,7

-10,0
53,5

48,3

-9,7
49,4

45,1

-8,7
44,8

41,8

-6,7
40,2

38,5

-4,2
36,1

35,2

-2,5
31,9

31,9

0,0
-

31,0

-

Сталь 20

(Nф = 0,97;

Nц = 0,03)
Опытные

Расчетные

Погрешность,%
51,9

54,4

+4,8
51,1

51,2

+0,2
48,5

47,9

-1,2
44,4

44,7

+0,6
42,7

41,4

-3,0
39,3

38,2

-2,8
35,6

35,0

-1,7
31,9

31,8

-0,3
-

30,9

-

Сталь 40

(Nф = 0,94;

Nц = 0,06)
Опытные

Расчетные

Погрешность,%
51,9

53,3

+2,7
50,6

50,2

-0,8
48,1

47,0

-2,3
45,6

43,9

-3,8
41,9

40,8

-2,6
38,1

37,6

-1,3
33,6

34,5

+2,7
30,0

31,4

+4,5
-

30,5

-

Сталь У8

(Nф = 0,88;

Nц = 0,12)
Опытные

Расчетные

Погрешность,%
49,8

51,9

+0,4
48,1

49,0

+1,8
45,1

46,0

+2,0
41,4

43,1

+4,1
38,1

40,2

+5,5
35,2

37,2

+5,7
32,7

34,3

+4,9
30,1

31,4

+4,3
-

30,6

-

Сталь У12

(Nф = 0,82;

Nц = 0,18)
Опытные

Расчетные

Погрешность,%
45,2

49,9

+10,0
44,8

47,2

+6,0
42,7

44,4

+4,0
40,2

41,7

+3,7
37,2

39,0

+4,8
34,7

36,2

+4,3
31,9

33,5

+5,0
28,3

30,8

+8,8
-

30,0

-

Феррит

(Nф = 1,0;

Nц = 0,0)
Опытные

Расчетные

Погрешность,%
76,8

76,8

0,0
-

73,5

-
-

70,1

-
-

66,8

-
-

65,3

-
-

60,1

-
-

56,8

-
-

53,6

-
-

52,6

-

Цементит

(Nф = 0,0;

Nц = 1,0)
Опытные

Расчетные

Погрешность,%
7,1

7,1

0,0
-

7,1

-
-

7,1

-
-

7,1

-
-

7,1

-
-

7,1

-
-

7,1

-
-

7,1

-
-

7,1

-


Таким образом, зная марку стали и температуру, можно определить ее коэффициент теплопроводности.

Из полученных формул (4) и (5) следует: при снижении доли цементита теплопроводность сплавов повышается, при повышении температуры теплопроводность понижается. При уменьшении доли феррита теплопроводность сплавов все меньше зависит от температуры, т.е. при доле феррита, равной 0, независимо от температуры теплопроводность сплава постоянна, т.е. теплопроводность чистого цементита при повышении температуры до 727°С практически не изменяется и остается равной 7,1 Вт/м·°С.

Для удобства применения формулы (4) в практических расчетах на рисунке представлена номограмма, по которой можно определить теплопроводность углеродистых сплавов без математических вычислений.

Р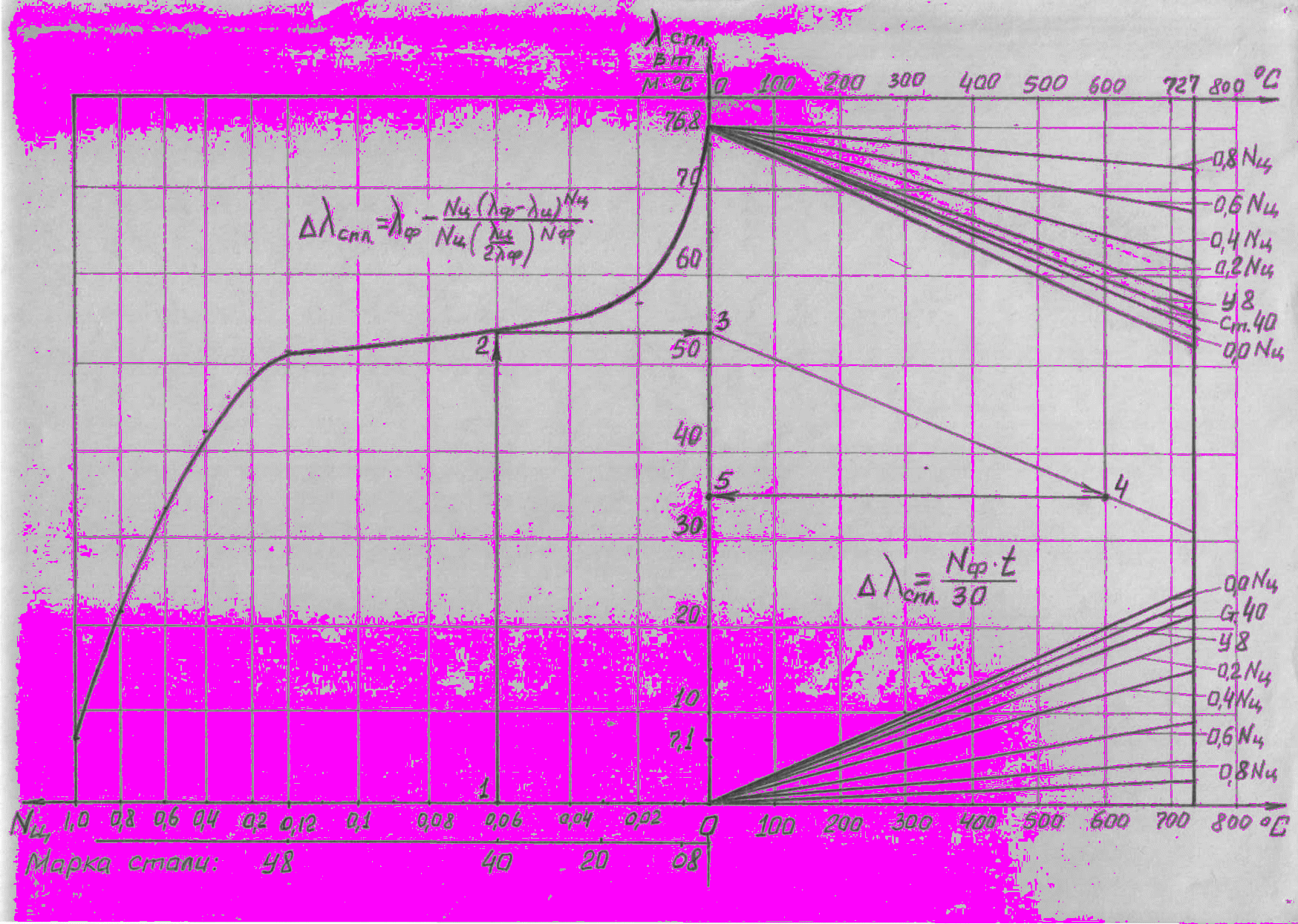ис. Номограмма для определения коэффициента теплопроводности углеродистых сталей


Рассмотрим принцип построения и использования номограммы. По оси абсцисс вправо откладывается температура сплава до 727°С, влево – доля цементита в сплаве, т.е. марка сплава. По оси ординат откладывается коэффициент теплопроводности в Вт/м·°С. Наивысшей теплопроводностью обладает феррит, поэтому теплопроводность феррита, равная 76,8 Вт/м·°С, является конечной точкой номограммы. В правом нижнем углу номограммы построены графики, показывающие снижение теплопроводности сплава в зависимости от температуры, т.е.падение теплопроводности по формуле (3). В правом верхнем углу номограммы построены данные графики в зеркальном отображении, причем за точку 0 взята теплопроводность феррита, т.е. по правой части номограммы можно определить падение теплопроводности сплава при повышении температуры до 727 °С. Например, требуется определить теплопроводность феррита при 500 °С. Для этого определяем точку пересечения линии проекции точки температуры 500 °С с наклонной прямой «0,0 Nц» (рисунок). Проекция данной точки на ось ординат (теплопроводность) даст искомый результат: 60 Вт/м·°С.

В левой части номограммы построен график падения теплопроводности сплавов в зависимости от содержания цементита, т.е. график, отвечающий формуле (4). При комнатной температуре (0…20°С) теплопроводность стали, например стали 40, определяется следующим образом. из точки, отвечающей заданной марке стали, восстанавливается перпендикуляр до пересечения с графиком снижения теплопроводности (линия 1-2). Из точки 2 восстанавливается перпендикуляр к оси ординат (к теплопроводности). Полученная точка 3 покажет значение теплопроводности стали 40.

При определении теплопроводности стали при повышенных температурах поступают следующим образом. например, необходимо определить теплопроводность стали 40 при 600°С. Из построенной ранее точки 3 проводят наклонную прямую, параллельную прямой, отвечающей падению теплопроводности в зависимости от температуры (прямая для стали 40), до пересечения с заданной температурой (600°С). Из полученной точки 4 восстанавливают перпендикуляр к оси теплопроводности, и найденная таким образом точка 5 является искомой теплопроводностью стали 40 при 600°С.

На основании данной номограммы и формулы (4) можно сделать вывод, что чем больше цементита в стали, тем меньше падение теплопроводности сплава в зависимости от температуры. Следовательно, можно предположить, что теплопроводность чистого цементита практически не зависит от температуры и при 727°С также равна 7,1 Вт/м·°С. Теплопроводность феррита при 727°С, согласно табл.2 и номограмме, равна 52,6 Вт/м·°С. Следовательно, соотношение теплопроводностей феррита и цементита при 727°С равно 52,6: 7,1 = 7,35.

Таким образом, можно сделать вывод, что толщина пластин феррита аф и цементита ац в момент фазовых превращений зависит от соотношения теплопроводностей фаз в момент превращений: аф/ац = λф/λц.


Список литературы

  1. Технология термической обработки сталей: [пер. с нем.] / М.: Металлургия, 1981.- 607с.
  2. Казанцев, Е.И. Промышленные печи/ Е.И. Казанцев. – М.: Металлургия, 1975. – 367 с.
  3. Бокштейн, Б.С. Диффузия в металлах / Б.С. Бокштейн. – М.: Металлургия, 1978. - с.164-182.


Материал поступил в редколлегию 19.10.06.