Geum.ru

Питання до екзаменів І мі

Вид материалаДокументы
Подобный материал:
  1   2   3

Питання до екзаменів

І МІ
  1. Предмет і метод математики.
  2. Множина. Операції над множинами.
  3. Множина дійсних чисел.
  4. Взаємно однозначна відповідність між елементами множин. Аксіома Кантора.
  5. Властивості множини дійсних чисел.
  6. Аксіома Архімеда. Принцип вкладених відрізків.
  7. Числові проміжки.
  8. Модуль дійсного числа. Геометричний зміст, властивості модуля.
  9. Обмеженість числових множин.
  10. Теорема про існування точної верхньої (нижньої) грані числової множини.
  11. Функції. Означення. Способи задання функції.
  12. Елементарні функції.
  13. Деякі класи функцій (монотонні, парні та непарні, періодичні).
  14. Числова послідовність та її границя.
  15. Властивості збіжних послідовностей.
  16. Теорема Больцано-Вейерштрасса. Критерій Коші.
  17. Теорема про проміжну змінну. Нескінченно великі послідовності.
  18. Нескінченно малі послідовності та їх властивості. Нескінченно великі.
  19. Представлення збіжної послідовності у вигляді суми її границі та нескінченно малої послідовності. Теореми про границю суми і добутку двох послідовностей.
  20. Теореми про границю частки двох послідовностей.
  21. Теорема про існування граней монотонно зростаючої і обмеженої зверху послідовності. Число e. Натуральні логарифми.
  22. Границя функції в точці. Означення за Коші. Геометричне тлумачення границі функції в точці. Означення границі функції за Гейне.
  23. Властивості функцій, що мають границю функції в точці.
  24. Границя функції та нескінченності. Властивості границь. Нескінченні границі
  25. Перша важлива границя.
  26. Друга важлива границя.
  27. Нескінченно малі функції та їх властивості. Порівняння нескінченно малих.
  28. Теорема про еквівалентні нескінченно малі.
  29. Однобічні (односторонні) границі функції в точці. Їх зв’язок з границею. Приклади.
  30. Неперервність функцій в точці і на проміжку. Однобічна (одностороння) неперервність.
  31. Точки розриву функцій та їх класифікація.
  32. Властивості функцій, неперервних на відрізку.
  33. Границя точки. Означення границі числової послідовності через граничну точку. Теорема про збіжність.
  34. Теорема про існування і неперервність обмеженої функції.
  35. Первісна функція та невизначений інтеграл. Властивості невизначеного інтеграла.
  36. Таблиця основних невизначених інтегралів.
  37. Основні методи інтегрування. Метод розбивки. Метод підстановки.
  38. Метод інтегрування частинами у невизначеному інтегралі.
  39. Інтегрування раціональних функцій. Прості дроби. Інтегрування простих дробів перших трьох типів.
  40. Інтегрування четвертого типу простих дробів. Рекурентна формула.
  41. Представлення правильного алгебраїчного дробу у вигляді скінченного числа простих дробів.
  42. Метод невизначених коефіцієнтів інтегрування раціональних функцій.
  43. Метод М.В.Остроградського інтегрування алгебраїчних дробів.
  44. Інтегрування деяких класів ірраціональних функцій.
  45. Підстановки Ейлера.
  46. Інтегрування біноміального диференціала. Підстановки Чебишева.
  47. Інтегрування тригонометричних функцій.
  48. Задачі, що приводять до поняття визначеного інтеграла.
  49. Визначений інтеграл та його геометричний зміст.
  50. Необхідні і достатні умови інтегровності функції.
  51. Класи інтегровних функцій.
  52. Властивості визначеного інтеграла.
  53. Теореми про середнє для визначеного інтеграла.
  54. Інтеграл із верхньою змінною межею. Формула Ньютона – Лейбніца.
  55. Основні способи обчислення визначеного інтеграла. Метод розбивки. Метод підстановки.
  56. Метод інтегрування частинами у визначеному інтегралі.
  57. Невласні інтеграли. Інтеграли на нескінченних проміжках. Ознаки збіжності та розбіжності.
  58. Інтеграли від необмежених функцій. Ознаки збіжності та розбіжності.
  59. Застосування визначеного інтеграла в геометрії. Обчислення площ плоских фігур.
  60. Обчислення довжини дуги кривої.
  61. Диференціал дуги.
  62. Обчислення об’єму тіла обертання.
  63. Обчислення площі поверхні обертання.
  64. Знаходження статичних моментів і координат центра маси плоскої кривої.
  65. Знаходження статичних моментів і координат центра маси плоскої фігури.
  66. Теореми Гульдіна.
  67. Знаходження моментів інерцій плоскої фігури та плоскої кривої відносно координатних осей.
  68. Наближене інтегрування. Формули прямокутників, трапецій та парабол.
  69. Поняття числового ряду. Основні означення. геометричний ряд. Необхідна умова збіжності ряду.
  70. Гармонічний ряд. Довести розбіжності гармонічного ряду.
  71. Властивості збіжних рядів.
  72. Додатні числові ряди. Порівняльні ознаки збіжності.
  73. Ознака д’Аламбера збіжності додатного числового ряду.
  74. Ознака Коші збіжності додатного числового ряду.
  75. Інтегральна ознака Коші збіжності додатного числового ряду.
  76. Знакозмінні ряди. Теорема Лейбніца. Абсолютна та умовна збіжність.
  77. Критерій Коші збіжності числового ряду.
  78. Теорема про збіжність абсолютно збіжного ряду. Властивості числових рядів.
  79. Функціональні ряди. Основні поняття. Область збіжності функціонального ряду. Збіжність та абсолютна збіжність функціонального ряду.
  80. Теорема Вейєрштраса.
  81. Властивості рівномірно збіжних рядів. Довести, що сума рівномірно збіжного ряду є неперервного.
  82. Інтегрування рівномірно збіжних рядів.
  83. Диференціювання функціональних рядів.
  84. Степеневі ряди. Означення. Теорема Абеля.
  85. Радіус збіжності, інтервал збіжності та область збіжності степеневого ряду.
  86. Властивості степеневих рядів.
  87. Ряд Тейлора.
  88. Розвинення елементарних функцій у ряд Тейлора.


І МФ, МЕ
  1. Аксіоми множини дійсних чисел. Різні форми аксіоми неперервності (Деде­кінда, Кантора, Вейєрштрасса) та їх рівносильність.
  2. Обмежені та необмежені числові множини. Їхні межі і точні межі. Найбіль­ший та найменший елементи множини.
  3. Модуль дійсного числа, його властивості і геометричний зміст.
  4. Принцип і метод математичної індукції. Нерівність Бернуллі. Формула біно­ма Ньютона.
  5. Загальне поняття функції, сюр’єкції, ін’єкції, бієкції, оберненої і складеної функцій та послідовності.
  6. Функції дійсної змінної. Способи їх задання, графіки. Основні елементарні функції та вигляд їхніх графіків. Елементарні функції та їх класифікація.
  7. Найпростіші властивості функцій дійсної змінної (парність, непарність, монотонність, періодичність та обмеженість).
  8. Границя послідовності. Властивості збіжних числових послідовностей.
  9. Теорема про границю монотонної обмеженої послідовності. Число .
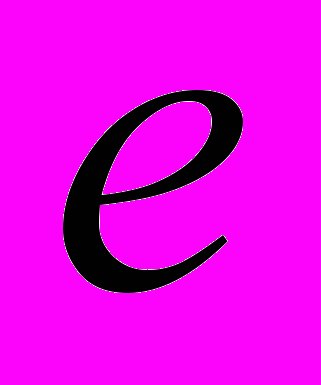  10. Часткові границі послідовності. Критерій часткової границі на мові околів.
  11. Теорема Больцано – Вейєрштрасса про існування часткових границь.
  12. Теорема про множину всіх часткових границь деякої послідовності.
  13. Верхня та нижня границі послідовності. Їх існування.
  14. Фундаментальні послідовності. Критерій Коші збіжності послідовності.
  15. Означення границі функції в точці за Коші, за Гейне та мовою околів. Їх еквівалентність.
  16. Властивості функцій, які мають границю в точці.
  17. Ліва та права границі функції в точці. Критерій існування границі. Теорема про ліву та праву границі монотонної функції.
  18. Деякі важливі границі (таблиця основних границь).
  19. Нескінченно малі функції в точці та їх порівняння між собою. Метод еквівалентних нескінченно малих при обчисленні границь.
  20. Поняття функції, неперервної у точці і на множині. Критерій рівномірно неперервної функції.
  21. Властивості функцій, неперервних у точці.
  22. Точки розриву та їх класифікація.
  23. Властивості функцій, неперервних на відрізку.
  24. Теорема про існування, монотонність і неперервність оберненої функції.
  25. Степінь з ірраціональним показником. Теорема про обгрунтування його означення.
  26. Показникова, логарифмічна і загальна степенева функції. Неперервність елементарних функцій.
  27. Задачі, що приводять до похідної.
  28. Означення похідної. Зв’язок похідної з неперервністю. Похідна суми, різниці, добутку і частки.
  29. Похідна складеної та оберненої функцій.
  30. Таблиця похідних та її обгрунтування.
  31. Диференційовні функції та їхні диференціали. Геометричний і фізичний зміст диференціала. Інваріантність форми диференціала.
  32. Похідні та диференціали вищих порядків.
  33. Диференціювання параметричної функції (формули для першої та другої похідної).
  34. Теореми Ферма, Ролля. Їхній геометричний і фізичний зміст.
  35. Теореми Лагранжа і Коші про середнє значення похідних.
  36. Однобічні похідні. Теореми про границю і точки розриву похідної.
  37. Теорема Дарбу про множину значень похідної.
  38. Формула Тейлора для многочлена. Приклад.
  39. Формула Тейлора для довільної функції із залишковим членом у формі Лагранжа.
  40. Формула Тейлора для довільної функції із залишковим членом у формі Коші.
  41. Формули Тейлора для синуса і косинуса.
  42. Формула Тейлора для експоненти. Ірраціональність числа .
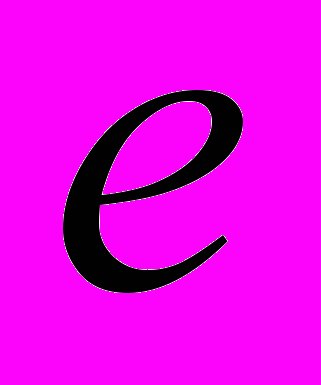  43. Умови сталості, монотонності і строгої монотонності диференційовної функції.
  44. Локальні екстремуми функції.
  45. Глобальні екстремуми функції. Приклади.
  46. Опуклість функцій і точки перегину.
  47. Асимптоти кривих.
  48. Схема повного дослідження функції та побудови її графіка. Приклад.
  49. Розкриття невизначеностей. Перше правило Лопіталя.
  50. Розкриття невизначеностей. Друге правило Лопіталя.
  51. Поняття первісної і невизначеного інтеграла. Необхідні умови існування первісної. Теорема про множину всіх первісних.
  52. Основні методи інтегрування.
  53. Інтегрування раціональних функцій. Елементарні дроби І – ІІІ типів.
  54. Інтегрування раціональних функцій. Елементарні дроби ІV типу.
  55. Інтегрування найпростіших та дробово-лінійних ірраціональностей.
  56. Інтегрування квадратичних ірраціональностей. Підстановки Ейлера.
  57. Біноміальний диференціал і підстановки Чебишова.
  58. Інтегрування тригонометричних функцій. Загальний і частинний випадки.
  59. Визначений інтеграл: задача про площу криволінійної трапеції, означення, необхідна умова інтегровності.
  60. Суми Дарбу та їхні властивості.
  61. Нижній і верхній інтеграли Дарбу. Теорема Дарбу про границі сум Дарбу.
  62. Критерії інтегровності (Дарбу, Рімана, мовою коливань і мовою послідов­ностей).
  63. Класи інтегровних функцій.
  64. Властивості визначеного інтеграла.
  65. Орієнтовані інтеграли та деякі їхні властивості.
  66. Інтеграл із змінною верхньою межею. Його неперервність і диференці­йовність.
  67. Існування первісної для неперервної функції. Формула Ньютона – Лейб­ніца.
  68. Формули заміни змінної та інтегрування частинами для визначеного інтеграла.
  69. Теорема про заміну змінної у визначеному інтегралі на монотонну функцію .
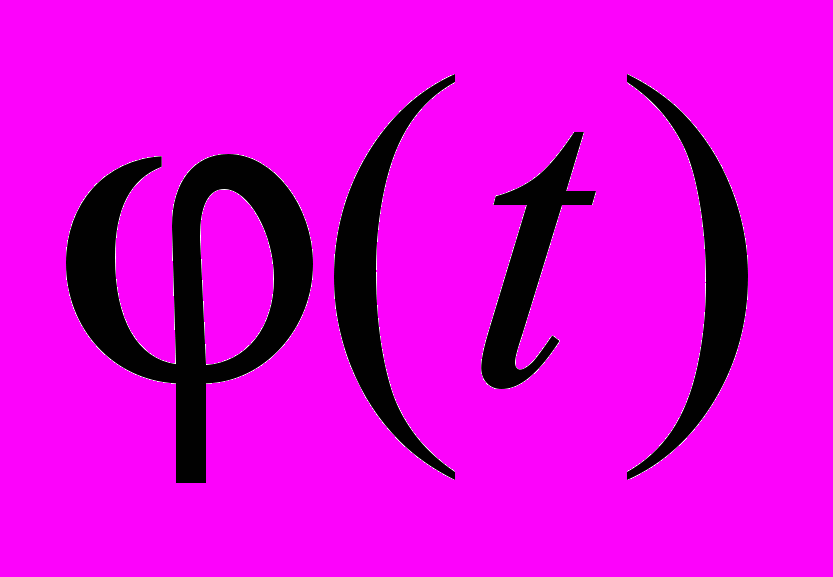  70. Властивості інтегралів від парних, непарних та періодичних функцій.
  71. Невласні інтеграли І-го роду. Критерій та ознаки збіжності додатних невласних інтегралів. Абсолютна та умовна збіжність.
  72. Невласні інтеграли ІІ-го роду для різних випадків розміщення особливих точок функції.
  73. Обчислення площі узагальненої криволінійної трапеції.
  74. Обчислення площі криволінійного сектора.
  75. Обчислення об’єму тіла обертання.
  76. Обчислення довжини дуги кривої, заданої параметрично.
  77. Обчислення довжини дуги кривої, заданої явно у декартовій чи в полярній системі координат.
  78. Обчислення площі поверхні обертання.
  79. Відшукання координат центра маси однорідної пластинки.
  80. Поняття числового ряду та його суми. Геометричний і гармонічний ряди.
  81. Необхідна умова та критерій Коші збіжності числового ряду.
  82. Властивості збіжних числових рядів.
  83. Додатні ряди. Критерій збіжності, ознаки порівняння.
  84. Ознаки Даламбера і Коші збіжності додатних рядів.
  85. Інтегральна ознака Коші.
  86. Знакозмінні ряди. Ознака Лейбніца.
  87. Абсолютно та умовно збіжні ряди.
  88. Переставна властивість абсолютно збіжних рядів. Теорема Рімана (без доведення).
  89. Добуток рядів за Коші. Теорема про множення рядів. Істотність умови абсолютної збіжності рядів.
  90. Поняття функціональної послідовності та її границі, а також функціональ­ного ряду та його суми. Область збіжності. Приклади.
  91. Рівномірно збіжні функціональні послідовності. Критерії рівномірної збіж­ності. Приклади.
  92. Найпростіші властивості рівномірно збіжних функціональних послідов­ностей. Чи зберігається рівномірна збіжність при множенні послідовності на функцію?
  93. Рівномірно збіжні функціональні ряди. Критерії та найпростіші властивості рівномірної збіжності рядів. Необхідна умова та ознака Вейєрштрасса рівномірної збіжності функціонального ряду.
  94. Властивості функціональних рядів, пов’язані з границею, неперервністю, інтегруванням та диференціюванням. Теорема про граничний перехід.
  95. Властивості функціональних рядів, пов’язані з границею, неперервністю, інтегруванням та диференціюванням. Теорема про почленне інтегрування.
  96. Властивості функціональних рядів, пов’язані з границею, неперервністю, інтегруванням та диференціюванням. Теорема про почленне диференцію­вання.


І ФІА
  1. Предмет та метод математики. Множини дії над множинами.
  2. Множини дійсних чисел. Аксіоматична теорія дійсних чисел.
  3. Наслідки з аксіом додавання та множення.
  4. Модуль дійсного числа. Властивості модуля.
  5. Основні числові множини. Межі числових множин. Обмежені множини.
  6. Метод математичної індукції. Приклад.
  7. Числова функція. Способи задання функції.
  8. Елементарні функції.
  9. Монотонні функції.
  10. Парні та непарні функції.
  11. Періодичні функції.
  12. Числова послідовність та її границя.
  13. Властивості збіжних послідовностей.
  14. Нескінченно малі та нескінченно великі послідовності.
  15. Властивості нескінченно малих послідовностей.
  16. Теореми про границі числових послідовностей.
  17. Обмежені числові послідовності. Теорема про існування границі монотонно-зростаючої (спадної) і обмеженої зверху (знизу) послідовності.
  18. Теорема Больцано-Вейерштрасса.
  19. Критерій Коші.
  20. Деякі види невизначеності. Число e. Натуральні логарифми.
  21. Границя функцій в точці. Означення за Коші. Геометричний зміст. Означення границі за Гейне.
  22. Властивості функції, що має границю в точці.
  23. Властивості границь.
  24. Границя функції на нескінченності. Геометричний зміст. Нескінченні границі.
  25. Перша важлива границя.
  26. Друга важлива границя.
  27. Теореми про границі функцій (в точці і на нескінченності).
  28. Нескінченно малі функції та їх властивості.
  29. Теорема про зв’язок функції, що має границю, з нескінченно малою функцією.
  30. Порівняння нескінченно малих функцій.
  31. Однобічні (односторонні) границі функції в точці. Зв’язок границі функції в точці з однобічними границями.
  32. Неперервність функції в точці. Означення. Геометричний зміст. Неперервність функції на проміжку.
  33. Теорема про неперервність складеної функції. Односторонні неперервності.
  34. Арифметичні дії над неперервними функціями.
  35. Точки розриву функції та їх класифікація.
  36. Властивості функцій, неперервних на відрізку.
  37. Рівномірна неперервність функції на деякому проміжку.
  38. Обернена функція, її існування та неперервність.
  39. Приклади обернених функцій до степеневих та показникових функцій.
  40. Приклади обернених функцій до тригонометричних функцій.
  41. Задачі, що приводятьдо поняття похідної.
  42. Означення похідної, її геометричний та механічний зміст.
  43. Означення диференційовності функції в точці. Неперервність диференційовної функції.
  44. Правила диференціювання.
  45. Диференціювання складеної та оберненої функції.
  46. Друге означення диференційовності функції, його еквівалентність першому. Диференціал, його геометричний та механічний зміст.
  47. Правила диференціювання (для диференціала).
  48. Застосування диференціала до наближених обчислень.
  49. Диференціювання параметрично заданих функцій.
  50. Похідні і диференціали вищих порядків.
  51. Похідні вищих порядків від параметрично заданих функцій.
  52. Теорема Ролля. Геометричний зміст.
  53. Теорема Лагранжа. Геометричний зміст. Формула Лагранжа. Наслідки з теореми Лагранжа.
  54. Теорема Коші. Наслідок.
  55. Логарифмічне диференціювання.
  56. Формула Тейлора для многочлена.
  57. Формула Тейлора для довільної функції із залишковим членом у формі Лагранжа.
  58. Залишковий член формули Тейлора у формі Коші. Формула Тейлора для деяких елементарних функцій.
  59. Застосування формули Тейлора до наближених обчислень.
  60. Монотонні функції. Зв’язок між знаком похідної і характером монотонності в даній точці.
  61. Точки екстремуму функцій. Екстремум. Необхідні і достатні умови екстремуму.
  62. Найбільше і найменше значення функцій на відрізку.
  63. Опуклість та вгнутість кривої. Точки перегину. Інтервали опуклості та вгнутості кривої.
  64. Асимптоти кривої. Знаходження похилих, горизонтальних та вертикальних асимптот.
  65. Перше правило Лопіталя.
  66. Друге правило Лопіталя. Теорема (без доведення). Приклад.
  67. Первісна функція та її властивості.
  68. Невизначений інтеграл та його властивості.
  69. Таблиця інтегралів.
  70. Основні методи інтегрування.
  71. Інтегрування елементарних раціональних дробів.
  72. Інтегрування раціональних функцій.
  73. Інтегрування в скінченному вигляді.
  74. Інтегрування ірраціональних функцій 1-го і 2-го типу.
  75. Інтегрування ірраціональних функцій. підстановки Ейлера.
  76. Інтегрування диференціальних біномів.
  77. Інтегрування тригонометричних функцій.
  78. Задача про площу криволінійної трапеції.
  79. Поняття визначеного інтеграла. Необхідна умова інтегровності функції.
  80. Достатні умови інтегровності функції.
  81. Властивості визначеного інтегралу.
  82. Теореми про середнє значення визначеного інтеграла.
  83. Визначений інтеграл із змінною верхньою межею. Теорема.
  84. Формула Ньютона-Лейбніца.
  85. Замінна змінної та формула інтегрування частинами для визначеного інтеграла.
  86. Застосування визначених інтегралів до обчислення площ плоских фігур.
  87. Застосування визначених інтегралів до обчислення довжини дуги кривої.
  88. Застосування визначених інтегралів до обчислення об’єму тіл обертання.
  89. Застосування визначених інтегралів до обчислення площі поверхні обертання.
  90. Застосування визначених інтегралів до розв’язування задач механіки (центр мас матеріальної дуги та пластинки).
  91. Невласні інтеграли.
  92. Числові ряди. Основні поняття.
  93. Геометрична прогресія.
  94. Основні властивості збіжних рядів.
  95. Знакододатні числові ряди. Необхідна і достатня умова збіжності.
  96. Ознаки збіжності знакододатних числових рядів (ознаки порівняння, Д’Аламбера, Коші, інтегральна ознака Коші).
  97. Знакозмінні числові ряди. Теорема Лейбніца і наслідки до неї.
  98. Абсолютна та умовна збіжність ряду.
  99. Функціональна послідовність та функціональний ряд.
  100. Теорема Вейєрштрасса про рівномірну збіжність функціонального ряду.
  101. Властивості рівномірно-збіжних функціональних рядів.
  102. Степеневі ряди. Теорема Абеля.
  103. Властивості степеневих рядів.
  104. Ряд Тейлора.
  105. Розклад елементарних функцій в степеневий ряд.
  106. Наближені обчислення за допомогою числових рядів.
  107. Тригонометричні ряди Фур’є.
  108. Ряд Фур’є для парних і непарних функцій.
  109. Ряд Фур’є для 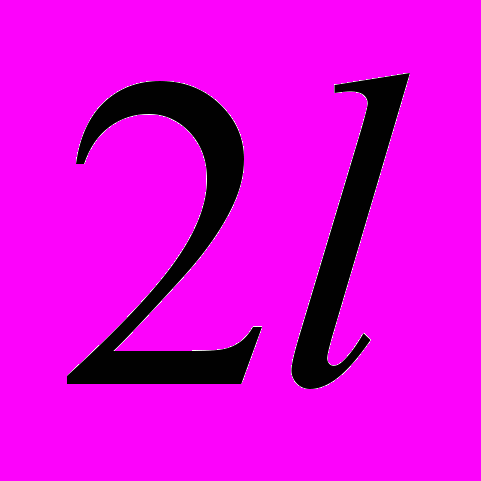-періодичних функцій.
  110. Ряд Фур’є для неперіодичних функцій.
  111. Застосування рядів Фур’є.