Питання до екзаменів І мі

Вид материала

Документы

Подобный материал:

1 2 3

ІІІ МІ

Означення і властивості комплексних чисел (аксіоми поля, тригонометрична форма, властивості модулів і аргументів комплексних чисел).
Формула Муавра, корінь n-го степеня та формула його обчислення.
Збіжні послідовності комплексних чисел та їхні основні властивості. Зв’язок з дійсними послідовностями. Нескінченна границя послідовності.
Часткова границя послідовності. Критерій часткової границі. Теореми про існування часткової границі та про множину часткових границь.
Збіжні і розбіжні ряди з комплексними членами та їхні основні властивості. Зв’язок з дійсними рядами.
Абсолютно та умовно збіжні комплексні ряди. Зв’язок абсолютно збіжних комплексних рядів з дійсними рядами. Переставна властивість і властивість про добуток рядів за Коші.
Границя функції комплексної змінної. Зв’язок границі комплексної функції з границями дійсних функцій.
Властивості функцій, які мають границю в точці.
Неперервні функції. Зв’язок неперервності комплексної функції з неперервністю дійсних функцій. Загальні властивості неперервних функцій.
Рівномірно неперервні функції. Властивості функцій, неперервних на компактних множинах.
Збіжні й рівномірно збіжні функціональні послідовності з комплексними членами. Зв’язок з дійсними послідовностями. Критерії рівномірної збіжності. Неперервність рівномірної границі.
Збіжні й рівномірно збіжні функціональні ряди з комплексними членами. Зв’язок з дійсними рядами. Критерії рівномірної збіжності. Ознака Вейєрштрасса. Неперервність суми ряду.
Степеневі ряди з комплексними членами. Теорема Абеля. Формула Коші – Адамара. Неперервність суми.
Означення і властивості функцій , , .
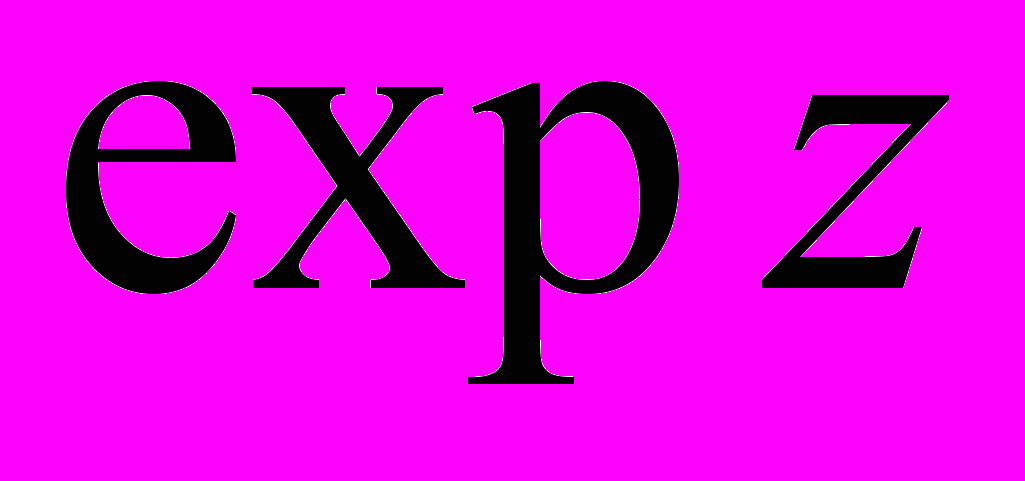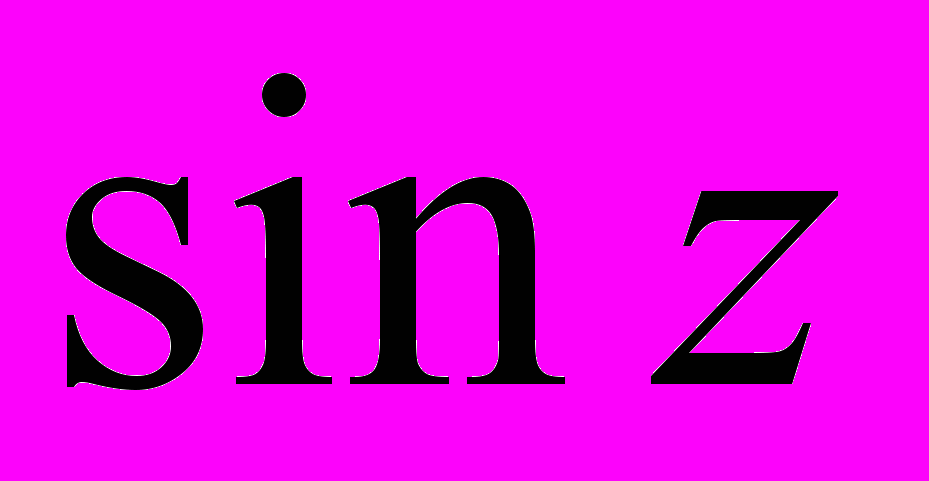Логарифм комплексного числа і логарифмічна функція.
Поняття арксинуса комплексного числа, його існування. Формула для обчислення.
Поняття арккосинуса комплексного числа, його існування. Формула для обчислення.
Зв’язок між комплексним і дійсним (шкільним) арккосинусами.
Зв’язок між комплексним і дійсним (шкільним) арксинусами.
Тангенс та арктангенс комплексного числа.
Гіперболічні синус і косинус та їх зв’язок з тригонометричними.
Гіперболічні ареакосинус та ареасинус. Формули для їх обчислення.
Поступове визначення поняття степеня 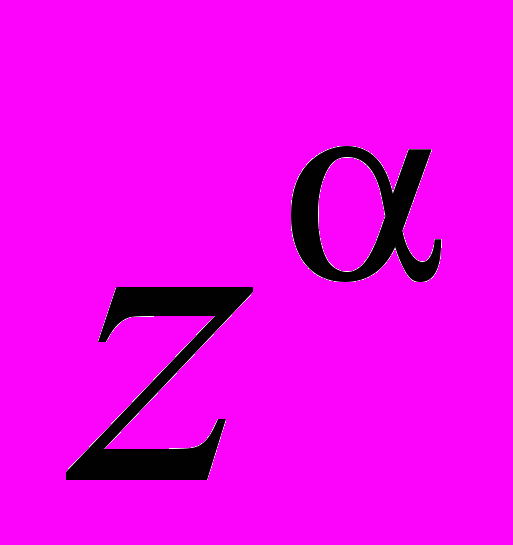і загальне означення степеня з комплексним показником. Загальна показникова і загальна степенева функції.
Основні елементарні та елементарні функції комплексної змінної. Вказати однакові та відмінні властивості дійсних та відповідних їм комплексних основних елементарних функцій.
Загальне означення похідної функції комплексної змінної. Властивості функцій, що мають похідні.
Диференційовні функції комплексної змінної. Критерій диференційовності. Умови Коші – Рімана.
Поняття аналітичної функції у розумінні Коші та у розумінні Рімана. Їх еквівалентність.
Геометричний зміст похідної комплекснозначної функції дійсної змінної та функції комплексної змінної. Конформні відображення.
Теорема про диференціювання степеневого ряду. Наслідки. Ряд Тейлора.
Інтеграл функції комплексної змінної. Його існування та обчислення.
Основні властивості інтеграла функції комплексної змінної.
Інтегральна теорема Коші.
Лема про рівність інтегралів за різними контурами.
Інтегральна формула Коші.
Розвинення аналітичної функції у степеневий ряд.
Означення аналітичності за Вейєрштрассом та його рівносильність з означенням аналітичності за Коші.
Нерівність Коші для коефіцієнтів степеневого ряду. Теорема Ліувілля. Основна теорема алгебри многочленів.
Властивість єдиності аналітичної функції для круга.
Властивість єдиності аналітичної функції для довільної області.
Узагальнена інтегральна формула Коші.
Первісна функції комплексної змінної, необхідна умова її існування. Критерій існування первісної (довести необхідність).
Критерій існування первісної (довести достатність). Формула Ньютона – Лейбніца.
Означення аналітичної функції за Осгудом та його рівносильність з означенням аналітичності за Коші.
Гармонічні функції та їх зв’язок з аналітичними функціями.
Відновлення аналітичної функції за відомою її дійсною або уявною частиною.
Поняття ряду Лорана. Кільце його збіжності та аналітичність суми.
Теорема Лорана про розклад аналітичної в круговому кільці функції у ряд Лорана.
Теорема про єдиність ряду Лорана.
Ізольовані особливі точки аналітичних функцій та їх класифікація. Критерій усувної точки. Критерій полюса через представлення.
Поняття m-кратного нуля аналітичної функції. Зв’язок між нулем і полюсом. Критерій полюса через границю.
Критерій суттєво особливої ізольованої точки аналітичної функції. Теорема Сохоцького про часткові границі в суттєво особливій точці.
Поняття лишку. Обчислення лишків відносно різних типів ізольованих точок.
Теорема про обчислення логарифмічного лишку.
Основна теорема про лишки (з повним доведенням).
Поняття про диференціальне рівняння I-го порядку та його розв’язки (загальний, частинний, особливий).
Приклади задач, які приводять до диференціальних рівнянь.
Диференціальне рівняння I-го порядку. Задача Коші. Теорема про існування та єдиність розв’язку задачі Коші (формулювання).
Зведення задачі Коші до інтегрального рівняння. Метод послідовних наближень відшукання розв’язку інтегрального рівняння.
Доведення теореми про існування розв’язку інтегрального рівняння (теорема Коші).
Доведення єдиності розв’язку інтегрального рівняння (задача Коші).
Продовження розв’язку задачі Коші. Означення загального розв’язку диференціального рівняння I-го порядку; означення частинного розв’язку, означення особливого розв’язку.
Поле напрямів, задане диференціальним рівнянням. Ізокліни, ламані Ейлера.
Диференціальні рівняння з відокремленими змінними: типи рівнянь, які зводяться до рівнянь з відокремленими змінними.
Однорідні диференціальні рівняння. Рівняння, які зводяться до однорідних.
Лінійні диференціальні рівняння I-го порядку. Метод варіації знаходження розв’язку лінійних неоднорідних диференціальних рівнянь першого порядку.
Рівняння Бернуллі.
Інтегрування лінійного рівняння методом підстановки. Метод Ейлера.
Рівняння в повних диференціалах. Критерій про диференціальне рівняння в повних диференціалах.
Інтегрувальний множник та його знаходження.
Диференціальні рівняння, які не розв’язані відносно похідної. Задача Коші. Теорема про існування і єдиність розв’язку задачі Коші для цього рівняння.
Типи диференціальних рівнянь, які не розв’язані відносно похідної і які інтегруються в квадратурах.
Рівняння Лагранжа і рівняння Клеро.
Знаходження особливого розв’язку для рівняння, розв’язаного відносно похідної.
Знаходження особливих розв’язків для рівняння, яке не розв’язане відносно похідної.
Обвідна сім’ї кривих. Знаходження похідної.
Обвідна сім’ї інтегральних кривих - особливий розв’язок.
Задача про ізогональні траєкторії.
Задача про ортогональні траєкторії до сім’ї кривих.
Диференціальні рівняння вищих порядків. Основні означення і поняття. Теорема про існування та єдність розв’язку задачі Коші.
Окремі класи диференціальних рівнянь вищих порядків, що інтегруються в квадратурах або за допомогою зниження порядку.
Лінійні диференціальні рівняння вищих порядків. Основні означення і поняття. Властивості.
Лінійні однорідні диференціальні рівняння. Поняття про фундаментальну систему розв’язків.
Детермінант Вронського. Необхідна і достатня умови лінійної незалежності розв’язків лінійного однорідного диференціального рівняння.
Структура загального розв’язку лінійного однорідного диференціального рівняння порядку п.
Формула Остроградського-Ліувілля.
Лінійні неоднорідні диференціальні рівняння порядку п. Теорема про структуру загального розв’язку такого рівняння.
Метод варіації довільних сталих (метод Лагранжа) розв’язування лінійних неоднорідних диференціальних рівнянь порядку п.
Лінійні однорідні диференціальні рівняння порядку п зі сталими коефіцієнтами. Метод Ейлера.
Структура загального розв’язку однорідних лінійних диференціальних рівнянь порядку п зі сталими коефіцієнтами у випадку дійсних та різних коренів характеристичного рівняння.
Структура загального розв’язку однорідних лінійних рівнянь у випадку кратних коренів характеристичного рівняння.
Диференціальні рівняння ІІ порядку зі сталими коефіцієнтами. Структура загального розв’язку цього рівняння.
Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами. Метод невизначених коефіцієнтів.
Вільні та вимушені гармонічні коливання.
Системи лінійних диференціальних рівнянь з п невідомими. Теорема про існування та єдиність розв’язку задачі Коші. Теорема про достатні умови виконання умови Ліпшиця.
Лінійні диференціальні системи диференціальних рівнянь зі сталими коефіцієнтами. Метод Ейлера.
Векторно-матричний метод розв’язування лінійних диференціальних систем зі сталими коефіцієнтами.

ІІІ МФ, МЕ

Означення і властивості комплексних чисел (аксіоми поля, тригонометрична форма, властивості модулів і аргументів комплексних чисел).
Формула Муавра, корінь n-го степеня та формула його обчислення.
Збіжні послідовності комплексних чисел та їхні основні властивості. Зв’язок з дійсними послідовностями. Нескінченна границя послідовності.
Часткова границя послідовності. Критерій часткової границі. Теореми про існування часткової границі та про множину часткових границь.
Збіжні і розбіжні ряди з комплексними членами та їхні основні властивості. Зв’язок з дійсними рядами.
Абсолютно та умовно збіжні комплексні ряди. Зв’язок абсолютно збіжних комплексних рядів з дійсними рядами. Переставна властивість і властивість про добуток рядів за Коші.
Границя функції комплексної змінної. Зв’язок границі комплексної функції з границями дійсних функцій.
Властивості функцій, які мають границю в точці.
Неперервні функції. Зв’язок неперервності комплексної функції з неперервністю дійсних функцій. Загальні властивості неперервних функцій.
Рівномірно неперервні функції. Властивості функцій, неперервних на компактних множинах.
Збіжні й рівномірно збіжні функціональні послідовності з комплексними членами. Зв’язок з дійсними послідовностями. Критерії рівномірної збіжності. Неперервність рівномірної границі.
Збіжні й рівномірно збіжні функціональні ряди з комплексними членами. Зв’язок з дійсними рядами. Критерії рівномірної збіжності. Ознака Вейєрштрасса. Неперервність суми ряду.
Степеневі ряди з комплексними членами. Теорема Абеля. Формула Коші – Адамара. Неперервність суми.
Означення і властивості функцій , , .
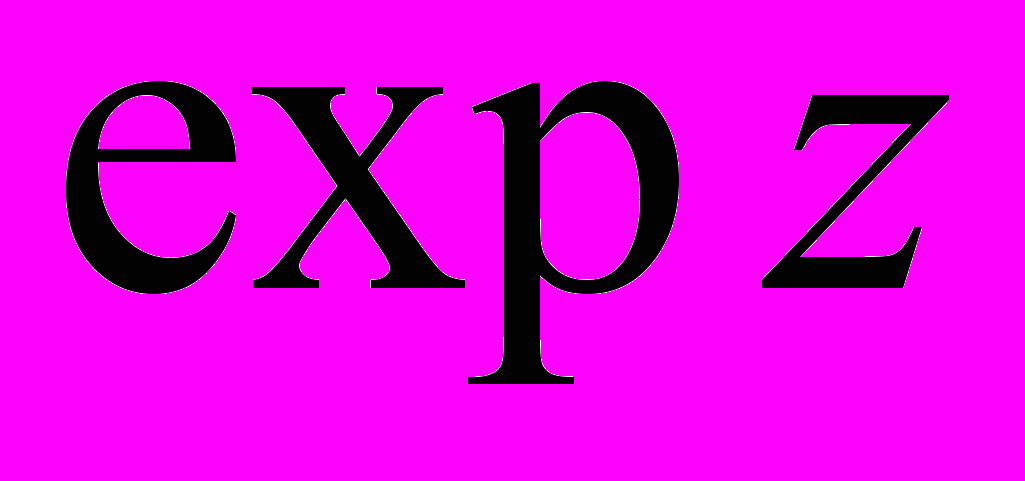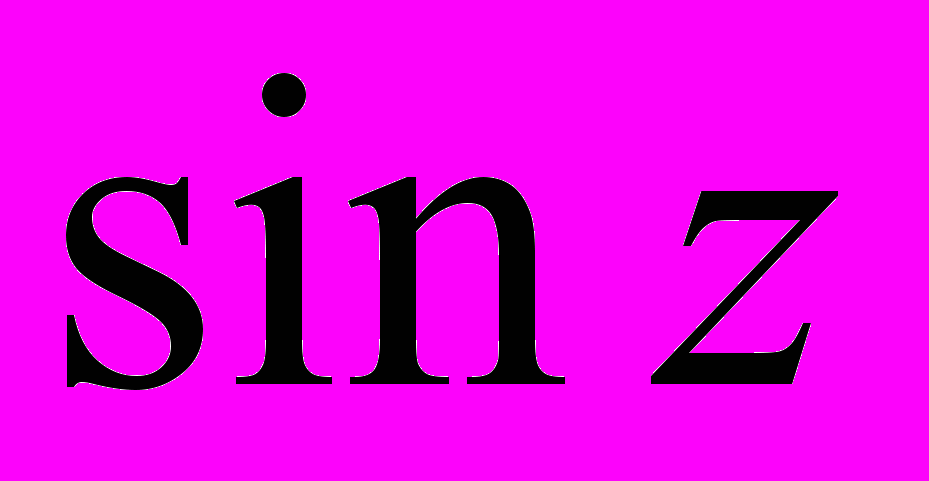Логарифм комплексного числа і логарифмічна функція.
Поняття арксинуса комплексного числа, його існування. Формула для обчислення.
Поняття арккосинуса комплексного числа, його існування. Формула для обчислення.
Зв’язок між комплексним і дійсним (шкільним) арккосинусами.
Зв’язок між комплексним і дійсним (шкільним) арксинусами.
Тангенс та арктангенс комплексного числа.
Гіперболічні синус і косинус та їх зв’язок з тригонометричними.
Гіперболічні ареакосинус та ареасинус. Формули для їх обчислення.
Поступове визначення поняття степеня 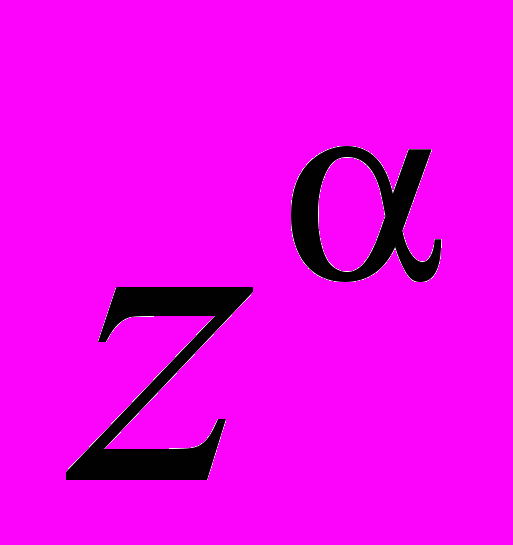і загальне означення степеня з комплексним показником. Загальна показникова і загальна степенева функції.
Основні елементарні та елементарні функції комплексної змінної. Вказати однакові та відмінні властивості дійсних та відповідних їм комплексних основних елементарних функцій.
Загальне означення похідної функції комплексної змінної. Властивості функцій, що мають похідні.
Диференційовні функції комплексної змінної. Критерій диференційовності. Умови Коші – Рімана.
Поняття аналітичної функції у розумінні Коші та у розумінні Рімана. Їх еквівалентність.
Геометричний зміст похідної комплекснозначної функції дійсної змінної та функції комплексної змінної. Конформні відображення.
Теорема про диференціювання степеневого ряду. Наслідки. Ряд Тейлора.
Інтеграл функції комплексної змінної. Його існування та обчислення.
Основні властивості інтеграла функції комплексної змінної.
Інтегральна теорема Коші.
Лема про рівність інтегралів за різними контурами.
Інтегральна формула Коші.
Розвинення аналітичної функції у степеневий ряд.
Означення аналітичності за Вейєрштрассом та його рівносильність з означенням аналітичності за Коші.
Нерівність Коші для коефіцієнтів степеневого ряду. Теорема Ліувілля. Основна теорема алгебри многочленів.
Властивість єдиності аналітичної функції для круга.
Властивість єдиності аналітичної функції для довільної області.
Узагальнена інтегральна формула Коші.
Первісна функції комплексної змінної, необхідна умова її існування. Критерій існування первісної (довести необхідність).
Критерій існування первісної (довести достатність). Формула Ньютона – Лейбніца.
Означення аналітичної функції за Осгудом та його рівносильність з означенням аналітичності за Коші.
Гармонічні функції та їх зв’язок з аналітичними функціями.
Відновлення аналітичної функції за відомою її дійсною або уявною частиною.
Поняття ряду Лорана. Кільце його збіжності та аналітичність суми.
Теорема Лорана про розклад аналітичної в круговому кільці функції у ряд Лорана.
Теорема про єдиність ряду Лорана.
Ізольовані особливі точки аналітичних функцій та їх класифікація. Критерій усувної точки. Критерій полюса через представлення.
Поняття m-кратного нуля аналітичної функції. Зв’язок між нулем і полюсом. Критерій полюса через границю.
Критерій суттєво особливої ізольованої точки аналітичної функції. Теорема Сохоцького про часткові границі в суттєво особливій точці.
Поняття лишку. Обчислення лишків відносно різних типів ізольованих точок.
Теорема про обчислення логарифмічного лишку.
Основна теорема про лишки (з повним доведенням).
Диференціальні рівняння. Основні поняття.
Приклади задач, які приводять до диференціальних рівнянь.
Диференціальні рівняння 1-го порядку. Основні поняття.
Диференціальні рівняння з відокремлюваними змінними.
Однорідні диференціальні рівняння 1-го порядку.
Лінійні диференціальні рівняння 1-го порядку.
Рівняння Бернуллі.
Диференціальні рівняння 1-го порядку в повних диференціалах.
Інтегруючий множник.
Метод послідовних наближень розв’язування диференціальних рівнянь 1-го порядку.
Теорема Пікара про існування та єдиність розв’язку задачі Коші для диференціального рівняння 1-го порядку.
Обвідна однопараметричної сім’ї кривих.
Особливі розв’язки диференціальних рівнянь 1-го порядку.
Диференціальні рівняння 1-го порядку не розв’язані відносно похідної: а) рівняння Клеро; б) рівняння Лагранжа.
Поле напрямів. Ізокліни. Метод Ейлера. Ламані Ейлера.
Диференціальні рівняння вищого порядку. Основні поняття.
Найпростіші типи диференціальних рівнянь вищого порядку.
Лінійні диференціальні рівняння вищого порядку. Основні поняття.
Теорема про властивості частинних розв’язків лінійних неоднорідних диференціальних рівнянь вищого порядку.
Критерій лінійної незалежності частинних розв’язків рівнянь лінійного неоднорідного диференціального рівняння.
Теорема про структуру загального розв’язку лінійного однорідного диференціального рівняння вищого порядку.
Лінійні однорідні диференціальні рівняння вищого порядку із сталими коефіцієнтами. Схема розв’язування.
Лінійні неоднорідні диференціальні рівняння вищого порядку. Структура загального розв’язку.
Метод Лагранжа знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння вищого порядку.
Лінійні неоднорідні диференціальні рівняння вищого порядку із сталими коефіцієнтами. Метод невизначених коефіцієнтів: а) для рівнянь 2-го порядку; б) для рівнянь п-го порядку.
Лінійні диференціальні рівняння і коливні процеси.
Нормальні системи диференціальних рівнянь. Основні поняття.
Метод виключення розв’язування нормальних систем диференціальних рівнянь.
Основні типи диференціальних рівнянь в частинних похідних.
Мішана задача для диференціального рівняння коливання струни.
Мішана задача для неоднорідного рівняння коливання струни.
Мішана задача для однорідного рівняння теплопровідності з нульовими крайовими умовами.
Мішана задача для однорідного рівняння теплопровідності з ненульовими крайовими умовами.
Задача Коші для рівняння коливання струни.
Лапласіан в полярних і циліндричних координатах.
Задача Діріхле для круга для рівняння Лапласа (внутрішня та зовнішня).
Інтеграл Пуассона.

Blog

Питання до екзаменів І мі