Питання до екзаменів І мі
| Вид материала | Документы |
- Питання по курсу "Хімія та методи дослідження сировини та матеріалів" для підготовки, 253.51kb.
- Пам’ятка робочій групі з підготовки питання щодо стану курсового, дипломного, магістерського, 27.58kb.
- Пам’ятка робочій групі з підготовки питання щодо стану методичного забезпечення навчального, 31.74kb.
- Директору/начальнику, 39.07kb.
- Директору/начальнику, 39.6kb.
- Директору Харківського торговельно-економічного коледжу кнтеу радченко, 22.18kb.
- 2. Мікроекономіка Тема Економічна політика, 1231.15kb.
- Олександр Новицький цад лраа «Helios», 136.54kb.
- Затверджено Атестаційною колегією Міносвіти та науки України Протокол №4/9 – 2/4 від, 104.83kb.
- Робоча навчальна програма для студентів 2-го курсу, 4-й семестр (групи г-26, г-27), 313.53kb.
ІІ МІ
- Ортогональна система функцій. Тригонометричний ряд формули Ейлера-Фур’є. Ряд Фур’є.
- Кусково-диференційовні функції. Теорема про розвинення функцій в ряд Фур’є.
- Ряд Фур’є для парної та непарної функцій.
- Ряд Фур’є для функцій з довільним періодом.
- Ряд Фур’є для неперіодичної функції.
- Комплексна форма для ряду Фур’є.
- Метричні простори в шкільному курсі математики.
- Означення метричного простору. Приклади метричних просторів.
- Основні метричні простори. п-вимірний евклідовий простір.
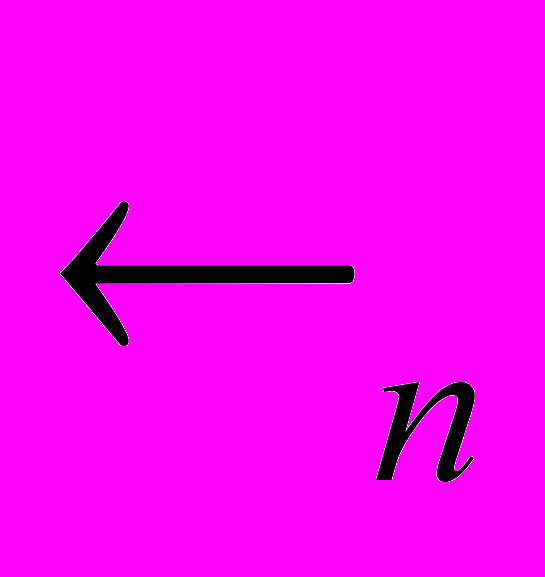 . Простір
. Простір 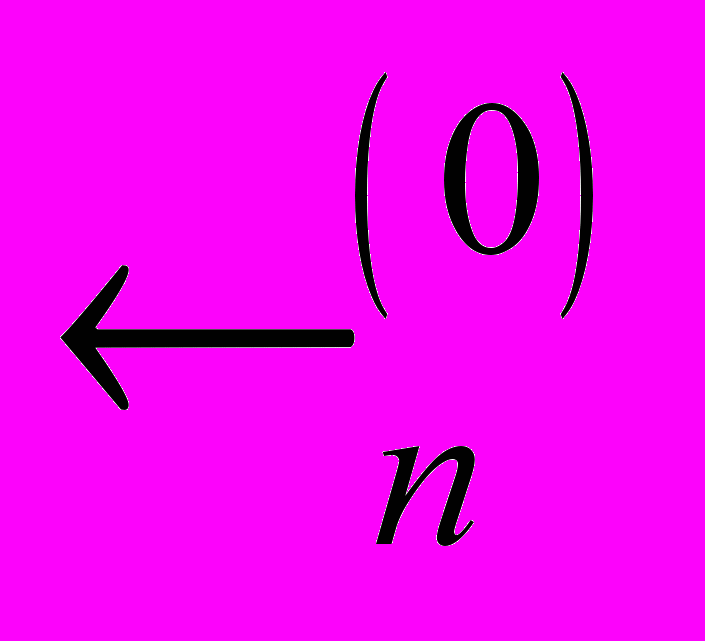 .
.
- Простір
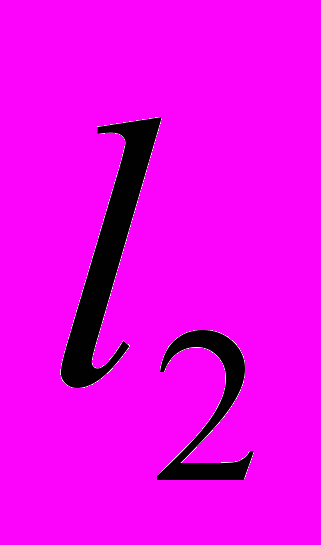 .
.
- Простір
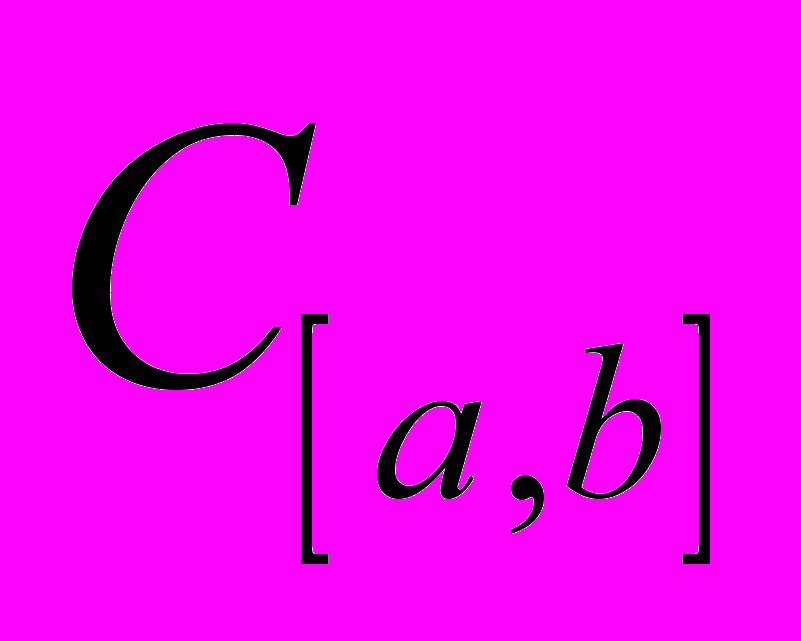 . Простір
. Простір 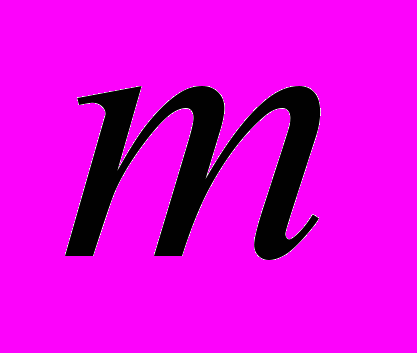 .
.
- Збіжні послідовності та їх властивості.
- Поняття відкритої та замкнутої кулі,
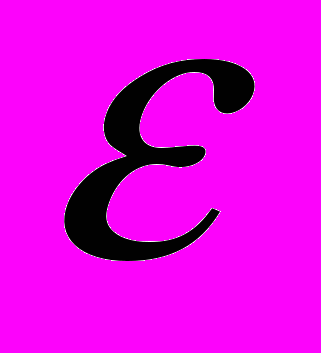 -околу точки, граничної та узагальненої точки у метричному просторі.
-околу точки, граничної та узагальненої точки у метричному просторі.
- Класифікація точок множини, що лежить у метричному просторі.
- Необхідна і достатня умова того, щоб деяка точка множини, що належить метричному простору, була граничною.
- Теорема про зв’язок відкритої та замкненої множин.
- Критерій відкритої множини.
- Критерій замкненої множини.
- Об’єднання і переріз відкритих множин.
- Об’єднання і переріз замкнених множин.
- Повні метричні простори. Означення. Теорема: якщо послідовність має границю, то вона є фундаментальною.
- Теорема: для того, щоб послідовність точок евклідового простору збігалась, необхідно й достатньо, щоб вона була фундаментальною.
- Теорема: для того, щоб фундаментальна послідовність метричного простору була збіжною необхідно і достатньо, щоб вона мала збіжну послідовність у цьому просторі.
- Довести повноту евклідового метричного простору
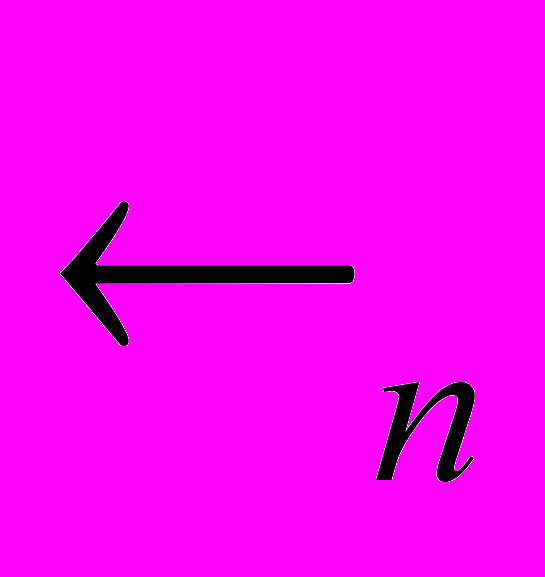 .
.
- Довести повноту простору
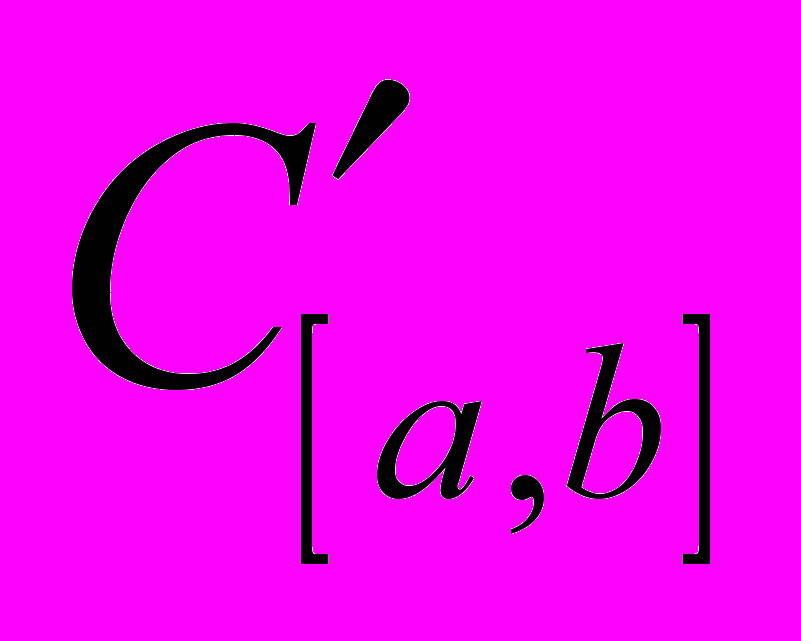 .
.
- Компактні множини. Означення. Теорема. Непорожня множина Д метричного простору
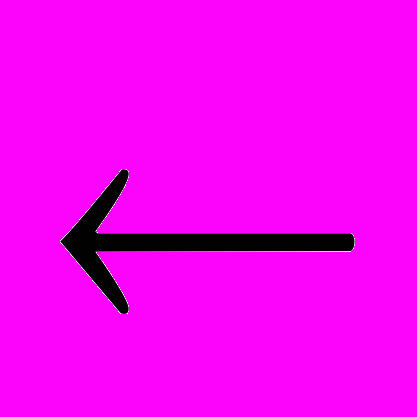 є компактною, якщо будь-яка нескінченна підмножина Д1 має принаймні одну граничну точку.
є компактною, якщо будь-яка нескінченна підмножина Д1 має принаймні одну граничну точку.
- Означення
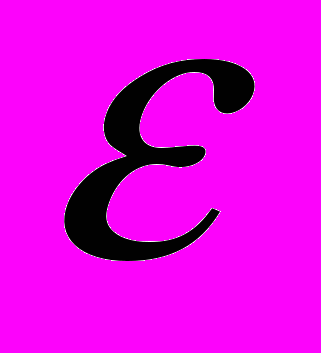 -сітки. Цілком обмежена множина. Теорема Хаусдорфа, наслідки.
-сітки. Цілком обмежена множина. Теорема Хаусдорфа, наслідки.
- Теорема: у евклідовому просторі
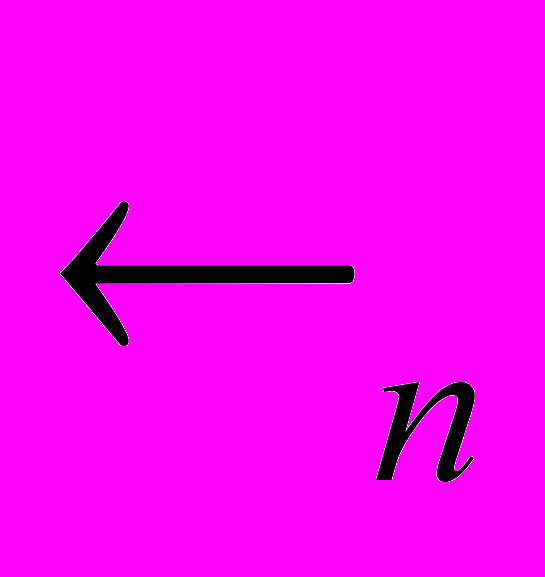 множина всіх неперервних непорожніх замкнених обмежених множин утворюють компакт і тільки вони.
множина всіх неперервних непорожніх замкнених обмежених множин утворюють компакт і тільки вони.
- Неперервні оператори та функціонали. Основні поняття. Означення неперервності за Коші і за Гейне.
- Критерій неперервності оператора в точці.
- Властивості неперервних операторів.
- Стискуючі відображення. Нерухомі точки відображення. Метод послідовних наближень.
- Теорема Банаха.
- Розв’язування системи лінійних алгебраїчних рівнянь методом стислих відображень.
- Функції багатьох змінних. Границя функцій багатьох змінних. Означення. Приклади.
- Неперервність функцій багатьох змінних. Означення, приклади.
- Теореми про властивості функцій багатьох змінних, неперервних на обмежених замкнених множинах.
- Частинні похідні функцій багатьох змінних. Геометричний зміст частинних похідних для функцій двох змінних.
- Диференційовність функцій багатьох змінних. Зв’язок між диференційовністю та неперервністю, між диференційовністю та частинними похідними.
- Повний диференціал функцій багатьох змінних. Застосування певного диференціала до наближених обчислень.
- Скалярне поле. Лінії та поверхні рівня.
- Похідна за напрямом. Градієнт.
- Похідні складених функцій.
- Диференціал складеної функції. Інваріантність форми першого диференціала.
- Похідна вищих порядків. Теорема про рівність мішаних похідних.
- Диференціали вищих порядків.
- Формула Тейлора для функції двох змінних.
- Дотична площина і нормаль до поверхні. Геометричний зміст повного диференціала.
- Неявні функції. Теорама 1.
- Неявні функції. Теореми 2 і 3.
- Екстремум функції багатьох змінних. Основні поняття. Необхідні умови екстремуму. Правило дослідження на екстремум.
- Достатні умови екстремуму для функції багатьох змінних.
- Найбільше і найменше значення функції в замкненій області. Правило дослідження на глобальний екстремум.
- Умовний екстремум для функції двох змінних.
- Умовний екстремум для функції трьох змінних.
- Еквівалентні множини. Поняття потужності. Властивості еквівалентних множин.
- Поняття зчисленної множини. Приклади зчислених множин.
- Властивості зчисленних множин.
- Поняття континуальної множини. Приклади континуальних множин. Властивості континуальних множин.
- Гіпотеза континууму. Існування як завгодно великих потужностей.
- Поняття частинних похідних та їхній геометричний зміст.
- Диференційовність функції кількох змінних. Необхідні умови диференційованості.
- Достатні умови диференційовності функції двох змінних..
- Повний диференціал функції, його геометричний зміст.
- Застосування повного диференціала до наближених обчислень.
- Похідні складних функцій. Приклади.
- Диференціали складних функцій, інваріантність їхньої форми. Правила диференціювання.
- Похідна за напрямом та її обчислення. Приклади.
- Градієнт функції та його зв'язок з похідною за напрямом.
- Частинні похідні вищих порядків. Приклади.
- Теорема про рівність мішаних похідних.
- Диференціали вищих порядків, неінваріантність їхньої форми.
- Формула Тейлора для функції двох змінних.
- Поняття екстремуму функції кількох змінних. Необхідна умова існування екстремуму.
- Достатні умови існування екстремуму функції двох змінних.
- Найбільше та найменше значення функції в обмеженій замкненій області.
- Розвязування прикладних задач на відшукання екстремуму.
- Неявні функції однієї змінної. Умови існування та диференційовності.
- Неявні функції двох змінних. Умови існування та диференційовності.
- Поняття та необхідні умови існування умовного екстремуму.
- Достатні умови існування умовного екстремуму.
- Міра Жордана у просторі
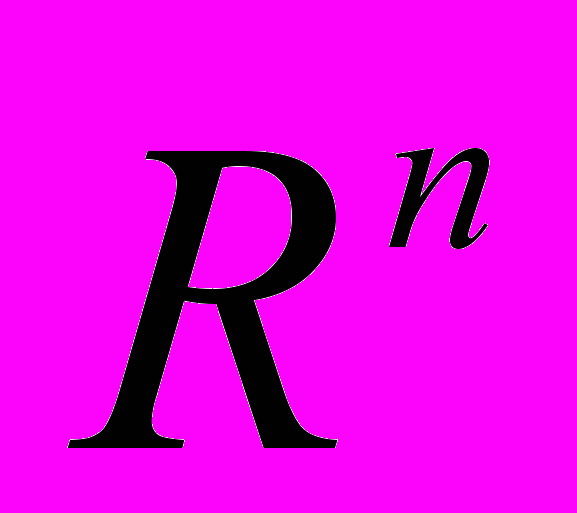 та її основні властивості.
та її основні властивості.
- Поняття елементарного прямокутника у проторі
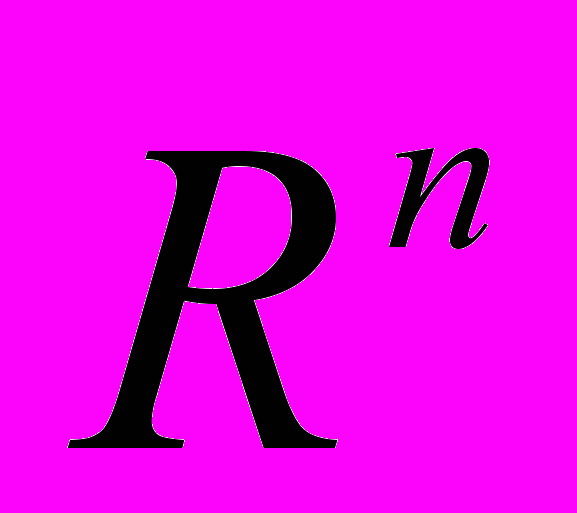 та його міри.
та його міри.
- Поняття подвійного інтеграла та умови його існування.
- Основні властивості подвійного інтеграла.
- Обчислення подвійних інтегралів у випадку прямокутної області.
- Обчислення подвійних інтегралів у випадку криволінійної області.
- Заміна змінної у подвійних інтегралах (загальний випадок).
- Подвійні інтеграли в полярних координатах.
- Потрійні інтеграли, їхні властивості. Обчислення потрійних інтегралів.
- Потрійні інтеграли у сферичних та циліндричних координатах.
- Застосування кратних інтегралів у геометрії.
- Застосування кратних інтегралів у фізиці.
- Криволінійні інтеграли першого роду (поняття, властивості, умови існування, обчислення).
- Застосування криволінійних інтегралів першого роду.
- Криволінійні інтеграли другого роду (поняття, властивості, умови існування).
- Формула Гріна.
- Умови незалежності криволінійного інтеграла другого роду від шляху інтегрування.
- Застосуваня криволінійних інтегралів другого роду.
- Означення міри Жордана через характеристичну функцію множини. Основні властивості міри.
- Множини L-міри нуль, їхні властивості та приклади.
- Східчасті функції та їхні властивості.
- L інтеграл від східчастої функції та його основні властивості.
- L-інтеграл функції по прямокутнику та його властивості.
- L-міра для довільної множини з
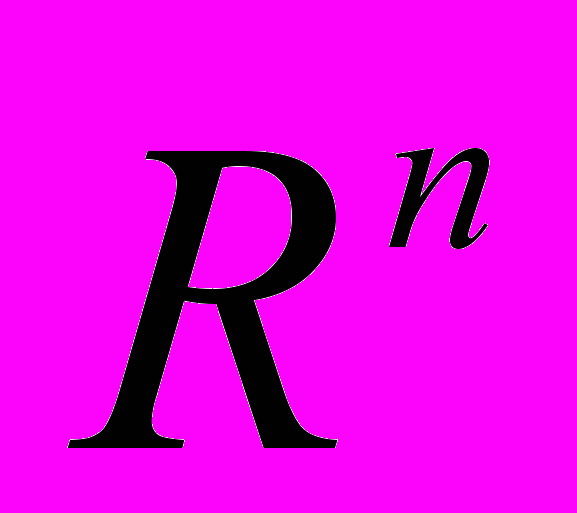 . Властивості міри.
. Властивості міри.
- L-інтеграл функції по довільній вимірній множині з
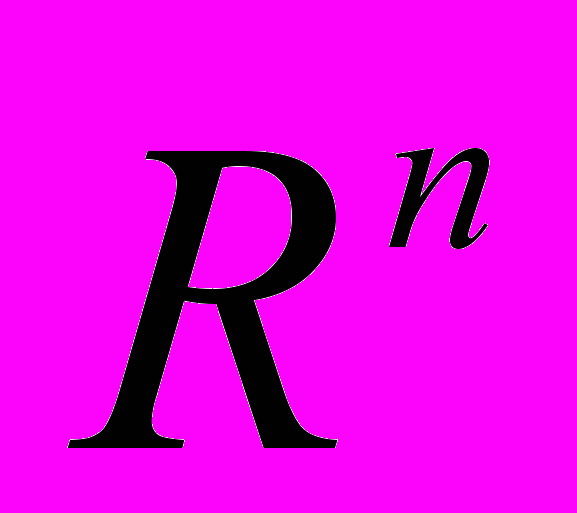 .
.
ІІ МФ, МЕ
- Степеневий ряд. Інтервал і радіус збіжності. Теорема Коші – Адамара.
- Властивості суми степеневого ряду.
- Розкладання функцій у степеневий ряд. Необхідна умова, критерій і достатня умова.
- Поняття тригонометричного ряду і ряду Фур’є. Теорема про єдиність тригонометричного ряду.
- Мінімальна властивість многочленів Фур’є та наслідки з неї.
- Інтегральне представлення многочленів Фур’є.
- Збіжність ряду Фур’є у випадку кусково диференційовної функції.
- Розкладання функцій у тригонометричний ряд. Різні способи. Приклади.
- Потужність множин. Порівняння потужностей.
- Зчисленні множини та їхні властивості. Довести теореми про потужність об’єднання і про нерівність
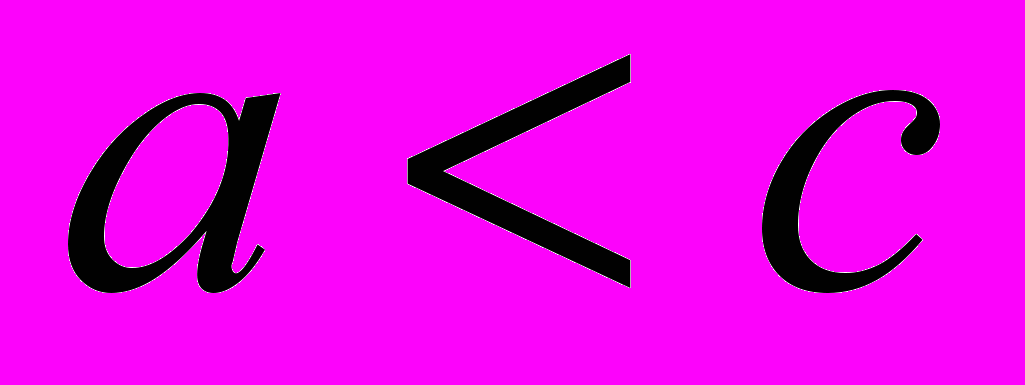 .
.
- Зчисленні множини та їхні властивості. Довести теореми про потужність індексованої множини і про об’єднання нескінченної множини з не більш ніж зчисленною.
- Континуальні множини та їхні властивості. Довести теореми про об’єднання континуальних множин і про потужність множин
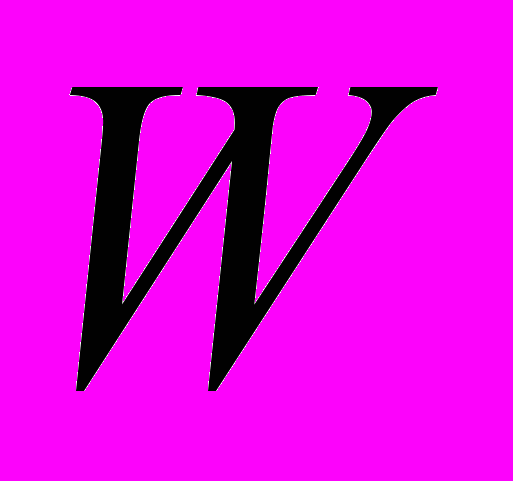 та
та 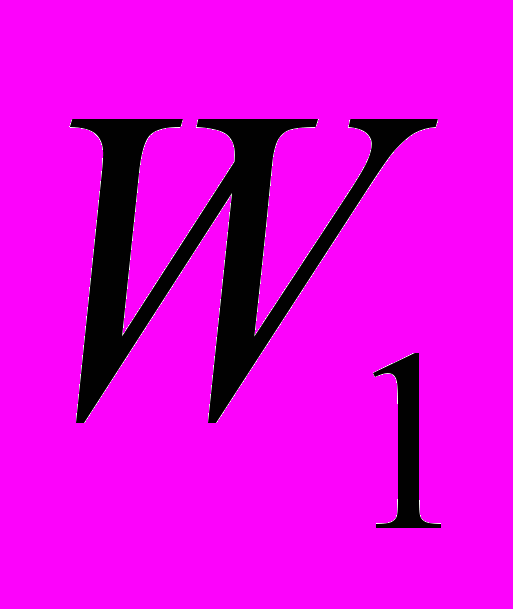 .
.
- Континуальні множини та їхні властивості. Довести теорему про континуальність індексованої множини.
- Континуальні множини та їхні властивості. Довести теореми про потужність просторів
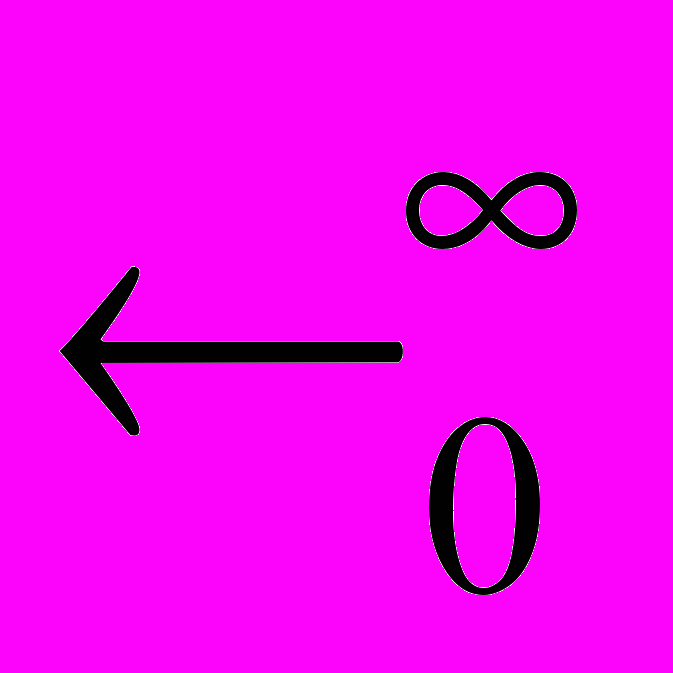 і
і 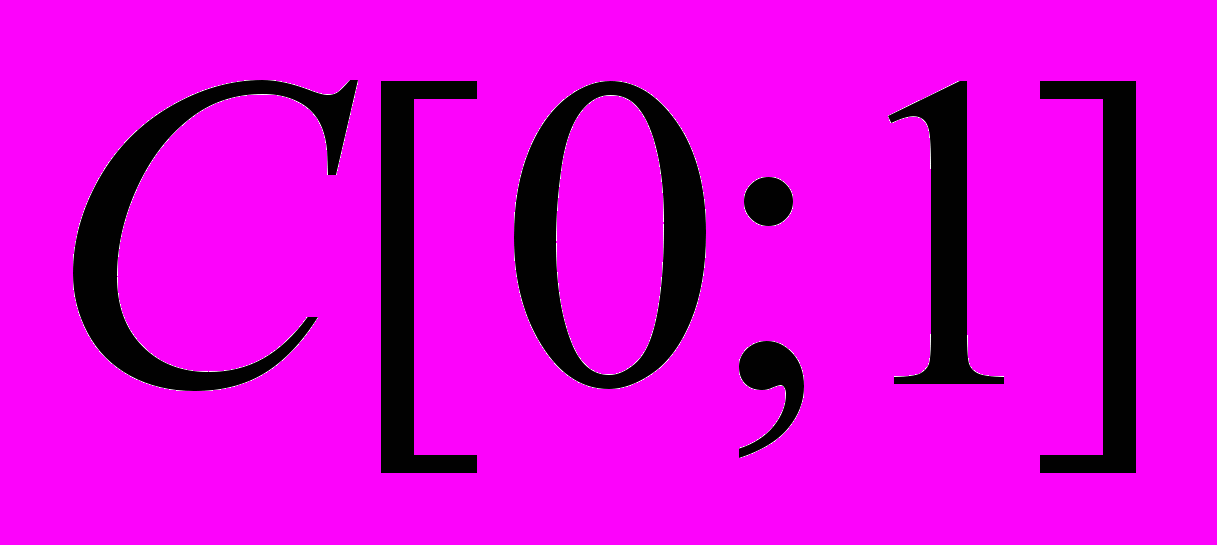 та про нерівність
та про нерівність 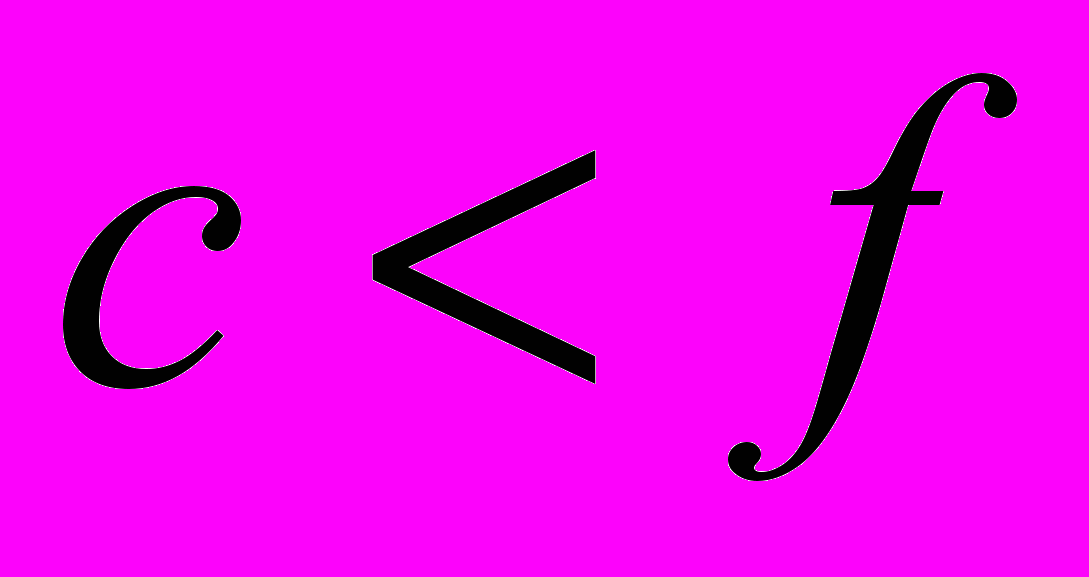 .
.
- Множина всіх підмножин даної множини. Неіснування найбільшої потужності. Континуум-гіпотеза.
- Означення метричного простору. Основні метричні простори. Довести метричність простору
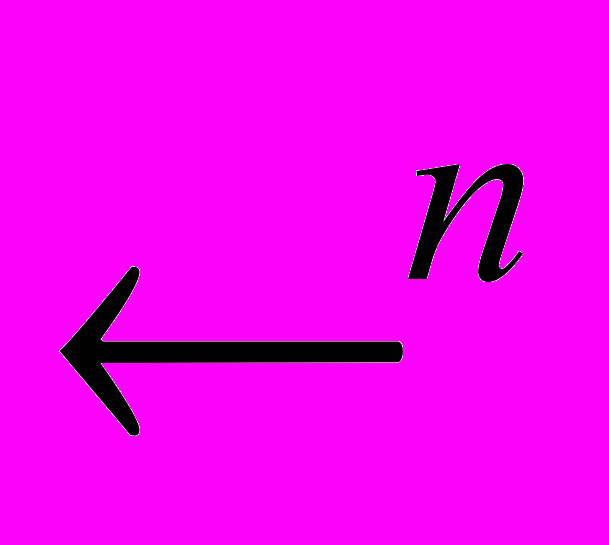 .
.
- Означення метричного простору. Основні метричні простори. Довести метричність просторів
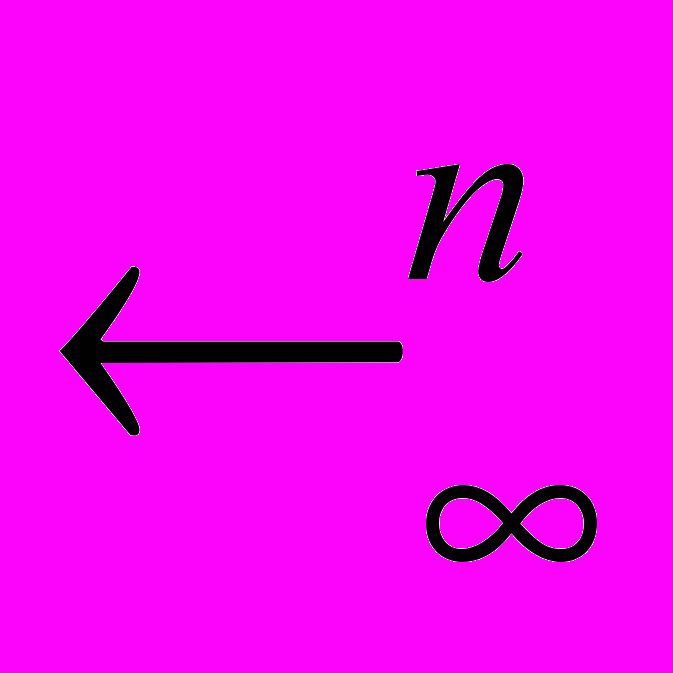 і
і 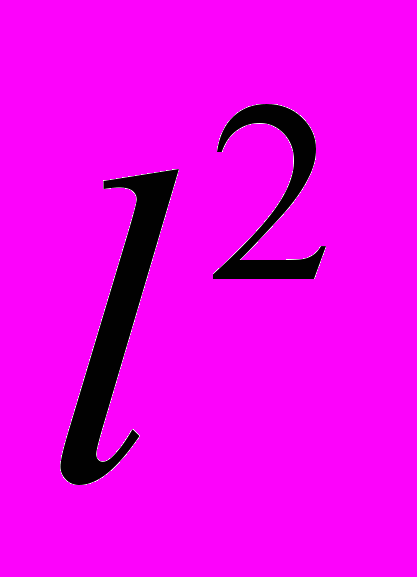 .
.
- Означення метричного простору. Основні метричні простори. Довести метричність просторів
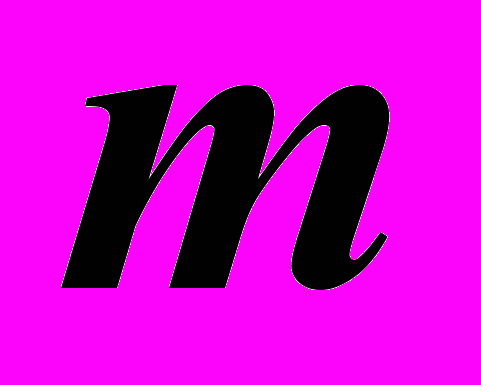 і
і  .
.
- Означення метричного простору. Основні метричні простори. Довести метричність простору
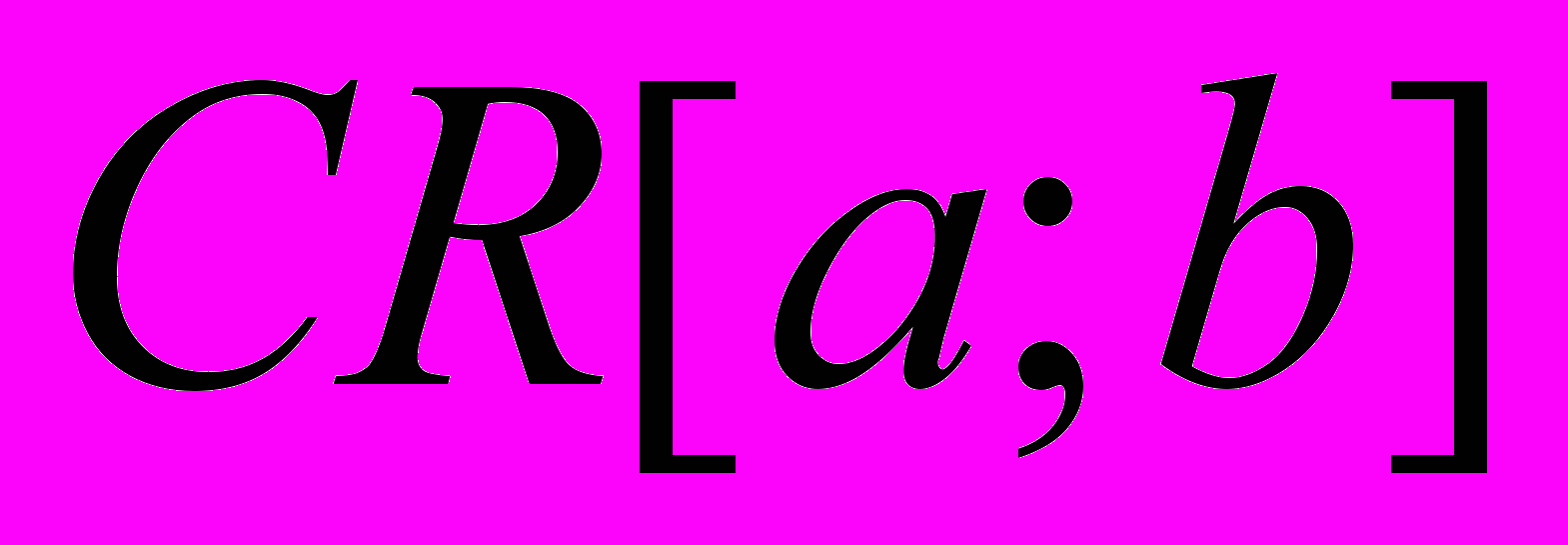 .
.
- Збіжні послідовності у метричному просторі. Умови збіжності в
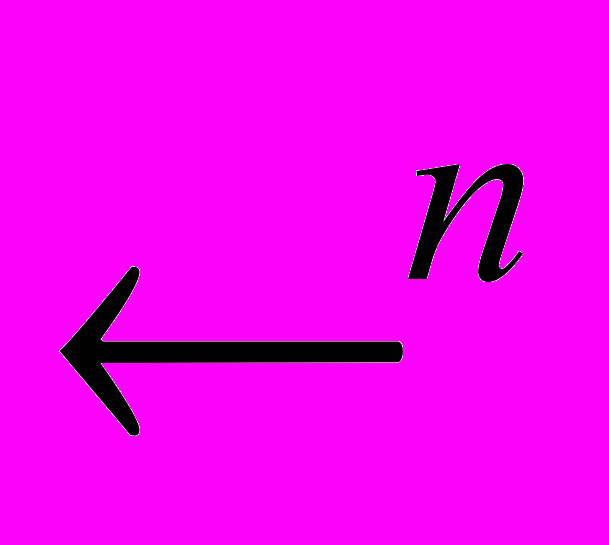 ,
, 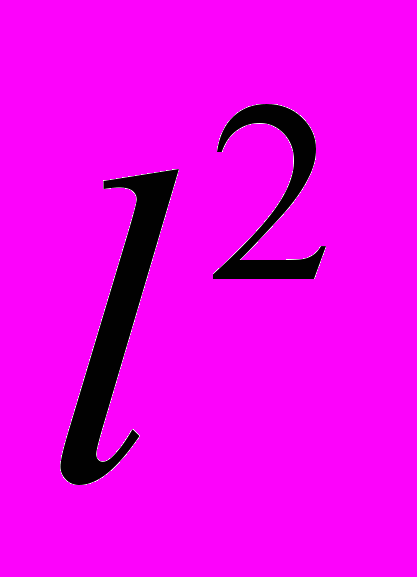 і
і  .
.
- Класифікація точок метричного простору відносно множини. Приклади.
- Основні типи множин у метричному просторі. Властивості відкритих і замкнених множин. Необхідні умови компактності.
- Будова відкритої лінійної множини.
- Будова замкненої лінійної множини, зокрема обмеженої.
- Будова досконалої лінійної множини, у тому числі обмеженої.
- Відкрита і досконала множини Кантора. Їхня потужність і довжина.
- Повні метричні простори. Довести повноту простору
 .
.
- Повні метричні простори. Довести повноту простору
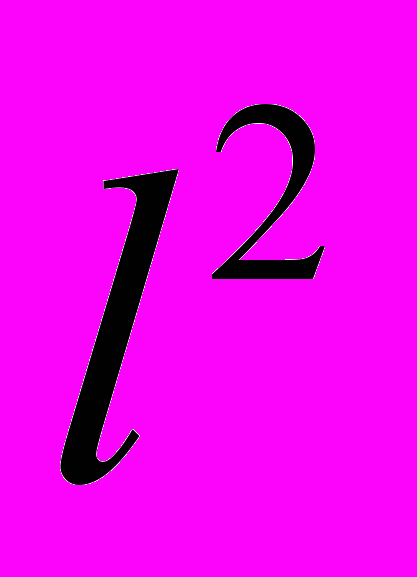 .
.
- Повні метричні простори. Довести повноту простору
 .
.
- Повні метричні простори. Довести неповноту простору
 .
.
- Границя і неперервність функцій у метричних просторах. Властивості функцій, неперервних на компактних і зв’язних множинах.
- Оператори стиску і теорема Банаха про нерухому точку.
- Функції двох змінних: їхній графік, лінії рівня, границя й неперервність, частинні похідні.
- Властивості границь і неперервних функцій двох змінних.
- Два означення диференційовної функції двох змінних та їх рівносильність.
- Необхідні умови диференційовності функції двох змінних.
- Достатня умова диференційовності функції двох змінних.
- Диференціал функції двох змінних, застосування його до наближених обчислень. Дотична площина і нормаль до графіка функції.
- Похідна за напрямком, її існування та обчислення. Градієнт.
- Диференціювання складеної функції однієї змінної.
- Диференціювання складеної функції двох і більше змінних.
- Інваріантна властивість диференціала першого порядку.
- Критерій сталості функції двох змінних.
- Неявна функція, її існування, єдиність і неперервність.
- Диференціювання неявної функції.
- Частинні похідні вищих порядків. Теорема про рівність мішаних похідних.
- Поняття
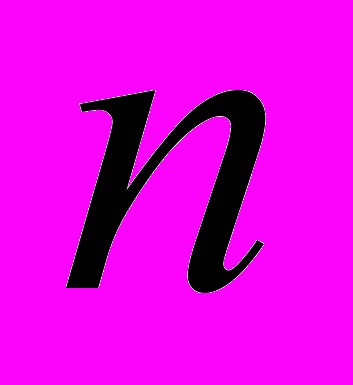 разів диференційовної функції багатьох змінних та диференціала
разів диференційовної функції багатьох змінних та диференціала 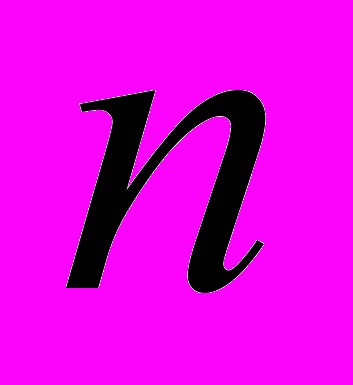 -го порядку, формула його обчислення.
-го порядку, формула його обчислення.
- Формула Тейлора для функції двох змінних.
- Локальні екстремуми функції багатьох змінних. Необхідні та достатні умови.
- Глобальні екстремуми функцій багатьох змінних. Способи їх відшукання та доведення існування.
- Означення кратного інтеграла по елементарному прямокутнику. Необхідна умова інтегровності.
- Суми Дарбу та їхні властвості.
- Інтеграли Дарбу. Теорема Дарбу.
- Критерії інтегровності функції багатьох змінних на прямокутнику.
- Достатні умови інтегровності на прямокутнику.
- Властивості кратного інтеграла по прямокутнику.
- Обчислення подвійного інтеграла по прямокутнику за допомогою повторних інтегралів.
- Обчислення потрійного інтеграла по прямокутнику за допомогою повторних інтегралів.
- Означення міри Жордана.
- Зв’язок між мірою Жордана та інтегралом Рімана.
- Властивості міри Жордана.
- Лема про множину нульової міри та критерій множини нульової міри через покриття прямокутниками.
- Теорема про зв’язок між вимірністю множини та її межі.
- Лема про міру графіка функції. Достатні умови квадровності множини.
- Означення кратного інтеграла по вимірній за Жорданом множині. Теорема про його існування.
- Обчислення подвійних інтегралів по елементарних областях I та II типів.
- Обчислення потрійного інтеграла по циліндричному тілу.
- Властивості кратних інтегралів по вимірній множині.
- Незалежність кратного інтеграла від множини нульової міри.
- Перехід до полярних координат у подвійному інтегралі.
- Перехід до сферичних координат у потрійному інтегралі.
- Задача про обчислення маси неоднорідної дротини.
- Означення криволінійного інтеграла I роду, його існування та обчислення у випадку задання кривої натуральним параметром.
- Існування та обчислення криволінійного інтеграла I роду у випадку довільного параметричного задання кривої.
- Властивості криволінійних інтегралів I роду.
- Задача про роботу змінної сили вздовж кривої.
- Означення криволінійних інтегралів II роду: за абсцисою, за ординатою і повного.
- Обчислення криволінійних інтегралів II роду.
- Властивості криволінійних інтегралів II роду.
- Формула Гріна.
- Обчислення площі фігури за допомогою криволінійного інтеграла.
- Незалежність криволінійного інтеграла від форми кривої і його рівність нулю.
- Незалежність криволінійного інтеграла від форми кривої і умова повного диференціала.
- Умова незалежності криволінійного інтеграла від форми кривої в однозв’язній області.
ІІ ФІА
- Ортогональна система функцій. Тригонометричний ряд. Формули Ейлера-Фур’є. Ряд Фур’є.
- Кусково-диференційовна функція. Теорема про розвинення функції в ряд Фур’є.
- Ряди Фур’є для парної та непарної функцій.
- Ряд Фур’є для функцій з довільним періодом.
- Ряд Фур’є для неперіодичної функції.
- Комплексна форма ряду Фур’є.
- Поняття функцій багатьох змінних. Лінії та поверхні рівня.
- Метричні простори. аксіоми метричного простору. п-вимірний евклідовий простір
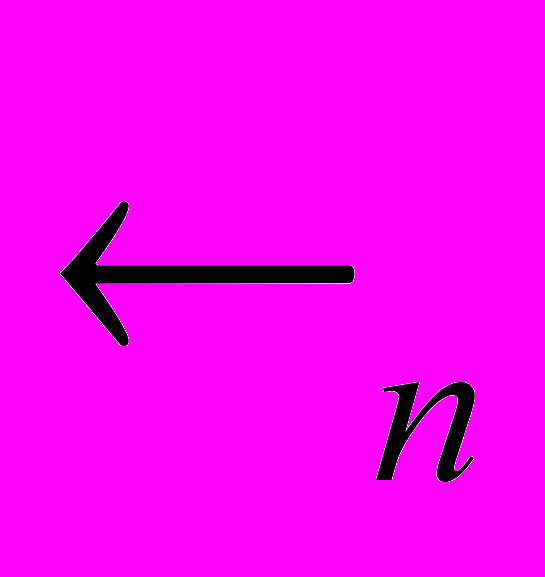 .
.
- Відкрита та замкнена куля, сфера. Окіл точки п-вимірного простору.
- Класифікація точок множини метричного простору.
- Послідовності точок метричного простору. Збіжність. Властивості збіжних послідовностей.
- Границя функції багатьох змінних. Різні означення границі.
- Неперервність функції багатьох змінних.
- Класифікація множин метричного простору.
- Властивості функцій, заданих і неперервних на однозв’язній замкненій множині.
- Частинні похідні. Означення. Геометричний зміст частинних похідних функцій двох змінних.
- Повний приріст функцій. Диференційовність функцій двох змінних. Зв’язок між диференційовністю і неперервністю функцій кількох змінних.
- Зв’язок між диференційовністю і частинними похідними.
- Повний диференціал функції двох змінних.
- Частинні похідні складеної функції двох змінних.
- Інваріантність форми першого диференціала.
- Застосування повного диференціала.
- Похідні вищих порядків. Теорема про рівність мішаних похідних другого порядку.
- Диференціали вищих порядків.
- Формула Тейлора для функції двох змінних.
- Скалярне поле. Похідна за напрямом.
- Градієнт, його зв’язок з похідною за напрямом. Оператор Гамільтона.
- Дотична площина і нормаль до поверхні.
- Неявні функції. Теорема 1 і 2.
- Екстремум функції багатьох змінних. Похідні умови екстремуму.
- Достатні умови екстремуму. Правило дослідження функції на екстремум.
- Найбільше і найменше значення функції в замкненій області. Правило дослідження функції на найбільше і найменше значення.
- Задачі. Що приводять до поняття подвійного інтеграла.
- Означення подвійного інтеграла, умови інтегровності.
- Властивості подвійного інтеграла.
- Обчислення подвійних інтегралів.
- Поняття потрійного інтеграла та його властивості.
- Обчислення потрійних інтегралів.
- Застосування подвійних інтегралів.
- Застосування потрійних інтегралів.
- Диференціальні рівняння. Основні поняття.
- Приклади і задачі, які приводять до диференціальних рівнянь.
- Диференціальні рівняння І порядку з відокремлюваними змінними.
- Однорідні диференціальні рівняння І порядку.
- Лінійні диференціальні рівняння І порядку.
- Рівняння Бернулі.
- Диференціальні рівняння І порядку в повних диференціалах.
- Інтегруючий множник.
- Метод послідовного наближення розв’язування диференціальних рівнянь.
- Теорема Пікара про існування та єдиність розв’язку задачі Коші для диференціальних рівнянь І порядку.
- Обвідна однопараметричної сім’ї кривих.
- Особливі розв’язки диференціальних рівнянь І порядку.
- Рівняння Клеро.
- Рівняння Лагранжа.
- Диференціальні рівняння вищих порядків. Основні поняття.
- Найпростіші типи диференціального рівняння вищого порядку.
- Лінійні диференціальні рівняння вищого порядку. Основні поняття.
- Теорема про властивості частинних розв’язків лінійного, однорідного диференціального рівняння вищого порядку.
- Критерій лінійної незалежності частинних розв’язків лінійного однорідного диференціального рівняння вищого порядку.
- Теорема про структуру загального розв’язку лінійного, однорідного диференціального рівняння вищого порядку.
- Лінійні однорідні диференціальні рівняння ІІ порядку із сталими коефіцієнтами.
- Схема розв’язування лінійного однорідного диференціального рівняння п-го порядку із сталими коефіцієнтами.
- Структура загального розв’язку лінійного неоднорідного диференціального рівняння вищого порядку.
- Метод Лагранжа знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння ІІ порядку.
- Метод Лагранжа знаходження частинних розв’язків лінійних неоднорідних диференціальних рівнянь п-го порядку.
- Метод невизначеного коефіцієнта знаходження частинних розв’язків лінійних неоднорідних диференціальних рівнянь п-го порядку.
- Лінійні диференціальні рівняння і коливання.
- Диференціальні рівняння І порядку, як поля напрямів. Ізокліни.
- Ламані Ейлера.
- Ізогональні та ортогональні проекції.
- Нормальні системи диференціальних рівнянь.
- Системи лінійних однорідних диференціальних рівнянь із сталими коефіцієнтами.
- Основні типи інтегральних рівнянь.
- Метод ітерації для рівняння Фредгольма.
- Метод ітерації для рівняння Вольтера.
- Метод ітерації для нелінійних інтегральних рівнянь.
- Розв’язування інтегральних рівнянь за допомогою квадратичних формул.
- Інтегральні рівняння з виродженим ядром. теорема Фредгольма.
- Диференціальні та інтегральні рівняння і математичні моделі.
- Диференціальні рівняння. Основні поняття.
- Прикладні задачі, які приводять до диференціальних рівнянь.
- Диференціальні рівняння 1-го порядку з відокремлюваними змінними.
- Однорідні диференціальні рівняння 1-го порядку.
- Лінійні диференціальні рівняння 1-го порядку.
- Рівняння Бернуллі.
- Диференціальні рівняння 1-го порядку в повних диференціалах.
- Інтегруючий множник.
- Метод послідовних наближень розв’язування диференціальних рівнянь.
- Теорема Пікара про існування та єдиність розв’язку задачі Коші для диференціальних рівнянь 1-го порядку.
- Обвідна однопараметричної сім’ї кривих.
- Особливі розв’язки диференціальних рівнянь 1-го порядку.
- Рівняння Клеро.
- Рівняння Лагранжа.
- Диференціальні рівняння 1-го порядку, як поля напрямів. Ізокліни.
- Ламані Ейлера.
- Ізогональні та ортогональні траєкторії.
- Диференціальні рівняння вищого порядку. Основні поняття.
- Найпростіші типи диференціальних рівнянь вищого порядку.
- Лінійні диференціальні рівняння вищого порядку. Основні поняття.
- Теорема про властивості частинних розв’язків лінійного однорідного диференціального рівняння вищого порядку.
- Критерій лінійної незалежності частинних розв’язків лінійного однорідного диференціального рівняння вищого порядку.
- Теорема про структуру загального розв’язку лінійного однорідного диференціального рівняння вищого порядку.
- Лінійні однорідні диференціальні рівняння 2-го порядку із сталими коефіцієнтами.
- Схема розв’язування лінійного однорідного диференціального рівняння п-го порядку із сталими коефіцієнтами.
- Структура загального розв’язку лінійного неоднорідного диференціального рівняння вищого порядку.
- Метод Лагранжа знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння 2-го порядку.
- Метод Лагранжа знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння п-го порядку.
- Метод невизначених коефіцієнтів знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння 2-го порядку із сталими коефіцієнтами.
- Метод невизначених коефіцієнтів знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння п-го порядку із сталими коефіцієнтами.
- Лінійні диференціальні рівняння і коливання.
- Нормальні системи диференціальних рівнянь. Метод виключення.
- Системи лінійних однорідних диференціальних рівнянь із сталими коефіцієнтами.
- Основні типи інтегральних рівнянь.
- Метод ітерації для інтегральних рівнянь Фредгольма 1-го та 2-го роду.
- Метод ітерації для інтегральних рівнянь Вольтера 1-го та 2-го роду.
- Метод ітерації для нелінійних інтегральних рівнянь.
- Розв’язування інтегральних рівнянь за допомогою квадратурних формул.
- Інтегральні рівняння з виродженим ядром. Теорема Фредгольма.
- Диференціальні та інтегральні рівняння і математичні моделі.
