О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А. Кизим, д-р екон. наук, проф. Харківського

Вид материала

Документы

Содержание ОПЕРАЦІЯ векторизацІЇ Матричний спосіб розв’язання систем лінійних рівнянь Х1 (вектор розв’язань) знаходиться як X1:=A1 РОЗВ’язання СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ЗА ДОПОМОГОЮ ФУНКЦІЇ LSOLVE(...) ПОШУК ВЛАСТИВИХ ВЕКТОРІВ та значень МАТРИЦЬ Питання для самоконтролю Практична робота № 3.1 Розрахунок обсягу перевезень. Визначення витрат матеріалів. Визначення потреби в ресурсах. Визначення потреби в матеріалах. Розрахунок необхідної кількості та вартості сировини. Практична робота № 3.2 Практична робота № 3.3 A невід’ємні, тобто A  0 А. Однією з умов продуктивності невід’ємної квадратної матриці A

Подобный материал:

• А. В. Ковалевська Рецензенти: доцент, канд екон наук, доцент Харківського національного, 739.76kb.
• А. А. Гвоздев руководительтемы; доктора техн наук, 3579.39kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Дипломных проектов по специальностям, 283.96kb.
• Конкурс-захист проходив на базі Харківського національного університету ім. В. Н. Каразіна,, 342.15kb.
• «Сторінки історії Харківського університету за архівними документами», 72.28kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Строительные нормы и правила бетонные и железобетонные конструкции, 3448.03kb.
• Надійності та безпеки в будівництві, 692.13kb.

ОПЕРАЦІЯ векторизацІЇ

Є ще одна цікава можливість: за допомогою операції векторизації здійснювати поелементні обчислення над матрицями (уводиться комбінацією клавіш Ctrl / – або кнопкою палітри векторів і матриць). При її використанні операції здійснюються над кожним елементом вектора незалежно, наприклад:



Або інший приклад:_.

Корені квадратного рівняння для трьох наборів вихідних даних:

5. МАТРИЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ

Для розв’язання систем лінійних рівнянь, як і для будь-яких інших, можна застосувати функції given … find( ) або given … minerr( ) (див. п. 2.4, 2.5), однак для них існують інші, більш зручні способи. Наведені вище матриця А та вектор В визначають таку систему лінійних рівнянь:

.

Можна розв’язати цю систему рівнянь матричним способом:

.

Розв’язання розглянутої вище задачі можна вивести ще й так:



Таким чином, для розв’язання системи лінійних рівнянь матричним способом необхідно представити цю систему в матричній формі, тобто виписати матрицю коефіцієнтів і вектор вільних членів рівняння. Наприклад, для системи рівнянь:




Матрична форма має вигляд А1X1 = C1, де:




Тоді Х1 (вектор розв’язань) знаходиться як X1:=A1^-1C1_{, .}

В Excel цю систему можна розв’язати, використовуючи функції для роботи з матрицями МУМНОЖ() і МОБР():


.

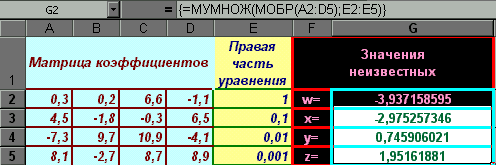6. РОЗВ’язання СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ЗА ДОПОМОГОЮ ФУНКЦІЇ LSOLVE(...)

У професіональних версіях MathCAD (MathCAD Professional) для розв’язання систем лінійних рівнянь можна використовувати вбудовану функцію lsolve(A,C) із категорії функцій Solving (не плутати з ключовим ідентифікатором solve!). Як її аргументи вказуються матриця коефіцієнтів рівнянь та вектор правої частини:

7. ПОШУК ВЛАСТИВИХ ВЕКТОРІВ та значень МАТРИЦЬ

Властивим вектором матриці називається такий вектор, що є розв’язком рівняння:

_, (1)

де  – скаляр, що називається властивим значенням матриці.

Для отримання властивих векторів х, що відповідають властивому значенню , необхідно розв’язати рівняння:

, (2)

яке отримуємо з (1) переносом х у ліву частину рівняння (Е – одинична матриця).

Властиві значення матриці А знаходяться як розв’язок рівняння

|A-E|=0, (3)

яке називається характеристичним рівнянням.

Таким чином, для розв’язання в MathCAD задачі пошуку властивих значень та відповідних їм властивих векторів матриці необхідно:

1. Розв’язати характеристичне рівняння det(A-E)=0 solve,  ;
   
2. Для кожного з отриманих значень  розв’язати рівняння . Для цього можуть бути використані:
   

• функція lsolve( ) та оператор символьної рівності:
  

• або блок given … find( ) та оператор символьної рівності:
  

…

• або ключове слово solve разом з оператором символьної рівності:
  

ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. Які види масивів існують у MathCAD?
   
2. Яка системна змінна визначає нижню границю індексації елементів масиву?
   
3. Опишіть способи створення масивів у MathCAD.
   
4. Як переглянути вміст масиву, визначеного через ранжируваний аргумент?
   
5. Як вибрати рядок із масиву?
   
6. Як вибрати стовпець із масиву?
   
7. Як розрахувати визначник (детермінант) матриці?
   
8. Як обчислити векторний і скалярний добутки векторів?
   
9. Які способи об’єднання двох масивів у один Ви знаєте?
   
10. Що таке операція векторизації, для чого вона застосовується?
    
11. Як сформувати одиничну матрицю?
    
12. Як визначити число елементів у векторі? Число рядків (стовпців) у матриці?
    
13. Які рівняння називаються матричними?
    
14. Як розв’язувати матричні рівняння? Назвіть способи розв’язання матричних рівнянь.
    

ПРАКТИЧНА РОБОТА № 3.1

1. Використовуючи команду Вставка / Матриця створіть матрицю Q розміром 4×4, заповніть її довільними значеннями. Розрахуйте для неї зворотну матрицю. Пересвідчіться, що розрахована матриця є зворотною: перемножте обидві матриці. Транспонуйте зворотну матрицю. Установіть для всіх цих матриць поріг експоненти рівним 5. Обчисліть визначник матриці.
   

Видаліть із матриці другий рядок (за допомогою кнопки палітри «Матриця»). Додайте стовпець після третього стовпця. Уставте ще два рядки в матрицю. Заповніть відсутні значення.

Виведіть перший стовпець матриці. Складіть другий і третій рядки матриці. Помножте останній стовпець матриці на її ж останній рядок.

2. Створіть матрицю розмірності 88 за правилом:
   

Q_i,j = 2*i-j.

Обчисліть:

а) суму всіх рядків;

б) суму всіх стовпців.

3. Побудуйте матрицю:
   

.

Обчисліть:

а) добуток елементів головної діагоналі;

б) повну суму всіх елементів.

4. Розрахунок випуску виробів. Два залізобетонні комбінати випускають вироби M, N, P вищої, першої та другої категорій якості. Кількість випущених кожним комбінатом виробів за кожною категорією якості характеризується такою таблицею:
   

Категорія якості	ЗБК-4			ЗБК-17
	M	N	P	M	N	P
Вища	150	240	320	280	300	450
Перша	100	130	175	120	150	170
Друга	25	15	20	30	20	18

Розрахувати загальний випуск виробів за зазначеними категоріями якості.

Вказівка. Визначити дві матриці ЗБК4 і ЗБК17, а потім складіть їх.

5. Розрахунок випуску виробів. Три підприємства випускають 4 види виробів.
   

Задана матриця випуску продукції:

1150	1250	1020	1 , 384
2030	3700	2700	1856
1500	990	1058	720

у комірках якої зазначений накопичений із початку року на кінець 1 кварталу обсяг випуску виробів k-го виду i-го підприємства. Знайти обсяг випуску виробів за 2 квартал на кожному підприємстві, якщо аналогічна матриця до кінця півріччя мала вигляд:

2370	1980	1790	1 . 880
3500	4736	4015	2750
2220	2112	2010	1830

6. Розрахунок обсягу перевезень. Три типи транспортних літаків розподілені між чотирма авіалініями. Задано матриці обсягу перевезень, де зазначені накопичені з початку року обсяги перевезень одним літаком i-го типу на k-ій авіалінії за станом на кінець травня й кінець серпня відповідно:
   

Травень:

15	10	20	5 . 0
20	25	10	17
35	50	30	45

Серпень:

97	54	75	200
83	102	49	79
71	210	150	180

Визначити обсяги перевезень, здійснених літаками кожного типу на кожній авіалінії за літній період.

7. Визначення витрат матеріалів. Відповідно до програми будівельно-монтажних робіт споруджується в галузі О₁ 10 об’єктів А та 15 об’єктів В; у галузі О₂ – 20 об’єктів С, у галузі О₃ – 10 об’єктів В та 100 об’єктів D. Відомі норми витрат будівельних матеріалів p і q (у відповідних одиницях виміру) на кожний тип об’єкта:
   

Тип об’єкта	p	q
A	2	15
B	10	20
C	10	100
D	5	50

Визначити витрати будівельних матеріалів p та q у кожній галузі.

Вказівка. Уведіть матриці вихідних даних по об’єктах Об’єкти та норми витрат матеріалу Норми.

8. Визначення потреби в ресурсах. При виготовленні деталей чотирьох видів m, n, p, q витрата матеріалів, робочої сили й електроенергії задається такою таблицею:
   

Ресурси	Деталь m	Деталь n	Деталь p	Деталь q
Матеріали	1	3	0,5	2
Робоча сила	1,5	2	3	1
Електроенергія	2	1	1	0,5

Обчисліть загальну потребу в матеріалах, робочій силі та електроенергії для виготовлення заданої кількості деталей кожного виду: m – 10 деталей, n – 2 деталі, p – 3 деталі, q – 4 деталі.

9. Розрахунок заробітної платні. Виконати розрахунок заробітної платні, що припадає на кожне замовлення при виготовленні різних деталей, якщо відомі такі дані.
   

а) витрати робочого часу в годинах на кожному робочому місці й на кожен виріб:

Виріб	Працівник 1	Працівник 2	Працівник 3	Працівник 4	Працівник 5
А	2	1	4	5	0
В	1	4	2	5	2
С	0	1	0	3	4

б) кількість виробів (у штуках) у кожному замовленні:

	А	В	С
Замовлення 1	0	4	2
Замовлення 2	0	2	4
Замовлення 3	5	1	0

в) годинна заробітна платня (у грош. од.) на кожному робочому місці:

1,25

1,50

1,40

1,40

1,25

10. Визначення потреби в матеріалах. Два цехи випускають трансформатори видів А, В та С. На один трансформатор виду А витрачається 5 кг трансформаторного заліза і 3 кг дроту, на трансформатор виду В – 3 кг заліза й 1,5 кг дроту, на трансформатор виду С – 3,2 кг заліза та 2 кг дроту. Відомий план випуску трансформаторів (відповідно А, В, С): для першого цеху – (100, 120, 150), для другого – (80, 50, 0). Визначити потребу в матеріалах за цехами та загальну потребу в матеріалах для виконання плану випуску.
    
11. Розрахунок необхідної кількості та вартості сировини. Підприємство випускає три види продукції, що характеризуються вектором-планом (10, 7, 4). При випуску продукції використовують п’ять видів сировини. Задана матриця витрат сировини:
    

5	10	3	9	. 2
4	8	5	6	8
6	12	4	3	10

Вектор (7, 4, 5, 10, 2) задає вартість однієї одиниці кожного виду сировини.


Визначити:

а) необхідну кількість одиниць сировини кожного виду для забезпечення плану;

б) вартість сировини для одиниці кожного виду продукції;

в) загальну вартість сировини при виконанні плану випуску.

12. **Оцінка виконання плану за асортиментом. Дані показники планового та фактичного випуску в січні виробів 6 найменувань:
    

		План		Факт
A		4000		4160
B		2200		2000
C		2000		2060
D		1500		1485
E		1000		1090
F		400		420

Оцініть виконання плану за асортиментом трьома способами: за найменшим відсотком; за питомою вагою номенклатур, за якими виконаний план; за середнім відсотком.

Вказівка. Способи оцінки виконання плану за асортиментом.

Перший спосіб (найменшого відсотка): для кожного виду продукції знаходиться відсоток виконання плану, а потім визначається min.

Другий спосіб – підраховується кількість видів продукції, за якими виконаний план, і визначається їх питома вага в загальній кількості виробів, що випускаються .

Третій спосіб (середнього відсотка): для кожного виду продукції визначається величина фактичного випуску продукції в межах плану (продукція понадпланова не враховується). Для кожного виду продукції обчислюється відсоток як частка розрахованої величини до планової кількості, а потім – середній відсоток за всіма виробами.

13. **Оцінка ритмічності виробництва. На додаток до умови попередньої задачі (п. 12) дані показники планового й фактичного випуску продукції в лютому та березні: у лютому – план 11620, факт 11260, у березні – план 11600, факт 11540. Визначити ритмічність виробництва продукції за місяцями.
    

Вказівка. Коефіцієнт ритмічності розраховується як частка загального фактичного випуску продукції в межах плану до загального плану випуску продукції.

ПРАКТИЧНА РОБОТА № 3.2

Розв’яжіть наведені задачі.

1. Із деякого листового матеріалу необхідно викроїти 200 заготовок типу А, 260 – типу В та 290 – типу С. При цьому можна застосовувати три способи розкрою. Кількість заготовок, отримуваних з кожного листа при кожному способі розкрою, зазначено в таблиці.
   

Тип заготовки	Спосіб розкрою
	1-й	2-й	3-й
А	3	2	1
В	1	6	2
С	4	1	5

Визначити, скільки листів повинно бути розкроєно першим, другим і третім способами

1. Запишемо в математичній формі умови виконання завдання: позначимо через x₁, x₂, x₃ кількість листів матеріалу, що розкроюються відповідно першим, другим і третім способами. Тоді при першому способі розкрою x₁ листів буде отримано 3x₁ заготовок типу А, при другому – 2x₂, при третьому – x₃. Для повного виконання завдання по заготовках типу А сума 3x₁ +2x₂ + x₃ повинна дорівнювати 200, тобто:
   

3x₁ + 2x₂ + x₃ = 200.

Аналогічно одержуємо рівняння: x₁ + 6x₂ + 2x₃ = 260,

4x₁ + x₂ + 5x₃ = 290,

яким повинні задовольняти невідомі для того, щоб виконати завдання по заготовках В і С.

Отримана система лінійних рівнянь виражає в математичній формі умови виконання всього завдання по заготовках А, В, С.

2. Для розв’язання даної системи лінійних рівнянь у MathCAD найкраще використовувати матричний метод. Для цього сформуємо матрицю системи:
   

Тепер можна розв’язати систему матричним способом:



або викликати функцію lsolve( ):



або скористатися блоком given … find( ), записавши систему рівнянь:



або вставити з панелі Символіка ідентифікатор solve:

3. Для розв’язання цієї ж задачі в Excel варто скористатися матричними функціями МЗВОР і МПОМНОЖ:
   

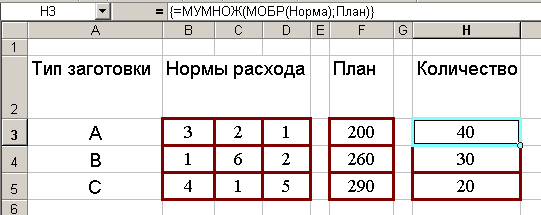
Зверніть увагу, що діапазонам В3:D5 і F3:F5 присвоєні імена Норма й План відповідно.

4. Однак можна використовувати й інші, не такі традиційні, методи розв’язання. Наприклад, розв’яжемо систему рівнянь, використовуючи Пошук розв’язку Excel:
   

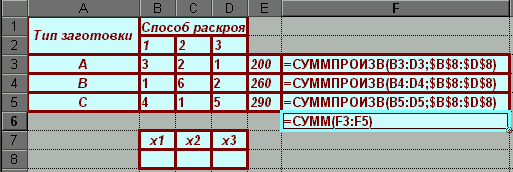
Скористаємося сервісом Пошук розв’язку:





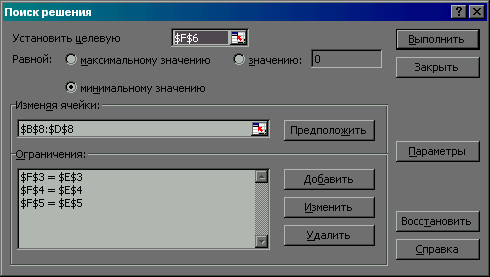
У результаті одержимо:

5. Розв’яжемо цю ж систему рівнянь, використовуючи можливості символьних обчислень MathCAD.
   

Застосуємо для розв’язання нашої задачі символ «Дозволити змінні» з панелі інструментів Символіка. Цей символ (або ідентифікатор) називається solve.

Щоб розв’язати систему рівнянь щодо 3-х невідомих:

• натисніть кнопку Створити матрицю:
  

на Панелі інструментів Матриці, щоб уставити вектор, що складається із 3-х рядків і одного стовпця;

• заповніть позиції вектора рівняннями, що складають систему (використовуйте жирний знак рівності або Ctrl =);
  
• натисніть кнопку Дозволити змінні:
  

на Панелі інструментів Символіка. Позицію після solve заповніть вектором, що складається з позначень невідомих.

У результаті одержимо:





Перевірте правильність розв’язку.

2. Припустимо, що функція, яка характеризує валовий прибуток підприємства, має вигляд: де – валовий прибуток, – випуск продукції за період t. Спостереження охоплюють два періоди, для яких значення , наведені в таблиці:
   

Період t
1	10	100
2	20	150

1. Скласти систему рівнянь для визначення , , і розв’язати її.
   
2. Визначити всю сукупність функцій валового прибутку, що задовольняють даній системі рівнянь.
   

Розв’язання.

Оскільки спостереження охоплюють два періоди, то ми маємо систему з двох лінійних рівнянь, а кількість шуканих змінних – 3.

Сформуємо ці рівняння, використовуючи знак символьної рівності  (або Ctrl +). Для цього запишемо функцію валового прибутку у вигляді:



де за даними таблиці:



Таким чином, одержуємо систему рівнянь:



Система сумісна і має незліченну множину розв’язків. Виберемо одну змінну як вільну. Нехай це буде змінна с. Змінні a, b – базисні. Виразимо базисні змінні через вільну змінну:



(тобто: , )


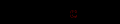і


Тоді вся сукупність валового прибутку:



або

3. Застосування властивих векторів при розв’язанні економічних задач. Модель лінійного обміну (модель міжнародної торгівлі).
   

Структурна матриця торгівлі трьох країн S₁, S₂, S₃ має вигляд:



Знайти співвідношення національних доходів країн для збалансованої торгівлі.

Розв’язання.

Розглянемо теоретичну модель міжнародної торгівлі.

Нехай є n країн S₁, S₂,…, S_n, національний доход кожної з яких дорівнює відповідно x₁, x₂,…, x_n. Позначимо коефіцієнтами a_ij частину національного доходу, яку країна S_j витрачає на закупівлю товарів у країни S_i. Будемо вважати, що весь національний доход витрачається або на закупівлю товарів усередині країни, або на імпорт з інших країн, тобто:



Розглянемо матрицю:



яка одержала назву структурної матриці торгівлі.

З урахуванням попередньої рівності, сума елементів будь-якого стовпця матриці дорівнює одиниці.

Для будь-якої країни виторг від внутрішньої та зовнішньої торгівлі становитиме:



Для збалансованої торгівлі необхідна бездефіцитність торгівлі кожної країни , тобто виторг від торгівлі кожної країни повинен бути не меншим за її національний доход:



Якщо вважати, що , то одержимо систему нерівностей.

Склавши ліві й праві частини нерівностей, після групування запишемо:



З огляду на те, що вирази в дужках дорівнюють одиниці, приходимо до суперечливої нерівності:



Таким чином, нерівність неможлива, й умова набуває вигляду: , (з економічних міркувань це зрозуміло, тому що всі країни не можуть одночасно отримувати прибуток).

Уводячи вектор національних доходів країн, отримуємо рівняння:

,

тобто задача звелася до пошуку властивого вектора матриці А, що відповідає властивому значенню .


Відповідно до вищевикладеної теорії властивим значенням заданої матриці А є .

Перевіримо, чи задовольняє характеристичному рівнянню

^{det(A–E) = 0, де}

Знаходимо властивий вектор 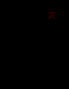, що відповідає властивому значенню , розв’язуючи систему:








або іншим способом:


^,


знаходимо, що x = C, y = 2C, z = 1,5C.

Отриманий результат означає, що для збалансованої торгівлі співвідношення національних доходів повинно бути 1:2:1,5 або 2:4:3.

ПРАКТИЧНА РОБОТА № 3.3

Міжгалузевий баланс суспільного продукту (МГБ).

1. Позначення й теоретичні положення:

x – матриця міжгалузевих потоків, де x_ij (i, j = 1,…,n) – обсяг продукції i-ої галузі, що надходить на виробничі потреби j-ої галузі;

n – загальне число галузей матеріального виробництва;

Y_i – обсяг кінцевої продукції i-ої галузі;

X_i – обсяг валової продукції i-ої галузі, що визначається як сума кінцевої та проміжної продукції:

(1)

Основним елементом математичної моделі міжгалузевого балансу «витрати-випуск» є квадратна матриця технологічних коефіцієнтів А=(a_ij). Числа a_ij показують, скільки продукції i-ої галузі необхідно затратити для виробництва одиниці продукції j-ої галузі безпосередньо у виробничому циклі j-ої галузі. Тому матрицю А називають матрицею прямих витрат.

Записана в матричній формі система балансів є системою лінійних рівнянь:

X = AX + Y (2)

Ця модель міжгалузевого балансу (модель Леонтьєва) пов’язує обсяги валових випусків з обсягами кінцевої продукції й може бути використана для згідного розрахунку цих розмірів.


Якщо розміри X_i, Y_i та x_ij виміряні в натуральних одиницях, то говорять про моделі міжгалузевого балансу в натуральному вираженні, якщо у вартісному, то про модель у вартісному вираженні. Позначимо через р=(p₁, p₂,…,p_n) набір цін на продукцію відповідних галузей, а зірочкою * – виміри, зроблені по вартості. Тоді зв’язок між показниками моделей у вартісному й натуральному вираженні:

X_j^* = p_j X_j x_ij^* = p_i x_ij Y_i^* = p_i Y_i. (3)

Отже,

a_ij^* = x_ij^* / X_j^* = (p_i / p_j) a_ij. (4)


Для того щоб за даним вектором кінцевого випуску Y знайти вектор валового випуску X, необхідно розв’язати систему рівнянь:

X – AX = Y. (5)

З економічних міркувань усі коефіцієнти матриці прямих затрат A невід’ємні, тобто A  0. Невід’ємні також компоненти заданого вектора Y  0. Розв’язок X, що має бути знайденим, за змістом також повинен мати невід’ємні компоненти, тобто потрібний X  0.

Якщо існують два такі вектори Y > 0 та X  0, що X – AX = Y, то матрицю A називають продуктивною. Продуктивність матриці означає, що виробнича система здатна забезпечити деякий позитивний кінцевий випуск за всіма продуктами. Цей випуск у випадку продуктивності матриці А може бути знайдений як розв’язок системи (5):

X = (E – A)^-1Y. (6)

Матриця (Е – A) –¹ називається матрицею повних витрат.

Існує декілька критеріїв продуктивності матриці А. Однією з умов продуктивності невід’ємної квадратної матриці A є невід’ємність матриці повних витрат, тобто виконання умови (Е – A) ^–1  0.

Крім цього, продуктивність матриці можна визначити, знайшовши всі її властиві значення, які у випадку продуктивності матриці повинні бути за модулем меншими за одиницю.

Можна скористатися й таким критерієм: матриця А продуктивна, якщо максимум сум елементів її стовпців не перевищує одиниці (причому хоча б для одного стовпця сума його елементів строго менша за одиницю).

1. Умова задачі.
   

Дані: матриця міжгалузевих зв’язків x у натуральному вираженні; вектор р цін продукції галузей і вектор кінцевої продукції Y.

Необхідно:

• визначити, чи є матриця коефіцієнтів прямих затрат A в натуральному вираженні продуктивною, і зробити висновок про можливості випуску продукції;
  
• перейти від натуральної форми моделі до вартісної й визначити, чи є вартісна матриця коефіцієнтів прямих витрат продуктивною;
  
• у випадку продуктивності розрахувати валовий обсяг випуску.
  

Послідовність обчислень та аналізу результатів:

1. За заданою матрицею міжгалузевих зв’язків та вектором кінцевої продукції розрахувати валовий випуск (формула 1).
   
2. За заданим вектором цін та векторами кінцевої й валової продукції розрахувати матрицю міжгалузевих зв’язків у вартісному вираженні, а також вартісні вектори кінцевої продукції й валового випуску (формули 3).
   
3. Розрахувати матрицю прямих витрат у натуральному й вартісному вираженнях (формули 4).
   
4. Розрахувати матрицю повних витрат у вартісному й натуральному вираженнях і зробити висновок про продуктивність або непродуктивність матриці A.
   
5. У випадку продуктивності матриць розв’язати систему рівнянь (5), розрахувавши обсяг валової продукції (6).