Зміст навчальної програми з вищої математики для студентів 1 курсу фармацевтичного факультету за спеціальністю " фармація"(освітньо-кваліфікаційний рівень -бакалавр, заочна форма навчання)
| Вид материала | Документы |
- Тематичний план лекцій з фармакогнозії для студентів III курсу фармацевтичного факультету, 200.56kb.
- Основна мета викладання фізичних методів аналізу та метрології для студентiв II курсу, 17.72kb.
- Білетна програма іспиту з інформаційних технологій у фармації для студентів за спеціальністю, 49.83kb.
- Київский національний університет імені тараса шевченка юридичний факультет, 427.74kb.
- Зміст навчальної програми з фармацевтичної хімії факультету №4 бакалаврів з відділенням, 57.92kb.
- Тематичний план занять «Патофізіологія ендокринної та нервової систем» Для студентів, 1055.52kb.
- Програма вступного випробування з математики для вступників на освітньо-кваліфікаційний, 102.33kb.
- Програма вступного випробування з математики для вступників на освітньо-кваліфікаційний, 85.8kb.
- Тематичний план лекцій з менеджменту та маркетингу у фармації для студентів ІV курсу, 162.83kb.
- Програма вступного іспиту на базі освітньо-професійної програми підготовки молодшого, 104.91kb.
Зміст навчальної програми з вищої математики для студентів 1 курсу фармацевтичного факультету
за спеціальністю “ фармація”(освітньо-кваліфікаційний рівень -бакалавр, заочна форма навчання)
Загальні відомості про функції. Поняття про множину. Числові множини. Поняття про функцію. Функція однієї змінної. Границя функцій. Нескінченно малі та нескінченно великі. Основні теореми про границі. Неперервність функцій.
Елементи диференціального числення. Похідна функції, її фізичний і геометричний зміст. Основні правила диференціювання. Похідні елементарних функцій. Правило диференціювання складної функції. Похідні вищих порядків. Застосування похідних для дослідження функцій: зростання і спадання функцій на інтервалі, екстремуми функцій, опуклість та вгнутість графіка функцій, точки перегину, асимптоти кривої. Дослідження функцій і побудова графіків. Диференціал функції. Диференціали вищих порядків. Застосування диференціала для лінійної апроксимації функції в околі точки.
Функції багатьох змінних. Частинні похідні і частинні диференціали функцій багатьох змінних. Повний диференціал. Застосування диференціалу функцій для обчислення похибок.
Елементи інтегрального числення. Первісна. Невизначений інтеграл. Властивості невизначених інтегралів. Таблиця основних інтегралів. Методи інтегрування: безпосереднє, методом заміни змінної або підстановки, інтегрування частинами.
Визначений інтеграл. Властивості визначеного інтеграла. Формула Ньютона-Лейбніца. Невласні інтеграли. Деякі фізичні, біофізичні та геометричні застосування визначеного інтеграла. Теорема про середнє значення. Наближення обчислення визначених інтегралів.
Диференціальне рівняння. Поняття про диференціальні рівняння. Рівняння з відокремленими змінними. Рівняння з відокремлюваними змінними. Лінійні диференціальні рівняння першого порядку. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами.
Прикладні задачі фармації, біології та медицини. Моделювання процесів лінійним однорідним диференціальним рівнянням першого порядку. Теорія епідемій. Фармакокінетичні моделі: однокамерна лінійна фармакокінетична модель; однокамерна лінійна фармакокінетична модель із всмоктуванням; однокамерна лінійна модель з крапельницею.
Основи теорії імовірностей. Частота та імовірність події. Сумісні та несумісні події. Теореми додавання імовірностей. Залежні та незалежні події. Умовна імовірність. Теорема множення імовірностей. Протилежні події. Формула повної імовірності. Формула Байєса. Повторні випробування. Формула Бернуллі.
Випадкова величина. Дискретні та неперервні випадкові величини. Інтегральна та диференціальна функції розподілу. Основні числові характеристики розподілу випадкових величин: математичне сподівання, дисперсія, середнє квадратичне відхилення. Квантилі. Медіана. Мода. Основні закони розподілу дискретних випадкових величин: біномний розподіл, розподіл Пуассона. Основні закони розподілу неперервних випадкових величин: рівномірний розподіл, експоненціальний розподіл, нормальний закон розподілу (закон Гауса). Імовірність попадання значень нормально розподіленої випадкової величини в заданий інтервал. Функція Лапласа. Інші розподіли випадкових величин: розподіл „
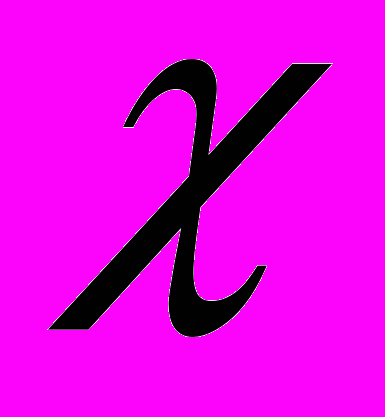і - квадрат”, розподіл Стьюдента, розподіл Фішера-Снедекора. Центральна гранична теорема (теорема Ляпунова). Локальна та інтегральна теореми Лапласа. Формула Муавра-Лапласа. Закон великих чисел Чебишова.Вибірковий метод. Знаходження характеристик розподілу. Предмет математичної статистики. Генеральна та вибіркова сукупності. Оцінка параметрів генеральної сукупності за її вибіркою. Генеральна та вибіркова дисперсії. Стандарт. Точність та надійність оцінки. Довірчий інтервал.
Статистична перевірка гіпотез. Статистична гіпотеза та статистичний критерій. Критична область. перевірка вибірки та однорідність. Порівняння дисперсій нормально розподілених величин. порівняння виправленої вибіркової дисперсії з гіпотетичною генеральною дисперсією нормальної сукупності. Порівняння вибіркових середніх двох нормально розподілених сукупностей, дисперсії яких невідомі. Перевірка гіпотези про нормальний розподіл генеральної сукупності. критерій згоди Персона.
Елементи теорії кореляції. Статистична та кореляційна залежності. Кореляційна таблиця. Рівняння прямих регресій. Коефіцієнт лінійної кореляції. Перевірка значущості вибіркового коефіцієнта кореляції. Метод найменших квадратів.
Дисперсійний аналіз. Однофакторний дисперсійний аналіз. Загальна, факторна та залишкова дисперсії. Оцінка впливу факторної ознаки. Двохфакторний дисперсійний аналіз.
Ряди динаміки. Класифікація часових рядів. Показники порівняння рівнів часового ряду. Вирівнювання часового ряду способом усереднення. Експоненціальне вирівнювання. Моделювання тренду. Прогнозування часових рядів.