Програма вступного випробування з математики для вступників на освітньо-кваліфікаційний рівень бакалавр полтава 2012

Вид материала

Документы

Содержание Пояснювальна записка Зміст програми Вимоги до рівня сформованості знань, умінь і навичок Критерії оцінювання знань і вмінь Рекомендована література

Подобный материал:

• Програма вступного випробування з математики для вступників на освітньо-кваліфікаційний, 85.8kb.
• Програма вступного випробування з соціальної педагогіки для вступників на освітньо-кваліфікаційний, 3535.82kb.
• Програма вступного випробування з соціальної педагогіки для вступників на освітньо-кваліфікаційний, 2907.34kb.
• Програма вступного випробування з хімії Галузь знань: 0401 Природничі науки, 252.73kb.
• Програма Вступного випробування з біології Галузь знань: 0401 Природничі науки, 410.48kb.
• Програма вступного випробування з історії України для вступників на освітньо-кваліфікаційний, 570.76kb.
• Програма вступного випробування з математики та інформатики для вступників на навчання, 237.73kb.
• Програма вступного випробування з математики для вступу на навчання для здобуття освітньо-кваліфікаційного, 107.58kb.
• Програма фахового вступного випробування на здобуття освітньо-кваліфікаційного рівня, 471.07kb.
• Програма вступного випробування з російської мови для вступників на освітньо-кваліфікаційний, 105.02kb.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ

імені В.Г. КОРОЛЕНКА


ЗАТВЕРДЖУЮ


Голова приймальної комісії

ПНПУ імені В.Г.Короленка

__________ проф. М.І. Степаненко

23 лютого 2012 р.


ПРОГРАМА

ВСТУПНОГО ВИПРОБУВАННЯ З МАТЕМАТИКИ

ДЛЯ ВСТУПНИКІВ НА ОСВІТНЬО-КВАЛІФІКАЦІЙНИЙ РІВЕНЬ БАКАЛАВР


Полтава – 2012

Програма вступного випробування з математики для вступників на освітньо-кваліфікаційний рівень бакалавр / Укладачі: Т.М. Барболіна, О.П. Губачов, В.О.Марченко.


Рецензенти: Мельниченко О.С., кандидат фіз.-мат. наук, професор кафедри математичного аналізу та інформатики ПНПУ імені В.Г. Короленка;

Флегантов О.О., кандидат. фіз.-мат. наук, доцент кафедри вищої математики Полтавської державної аграрної академії.


Затверджено на засіданні кафедри математичного аналізу та інформатики.

Протокол № 12 від 21 лютого 2012 року

ПОЯСНЮВАЛЬНА ЗАПИСКА


Програма вступного випробування з математики для вступників до бакалаврату складена на основі діючої програми для загальноосвітньої школи. Вона містить основні поняття і факти, знання, уміння і навички, якими повинен володіти випускник, щоб успішно навчатися за програмами підготовки бакалаврів у ВНЗ.

Випробування проводиться у вигляді тестування.

На випробуванні з математики до вищого навчального закладу вступник повинен виявити:

а) чітке знання означень, математичних понять, термінів, формулювань правил, ознак теорем, передбачених програмою, уміння доводити їх;

б) уміння точно і стисло висловити математичну думку в усній і письмовій формі, використовуючи відповідну символіку;

в) упевнене володіння практичними математичними уміннями і навичками, передбаченими програмою, вміння застосовувати їх у процесі розв'язування задач і вправ.

ЗМІСТ ПРОГРАМИ


Арифметика, алгебра і початки аналізу

1. Натуральні числа і нуль. Читання і запис натуральних чисел. Порівняння натуральних чисел. Додавання, віднімання, множення та ділення натуральних чисел.
   
2. Подільність натуральних чисел. Дільники і кратні натурального числа. Парні і непарні числа. Ознаки подільності на 2, 5, 3, 9, 10. Ділення з остачею.
   
3. Звичайні дроби. Порівняння звичайних дробів. Перетворення звичайного дробу у десятковий та нескінченного періодичного десяткового дробу — у звичайний.
   
4. Відношення та пропорції. Відсотки. Основні задачі на відсотки.
   
5. Степінь із натуральним і раціональним показником. Арифметичний корінь та його властивості.
   
6. Логарифми та їхні властивості. Основна логарифмічна тотожність.
   
7. Одночлен і многочлен. Дії над ними. Формули скороченого множення.
   
8. Многочлен з однією змінною. Корінь многочлена (на прикладі квадратного тричлена).
   
9. Поняття функції. Способи задання функції. Область визначення, область значень функції. Функція, обернена до даної.
   
10. Графік функції. Зростання і спадання функції, періодичність, парність, непарність функції.
    
11. Достатня умова зростання (спадання) функції на проміжку. Поняття екстремуму функції. Необхідна умова екстремуму функції. Найбільше і найменше значення функції на проміжку.
    
12. Означення й основні властивості функцій: лінійної y=kx+b, квадратичної у=ах²+bх+c, степеневої y=xⁿ 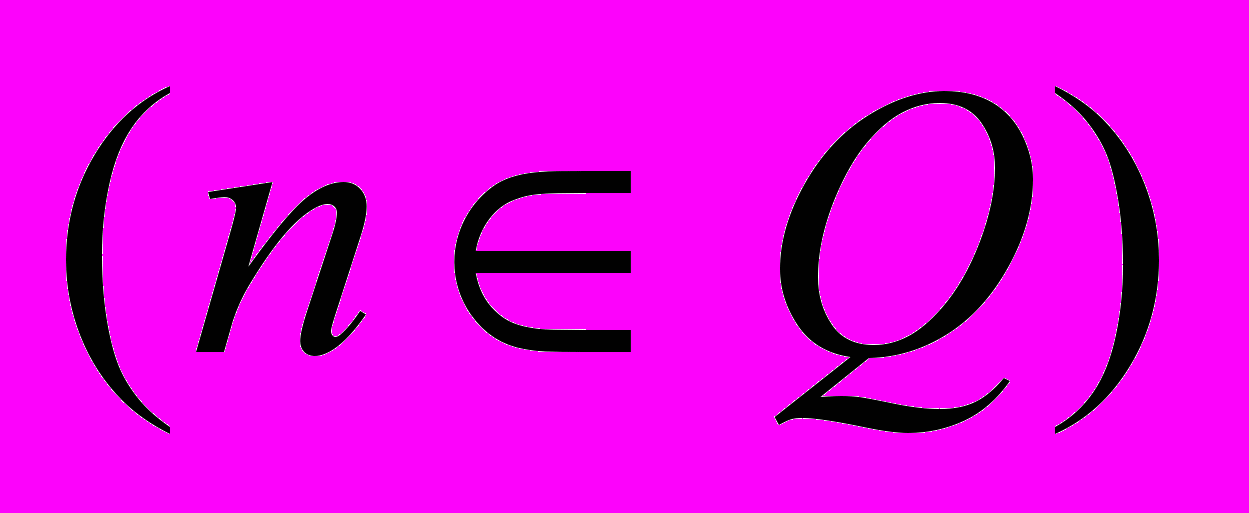, показникової у=а^x, а>0, а0 логарифмічної y=log _a x, а>0, а0 тригонометричних функцій (y=sinx, y=cosx, y=tgx).
    
13. Рівняння. Розв'язування рівнянь, корені рівняння. Рівносильні рівняння. Графік рівняння з двома змінними.
    
14. Нерівності. Розв'язування нерівностей. Рівносильні нерівності.
    
15. Системи рівнянь і системи нерівностей. Розв'язування систем. Розв’язок системи. Рівносильні системи рівнянь.
    
16. Арифметична та геометрична прогресії. Формули n-го члена і суми n перших членів прогресій. Нескінченна геометрична прогресія зі знаменником |q| <1 та її сума.
    
17. Тригонометричні функції подвійного аргументу.
    
18. Перетворення в добуток сум sina ± sinb та cosa ± cosb.
    
19. Означення похідної, її фізичний та геометричний зміст.
    
20. Похідні суми, добутку, частки та функцій у=kх+b, y=sinx; y=cosx; y=tgx; у=хⁿ, де n – натуральне число.
    

Геометрія

1. Пряма, промінь, відрізок, ламана, довжина відрізка. Кут, величина кута. Вертикальні та суміжні кути. Паралельні прямі. Рівність і подібність геометричних фігур. Відношення площ подібних фігур.
   
2. Приклади перетворення геометричних фігур, види симетрії.
   
3. Вектори. Операції над векторами.
   
4. Прямокутна система координат на площині та в просторі. Формула для обчислення відстані між двома точками та формула для обчислення координат середини відрізка.
   
5. Многокутник. Вершини, сторони, діагоналі многокутника. Правильний многокутник та його властивості.
   
6. Трикутник. Медіана, бісектриса, висота трикутника, їх властивості. Види трикутників. Співвідношення між сторонами та кутами прямокутного трикутника. Теорема синусів, теорема косинусів.
   
7. Паралелограм, прямокутник, ромб, квадрат, трапеція; їх основні властивості.
   
8. Коло і круг та їх елементи. Центр, діаметр, радіус, хорди, січні кола. Дотична до кола.
   
9. Центральні і вписані кути; їх властивості.
   
10. Формули площ геометричних фігур: трикутника, прямокутника, паралелограма, квадрата, ромба, трапеції.
    
11. Довжина кола і довжина дуги кола. Радіанна міра кута. Площа круга і площа сектора.
    
12. Площина. Паралельні площини і площини, що перетинаються.
    
13. Паралельність прямої і площини.
    
14. Куг прямої з площиною. Перпендикуляр до площини.
    
15. Двогранні кути. Лінійний кут двогранного кута. Перпендикулярність двох площин.
    
16. Многогранники. Вершини, ребра, грані, діагоналі многогранника. Пряма і похила призми. Піраміда. Правильна призма і правильна піраміда. Паралелепіпеди, їх види.
    
17. Тіла обертання: циліндр, конус, сфера, куля. Центр, діаметр, радіус сфери і кулі. Площина, дотична до сфери.
    
18. Формули площі поверхні й об'єму призми, піраміди, циліндра, конуса.
    
19. Формули площі сфери, об'єму кулі.
    

ВИМОГИ ДО РІВНЯ СФОРМОВАНОСТІ ЗНАНЬ, УМІНЬ І НАВИЧОК


Вступник повинен знати:

• властивості і графік функції у=ах+b;
  
• властивості і графік функції у=к/х;
  
• властивості і графік функції у=ах²+bх+с;
  
• формулу коренів квадратного рівняння;
  
• властивості числових нерівностей;
  
• формули логарифма добутку, степеня, частки;
  
• означення, властивості і графіки функцій y=sinx, y=cosx, y=tgx;
  
• формули коренів рівнянь sinx=a, cosx=a, tgx=a;
  
• формули залежності між тригонометричними функціями одного й того ж apryмента;
  
• формули тригонометричних функцій подвійного аргументу;
  
• формули похідних суми, добутку і частки двох функції, степеневої функції;
  
• формули похідних тригонометричних функцій, показникової і логарифмічної функції;
  
• рівняння дотичної до графіка функції;
  
• властивості рівнобедреного трикутника;
  
• властивості точок, рівновіддалених від кінців відрізка;
  
• ознаки паралельності прямих;
  
• ознаки паралелограма;
  
• основні твердження про коло, описане навколо трикутника;
  
• основні твердження про коло, вписане в трикутник;
  
• означення і властивості дотичної до кола;
  
• ознаки рівності, подібності трикутників;
  
• теорему Піфагора;
  
• формули площ паралелограма, трикутника, трапеції;
  
• формули відстані між двома точками площини; рівняння кола;
  
• ознаки паралельності прямої і площини, площин;
  
• теореми про перпендикулярність прямої і площини, двох площин;
  

Вступник повинен уміти:

• будувати математичні моделі реальних об’єктів, процесів і явищ та досліджувати ці моделі засобами математики;
  
• виконувати арифметичні дії з натуральними числами, десятковими і звичайними дробами;
  
• виконувати тотожні перетворення многочленів, алгебраїчних дробів, виразів, що містять степеневі, показникові, логарифмічні і тригонометричні функції;
  
• розкладати квадратний тричлен на лінійні множники;
  
• будувати і читати графіки лінійної, квадратичної, степеневої, показникової, логарифмічної та тригонометричних функцій;
  
• розв'язувати рівняння і нерівності першого і другого степеня, а також рівняння і нерівності, що зводяться до них; розв'язувати системи рівнянь та нерівностей першого і другого степеня і ті, що зводяться до них.
  
• розв’язувати найпростіші рівняння і нерівності, що мають степеневі, показникові, логарифмічні і тригонометричні функції;
  
• розв'язувати задачі за допомогою рівнянь і систем рівнянь;
  
• зображати геометричні фігури на площині і виконувати найпростіші побудови на площині;
  
• знаходити кількісні характеристики геометричних фігур (довжини, величини кутів, площі, об’єми);
  
• застосовувати похідну у процесі дослідження функцій на зростання (спадання), на екстремуми і для побудови графіків функцій.
  

КРИТЕРІЇ ОЦІНЮВАННЯ ЗНАНЬ І ВМІНЬ

Тест для вступного випробування складається із 15 тестових завдань, за розв’язання яких абітурієнт може отримати щонайбільше 200 балів. Перші 10 завдань оцінюються десятьма балами кожне, а завдання 11-15 – двадцятьма балами кожне.


Програма складена на основі програми з математики для загальноосвітньої школи, надрукованої у збірнику:

Збірник програм з математики для допрофільного навчання та профільної підготовки / Упор. Прокопенко Н.С., Єригіна О.В., Вашуленко О.П. — Харків: Ранок, 2011.


РЕКОМЕНДОВАНА ЛІТЕРАТУРА

1. Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика : підручник для 5 класу. — Х. :Гімназія, 2005.
   
2. Бевз Г.П., Бевз В.Г. Математика : підручник для 5 класу. — К. : Зодіак-ЕКО, 2005.
   
3. Кравчук В.Р., Янченко Г.М. Математика : підручник для 5 класу. — Тернопіль : Підручники і посібники, 2005.
   
4. Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика : підручник для 6 класу. — Х. : Гімназія, 2006.
   
5. Бевз Г.П., Бевз В.Г. Математика : підручник для 6 класу. — К. : Генеза, 2006.
   
6. Янченко Г.М., Кравчук В.Р. Математика : підручник для 6 класу. —Тернопіль : Підручники і посібники, 2006.
   
7. Бевз Г.П., Бевз В.Г. Алгебра : підручник для 7 класу. — К. : Зодіак-ЕКО, 2007.
   
8. Кравчук В.Р., Янченко Г.М. Алгебра : підручник для 7 класу. — Тернопіль : Підручники і посібники, 2007.
   
9. Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра : підручник для 7 класу. — Х. : Гімназія, 2007.
   
10. Бурда М.І., Тарасенкова Н.А. Геометрія : підручник для 7 класу. — К. : Зодіак-ЕКО, 2007.
    
11. Мерзляк А.Г.,Полонський В.Б., Якір М.С. Геометрія : підручник для 7 класу. — Х. : Гімназія, 2007.
    
12. Апостолова Г.В. Геометрія : підручник для 7 класу. К. : Генеза, 2008.
    
13. Мерзляк А.Г.,Полонський В.Б., Якір М.С. Алгебра : підручник для 8 класу. — Х. : Гімназія, 2008.
    
14. Бевз Г.П., Бевз В.Г. Алгебра : підручник для 8 класу. — К. : Зодіак-ЕКО, 2008.
    
15. Бурда М.І., Тарасенкова Н.А. Геометрія : підручник для 8 класу. — К. : Зодіак-ЕКО, 2008.
    
16. Єршова А.П., Голобородько В.В., Крижанівський О.Ф. Геометрія : підручник для 8 класу. — К. :АН ГРО ПЛЮС, 2008.
    
17. Апостолова Г.В. Геометрія : підручник для 8 класу. К. : Генеза, 2008
    
18. Мерзляк А.Г., Полонський В.Б., Якір М.С. Геометрія : підручник для 8 класу. — Х. : Гімназія, 2008
    
19. Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра : підручник для 9 класу. — Х. : Гімназія, 2009.
    
20. Кравчук В.Р., Підручна М.В., Янченко Г.М. Алгебра : підручник для 9 класу. — Тернопіль : Підручники і посібники, 2009.
    
21. Бевз Г.П., Бевз В.Г. Алгебра : підручник для 9 класу. — К. :Зодіак – ЕКО, 2009.
    
22. Мерзляк А.Г., Полонський В.Б., Якір М.С. Геометрія : підручник для 9 класу. — Х. : Гімназія, 2009.
    
23. Єршова А.П., Голобородько В.В., Крижанівський О.Ф., Єршов С.В. Геометрія : підручник для 9 класу. — Х. : Ранок, 2009.
    
24. Апостолова Г.В. Геометрія : підручник для 9 класу. К. : Генеза, 2009.
    
25. Бурда М.І., Тарасенкова Н.А. Геометрія : підручник для 9 класу. — К. : Зодіак – ЕКО, 2009.
    
26. Нелін Є.П. Алгебра і початки аналізу : підруч. для 10 кл. загальноосвіт. навчальн. закладів : академ. рівень . — Х. : Гімназія 2010.
    
27. Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С. Алгебра і початки аналізу : підруч. для 10 кл. загальноосвіт. навчальн. закладів : академ. рівень. — Х. : Гімназія, 2010.
    
28. Нелін Є.П Алгебра і початки аналізу підруч. для 10 кл. загальноосвіт. навчальн. закладів : профільн. рівень. — Х. : Гімназія, 2010.
    
29. Єршова А.П.,Голобородько В.В., Крижановський О.Ф., Єршов С.В. Геометрія : підруч. для 10 кл. загальноосвіт. навчальн. закладів : академ рівень, профільн. рівень. — Х. : Ранок, 2010.
    
30. Нелін Є.П. Геометрія. Дворівневий підручник для 10 класу : академічний та профільний рівні. — Х. : Гімназія, 2010.
    
31. Бурда М.І., Тарасенкова Н.А. Геометрія підруч. для 10 кл. загальноосвіт. навчальн. закладів : академ. рівень . — К. : Зодіак-ЕКО, 2010.
    
32. Біляніна О.Я., Біляніна Г.І., Швець В.О. Геометрія підруч. для 10 кл. загальноосвіт. навчальн. закладів : академ. рівень. — К. : Генеза, 2010.
    
33. Нелін Є.П., Долгова О.Є. Алгебра : підруч. для 11 кл. загальноосвіт. навчальн. закладів : академ., профільн. рівень. — Х. : Гімназія, 2011.
    
34. Мерзляк А.Г., Полонський В.Б., Якір М.С., Номіровський Д.А. Алгебра : підруч. для 11 кл. загальноосвіт. навчальн. закладів : академ., профільн. рівень. — Х. : Гімназія, 2011.
    
35. Бевз Г.П., Бевз В.Г., Владімрова Н.Г., Владіміров В.М. Геометрія : підруч. для 11 кл. загальноосвіт. навчальн. закладів : академ., профільн. рівень. — К. : Генеза, 2011.
    
36. Апостолова Г.В. Геометрія : підруч. для 11 кл. загальноосвіт. навчальн. закладів : академ., профільн. рівень. — К. : Генеза, 2011.
    

Голова предметної комісії

к. ф-м. н., доцент, завідувач кафедри математичного аналізу та інформатики Т.М. Барболіна