Geum.ru

Східноукраїнський національний університет ім. В. Даля Інститут хімічних технологій м

Вид материалаДокументы

Содержание


1 Витяг з робочого навчального плану. система оцінювання та критерії оцінок за всіма видами навчальної роботи
3 Програма дисципліни
Подобный материал:

Міністерство освіти та науки України

Східноукраїнський національний університет ім. В. Даля

Інститут хімічних технологій (м. Рубіжне)

Факультет хімічних та інформаційних систем

Кафедра вищої математики та комп’ютерних технологій


ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ


самостійна робота студентів


2009

Диференціальні рівняння. Самостійна робота студентів (для студентів напряму 6.040302 “Інформатика”) \ Укладачі Баранов Ю.С., Євтушенко Ю.О. – Рубіжне: ІХТ СНУ, 2009. – 16 с.


Методичні вказівки для студентів денної і заочної форми навчання містять рекомендації до самостійного вивчення дисципліни «Диференціальні рівняння», дані про порядок та зміст поточного та семестрового контролю виконання навчальної програми, інформацію про робочу навчальну програму, завдання для контрольної роботи.


Схвалено кафедрою ВМКТ

Протокол № _____ «___» _____________ 2009 р.

Зав. кафедрою ______________ Кондратов С.О.


Затверджено методичною радою ІХТ СНУ ім. В.Даля

Протокол № ______ від «______» ___________ 2009 р.

Голова методичної ради ________________ Тімошин А.С.


1 ВИТЯГ З РОБОЧОГО НАВЧАЛЬНОГО ПЛАНУ. СИСТЕМА ОЦІНЮВАННЯ ТА КРИТЕРІЇ ОЦІНОК ЗА ВСІМА ВИДАМИ НАВЧАЛЬНОЇ РОБОТИ


1.1 Витяг з робочого навчального плану


Дисципліна „Диференціальні рівняння” входить до складу дисциплін професійної підготовки і вивчається студентами денної та заочної форми навчання у 5 семестрі.

Дисципліна „Диференціальні рівняння”, згідно з програмою освітньо-професійної підготовки зазначеного напрямку і спеціальності, вміщує в себе основні поняття диференціальних рівнянь першого та вищих порядків, систем диференціальних рівнянь та стійкість розв’язків диференціальних рівнянь. Зміст дисципліни за даною програмою побудовано таким чином, що приклади і твердження попередніх тем обов’язково використовуються у наступних темах і розділах. Дисципліна насичена великою кількістю понять, термінів і методів, які складають основну базу знань студентів вказаного напряму і без засвоєння яких неможливо повноцінно засвоїти елементи програмування та інші фахові дисципліни.

Для денної форми навчання в кожному семестрі передбачені такі аудиторні заняття: лекції – 2, практичні заняття – 2 (академічні години на тиждень)


Таблиця 1.1


Види роботи і занять
Форми навчання

Денна
Заочна

Всього відведено годин на

вивчення дисципліни
162
162

Самостійна робота
106
158

Аудиторні заняття
56
4

Лекції
28
2

Практичні заняття
28
2

Форма семестрового контролю
іспит
іспит


1.2 Система оцінювання


1.2.1 Денна форма


Об’єктами поточного контролю є: виконання індивідуальних практичних завдань, опитування по теоретичному матеріалу, виконання аудиторних та домашніх контрольних робіт.

Для студентів денної форми навчання поточний контроль засвоєння ними навчального матеріалу проводиться під час практичних занять.

За підсумками поточного контролю студент отримує атестаційні оцінки.

Студент, який пропустив практичне заняття або отримав незадовільну оцінку за результатами поточного контролю, може ліквідувати заборгованість, самостійно виконав практичне завдання і відповівши викладачеві на контрольні питання. Заборгованість належить ліквідувати не пізніше, ніж до початку екзаменаційної сесії.


1.2.2 Заочна форма


Для студентів заочної форми навчання поточний контроль засвоєння ними навчального матеріалу проводиться на підставі виконання ними письмової контрольної роботи, зміст і обсяг якої приведено в додатку А.

Зарахована контрольна робота є підставою для допуску студента до іспиту.


1.3 Критерії оцінок семестрового контролю


1.3.1 Денна форма навчання


Для студентів денної форми навчання двічі на семестр проводиться модульний контроль, відповідно до графіку навчального процесу. Метою модульного контролю є оцінювання рівня знань і ступеня засвоєння навчального матеріалу.

Оцінка за кожний модульний контроль виставляється як середнє арифметичне з оцінок отриманих на практичних заняттях, оцінки за виконання аудиторної контрольної роботи і оцінки за опитування на модульному контролі.

Відвідування практичних занять обов’язково.

Екзаменаційна оцінка є середньозважена з оцінок першого та другого модульного контролю.

Студенти, які бажають підвищити оцінку, отриману за результатами підсумкового контролю, та мають на це дозвіл, можуть додатково скласти аудиторну контрольну роботу, яка буде містити в собі всі основні питання лекційного курсу та практичних занять.


1.3.2 Заочна форма навчання


Для студентів заочної форми навчання семестровий контроль проводиться у формі письмового іспиту, до якого студент допускається після зарахування контрольної роботи. Тривалість іспиту 2 академічні години.

На іспиті студент отримує екзаменаційний білет, який містить 4 питання: 2 теоретичні та 2 практичні. На теоретичні питання студент повинен дати стислі відповіді, а на практичні питання навести повне рішення зі всіма необхідними поясненнями.

На іспиті студенти мають право користуватися будь-якою особистою літературою та зарахованою контрольною роботою.

При оцінюванні відповідей студентів екзаменатор повинен користуватися такими критеріями: відповідь на кожне питання білету оцінюється за такою шкалою:
  • 3 бали – вичерпна відповідь на питання;
  • 2 бали – відповідь принципово вірна, але допущені непринципові помилки;
  • 1 бал – у відповіді показано знання основних складових дисципліни, але допущені суттєві помилки принципового характеру;
  • 0 балів – відповідь на питання принципово невірна або взагалі відсутня.

За сумою балів за кожне питання білету виставляється оцінка студенту на екзамені за дванадцятибальною шкалою.

В залежності від суми балів студент одержує таку оцінку:
  • сума балів 10 – 12 – «відмінно»;
  • сума балів 7 – 9 – «добре»;
  • сума балів 4 – 6 – «задовільно»;
  • сума балів 0 – 3 – «незадовільно».

2 Мета вивчення дисципліни


В результаті вивчення дисципліни студент повинен знати:
  • основні поняття з курсу „Диференціальні рівняння”;
  • основну термінологію;
  • літературу та інші джерела інформаційного забезпечення.

Мати уявлення про:
  • диференціальні рівняння першого порядку;
  • диференціальні рівняння вищих порядків;
  • лінійні диференціальні рівняння другого порядку;
  • системи диференціальних рівнянь;
  • стійкість розв’язків диференціальних рівнянь;
  • диференціальні рівняння Ейлера в задачах варіаційного числення.

Вміти:
  • розв’язувати диференційні рівняння;
  • вміти користуватися літературою за спеціальністю;
  • за допомогою літератури розв’язувати диференціальні рівняння.



3 ПРОГРАМА ДИСЦИПЛІНИ


3.1 Лекційні заняття


Тема 1. Диференціальні рівняння першого порядку. [6] с. 18 – 109, [7] с. 7 – 32

1.1 Загальний розв’язок. Інтегральна крива. Задача Коші. Поле напрямків.

1.2 Диференціальні рівняння з подільними змінними. Особливі точки векторного поля.

1.3 Однорідні відносно 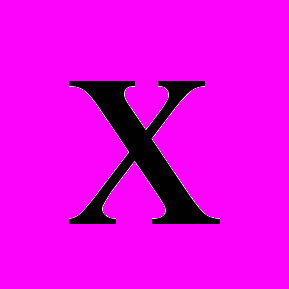та рівняння. Квазіоднорідні рівняння.

1.4 Рівняння виду .

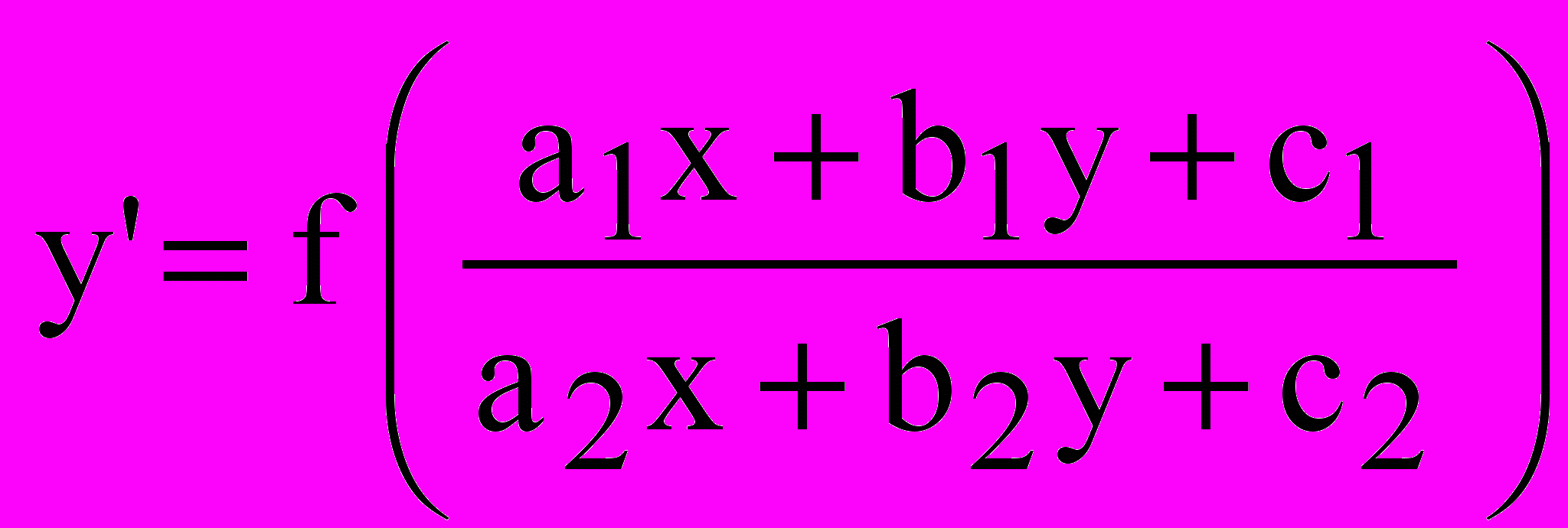1.5 Метод варіації сталих. Розв’язання лінійного диференціального рівняння першого порядку.

1.6 Метод Бернуллі розв’язання лінійного диференціального рівняння першого порядку. Рівняння Бернуллі.

1.7 Рівняння Ріккаті.

1.8 Теорема Пеано існування розв’язання задачі Коші. Особливі точки. Особливі розв’язки.


Тема 2. Диференціальні рівняння вищих порядків. [6] с. 113 – 255, [7] с. 35 – 58

2.1 Диференціальне рівняння 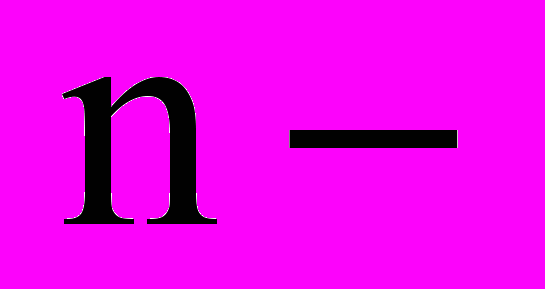го порядку.

2.2 Рівняння виду .

2.3 Рівняння виду .

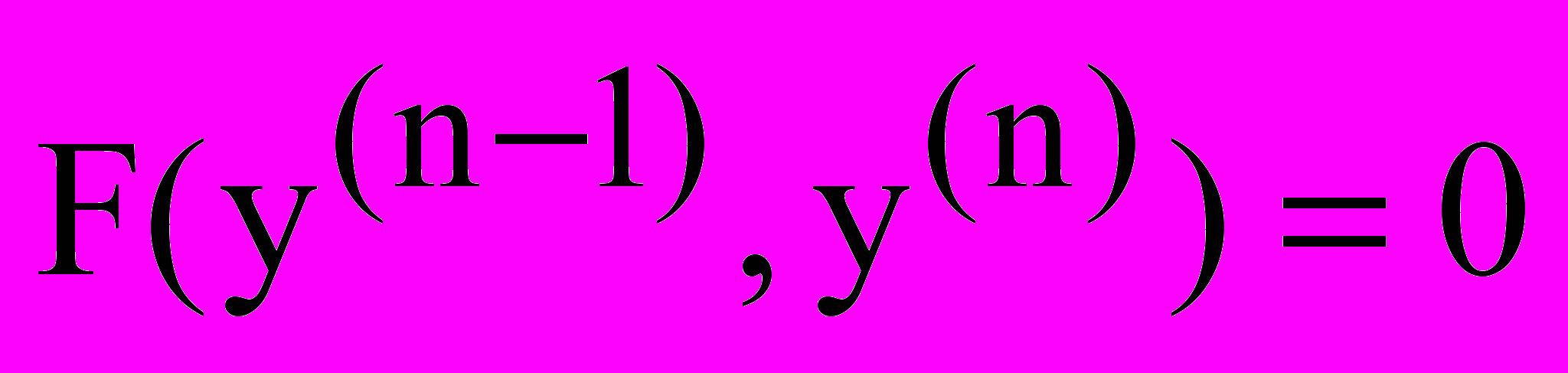2.4 Рівняння виду .

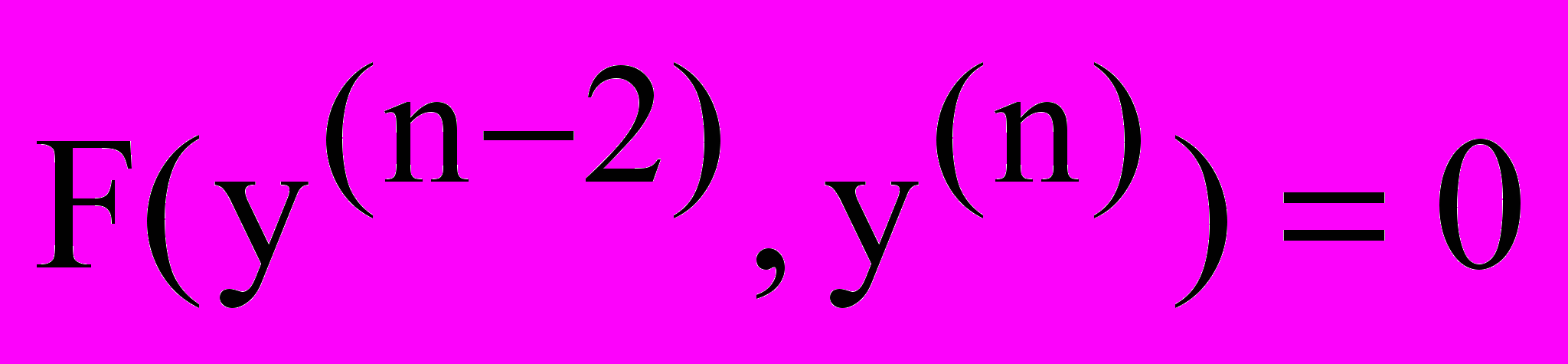2.5 Рівняння виду .

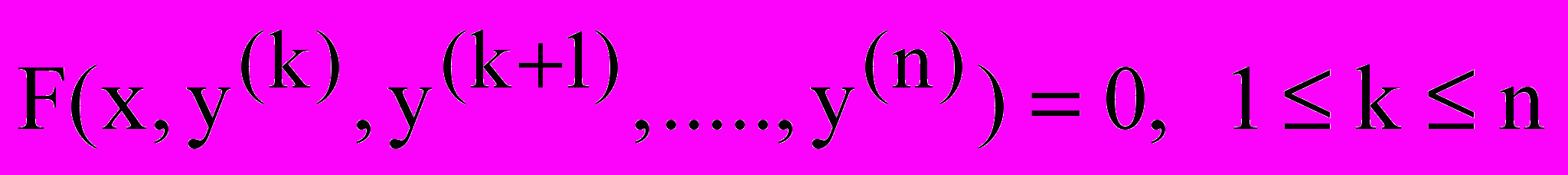2.6 Рівняння виду .

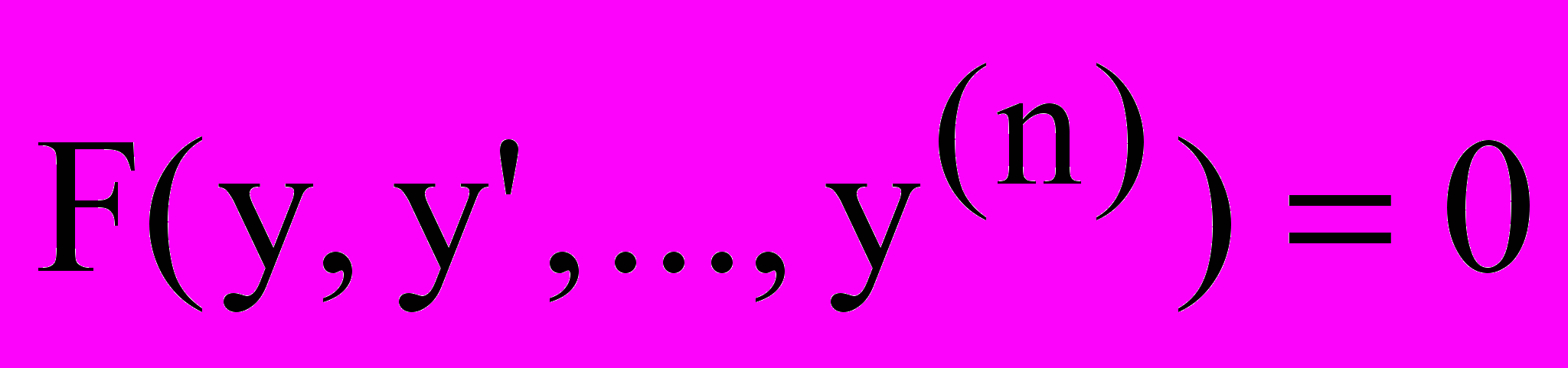2.7 Лінійні диференціальні рівняння 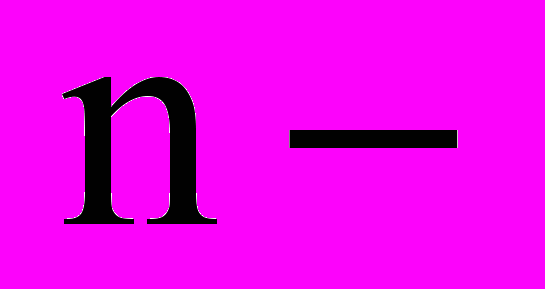го порядку. Фундаментальна система розв’язків.

2.8 Умови лінійної залежності та незалежності системи функцій. Визначник Грама. Визначник Веронського.

2.9 Формула Остроградського-Ліувілля.

2.10 Лінійне неоднорідне рівняння 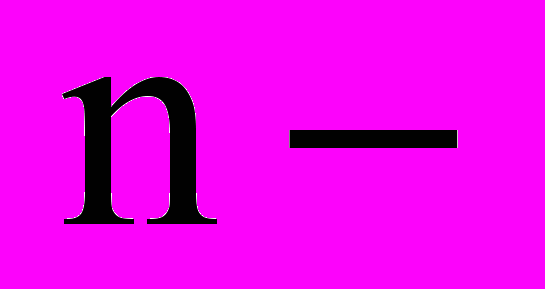го порядку. Метод варіації сталих Лагранжа.


Тема 3. Системи диференціальних рівнянь [6] с. 258 - 306

3.1 Системи диференціальних рівнянь у нормальній формі. Зведення нормальної системи 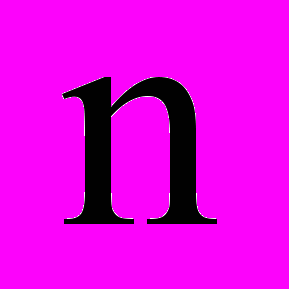диференціальних рівнянь до рівняння 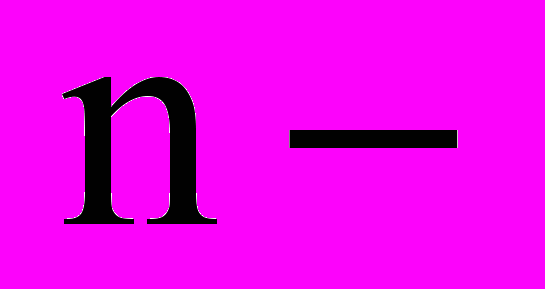го порядку.

3.2 Системи диференціальних рівнянь у симетричній формі.

3.3 Однорідні системи лінійних диференціальних рівнянь. Фундаментальна матриця.

3.4 Лінійні системи зі сталими коефіцієнтами. Метод Ейлера.

3.5 Розв’язання систем лінійних рівнянь зі сталими коефіцієнтами методом матричної експоненти.

3.6 Лінійні неоднорідні системи. Метод варіації сталих.

3.7 Лінійна неоднорідна система диференціальних рівнянь зі сталими коефіцієнтами. Метод невизначених коефіцієнтів у випадку вільних членів спеціального виду.


Тема 4. Стійкість розв’язків диференціальних рівнянь [6] с. 310 - 358

4.1 Стійкі та нестійкі розв’язки системи диференціальних рівнянь. Асиметрична стійкість.

4.2 Стійкість розв’язків лінійної однорідної системи виду .

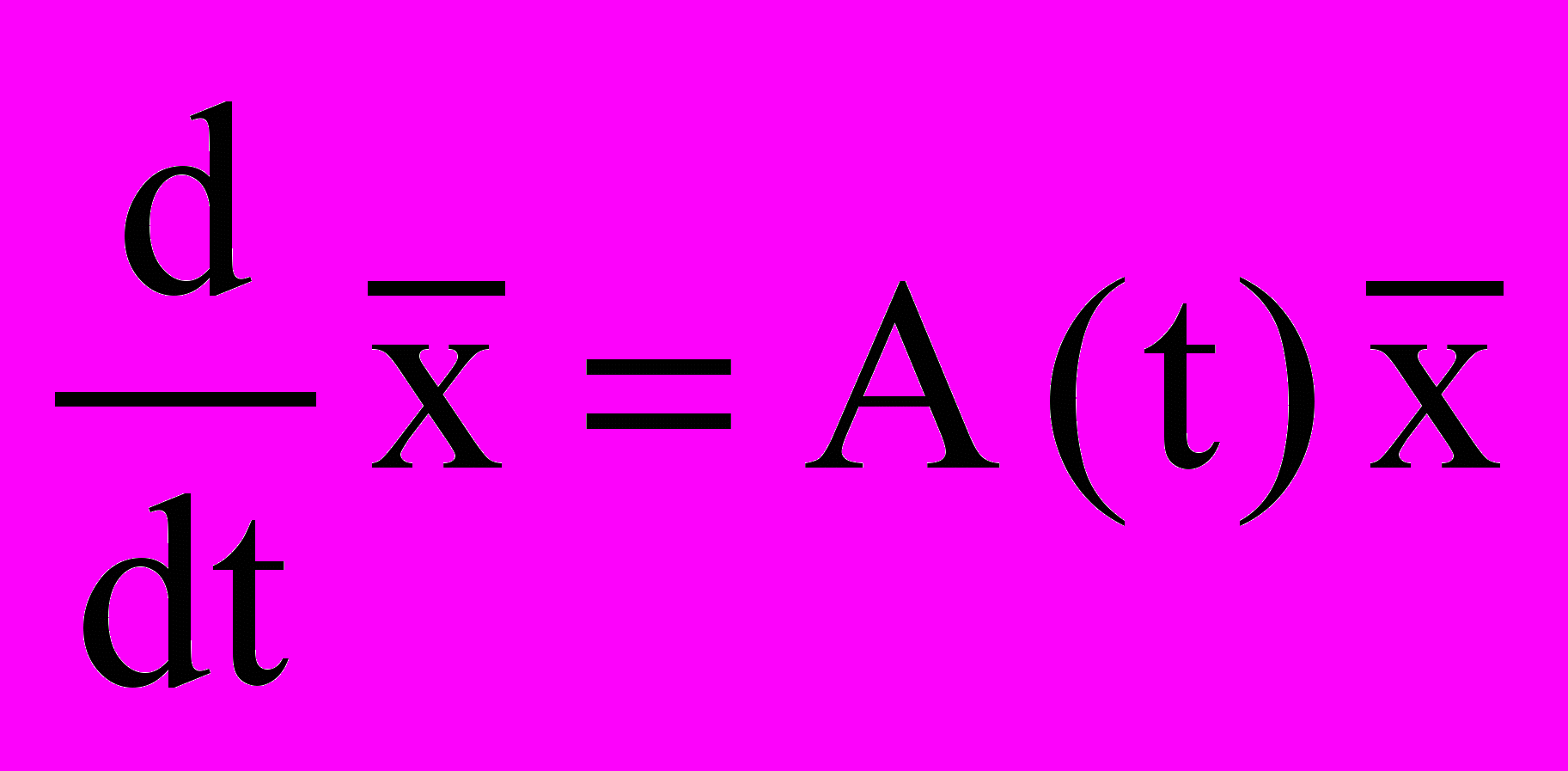4.3 Стійкість розв’язків лінійної системи зі сталими коефіцієнтами.

4.4 Критерій стійкості за першим наближенням.

4.5 Теореми Ляпунова про стійкість та нестійкість нульового розв’язку системи

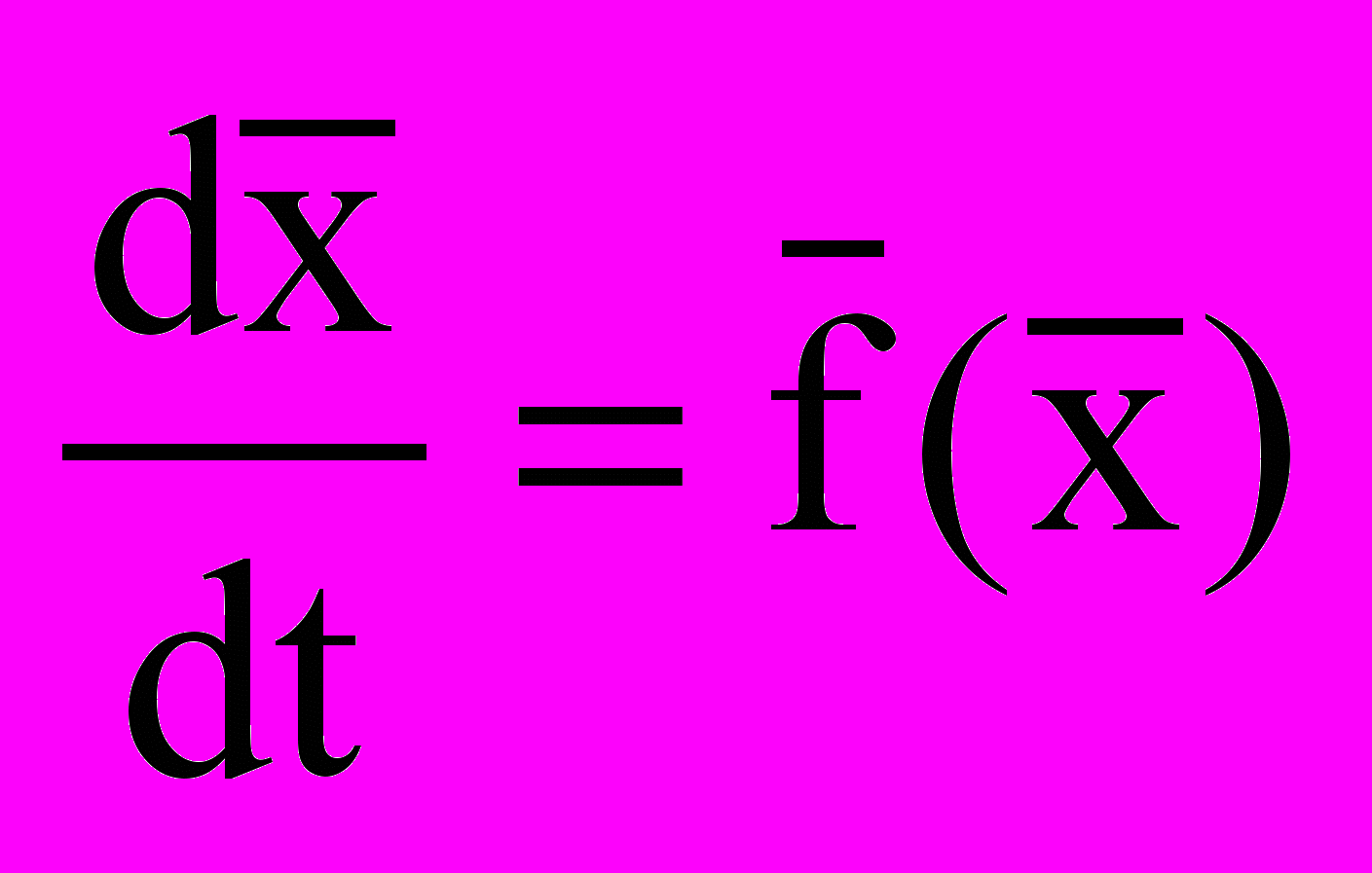
4.6 Динамічна система другого порядку. Фазні криві. Граничні цикли. Сепаратриси.

4.7 Лінійна однорідна динамічна система другого порядку. Особливі точки: вузол, сідло, фокус, центр. Стійкість особливих розв’язків.


Тема 5. Лінійні рівняння першого порядку з частинними похідними. [6] с. 362 - 374

5.1 Лінійні однорідні рівняння першого порядку з частинними похідними. Характеристика.

5.2 Задача Коші для лінійного однорідного рівняння першого порядку з частинними похідними. Нехарактеристичні точки.

5.3 Квазілійнійне рівняння першого порядку з частинними похідними.

5.4 Побудова загального розв’язку квазілінійного рівняння першого порядку з частинними похідними за допомогою перших інтегралів системи характеристик.


Тема 6. Деякі задачі варіаційного числення. [4] с. 257 – 300, [2] с. 385 - 398


6.1 Функціонал. Варіація функціоналу. Рівняння Ейлера.

6.2 Друга варіація функціоналу. Умова екстремуму у термінах другої варації.


3.2 Практичні заняття


1. Рівняння першого порядку, що розв’язуються відносно похідної. Розподілення змінних. – 2 год., [7] с. 7 – 9, [6] с. 29 – 35

2. Однорідні диференціальні рівняння. – 2 год., [7] с. 14 – 17

3. Рівняння у повних диференціалах. Інтегруючий множник. – 2 год., [6] с. 86 – 96

4. Задачі на складання диференціальних рівнянь. – 2 год., [6] с. 37 – 55

5. Наближені методи розв’язання диференціальних рівнянь. – 2 год., [6] с. 271 – 281

6. Рівняння, що допускають зниження порядку. – 2 год., [7] с. 35 – 38

7. Лінійні рівняння зі сталими коефіцієнтами. – 2 год., [7] с. 38 – 48

8. Лінійні рівняння зі змінними коефіцієнтами. – 2 год., [7] с. 49 – 50

9. Лінійні системи зі сталими коефіцієнтами. – 2 год., [5] с. 42 – 56, [7] с. 58 – 63

10. Стійкість. – 2 год., [6] с. 310 – 313

11 Особливі точки. Фазна площина. – 2 год., [7] с. 78 – 82

12. Залежність розв’язків від початкових умов та параметрів. Наближене розв’язання диференціальних рівнянь. – 2 год., [7] с. 88 – 91

13. Нелінійні системи. – 2 год., [7] с. 97 – 98

14. Задачі варіаційного числення. – 2 год., [4] с. 257 – 275, с. 237 – 300


3.3 Самостійна робота


1. Диференціальні рівняння першого порядку – 90 год., [6] с. 18 – 109

2. Диференціальні рівняння вищих порядків – 90 год., [6] с. 113 – 255

3. Системи диференціальних рівнянь -– 90 год., [5] с. 42 – 56, [6] с. 258 – 306

4. Стійкість розв’язків диференціальних рівнянь – 90 год., [6] с. 310 – 358

5. Лінійні рівняння першого порядку з частинними похідними – 90 год., [7] с. 100 – 101

6. Задачі варіаційного числення – 16 год., [4] с. 237 – 300


4 Література


1. Гутер Р.С., Янпольский А.Р. Дифференциальные уравнения. – М.: Высшая школа, 1976.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школ. Часть 2. 1986.

3. Кузнєцов Л.А. Сборник заданий по высшей математике (типовые расчёты). – М.: Высшая школа, 1983.

4. Мышкис А.Д. Математика для втузов. Специальные курсы. – М.: Наука, 1971.

5. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1970.

6. Самойленко А.М., Кривошея С.А., Перестюк Н.Я. Дифференциальные уравнения: примеры и задачи. – М.: Наука, 1989.

7. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – М.: Наука, 1973.


5 Контрольні роботи студентів заочної форми навчання


5.1 Зміст контрольної роботи


Для заочної форми навчання поточний контроль засвоєння студентами навчального матеріалу здійснюється на підставі виконання ними письмової контрольної роботи, зміст якої наведено у додатку А.

Зарахована контрольна робота є підставою для допуску до іспиту

Контрольна робота може бути зарахованою, якщо виконано вірно не менш 60% від її об’єму.


5.2 Рекомендації з вибору варіанту


Контрольна робота складається з 13 завдань, які наведено у додатку А. Кожне завдання містить 31 варіант. Номер варіанту співпадає з порядковим номером студента у журналі групи на початок навчального семестру. Якщо варіант більший за 31, то номер варіанту визначається як різниця номеру за журналом та 31, тобто





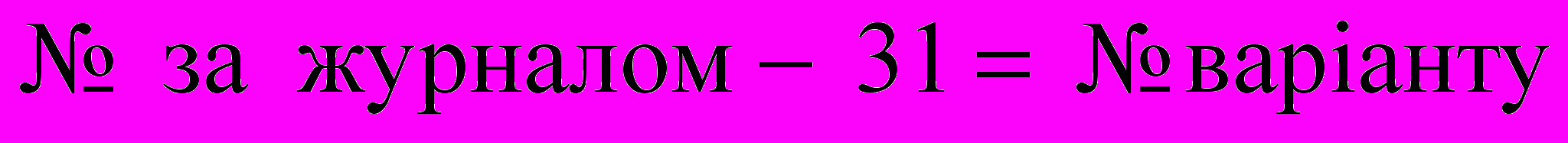
5.3 Рекомендації щодо виконання контрольної роботи


Контрольна робота виконується у зошиті в клітинку. Всі записи робити через клітинку, синьою пастою розбірливо та старанно. Рішення повинні бути вичерпані, з необхідними поясненнями. Уникати закреслень та виправлень. Обов’язково залишати поля для поміток викладача.

Приклад оформлення титульного аркушу контрольної роботи наведено у додатку Б.

Якщо контрольна робота не зарахована, студент повинен виправити неправильно розв’язані задачі в тому ж зошиті (щоб викладач зміг побачити роботу над помилками).

Якщо студент виконав контрольну роботу не свого варіанту, робота повертається і вважається не зарахованою.

Приклади розв’язання задач містяться у підручниках, посилка на які наведена у таблиці 5.3.1.


Таблиця 5.3.1. Приклади розв’язання задач


Номер задачі
Посилання на підручники

з прикладами рішень

1
[2] с.118 №№507, 509

2
[6] с.57 №№1.53 – 1.57

3
[6] с.30 №№1.22 – 1.25

4
[7] с.22 – 23

5
[6] с.33 №№1.28 – 1.31

6
[2] с.141 №649, с.142 №№656, 657

7
[6] с.151 №№2.9 – 2.11

8
[2] с.156 №714

9
[2] с.156 №№715 – 719

10
[6] с.362 №№4.40 – 4.41

11
[6] с.377 №4.54

12
[6] с.397 №№5.5 – 5.9, 5.11, 5.15

13
[6] с.411 №5.23, с.415 №5.27



6 Перелік основних теоретичних і практичних питань, що виносяться на екзамен (модульний контроль)


1. Які рівняння називаються диференціальними? [6] с.3

2. Які питання вивчає теорія диференціальних рівнянь? [6] с.8

3. сформулюйте означення диференціального рівняння першого порядку. [6] с.14

4. Які диференціальні рівняння першого порядку називаються розв’язаними відносно похідної? [6] с.14

5. Що ми називаємо інтегралом рівняння? [6] с.15

6. Що називається інтегральною кривою диференціального рівняння? [6] с.15

7. Що таке фазна крива? [6] с.15

8. Дайте означення ізокліни. [6] с.15

9. Сформулюйте означення диференціального рівняння з відокремлюваними змінними. [6] с.28

10. Однорідні диференціальні рівняння. Означення. [6] с.58

11. В чому полягає метод варіації довільної сталої (метод Лагранжа) розв’язання лінійного диференціального рівняння першого порядку? [6] с.69

12. В чому полягає метод Бернуллі розв’язання лінійного диференціального рівняння першого порядку? [6] с.69

13. В чому полягає метод інтегрувального множника розв’язання лінійного диференціального рівняння першого порядку? [6] с.70

14. Запишіть загальний вид рівняння Ріккаті. [6] с.70

15. Запишіть рівняння у повних диференціалах. [6] с.86

16. Що є інтегрувальним множником для рівняння у повних диференціалах? [6] с.87

17. Сформулюйте достатні умови існування та єдиності розв’язку задачі Коші (теореми Пікара та Пеано). [6] с.97

18. В чому полягає суть методу введення параметру при розв’язанні диференціальних рівнянь, не розв’язаних відносно похідної? [6] с.112

19. В чому полягає метод виключення при розв’язанні системи диференціальних рівнянь? [6] с.323

20. В чому полягає метод інтегрованих комбінацій при розв’язанні системи диференціальних рівнянь? [6] с.323

21. Що називається фундаментальною системою розв’язків лінійної однорідної системи рівнянь? [6] с.341

22. Що таке визначник Вронського? [6] с.341

23. Що називають матрицантом системи? [6] с.341

24. В чому полягає метод Ейлера при розв’язанні лінійної системи зі сталими коефіцієнтами? [6] с.350

25. На чому ґрунтується матричний метод інтегрування лінійної системи зі сталими коефіцієнтами? [6] с.350

26. Лінійна неоднорідна система. Означення. [6] с.370

27. Способи розв’язання лінійної неоднорідної системи. [6] с.370 – 371

28. Поняття стійкості розв’язку. [6] с.390

29. Система збурень. Означення. [6] с.391

30. Сформулюйте основні теореми про стійкість розв’язків лінійних систем диференціальних рівнянь. [6] с.395 – 397

31. Сформулюйте критерій стійкості за першим наближенням. [6] с.408

32. В чому полягає дослідження системи диференціальних рівнянь на стійкість за методом функцій Ляпунова? [6] с.417

33. Динамічна система. Означення. [6] с.427

34. Фазна площина. Означення. [6] с.427

35. Що називається граничним циклом системи? [6] с.428

Додаток А


Завдання 1. Знайти загальний інтеграл диференціального рівняння: [3] с.70 №1


Завдання 2. Знайти загальний інтеграл диференціального рівняння: с.71 №3.


Завдання 3. Розв’язати задачу Коші: [3] с.73 №5


Завдання 4. Знайти загальний інтеграл диференціального рівняння: [3] с.74 №7


Завдання 5. Для даного диференціального рівняння методом ізоклін побудувати інтегральну криву, що проходить через точку М: [3] с.75 №8


Завдання 6. Знайти загальний розв’язок диференціального рівняння: [3] с.76 №10


Завдання 7. Знайти розв’язок задачі Коші: [3] с.77 №11


Завдання 8. Знайти загальний розв’язок диференціального рівняння: [3] с.78 №12


Завдання 9. Знайти загальний розв’язок диференціального рівняння: [3] с.79 №15


Завдання 10. Розв’язати систему рівнянь


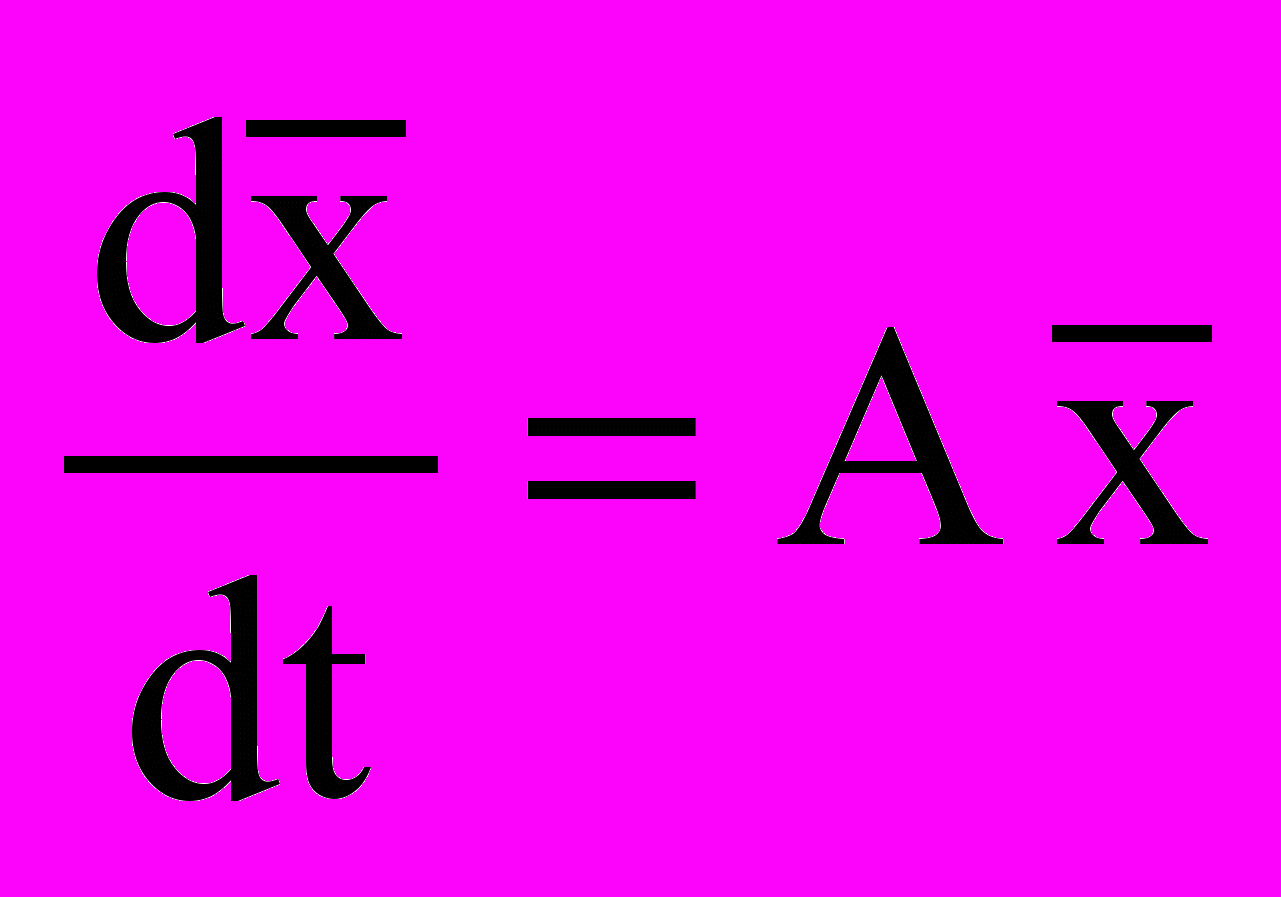, де ,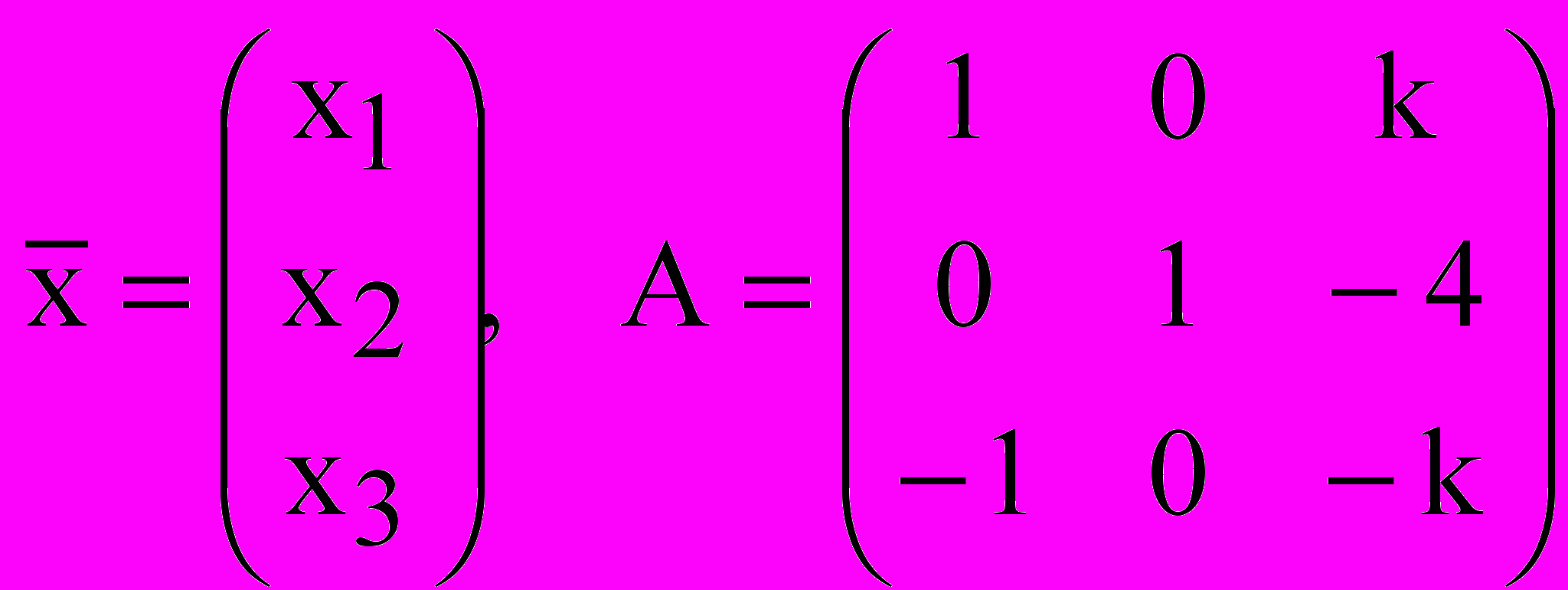


та знайти матрицю (де 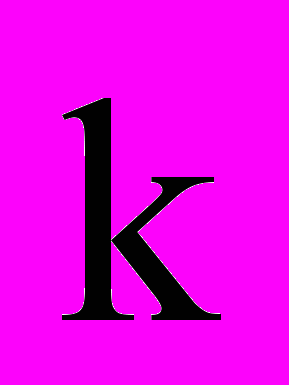- номер Вашого варіанту).


Завдання 11. Розв’язати систему рівнянь


,


(де 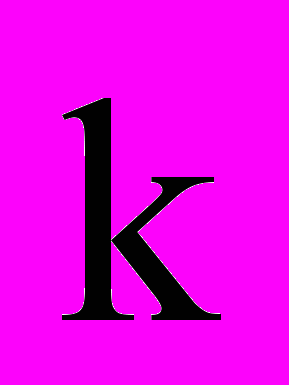- номер Вашого варіанту).


Завдання 12. Дослідити стійкість усіх особливих точок системи рівнянь


,


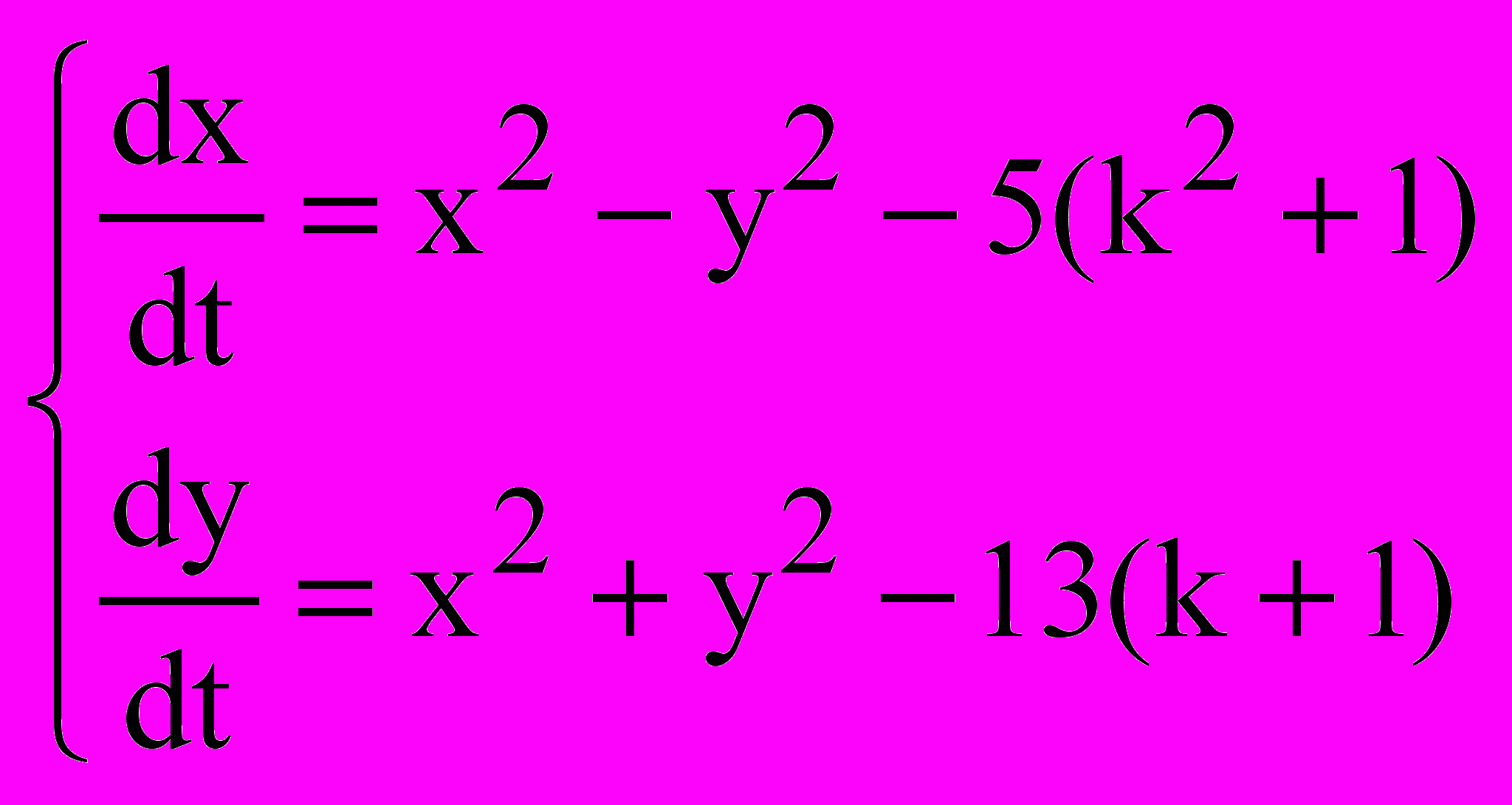(де 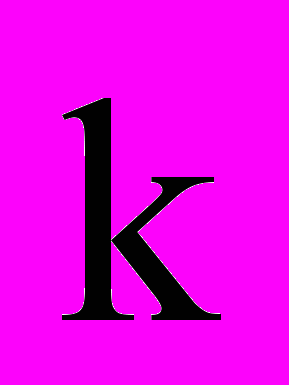- номер Вашого варіанту).


Завдання 13. Дослідити тип кожного з положень рівноваги системи


,


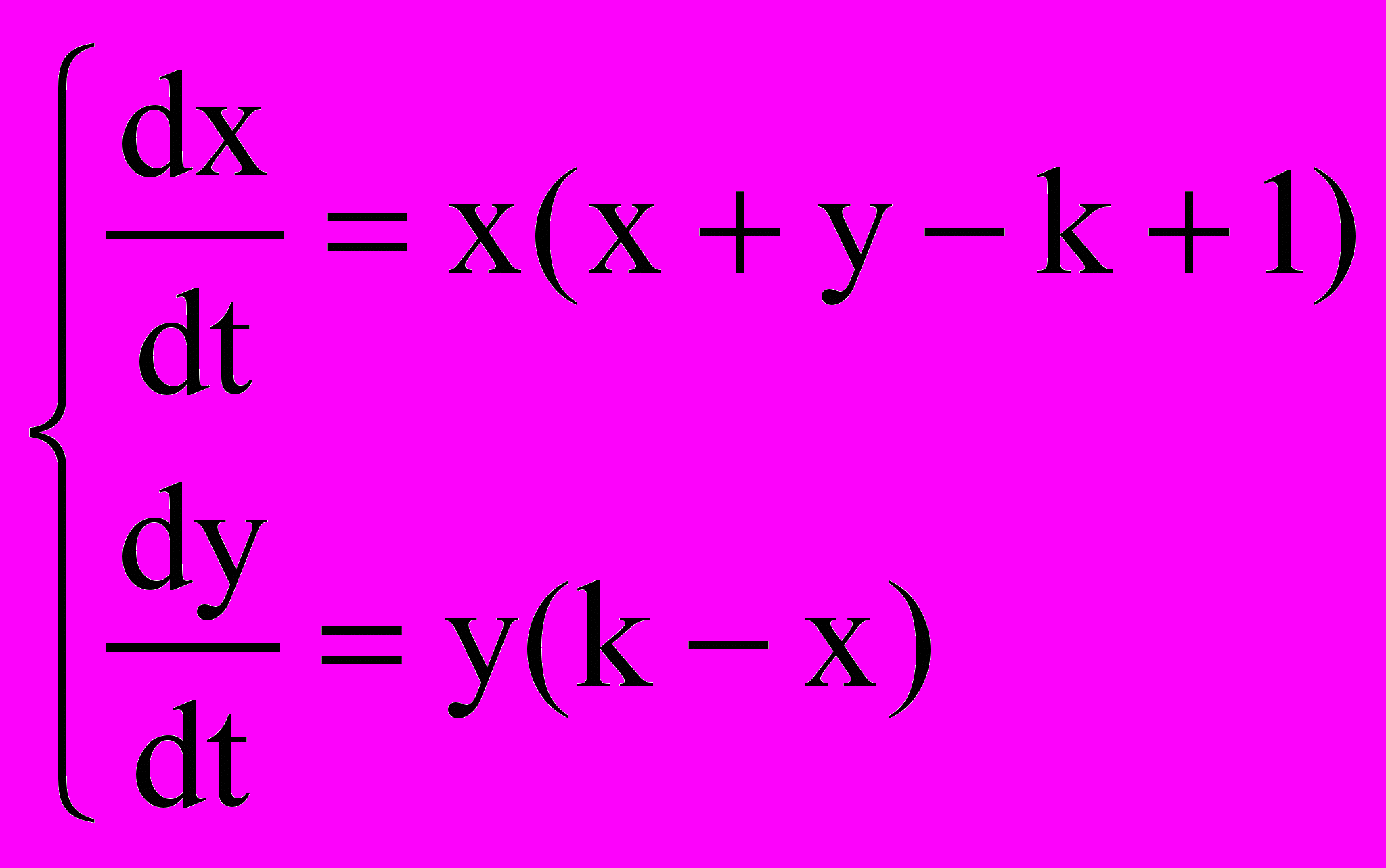(де 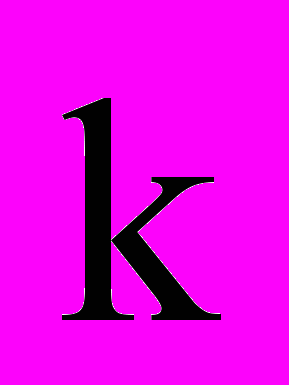- номер Вашого варіанту).

Додаток Б


Приклад оформлення титульного аркушу контрольної роботи


Міністерство освіти та науки України

Інститут хімічних технологій (м. Рубіжне)

Східноукраїнського національного університету ім. В. Даля


Факультет хімічних та інформаційних систем


Кафедра вищої математики та комп’ютерних технологій


ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ


Контрольна робота


Варіант ___


Група _______________

Студент _____________

Зал. книжка __________

Здано________________

Підпис _______________


2009-2010, осінній (весняний)