Geum.ru

За переліком дисциплін програми підготовки бакалаврів з економіки підприємства дисципліна „ Теорія ймовірностей та математична статистика має код пнзе- 03/1 І викладається в обсязі 7 кредитів ects

Вид материалаДокументы

Содержание


VІІ. Характеристика індивідуальних завдань
VІІІ. Методика оцінювання
Rс= 100 балів
Розмір шкали рейтингу R=100 бали
Подобный материал:

Опис кредитного модуля (дисципліни)

Математика для економістів:

ПНЗЕ-05/1 „Вища математика”

Статус кредитного модуля (дисципліни) обов’язковий

Лектор Диховичний Олександр Олександрович

Факультет фізико-математичний

Кафедра математичного аналізу та теорії ймовірностей


І. Загальні відомості

В умовах технічного ВНЗ курс вищої математики є одним з основних, визначальних як для всього процесу навчання, так і подальшої практичної діяльності спеціаліста. Він є необхідним для успішного засвоєння спеціальних дисциплін.

Згідно з навчальним планом підготовки бакалаврів за напрямом підготовки “Економіка підприємства” на факультеті менеджменту та маркетингу Національного технічного університету „України „Київський політехнічний інститут” дисципліна „Вища математика” відноситься до нормативної частини програми, циклу природничо-наукової та загальноекономічної підготовки.

За переліком дисциплін програми підготовки бакалаврів з економіки підприємства дисципліна „ Теорія ймовірностей та математична статистика” має код ПНЗЕ-03/1 і викладається в обсязі 7 кредитів ECTS.


ІІ. Розподіл навчального часу

Семестр
Код кредитного модуля
Всього кредитів / годин
Розподіл за видами занять

(всього год. / год. у тижні)

СРС
Кількість МКР
Індивід. завдання
Семестрова атестація

Лекції
Практичні

1
ПНЗЕ-03/1
3 / 108
18
36

54
1
РР
залік

2
ПНЗЕ-03/1
4 / 144
18
36

90
1
РР
екзамен



ІІІ. Мета і завдання дисципліни (кредитного модуля)

Викладання вищої математики має за мету:
  • оволодіння студентами основами математичного апарату;
  • розвиток логічного мислення;
  • вироблення навичок самостійного вивчення наукової літератури з математики та її застосування;
  • вироблення навичок математичного дослідження прикладних задач.

Для вивчення вищої математики необхідні знання математики в об’ємі середньої школи

“Вища математика” належить до циклу фундаментальних дисциплін і забезпечує вивчення загальнонаукових, загальноінженерних та спеціальних дисциплін.

ІV. Зміст дисципліни (кредитного модуля)

Модуль 1

Розділ 1. Аналітична геометрія та лінійна алгебра.

Тема 1.1. Елементи лінійної алгебри.

Поняття матриці, класифікація матриць. Дії над матрицями: додавання, віднімання, множення на число, добуток матриць. Означення та обчислення детермінантів 2-го, 3-го та n-го порядків. Властивості детермінантів. Мінори та алгебраїчні доповнення елементів матриці. Ранг матриці, його властивості та методи обчислення. Обернена матриця та обчислення оберненої матриці. Власні числа та власні вектори матриці. Лінійні системи алгебраїчних рівнянь. Теорема Кронекера-Капеллі. Формули Крамера. Матричний метод і метод Гауса розв’язування лінійних систем.

Тема 1.2. Елементи векторної алгебри.

n-вимірні вектори. Векторний простір. Лінійна залежність та незалежність векторів. Базис лінійного простору. Розклад вектора у базисі.

Тема 1.3. Аналітична геометрія на площині та в просторі.

Основні задачі аналітичної геометрії. Пряма лінія на площині та в просторі: різні види рівнянь. Рівняння площини в 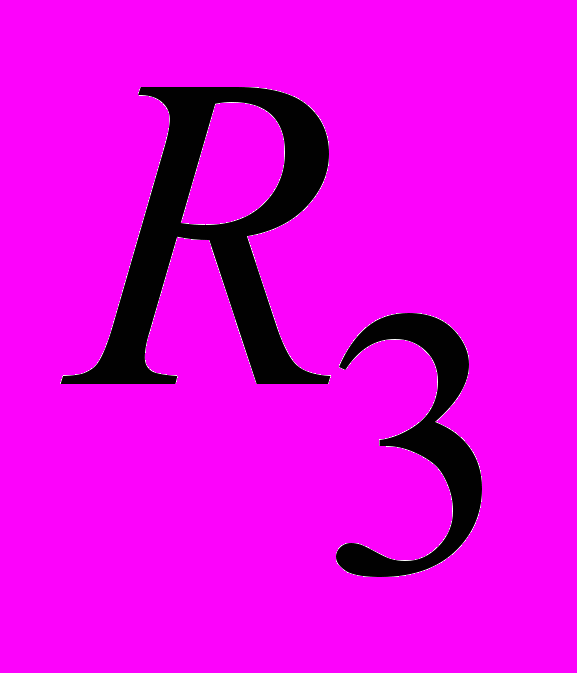. Лінії на площині. Криві другого порядку: коло, еліпс, гіпербола, парабола: канонічні рівняння.

Розділ 2. Диференціальне та інтегральне числення функцій однієї змінної.

Тема 2.1. Вступ до математичного аналізу.

Основні логічні символи. Операції над множинами. Функція як відображення, обернене відображення, графік функції. Числові послідовності. Границя числової послідовності, властивості збіжних числових послідовностей. Теорема Вейєрштраса про існування границі монотонної обмеженої числової послідовності. Число ℮. Границя функції в точці за Коші та за Гейне. Односторонні границі, властивості функцій, що мають границю (про арифметичні дії, збереження знаку, перехід до границі в нерівностях). Перша і друга важливі границі. Нескінченно малі і нескінченно великі функції та їх властивості, зв’язок між нескінченно малими та нескінченно великими функціями, символи Ландау. Порівняння нескінченно малих функцій. Умова еквівалентності. Заміна нескінченно малих еквівалентними.

Неперервність функції в точці. Означення та властивості функцій, неперервних в точці: неперервність суми, добутку і частки; границя і неперервність складеної функції, неперервність елементарних функцій. Стійкість знаку. Одностороння неперервність.

Неперервність функції на відрізку. Властивості неперервних функцій на відрізку: обмеженість, існування найменшого та найбільшого значень, існування проміжних значень.

Тема 2.2. Диференціальне числення та його застосування.

Означення похідної у точці. Односторонні похідні. Неперервність і існування похідної у точці. Геометричний, фізичний, економічний зміст похідної. Дотична і нормаль до графіка функції. Похідна оберненої, складеної функцій, функцій, заданих неявно і параметричним чином. Похідні гіперболічних функцій. Похідна степенево-показникової функції.

Диференційовність функції в точці. Диференціал: означення і геометричний зміст. Властивості диференціалу, інваріантність форми. Похідні і диференціали вищих порядків. Формула Лейбніца. Неінваріантність форми другого диференціалу.

Теорема Ферма. Основні теореми диференціального числення: Лагранжа, Ролля, Коші. Правило Лопіталя.

Тема 2.3. Дослідження функцій однієї змінної за допомогою похідної.

Дослідження монотонності функції. Локальні екстремуми функції, їх необхідні та достатні умови. Найбільше та найменше значення функції на відрізку.

Опуклі функції. Необхідні і достатні умови опуклості функції на інтервалі. Точки перегину, достатні умови існування точок перегину.


Модуль 2


Розділ 3. Інтегральне числення функцій однієї змінної.

Тема 3.1. Невизначений інтеграл.

Первісна функції та невизначений інтеграл: означення та їх властивості. Таблиця основних формул інтегрування. Безпосереднє інтегрування. Основні методи інтегрування: заміна змінної у невизначеному інтегралі та інтегрування частинами.

Основна теорема алгебри. Розклад раціональних дробів на елементарні. Інтегрування раціональних дробів та найпростіших ірраціональних функцій. Поняття про функції, що неінтегровані в скінченному вигляді.

Інтегрування тригонометричних функцій. Мішані задачі на інтегрування.

Тема 3.2. Визначений інтеграл.

Задачі, що приводять до поняття визначеного інтеграла. Визначений інтеграл як границя інтегральних сум. Необхідні і достатні умови інтегрованості функцій на відрізку. Основні властивості визначеного інтеграла.

Визначений інтеграл із змінною верхнею межею інтегрування та його властивості. Формула Ньютона-Лейбніца. Інтегрування частинами і заміною змінної у визначеному інтегралі. Застосування визначеного інтеграла до обчислення площ плоских фігур, довжин дуг кривих та об’ємів тіл обертання.

Невласні інтеграли 1-го та 2-го роду. Ознаки збіжності невласних інтегралів.

Розділ 4. Диференціальне числення функцій багатьох змінних.

Тема 4.1. Диференційовність функцій багатьох змінних.

Функції багатьох змінних: означення, область визначення, приклади з економіки: функції попиту і пропозицій, Кобба-Дугласа, корисливості. Границя функції в точці та неперервність функцій багатьох змінних в точці і області.

Повний та частинний приріст функцій. Частинні похідні. Диференційовність функцій Повний диференціал функцій, його зв’язок з частинними похідними. Інваріантність форми повного диференціала.

Диференціювання складених і неявних функції багатьох змінних. Повна похідна. Похідна за напрямком. Градієнт скалярного поля, його властивості і зв’язок з похідною за напрямком.

Тема 4.2. Екстремуми функцій багатьох змінних.

Локальний екстремум функцій багатьох змінних: означення, необхідні умови. Достатні умови існування локального екстремуму. Умовний екстремум. Метод множників Лагранжа.

Розділ 5. Звичайні диференціальні рівняння.

Тема 5.1. Диференціальні рівняння першого порядку.

Основні поняття диференціальних рівнянь: порядок, розв’язок, загальний розв’язок, інтегральна крива. Диференціальні рівняння 1-го порядку. Задача Коші: постановка, достатні умови існування та єдиності розв’язку задачі Коші.

Деякі класи диференціальних рівнянь 1-го порядку, які інтегруються в квадратурах: рівняння з відокремлюваними змінними, лінійні, однорідні.

Тема 5.2. Диференціальні рівняння вищих порядків.

Диференціальні рівняння вищих порядків: означення, постановка задачі Коші. Поняття загального та частинного розв’язку. Диференціальні рівняння, що допускають зниження порядку. Лінійні однорідні диференціальні рівняння (ЛОДР) n-го порядку зі сталими коефіцієнтами.

Неоднорідні лінійні диференціальні рівняння (НЛДР) n-го порядку: означення, теорема про структуру загального розв’язку, принцип суперпозиції. Знаходження частинного розв’язку НЛДР методом невизначених коефіцієнтів.

Розділ 6. Ряди.

Тема 6.1. Числові ряди.

Числові ряди: означення ряду, частинної суми, збіжності та розбіжності ряду, залишку ряду. Необхідна умова збіжності. Дії над збіжними числовими рядами. Ряди з додатними членами. Ознаки збіжності додатних числових рядів. Знакозмінні числові ряди. Ознака Лейбніца про збіжність знакопочергових рядів, оцінка залишку ряду. Абсолютна та умовна збіжність.


Тема 6.2. Степеневі ряди

Степеневі ряди. Радіус та інтервал збіжності степеневого ряду. Властивості та застосування степеневого ряду. Ряд Тейлора-Маклорена.

Тема 6.3. Ряди Фур’є.

Ряд Фур’є для 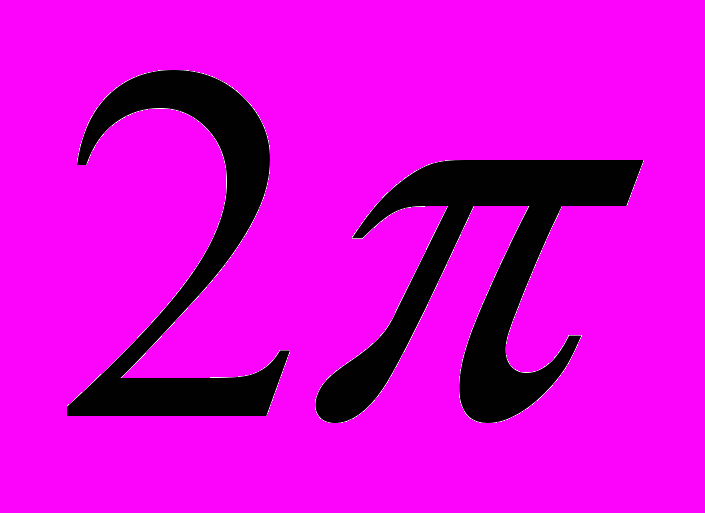-періодичних функцій. Теорема Діріхле.


V. Методи навчання та інформаційно-методичне забезпечення


Повноцінне оволодіння студентами тем навчальної дисципліни відбувається під час аудиторних занять, індивідуальної та самостійної роботи згідно з навчальним планом.

Важливе місце відводиться самостійній роботі студенті, яка в рамках Болонського процесу розглядається як один із найважливіших елементів нових освітніх технологій.

Навчальний матеріал дисципліни, передбачений робочою навчальною програмою для засвоєння студентами під час самостійної роботи, виноситься на поточний та підсумковий контроль поряд з навчальним матеріалом, який опрацьовується під час аудиторних навчальних занять.

Викладач призначає щотижневі індивідуальні консультації для того, щоб студенти змоги з’ясувати всі проблемні питання стосовно даної дисципліни.


Література:

  1. Барковський В.В., Барковська Н.В. математика для економістів. Вища математика.-К.:Нац. Академія управління, 1997.-382с.
  2. Боярский А.К. Математика для экономистов. М.: Вісшая школа, 1961.-264с.
  3. Бугір М.К. математика для економістів.-Тернопіль: Підручники & посібники, 1998.-80с.
  4. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1980.-176с.
  5. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. М. Наука. 1980.-482с.
  6. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов в 3 ч. -М.: Наука,- 1981.
  7. Краас В.М. Высшая математика для экономических специальностей. М.: Вісшая школа, 1997.-256с.
  8. Кремер Н.Ш. Высшая математика для экономистов. -М.: Юнити, 1998.-378с.
  9. Кудрявцев Л.Д., Демидович Б.П. Курс высшей математики. М.: Наука, 1984.-592с.
  10. Мантуров О.В., Матвеев Н.М. Курс высшей математики. - М.: Вісшая школа,-1986.-296с.
  11. Ординська З.П., Репета Л.А., Дем’яненко О.О. Елементи лінійної алгебри та аналітичної геометрії. Методичні вказівки до виконання типової роботи з вищої математики Ч.1. -К.: КПІ, 200.-58с.
  12. Іванов О.В., Ординська З.П., Репета Л.А., Дем’яненко О.О. Вступ до математичного аналізу. Диференціальне числення функцій однієї та багатьох змінних. Методичні вказівки до виконання типової розрахункової роботи з вищої математики Ч.2 -К.: КПІ, 200.-82с.
  13. Письменный Д. Конспект лекций по высшей математике. Ч.1.-М.:Айрис пресс, -2004.-288с.
  14. Барковський В.В., Барковська Н.В. математика для економістів. Вища математика.-К.:Нац. Академія управління, 1997.-382с.
  15. Боярский А.К. Математика для экономистов. М.: Высшая школа, 1961.-264с.
  16. Бугір М.К. математика для економістів. - Тернопіль: Підручники & посібники, 1998.-80с.
  17. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. М. Наука. 1980.-482с.
  18. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Теория функций комплексного переменного. М.: Наука, 1981. – 448 с.
  19. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов в 3 ч. -М.: Наука,- 1981.
  20. Краас В.М. Высшая математика для экономических специальностей. М.: Высшая школа, 1997.-256с.
  21. Кремер Н.Ш. Высшая математика для экономистов. - М.: Юнити, 1998.-378с.
  22. Кудрявцев Л.Д., Демидович Б.П. Курс высшей математики. М.: Наука, 1984.-592с.
  23. Мантуров О.В., Матвеев Н.М. Курс высшей математики. - М.: Высшая школа,-1986.-296с.
  24. Іванов О.В., Ординська З.П., Репета Л.А., Дем’яненко О.О. Вступ до математичного аналізу. Диференціальне числення функцій однієї та багатьох змінних. Методичні вказівки до виконання типової розрахункової роботи з вищої математики Ч.2 -К.: КПІ, 200.-82с.
  25. Іванов О.В., Ординська З.П., Репета Л.А., Дем’яненко О.О. Інтегральне числення функцій однієї змінної. Диференціальні рівняння. Ряди. Методичні вказівки до виконання типової розрахункової роботи з вищої математики Ч.3 - К.: КПІ, 2002.-140с.
  26. Письменный Д. Конспект лекций по высшей математике. Ч.1.-М.:Айрис-пресс, -2004.-288с.
  27. Письменный Д. Конспект лекций по высшей математике. Ч.2.-М.:Айрис-пресс, -2005.-256с.


VI. Мова

Викладання дисципліни здійснюється українською мовою, для іноземних студентів – російською.


VІІ. Характеристика індивідуальних завдань


З метою кращого засвоєння курсу вищої математики та інтенсифікації самостійної роботи студентам пропонуються індивідуальні розрахункові роботи, які містить завдання з усіх розділів кредитних модулів. Контроль за виконанням проводиться у два етапи: 1) попередня перевірка правильності письмового розв’язку задач та прикладів; 2) захист розрахункових робот (усний чи письмовий).


VІІІ. Методика оцінювання


Бально-рейтингова система оцінювання якості навчально – пізнавальної діяльності студентів розроблена у відповідності з загально університетськими методичними рекомендаціями щодо розробки та застосування рейтингових систем оцінювання успішності студентів з навчальних дисциплін «Положення про рейтингову систему оцінювання успішності студентів». Сутність РСО з дисципліни, права та обов’язки студентів, тобто всі правила застосування РСО, доводяться до студентів на першому занятті з дисципліни.


Модуль 1

Рейтинг студента складається з балів, що отримуються за відповіді на практичних заняттях, експрес-контролі на практичних заняттях, балів по МКР та розрахункову роботу.

Розрахунок шкали R рейтингу :

Сума вагових балів контрольних заходів протягом семестру складає:

Rс= 100 балів

Студенти, які набрали протягом семестру рейтинг з кредитного модулю менше 60 балів, забов’язані виконувати залікову контрольну роботу.

Студенти, які набрали протягом семестру необхідну кількість балів (RD≥60), мають можливості:
  • отримати залікову оцінку (залік) так званим «автоматом»

відповідно до набраного рейтингу;
  • виконувати залікову контрольну роботу з метою підвищення оцінки;
  • у разі отримання оцінки, більшої ніж «автоматом» з рейтингу, студент отримає оцінку за результатами залікової контрольної

роботи.


Для отримання студентом відповідних оцінок (ECTS та традиційних) його рейтингова оцінка переводиться згідно з таблицею:


RD
Оцінка ECTS та визначення
Оцінка традиційна

95…100
А
Відмінно

85…94
В

Добре

75…84
С

65…74
D

Задовільно

60…64
E

RD<60
FX

незадовільно

RD <40
F

не допущений


Модуль 2

Рейтинг студента складається з балів, що отримуються за відповіді на практичних заняттях, експрес-контролі на практичних заняттях, балів по МКР та розрахункову роботу .


Розмір шкали рейтингу R=100 бали

Розмір стартової шкали RC=60 балів

Розмір екзаменаційної шкали RЕ =40 бали


Розрахунок шкали (R) рейтингу:

Сума вагових балів контрольних заходів протягом семестру складає:

Rc=60 балів.

Екзаменаційна складова шкали дорівнює 40% від R. Максимальна кількість балів дорівнює 40 балів.

RE=40 балів.

Таким чином, рейтингова шкала складає:

R=RC+RE=60+40=100 балів


Необхідною умовою допуску до екзамену є зарахування розрахункової роботи, а також стартовий рейтинг (rc) не менше 50 % від RC тобто 30 балів.


Для отримання студентом відповідних оцінок (ECTS та традиційних) його рейтингова оцінка RD переводиться згідно з таблицею:


RD = rC+ rE
Оцінка ECTS
Традиційна оцінка

95...100
A
Відмінно

85…94
B
Добре

75…84
C

65…74
D
Задовільно

60…64
E

RD<60
FX
Не задовільно

rC<30 або не виконані інші умови допуску до екзамену
F
Не допущений


ІХ. Організація


Організація навчання проходить у групах, визначених деканатом у відповідності до розкладу занять.

Семестрова атестація проводиться на основі відомостей, підготовлених деканатом..