Робоча навчальна програма для студентів спеціальності 040203 фізика Затверджено
| Вид материала | Документы |
- Робоча навчальна програма для студентів спеціальності 030301 „Журналістика Затверджено, 278.32kb.
- Робоча навчальна програма для студентів спеціальності 040103 геологія Затверджено, 628.51kb.
- Робоча навчальна програма для студентів спеціальності "060101 Правознавство" Затверджено, 408.94kb.
- Робоча навчальна програма для студентів спеціальності 030401 «Право» Затверджено, 944.73kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 176.29kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 280.46kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 321.43kb.
- Робоча навчальна програма для студентів спеціальності 030401 «Право» Затверджено, 797.55kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 208.66kb.
- Робоча навчальна програма для студентів спеціальності 030401 «Право» Затверджено, 1918.21kb.
Київський національний університет імені Тараса Шевченка
Радіофізичний факультет
Кафедра математики і теоретичної радіофізики
Укладач доц. Кривошея С. А.
ДИФЕРЕНЦІАЛЬНІ ТА ІНТЕГРАЛЬНІ
РІВНЯННЯ
РОБОЧА НАВЧАЛЬНА ПРОГРАМА
для студентів спеціальності 6.040203 - фізика
Затверджено
на засіданні кафедри
Протокол № 6
від 16 травня 2008 р.
З
 ав. кафедри
ав. кафедри_____________ Висоцький В. І.
Декан факультету
_____________ Анісімов І. О.
КИЇВ – 2008
Робоча навчальна програма з дисципліни «Диференціальні та інтегральні рівняння».
Укладач кандидат фіз.-мат. наук, доцент Кривошея Сергій Арсенович
Лектор кандидат фіз.-мат. наук, доцент Кривошея Сергій Арсенович
Викладачі:
доктор фіз.-мат. наук, професор, Макарець Микола Володимирович,
доктор фіз.-мат. наук, професор, Решетняк Віктор Юрійович,
кандидат фіз.-мат. наук, асистент Шмельова Людмила Володимирівна,
кандидат фіз.-мат. наук, асистент Субота Світлана Леонидівна,
кандидат фіз.-мат. наук, доцент Майко Наталія Валентинівна,
асистент Іваненко Дмитро Олександрович.
Погоджено
з науково-методичною комісією
19 травня 2008 р.
____________ Обуховський В. В.
ВСТУП
Дисципліна "Диференціальні та інтегральні рівняння" є базовою нормативною дисципліною для спеціальності "фізика", що вивчається в другому і третьому семестрах. Її обсяг становить 216 годин (6 кредитів за Європейською Кредитно-Трансферною Системою ECTS), в тому числі: 105 годин аудиторних занять (з них 35 годин лекцій і 70 годин практичних занять) та 111 години самостійної роботи.
2-ий семестр –– 108 години (3 кредити), в тому числі:
лекції –– 17 години,
практичні –– 34 годин,
самостійна робота –– 57 години;
3-ій семестр –– 108 години (3 кредити), в тому числі:
лекції –– 18 годин,
практичні –– 36 годин,
самостійна робота –– 54 години.)
Формою підсумкового контролю є залік за другий семестр та іспит за третій семестр.
Мета і завдання навчальної дисципліни "Диференціальні та інтегральні рівняння": ознайомлення й оволодіння методами теорії диференціальних і інтегральних рівнянь та їх основними застосуваннями; сприяння розвитку логічного й аналітичного мислення студентів.
Предмет навчальної дисципліни "Диференціальні та інтегральні рівняння" включає основні поняття, теореми, методи та моделі теорії диференціальних і інтегральних рівнянь.
Вимоги до знань і вмінь. Знати: основні поняття теорії диференціальних та інтегральних рівнянь.
Уміти: розв’язувати основні типи елементарно інтегровних рівнянь, застосовувати теоретичні методи до дослідження математичних моделей фізичних явищ.
Місце в структурно-логічній схемі спеціальності. Нормативна навчальна дисципліна "Диференціальні та інтегральні рівняння" є складовою циклу професійної підготовки фахівців освітньо-кваліфікаційного рівня "бакалавр", є базовою для вивчення всіх фізико-математичних дисциплін.
Система поточного і підсумкового контролю з навчальної дисципліни. Навчальна дисципліна "Диференціальні та інтегральні рівняння" складається з 4 змістових модулів і оцінюється за модульно-рейтинговою системою.
Для оцінювання знань студентів використовується 100-бальна шкала в кожному семестрі окремо.
РОЗДІЛ 1
ФОРМИ ПРОВЕДЕННЯ ПОТОЧНОГО ТА ПІДСУМКОВОГО КОНТРОЛЮ
Курс "Диференціальні та інтегральні рівняння" складається з двох змістових модулів (ЗМ-1 і ЗМ-2) у другому семестрі та двох змістових модулів (ЗМ-3 і ЗМ-4) у третьому семестрі.
В другому семестрі (3 кредити) передбачено:
1) 2 модульні контрольні роботи (ПМК-1, ПМК-2);
2) 4 контролі самостійної роботи студентів (СРС-1, СРС-2);
3) потокова письмова робота (колоквіум);
4) комплексний підсумковий модуль-залік (КПМ-1).
В третьому семестрі (3 кредити) передбачено:
1) 2 модульні контрольні роботи (ПМК-3, ПМК-4);
2) 4 контролі самостійної роботи студентів (СРС-3, СРС-4);
3) потокова письмова робота (колоквіум);
4) комплексний підсумковий модуль-іспит (КПМ-2).
За результатами кожного семестру студент отримує підсумкову оцінку за 100-бальною шкалою, в тому числі 10 балів за активну участь у практичних заняттях.
Табл.1 Семестр II
| | ЗМ-1 | ЗМ-2 | Колоквіум | Активність | Залік | Разом | ||
| | ПМК-1 | СРС-1 | ПМК-2 | СРС-2 | ||||
| Бали | 10 | 10 | 20 | 15 | ||||
| Всього балів | 20 | 35 | 10 | 10 | 25 | 100 | ||
Табл.2 Семестр III
| | ЗМ-3 | ЗМ-4 | Колоквіум | Активність | Іспит | Разом | ||
| | ПМК-3 | СРС-3 | ПМК-4 | СРС-4 | ||||
| Бали | 5 | 5 | 20 | 10 | ||||
| Всього балів | 10 | 30 | 10 | 10 | 40 | 100 | ||
Кількість балів за кожну з СРС-1–СРС-4 отримується як середнє арифметичне кількості білів за дві письмові контрольні роботи. Так, за кожну з двох контрольних робіт в СРС-1 і СРС-4 максимальна кількість балів 10; за кожну з двох контрольних робіт в СРС-2 –– 15 балів, за кожну з двох контрольних робіт в СРС-3 –– 5 балів.
Студентам, які протягом другого семестру набрали кількість балів, меншу за 60, надається можливість набрати необхідну кількість балів (25) на заліку. Студентам які протягом другого семестру набрали кількість балів, більшу за 60, додається 25 балів і залік виставляється автоматично.
РОЗДІЛ 2
НАВЧАЛЬНО-ТЕМАТИЧНИЙ ПЛАН ВИВЧЕННЯ ДИСЦИПЛІНИ
СЕМЕСТР I
| № теми | Назва теми | Кількість годин | ||
| Лекції | Практичні | Самостійна робота | ||
| Змістовий модуль 1 Скалярні диференціальні рівняння | ||||
| 1. | Елементарно інтегровні типи диференціальних рівнянь 1-го порядку | 4 | 8 | 10 |
| 2. | Скалярні диференціальні рівняння вищих порядків. Випадки зниження порядку | 2 | 4 | 8 |
| 3. | Теорема існування і єдиності розв’язку задачі Коші. Неявні диференціальні рівняння | 2 | 2 | 6 |
| Контроль СРС-1 | | | 1 | |
| Контроль СРС-2 | | | 1 | |
| Модульна контрольна робота ПМК-1 | | 2 | | |
| Всього за змістовий модуль 1 | 8 | 16 | 26 | |
| Змістовий модуль 2 Лінійні рівняння вищих порядків і системи лінійних рівнянь | ||||
| 4. | Загальні властивості розв’язків лінійних рівнянь і систем | 2 | | 2 |
| 5. | Фундаментальна матриця і фундаментальна система розв’язків. Метод Лагранжа | 2 | 2 | 4 |
| 6. | Метод Ейлера побудови загального розв’язку систем зі сталими коефіцієнтами | 2 | 10 | 12 |
| 7. | Метод Ейлера побудови загального розв’язку скалярного рівняння зі сталими коефіцієнтами | 2 | | |
| 8. | Інтегрування лінійних систем зі сталими коефіцієнтами | 1 | 4 | 10 |
| Контроль СРС-3 | | | 1 | |
| Контроль СРС-4 | | | 2 | |
| Модульна контрольна робота ПМК-2 | | 2 | | |
| Всього за змістовий модуль 2 | 9 | 18 | 31 | |
| ВСЬОГО ЗА 1-ИЙ СЕМЕСТР | 17 | 34 | 57 | |
СЕМЕСТР III
| № теми | Назва теми | Кількість годин | ||
| Лекції | Практичні | Самостійна робота | ||
| Змістовий модуль 3 Лінійні диференціальні задачі та теорія стійкості за Ляпуновим | ||||
| 1. | Схема застосування інтегрального перетворення Лапласа до інтегрування лінійних диференціальних рівнянь і систем зі сталими коефіцієнтами | 2 | 4 | 6 |
| 2. | Лінійні диференціальні (крайові) задачі. Метод функції Гріна | 2 | 2 | 4 |
| 3. | Спектральні крайові задачі. Задача Штурма–Ліувілля | 2 | 2 | 6 |
| 4. | Стійкість лінійних систем. Стійкість за першим наближенням | 2 | 4 | 4 |
| 5. | Стійкість точки спокою двох лінійних рівнянь зі сталими коефіцієнтами | 2 | 2 | 2 |
| Контроль СРС-5 | | | 2 | |
| Контроль СРС-6 | | | 2 | |
| Модульна контрольна робота ПМК-3 | | 2 | | |
| Всього за змістовий модуль 3 | 10 | 16 | 26 | |
| Змістовий модуль 4 Лінійні рівняння 1-го порядку з частинними похідними і елементи теорії інтегральних рівнянь | ||||
| 6. | Методи інтегрування нормальних систем диференціальних рівнянь. Регулярний метод степеневих рядів | 2 | 10 | 10 |
| 7. | Лінійні однорідні і квазіоднорідні рівняння з частинними похідними першого порядку | 2 | 6 | 6 |
| 8. | Інтегральні рівняння Фредгольма з виродженим ядром. Альтернатива Фредгольма | 2 | 2 | 6 |
| 9. | Метод послідовних наближень для рівняння Фредгольма і Вольтерра | 2 | | 2 |
| Контроль СРС-7 | | | 2 | |
| Контроль СРС-8 | | | 2 | |
| Модульна контрольна робота ПМК-4 | | 2 | | |
| Всього за змістовий модуль 4 | 8 | 20 | 28 | |
| ВСЬОГО ЗА 3-ИЙ СЕМЕСТР | 18 | 36 | 54 | |
| ВСЬОГО ЗА КУРС | 35 | 70 | 111 | |
РОЗДІЛ 3
ЗМІСТ ДИСЦИПЛІНИ ЗА ТЕМАМИ
(ЛЕКЦІЇ)
СЕМЕСТР II
Змістовий модуль 1. Скалярні диференціальні рівняння (8 год.)
Лекція 1 (2 год.)
Типи рівнянь. Поле напрямів. Метод ізоклін. Диференціальні рівняння з відокремлюваними змінними і звідні до них. Лінійні рівняння першого порядку
Лекція 2 (2 год.)
Рівняння в повних диференціалах. Інтегрувальний множник. Поняття загального розв‘язку і загального інтеграла.
Лекція 3 (2 год.)
Інтегровні типи скалярних рівнянь вищих порядків. Випадки зниження порядку.
Лекція 4 (2 год.)
Існування і єдиність розв‘язку задачі Коші. Існування і єдиність розв‘язку задачі Коші для лінійних рівнянь і систем. Неявні скалярні рівняння. Відшукання особливого розв‘язку за відомим загальним.
Змістовий модуль 2 . Лінійні рівняння вищих порядків і системи лінійних рівнянь (9 год.)
Лекція 1 (2 год.)
Лінійні рівняння і системи. Основні поняття і властивості розв‘язків.
Лекція 2 (2 год.)
Фундаментальна матриця і фундаментальна система розв‘язків. Загальний розв‘язок. Метод Лагранжа.
Лекція 3 (2 год.)
Метод Ейлера побудови загального розв‘язку скалярного рівняння зі сталими коефіцієнтами. Загальний розв‘язок неоднорідного рівняння. Випадок неоднорідності – квазіполінома.
Лекція 4, 5 (3 год.)
Метод Ейлера побудови загального розв‘язку лінійної системи зі сталими коефіцієнтами. Лінійні неоднорідні системи зі сталими коефіцієнтами.
СЕМЕСТР III
Змістовий модуль 3. Лінійні диференціальні задачі та теорія стійкості за Ляпуновим (10 год.)
Лекція 1 (2 год.)
Короткий огляд властивостей інтегрального перетворення Лапласа. Загальна схема застосування перетворення Лапласа до інтегрування рівнянь і систем зі сталими коефіцієнтами.
Лекція 2 (2 год.)
Лінійні крайові задачі. Їх типи. Метод функцій Гріна.
Лекція 3 (2 год.)
Спектральні крайові задачі. Задача Штурма – Ліувілля.
Лекція 4 (2 год.)
Стійкість за Ляпуновим. Система збурень. Стійкість лінійних систем. Стійкість за першим наближенням.
Лекція 5 (2 год.)
Стійкість точки спокою системи двох лінійних рівнянь зі сталими коефіцієнтами. Типи особливих точок. Поняття про функції Ляпунова.
Змістовий модуль 4. Лінійні рівняння 1-го порядку з частинними похідними
і елементи теорії інтегральних рівнянь (8 год.)
Лекція 1 (2 год.)
Методи інтегрування нормальних систем (виключення і інтегровних комбінацій). Регулярні методи степеневих рядів і малого параметра. Рівняння Бесселя.
Лекція 2 (2 год.)
Лінійні і квазілінійні рівняння з частинними похідними першого порядку. Загальний розв‘язок. Розв‘язок задачі Коші.
Лекція 3 (2 год.)
Інтегральні рівняння Фредгольма з виродженим ядром. Альтернатива Фредгольма.
Лекція 4 (2 год.)
Методи послідовних наближень для рівнянь Фредгольма і Вольтерра. Рівняння з симетричним ядром.
РОЗДІЛ 4
ПЛАН ПРАКТИЧНИХ ЗАНЯТЬ
СЕМЕСТР II
Змістовий модуль 1. Скалярні диференціальні рівняння (16 год.)
Практичне заняття 1 (2 год.)
1. Рівняння з відокремлюваними змінними
2. Метод ізоклін
Практичне заняття 2 (2 год.)
1. Однорідні рівняння першого порядку і звідні до них
2. Квазіоднорідні рівняння першого порядку
Практичне заняття 3 (2 год.)
1. Лінійні рівняння першого порядку. Методи Лагранжа і Бернуллі
2. Рівняння Бернуллі й інші рівняння, звідні до лінійних
Практичне заняття 4 (2 год.)
1. Рівняння в повних диференціалах
2. Інтегрувальний множник
Практичне заняття 5 (2 год.)
1. Неявні скалярні рівняння. Рівняння Лагранжа і Клеро
2. Відшукання особливого розв‘язку за відомим загальним
Практичне заняття 6 (2 год.)
Скалярні рівняння вищих порядків, інтегровні в квадратурах.
Практичне заняття 7 (2 год.)
Скалярні рівняння вищих порядків. Випадки зниження порядку.
Практичне заняття 8 (2 год.)
Контрольна модульна робота ПМК-1 (2 год.)
Змістовий модуль 2. Лінійні рівняння вищих порядків і системи лінійних рівнянь (18 год.)
Практичне заняття 1 (2 год.)
1. Лінійні рівняння вищих порядків (n = 2)
2. Метод Лагранжа
3. Формула Абеля (
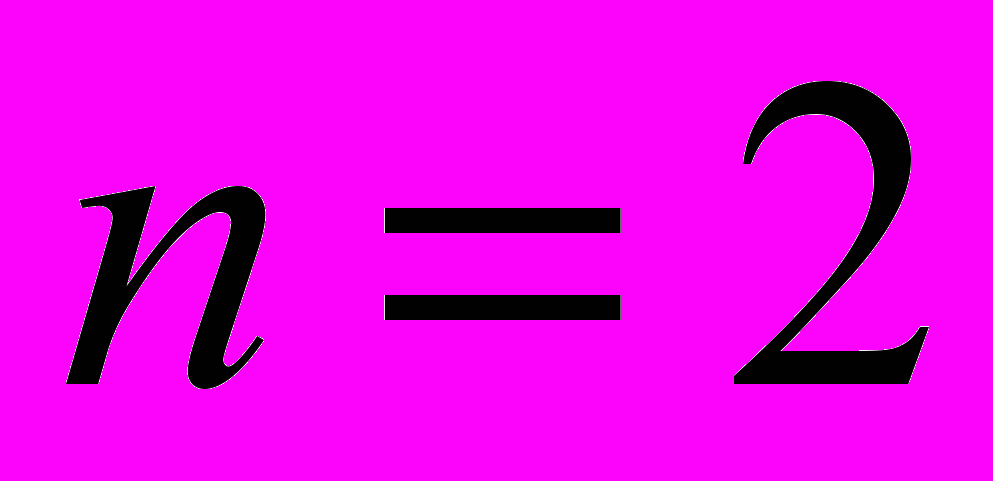 )
)Практичне заняття 2 (2 год.)
1. Лінійні однорідні рівняння зі сталими коефіцієнтами. Метод Ейлера
побудови загального розв‘язку
2. Рівняння Ейлера, Лагранжа, Чебишова
Практичне заняття 3 (2 год.)
1. Лінійні неоднорідні рівняння зі сталими коефіцієнтами. Принцип
суперпозиції
2. Випадок неоднорідності у вигляді квазіполінома
Практичне заняття 4 (2 год.)
Інтегрування лінійних однорідних систем зі сталими коефіцієнтами
методом Ейлера
Практичне заняття 5, 6 (4 год.)
1. Побудова матричних експонент у випадку жорданової нормальної форми
матриці
2. Інтегрування лінійних однорідних систем зі сталими коефіцієнтами
матричним методом
Практичне заняття 7, 8 (4 год.)
1. Інтегрування лінійних неоднорідних систем. Метод Лагранжа
2. Лінійні неоднорідні системи зі сталими коефіцієнтами. Випадок
неоднорідності у вигляді векторного квазіполінома
Практичне заняття 9 (2 год.)
Контрольна модульна робота ПМК-2 (2 год.)
СЕМЕСТР III
Змістовий модуль 3. Лінійні диференціальні задачі та теорія стійкості за Ляпуновим (16 год.)
Практичне заняття 1, 2 (4 год.)
1. Знаходження зображень і оригіналів
2. Інтегрування лінійних рівнянь і систем зі сталими коефіцієнтами
операційним методом
Практичне заняття 3 (2 год.)
1. Крайові задачі
2. Лінійні неоднорідні крайові задачі. Метод функцій Гріна
Практичне заняття 4 (2 год.)
Задача Штурма – Ліуввілля
Практичне заняття 5 (2 год.)
1. Означення стійкості за Ляпуновим
2. Стійкість лінійних систем зі сталими коефіцієнтами. Критерій Гурвіца
Практичне заняття 6 (2 год.)
1. Система збурень і її лінеаризація
2. Дослідження на стійкість за першим наближенням
Практичне заняття 7 (2 год.)
Дослідження на стійкість точок спокою лінійних систем. Типи точок спокою.
Практичне заняття 8 (2 год.)
Контрольна модульна робота ПМК-3 (2 год.)
Змістовий модуль 4. Лінійні рівняння 1-го порядку з частинними похідними
і елементи теорії інтегральних рівнянь (20 год.)
Практичне заняття 1, 2, 3 (6 год.)
1. Інтегрування нормальних систем. Метод виключення
2. Інтегрування нормальних систем. Метод інтегровних комбінацій
Практичне заняття 4 (2 год.)
Регулярний метод степеневих рядів. Рівняння Бесселя
Практичне заняття 5 (2 год.)
Регулярний метод малого параметра
Практичне заняття 6, 7 (4 год.)
1. Лінійні і квазілінійні рівняння з частинними похідними першого
порядку. Побудова загального розв‘язку
2. Побудова розв‘язку задачі Коші
Практичне заняття 8, 9 (4 год.)
1. Розв‘язування рівнянь Фредгольма з виродженим ядром
2. Розв‘язування рівнянь Фредгольма з параметром у випадку
виродженого ядра. Альтернатива Фредгольма
Практичне заняття 10 (2 год.)
Контрольна модульна робота ПМК-4 (2 год.)
РОЗДІЛ 5
ОРГАНІЗАЦІЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ
Складовими самостійної роботи студента є:
1) робота над лекційним матеріалом за конспектом лекцій;
2) підготовка до практичних занять;
3) виконання домашніх завдань;
4) опрацювання частини лекційного матеріалу, винесеного на самостійне вивчення за вказаними джерелами;
5) виконання індивідуальних завдань та їх захист під час контролю СРС.
ПИТАННЯ ДЛЯ САМОСТІЙНОГО ВИВЧЕННЯ
ЗМ-1
- Метод ізоклін
2.Відшукання особливих розв‘язків
3. Рівняння Лагранжа і Клеро. Неявні диференціальні рівняння 1-го порядку
Література [1, 2.4, 3.1 – 3.4]
ЗМ-2
1. Властивості розв‘язків лінійних рівнянь і систем (доведення)
2. Побудова матричної експоненти
Література [1, 4.1, 4.2, 5.1, 5.2], [2]
ЗМ-3
1. Основні теореми операційного числення
2. Методи відшукання оригіналів
3. Властивості розв‘язків задачі Штурма – Ліуввілля (доведення)
4. Функції Ляпунова
Література [1, 5.1, Д.1, 6.4, 8.3, 8.4], [2], [6]
ЗМ-4
1. Функції Бесселя і їх властивості
2. Задача Коші для квазілінійних рівнянь з частинними похідними першого порядку
3. Регулярні методи малого параметра
4. Інтегральні рівняння з симетричним ядром
Література [1: 7.3, 7.4, 9.2, 9.3, 10.3, 10.4, 10.5]
РОЗДІЛ 6
КОНТРОЛЬНІ ЗАПИТАННЯ ТА ЗАВДАННЯ;
ПРОБЛЕМНІ ТЕМИ ДЛЯ ОБГОВОРЕННЯ
ЗМ-1
1. Рівняння першого порядку. Геометричний смисл. Розв‘язок. Метод ізоклін.
2. Рівняння з відокремленими змінними і звідні до них: однорідні й квазіоднорідні.
3. Лінійні рівняння першого порядку і звідні до них. Методи Лагранжа і Бернуллі.
4. Метод інтегрування рівняння в повних диференціалах.
5. Інтегрувальний множник і методи його знаходження.
6. Скалярні рівняння вищих порядків, інтегровні в квадратурах.
Випадки зниження порядку.
7. Теорема існування і єдиності розв‘язку задачі Коші.
8. Рівняння Лагранжа і Клеро.
9. Відшукання особливих розв’язків.
ЗМ-2
1. Властивості розв‘язків лінійних однорідних рівнянь і систем.
Формула Остроградського – Ліуввілля. Формула Абеля.
2. Властивості розв‘язків лінійних неоднорідних рівнянь і систем.
Принцип суперпозиції.
3. Фундаментальна система розв‘язків, фундаментальна матриця і їх властивості.
4. Метод Лагранжа.
5. Метод Ейлера для рівнянь і систем зі сталими коефіцієнтами.
6. Інтегрування лінійних рівнянь і систем зі сталими коефіцієнтами у випадку
неоднорідності – квазіполінома.
7. Матричний метод інтегрування лінійних однорідних систем зі сталими
коефіцієнтами.
ЗМ-3
1. Основні теореми операційного числення.
2. Загальна схема застосування операційного методу.
3. Типи лінійних крайових задач.
4. Побудова функцій Гріна лінійних крайових задач для рівнянь другого порядку у
випадку розщеплених і нерозщеплених крайових умов.
5. Спектральні крайові задачі. Задача Штурма – Ліуввілля і її властивості.
6. Означення стійкості, асимптотичної стійкості і нестійкості за Ляпуновим.
Система збурень.
7. Стійкість лінійних систем.
8. Стійкість лінійних систем зі сталими коефіцієнтами.
9. Критерій Гурвіца.
10. Стійкість за першим наближенням.
11. Класифікація точок спокою і їх стійкість.
12. Функції Ляпунова. Теореми Ляпунова.
ЗМ-4
1. Метод виключення.
2. Метод інтегровних комбінацій.
3. Регулярний метод степеневих рядів.
4. Регулярний метод малого параметра.
5. Рівняння Бесселя і функції Бесселя.
7. Система характеристик. Загальний розв‘язок лінійного однорідного рівняння
з частинними похідними першого порядку.
8. Квазілінійні рівняння.
9. Розв‘язання задачі Коші.
10. Інтегральні рівняння Фредгольма з виродженим ядром.
11. Альтернатива Фредгольма.
12. Метод послідовних наближень для рівнянь Фредгольма і Вольтерра.
13. Інтегральні рівняння Фредгольма з симетричним ядром і їх властивості.
РОЗДІЛ 7
ПЕРЕЛІК ПИТАНЬ, ЯКІ ВИНОСЯТЬСЯ НА ІСПИТ
На залік (ПМК-1) винесено контрольні питання до ЗМ-1 і ЗМ-2.
На іспит (ПМК-2) винесено контрольні питання до ЗМ-1 - ЗМ-4.
ЛІТЕРАТУРА
1. Основні джерела
1. С.А. Кривошея, М.О. Перестюк, В.М. Бурим, Диференціальні та інтегральні
рівняння, К., „Либідь”, 2004.
2. А.М. Самойленко, С.А. Кривошея, М.О. Перестюк, Диференціальні рівняння в
задачах, К., „Либідь”, 2003.
3. А.Ф. Филиппов, Сборник задач по дифференциальным уравнениям, М., 1979.
2. Додаткові джерела
4. Л.Э. Эльсгольц, Дифференциальные уравнения и вариационное исчисление,
М., 1965.
5. П.П. Головач, О.Ф. Калайда, Збірник задач з диференціальних та інтегральних
рівнянь, К., 1997.
6. С.А. Кривошея, Ю.В. Придатченко, А.Т. Янішевський, Операційне числення,
К., 1997.
