Теоретическая механика

Вид материала

Лекция

Содержание Введение в кинематику точки

Подобный материал:

• Рабочая программа Наименование дисциплины Теоретическая механика По специальности 220501., 218.91kb.
• Рабочая программа дисциплины «Теоретическая механика» наименование, 700.1kb.
• Программа дисциплины теоретическая механика цели и задачи дисциплины. "Теоретическая, 216.89kb.
• Учебное пособие для студентов механико-математического факультета специальностей «Механика»,, 1167.1kb.
• Программа-минимум кандидатского экзамена по специальности 01. 04. 02 «Теоретическая, 115.8kb.
• Общий курс физики т-1 Механика: учебное пособие М.: Физматлит, 2002. Сивухин Д. В.,, 679.32kb.
• Программа подраздела «История механики», 75.11kb.
• Аннотация программы дисциплины учебного плана и программ учебной и производственных, 24.01kb.
• «Теоретическая механика», 79.2kb.
• «Теоретическая механика», 75.26kb.

Теоретическая механика.

(ауд.Г-200, среда, 15.30-16.55)


Лекция №1 (Статика, 7 февраля 2001)

1. Введение. Предмет теоретической механики. Механическое движение. Сила. Абсолютно твердое тело. Статика, кинематика, динамика. История науки. Архимед (287-212 г. до н.э.), Галилей (1564-1642), Ньютон( 1643-1727), Эйлер (1707-1783), Д’Аламбер (1717-1783), Лагранж (1736-1813), Пуансо (1777-1859), Чебышев (1821-1894), Ковалевская (1850-1891), Циолковский (1857-1935), Жуковский (1847-1921).
   
2. Сила как вектор. Системы сил (сходящиеся, параллельные, плоская система). Эквивалентные системы сил. Уравновешенная система. Равнодействующая. Уравновешивающая сила. Внутренние и внешние силы. Сосредоточенные и распределенные силы (объемные, поверхностные).
   
3. Аксиомы. Роль аксиом в науке.
   
4. Аксиома связи.
   

Лекция №2 (Статика, 14 февраля 2001)

1. Теорема о трех силах.
   
2. Связи и их реакции.
   
3. Равнодействующая системы сходящихся сил. Главный вектор. Условие равновесия системы сходящихся сил. Сложение параллельных сил. Пара сил.
   

Лекция №3 (Статика, 21 февраля 2001: Подалков В.В.)

1. Момент силы относительно центра и относительно оси.
   
2. Свойства пары сил.
   

1. Сумма пар в одной плоскости.
   
2. Эквивалентность пар в параллельных плоскостях.
   

Лекция №4 (Статика, 28 февраля 2001)

1. Сумма пар в пересекающихся плоскостях.(Момент пары свободный вектор)
   
2. Равновесие системы пар.
   
3. Лемма Пуансо «Силу можно переносить эквивалентным образом на параллельную прямую, прибавляя пару с моментом, равным моменту силы относительно новой точки приложения»
   
4. Основная теорема статики (Пуансо). «Всякую систему сил можно заменить эквивалентным образом главным моментом относительно некоторой точки (центр приведения) и главным вектором, приложенным к этой точке».
   
5. Условие равновесия произвольной системы сил.
   
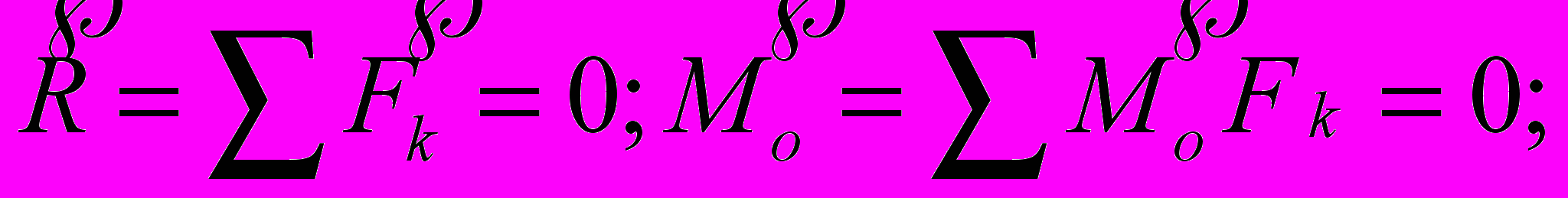
6. Теорема Вариньона «Момент равнодействующей системы равен сумме моментов сил системы относительно того же центра.»
   
7. Варианты условия равновесия плоской системы сил.
   
8. Силы, распределенные по линейному закону. 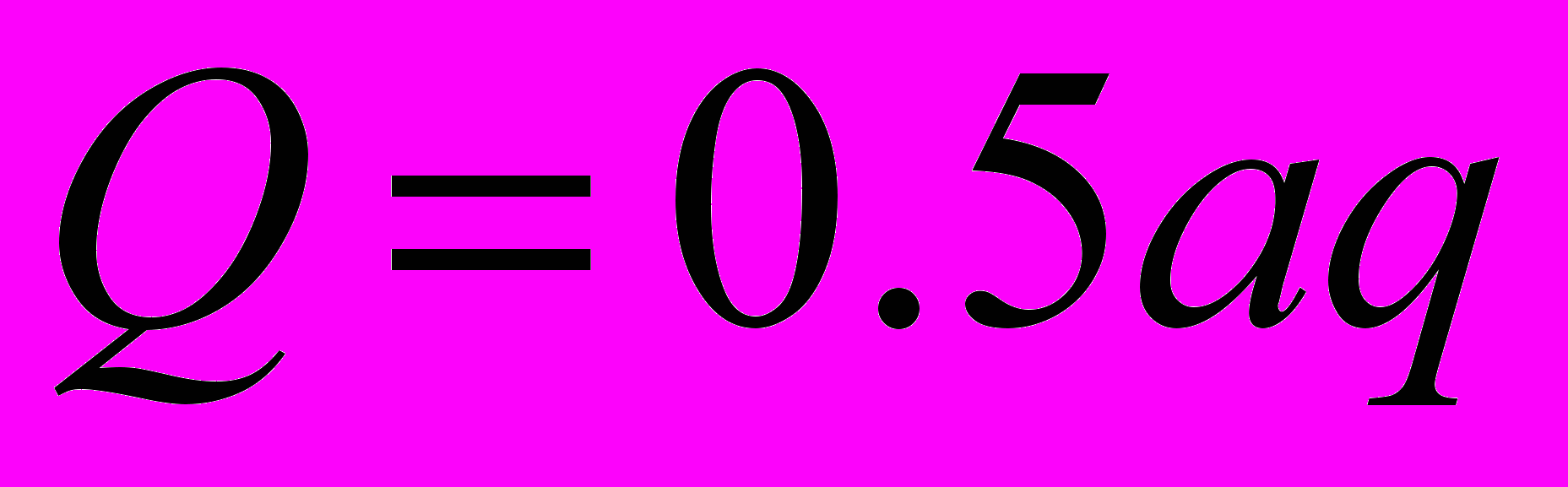. Силы, равномерно распределенные по дуге S окружности радиуса R. (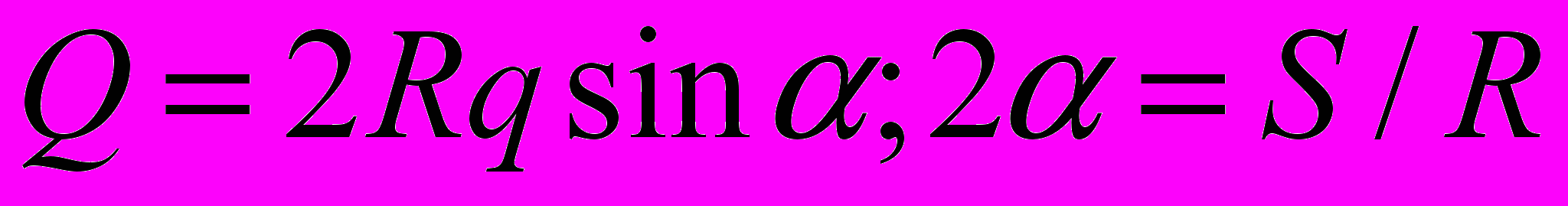)Тарг, § 21
   
9. Реакция заделки (Тарг, § 21)
   
10. Статические инварианты., 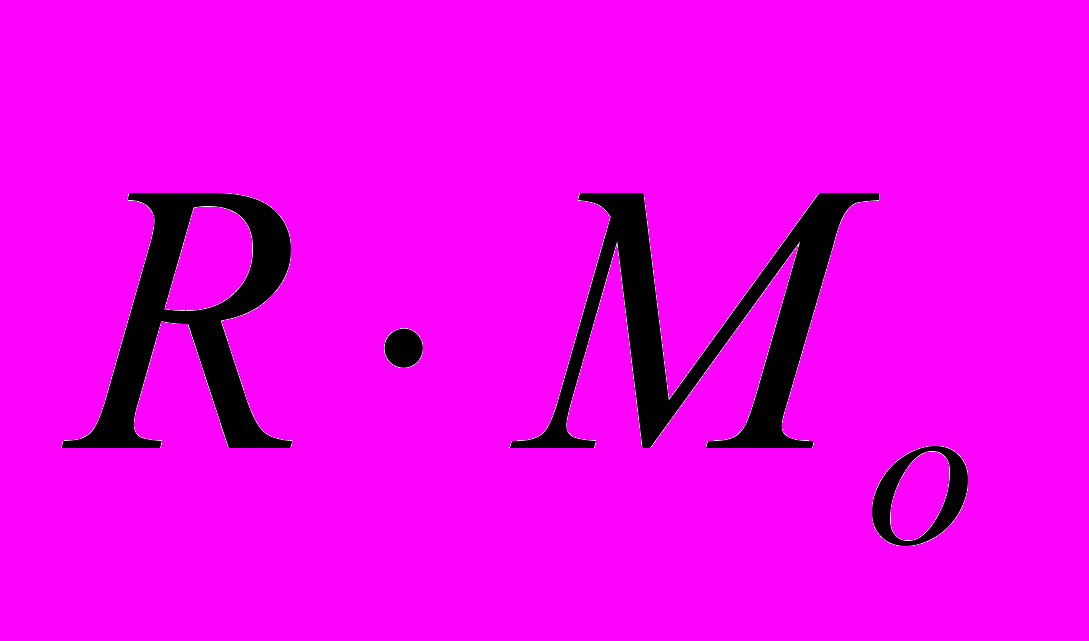Динама.
    

Лекция №5 (Статика,Кинематика, 7марта 2001)

1. Минимальный момент приведения 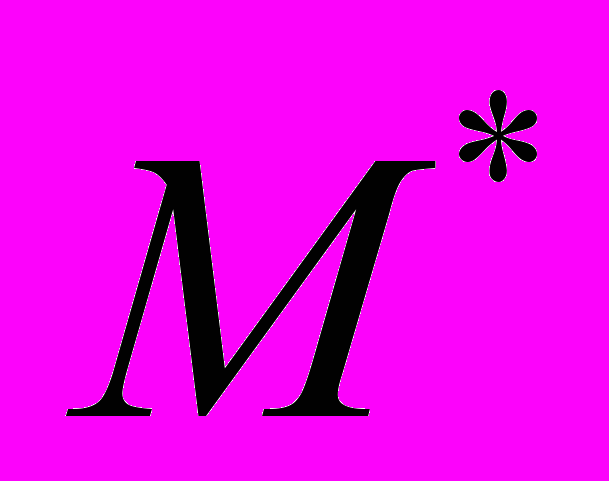. Центральная винтовая ось.
   

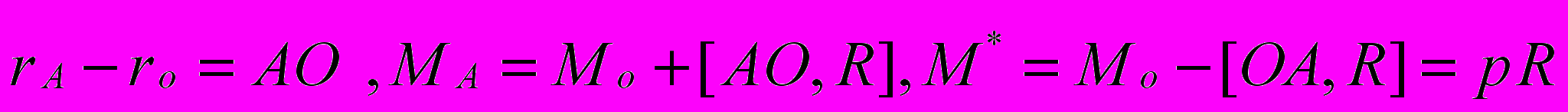
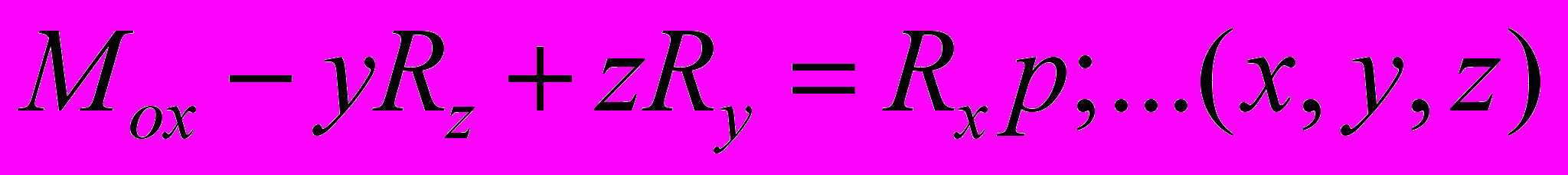
2. Введение в кинематику точки. Система отсчета. Траектория. Способы задания движения точки (координатный, векторный, естественный).
   
3. Радиус-вектор точки. Скорость и ускорение точки в декартовой системе координат.
   
4. Трехгранник Френе. Соприкасающаяся плоскость, нормальная, спрямляющая. Нормаль, касательная, бинормаль.
   

Лекция №6 (Кинематика, 14марта 2001)

1. Годограф вектора. Производная вектора по скалярному аргументу.
   
2. Скорость и ускорение точки в естественных осях. Угол смежности. Кривизна кривой. Радиус кривизны. Нормальное и касательное ускорение. Физический смысл компонент ускорения в естественных осях. Вектор кривизны.
   
3. Полярные координаты. Скорость и ускорение точки в полярных координатах.
   
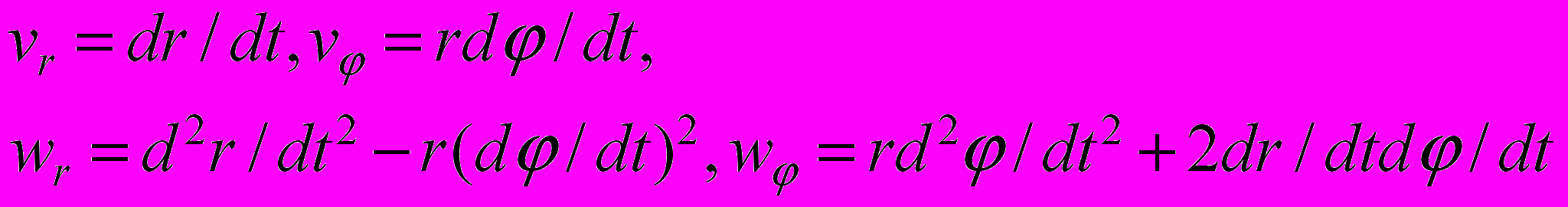
4. Простейшие движения твердого тела. Поступательное движение. Закон движения. Скорости и ускорения точек тела.
   
5. Вращательное движение. Закон движения. Угловая скорость и угловое ускорение тела.
   

Лекция №7 (Кинематика, 21марта 2001)

1. Вектора угловой скорости и углового ускорения. Замедленное и ускоренное вращение. Равномерное и равноускоренное (замедленное) движение. Формула Эйлера для скорости точки тела. 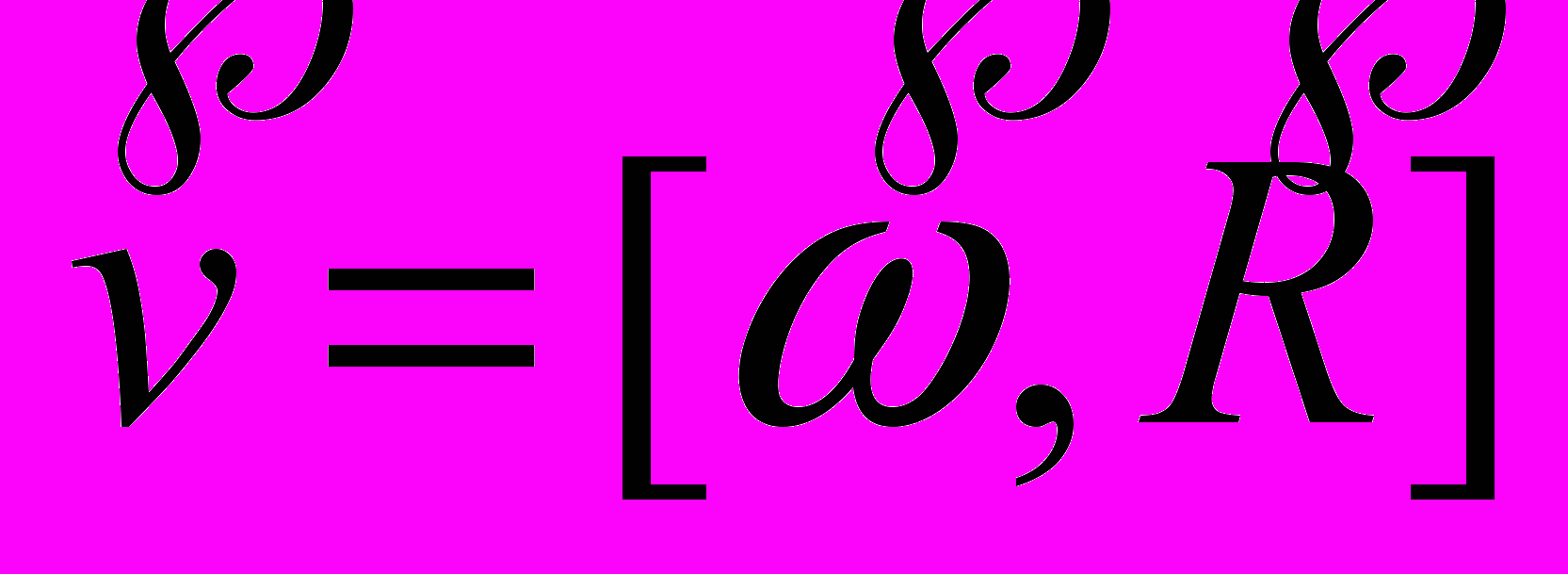. Распределение скоростей в теле.
   
2. Центростремительное и вращательное ускорение. Формула Ривальса 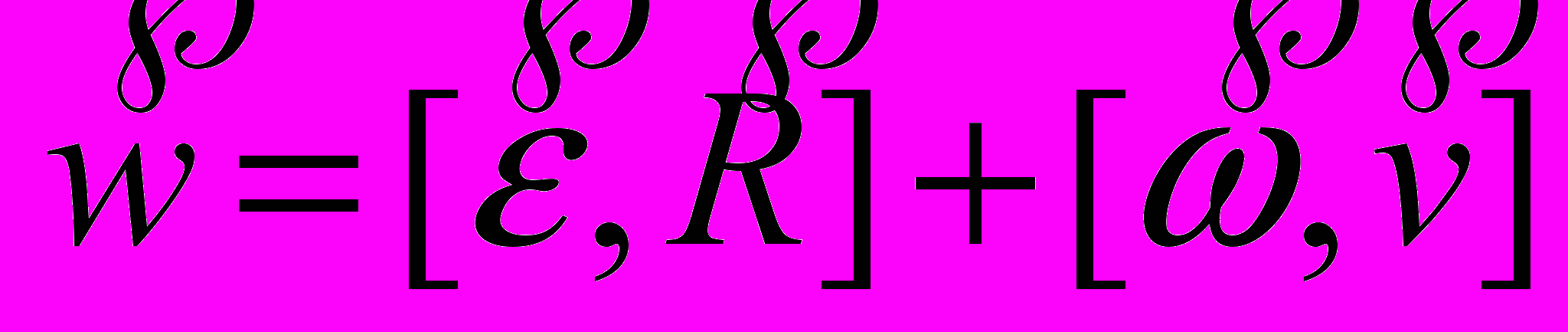. Распределение ускорений в теле.
   
3. Плоское движение. Закон движения. Зависимость (или независимость) уравнений закона движения от выбора полюса. Скорости точек. (Скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости В вокруг полюса)
   
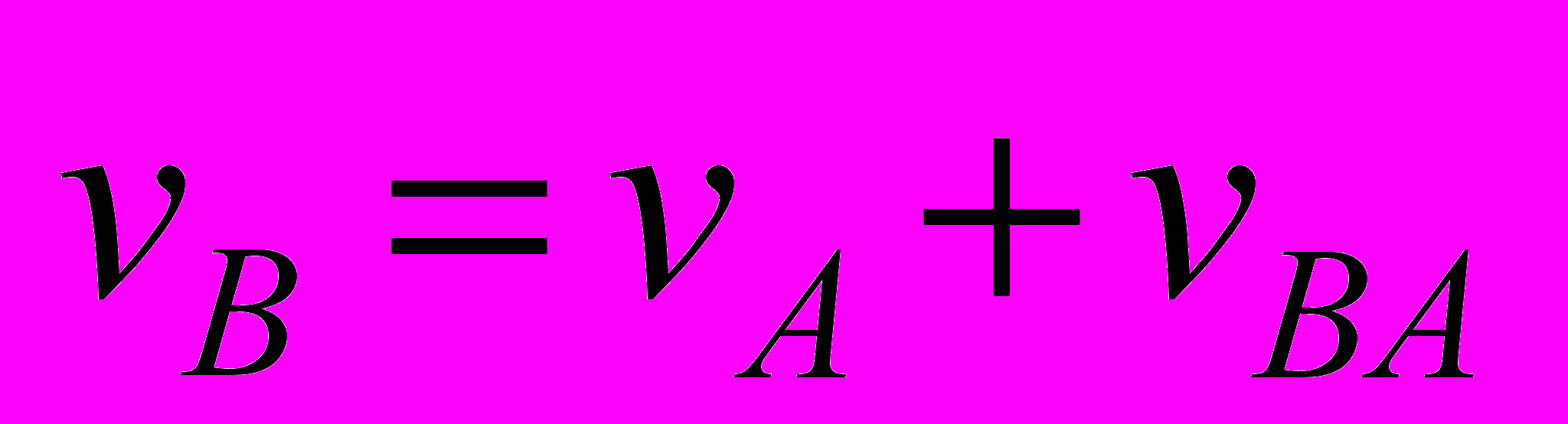
4. Ускорения точек тела при плоском движении .
   
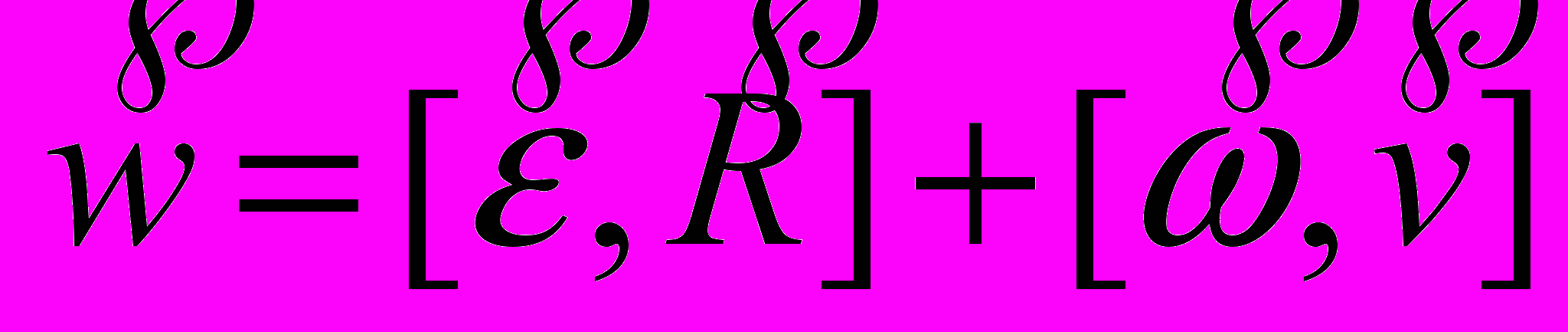5. Теорема о скоростях точек неизменяемого отрезка. (Проекции скоростей двух точек тела на ось, проходящую через эти точки, равны).
   

Лекция №8 (Кинематика, 28 марта )

1. Теорема о концах векторов скоростей точек неизменяемого отрезка. (Концы векторов скоростей точек отрезка лежат на одной прямой и делят ее на части пропорциональные расстояниям между точками)
   
2. Мгновенный центр скоростей. Существование и единственность. Частные случаи положения МЦС. Центроиды (подвижные и неподвижные).
   
3. Графоаналитический метод решения задач кинематики многозвенных механизмов.
   
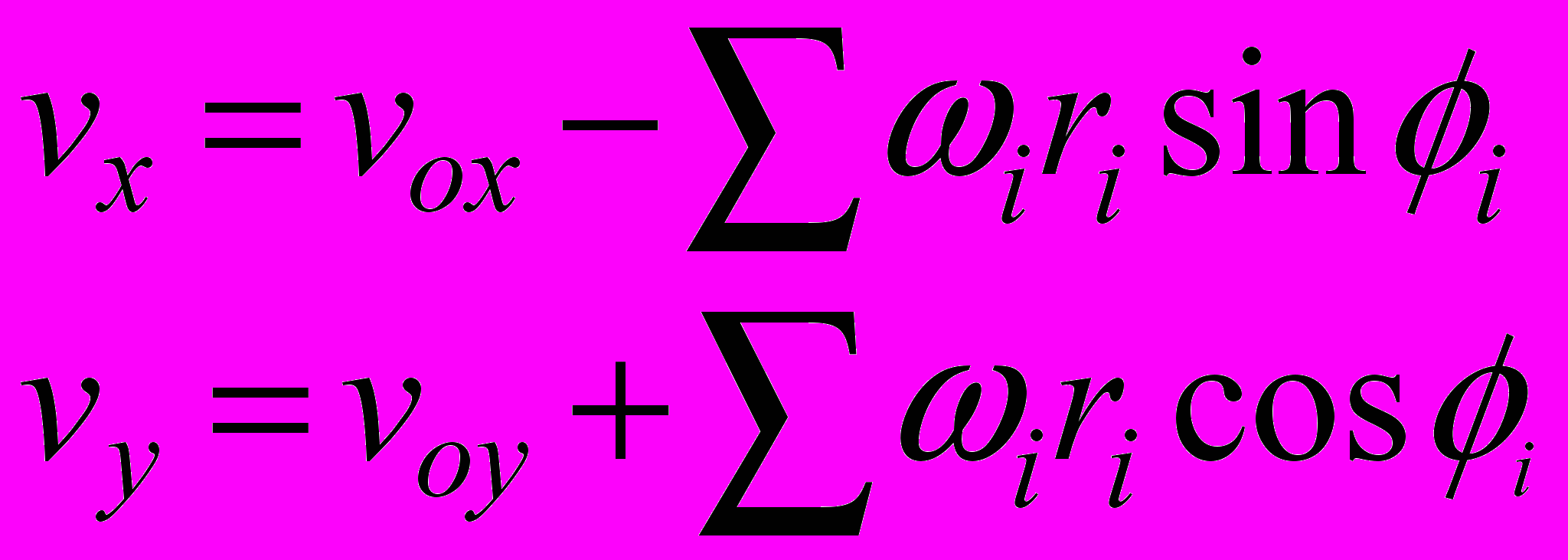
4. Кинематический четырехзвенник. Уравнение трех угловых скоростей 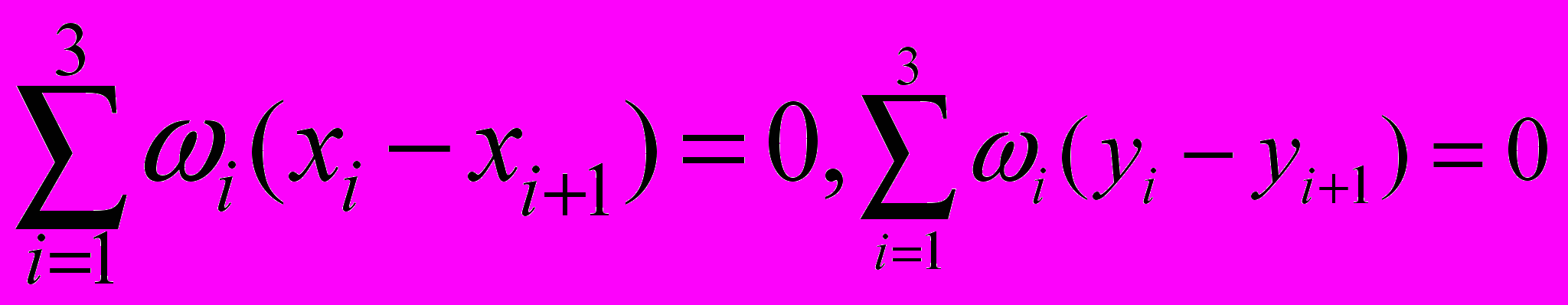и теорема трапеции. Следствие. ()
   
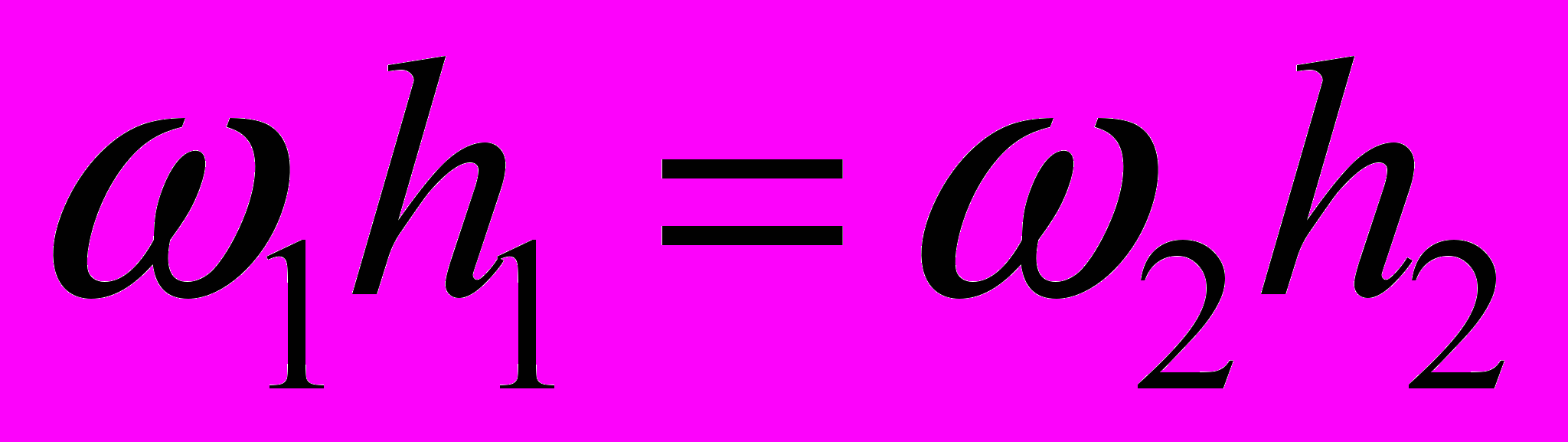5. Мгновенный центр ускорений.
   
6. Сферическое движение. Углы Эйлера (собственного вращения, прецессии, нутации).
   

Лекция №9 (Кинематика, 4 апреля )

1. Кинематические уравнения Эйлера (проекция на подвижные оси).
   
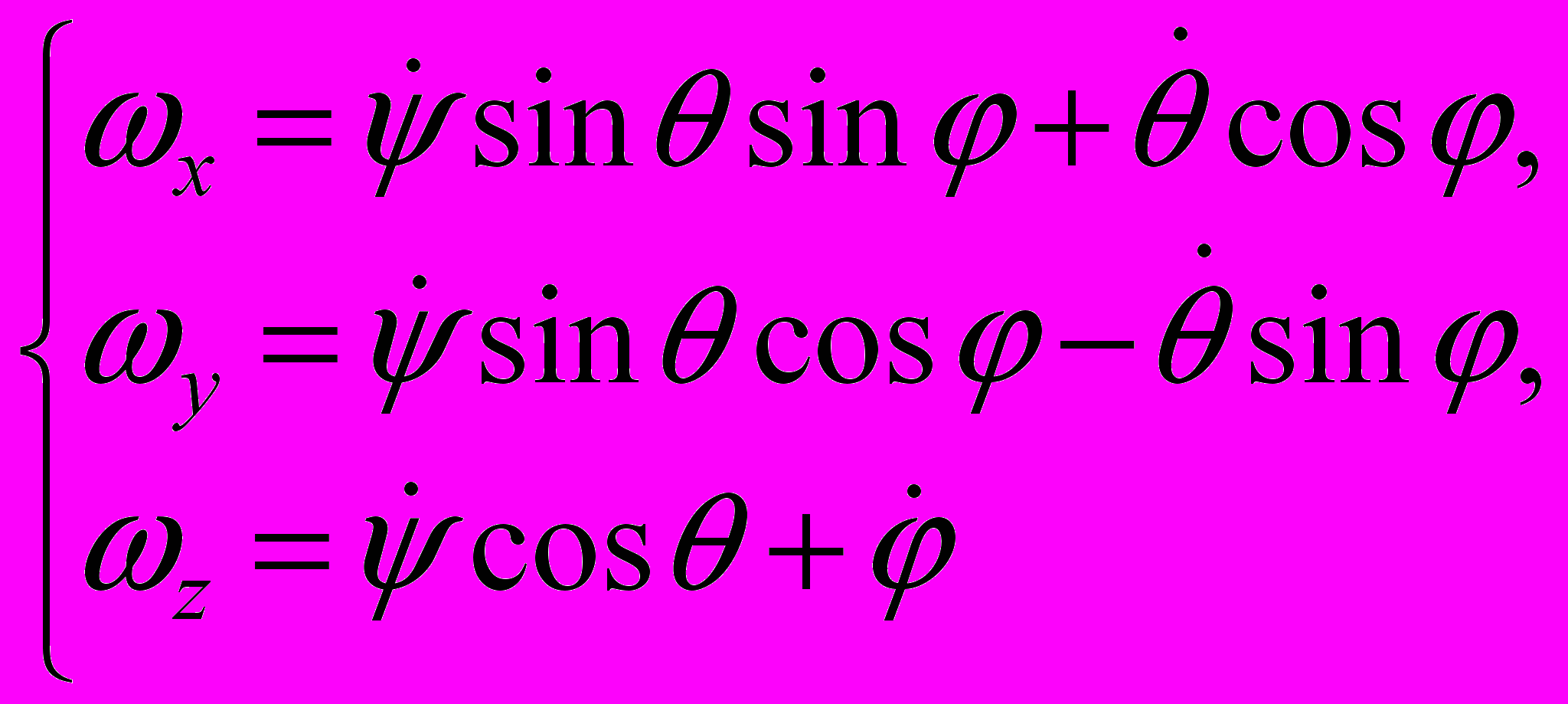
2. Скорости и ускорения точек тела при сферическом движении.
   
3. Общий случай движения свободного тела.
   
4. Сложное движение точки. Относительное, переносное и абсолютное движение.
   
5. Сложение скоростей.
   
6. Сложение ускорений. 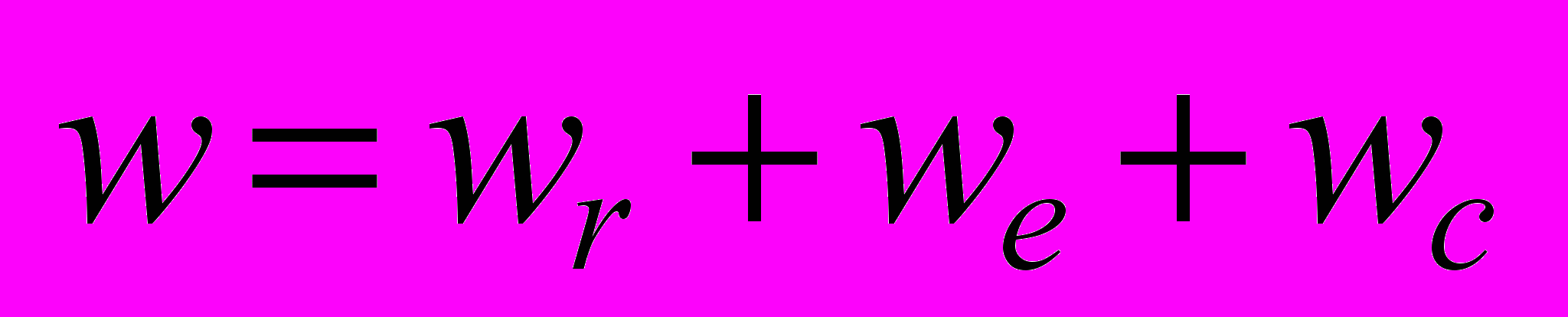.Ускорение Кориолиса (1792-1843).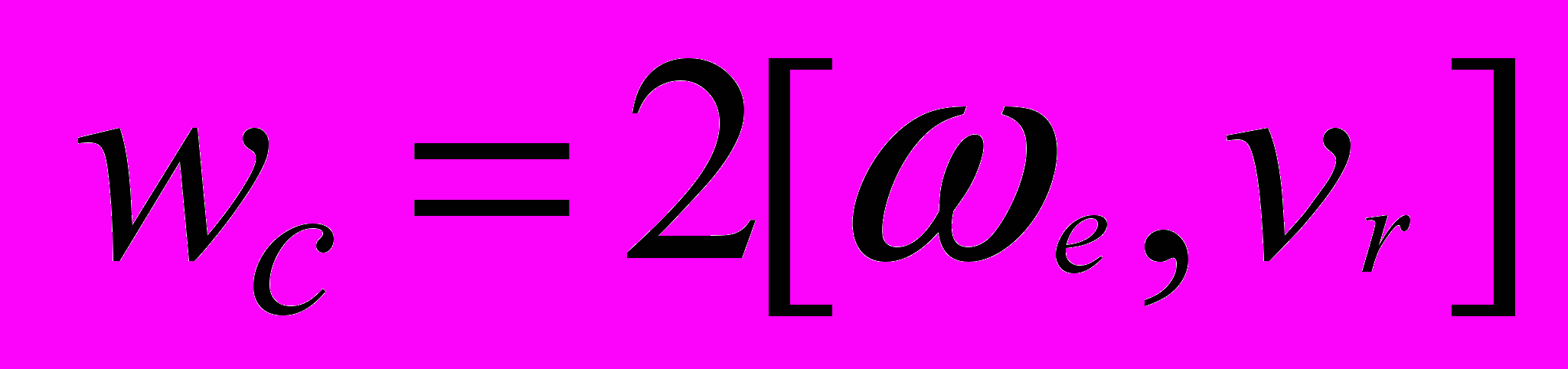
   

Правило Жуковского.


Лекция №10 (Кинематика. Динамика. 11 апреля)

1. Сложное движение твердого тела. Сложение поступательных движений. Сложение вращений вокруг параллельных осей. Пара вращений. Сложение вращений вокруг пересекающихся осей.
   
2. Основные понятия динамики. Законы динамики.
   
3. Дифференциальное уравнение движения точки в декартовых и естественных координатах.
   

Лекция №11 (Динамика. 18 апреля)

1. Интегрирование уравнения движения точки в случае
   а) постоянной силы,
   б) силы, зависящей от координаты,
   в) силы, зависящей от скорости,
   г) силы, зависящей от времени.
   
   
   
2. Импульс силы 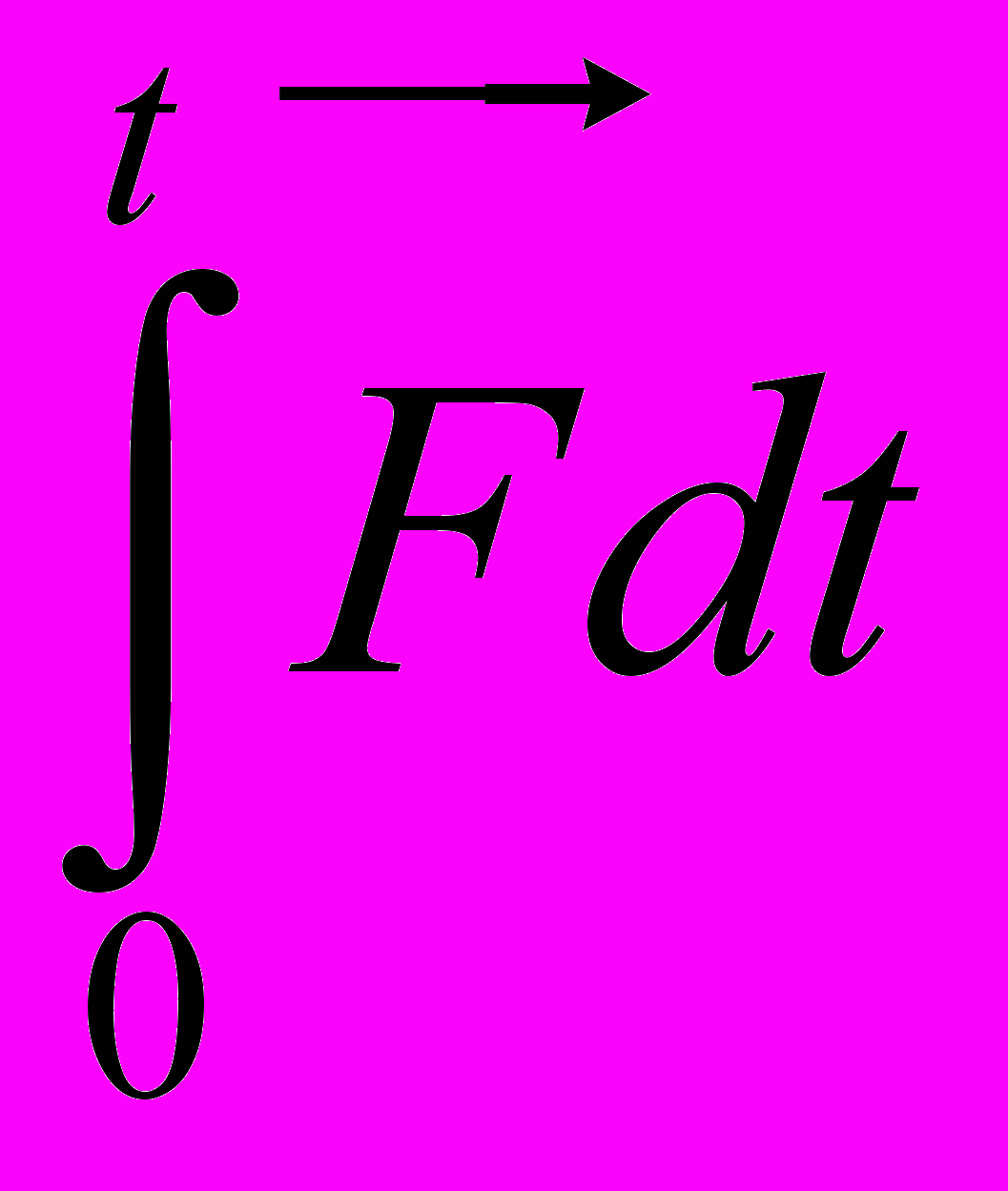. Количество движения точки 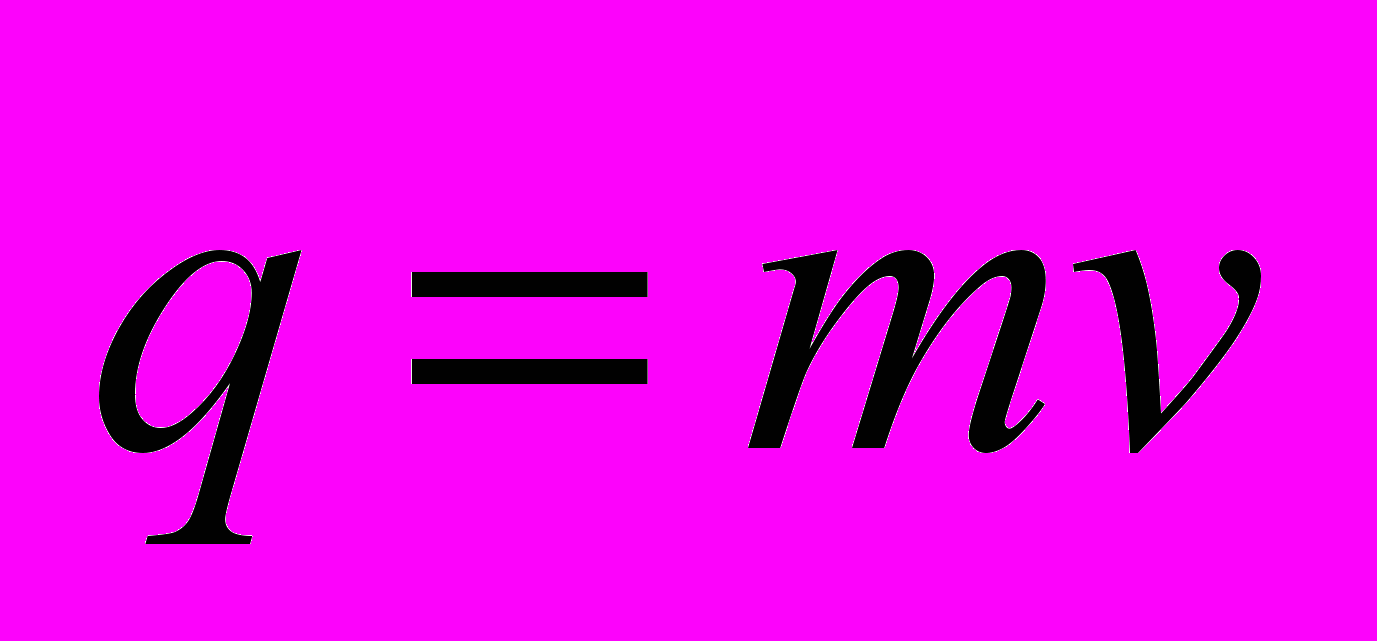. Теорема об изменении количества движения точки. .
   
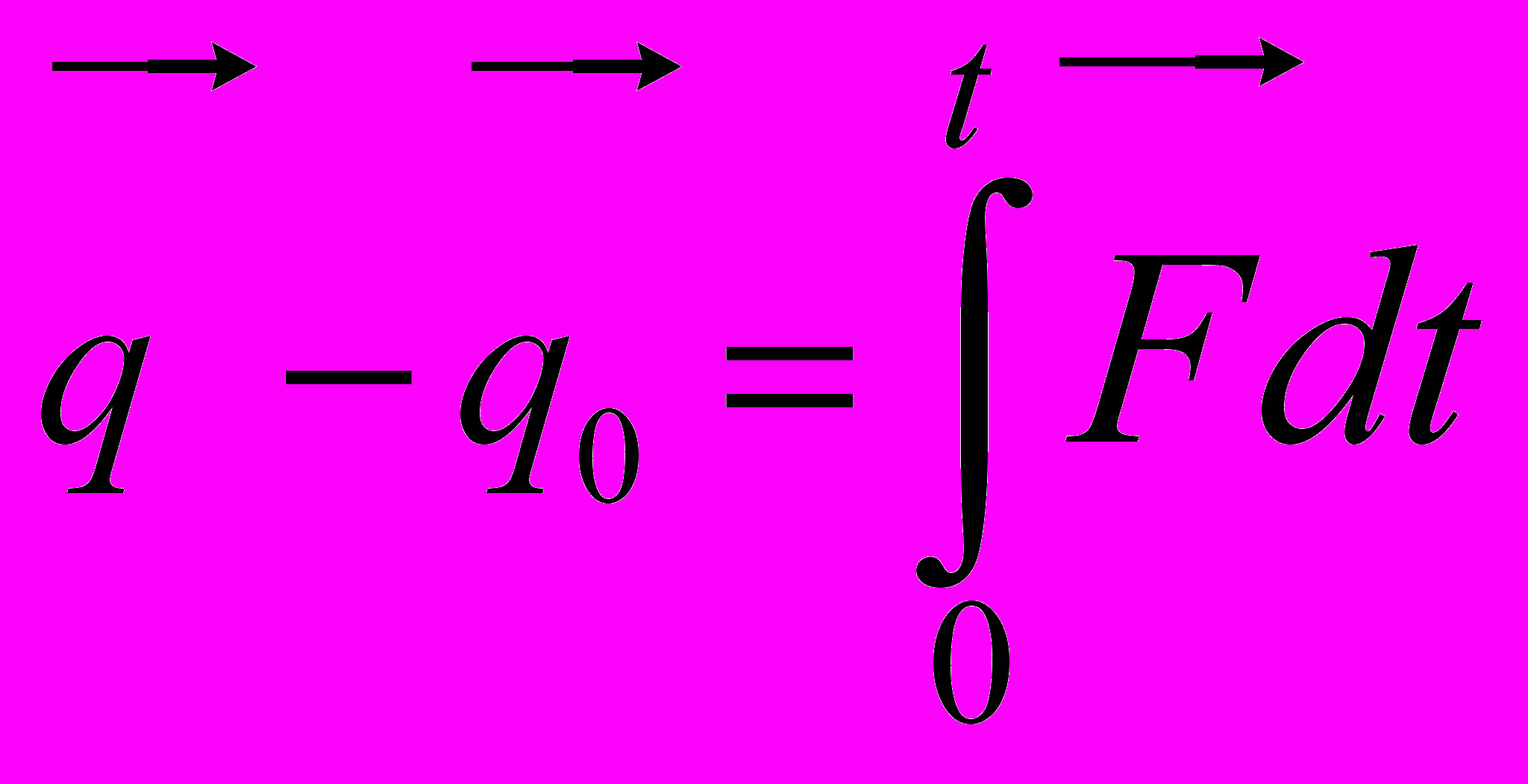3. Момент количества движения точки 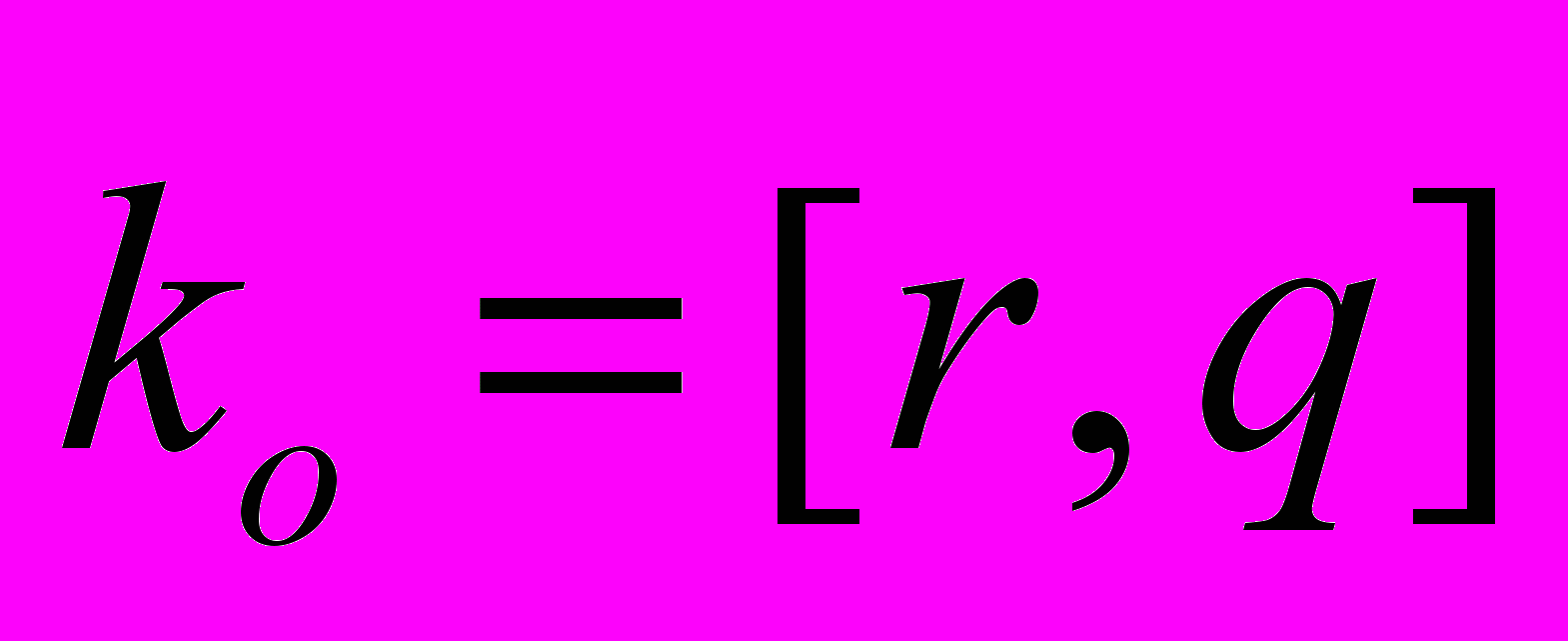. Теорема об изменении момента количества движения точки .
   
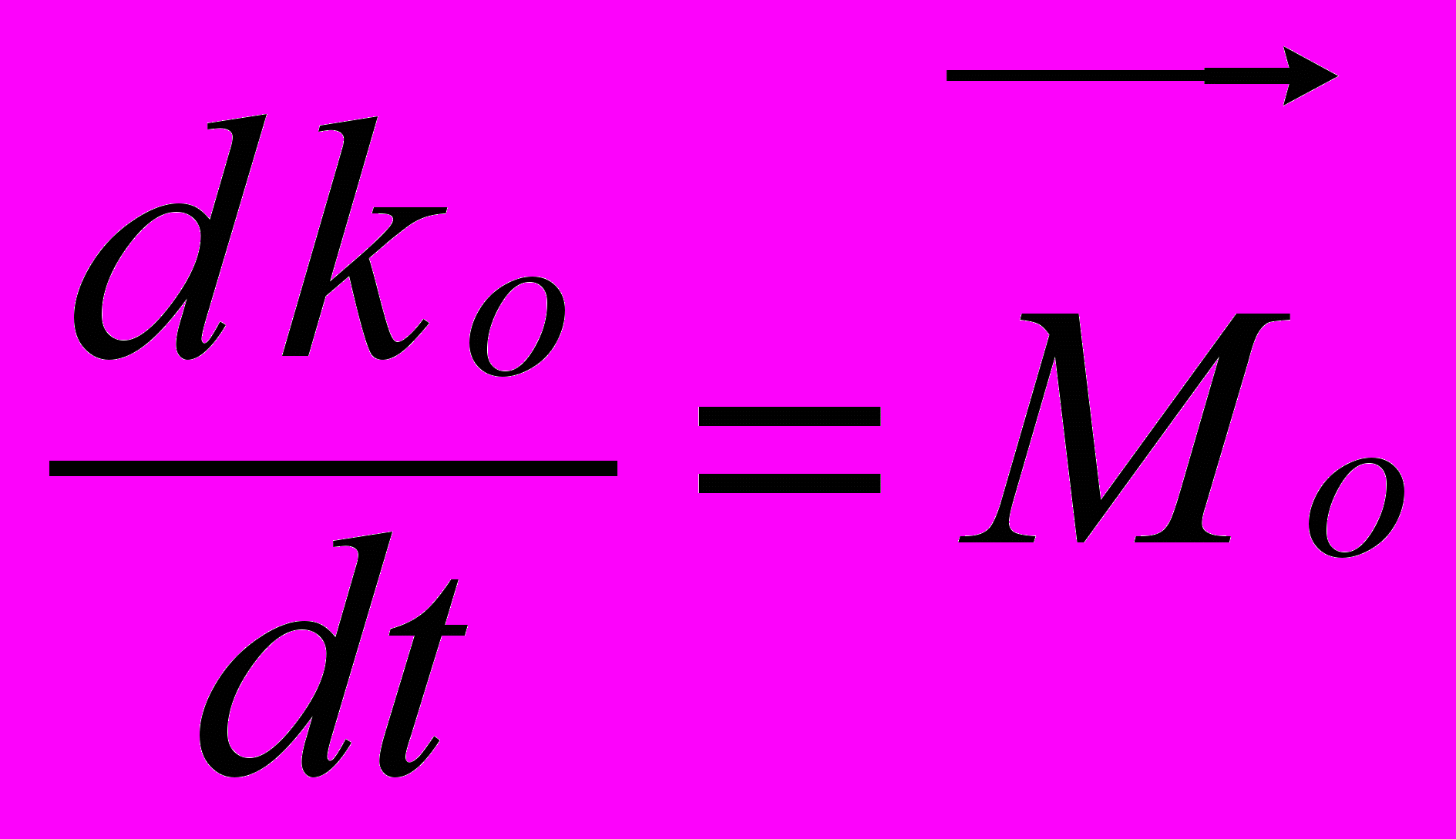4. Работа силы. 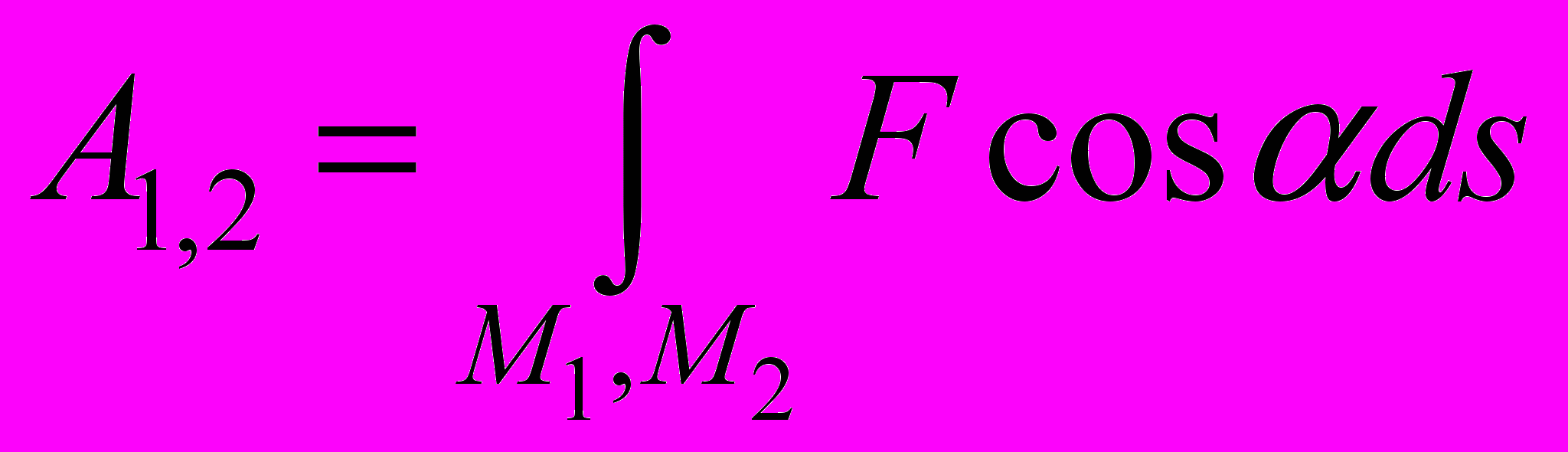. Мощность. Кинетическая энергия точки 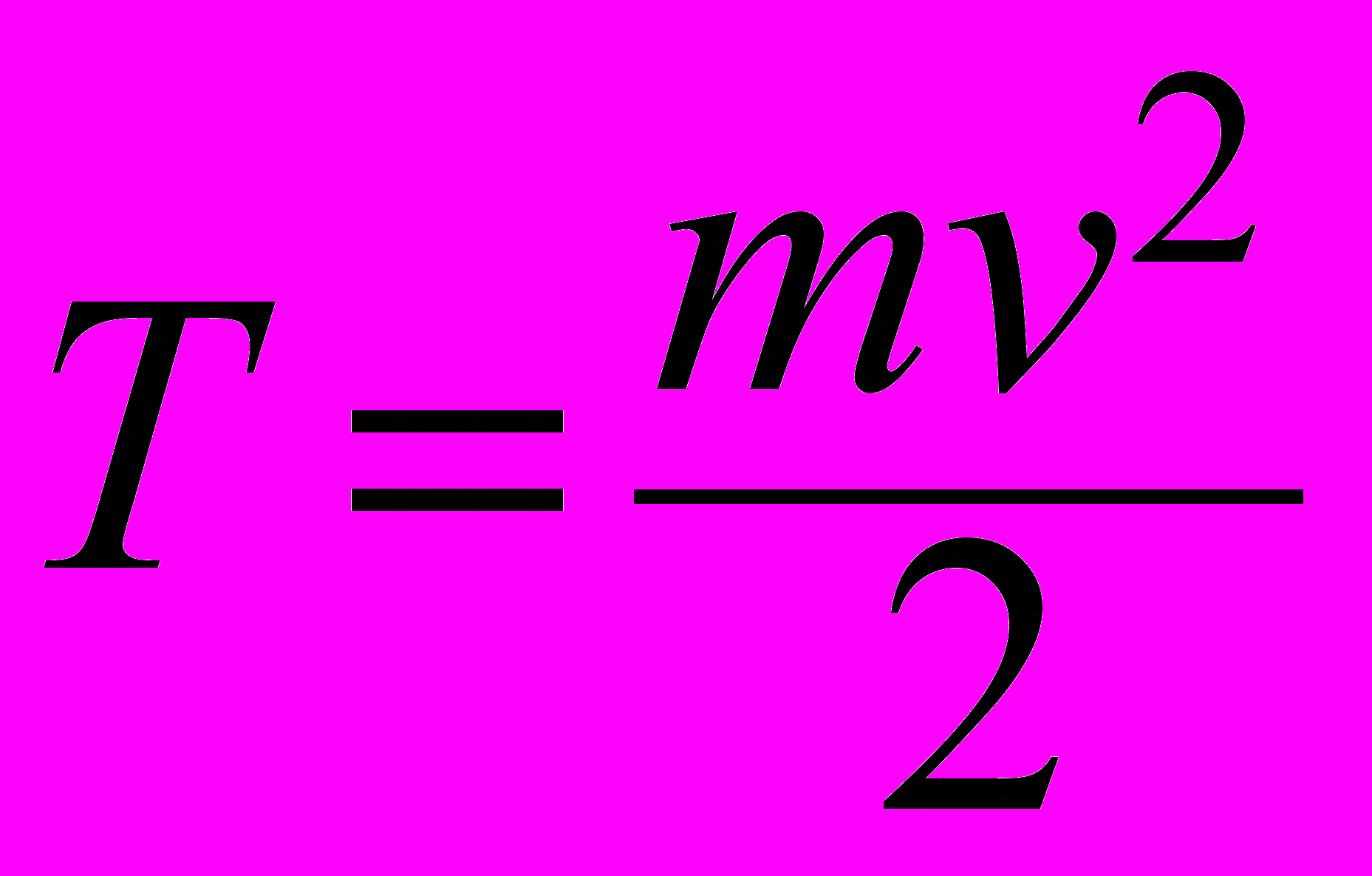.Теорема об изменении кинетической энергии точки.
   
5. Механическая (материальная) система. Силы внутренние и внешние. Масса системы. Центр масс 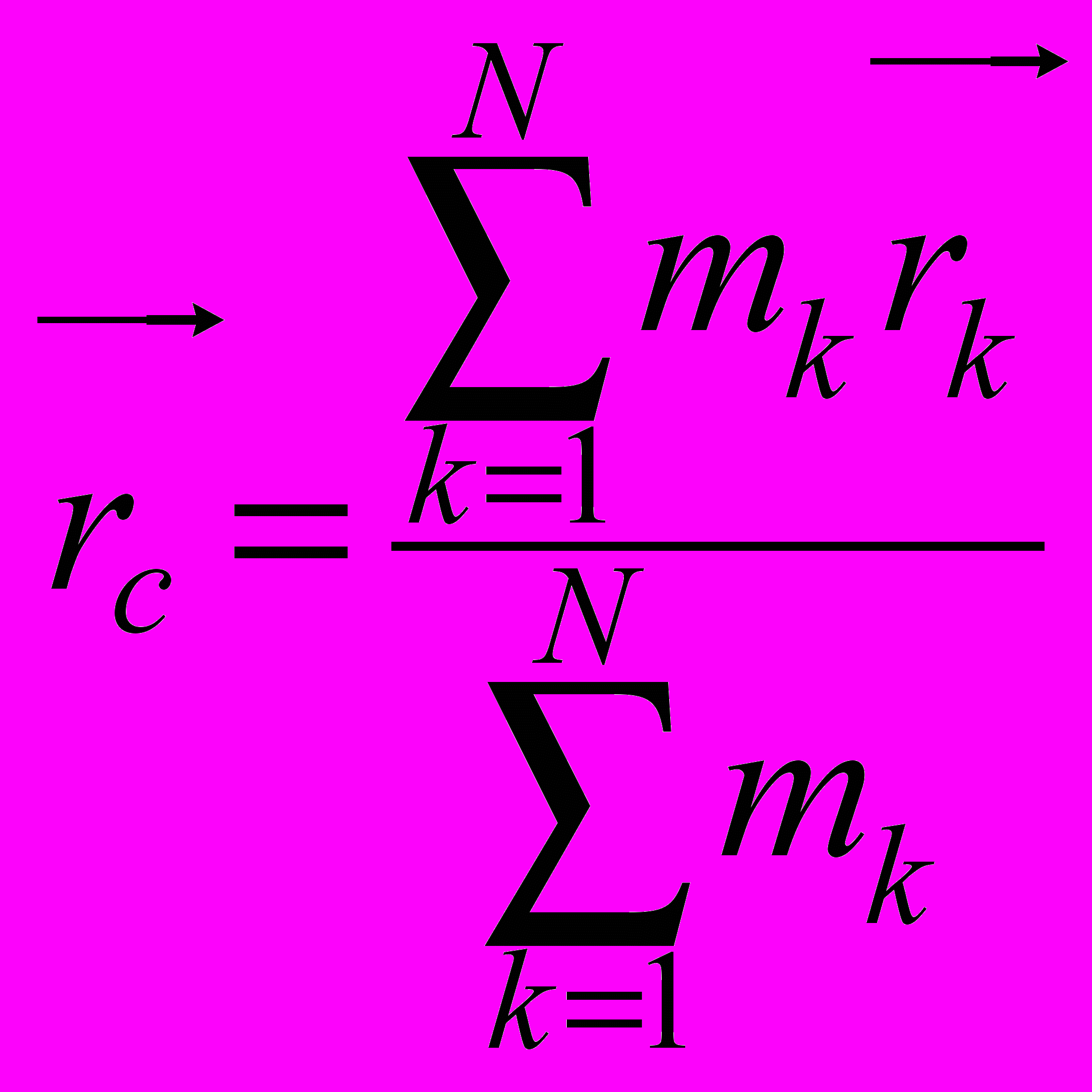. Дифференциальное уравнение движения системы.
   
6. Теорема о движении центра масс. Следствие (закон сохранения движения центра масс).
   

Лекция №12 (Динамика. 25 апреля)

1. Количество движения системы. 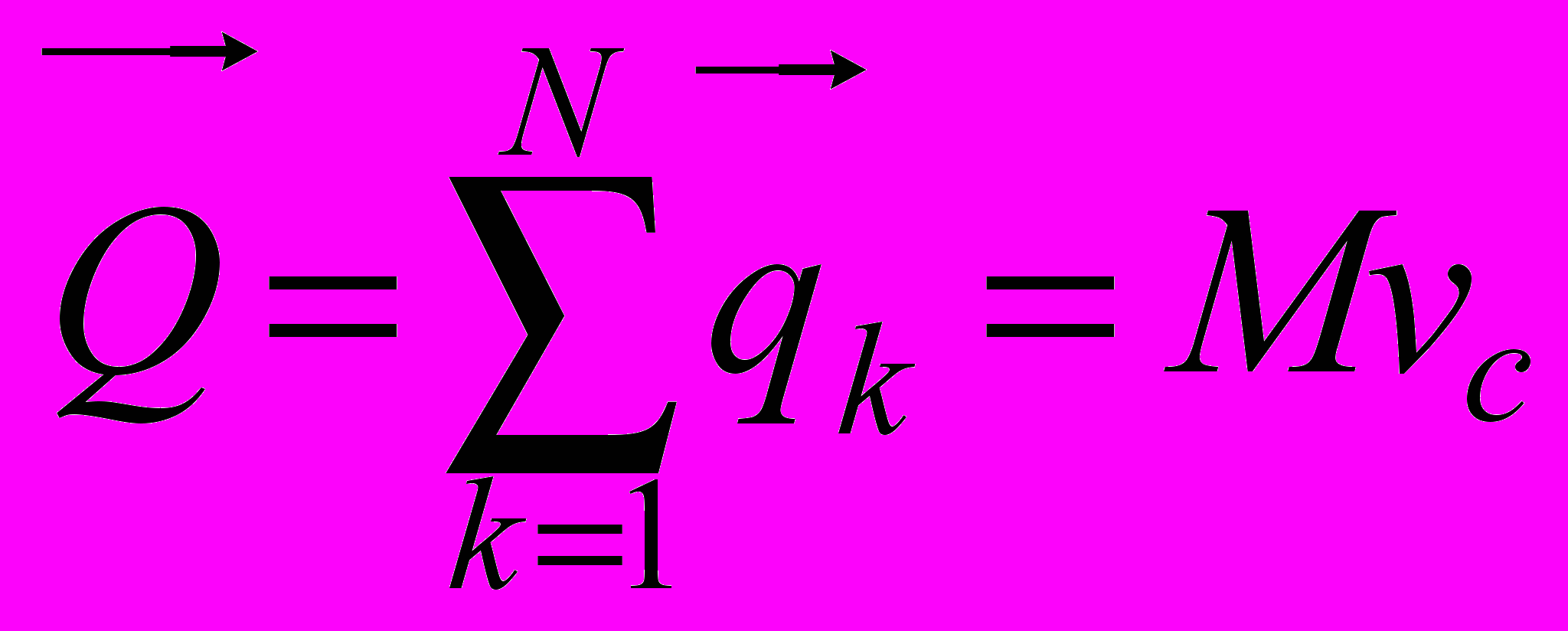. Теорема об изменении количества движения системы .
   
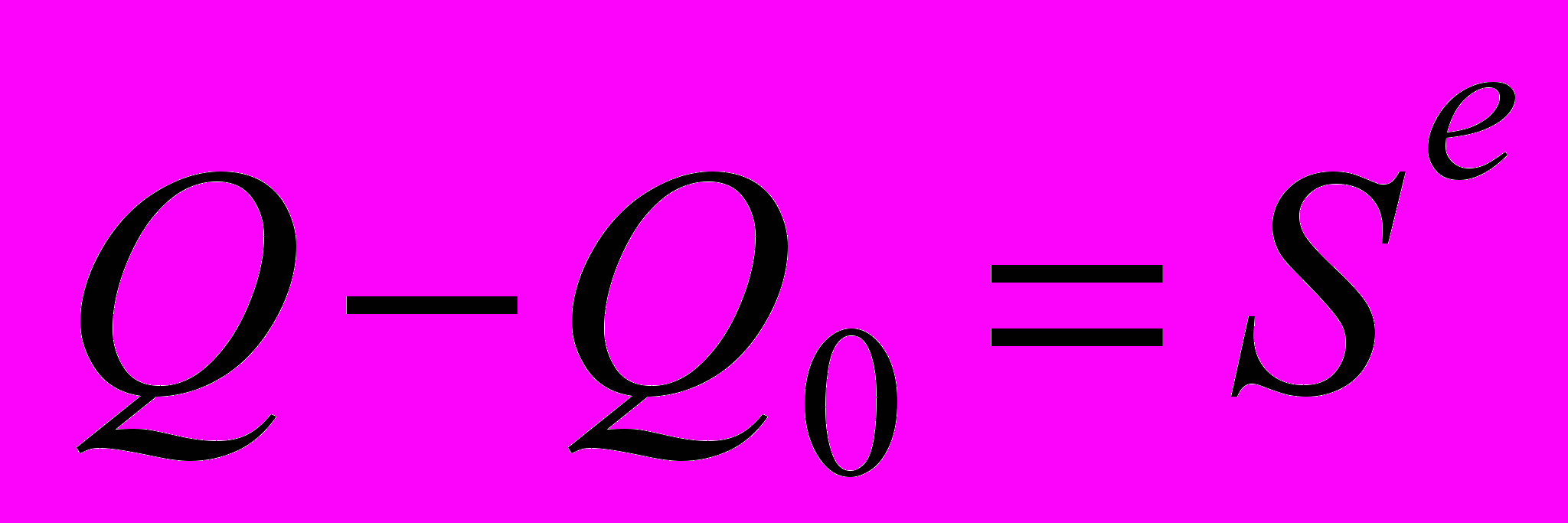2. Моменты инерции тела относительно центра, оси. Теорема Христиана Гюйгенса (1629-1695). Моменты инерции цилиндра, стержня. Радиус инерции.
   
3. Момент количество движения системы (кинетический момент). Теорема об изменении момента количества движения системы.
   
4. Теорема об изменении кинетической энергии системы. Кинетическая энергия тела при поступательном, вращательном и плоском движении. Работа момента сил. Неизменяемая система.
   
5. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
   
6. Дифференциальные уравнения плоского движения тела.
   

Лекция №13 (Динамика. 16 мая)

1. Принцип Даламбера. Силы инерции.
   
2. Классификация связей (геометрические и кинематические, односторонние и двусторонние, голономные и неголономные, стационарные и нестационарные) . , Идеальные связи.
   
3. Возможные перемещения, число степеней свободы, обобщенные координаты.
   
4. Принцип возможных перемещений.
   
5. Общее уравнение динамики.
   
6. Обобщенные силы.
   
7. Уравнение Лагранжа 2-го рода.
   

Лекция №14 (Динамика. 23 мая)

1. Поле сил. Потенциальные силы. Условие потенциальности поля. Потенциальная энергия.
   
2. Функция Лагранжа. Уравнение Лагранжа 2-го рода для потенциальных полей.
   
3. Циклические координаты.
   
4. Устойчивость положения равновесия. Теорема Лагранжа-Дирихле.
   

Лекция №15, заключительная 30 мая

1. Обобщенные коэффициенты жесткости (квазиупругие коэффициенты). Критерий Сильвестра.
   
2. Малые колебания системы с 2 степенями свободы. Инерционные коэффициенты. Уравнение частот. Коэффициенты формы.
   
3. Нормальные координаты.
   

Литература:

1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. СПб.: 1998, 736 с.
   
2. Тарг С.М. Краткий курс теоретической механики. М.:1998.
   
3. Бать М.И. , Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. М:1971.
   
4. Новожилов И.В., Зацепин М.Ф. Типовые расчеты по теоретической механике на базе ЭВМ, М.:1986.
   
5. Корецкий А.В., Осадченко Н.В. Методические указания по проведению практических занятий по курсу «Теоретическая механика» в классах ПЭВМ . М.: МЭИ, 1993. 44с.
   
6. Корецкий А.В., Осадченко Н.В., Устинов В.Ф. Методические указания по работе студентов с обучающими программами по динамике. . М.: МЭИ, 1996. 59с.