Geum.ru

Универсальный подход к вариационным расчетам колебательно-вращательных уровней энергии малоатомных молекул c использованием поверхности потенциальной энергии

Вид материалаАвтореферат диссертации

Содержание


Общая характеристика работы
Целью настоящей работы
Основные методы исследования
Положения, выносимые на защиту
Обоснованность и достоверность
Научная значимость
Практическая значимость
Вклад автора
Апробация результатов работы
Содержание работы
Во второй главе
P. И размер базисного набора ограничивается предельным значением P
В третьей главе
В заключении
Список основных публикаций
Оглавление диссертации
Подобный материал:

На правах рукописи





Овсянников Роман Ильич


УНИВЕРСАЛЬНЫЙ ПОДХОД К ВАРИАЦИОННЫМ РАСЧЕТАМ КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫХ УРОВНЕЙ ЭНЕРГИИ

МАЛОАТОМНЫХ МОЛЕКУЛ C ИСПОЛЬЗОВАНИЕМ

ПОВЕРХНОСТИ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ


Специальность 01.04.03 – радиофизика


А в т о р е ф е р а т

диссертации на соискание ученой степени

кандидата физико-математических наук


Нижний Новгород – 2010

Работа выполнена в Учреждении Российской академии наук Институте прикладной физики РАН г. Нижнего Новгорода и университете г. Вупперталь (Германия)


Научные руководители: кандидат физико-математических наук

Третьяков Михаил Юрьевич (ИПФ РАН),


профессор Пер Йенсен

(университет г. Вупперталь)


Официальные оппоненты: доктор физико-математических наук

Быков Александр Дмитриевич,


кандидат физико-математических наук

Вакс Владимир Лейбович


Ведущая организация: Химический факультет Московского государственного университета имени М.В. Ломоносова


Защита состоится 2010 г. в 15 часов 00 минут на заседании диссертационного совета Д 002.069.02 при Учреждении Российской академии наук Институте прикладной физики РАН по адресу: 603950, г. Нижний Новгород, ул. Ульянова, д. 46.


С диссертацией можно ознакомиться в библиотеке Учреждения Российской академии наук Института прикладной физики РАН.


Автореферат разослан 2010 г.


Ученый секретарь диссертационного совета

доктор физико-математических наук

профессор Ю.В. Чугунов

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ




Актуальность

Теория молекулярных спектров возникла вместе с квантовой механикой и к настоящему времени составляет развитый раздел этой науки. Молекулярная спектроскопия имеет большое значение, являясь источником информации о строении и состоянии молекулярных систем. Интенсивная экспериментальная работа в этой области, большое число результатов стимулировали быстрое и глубокое развитие теории. Молекулярная спектроскопия важна как методически, поскольку содержит много задач, иллюстрирующих применение методов квантовой механики, так и для приложений, поскольку содержит разделы, необходимые в физике и технике лазеров, в химическом анализе, в космических исследованиях, в физике твёрдого тела.

Исследования уровней энергии молекул позволяют точно определить характеристики молекул [1, 2], такие как молекулярная конфигурация, потенциальные функции, потенциальный барьер для внутреннего вращения, потенциальный барьер для молекулярной инверсии, электродипольные моменты. Ещё одно важное приложение колебательно-вращательной спектроскопии – интерпретация переходов в молекулярных газовых лазерах и мазерах, и предсказание новых переходов. Теоретическое исследование колебательно-вращательных состояний молекул для этих новых междисциплинарных полей исследования не менее важно, чем экспериментальное.

Решить аналитически уравнение Шрёдингера для молекулярных ядер невозможно. Да и численное решение сталкивается с рядом трудностей, связанных прежде всего с большим объёмом необходимых вычислений.


Целью настоящей работы является усовершенствование методов вариационных расчетов спектров молекул, расчёт и анализ молекулярных спектров и уровней энергий молекул. Расчёты посвящены исследованию энергетических кластеров молекул XH2D и XHD2 (X = Bi, P, или Sb), торсионному расщеплению уровней энергии в молекуле HSOH, электродипольным моментам колебательных переходов молекулы PH3, идентификации линий горячего спектра молекулы воды, и спискам линий трёх изотопических модификаций молекулы воды H216O, H217O и H218O.


Основные методы исследования: вариационные методы расчетов спектров молекул, реализованные в виде наборов программ DVR3D [3] и TROVE [4]. Метод конечных разностей использовался для разложения функции потенциальной энергии многоатомных молекул в ряд Тейлора. Для наиболее точного воспроизведения экспериментальных данных в расчётах использовались полуэмпирические методы. Использовался метод экстраполяции для моделирования полного базисного набора; квазиклассический метод расчёта молекулярных состояний для их анализа; метод эффективных вращательных гамильтонианов для аппроксимации структуры уровней энергии, полученной из эксперимента; метод Нумерова для численного решения одномерного уравнения Шрёдингера [5, 6]; методы приписывания приближённых квантовых чисел [7].


Положения, выносимые на защиту:

1. Теоретическое исследование структур сильно возбуждённых вращательных состояний пирамидальных молекул классов XH2D и XHD2 (X=Bi, P или Sb) позволило установить наличие чётких чётырёхкратных кластеров энергии в молекулах XHD2, и отсутствие таковых в молекулах XH2D при высоких значениях J. Наличие или отсутствие кластеров энергии объясняется наличием или отсутствием бифуркации поверхности вращательной энергии.

2. Расчёт вращательно-торсионных уровней энергии молекулы HSOH в основном электронном состоянии и использование специальной полуэмпирической поверхности потенциальной энергии для этой молекулы позволили рассчитать расщепление в этих уровнях с точностью 0.0002 см-1, что привело к улучшению процесса идентификации линии в экспериментальном спектре этой молекулы.

3. Оптимизация поверхности потенциальной энергии молекулы PH3 в диапазоне энергий 0 – 7000 см-1 позволяет рассчитать список матричных элементов электродипольных моментов колебательных переходов этой молекулы с точностью, которая соответствует точности имеющихся экспериментальных данных, что превышает точность предыдущих теоретических исследований в 3 раза.

4. Идентифицировано около 75% линии в лабораторном спектре высокого разрешения молекулы воды в диапазоне длин волн 4750 – 12000 см-1, записанного при 3000 К.

5. Использование полуэмпирической поверхности потенциальной энергии в расчёте списка линий колебательно-вращательных переходов для изотопических модификаций молекулы воды H216O, H217O и H218O (в диапазоне частот 0 – 20000 см-1, для вращательных чисел до J=20 (J=30 для H216O)) позволяет получить не достигавшуюся ранее расчётную точность 0.025 см-1 для таких широкодиапазонных расчетов. Полученная точность близка к экспериментальной.


Научная новизна

1. Впервые проведено теоретическое исследование образования энергетических кластеров в пирамидальных молекулах классов XH2D и XHD2 (X=Bi, P или Sb).

2. Улучшена идентификация линий в экспериментальном спектре молекулы HSOH.

3. Достигнута рекордная точность расчётов матричных элементов электродипольных моментов колебательных переходов молекулы PH3 в основном электронном состоянии в диапазоне энергий до 7000 см-1.

4. Впервые идентифицировано 75% линий в лабораторном спектре высокого разрешения молекулы воды в диапазоне длин волн 4750 – 12000 см-1, записанного при 3000 К.

5. Достигнута рекордная точность в расчётах списка линий колебательно-вращательных переходов для изотопических модификаций молекулы воды H216O, H217O и H218O в диапазоне частот 0 – 20000 см-1. Полученная точность близка к экспериментальной.


Обоснованность и достоверность полученных в диссертации результатов подтверждается использованием широко известных спектроскопические методов и методов численного моделирования; хорошим совпадением с результатами других авторов, как теоретическими, так и экспериментальными, совпадением результатов, полученных различными методами, а также воспроизводимостью всех численных результатов.


Научная значимость

Проведённые в работе расчёты важны для фундаментальных исследований, объясняющих структуру уровней энергии молекул. Улучшение метода расчётов молекулярных уровней энергии приводит к увеличению расчётной точности, что повышает достоверность полученных результатов.


Практическая значимость

Рассчитанные в работе уровни энергии и спектры молекул открывают новые возможности для идентификации экспериментально полученных молекулярных спектров. Также расчётные молекулярные спектры можно использовать в большом количестве приложений: моделирование поглощения солнечного излучения в атмосфере, исследование спектра солнечных пятен, расчет прозрачности звездных атмосфер, астрофизические приложениях и для анализа экспериментальных спектров. Определенные спектроскопические характеристики молекул можно использовать при исследовании процессов горения, в лазерной физике и производстве сверхчистых материалов.


Вклад автора

При получении результатов настоящей работы автором внесен существенный вклад, выраженный участием в постановке задач, разработке алгоритмов и программ их реализации, оптимизации поверхностей потенциальной энергии, проведении расчётов уровней энергии в приближении полного базисного набора, расчёте спектров и анализе экспериментальных данных.

Постановка большинства задач осуществлялась совместно с к. ф.-м. н. М.Ю. Третьяковым, проф. П. Йенсеном (университет г. Вупперталь, Германия) и С.Н. Юрченко (Технический университет Дрездена, Германия).


Апробация результатов работы

Результаты работы докладывались на 20-м коллоквиуме по молекулярной спектроскопии высокого разрешения в Дижоне (Франция), 20-й международной конференции по молекулярной спектроскопии высокого разрешения в Праге (Чешская республика), 15-м и 16-м симпозиуме по молекулярной спектроскопии (Томск и пос. Листвянка), 9-й, 10-й и 12-й конференциях по радиофизике в Нижнем Новгороде, 10-й, 11-й и 13-й Нижегородских сессиях молодых ученых, 13-й научной школе "Нелинейные волны".


Публикации

По тематике диссертации автором опубликовано 28 работ, включая 10 статей в реферируемых российских и зарубежных научных журналах и 18 тезисов докладов на российских и международных научных конференциях. Все основные результаты диссертации опубликованы в реферируемых журналах. Работа выполнялась при финансовой поддержке РФФИ и еврокомисии по контракту “Quantitative Spectroscopy for Atmospheric and Astrophysical Research” (QUASAAR).


Структура и объем работы

Диссертационная работа состоит из введения, трех глав и заключения. Общий объем работы – 144 страницы, рисунков – 29, таблиц – 15, библиография – 161 наименование.


СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы, ставится цель исследования, приводится краткое изложение диссертационной работы.

В первой главе проводится обзор общих принципов и некоторых этапов, из которых состоят вариационные расчёты уровней энергии молекул. Также здесь представлены два метода расчётов уровней энергии молекул: DVR3D (Discrete Variable Representation 3 Dimensional – расчёт с использованием представления дискретной переменной в 3-мерном пространстве) и TROVE (Theoretical ROtational-Vibrational Energies – теоретические колебательно-вращательные уровни энергии).

В основе расчетов лежит уравнение Шрёдингера

, (1)

которое традиционно упрощается в рамках приближения Борна-Оппенгеймера (разделение “движения” на быстрое – электронное и медленное – ядерное). Для удобства определяется внутренняя система координат, к которой преобразуется гамильтониан системы. Рассматриваются основы вариационного метода, позволяющего свести решение уравнения Шрёдингера к решению секулярного уравнения:

, (2)

где Hkl – элементы матрицы гамильтониана, а ε – значения энергии. Так же обсуждаются вопросы выбора базисных функций, определяющих конкретный вид секулярного уравнения.

В методе DVR3D [3] используется аналитическое выражение для кинетической части оператора Гамильтона. Аналитические выражения гамильтонианов во внутренней системе координат молекул являются существенно различными для каждого отдельного класса молекул, а также для каждого отдельного типа координат. Метод DVR3D разработан и применяется лишь для трехатомных молекул. Во внутренних координатах колебательная часть оператора кинетической энергии ядер записывается в виде [8]:

, (3)

где:

, (4)

, (5)

μ1-1, μ12-1, μ2-1 – обратные приведенные массы, а r1, r2, θ – внутренние координаты.

Существует частный класс координат, в котором перекрестные члены с частными производными в операторе кинетической энергии оказываются равными нулю. Такие координаты называются ортогональными. В рамках рассматриваемой здесь теории ортогональными являются координаты, удовлетворяющие следующему условию

μ12-1 = 0 . (6)

Этого условия достаточно для превращения оператора KV(2) в нулевой.

Полученный гамильтониан используется для расчета энергий колебательно-вращательных уровней энергии и их волновых функций.

Метод TROVE [4] предоставляет огромный выбор различных способов расчёта колебательно-вращательных уровней энергии молекул в изолированных электронных состояниях. Авторы этого метода поставили цель – создать возможность расчёта спектра любой молекулы с произвольной структурой в различных системах колебательных координат. Общность подхода TROVE достигается за счёт включения преобразования координат в общий расчётный процесс в виде численной процедуры.

Общность подхода в методе TROVE обеспечивается тем, что оператор Гамильтона выражен в виде ряда по внутренним координатам с численно определяемыми коэффициентами. Преобразование координат, как и коэффициентов гамильтониана, из неподвижной декартовой системы координат к выбранному набору колебательных координат производится с использованием разложений в ряд Тейлора с численной рекурсивной схемой определения значений коэффициентов. Данная схема – универсальная, она не требует предварительных аналитических выводов оператора кинетической энергии.

Известно (см. например [9]), что преобразованный оператор кинетической энергии во внутренней системе координат может быть выражен в виде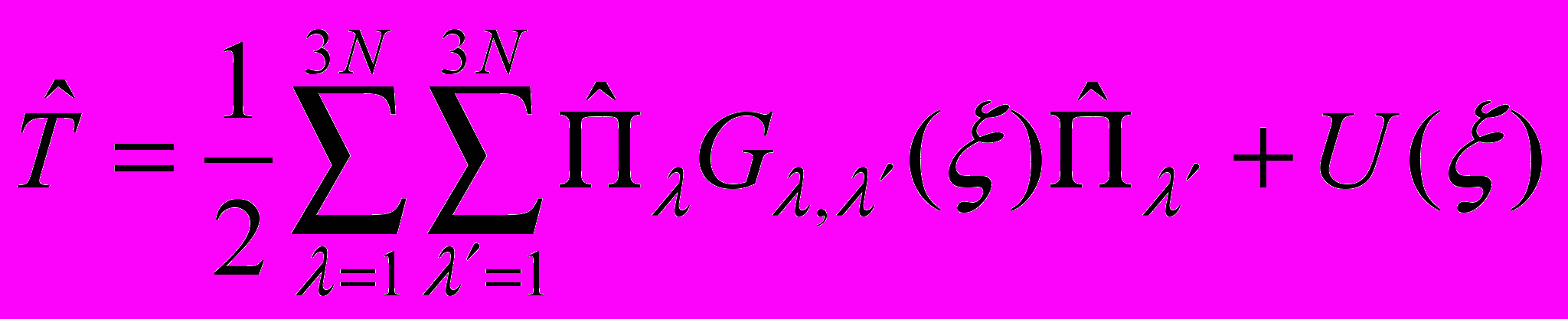

, (7)

где 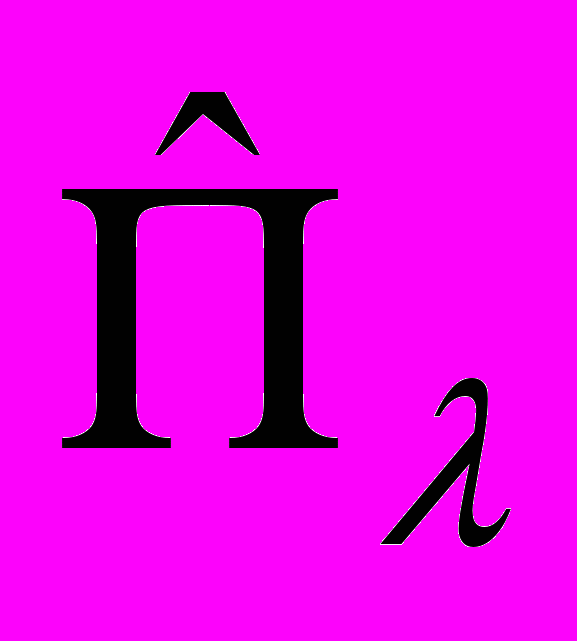– операторы обобщённого момента, а Gλ,λ´(ξ) и U(ξ) – функции, зависящие от внутренних координат ξ.

Расчётная схема метода TROVE является общей еще и в том смысле, что она может быть использована совместно с произвольным выбором удовлетворяющих физическим условиям колебательных координат, а также произвольным выбором физически обоснованных базисных волновых функций.

Во второй главе содержатся модификации схемы вариационных расчетов методом TROVE, сделанные автором. Они позволили расширить класс молекул, для которых рассчитываются уровни энергии, а также увеличить точность и устойчивость расчётов, ослабить требования к компьютерным ресурсам.

В разделе 2.1 проведена модификация метода TROVE, основанная на численном подходе к определению неприводимых представлений колебательно-вращательных базисных функций. Этот подход позволяет привести матрицу гамильтониана произвольной молекулы к блочно-диагональному виду. За счёт этого можно ослабить требования к компьютерным ресурсам, необходимым для расчёта уровней энергии молекулы, или расширить используемый базисный набор для увеличения точности расчётов.

Для симметризации базисных функций необходима информация о том, как эти функции преобразуются под действием операций симметрии. Традиционно преобразования симметрии определяются в расчётах аналитически. Однако в методе TROVE проводится непосредственный расчёт свойств симметрии волновых функций. Для этого случайным образом выбираются несколько конфигураций молекулы (например, 50), и к этому набору конфигураций применяются операции симметрии. С использованием выбранных конфигураций рассчитываются матрицы преобразования волновых функций, из которых определяется их симметрия.

Удобство использования свойств симметрии демонстрируется в диссертации на примере молекулы PH3. В работе проводились сравнения размеров базиса, полученного как с использованием свойств симметрии, так и без использования. Полная матрица гамильтониана системы (принадлежащая приводимому представлению) с использованием преобразований симметрии приводится к блочно-диагональному виду. Диагонализация всех блоков по отдельности является гораздо более простой вычислительной задачей, чем диагонализация всей матрицы целиком. Чем большей степенью симметрии обладает молекула, тем больше отдельных блоков можно получить, используя свойства симметрии. Из анализа данных в диссертации становится очевидным эффективность симметризации базисных функций. Максимальный размер матричных блоков для молекулы PH3 уменьшается приблизительно в 3 раза, что позволяет ослабить требования к компьютерным ресурсам приблизительно в 10 раз. А поскольку в расчётах колебательно-вращательных уровней энергий молекул методом TROVE наилучшие результаты были получены с использованием численных базисных функций, то и симметризация этих функций должна выполняться в численном виде. Проведение симметризации в численном виде также важно для универсальности всего метода TROVE.

В разделе 2.2 Показана возможность использования приближения полного базисного набора, аналогичного широко известному подходу в расчётах электронной структуры. Это приближение позволяет повысить точность расчётов, что важно при расчёте уровней, чья энергия сильно зависит от размера базиса.

В методе TROVE каждой базисной функции некоторым образом ставится в соответствие полиадное число P. И размер базисного набора ограничивается предельным значением Pmax. Для проведения экстраполяции на полный базисный набор необходимо рассчитать значения энергии для нескольких значений Pmax. Причём при проведении расчётов серьёзную проблему создаёт большая плотность уровней. Часто бывает достаточно трудно упорядочить энергии, полученные для различных значений Pmax наилучшим образом. Упорядочивание по возрастанию энергии иногда приводит к негладкому изменению энергий при вариации Pmax. Однако даже при большой плотности уровней возможна экстраполяция к полному колебательному базисному набору.

Для экстраполяции на полный колебательный базисный набор использовалась экспоненциально убывающая зависимость энергии состояния от полиадного числа (использованная ранее другими авторами в ряде работ [10 – 12]):

, (8)

где , ai, и λi – параметры, значения которых определяются из оптимизации, Ei(Pmax) – одно из значений энергии, рассчитанное при полиадном номере Pmax, а i – номер колебательного квантового состояния с квантовыми числами , которые являются общепринятыми спектроскопическими обозначениями, основанными на приближении невзаимодействующих гармонических осцилляторов для колебательных энергий. Предельное значение

, (9)

поэтому – значение энергии при экстраполяции на полный колебательный базисный набор.

В экстраполяции определялись значения , ai, и λi для каждого уровня энергии.

В разделе 2.3 проведена модификация метода конечных разностей (МКР) для разложения потенциальной энергии многоатомных молекул в ряд Тейлора. Модификация позволяет учесть взаимное влияние коэффициентов разложения при численном построении этого разложения, увеличить точность и устойчивость расчётов, что особенно важно при расчёте высоко возбуждённых уровней энергии молекул.

Основным недостатком традиционного МКР при вычислении производных высоких порядков является понижение точности расчетов при увеличении порядка разложения m (см., например [13]). Одной из причин является конечная точность представлений действительных чисел, присущая реальным компьютерным вычислениям.

Модификация метода разложения произвольной одномерной функции V(ξ) в ряд Тейлора m-го порядка с использованием конечных разностей заключается в следующем. Вычисление производных начинается с наивысшей степени m (и вводится обозначение ). Пусть на неком итерационном шаге i (i = m, m-1,..,0) рассчитан коэффициент разложения Vi. С его использованием определяется следующая «приведенная» функция

, (10)

которая используется в качестве объекта разложения на следующей итерации i-1, из которой затем аналогичным образом исключим найденный член разложения посредством (10) для вычисления (i-2)-й производной, и т.д. вплоть до i=0.

Представленная модификация МКР требует лишь незначительного изменения расчётного алгоритма и практически не влияет на время, затрачиваемое на расчёты. При этом модифицированный метод позволяет производить разложения со значительно меньшими ошибками по сравнению с традиционным методом.

В третьей главе представлены расчёты уровней энергии и спектров молекул, проведённые с использованием изложенных в первой главе методов TROVE и DVR3D, а также модернизаций расчётного метода TROVE, изложенных во второй главе.

В разделе 3.1 Проведено теоретическое исследование образования энергетических кластеров (близко лежащих уровней энергии, обычно ∆E/E убывает экспоненциально с ростом J) у высоко возбуждённых вращательных состояний различных пирамидальных молекул XH2D и XHD2 (X = Bi, P, или Sb). Исследование проводилось с помощью вариационных расчётов вращательных уровней энергии в основном колебательном и электронном состоянии этих молекул для J≤70. Было показано, что при высоких значениях J у молекул с двумя атомами дейтерия XHD2 рассчитанные уровни энергии образуют ярко выраженные четырёхкратные кластеры, аналогичные наблюдаемым для молекул класса H2X (X = Se, Te, S).

Было показано соответствие квантового и квазиклассического подходов к расчётам кластеризации уровней энергии в молекулах (совпадение направлений стационарных осей). А наличие или отсутствие кластеризации объяснено наличием или отсутствием бифуркации квазиклассической поверхности вращательной энергии, соответствующей рассматриваемой молекуле.

В разделе 3.2 Рассчитаны вращательно-торсионные уровни энергии молекулы HSOH с использованием ab initio (лат. из основных принципов) ППЭ, и оптимизированной ППЭ. За счёт проведённой оптимизации рассчитанные значения вращательного расщепления отлично согласуются с экспериментом; среднеквадратичное отклонение составило 0.0002 см-1 для всех полученных экспериментально значений (с J ≤ 40 и Ka ≤ 4). Расчёт расщепления позволил улучшить идентификацию линий в экспериментальном спектре.

Молекула HSOH обладает внутренним вращением, позволяющим перейти из одного минимума ППЭ в другой. Этим объясняется наличие расщеплений в структуре уровней энергии этой молекулы. Зависимость расщепления от квантового числа Ka нетривиальна, что отличает молекулу HSOH от близких ей молекул HSSH и HOOH.

В разделе 3.3 получен расширенный список рассчитанных матричных элементов электродипольных моментов колебательных переходов для молекулы PH3 в основном электронном состоянии. Точность расчёта оказалась близка к экспериментальной.

Таблица 1: равновесные значения углов αe и отклонения σ расчётных значений энергии от экспериментальных (σ – для всех уровней энергии, σ(ν2) – для уровней энергии с возбуждением ν2, σ(ν134) – для уровней энергии без возбуждения ν2) для трёх поверхностей потенциальной энергии: ab initio ППЭ с релятивисткой поправкой, без поправки, а также оптимизированная ППЭ.
ab initio ППЭ без поправок
ab initio ППЭ

с релятивистской поправкой
оптимизированная ППЭ

αe/рад
93.5560
93.49260
93.5650

σ/см-1
3.22
3.06
1.63

σ(ν2)/см-1
3.52
3.57
1.18

σ(ν134)/см-1
2.99
2.66
1.87



Было обнаружено, что уровни, соответствующие возбуждению изгибных колебаний, соответствующих моде ν2, рассчитываются со значительно большей ошибкой, чем остальные уровни (см. табл. 1). Оказалось, что точность расчёта этих уровней можно значительно улучшить через оптимизацию (отклонений расчётных уровней энергии от экспериментальных) только одного параметра αe (т. е. равновесного значения угла связи). Для ab initio поверхности с релятивисткой поправкой равновесное значение составило αe=93.49260 рад. Проведение оптимизации привело к замене этого значения на 93.5650; причём изменённое значение близко к равновесному значению 93.5560, соответствующему ab initio поверхности без поправок (см. табл. 1). Добавление релятивистской поправки к ab initio ППЭ приводит к улучшению описания колебательных уровней энергии, у которых не возбуждена мода ν2. Однако при этом ухудшается точность описания уровней энергии, соответствующих возбуждению моды ν2. Колебания типа ν2 сильно связаны с углом связи αe, поэтому оптимизация ППЭ проводилась именно по этому параметру.

В разделе 3.4 проведён анализ экспериментально полученного спектра молекулы воды в диапазоне 4750 – 13000 см-1 записанного при температуре 3000 K. Результаты анализа могут быть полезны при идентификации линий в спектрах излучения астрономических объектов: звёзд класса М и коричневых карликов.

В работе [14] определены частоты и квантовые числа примерно 50 сильных линий при T=2200 K в диапазоне 9392 – 9456 см-1. Идентификация 18 линий совпадает с идентификацией из диссертации. Идентификация остальных линий была изменена в диссертации. В работе [14] частоты линий рассчитаны с использованием ранее определённых экспериментальных уровней энергии, и являются точными (порядка экспериментальной точности). Однако многие идентифицированные линии не видны в списке линий из [15] (использованного в диссертации), поскольку их интенсивность слишком мала при температуре 3000 К. В результате анализа выяснилось, что использование информации об интенсивностях линий, является ключевым моментом в идентификации горячего спектра. Именно значения интенсивностей помогают избежать неоднозначностей в простейшей идентификации, использующей только значения частот линий.

В разделе 3.5 рассчитаны колебательно-вращательные спектры трёх изотопических модификаций молекулы воды H216O, H217O и H218O в диапазоне 0 – 20000 см-1 и вращательным квантовым числом J ≤ 20 (J ≤ 30 для H216O). В расчётах использовалась полуэмпирическая ППЭ, полученная из оптимизации ab initio ППЭ с использованием экспериментальных данных. Точность расчёта уровней энергии с J ≤ 5 (для которых существуют достоверные экспериментально полученные значения) составляет 0.025 см-1, что близко к средней оценке экспериментальной точности 0.02 см-1.

Несмотря на многочисленные исследования, идентификация водяного спектра ещё не является однозначной, рутинной процедурой. Различные процедуры идентификации (основанные как на анализе значений энергии уровней, волновых функций, так и на анализе поверхности потенциальной энергии) часто приводят к взаимно противоречащим результатам. Поэтому в работе была поставлена цель – сконструировать ППЭ и рассчитать соответствующий ей список линий, достаточно точный для того, чтобы значительно упростить и улучшить процесс идентификации экспериментальных спектров. Для достижения этой цели необходимо получить точность, близкую к экспериментальной для рассчитанных уровней энергии в основном электронном состоянии. Усреднённое определение экспериментальной точности можно принять равным 0.02 см-1, это значение приблизительно характеризует предел различий комбинационных разностей для одних и тех же уровней.

Полученная ППЭ воспроизводит экспериментальные данные достаточно точно на всём рассматриваемом диапазоне энергий. Рассчитанные значения многих колебательных уровней энергии соответствуют теоретическим оценкам, особенно для случаев, когда соответствующий уровень уже наблюдался для других изотопических модификаций.

Списки линий, а также использованная в расчётах ППЭ, приведены в электронном архиве EPAPS [16]. Порог по интенсивности составил 1.0x10-30 см мол-1 и использовался как для температуры 296 K, так и для 3000 K, полученные списки линий возможно использовать для анализа экспериментальных спектров, как для комнатной температуры, так и горячих спектров.

Рассчитанные списки линий для трёх основных изотопических модификаций молекулы воды являются наиболее точными списками линий, как по положениям центров линий, так и по интенсивностям.

В заключении сформулированы основные результаты работы:

1. Проведено теоретическое исследование образования энергетических кластеров в сильно возбуждённых вращательных состояниях пирамидальных молекул классов XH2D и XHD2 (X=Bi, P или Sb) с помощью вариационных расчётов вращательных уровней энергии в основном колебательном состоянии для J ≤ 70. Показано, что при высоких значениях J рассчитанные уровни энергии молекул XHD2 образуют чёткие чётырёхкратные кластерные структуры. Из анализа волновых функций и поверхностей вращательных энергий показано, что в состояниях, соответствующих энергетическим кластерам, молекула XHD2 квазиклассически вращается вокруг так называемой локальной оси, которая почти совпадает с одной из связей X-D. Аналогичные вращательные уровни энергии изотопических модификаций XH2D образуют структуры с двукратно вырожденными кластерами, что схоже со структурами уровней симметричных волчков. Наличие или отсутствие кластеров энергии объяснено наличием или отсутствием бифуркации поверхности вращательной энергии.

2. Рассчитаны вращательно-торсионные уровни энергии молекулы HSOH в основном электронном состоянии. Получена специальная полуэмпирическая поверхность потенциальной энергии, позволяющая рассчитывать расщепление в этих уровнях с точностью 0.0002 см-1, что позволило улучшить идентификацию линий в экспериментальном спектре.

3. Получен расширенный список рассчитанных матричных элементов электродипольных моментов колебательных переходов молекулы PH3 в основном электронном состоянии в диапазоне энергий 0 – 7000 см-1. Благодаря улучшению поверхности потенциальной энергии точность рассчитанного списка матричных элементов соответствует точности имеющихся экспериментальных данных.

4. Идентифицировано около 75% линии в лабораторном спектре высокого разрешения молекулы воды в диапазоне длин волн 4750 – 12000 см-1, записанного при 3000 К. Показано, что использование информации об интенсивностях линий, является ключевым моментом в идентификации горячего спектра.

5. Рассчитаны колебательно-вращательные спектры изотопических модификаций молекулы воды H216O, H217O и H218O в диапазоне частот 0 – 20000 см-1, для вращательных чисел до J=20 (J=30 для H216O). В расчётах получена рекордная расчётная точность 0.025 см-1 для таких широкодиапазонных расчетов за счёт использования полуэмпирической поверхности потенциальной энергии. Точность расчётов близка к экспериментальной.

6. Проведена модификация метода TROVE, предназначенного для вариационных расчётов уровней энергии молекул. Модифицирована процедура разложения функций потенциальной энергии молекул в ряд Тейлора с использованием конечных разностей. В процедуру построения матрицы гамильтониана в численном виде включено использование свойств молекулярной группы симметрии. Модификация метода позволяет повысить точность и уменьшить необходимое для расчётов время. Показано, что модифицированный метод более устойчив, и, таким образом, гарантирует более широкую область применения.

7. Показана эффективность использования приближения полного базисного набора при расчёте колебательно-вращательных уровней энергии молекулы PH3. Это приближение позволяет избежать трудновыполнимых расчётов с большим размером базиса.


Литература

1. Papoušek D., Aliev M. R. Theory and Applications of High Resolution Infrared Microwave and Raman Spectroscopy of polyatomic Molecules. Amsterdam: Elsevier, 1982.

2. Таунс Ч., Шавлов А. Радиоспектроскопия. Москва, издательство иностранной литературы, 1959, Townes C.H., Schawlow A.L. Microwave Spectroscopy, New York, 1955.

3. Tennyson J., Henderson J.R. and Fulton N.G., DVR3D – for the fully poinwise calculation of ro-vibrational spectra of triatomic molecules // Соmр. Phys. Comms., V. 86., P. 175 – 198, 1995.

4. Yurchenko S. N., Thiel W., and Jensen P. Theoretical ROVibrational Energies (TROVE): A robust numerical approach to the calculation of ro-vibrational energies for polyatomic molecules // J. Mol. Spectrosc., V. 245, P. 126 – 140 (2007).

5. Нумеров Б. // Публикации Центральной Астрофизической Обсерватории, 2, 188 (1923).

6. Cooley J. W. An Improved Eigenvalue Corrector Formula for Solving the Schrodinger Equation for Central Fields // Math. Comp., V. 15, N. 76, P. 363 – 374 (1961).

7. Зобов Н.Ф., Овсянников Р.И., Ширин С.В., Полянский О.Л. Приписывание квантовых чисел теоретическим спектрам молекул H216O, H217O и H218O, рассчитанных вариационными методами в диапазоне 0 – 26000 см-1 // Оптика и Спектроскопия, Т. 102, N. 3, С. 390 – 395 (2007).

8. Sutcliffe В.Т., Tennyson J. A general teatment of vibration-rotation coordinates for triatomic molecules // Intern. J. Quantum Chem., V. 39, P. 183 – 196, 1991.

9. Банкер Ф.Р., Йенсен П. Симметрия молекул и спектроскопия. Серия: Теоретические основы химии: Пер. с англ. Мир: Научный мир, 2004. Bunker P.R., Jensen P. Molecular symmetry and spectroscopy. Ottawa: NRC Research Press, 1998.

10. Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen // J. Chem. Phys., V. 90, I. 2, P. 1007 – 1023 (1989).

11. Feller D. Application of systematic sequences of wave functions to the water dimmer // J. Chem. Phys., V. 96, I. 8, P. 6104 (1992).

12. Feller D. The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water // J. Chem. Phys., V. 98, I. 9, P. 7059 (1993).

13. Калиткин Н.Н. Численные методы. М.: Наука, 1978.

14. Petrova T., Poplavskii Yu., Serdyukov V., Sinitsa L. Intracavity laser spectroscopy of high-temperature water vapour in the range 9390 – 9450 cm-1 // Mol. Phys., V. 104, I. 16, P. 2691 – 2700, 2006.

15. Barber R.J., Tennyson J., Harris G.J. and Tolchenov R.N. A high-accuracy computed water line list // Mon. Not. R. Astr. Soc., V. 368, P. 1087 – (2006).

16. See EPAPS Document No. E-JCPSA6-128-046821 for electronic versions of all the potential energy surfaces as FORTRAN programs and for copies of the linelists. For more information on EPAPS, see rg/pubservs/epaps.php.


Список основных публикаций по теме диссертации:

1. Shirin S.V., Polyansky O.L., Zobov N.F., Ovsyannikov R.I., Császár A.G., Tennyson J. Spectroscopically determined potential energy surfaces of the H216O, H217O and H218O Isotopologues of water // J. Mol. Spectrosc., V. 236, P. 216 – 223 (2006).

2. Zobov N.F., Ovsyannikov R.I., Shirin S.V., Polyansky O.L., Tennyson J., Janka A. and Bernath P.F. Infrared emission spectrum of hot D2O // J. Mol. Spectrosc., V 240, P. 132 – 139 (2006).

3. Зобов Н.Ф., Овсянников Р.И., Ширин С.В., Полянский О.Л., Приписывание квантовых чисел теоретическим спектрам молекул H216O, H217O и H218O, рассчитанных вариационными методами в диапазоне 0 – 26000 см-1 // Оптика и Спектроскопия, Т. 102, N. 3, С. 390 – 395 (2007).

4. Shirin S. V., Zobov N. F., Ovsyannikov R. I., Polyansky O. L. and Tennyson J. Water line lists close to experimental accuracy using a spectroscopically determined potential energy surface for H216O, H217O and H218O // J. Chem. Phys., V. 128, 224306 (2008).

5. Zobov N. F., Shirin S. V., Ovsyannikov R. I., Polyansky O. L., Barber R. J., Tennyson J., Bernath P. F., Carleer M., Colin R. and Coheur P.-F. Spectrum of hot water in the 4750 – 13,000 cm-1 wavenumber range (0.769 – 2.1 µm) // Monthly Notices of the Royal Astronomical Society, V. 387, P. 1093 – 1098 (2008).

6. Ovsyannikov R. I., Thiel W., Yurchenko S. N., Carvajal M., and Jensen P. Vibrational energies of PH3 calculated variationally at the complete basis set limit // J. Chem. Phys., V. 129, 044309 (2008).

7. Ovsyannikov R. I., Thiel W., Yurchenko S. N., Carvajal M., Jensen P. PH3 revisited: Theoretical transition moments for the vibrational transitions below 7000 cm-1 // J. Mol. Spectrosc., V. 252, I. 2, P. 121 – 128 (2008).

8. Ovsyannikov R. I., Melnikov V. V., Thiel W., Jensen P., Baum O., Giesen T. F., and Yurchenko S. N. Theoretical rotation-torsion energies of HSOH // J. Chem. Phys., V. 129, 154314 (2008).

9. Yurchenko S. N., Ovsyannikov R. I., Thiel W., and Jensen P. Rotation-vibration energy cluster formation in XH2D and XHD2 molecules (X = Bi, Sb, and P) // J. Mol. Spectrosc., V. 256, P. 119 – 127 (2009).

10. Овсянников Р. И., Йенсен П., Третьяков М. Ю., Юрченко С. Н. О применении метода конечных разностей при расчете колебательно-вращательных энергий // Оптика и Спектроскопия, Т. 107, № 2, С. 236 – 242 (2009).

Оглавление диссертации



Введение

Глава 1. Методы расчётов колебательно-вращательных спектров молекул

1.1 Основы вариационных расчётов

1.2 Расчёты спектров трёхатомных молекул с использованием аналитического представления гамильтониана на примере метода расчётов DVR3D

1.3 Расчёты уровней энергии молекул произвольной структуры с использованием численного представления гамильтониана на примере метода расчётов TROVE

1.4 Результаты и выводы главы 1

Глава 2. Модернизация метода расчётов TROVE

2.1 Учёт симметрии. Численный подход к определению молекулярной группы симметрии колебательно-вращательных базисных функций

2.2 Приближение полного базисного набора в применении к колебательным уровням энергии PH3

2.3 Модификация метода конечных разностей для разложения функции потенциальной энергии многоатомных молекул в ряд Тейлора

2.4 Результаты и выводы главы 2

Глава 3. Расчёт уровней энергии и спектров молекул, важных для спектроскопии

3.1 Образование кластеров колебательно-вращательных энергий в молекулах XH2D и XHD2 (X = Bi, Sb, или P)

3.2 Торсионное расщепление уровней энергии молекулы HSOH

3.3 Теоретические матричные элементы электродипольных переходов для колебательных уровней энергии молекулы PH3 ниже 7000 см-1

3.4 Анализ горячего спектра молекулы воды в диапазоне длин волн 4750 – 13000 см-1 (0.769 – 2.1 мкм)

3.5 Расчёт списков линий трёх изотопических модификаций молекулы воды с точностью близкой к экспериментальной

3.6 Результаты и выводы главы 3

Заключение

Библиография


Овсянников Роман Ильич


УНИВЕРСАЛЬНЫЙ ПОДХОД К ВАРИАЦИОННЫМ РАСЧЕТАМ КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫХ УРОВНЕЙ ЭНЕРГИИ МАЛОАТОМНЫХ МОЛЕКУЛ C ИСПОЛЬЗОВАНИЕМ ПОВЕРХНОСТИ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ


    А в т о р е ф е р а т


Подписано в печать

Формат 60 × 90 1/16. Бумага офсетная № 1.
Усл. печ. л. 1,0.
Тираж экз. Заказ № (2010)


Отпечатано в типографии Учреждения российской академии наук

института прикладной физики РАН,
603950 Н. Новгород, ул. Ульянова, 46