Лекция n2 Лекция 2
| Вид материала | Лекция |
- «Социальная стратификация и социальная мобильность», 46.19kb.
- Первая лекция. Введение 6 Вторая лекция, 30.95kb.
- Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
- Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
- Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
- Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
- Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
- Тема Лекция, 34.13kb.
- Лекция посвящена определению термина «транскриптом», 219.05kb.
- А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.
ЛЕКЦИЯ N2
Лекция 2.
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ в контуре. сохранение энергии.
ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ.
ФАЗОВЫЙ ПОРТРЕТ КОЛЕБАНИЙ
К
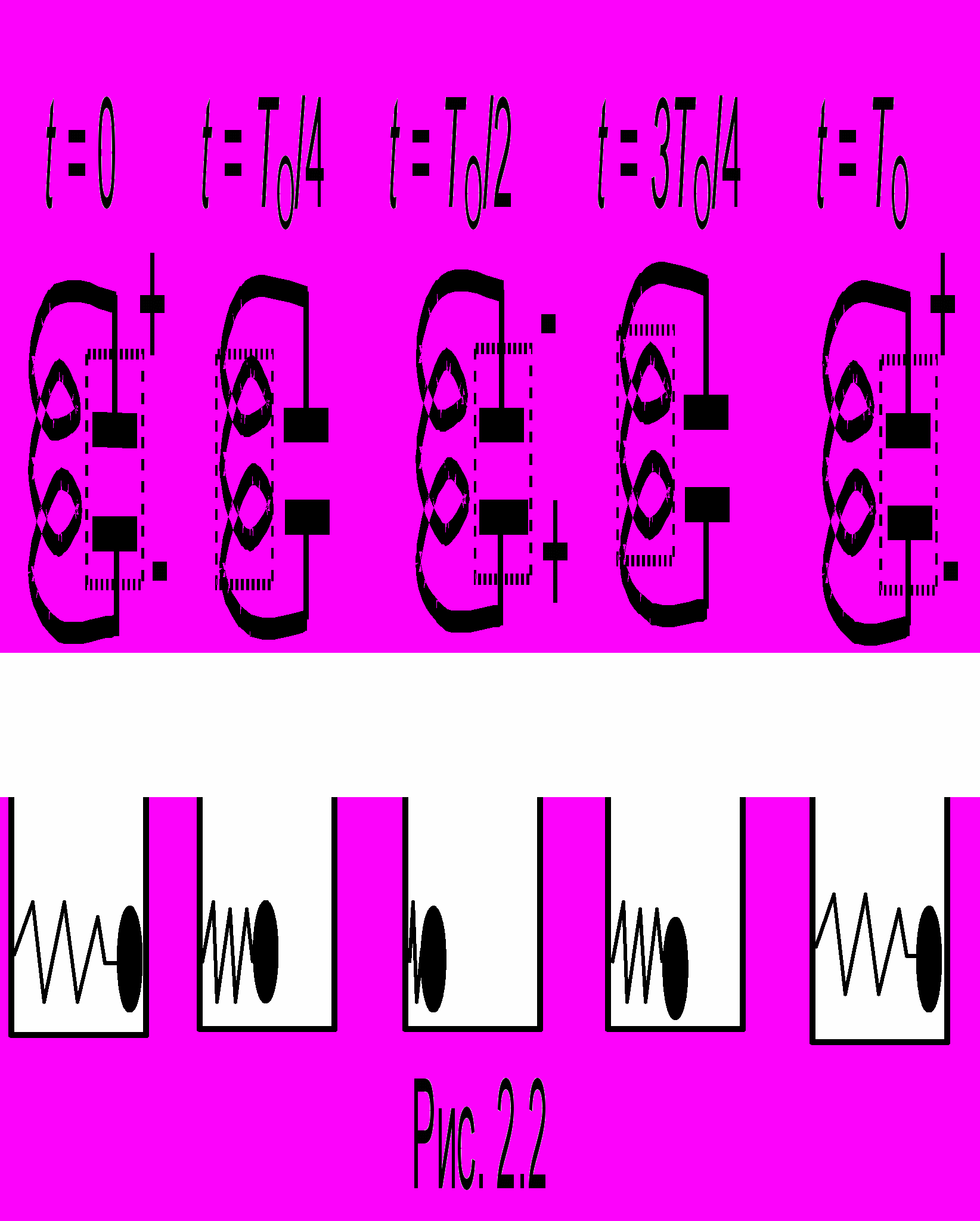
олебательный контур представляет собой катушку индуктивности, с
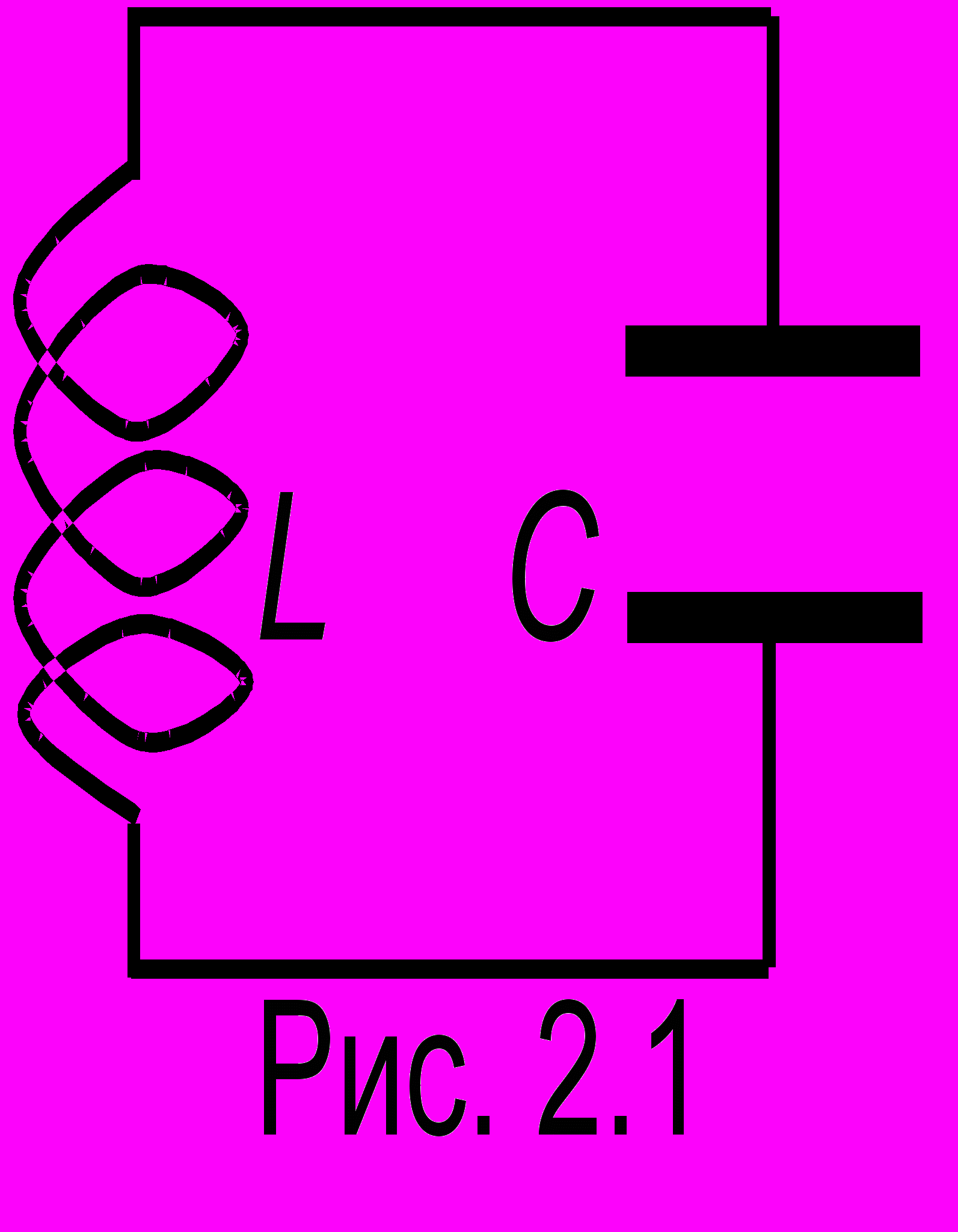
оединенную с конденсатором (рис. 2.1), и он также является гармоническим осциллятором. Рассмотрим характер протекания колебательных процессов в контуре. Пусть в начальный момент на конденсаторе имеется заряд q, полученный от некоторого источника, отключенного от конденсатора в момент t = 0. Пусть, например, верхняя пластина при этом заряжена положительно. Протекание тока через катушку в направлении против часовой стрелки будет приводить к разряду конденсатора и убыванию напряжения на его обкладках до нулевого значения. В этот момент запасенная изначально энергия электростатического поля в конденсаторе
 с = СU2 /2 обратится в ноль и полностью перейдет в энергию магнитного поля М = LJ2 /2, локализованную в катушке. Величина тока в ней достигает в этот момент максимального значения и затем начинает убывать. Возникающая при этом э.д.с. самоиндукции порождает ток, который в соответствии с правилом Ленца будет стремиться поддержать убывающий ток. Этот ток, протекая по цепи и убывая по величине, будет перезаряжать конденсатор. По завершении этого процесса ток обратится в нуль, а заряд на конденсаторе снова примет максимальное значение, но при этом верхняя пластина будет теперь заряжена отрицательно. Этот момент соответствует половине периода колебаний, и далее процесс будет развиваться аналогичным образом в обратном направлении. На рис. 2.2 схематически показан этот колебательный процесс. Он вполне аналогичен колебаниям пружинного маятника. Для более наглядной аналогии выбран горизонтальный маятник без трения с положением равновесия (пружина не растянута) точно посредине, когда t = TО/4 или t = 3TО/4. В этот момент величина скорости маятника максимальна, а в контуре максимальна величина тока. Полная энергия маятника при этом равна кинетической, а контура - энергии магнитного поля, локализованного в катушке индуктивности. Когда скорость маятника равна нулю, пружина максимально растянута (t = 0 и t = TО) или сжата (t = TО/2), и полная энергия маятника равна потенциальной, а контура - энергии электростатического поля, сосредоточенного в конденсаторе. Перераспределение энергии контура отмечено на рис. 2.2 пунктирными квадратами, а аналогии между электрическими и механическими величинами представлены в таблице 1.
с = СU2 /2 обратится в ноль и полностью перейдет в энергию магнитного поля М = LJ2 /2, локализованную в катушке. Величина тока в ней достигает в этот момент максимального значения и затем начинает убывать. Возникающая при этом э.д.с. самоиндукции порождает ток, который в соответствии с правилом Ленца будет стремиться поддержать убывающий ток. Этот ток, протекая по цепи и убывая по величине, будет перезаряжать конденсатор. По завершении этого процесса ток обратится в нуль, а заряд на конденсаторе снова примет максимальное значение, но при этом верхняя пластина будет теперь заряжена отрицательно. Этот момент соответствует половине периода колебаний, и далее процесс будет развиваться аналогичным образом в обратном направлении. На рис. 2.2 схематически показан этот колебательный процесс. Он вполне аналогичен колебаниям пружинного маятника. Для более наглядной аналогии выбран горизонтальный маятник без трения с положением равновесия (пружина не растянута) точно посредине, когда t = TО/4 или t = 3TО/4. В этот момент величина скорости маятника максимальна, а в контуре максимальна величина тока. Полная энергия маятника при этом равна кинетической, а контура - энергии магнитного поля, локализованного в катушке индуктивности. Когда скорость маятника равна нулю, пружина максимально растянута (t = 0 и t = TО) или сжата (t = TО/2), и полная энергия маятника равна потенциальной, а контура - энергии электростатического поля, сосредоточенного в конденсаторе. Перераспределение энергии контура отмечено на рис. 2.2 пунктирными квадратами, а аналогии между электрическими и механическими величинами представлены в таблице 1.От этих качественных рассмотрений перейдем теперь к составлению дифференциального уравнения колебаний в контуре. По закону Кирхгофа напряжение на конденсаторе Uc = q/C равно э.д.с. самоиндукции
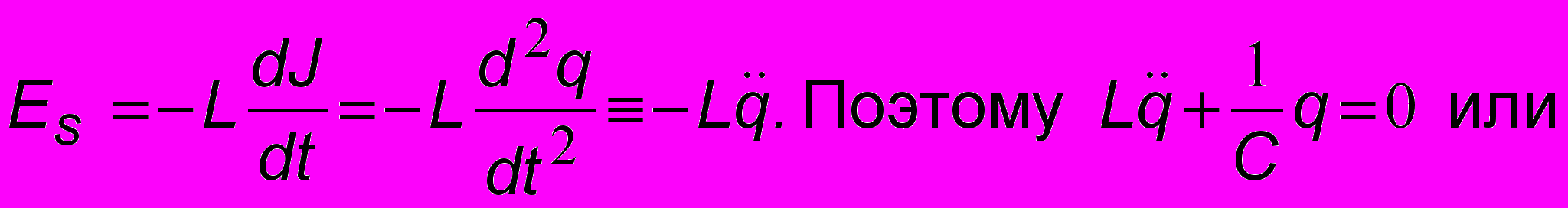
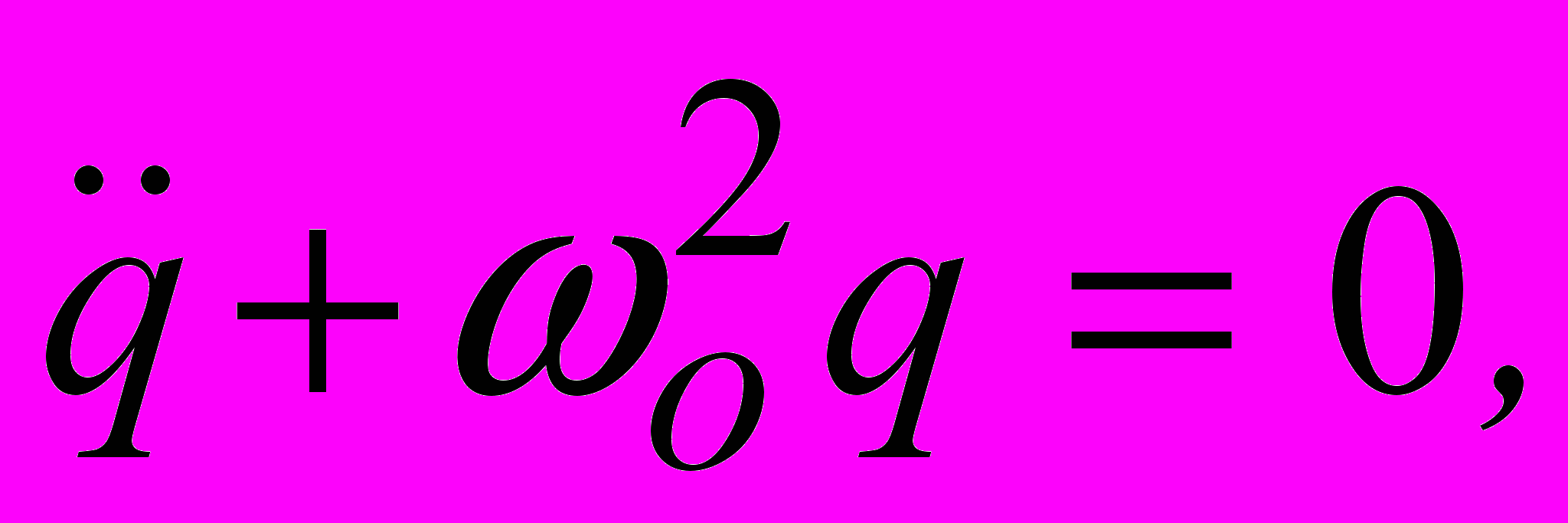 (2.1)
(2.1)где
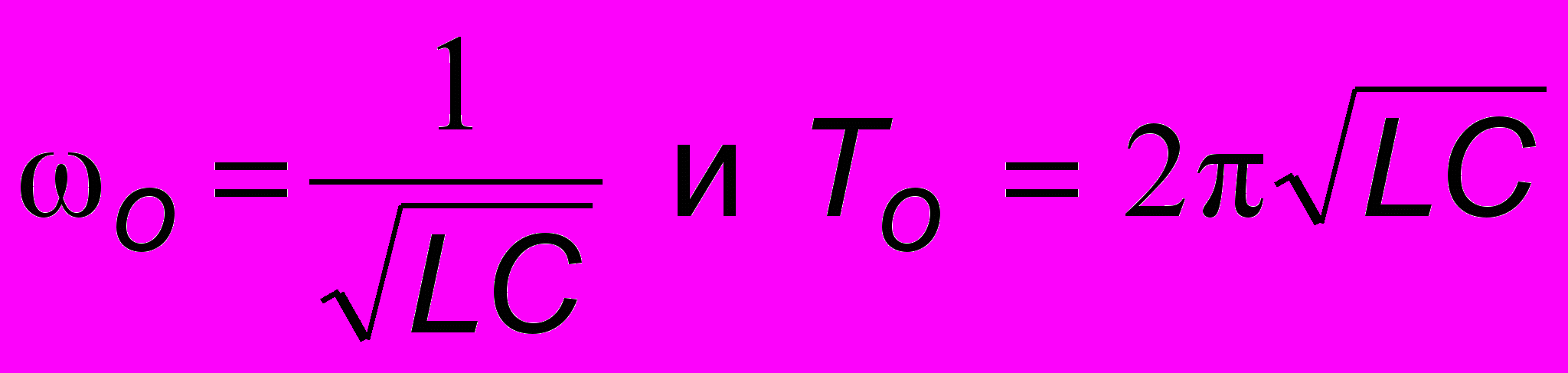 - формула Томсона. Решением (2.1) является гармоническое колебание q(t) = Q cos (Оt + ), где Q - амплитуда заряда. Вместо колебаний заряда q можно говорить о колебаниях тока в контуре
- формула Томсона. Решением (2.1) является гармоническое колебание q(t) = Q cos (Оt + ), где Q - амплитуда заряда. Вместо колебаний заряда q можно говорить о колебаниях тока в контуре 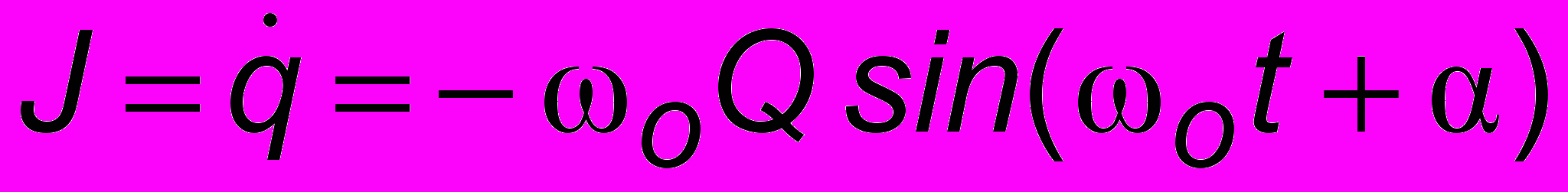 или же напряжения на конденсаторе Uc = q/C = (Q/C) cos (Оt + ).
или же напряжения на конденсаторе Uc = q/C = (Q/C) cos (Оt + ). Таблица 1 (Электромеханическая аналогия)
| Электрические величины | Механические величины | ||
| Величина | Ед. измер. | Величина | Ед. измер. |
| Заряд q | Кл | Смещение, х | м |
| Ток J = 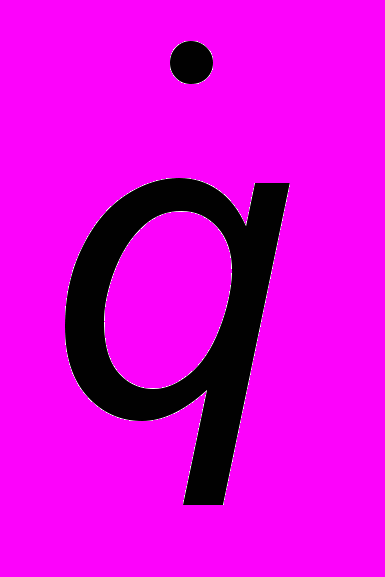 | Кл/с (A) | Скорость, v =  | м/с |
| Изменение тока 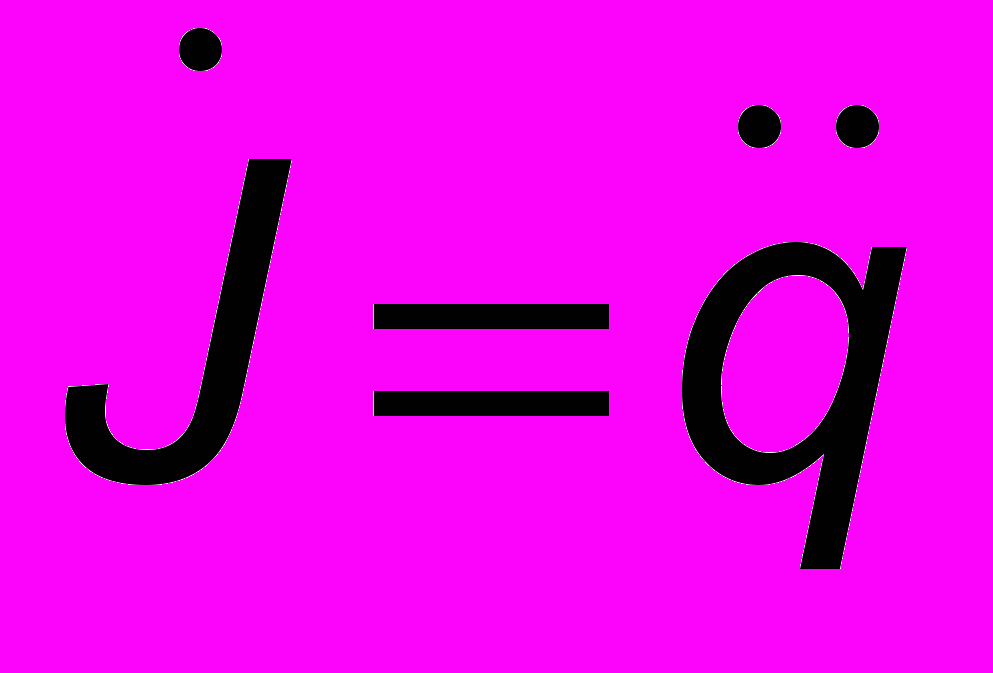 1 1 | А/с | Ускорение а = 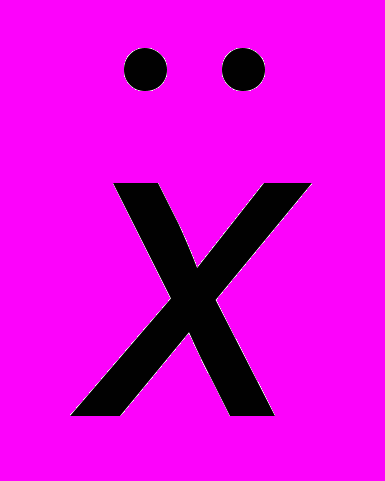 | м/с2 |
| Электростатическая энергия 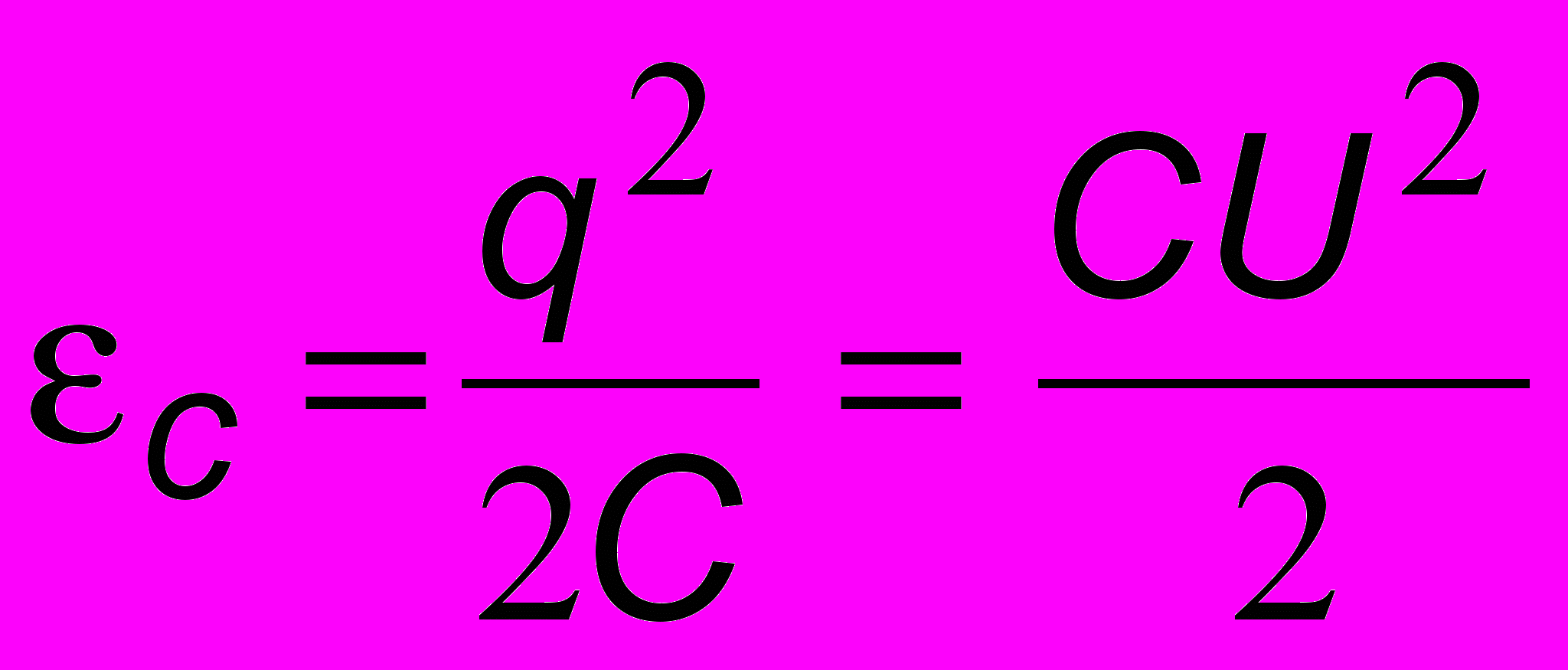 | Дж | Потенциальная энергия 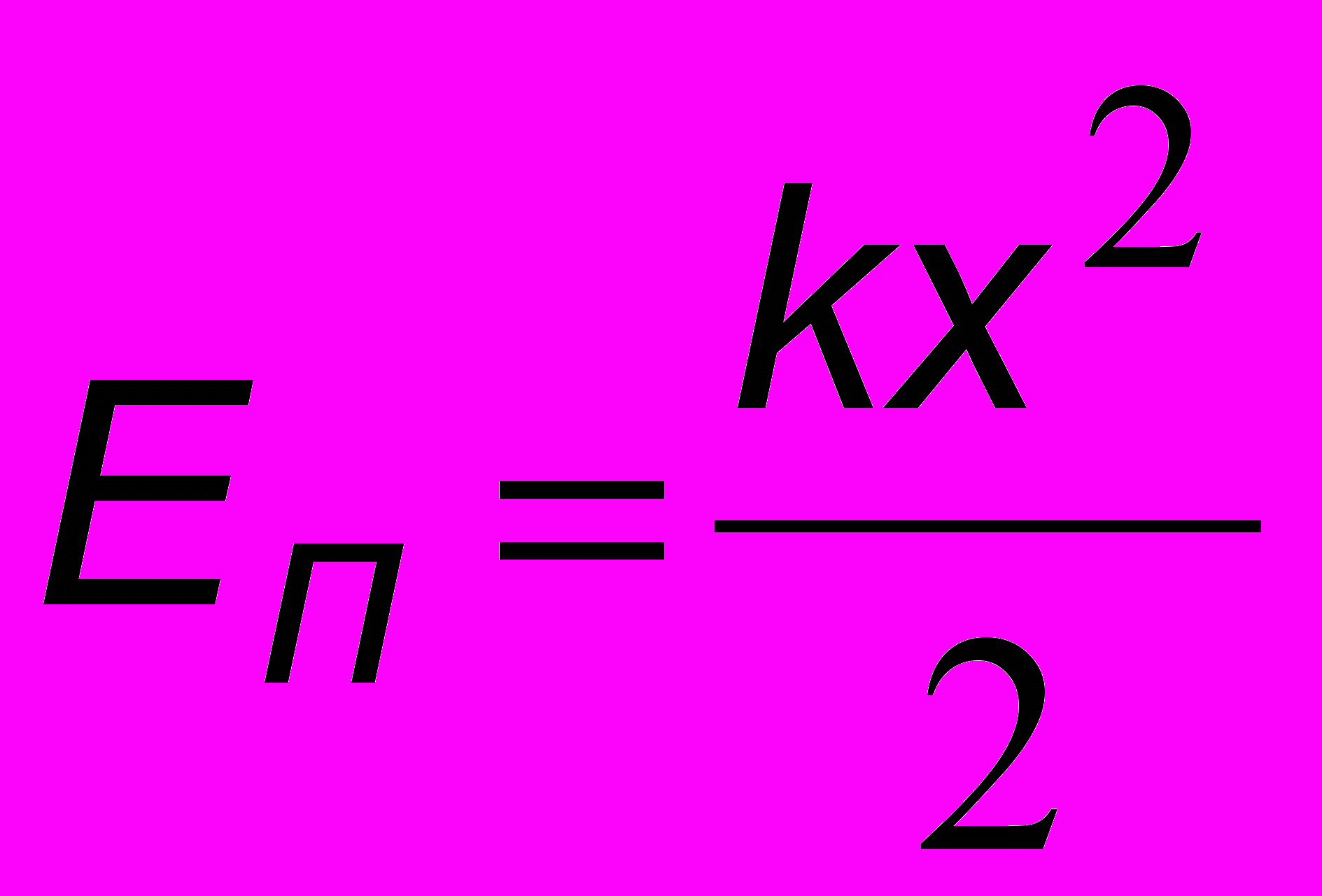 | Дж |
| Энергия магнитного поля 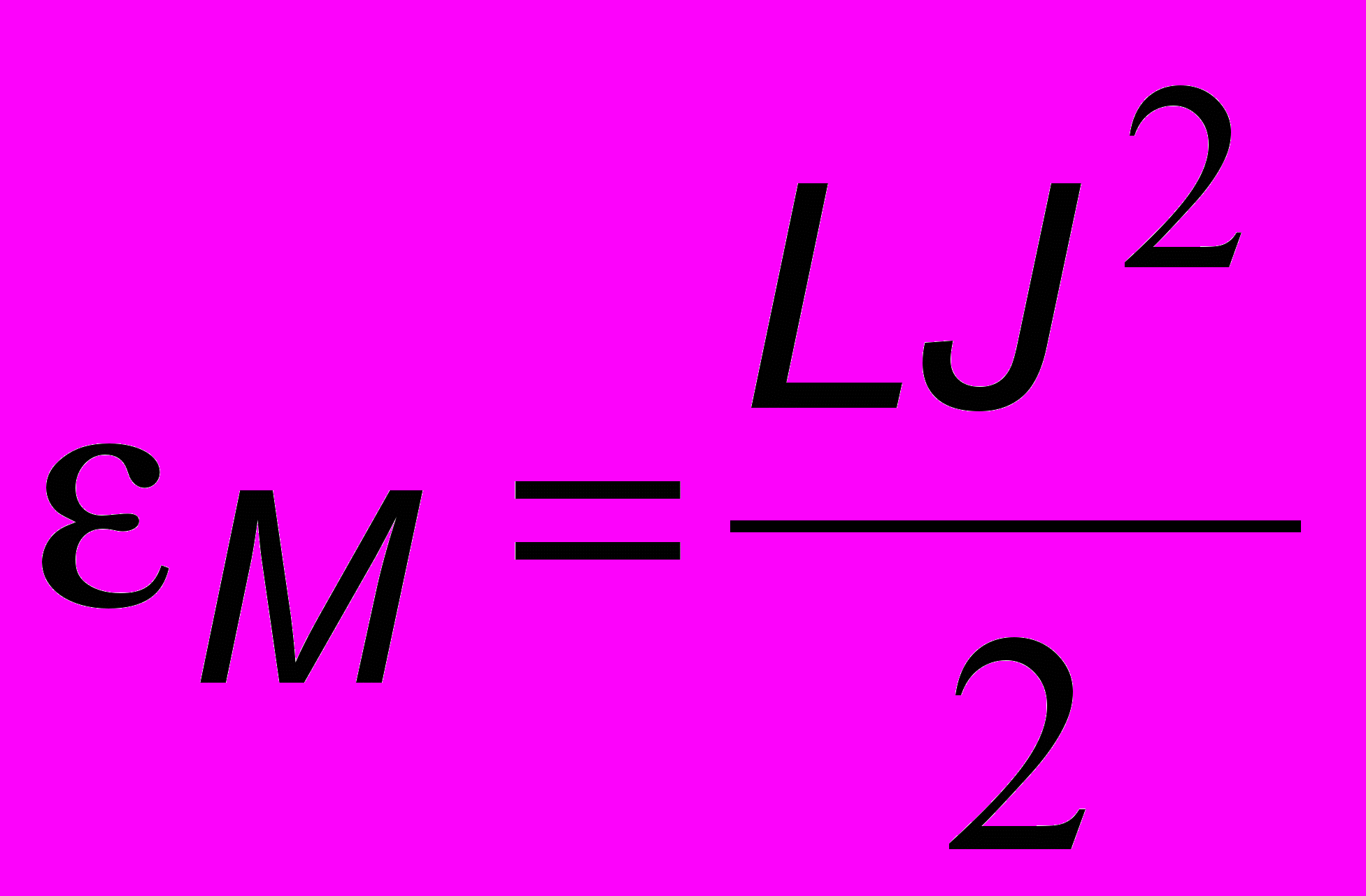 | Дж | Кинетическая энергия 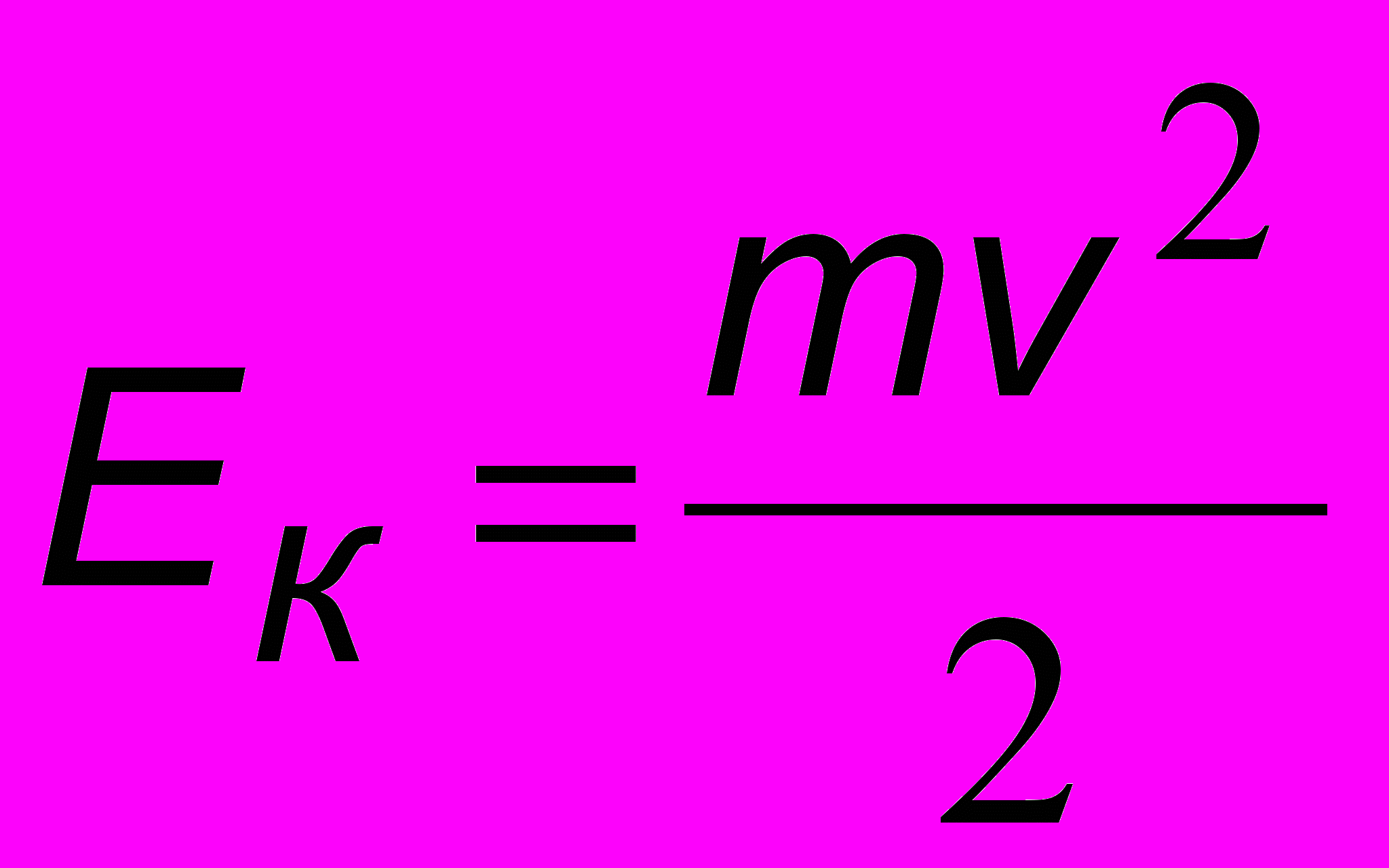 | Дж |
Чтобы определить Q и начальную фазу , нужно, как и в "механическом случае" (см. ЛЕКЦИЮ 1) задать q(0) = qo - начальный заряд и
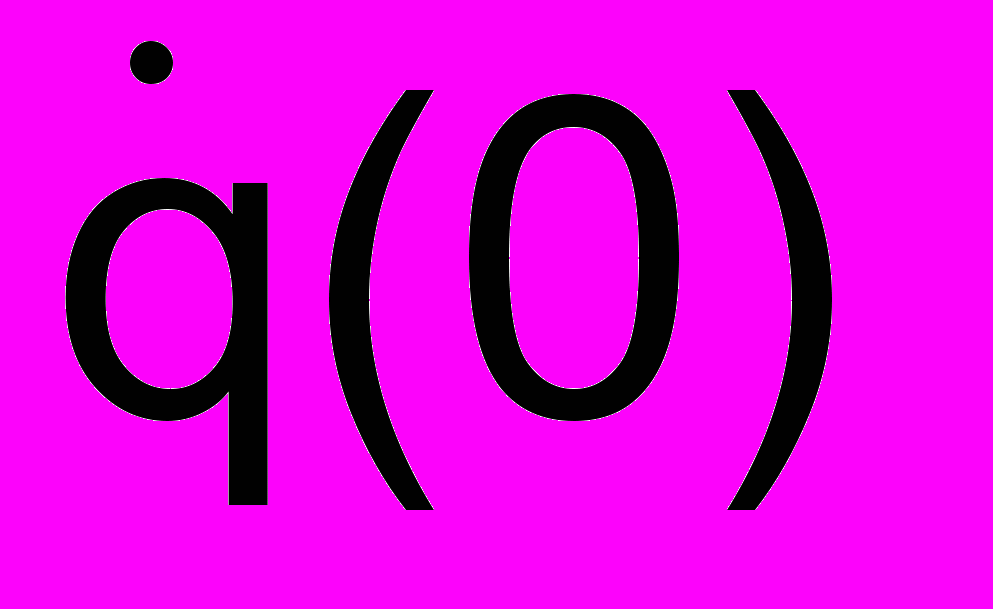 = JО - начальный ток, аналогичные начальному смещению и начальной скорости пружинного маятника. На рис. 2.3 показана временнáя диаграмма представленных в таблице параметров контура, которым соответствуют указанные в квадратных скобках механические параметры. (На графиках для простоты мы положили = 0).
= JО - начальный ток, аналогичные начальному смещению и начальной скорости пружинного маятника. На рис. 2.3 показана временнáя диаграмма представленных в таблице параметров контура, которым соответствуют указанные в квадратных скобках механические параметры. (На графиках для простоты мы положили = 0).Поскольку для контура
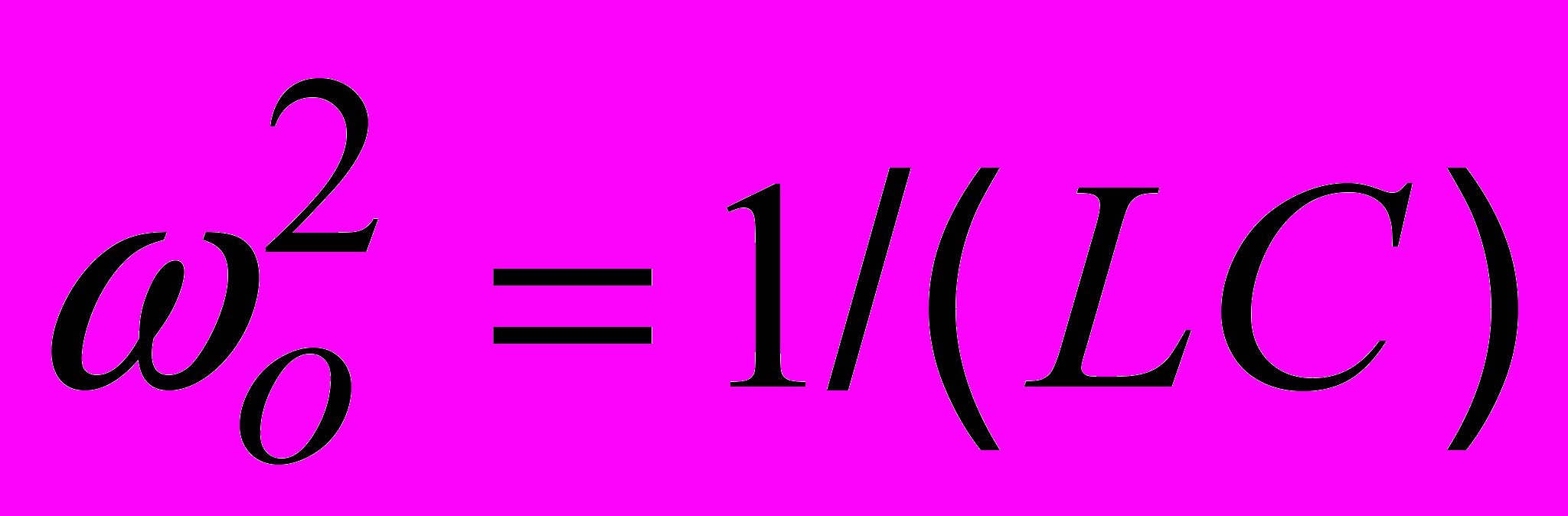 , то полная энергия контура
, то полная энергия контура 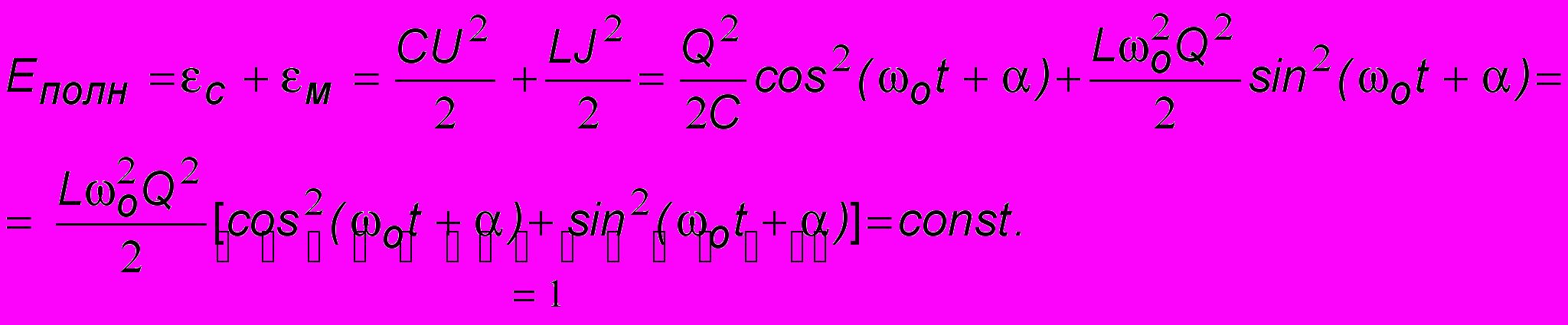 Аналогично для пружинного маятника
Аналогично для пружинного маятника 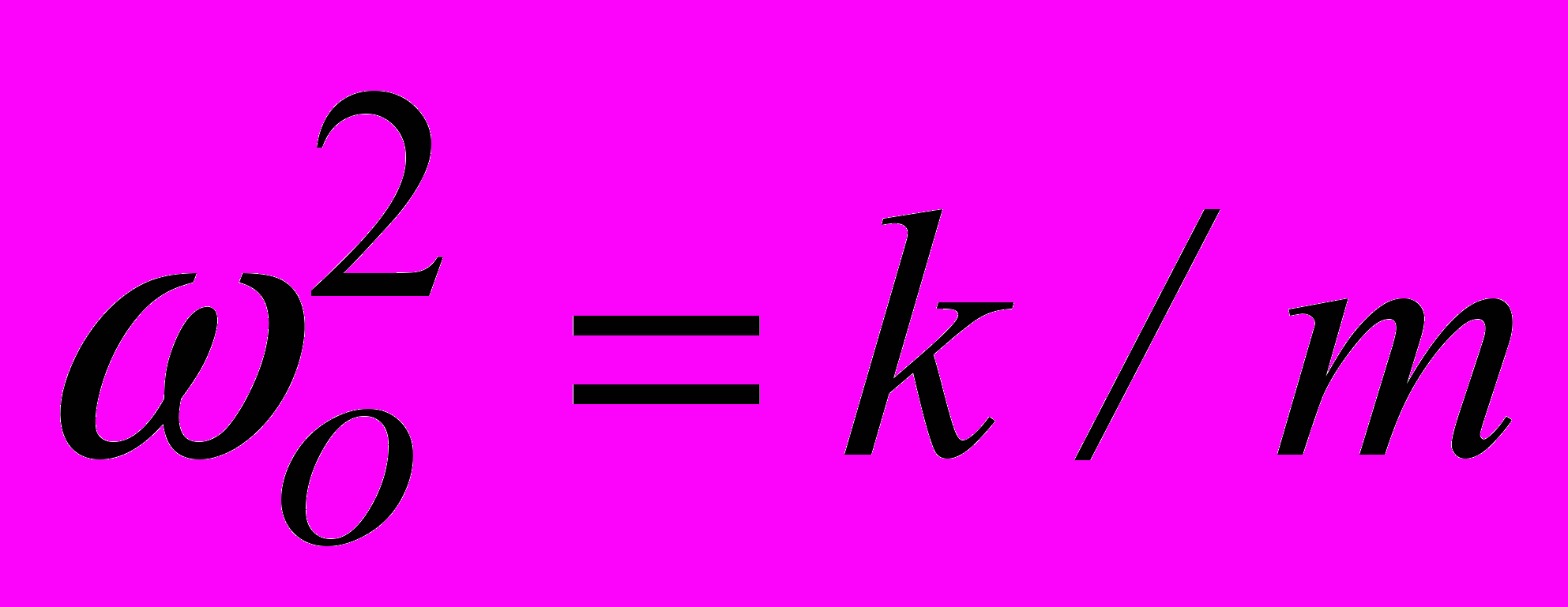 и
и 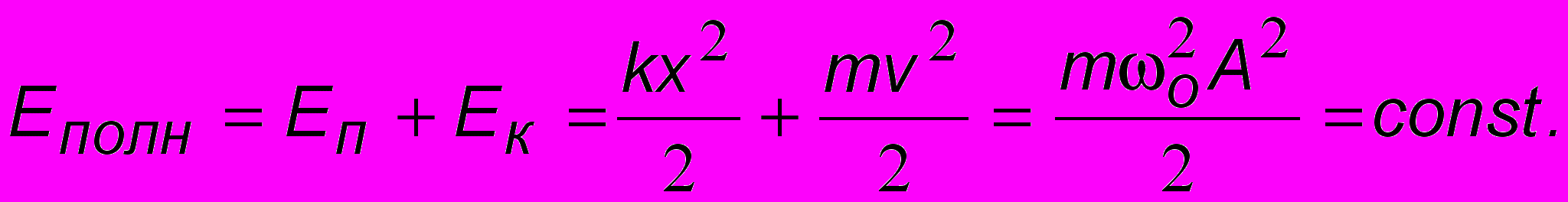
Т
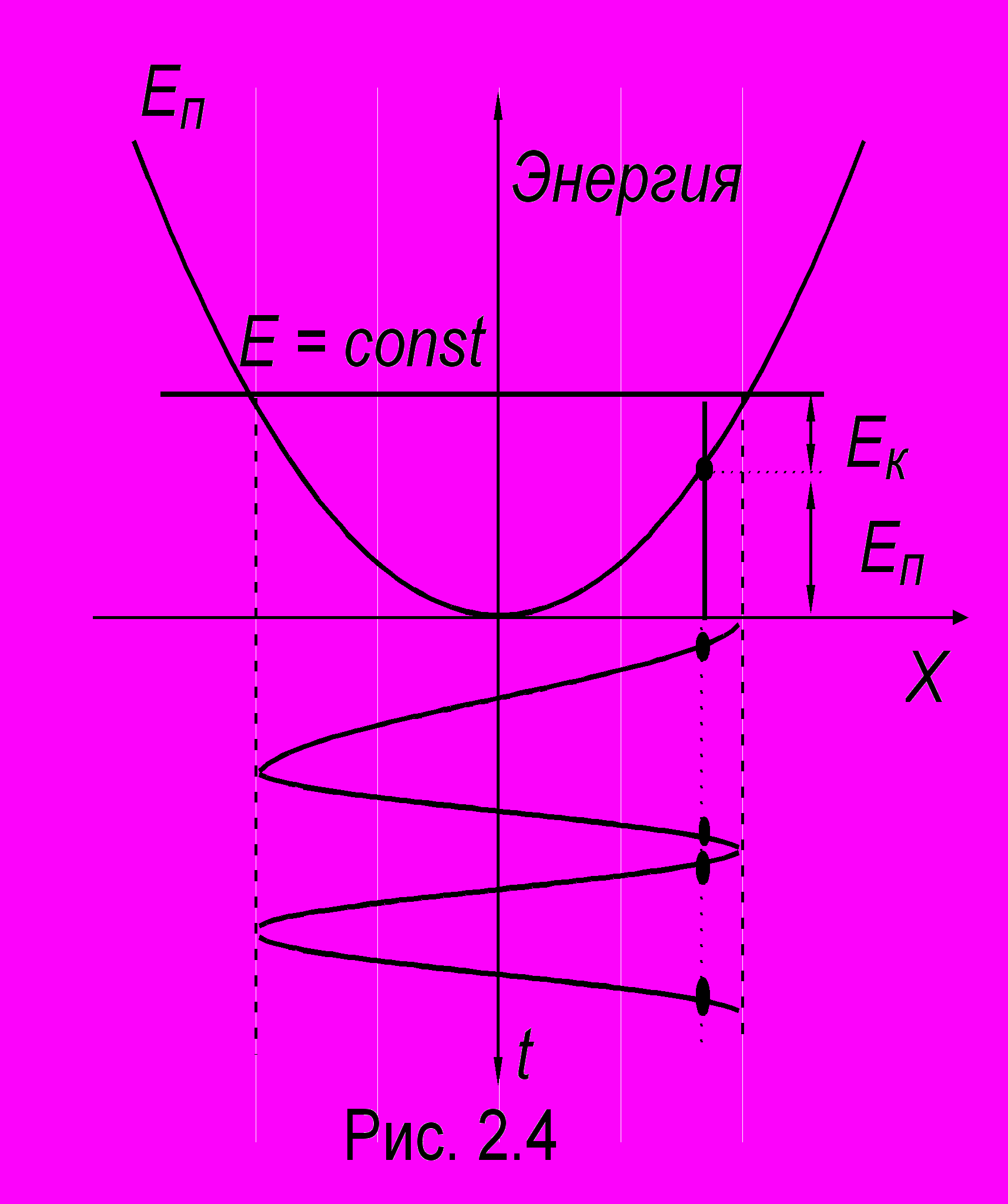
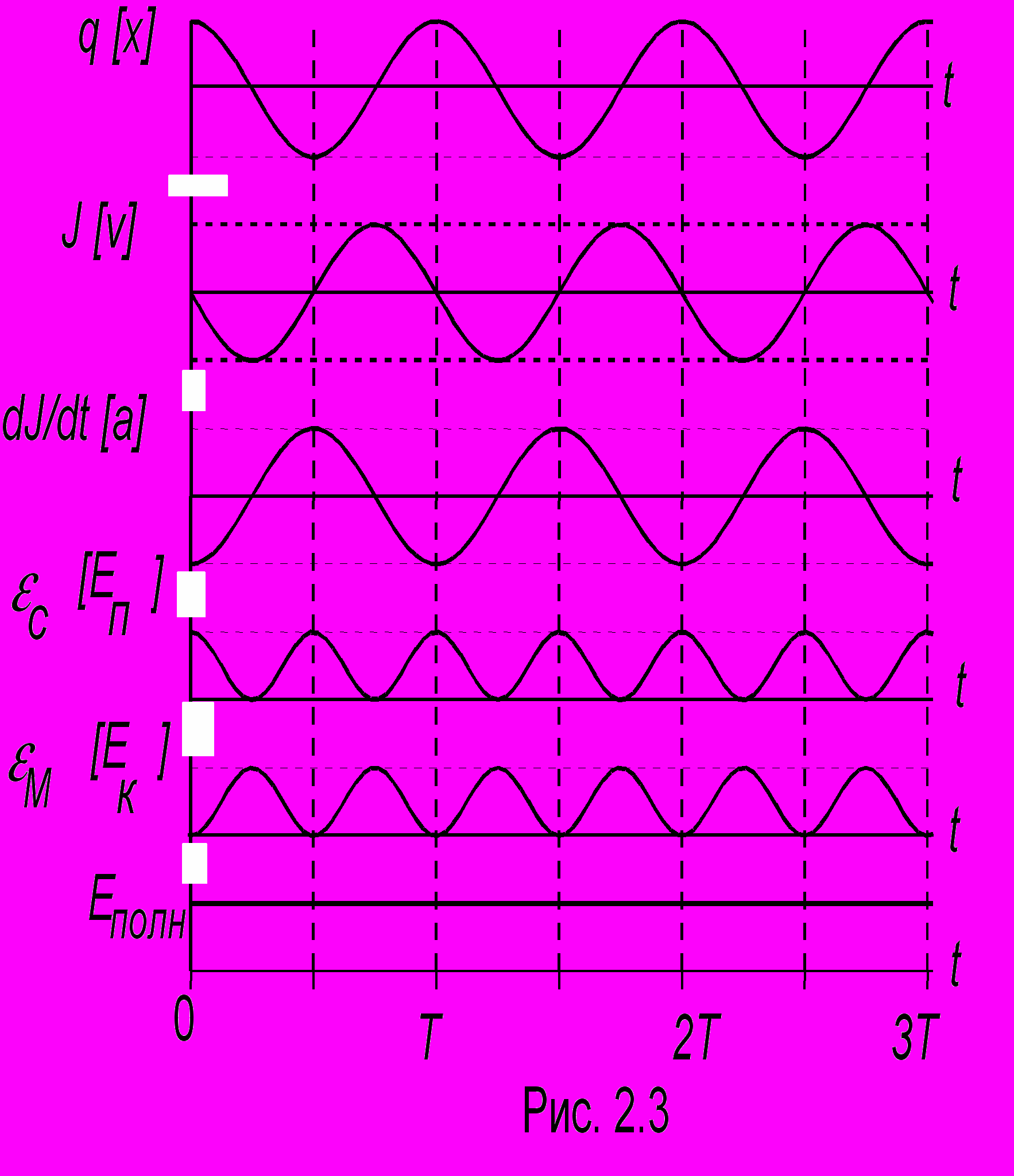 аким образом, полная энергия в каждой из этих систем сохраняется. Как видно из рис. 2.2, энергии С М и Еп Ек колеблются в противофазе и с удвоенной частотой. Еще более наглядно изменение энергий в процессе колебаний представлено на рис. 2.4. Любая прямая, проведенная вертикально вниз от горизонтальной прямой Еполн, пересекает параболу Еп = kx2/2. Получившиеся отрезки между осью Х и прямой Еполн соответствуют Еп и Ек. Нижний график иллюстрирует обычную временнýю зависимость x(t).
аким образом, полная энергия в каждой из этих систем сохраняется. Как видно из рис. 2.2, энергии С М и Еп Ек колеблются в противофазе и с удвоенной частотой. Еще более наглядно изменение энергий в процессе колебаний представлено на рис. 2.4. Любая прямая, проведенная вертикально вниз от горизонтальной прямой Еполн, пересекает параболу Еп = kx2/2. Получившиеся отрезки между осью Х и прямой Еполн соответствуют Еп и Ек. Нижний график иллюстрирует обычную временнýю зависимость x(t).Фазовый портрет также является способом наглядного представления колебаний. Рассмотрим колебания пружинного маятника, описываемые дифференциальным уравнением (1.2), и, обозначив в нем
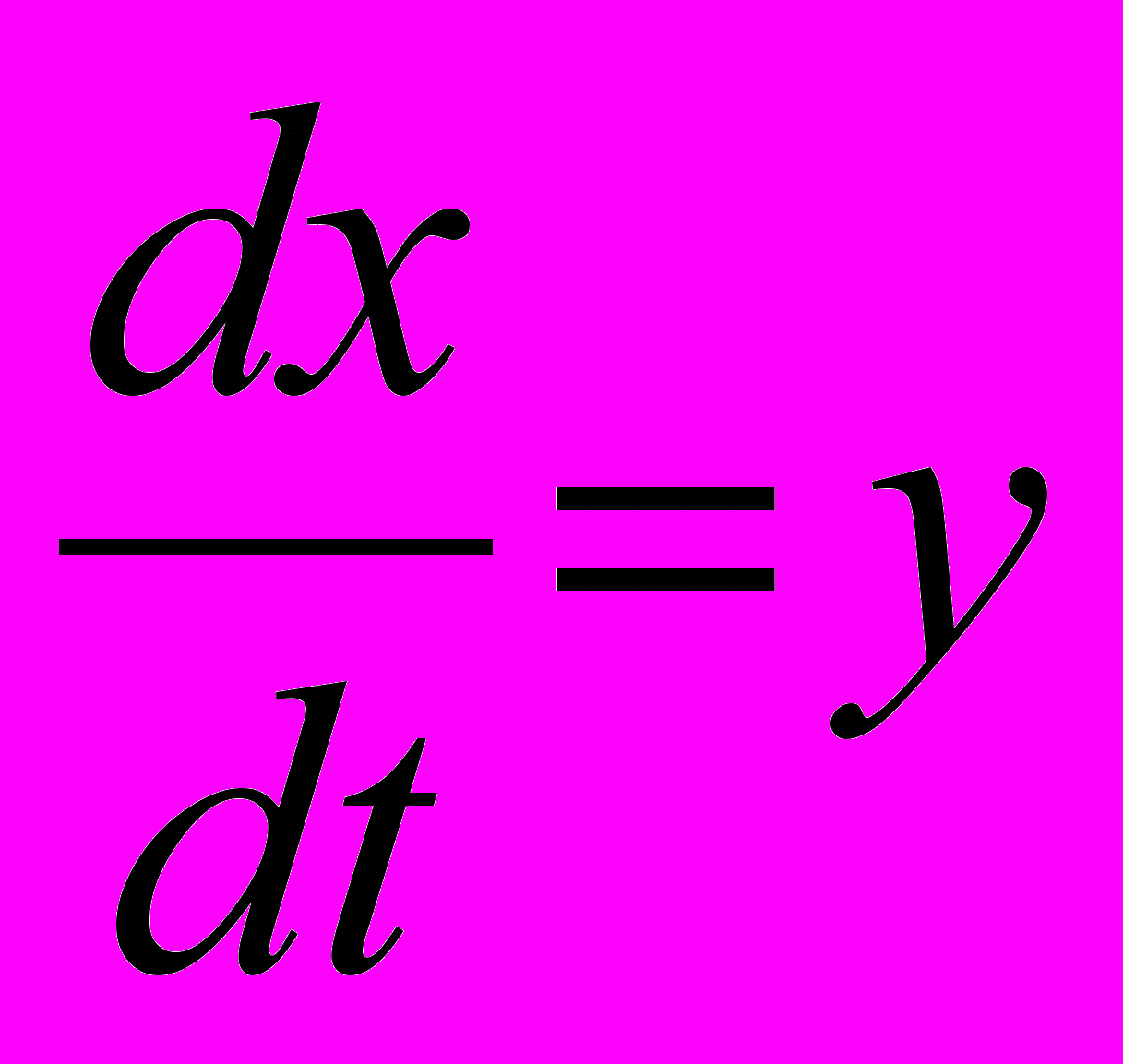 , представим (1.2) в виде
, представим (1.2) в виде 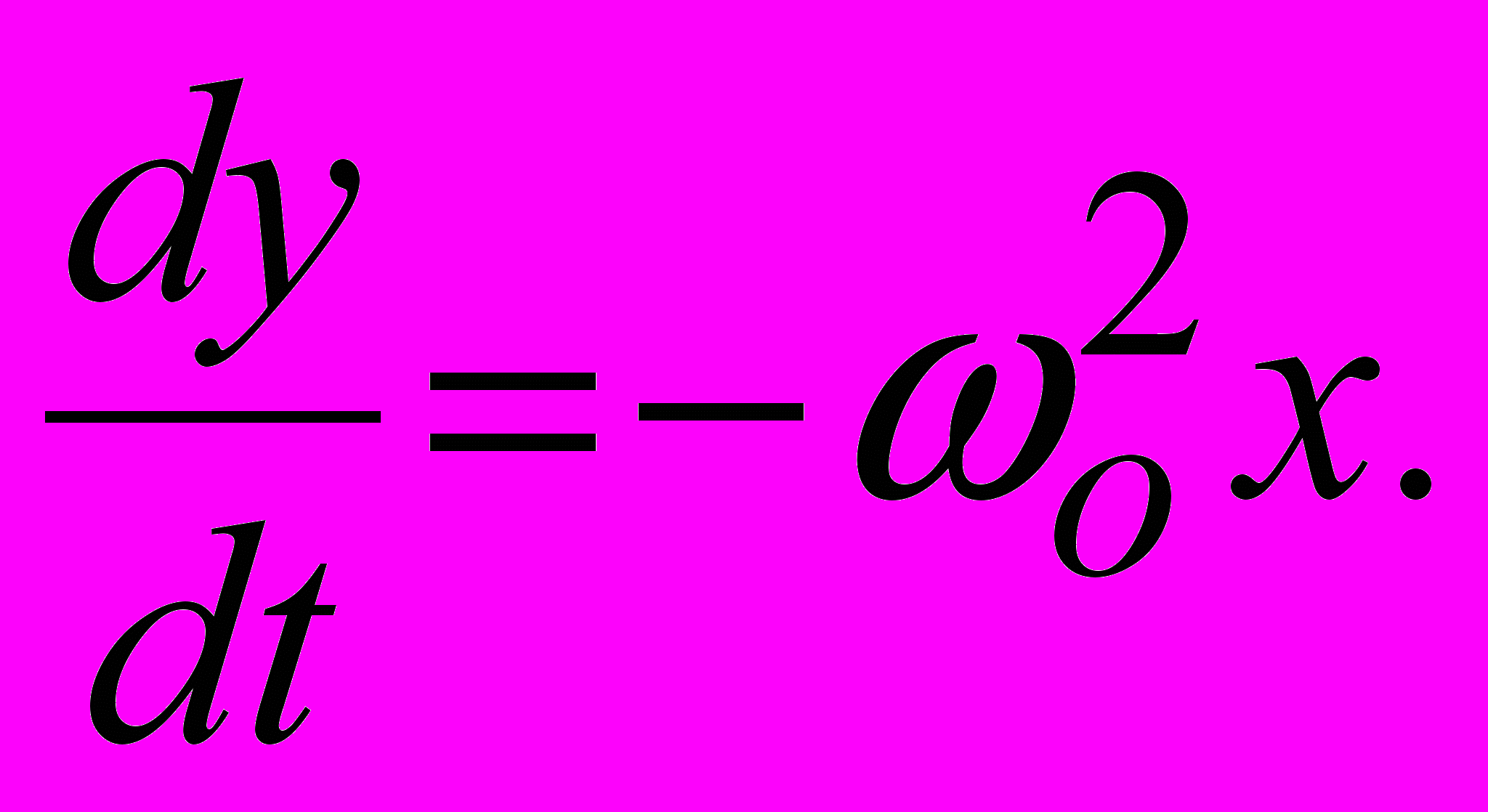 Поделив это соотношение на предыдущее, получим уравнение
Поделив это соотношение на предыдущее, получим уравнение 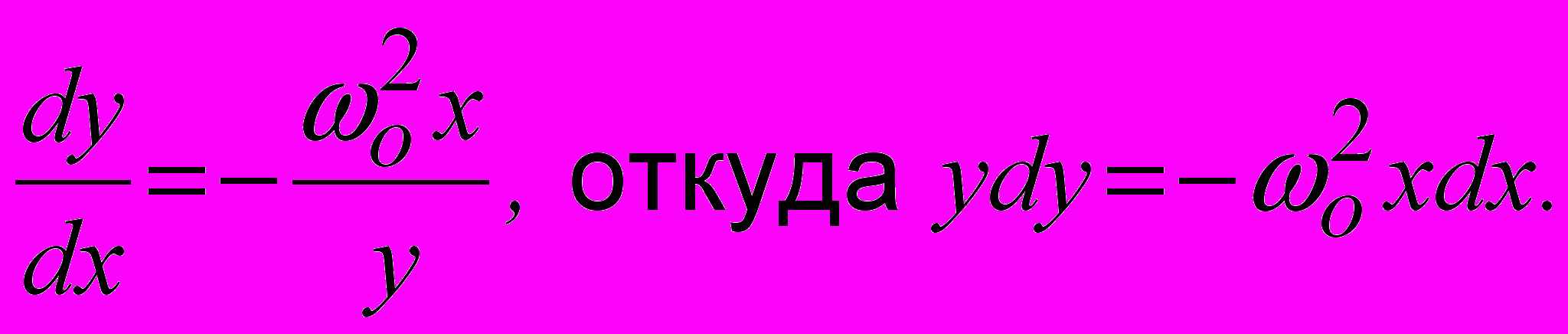 Проинтегрируем обе части этого уравнения:
Проинтегрируем обе части этого уравнения: 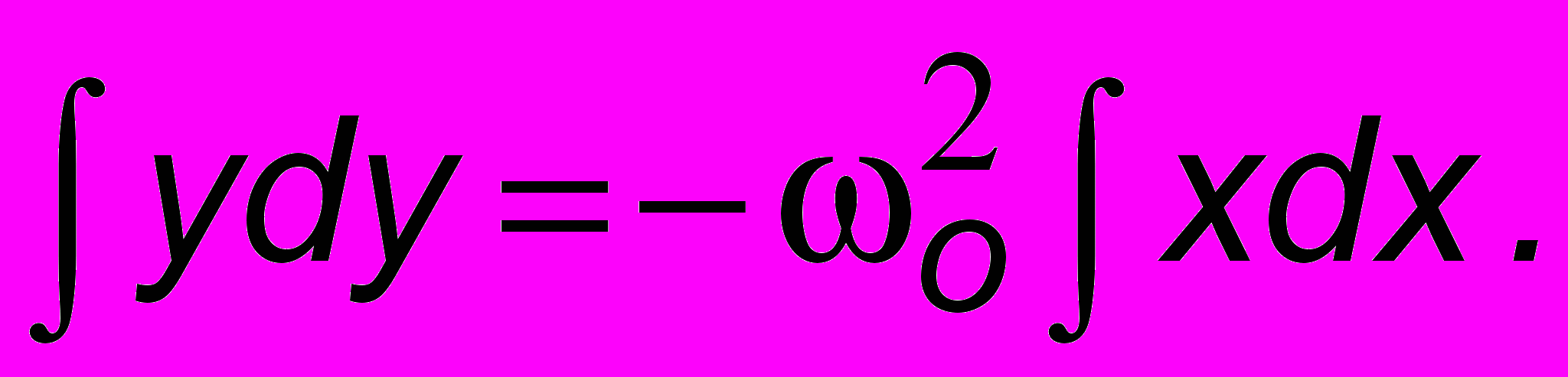 Получим
Получим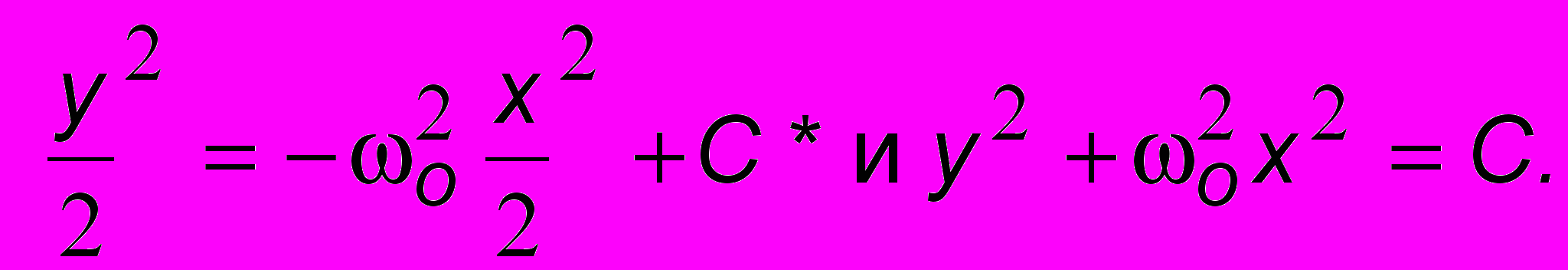
 (2.2)
(2.2)Здесь С* , С - константы (С = 2С*). Отсюда
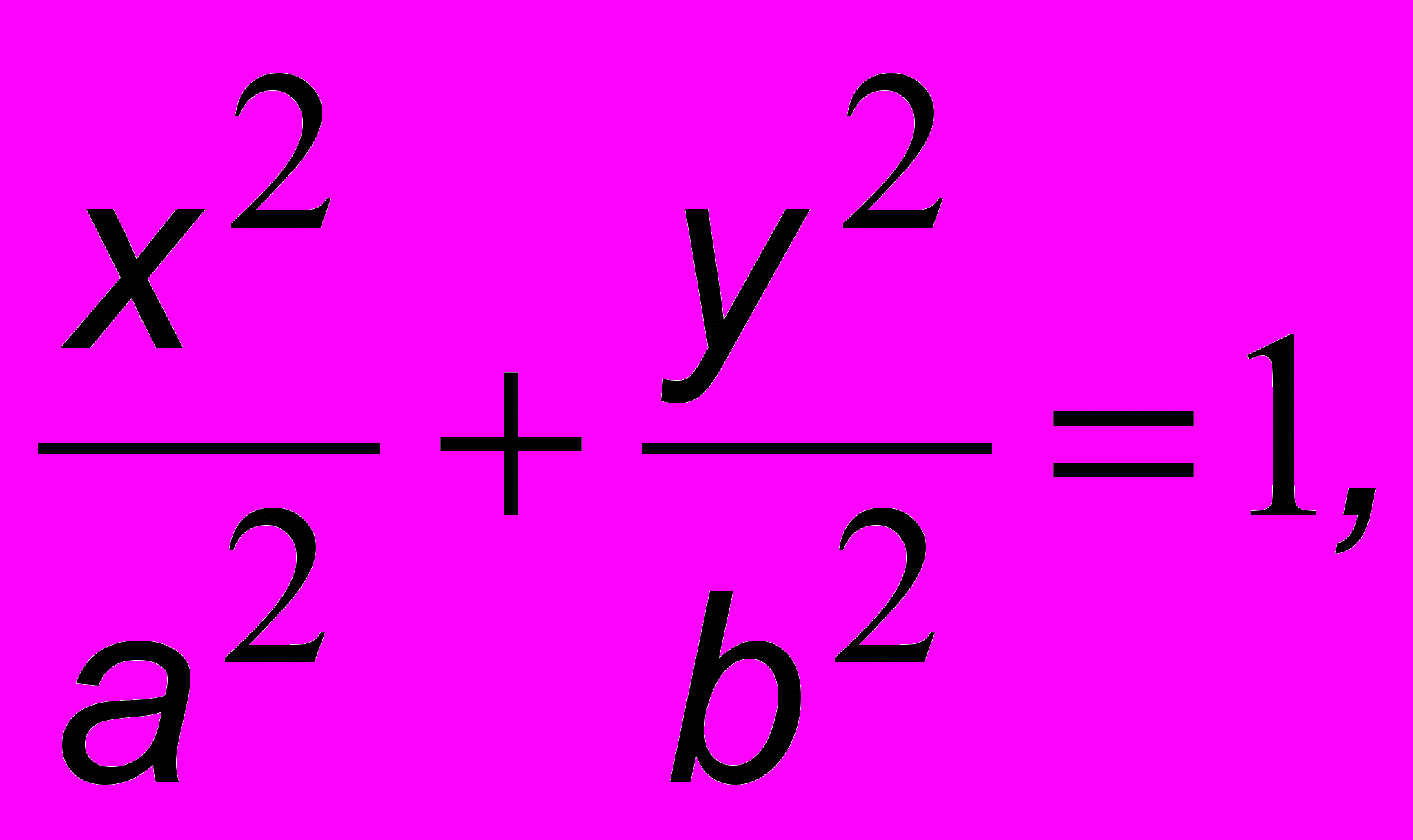 (2.3)
(2.3)г
де
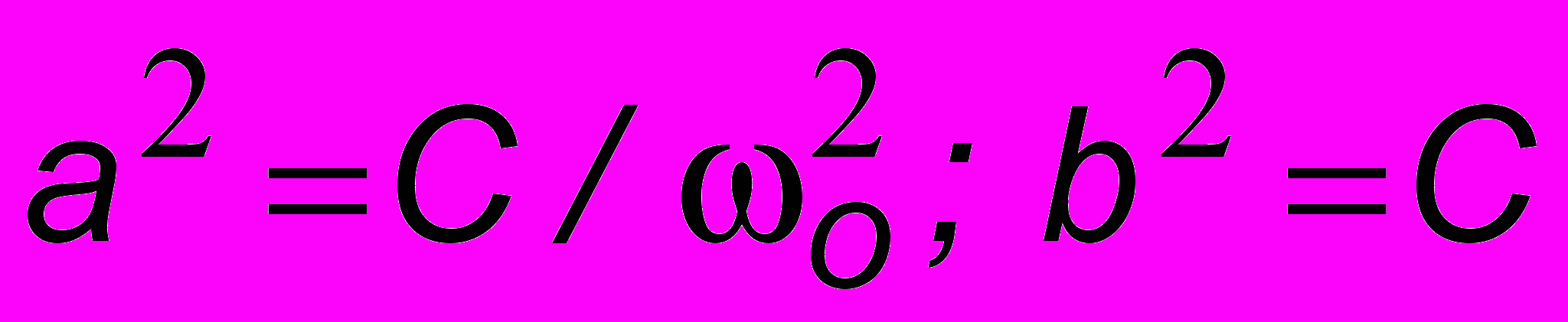 . Это уравнение семейства эллипсов; разным константам С будут соответствовать разные эллипсы, вложенные один в другой. Если задать конкретные начальные условия, то из всех эллипсов выделится один-единственный. Пусть при t = 0
. Это уравнение семейства эллипсов; разным константам С будут соответствовать разные эллипсы, вложенные один в другой. Если задать конкретные начальные условия, то из всех эллипсов выделится один-единственный. Пусть при t = 0 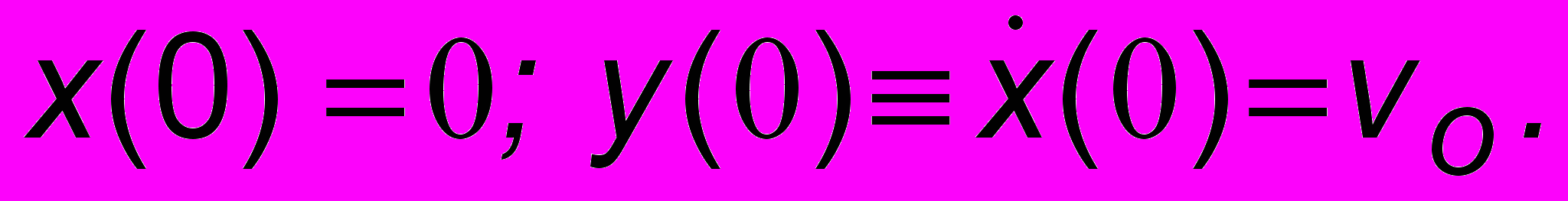 Из (2.2) следует, что
Из (2.2) следует, что 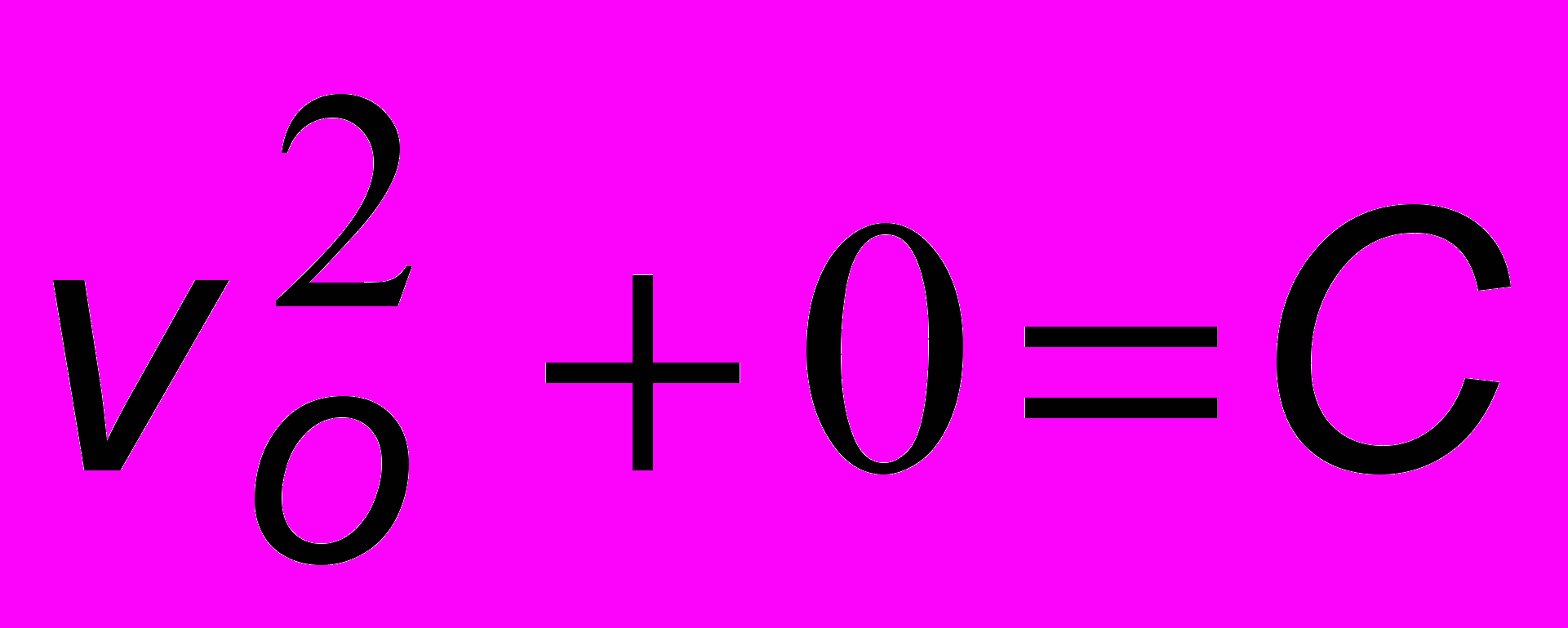 . Поэтому
. Поэтому 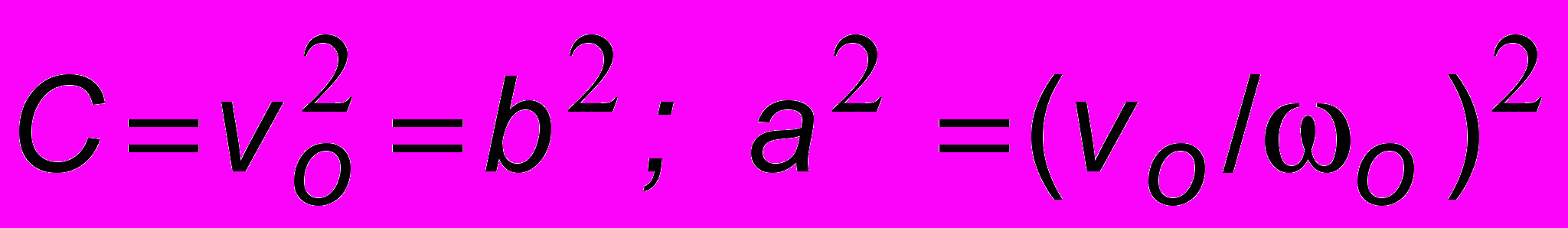 . Точка движется по эллипсу с большой полуосью, равной a =
. Точка движется по эллипсу с большой полуосью, равной a = 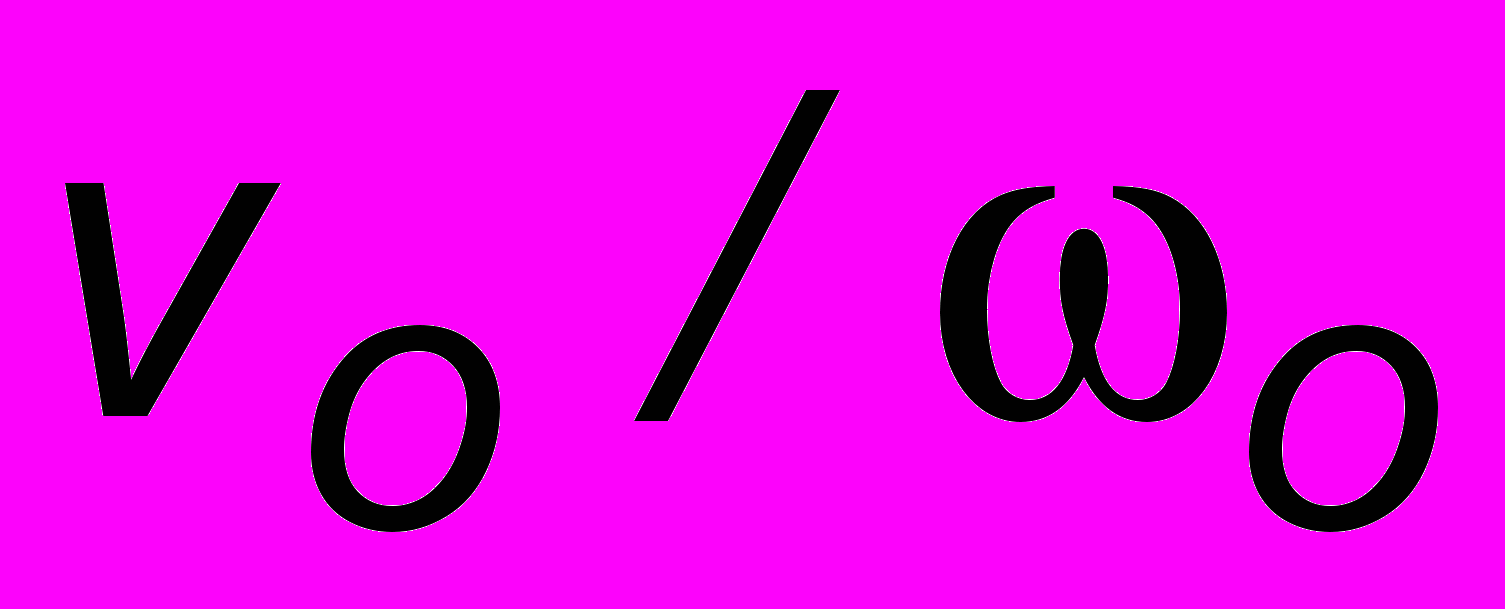 и малой, равной
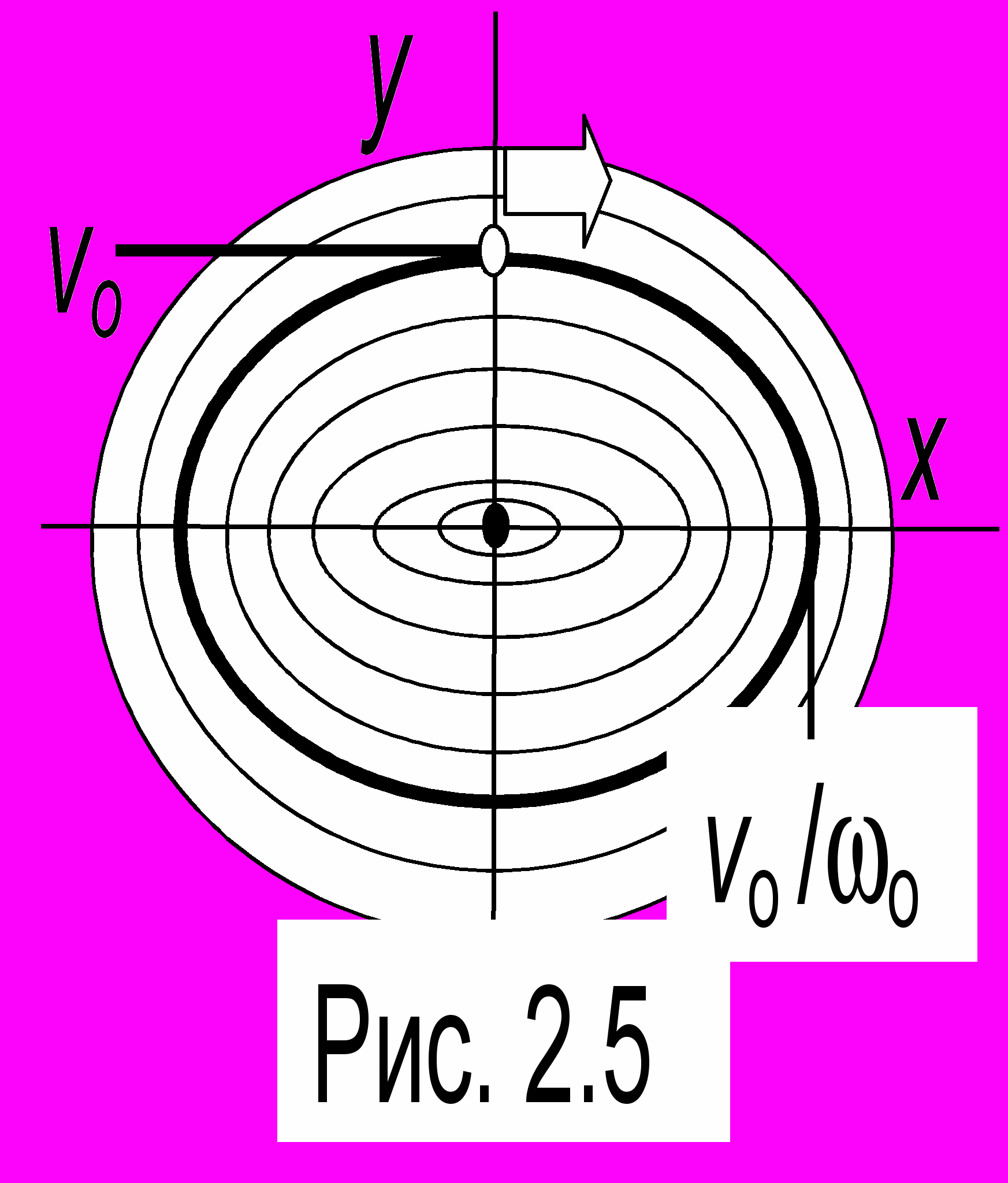
и малой, равной 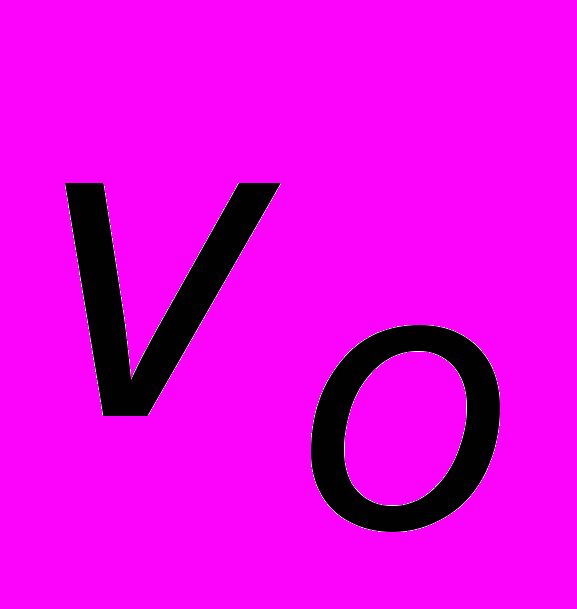 (рис. 2.5). Начальные условия определяют начальное положение точки (верхушка эллипса). Время, за которое точка обходит эллипс, равно периоду колебаний: TО = 2/О, а состояние равновесия - устойчивое состояние – является началом координат. Это как бы эллипс, свернутый в точку ("центр").
(рис. 2.5). Начальные условия определяют начальное положение точки (верхушка эллипса). Время, за которое точка обходит эллипс, равно периоду колебаний: TО = 2/О, а состояние равновесия - устойчивое состояние – является началом координат. Это как бы эллипс, свернутый в точку ("центр").1 В отличие от ускорения эта электрическая характеристика используется редко
