Поведение пузырьков в воде под действием сильных электрических полей: Обсуждение

Вид материала

Исследование

Содержание Обсуждение экспериментальных данных Силы, влияющие на поведение пузырьков Сопоставление с экспериментом.

Подобный материал:

• Региональная олимпиада по физике, 38.6kb.
• Е. К. Изменение абсорбции слабых электрических полей высокой частоты некоторыми жидкостями, 3.36kb.
• Содержани министрество образования российской федерации, 852.35kb.
• Естественные электрические поля электроннопроводящих рудных и нерудных объектов, 87.71kb.
• Эффекты облучения в твердых телах, 247.82kb.
• Большое влияние на дальнейшее развитие тепловых двигателей оказал Дени Папен, 34.83kb.
• Физические процессы в тканях при воздействии током и электромагнитными полями, 39.27kb.
• Фильтрация флюида в скважину с учетом двухтемпературной динамики флюида и матрицы, 29.14kb.
• Тся задача определения вероятности срыва управления для нелинейных динамических систем,, 8.46kb.
• 2. Электроника и радиотехника, 219.7kb.

Поведение пузырьков в воде под действием сильных электрических полей: Обсуждение^

Коробейников С.М.*, Мелехов А.В.**, Синих Ю.Н.*, Соловейчик Ю.Г.*

*Новосибирский Государственный Технический Университет

**Институт Лазерной Физики СО РАН

г. Новосибирск


Анализируются результаты экспериментов по образованию долгоживущих пузырьков в воде и их поведению под действием сильного электрического поля (ч.1 статьи). Показано, что наиболее значимым фактором является возникновение частичных разрядов.

Введение

Исследование поведения пузырьков в сильных полях важно не только для физики импульсных накопителей энергии, но и для создания управляемых коммутаторов [1], электрогидравлических и электрогидродинамических преобразователей энергии, криогенных кабелей [2], способов управления жидкими средами в условиях невесомости [3] и т.п.

В настоящей работе делается попытка анализа результатов экспериментального исследования поведения специально создаваемых микропузырьков в воде под действием сильного электрического поля [4] .

Обсуждение экспериментальных данных

Образование долгоживущих пузырьков

Ясно, что долгоживущие пузырьки должны быть наполнены газом, поскольку паровые пузырьки при температуре ниже точки кипения должны исчезать за микросекундные времена. Для газового пузырька время растворения _р пропорционально квадрату радиуса r, обратно пропорционально коэффициенту диффузии газа в жидкости D, растворимости Сs, и газосодержанию С в жидкости.

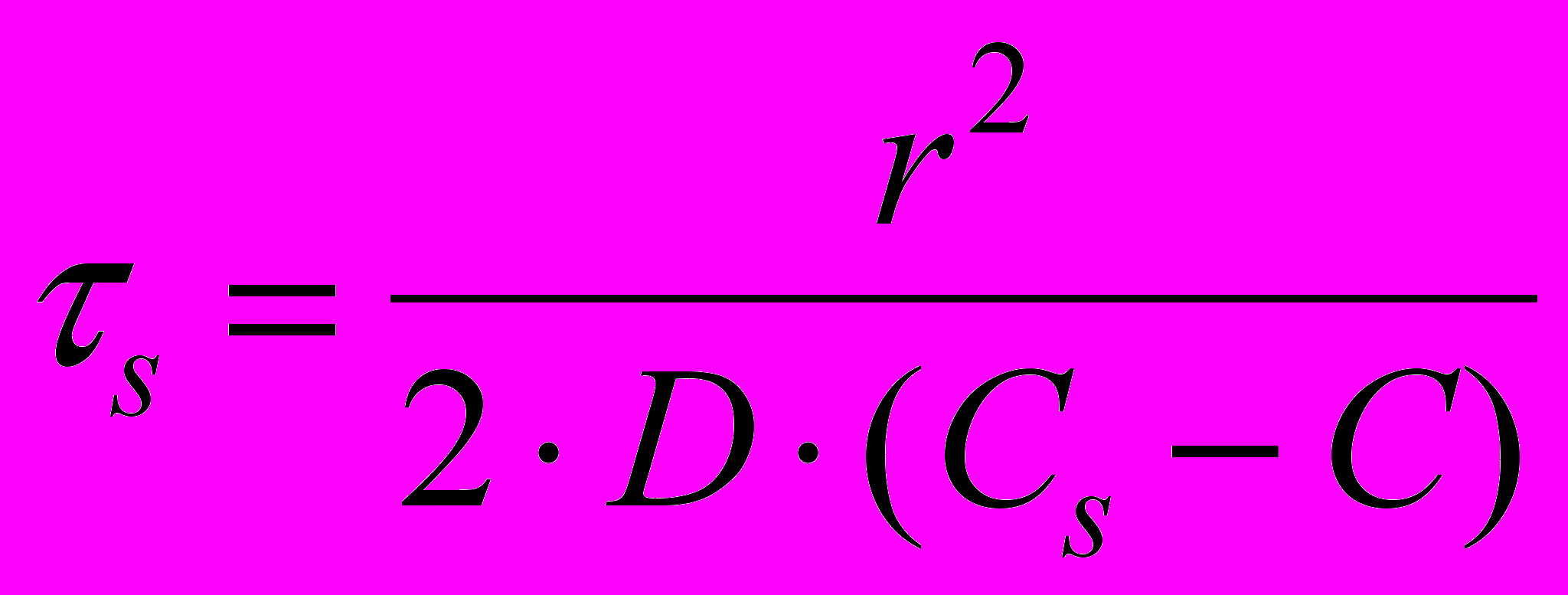(1)

Экспериментальные данные по растворению пузырьков были аппроксимированы в соответствии с выражением (1). На рис. 1 приведены экспериментальные результаты (точки) и расчет (линия).

Р
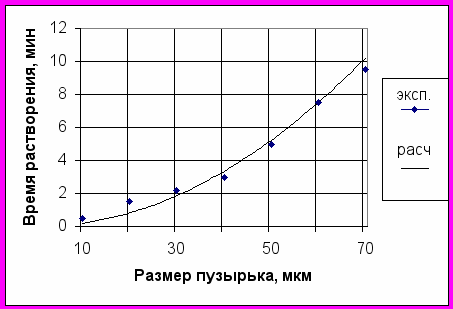
ис. 1. Аппроксимация экспериментальных данных по растворению микропузырьков в отстоянной дистиллированной воде.

Видно, что соответствие между ними достаточно убедительно. Если положить коэффициент диффузии D  210^-5 см²/с [5], то наилучшее соответствие достигается при C_s-C  410^-3 см³/см³. При растворимости воздуха в нормальных условиях C_s  210^-2 см³/см³ [5], это означает, что вода была насыщена чуть более 80% от максимального содержания, т.е. пузырьки находились в состоянии, близком к равновесному.

Для выяснения механизма образования были проведены теплофизические расчеты нестационарных тепловых полей в жидкости при импульсном нагреве проволочки. Расчеты проведены с помощью подсистемы «Тепло» пакета прикладных программ «Telma». На рис. 2 показана временная зависимость температуры в различных точках вблизи проволочки при воздействии импульса тока, амплитудой и длительностью, соответствующего пороговым значениям I=2.6 A, t=0,4 с.





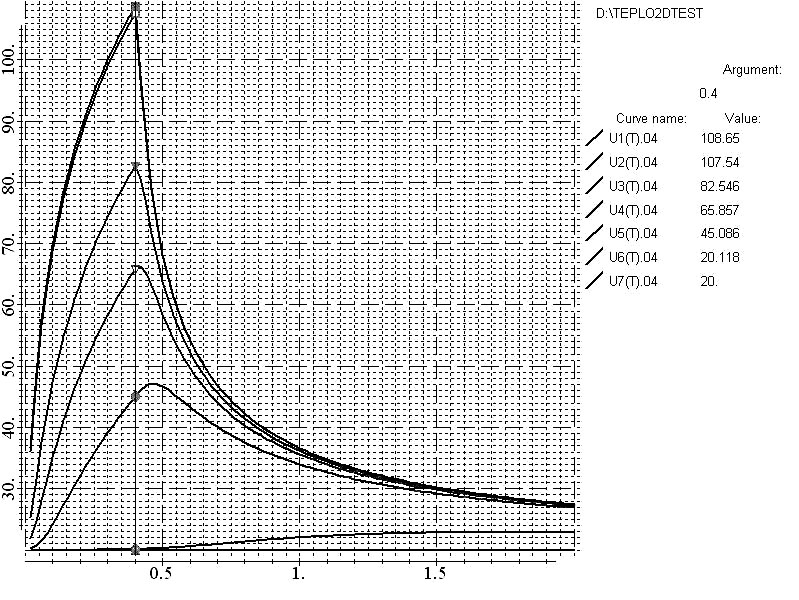
Рис. 2. Зависимость температуры от времени для различных точек. 1, 2 - в центре и на поверхности проволочки (практически сливаются), 3, 4, 5, 6, 7- на расстоянии 50 мкм, 100 мкм, 200 мкм, 1 мм, 2 мм от поверхности электрода


Видно, что температура вблизи поверхности незначительно превышает точку кипения воды. Расчеты температур при других пороговых условиях показали, что это достигается во всех случаях. При вскипании, на поверхности образуются паровые пузырьки. Ясно, что в пузырьки должен диффундировать газ, растворенный в жидкости и находящийся в пересыщенном состоянии при повышенной температуре. Оценки по диффузии газа в паровой пузырек радиусом r₀ в течение характерного времени t~0.1 c (см. рис.2) дают объем продиффундировавшего газа

V ~ 4r₀²(Dt)^1/2C (2)

При охлаждении пузырька пар должен сконденсироваться и паро-газовый пузырек должен превратиться в чисто газовый пузырек, согласно оценке (2), размером в 3-4 раза меньшим, чем максимальный размер исходного парового пузырька. Исходя из (2) легко объясняется и тот факт, что в дегазированной воде пузырьки не образуются.

Таким образом, механизм образования долгоживущих пузырьков состоит в следующем: локальное вскипание жидкости, диффузия газа в паровой пузырек, охлаждение электрода и пузырька, сопровождающееся конденсацией пара и уменьшением размеров пузырька. Затем следует более медленная стадия - диффузионное растворение газового микропузырька.

Силы, влияющие на поведение пузырьков

Проанализируем роль различных сил в движении и деформации пузырьков в неподвижной жидкости под действием электрического поля.

Во-первых, это сила, связанная с разницей диэлектрических проницаемостей жидкости и пузырька, которая приводит к некоторому удлинению пузырька в направлении поля и к более значительному сжатию пузырька в поперечном направлении. Деформация пропорциональна радиусу r и квадрату напряженности поля E² [6]

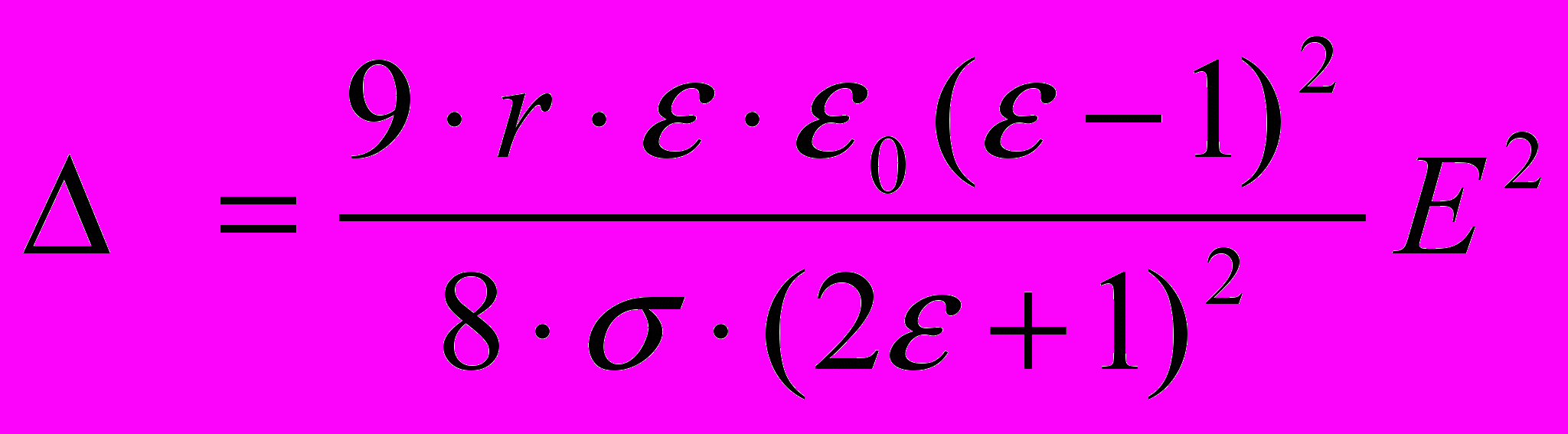(3)

Здесь  - коэффициент поверхностного натяжения. Относительное уменьшение объема пузырька вследствие действия этого фактора [7]:

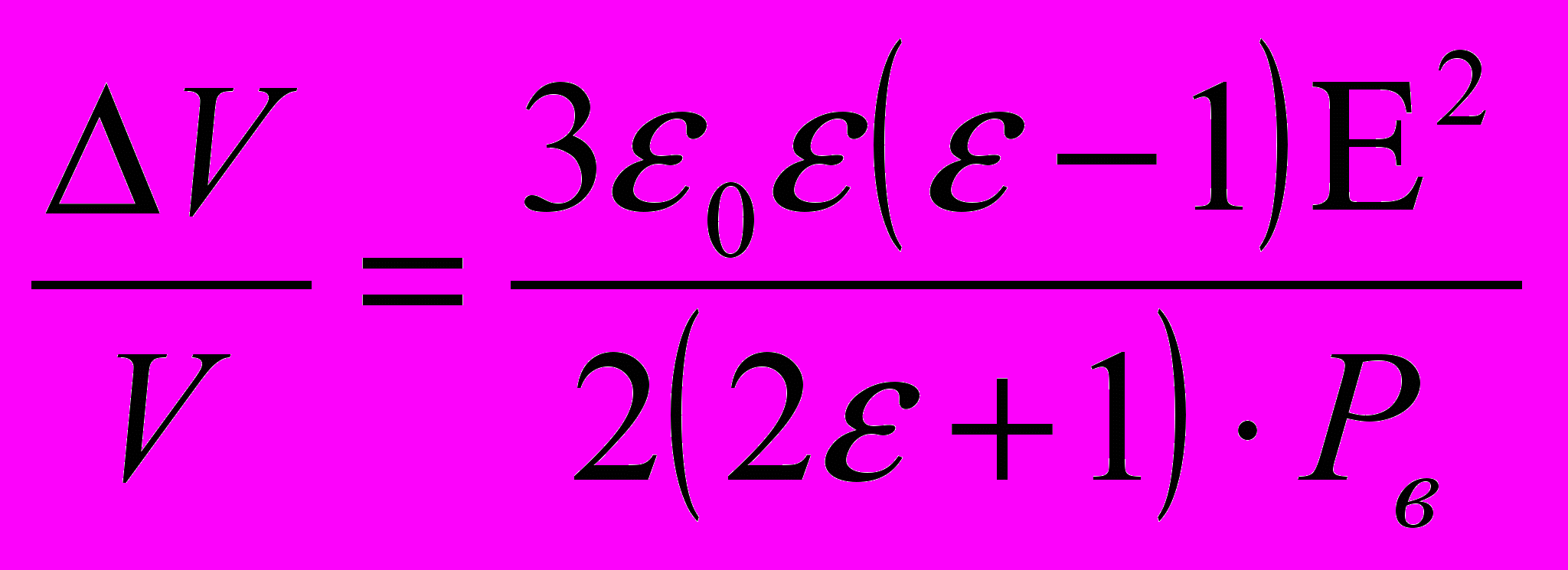(4)

где P_в - внешнее давление.

Вторая сила, вызванная различием диэлектрических проницаемостей и градиентом поля, действует при помещении пузырька в неоднородное электрическое поле. Это так называемая диэлектрофоретическая сила [8].

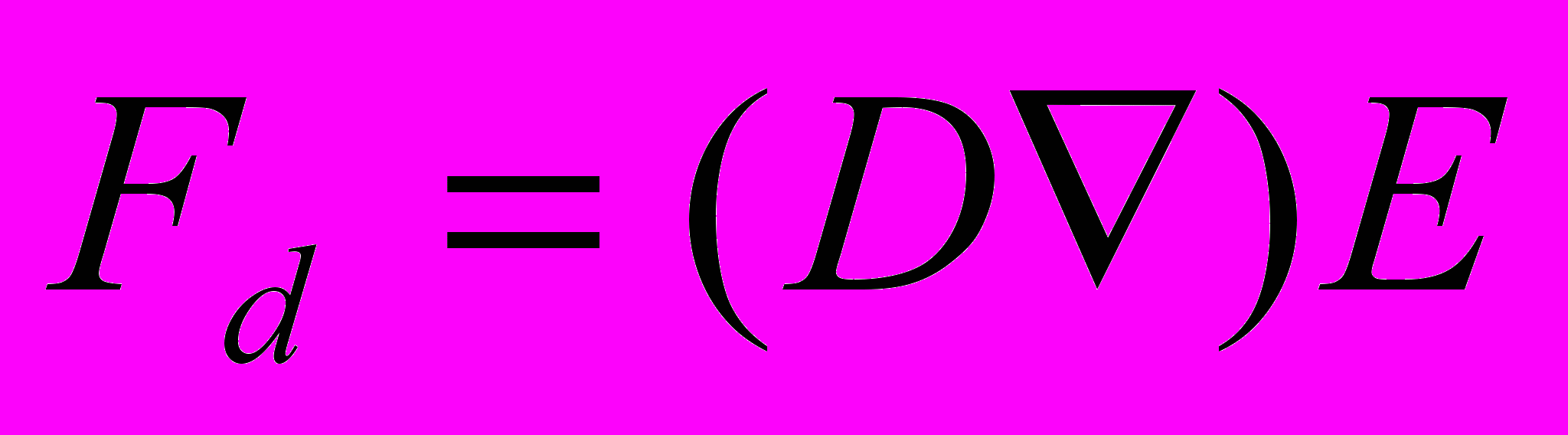(5)

где D - наведенный дипольный момент пузырька, который для сферического пузырька составляет

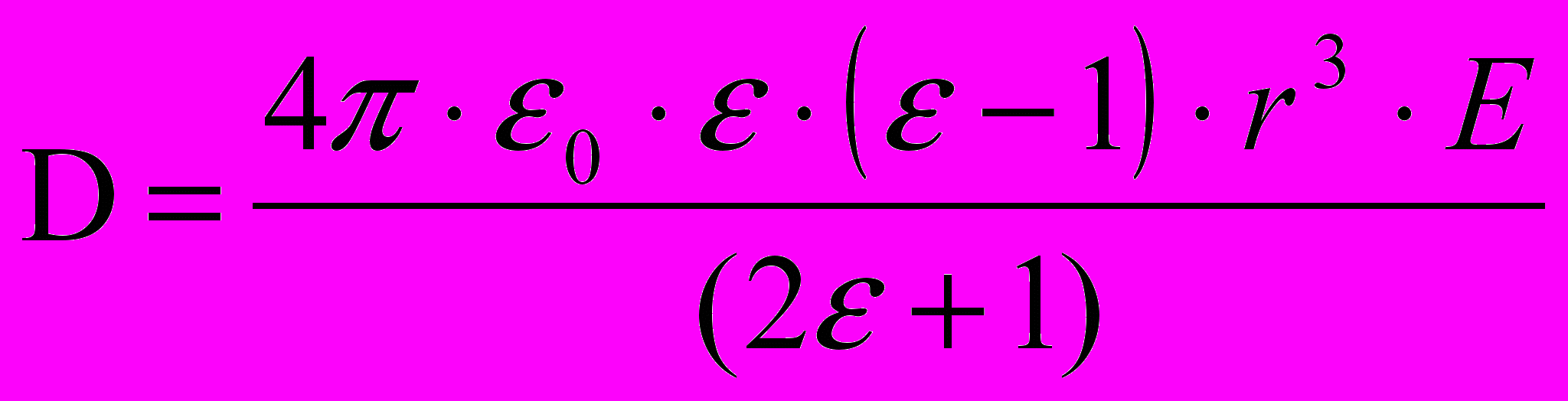(6)

Если пренебречь искривлением проволочного электрода, т.е. считать распределение поля вблизи проволочки цилиндрически симметричным, то F_d выражается через R- расстояние от оси проволочки

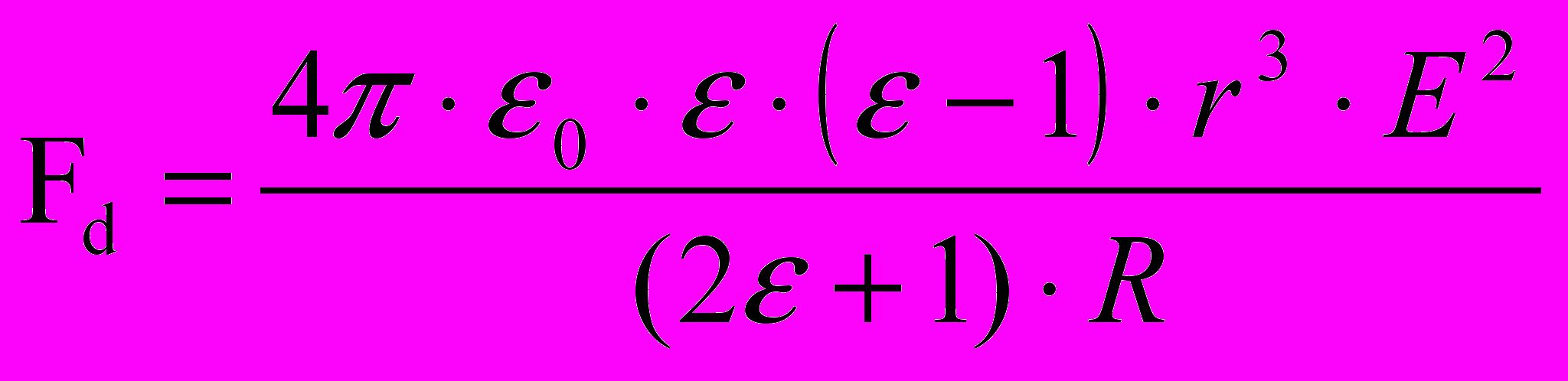(7)

Третьим фактором являются частичные разряды в пузырьках (ЧР). Удлинение пузырька в этом случае можно рассчитать согласно пузырьковой модели инициирования разряда [9,10]. Появление поверхностного и объемного зарядов вблизи полюсов пузырька вследствие ЧР приводит к деформации пузырька за счет кулоновских сил. Эквивалентное давление в направлении действия поля можно оценить по выражению

P = 3₀E²(E/r + 1 )/2 (8)

где  - подвижность носителей заряда в жидкости,  - длительность воздействия электрического поля.

Четвертый фактор является наиболее дискуссионным. На незаряженный пузырек, находящийся в зоне объемного заряда, должна действовать сила, направленная в противоположную сторону, по отношению к кулоновской силе. Дополнительным условием является наличие механического равновесия в жидкости. На первый взгляд, происхождение этой силы трудно понять. Однако можно воспользоваться аналогией с обычной выталкивающей силой, действующей в жидкости на пузырек в поле силы тяжести. И в том, и в другом случае сила действует на жидкость и это эквивалентно действию противоположно направленной силы на пузырек. По аналогии, выражение для силы F_sc в зоне объемного заряда плотностью _sc можно написать

F_sc = - _scEV_b (9)
где V_b - объем пузырька. В случае объемного гомозаряда у поверхности электрода сила F_sc должна прижимать пузырек к электроду. В случае гетерозаряда сила F_sc должна выталкивать пузырек из приэлектродной области.

Последний фактор, который следует рассмотреть - это нестабильность пузырьков. Предполагается, что пузырьки должны иметь несколько типов нестабильности. Ранее [11-13], были рассмотрены несколько типов неустойчивостей пузырьков в электрическом поле. Показано, что неионизованный пузырек стабилен в электрическом поле, а ионизованный, проводящий пузырек должен иметь «сосисочную» неустойчивость, длина волны которой [11]

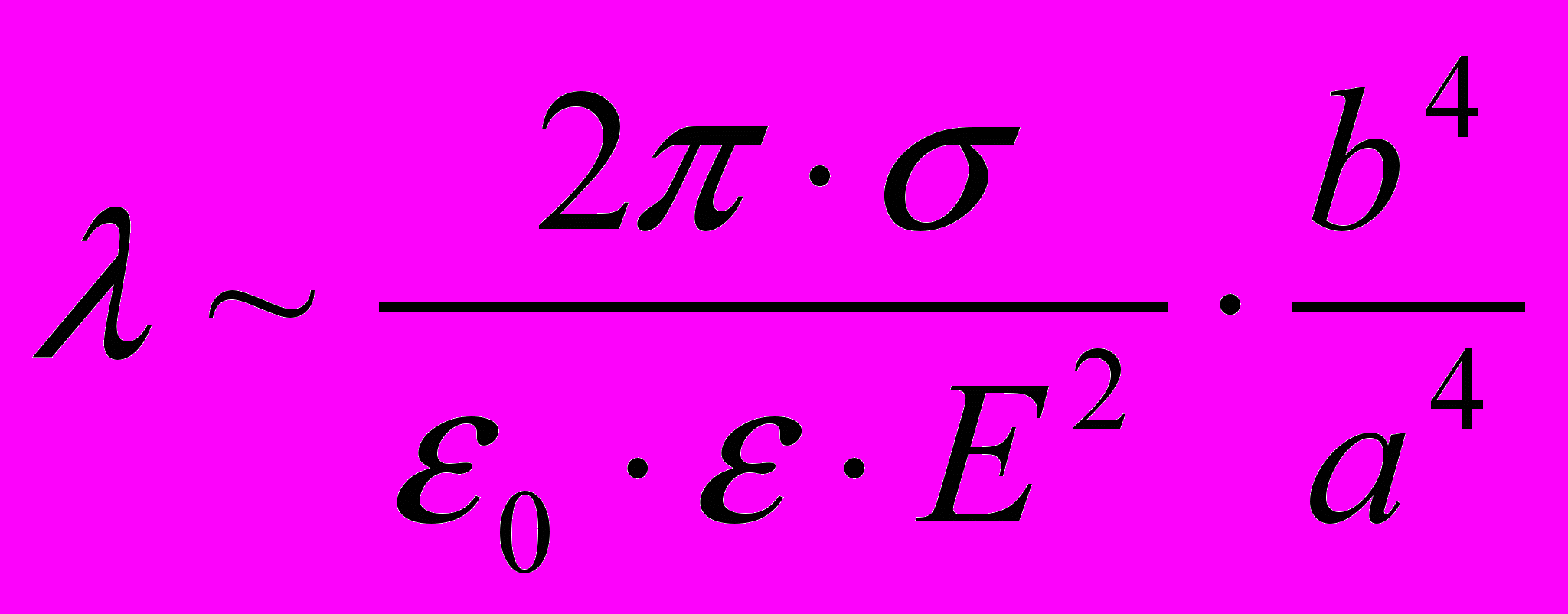(10)
где a,b - размер пузырька вдоль поля и поперек поля, соответственно. Неустойчивость должна возникать при достижении a/b значения a/b =1.85, в виде образования вблизи полюса пузырька серии мелких пузырьков. В выражении (10), полученном для уединенного пузырька, фактор (b/a)² характеризует усиление поля вблизи полюсов ионизованного пузырька [11]. Для пузырька, находящегося на поверхности электрода, усиление вблизи удаленного от поверхности полюса пузырька, будет превышать это значение, причем это дополнительное увеличение может достигать 3-4. Соответственно, длина волны «сосисочной» неустойчивости должна быть еще примерно на порядок меньше, чем по выражению (10).

Действие поля и кулоновских сил должны генерировать моду колебаний, соответствующую удлинению и делению пузырька на два или несколько пузырьков. Без электрического поля низшая частота осцилляций пузырька соответствует

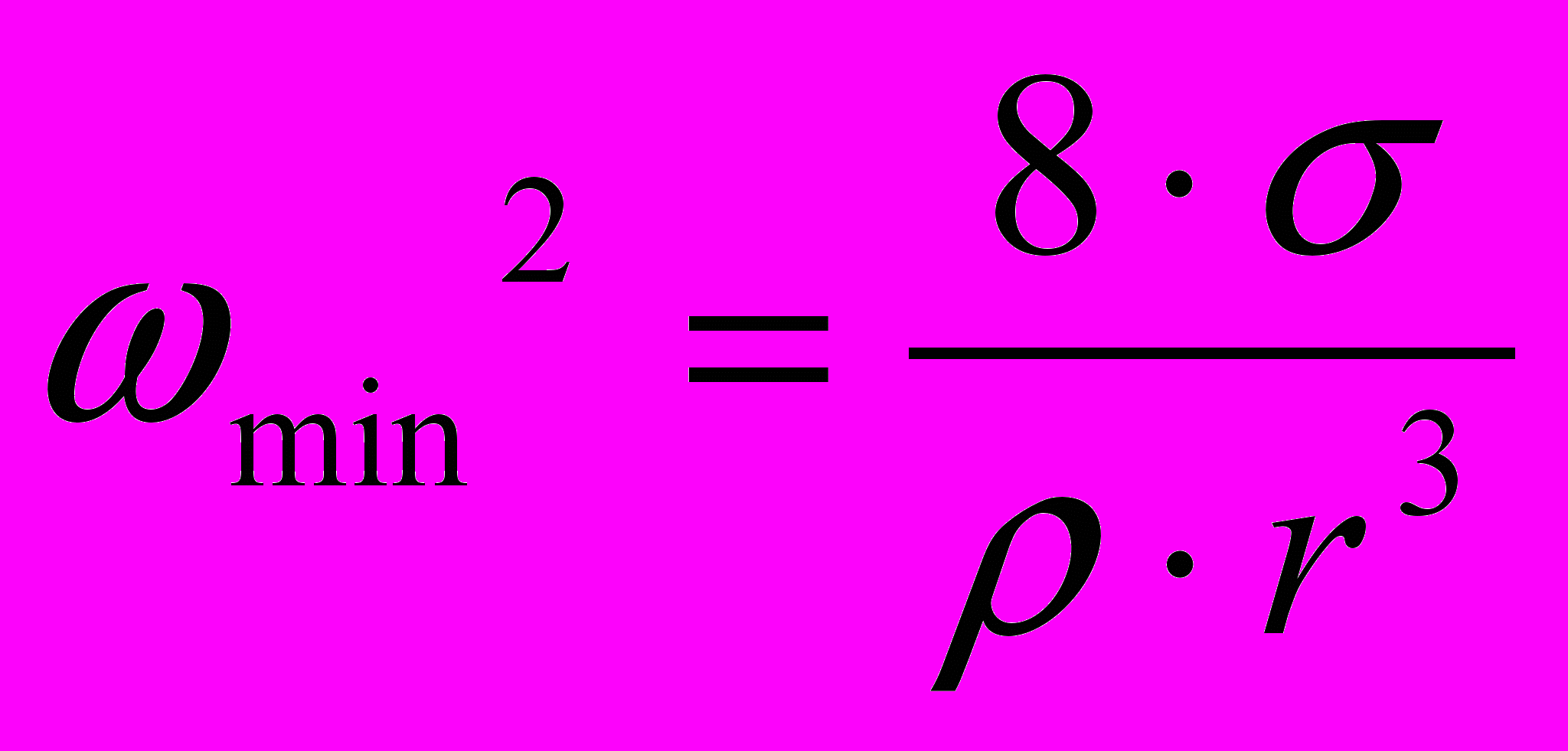(11)
Все вышеупомянутые факторы должны увеличивать частоту осцилляций.

Другим типом нестабильности должны быть мелкомасштабные возмущения поверхности вследствие нестабильности заряженной поверхности в электрическом поле. Длина волны нестабильности, согласно [12]:

(12)

Здесь _s - поверхностная плотность заряда. В случае полностью заряженной поверхности пузырька, находящегося на поверхности электрода (что означает, что пузырек полностью разряжен, как предполагается в пузырьковой модели [9,10]):

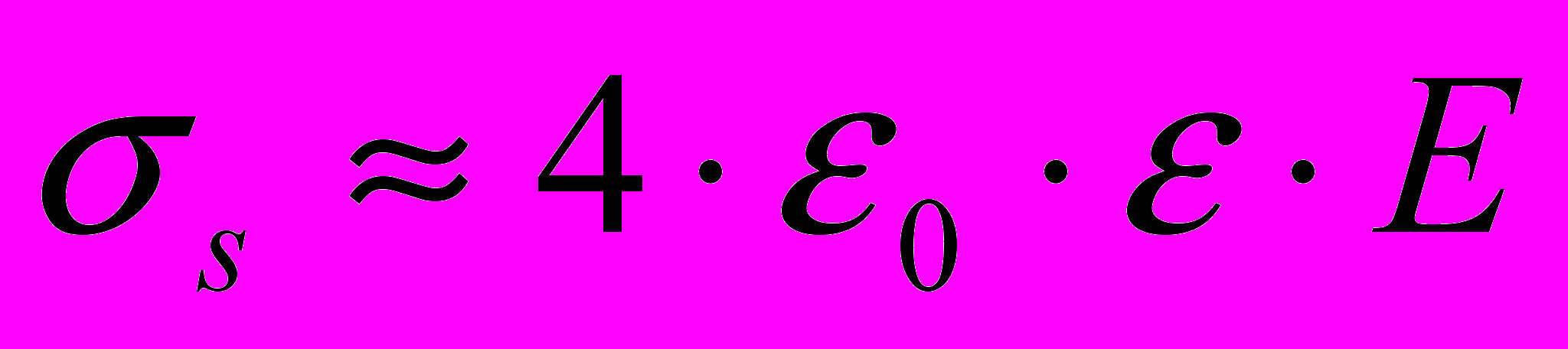(13)

Подставляя, получим

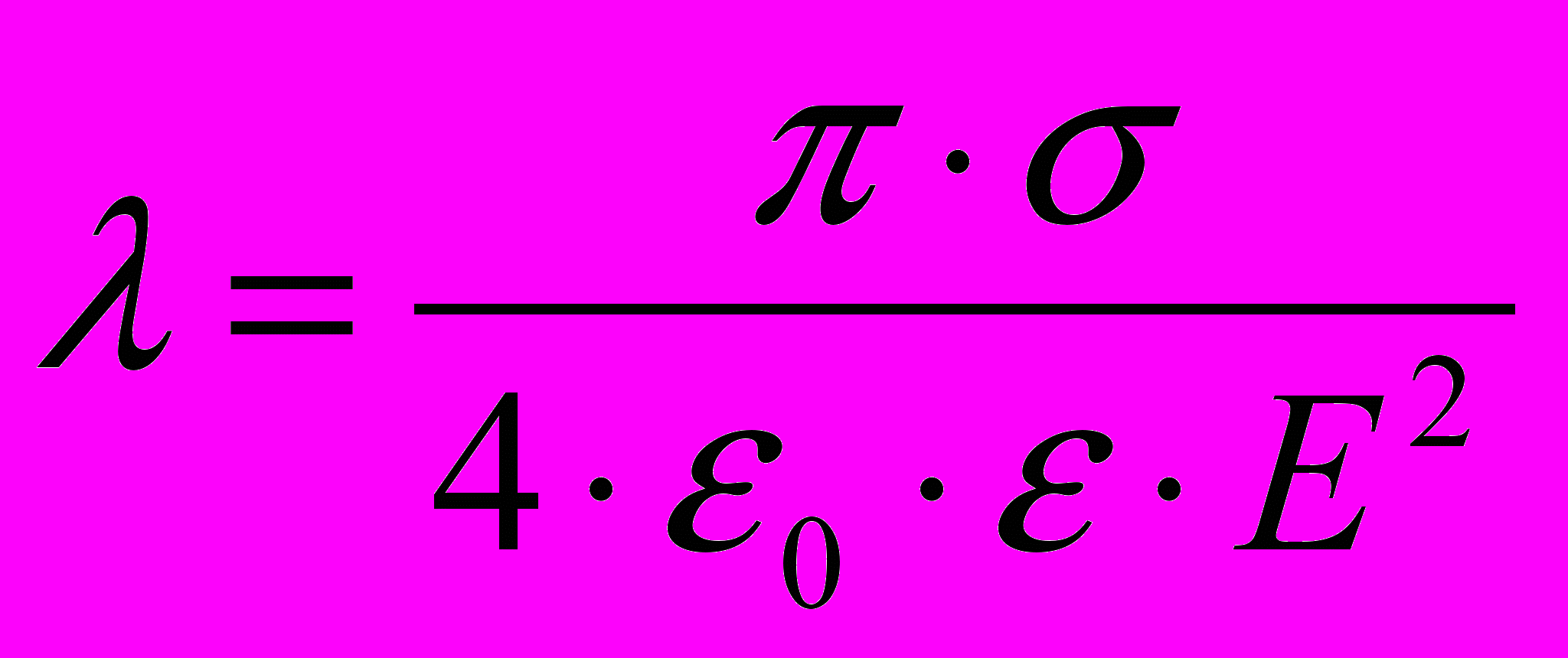(14)

Сопоставление с экспериментом.

Сравнение различных факторов, оценка их применимости к условиям экспериментов [4] по изучению поведения искусственных пузырьков в воде показывают следующее. Падение напряжения на пузырьке диаметром 30-60 мкм будет превышать напряжение пробоя в соответствии с законом Пашена (U_min~300500 В), при напряженности более 100 кВ/см. Следовательно, разряды должны возникать практически во всех зарегистрированных пузырьках. Кулоновская сила, действующая на заряженную стенку пузырька (ф-ла (8)) должна, по крайней мере в  (=80) раз превышать силу, которая вытягивает незаряженный пузырек (ф-ла (3)). Более того, деформация, согласно (3) пропорциональна r, поэтому должна приводить к большей деформации больших пузырьков. Это противоречит экспериментальным данным. Диэлектрофоретическая сила (7) в сравнении с кулоновской силой меньше в отношении R/r, что в нашем случае составляет R/r ~ 4-8. Что касается силы, действующей на пузырек в области объемного заряда, кажется, что в условиях экспериментов, она не реализовывалась. Здесь жидкость не находится в покое и нет сплошной зоны, занятой объемным зарядом.

Следовательно, кулоновская сила более всего подходит в качестве источника движения пузырьков. Сравнение рассчитанного и экспериментально измеренного удлинения пузырька представлено на рис. 3. Экспериментальные точки получены в разных сериях, выбраны пузырьки на катоде, радиусом r=275 мкм, при напряженности 10010 кВ/см. На рис. 3 экспериментальные точки показаны прямоугольными метками. Кривая 1 получена расчетом согласно пузырьковой модели. Видно, что кривая и точки не слишком хорошо соответствуют друг другу. Ясно, что какой-то фактор отсутствует в модели. Здесь следует вновь отметить, что в модели предполагается пузырек полностью разряженным. Это означает, что после разряда поле в пузырьке равно нулю. На самом деле, в пузырьке должна оставаться некоторая напряженность поля. Если предполагать, что в пузырьке постоянно «горит» разряд - значит в нем поддерживается напряженность не ниже пробивной напряженности. Если в пузырьке периодически возникают разряды, все равно напряженность не может опуститься ниже пробивной напряженности. В обоих вариантах поверхностный заряд после разряда в пузырьке меньше примерно в 1.5-3 раза по сравнению с полностью разряженным пузырьком. Точная цифра зависит от размеров пузырька и напряженности поля. Чем больше пузырек и напряженность поля - тем больше поверхностный заряд, тем ближе к случаю полностью разряженного пузырька.

Можно получить корректные выражения с учетом этого обстоятельства. В выражении (13) поверхностный заряд будет уменьшен

(15)
где U_p~300 В - напряжение пробоя по Пашену. Эквивалентное давление, которое движет стенку пузырька в направлении поля, также уменьшится

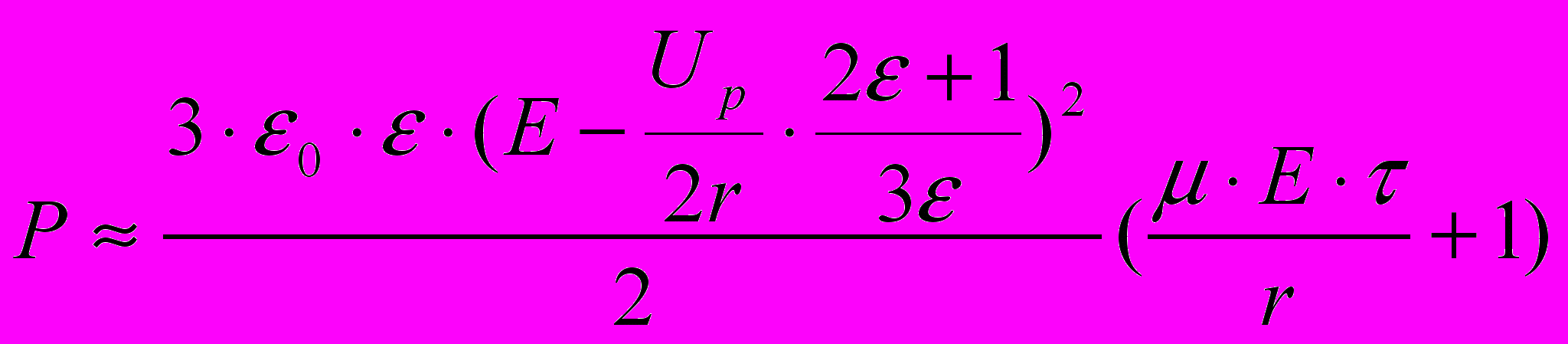(16)
Компьютерный расчет удлинения пузырька согласно скорректированной модели показан на рис. 3, кривая 2.




Рис. 3. Сопоставление расчетного и экспериментального удлинений пузырька диаметром 55 мкм под действием электрического поля напряженностью 100 кВ/см.

Видно, что модель хорошо соответствует экспериментальным точкам.

Что касается нестабильности пузырьков, то можно выделить несколько моментов. Пузырьки делятся на две части через 5-10 мкс. Это не противоречит выражению (11), т.к. в соответствии с этим выражением характерное время составляет 5-10 мкс для пузырьков размером 30-50 мкм. Наблюдаемые мелкомасштабные возмущения поверхности имеют длину волны примерно 4-5 мкм, причем они не обязательно находятся на полюсе пузырька, что не соответствует «сосисочной» неустойчивости. Против «сосисочной» неустойчивости свидетельствует и то, что оценки характерной длины, согласно (10), при a/b~23, E=200 кВ/см дают примерно 0.1 мкм. С учетом дополнительного усиления поля длина волны должна быть еще меньше. Оценки согласно (14) дают примерно 0.2 мкм.. Если поверхностный заряд изменить согласно выражению (15), длина волны неустойчивости увеличится до 1-5 мкм в зависимости от электрического поля и размера пузырька. Таким образом, мелкомасштабные возмущения поверхности пузырька могут быть связаны с действием кулоновских сил. При этом пузырек не следует считать проводящим, корректнее полагать, что на его поверхности находится заряд, частично уменьшающий поле в пузырьке.

Нетривиальное поведение анодных микропузырьков, похожее на мгновенное ухудшение смачиваемости жидкостью поверхности электрода, допускает несколько предположительных вариантов объяснений.

Наиболее простым, по-видимому, будет следующее. Как известно, поверхность электрода из нихрома на самом деле состоит из окислов NiO и Cr₂O₃ [14]. Хорошее смачивание электрода водой происходит, по-видимому, за счет водородных связей молекул воды с частично ионизованными атомами кислорода окислов. При воздействии электрического поля на диполи молекул воды они ориентируются атомами (скорее ионами) кислорода к поверхности анода. Возникающее взаимное отталкивание собственно и означает мгновенное возникновение несмачивания электрода водой.

Другой вариант может быть связан с наличием двойных электрических слоев на границе раздела «электрод-вода». При этом, подвижная часть двойного слоя, находящаяся в воде, может состоять, как из положительных, так и из отрицательных ионов в зависимости от типа поверхности электрода и типа электролитических примесей в воде. На границе электрода, содержащей оксидные слои, должен возникать двойной слой, и, скорее всего, у поверхности электрода в воде должны скапливаться положительные ионы. При воздействии электрического поля ионы поступают в объем жидкости. Возникающая кулоновская сила отталкивает жидкость от электрода, и в области касания пузырька возможен отрыв жидкости от электрода.

Если какая-либо из этих гипотез верна, то в неполярной жидкости подобный эффект не будет присутствовать.

Заключение

Проведены исследования поведения пузырьков в электрическом поле. Пузырьки создавались за счет вскипания жидкости на проволочке и диффузии растворенного газа в них. Главными факторами следует считать действия кулоновских сил на поверхностный заряд, появляющийся после частичного разряда в пузырьках. Это приводит к удлинению пузырька, возмущениям его поверхности, отрыву и движению пузырьков.

Список литературы

1. A.Sunesson, L.Walfridsson «Laser-triggering of electric breakdown in liquids», Proc. of the 11^th Int. Conf.on Conduction and Breakdown in Dielectric Liquids, IEEE No.93CH3204-6, Baden-Dattwill, Switzerland, 1993, pp.572-576.
   
2. M. Hara, Z.-c.Wang, H.Saito «Thermal bubble breakdown in cryogenic liquids under non-uniform fields» Proc. of the 11^th Int. Conf.on Conduction and Breakdown in Dielectric Liquids, IEEE No.93CH3204-6, Baden-Dattwill, Switzerland, 1993, pp.249-253.
   
3. Y. Suda, K.Mutoh and Y.Sakai «Bubble motion in liquid nitrogen between electrodes in a microgravity environment» Proc. of the 12^th Int. Conf.on Conduction and Breakdown in Dielectric Liquids, Rome, Italy, 1996, pp.144-147.
   
4. Коробейников С.М. и др. Поведение пузырьков в воде под действием сильных электрических полей. Эксперимент.//ТВТ, (1 часть статьи).
   
5. Краткий справочник физико-химических величин./ Под ред. Мищенко К.П., Равделя А.А.-М.-Л.:Химия, 1965, 160 с.
   
6. Коробейников С.М. Деформация пузырьков в электрическом поле. Инженерно-физический журнал т.36, N 5, с.882, 1979
   
7. Коробейников С.М. Влияние электрического поля на точку кипения жидкостей. Инженерно-физический журнал т.41, №6, с.1131, 1981 г.
   
8. Jones T.B., Bliss G.W. Bubble dielectrophoresis. -J. Appl. Phys., V.48, 4, p.1412-1417, 1977.
   
9. Коробейников С.М. О роли пузырьков в электрической прочности жидкостей. 1. Предпробивные процессы. Теплофизика высоких температур N 3, 1998.
   
10. Коробейников С.М. О роли пузырьков в электрической прочности жидкостей. 2. Сопоставление с экспериментом. Теплофизика высоких температур N 4, 1998.
    
11. Felici N.J. Bubbles, partial discharges and liquid breakdown. Inst. Phys..Conf., ser.No.48, 1979, pp.181-190.
    
12. Garton C.G., Krasucki Z. Bubbles in insulating liquids: stability in an electric fields. -Proc. Roy. Soc., 1964, V.A280, p.211-226.
    
13. I.Alexeff, M.O. Pace, T.V. Blalock and A.I. Winterberg. Possible Models for the Earliest Prebreakdown Events in DC Stressed Hexane. Conf. Record of 10 ICDL, Grenoble, France, pp.387-391.
    
14. Справочник по электротехническим материалам.: В 3-х т. Т.3./под ред. Ю.В.Корицкого и др.-3-е изд., М.:Энергоатомиздат, 1988.-728 с.