Спектральное представление
| Вид материала | Лекция |
- Тема 4: спектральное представление сигналов, 371.37kb.
- Программа вступительных экзаменов в аспирантуру по специальности 05. 11. 13 Приборы, 40.33kb.
- Тема спектральное представление сигналов ясогласен, что все состоит из атомов. Но какое, 527.75kb.
- Вопросы к экзамену по курсу " ЭВМ и периферийные устройства" для групп К2-121, -122,, 75.03kb.
- И представление налоговой отчетности, 394.07kb.
- И представление налоговой отчетности, 357.06kb.
- Дать детям представление о речевом этикете, как о правилах поведения в различных ситуациях;, 241.98kb.
- Дать общее представление о витаминах, познакомить учащихся с их классификацией, представителями, 180.08kb.
- Урок Окружающий мир 2 класс умк «Перспективная начальная школа», 44.76kb.
- Задачи:; развивать обобщенное представление о казахстанцах; сформировать представление, 49.53kb.
ЛЕКЦИЯ N5
Лекция 5.
Лекция 5.
СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ
СИГНАЛА. АМПЛИТУДНАЯ МОДУЛЯЦИЯ. ФУРЬЕ-АНАЛИЗ И СИНТЕЗ
В
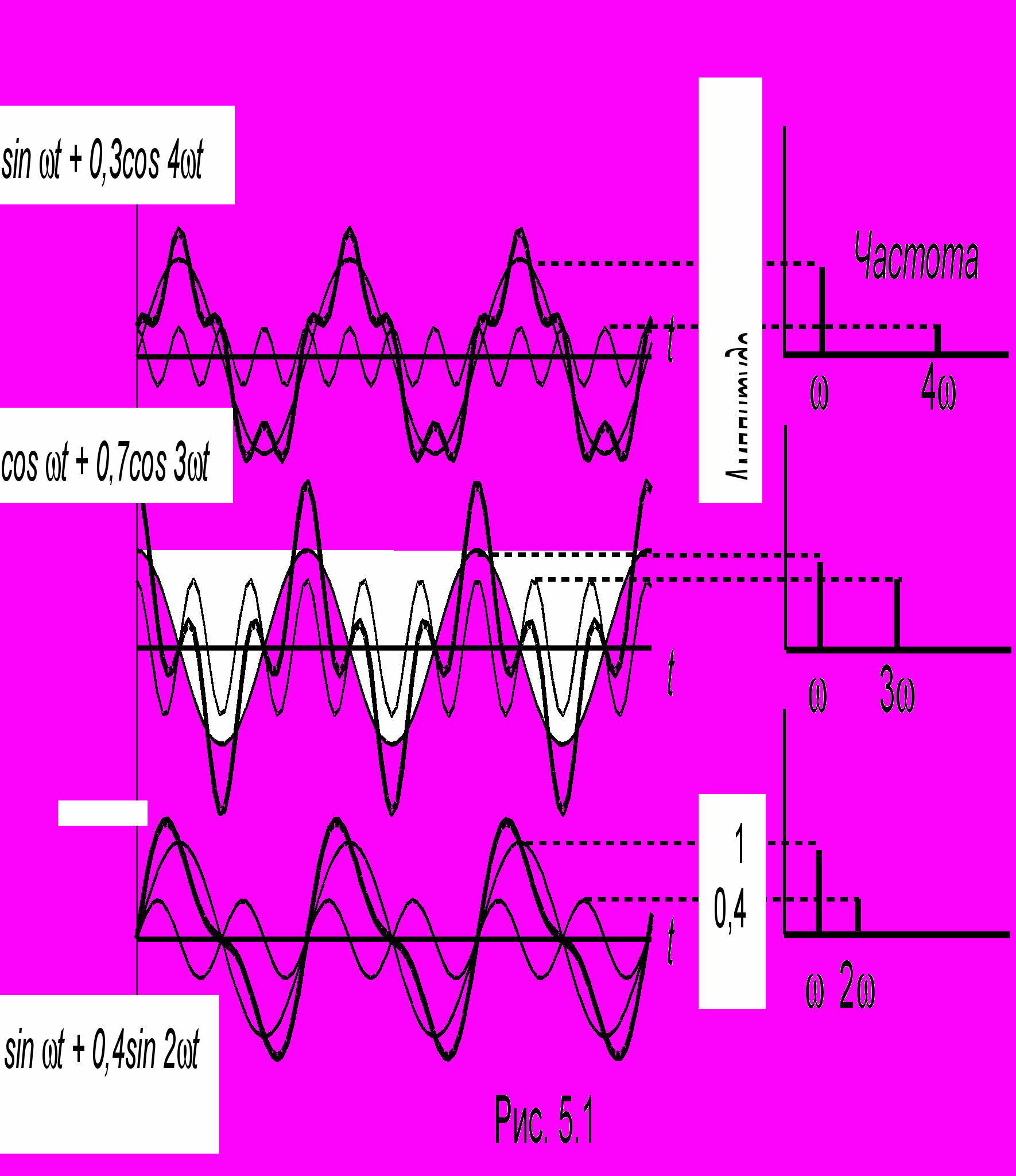
лекции 4 мы рассмотрели сложение коллинеарных колебаний близких частот. Пусть теперь складываемые коллинеарные колебания имеют кратные частоты (2:1 = 2; 3; 4 ...). Если на один чертеж нанести графики складываемых колебаний, то, пользуясь циркулем и изме-
а) б)
ряя соответствующие ординаты, можно получить графики типа показанных на рис. 5.1, а. Нетрудно видеть, что результирующее колебание (жирная линия) является периодическим, но не гармоническим. Каждое из этих колебаний содержит две частоты и может быть представлено спектральной диаграммой (рис. 5.1, б), показывающей, какие частоты складываемых гармонических колебаний присутствуют в сложном сигнале и каковы их амплитуды. При передаче информации по каналам связи используется тот или иной вид модуляции - низкочастотного воздействия на высокочастотный сигнал, как например, биения, рассмотренные в предыдущей лекции (рис. 4.2). Рассмотрим распространенную в радиотехнике амплитудную модуляцию (АМ ). Чистая синусоида - непрерывный сигнал постоянной амплитуды - полезной информации не несет. Если его послать в эфир, то зарегистрировав (каким-либо способом) такой сигнал, можно лишь получить информацию, что где-то работает передатчик на некоторой частоте . Чтобы пропеть ноту "ля", обычная частота которой = 440 Гц, а циклическая = 2 440 с-1, необходимо воспользоваться тем или иным видом модуляции, например АМ. Дело в том, что послать в эфир непосредственно "в чистом виде" низкочастотный сигнал довольно трудно: для этого потребовались бы большие антенны и большая мощность передатчика, не говоря о многочисленных низкочастотных помехах, с которыми бы предстояло побороться. Поэтому поступают так. Передатчик передает модулированное колебание на так называемой "несущей" высокой частоте ( > 105 Гц). Амплитудно-модулированный сигнал ноты "ля", которую мы собираемся пропеть в прямом эфире, имеет вид, изображенный на рис. 4.3. В общем виде такой сигнал описывается функцией
f(t) = A(1 + mcos t)cos t, (5.1)
которая при глубине модуляции m = 0 обращается в обычное гармоническое колебание. Чем больше m, тем сильнее "деформирован" модуляцией сигнал несущей частоты . Преобразуем (5.1), чтобы получить спектр сигнала. Складывая два известных тождества,
cos(+) = coscos-sinsin и cos(-) = coscos+sinsin, получим
coscos = [cos(+)+cos(-)]/2. Тогда (5.1) примет вид
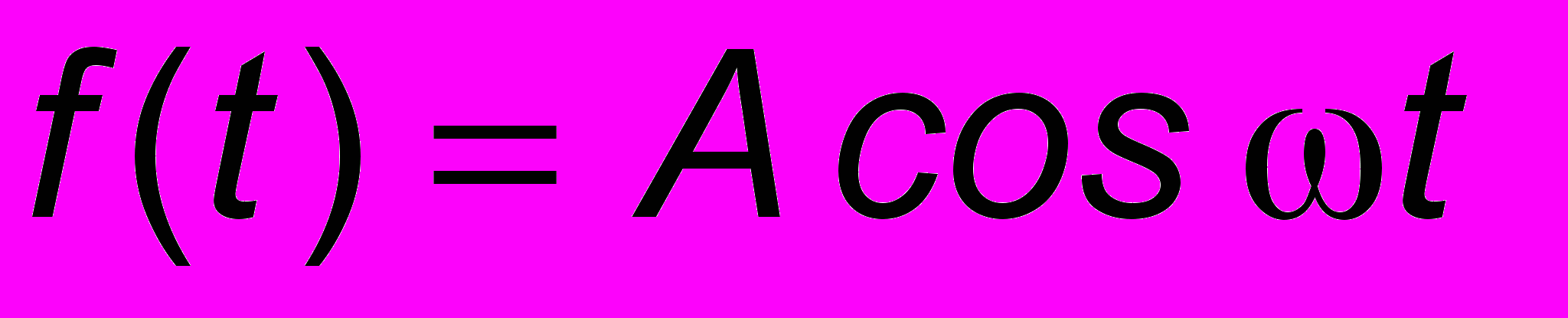 +
+ 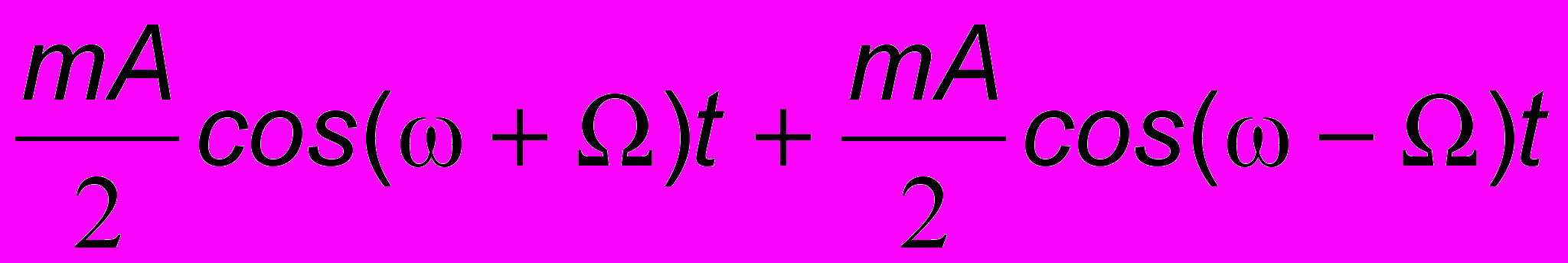 ,
,и таким образом в АМ-сигнале присутствуют основная частота и две "боковые" частоты + и -. Спектр сигнала показан на рис. 5.2.
"
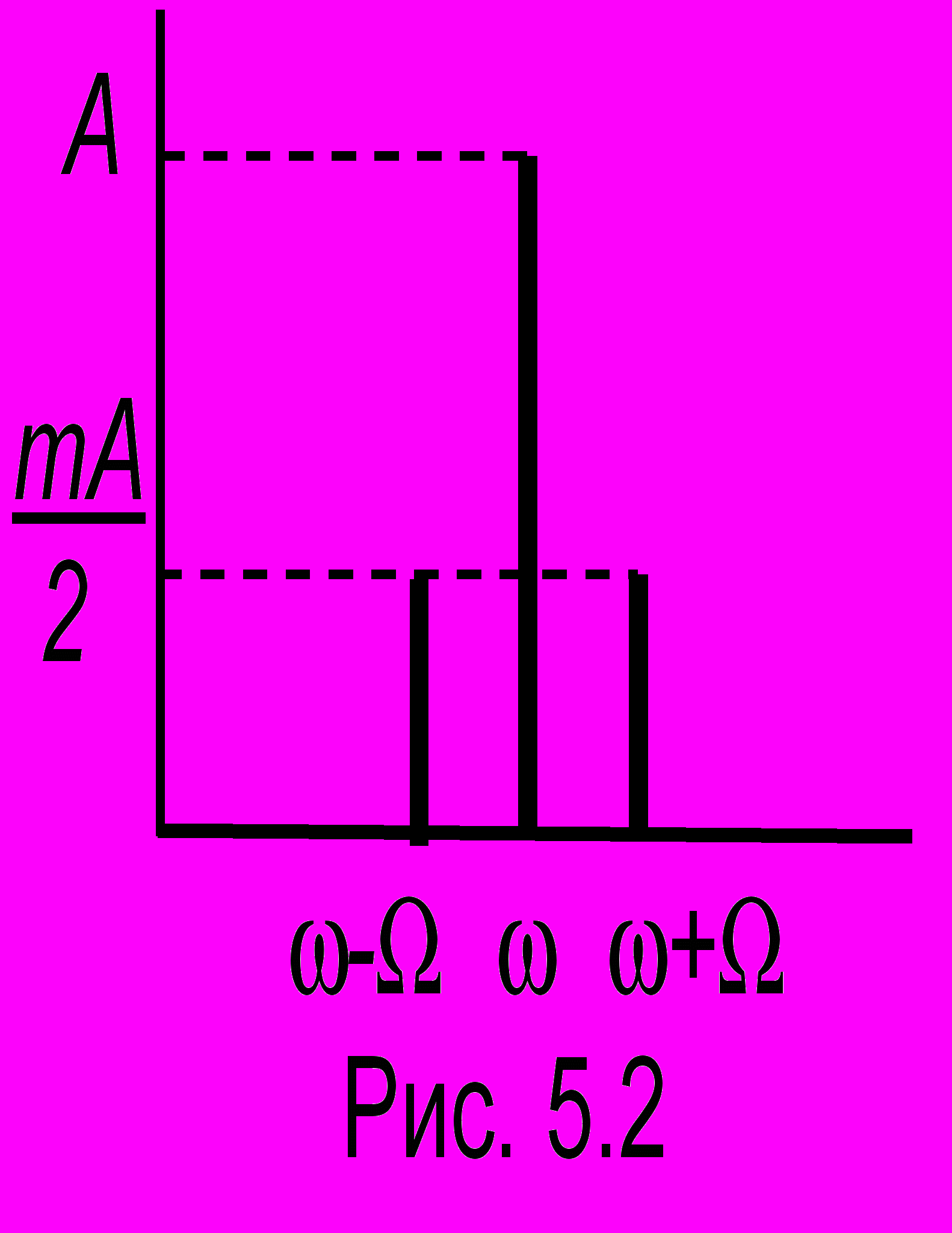 Полезная" частота в дальнейшем выделяется в радиоприемнике при помощи нелинейного преобразователя, который называется детектором. В эфир, конечно же, нужно передавать не одну только ноту, а большое количество низкочастотных составляющих. Поэтому и спектр будет гораздо сложнее.
Полезная" частота в дальнейшем выделяется в радиоприемнике при помощи нелинейного преобразователя, который называется детектором. В эфир, конечно же, нужно передавать не одну только ноту, а большое количество низкочастотных составляющих. Поэтому и спектр будет гораздо сложнее. Способ, при помощи которого мы разложили АМ-сигнал на простейшие гармонические составляющие может быть использован только для простейшего случая (5.1). В общем случае применяется теорема Фурье: всякая1 периодическая функция f(t) может быть представлена бесконечным тригонометрическим рядом:
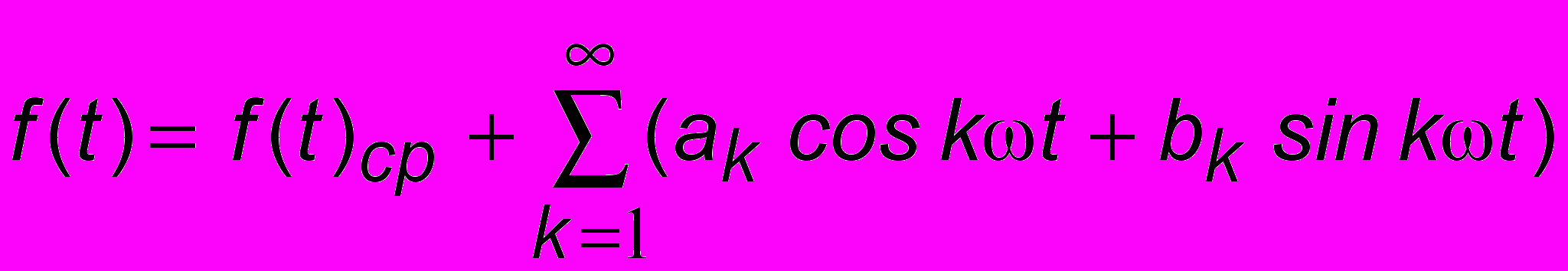 , (5.2)
, (5.2)где
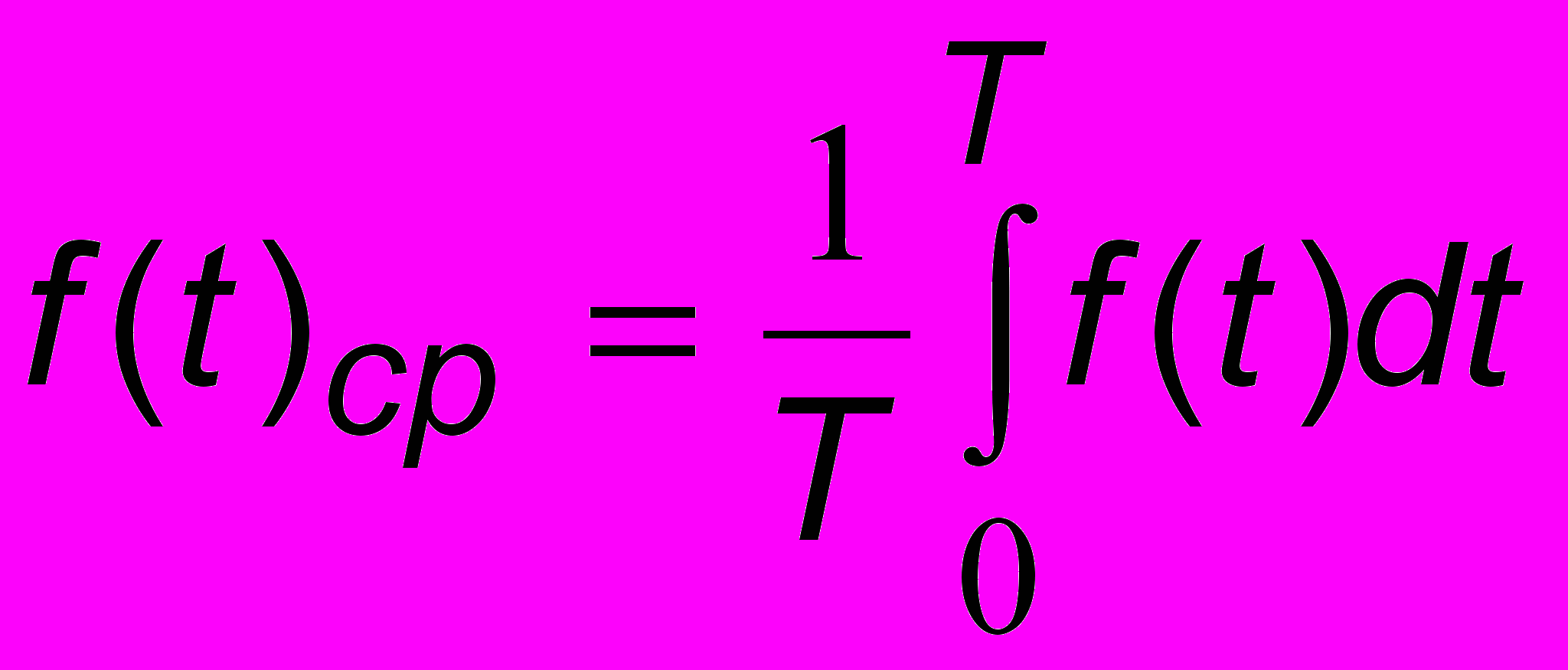 - среднее за период значение функции f(t),
- среднее за период значение функции f(t), а ak, bk - коэффициенты Фурье, определяемые по формулам:
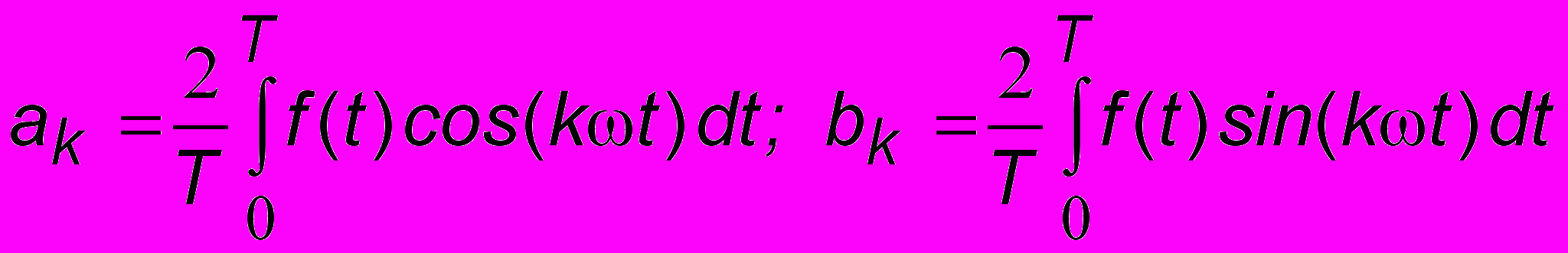 . При этом k = 1 соответствует основной частоте, а последующие значения k - удвоенной, утроенной и т.д. частотам, которые называются гармониками. Разложение сложного сигнала на гармонические составляющие называется Фурье-анализом, а обратный процесс Фурье-синтезом2. Ясное дело, что на практике невозможно иметь дело с бесконечным количеством гармоник. Это и не нужно, поскольку по мере увеличения k амплитуды гармоник быстро убывают и достаточно взять конечное их количество, чтобы достаточно точно воспроизвести форму оригинального сигнала. Так, на рис. 5.3 показана форма звукового сигнала f(t), характерн
. При этом k = 1 соответствует основной частоте, а последующие значения k - удвоенной, утроенной и т.д. частотам, которые называются гармониками. Разложение сложного сигнала на гармонические составляющие называется Фурье-анализом, а обратный процесс Фурье-синтезом2. Ясное дело, что на практике невозможно иметь дело с бесконечным количеством гармоник. Это и не нужно, поскольку по мере увеличения k амплитуды гармоник быстро убывают и достаточно взять конечное их количество, чтобы достаточно точно воспроизвести форму оригинального сигнала. Так, на рис. 5.3 показана форма звукового сигнала f(t), характерн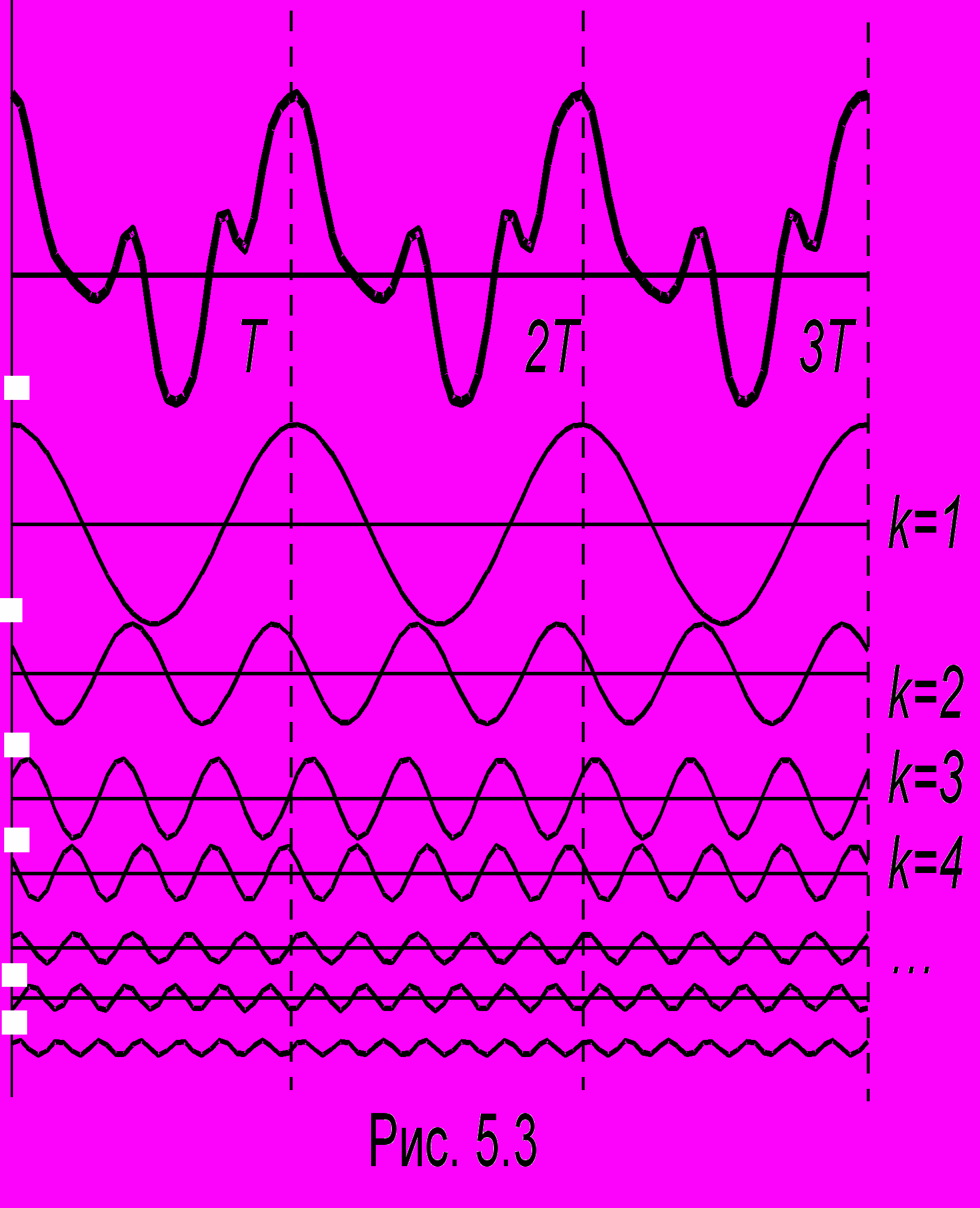
ого для духовых музыкальных инструментов (верхний график), и семь первых его гармоник (k = 1 ...7). Как видно из рисунка, вклад высших гармоник (начиная с пятой-шестой) невелик, и ряд Фурье (5.2) можно оборвать. Таким образом, для достаточно качественного воспроизведения о
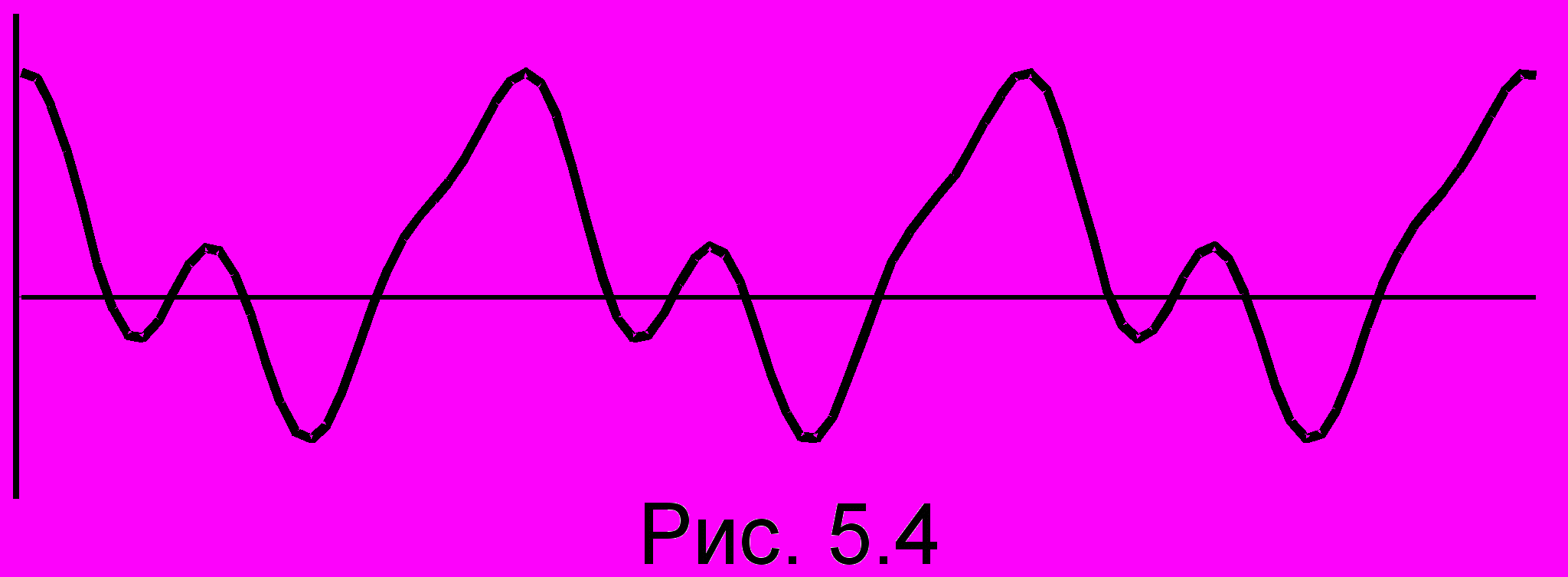
ригинального сигнала воспроизводящее устройство (радиоприемник, магнитофон, плеер и т.п.) должно быть способным обеспечивать одинаковое усиление в диапазоне частот, содержащем гармоники заметной амплитуды, т.е. иметь оптимальную полосу пропускания. Слишком широкая полоса пропускания открывает "ворота" не только для спектральных составляющих, но и для помех, а слишком узкая полоса даст заметное искажение сигнала. В телефонии, где не требуется высокого качества воспроизведения исходного голосового сигнала, используется узкая полоса. Поэтому не всегда по телефону можно узнать голос знакомого человека. На рис. 5.4 для сравнения показан тот же, что и на рис. 5.3, сложный сигнал, прошедший через воспроизводящее устройство, пропускающее только три первых гармоники (k = 1, 2, 3). Из рисунков легко видеть степень искажения исходного сигнала.
Т
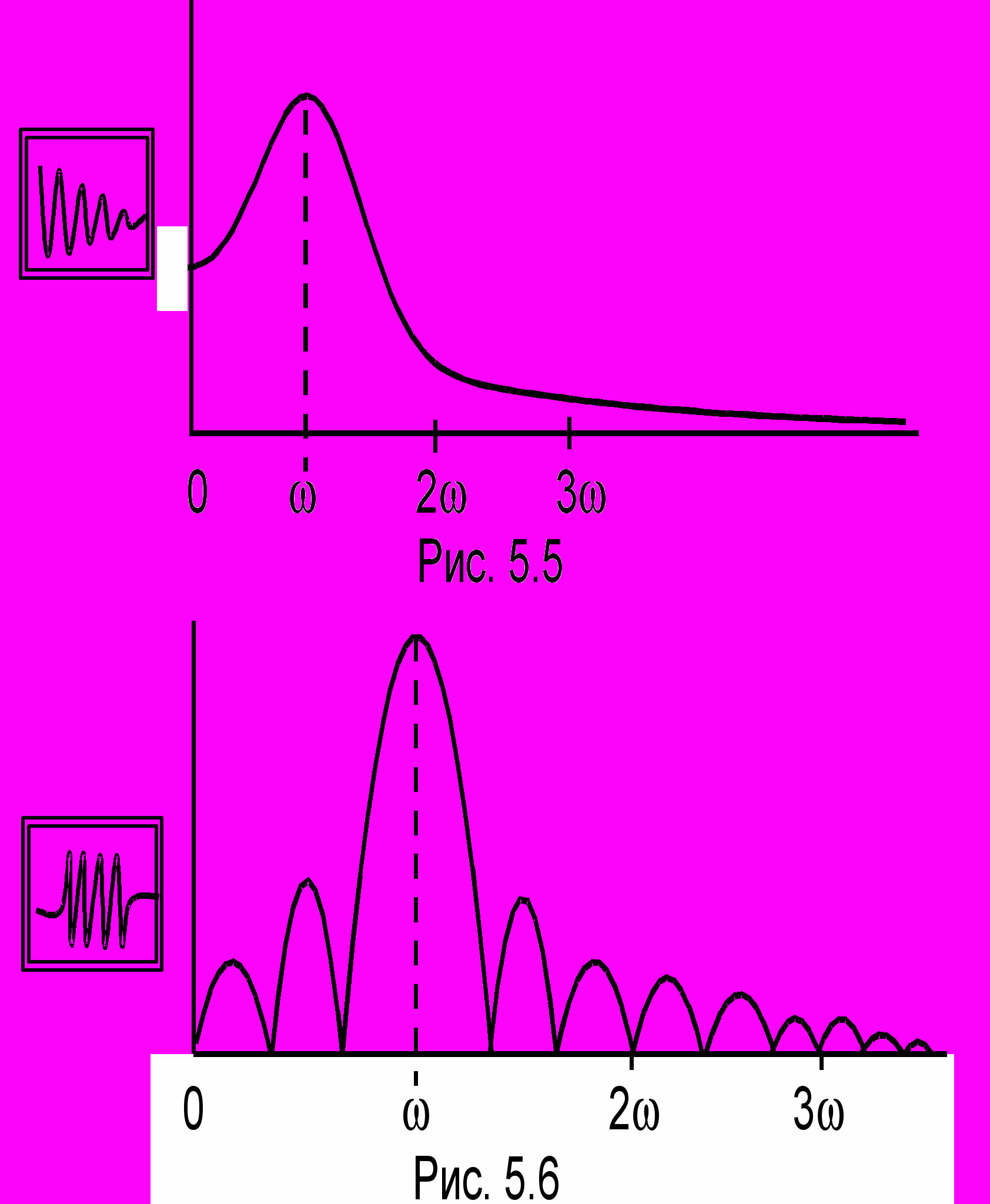 еория Фурье применима и для непериодических сигналов, например для одиночных импульсов. Такой одиночный импульс можно рассматривать как периодический сигнал с периодом Т . Подробный анализ таких сигналов выходит за рамки данного курса. Отметим только, что вместо рядов Фурье получим интегралы Фурье, а спектр станет не дискретным (т.е. состоящим из отдельных палочек, как на рис. 5.2), а непрерывным. В качестве примера на рис. 5.5 показан спектр затухающего колебания, а на рис. 5.6 спектр "обрывка" синусоиды. Таким образом, если спектр бесконечной синусоиды - единственная палочка, то обрывок синусоиды - одиночный сигнал, имеющий непрерывный спектр! По оси ординат на этих рисунках отложены амплитуды, а по оси абсцисс - частоты. На рис. 5.5 величина - условная циклическая частота затухающего колебания, а на рис. 5.6 это циклическая частота аналогичного бесконечного периодического сигнала.
еория Фурье применима и для непериодических сигналов, например для одиночных импульсов. Такой одиночный импульс можно рассматривать как периодический сигнал с периодом Т . Подробный анализ таких сигналов выходит за рамки данного курса. Отметим только, что вместо рядов Фурье получим интегралы Фурье, а спектр станет не дискретным (т.е. состоящим из отдельных палочек, как на рис. 5.2), а непрерывным. В качестве примера на рис. 5.5 показан спектр затухающего колебания, а на рис. 5.6 спектр "обрывка" синусоиды. Таким образом, если спектр бесконечной синусоиды - единственная палочка, то обрывок синусоиды - одиночный сигнал, имеющий непрерывный спектр! По оси ординат на этих рисунках отложены амплитуды, а по оси абсцисс - частоты. На рис. 5.5 величина - условная циклическая частота затухающего колебания, а на рис. 5.6 это циклическая частота аналогичного бесконечного периодического сигнала. 1 С некоторыми несущественными для практики математическими ограничениями.
2 Другая эквивалентная форма ряда (как нетрудно убедиться) имеет вид:
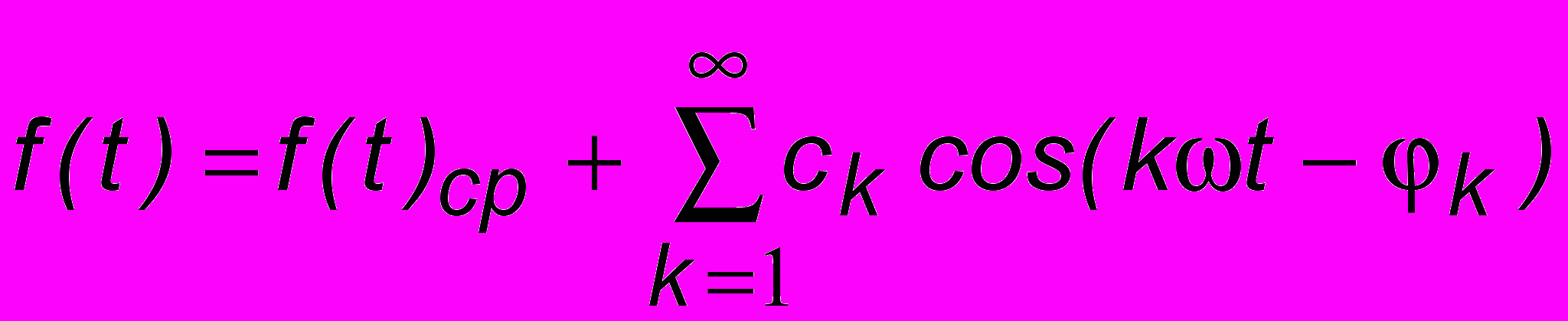 , где
, где 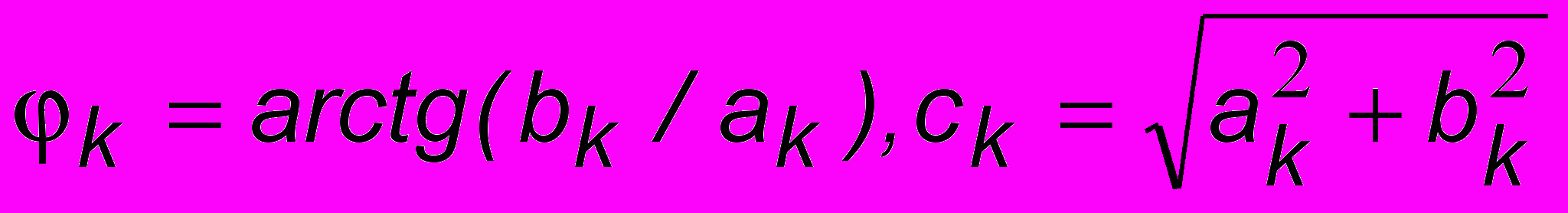 .
.