Исследование многошагового нечеткого вывода на примере построения экспертной системы оценки экологической безопасности производственной деятельности

Вид материала

Исследование

Содержание 1. Постановка задачи 2. Механизм нечеткого логического вывода 2.2. Иерархические нечеткие базы данных. 2.3. Иерархический нечеткий вывод 2.4. Модель иерархического (многошагового) нечеткого вывода 3. Решение задачи в среде Matlab Список литературы

Подобный материал:

• Удк 681. 03 Экспертная система анализа экологической безопасности, 79.34kb.
• Исследование применимости различных схем нечеткого вывода в иерархических нечетких, 89.29kb.
• Демидова Л. А., Коротаев А. Н. Генетический алгоритм настройки параметров системы нечеткого, 38.47kb.
• Документ разработан с учетом требований: законодательства Российской Федерации; нормативных, 356.52kb.
• Моделирование системы управления стеклоочистителем на базе нечеткого контроллера, 16.79kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 154.89kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 192.33kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 161.21kb.
• Формирование производственной программы предприятия в условиях рыночной конкуренции, 110.21kb.
• Прогнозирование на основе нечеткого логического вывода, 30.91kb.

УДК 681.03

Исследование многошагового нечеткого вывода на примере построения экспертной системы оценки экологической безопасности производственной деятельности.

Н.Н.Иванова¹, Н.Г. Ярушкина²

В работе описывается механизм многошагового (иерархического) нечеткого вывода и его применение в решении задач эколого-экономического анализа деятельности предприятия.

Введение

Сегодня во всем мире принято уделять большое внимание проблемам экологии. Поскольку ни один руководитель не будет работать себе в ущерб, очень важно соблюсти баланс между экологической безопасностью (экологичностью производственного процесса), требующей значительных денежных затрат, и экономической эффективностью деятельности хозяйствующего субъекта.

Стремясь к лучшим производственным ре­зультатам, руководители предприятий, иногда даже неожиданно для себя, вызывают побочные отрица­тельные эффекты в окружающей среде («экологические ущербы»). Возникновение крупного экологического ущерба может свести на нет даже самые, казалось бы, по­ложительные производственные итоги.

Чтобы этого не допустить, необходимо организовывать производственную деятельность таким образом, чтобы она обеспечива­ла разумный компромисс между производствен­ными целями и их экологическими последствиями.

В такой ситуации оценка и принятие решений становятся достаточно сложной задачей. Одним из путей решения этой задачи является разработка компьютерных моделей, базирующихся на нечетком выводе.

В настоящее время большую актуальность приобретает использование экспертных систем для решения объемных, трудно формализуемых задач в различных предметных областях. Эти задачи характеризуются, как правило, отсутствием или сложностью формальных алгоритмов решения, неполнотой и нечеткостью, а иногда и не репрезентативностью исходных данных, нечеткостью конечных целей и условий ограничений при принятии решений. Данные особенности приводят к необходимости использования в процессе решения данных задач знаний, полученных от человека-эксперта в предметной области, и разработки экспертных систем, осуществляющих сбор и управление этими знаниями, принимающими решения об оптимальном способе достижения целей в условиях неполноты и нечеткости.

1. Постановка задачи

При разра­ботке экспертной системы анализа экономического и экологического состояния предприятия необходимо обеспечить тесную увязку двух ведущих на­чал: экологии и экономики. Они отражают две объектив­ные, но взаимно противоположные стороны проблемы. Реально достижимая степень безопасности определяется величиной доступных источников денежных и других ре­сурсов, которые необходимо найти для осуществления средозащитных мероприятий.

Для выявления возможных источников собственного финансирования средозащитных мероприятий необходимо провести комплексный анализ финансового состояния предприятия. В ходе экономического анализа также может быть выявлена убыточность основного производства, тогда может быть принято решение о его консервации, если величина ущерба, наносимого окружающей среде, окажется выше приносимой прибыли.

Знания человека-эксперта о решении задач в условиях неполноты, нечеткости исходной информации и достигаемых целей, также имеют нечеткий характер. Для их формализации в настоящее время успешно применяется аппарат теории нечетких множеств и нечеткой логики.

Нечеткие понятия в данном случае формализуются в виде нечетких и лингвистических переменных, а нечеткость действий в процессе принятия решения – в виде нечетких алгоритмов. Экспертные системы, способные формализовывать нечеткую информацию и обрабатывать ее в рамках нечетких алгоритмов, получили название нечетких экспертных систем. Большую актуальность в настоящее время имеет использование нечетких экспертных систем для решения задач моделирования в области экономики, экологии, управления предприятием.

Проект экспертной системы для решения данной задачи предполагает способность накапливать знания специалистов в данной предметной области и управлять этими знаниями при принятии решения. Основное требование к модулю накопления и управления знаниями экспертов - возможность его легкого практического использования специалистом, не знакомым с языками программирования. В то же время, данный модуль должен обеспечить специалисту возможность качественного формирования базы знаний в соответствии с потребностями решаемой задачи.

Моделью проектирования является иерархически-блочный метод, сущность которого сводиться к декомпозиции функций с последующим выделением иерархий систем и подсистем. Проектируемая система формируется с помощью синтеза таких подсистем (см. рис.1).




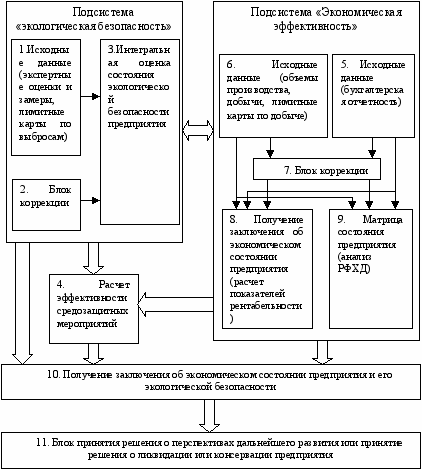
Рис. 1. Структурная схема модели экономически эффективного и экологически безопасного производства.

2. Механизм нечеткого логического вывода

2.1. Стандартный алгоритм

Стандартная интеллектуальная система осуществляет нечеткий логический вывод по следующим этапам[Ярушкина, 2004]:

1. Фаззификация: точное значение входной переменной интерпретируется как нечеткая точка.
   
2. Композиция входной переменной и условной части правила: вычисление уровня пригодности правила к ситуации.
   
3. Вычисление нечеткой импликации.
   
4. Агрегация среднего значения: построение нечеткого значения выхода.
   
5. Дефаззификация: выбор представляющего элемента по агрегированному нечеткому понятию.
   

Функциональная схема нечеткого вывода в упрощенном виде представлена на рис. 2.



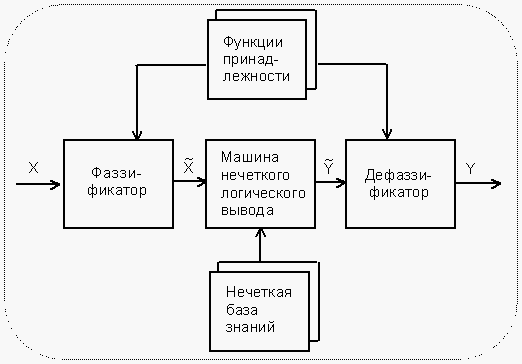
Рис.2. Нечеткий логический вывод

2.2. Иерархические нечеткие базы данных.

Для моделирования многомерных зависимостей "входы - выход" целесообразно использовать иерархические системы нечеткого логического вывода. В этих системах выходная переменная одной базы знаний является входной для другой базы знаний. На рис.3. приведен пример иерархической нечеткой базы знаний, моделирующей зависимость y=f(x₁,x₂,x₃,x₄,x₅,x₆) с использованием трех баз знаний. Эти базы знаний описывают такие зависимости: y₁=f₁(x₁,x₂) , y₂=f₂(x₄,x₅,x₆) и y=f₃(y₁,x₃,y₂) .



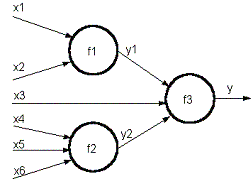
Рис 3. Пример иерархической нечеткой базы знаний

Применение иерархических нечетких баз знаний позволяет преодолеть "проклятие размерности": при большом количестве входов эксперту трудно описать причинно-следственные связи в виде нечетких правил. Это обусловлено тем, что в оперативной памяти человека может одновременно хранится не более 7±2 понятий-признаков [Index, 2003]. Поэтому, при большем количестве входных переменных необходимо их иерархически классифицировать. Обычно, выполнение такой классификации не составляет трудностей для эксперта, так как при принятии решений человек иерархически учитывает влияющие факторы.

Преимущество иерархических баз знаний заключается и в том, что они позволяют небольшим количество нечетких правил адекватного описать многомерные зависимости "входы.

2.3. Иерархический нечеткий вывод

Существует два способа моделирования систем многошагового нечеткого логического вывода. Первый способ состоит в выполнении нечеткого вывода для промежуточных переменных с последующей передачей четких значений этих переменных в нечеткие системы следующего уровня иерархии. Недостаток этого способа состоит в том, что над промежуточными переменными последовательно выполняются операции дефаззификации и фаззификации. Нечеткие результаты промежуточных логических выводов дефаззифицируют, потом эти четкие значения подают на вход нечетких систем следующего уровня иерархии и там они фаззифицируются, т.е становятся нечеткими. Следовательно, для промежуточных переменных надо задавать функции принадлежности. Кроме того, необходимо обеспечить эквивалентность нечетких множества до и после операций дефаззификации и фаззификации, на практике это часто не представляется возможным.

При втором способе процедуры дефаззификации и фаззификации для промежуточных переменных не выполняются. Результат логического вывода в виде нечеткого множества напрямую передается в машину нечеткого вывода следующего уровня иерархии. Поэтому, для описания промежуточных переменных в иерархических нечетких базах знаний достаточно задать только терм-множества, без определения функций принадлежностей. Понятно, что преимущества второго способа неоспоримы. Поэтому мы и выбрали его для решения поставленной задачи.

2.4. Модель иерархического (многошагового) нечеткого вывода

Представим модель нечеткого вычисления в виде следующей схемы (рис.4):



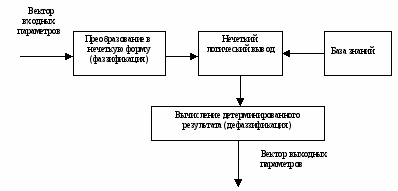
Рис. 4 Стандартная модель нечетких вычислений

Доработаем ее для реализации процедуры многошагового нечеткого логического вывода.

Алгоритм работы иерархического нечеткого логического вывода примет вид:

1.Вектор входных переменных, используемых на всех шагах нечеткого вывода ().

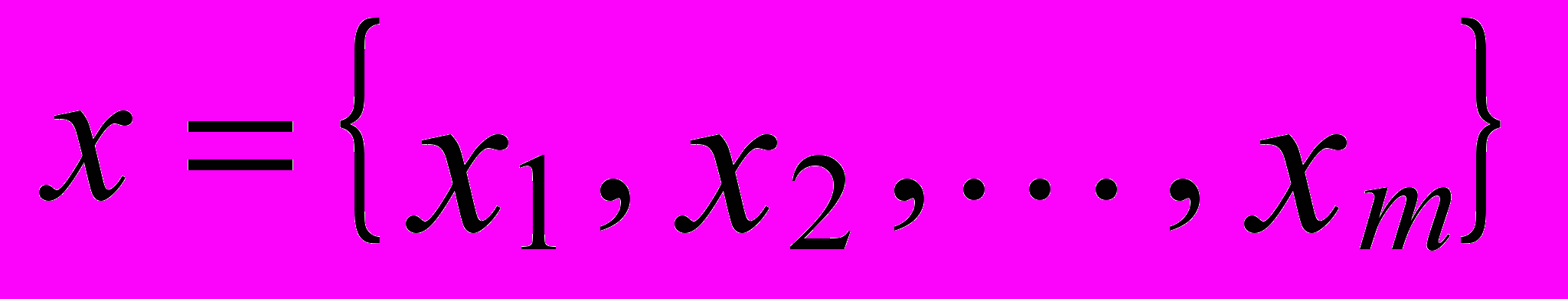2. Преобразование входных переменных в нечеткую форму – процедура фаззификации.

3. Цикл i:=1 to N do (где N – число шагов нечеткого вывода)

3.1. выполнить процедуру нечеткого логического вывода, с использованием соответствующих переменных и соответствующей базы правил.

3.2. if i=N then goto 4. (дефаззификация результата)

else полученное нечеткое множество y_i передать на вход процедуры нечеткого логического вывода следующего уровня (i:=i+1).

4. Дефаззификация.



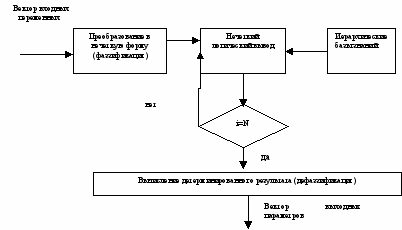
Рис. 5. Модель иерархического нечеткого логического вывода

3. Решение задачи в среде Matlab

Для решения задачи реализации на практике используем компоненту Matlab Fuzzy Logic Toolbox. Для расширения стандартного алгоритма нечеткого вывода, предусмотренного в системе, необходимо запрограммировать две процедуры. Первая процедура должна выдавать результат вывода по промежуточной базе знаний в виде нечеткого множества типа:

,
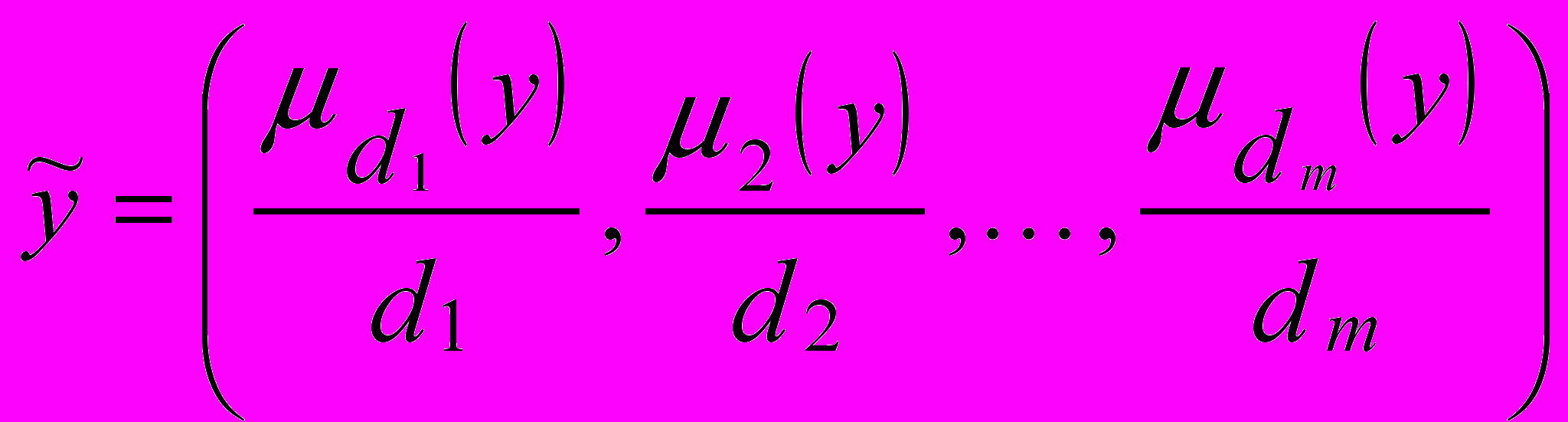где 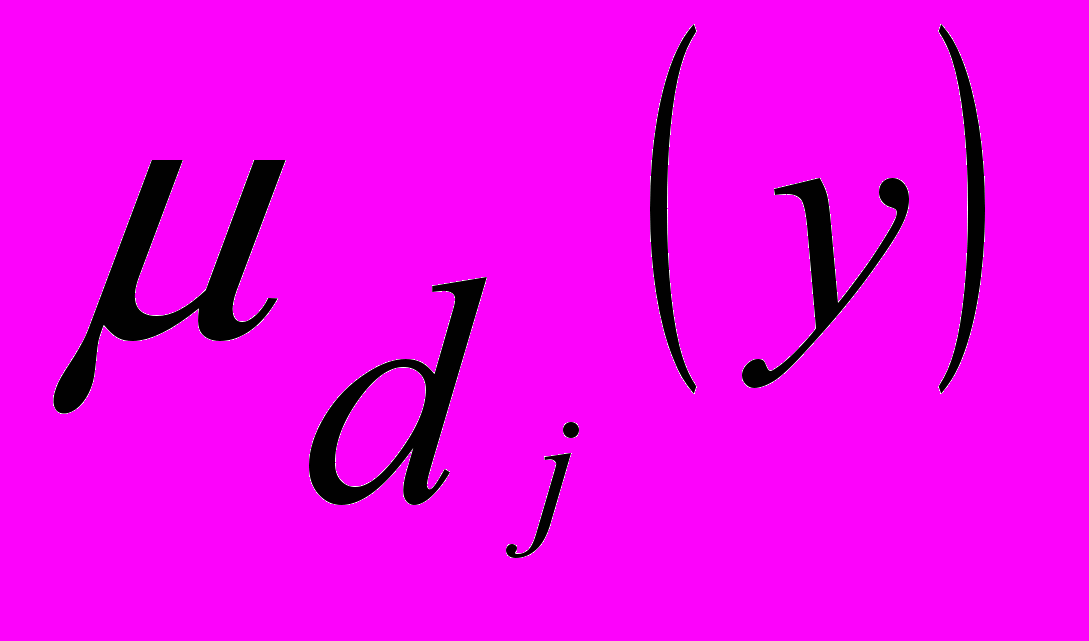степень принадлежности результата нечеткому терму 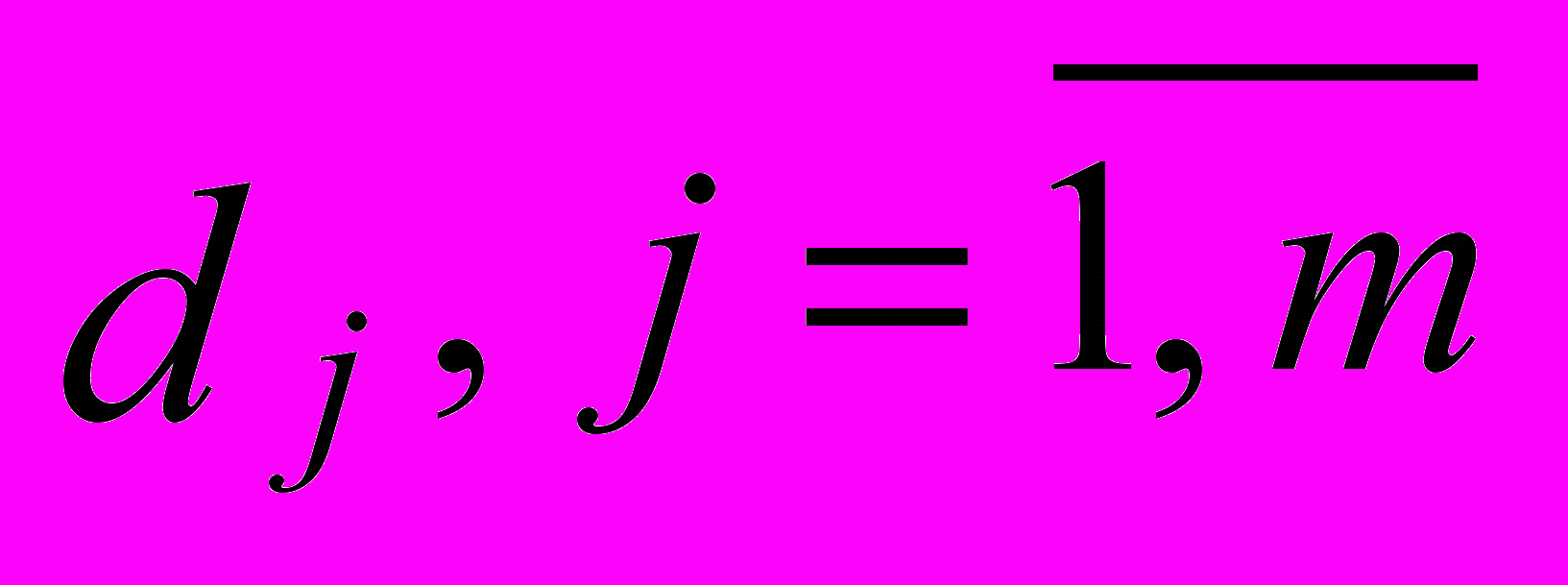, m - количество термов.

Вторая процедура должна передавать найденные степени принадлежности 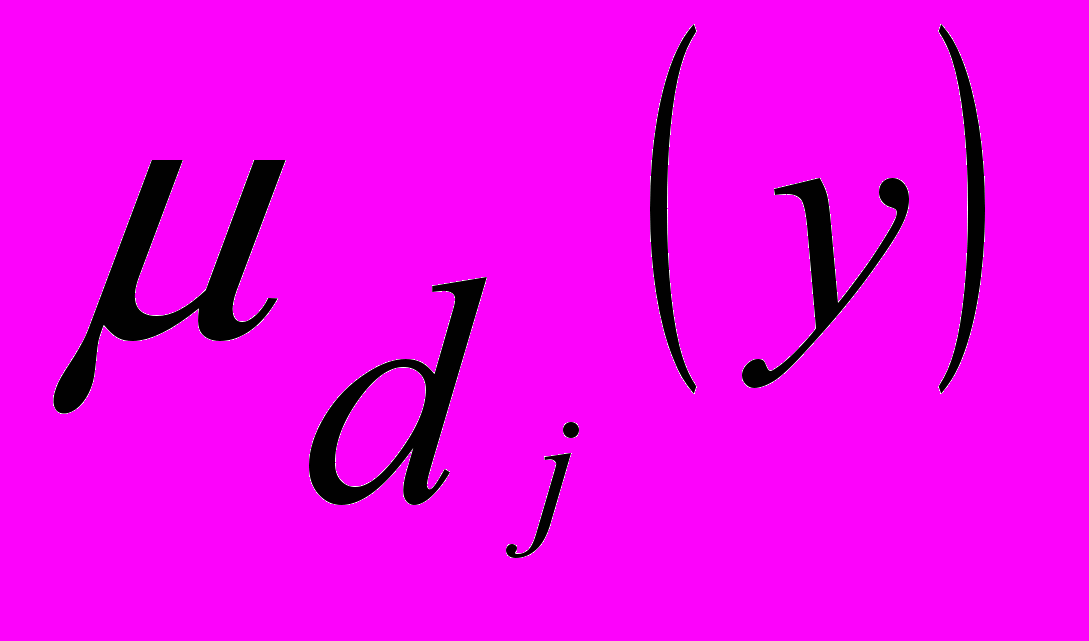, 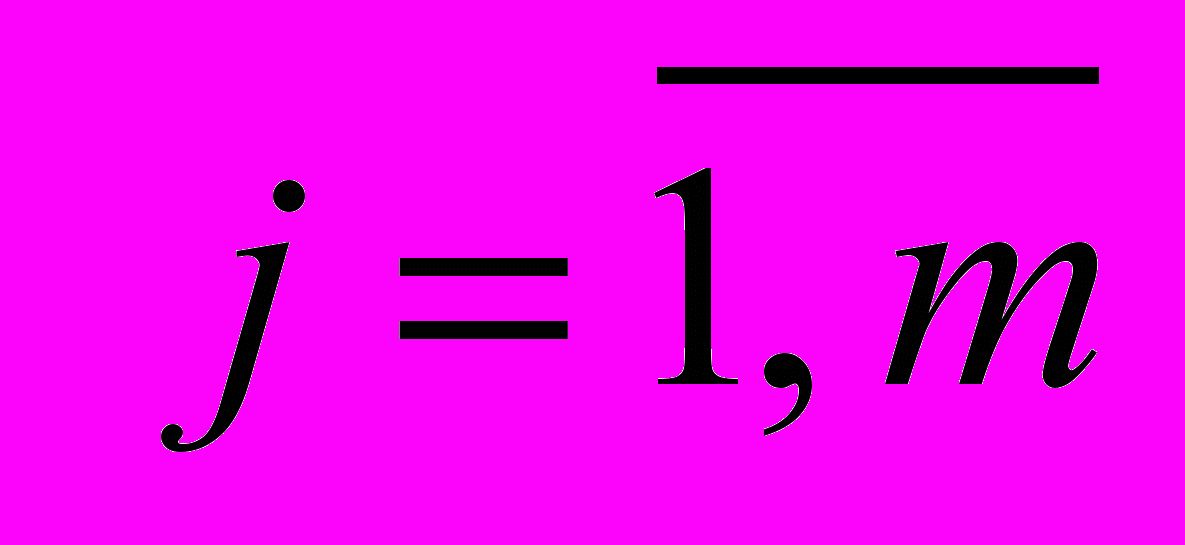в машину нечеткого вывода следующего уровня иерархии.

В качестве промежуточной нечеткой системы будем использовать систему нечеткого вывода Сугено. Классам решений поставим в соответствие "функции принадлежности" выходной переменной. Параметры "функций принадлежности" выходной переменной могут быть произвольными, т.к. они не влияют на результирующее нечеткое множество

Для получения результата вывода в виде нечеткого множества выполним следующие команды:

[a,b,c,d]=evalfis(inputs,fis);         %inputs - входы, fis - нечеткая система

number_of_terms=length(fis.output(1).mf);         %количество термов

mf_grades=zeros(1,number_of_terms);  %искомые степени принадлежности
number_of_rules=length(fis.rule);    %количество правил в базе знаний
for j=1:number_of_rules

term_index=fis.rule(j).consequent;

mf_grades(term_index)=max(mf_grades(term_index), d(j)); %s-норма - мax

end.

Для реализации второй процедуры предлагается специальная функция принадлежности treemf, которая возвращает степень принадлежности, равную ее первому параметру:

function mu = treemf(x, params)

mu=x; %Чтобы не определять размер

mu(:,:)=params(1);

Этот тип функции принадлежности следует устанавливаем для каждого терма входной промежуточной переменной. Для передачи в машину нечеткого вывода следующего уровня иерархии степеней принадлежности, найденных первой процедурой, необходимо первый параметр функции принадлежности treemf установить равным координате вектора mf_grades. Параметры функций принадлежности входных промежуточных переменных необходимо устанавливать при каждом нечетком выводе.

Заключение

В работе рассмотрена математическая модель иерархического нечеткого вывода и ее практическая реализация в среде Matlab Fuzzy Logic Toolbox, которая позволяет моделировать рассуждения человека-эксперта в ходе принятия сложных решений в процессе анализа экономической эффективности и экологической безопасности производственной деятельности.

Список литературы

[Ярушкина, 2004] Ярушкина Н.Г. Основы теории нечетких и гибридных систем: учебное пособие.- М.: Финансы и статистика, 2004.- 320 с.: ил.

[Index, 2003]ссылка скрыта

[Ротштейн, 2001] Ротштейн А.П., Штовба С.Д. Нечеткий многокритериальный анализ вариантов с применением парных сравнений // Известия РАН. Теория и системы управления.- 2001.- №3.- С.150-154.

[Орловский, 1981] Орловский С.А. Проблемы принятия решений при нечеткой исходной информации. - М.: Радио и связь, 1981. - 286 с.