Удк 681. 03 Экспертная система анализа экологической безопасности

Вид материала

Документы

Содержание Теоретические основы иерархического нечеткого вывода 1-го порядка 2). Результирующее значение выхода y Практическая реализация

Подобный материал:

• Удк 681. 51: 303. 732+681 066 вопросы анализа проблем рыбохозяйственных комплексов:, 87.72kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 134.1kb.
• З. О. Ибраимова уфимский государственный авиационный технический университет экспертная, 19.26kb.
• Удк 681 053: 681. 32: 007, 134.3kb.
• Удк 340. 6+681. 327+681 015 Д. В. Ландэ, В. Н. Фурашев, 450.24kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 154.89kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 192.33kb.
• Единая система оценки соответствия в области промышленной, экологической безопасности,, 161.21kb.
• Экспертная система разработана для имитации процесса принятия решения экспертом- человеком, 162.54kb.
• Концепция комплексного подхода решения вопросов энергосбережения, повышения энергетической, 94.05kb.

УДК 681.03

Экспертная система анализа экологической безопасности

Н.Г. Ярушкина¹, Н.Н.Ястребова², И.С.Ястребов³

В работе описываются основные принципы построения экспертных систем и способ решения задачи анализа экологической безопасности с помощью нового инструмента искусственного интеллекта – иерархического нечеткого вывода.

Введение

В настоящее время большую актуальность приобретает использование экспертных систем для решения объемных, трудно формализуемых задач в различных предметных областях. Эти задачи характеризуются, как правило, отсутствием или сложностью формальных алгоритмов решения, неполнотой и нечеткостью, а иногда и нерепрезентативностью исходных данных, нечеткостью конечных целей и условий ограничений при принятии решений. Задача оценки состояния экологической безопасности на предприятии – одна из таких.

Теоретические основы иерархического нечеткого вывода

В ходе решения задачи были проанализированы схемы нечеткого вывода, для выбора наиболее адекватной условиям задачи (табл. 1).

Таблица 1. Сравнение схем нечеткого вывода

Название схемы нечеткого вывода	Вид выходного нечеткого множества	Отсутствие накопления нечеткости в иерархических системах	Отсутствие суммирования одинаковых правил при дефаззификации
Эталон	1-ого порядка	+	+
E.H.Mamdani, P.M.Larsen, Y. Tsukamoto	2-ого порядка	-	+
M. Sugeno	1-го порядка	+	+
Синглетон	1-ого порядка	+	-

На основе этих данных был выбран нечеткий логический вывод по Сугено, так как только он удовлетворяет всем поставленным условиям.

Применение иерархических нечетких баз правил позволило преодолеть "проклятие размерности" (комбинаторный взрыв): при большом количестве входов эксперту трудно описать причинно-следственные связи в виде нечетких правил.

Другое преимущество иерархических систем заключается в том, что они позволяют небольшим количеством правил адекватного описать многомерные зависимости "входы - выход".

Существует два способа создания таких систем: c выполнением фаззификации/дефаззификации промежуточных переменных и без дефаззификации/фаззификации промежуточных переменных.

Для реализации в экспертной системе был выбран второй способ.

Оператор fuzzy 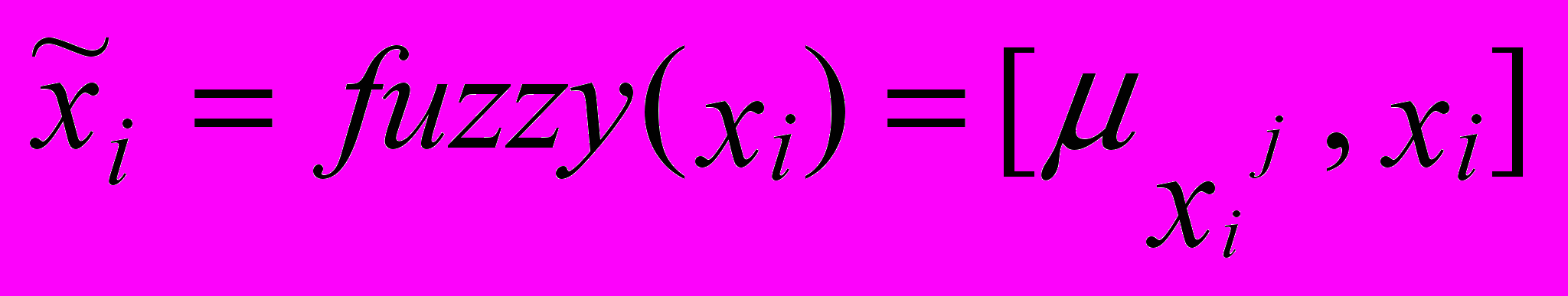(1) ставит в соответствие четкому числу нечеткое множество, содержащее число кортежей, равное числу функций принадлежности, заданных для данной лингвистической переменной. Результатом выполнения над фаззифицированным вектором входных переменных X композиционного правила Л.Заде будет множество: ( 2).

Результирующее значение выхода y определяется как суперпозиция линейных зависимостей, выполняемых в данной точке n-мерного пространства. Для этого дефаззифицируем нечеткое множество .

Обозначим дефаззификацию функционалом: (3)

Введем следующие обозначения:

- слой, где k – общее число слоев. Ранее понятие слой употреблялось только по отношению к нейронным сетям. Мы подразумеваем под слоем следующее определение: слой – структурная единица, содержащая все независимые задачи, которые могут выполняться параллельно и результат выполнения одной не влияет на ход вычисления других задач.

- задача слоя l, где - общее число задач слоя l. Под задачей мы подразумеваем атомарную расчетную единицу нечеткого логического вывода, представляющую собой схему нечеткого логического вывода по Сугено.

- лингвистические переменные задачи t слоя l.

Тогда с помощью правила Заде мы можем вывести следующую формулу:

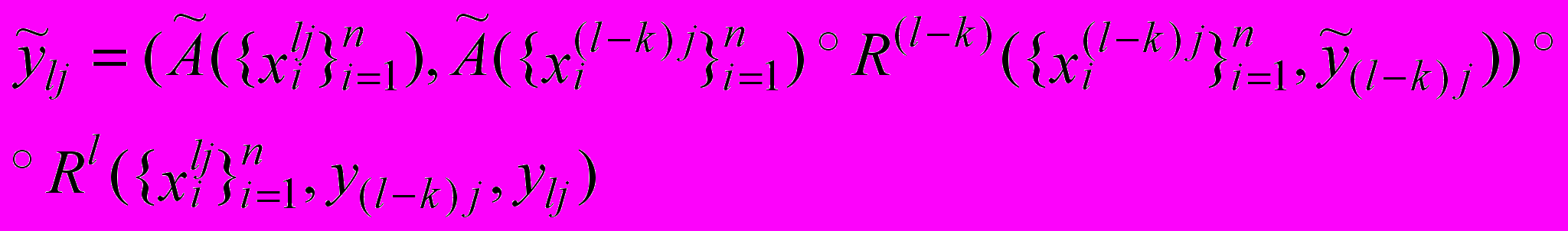(4)

И продеффазифировав полученное нечеткое множество (4) выведем общую формулу иерархического нечеткого вывода:

(5)

Теперь представим модель иерархического нечеткого вычисления в виде следующей схемы (рис.1):



Рисунок 1. Модель нечетких вычислений

Алгоритм работы иерархического нечеткого логического вывода примет вид:

1.Вектор входных переменных, используемых на всех шагах нечеткого вывода ().

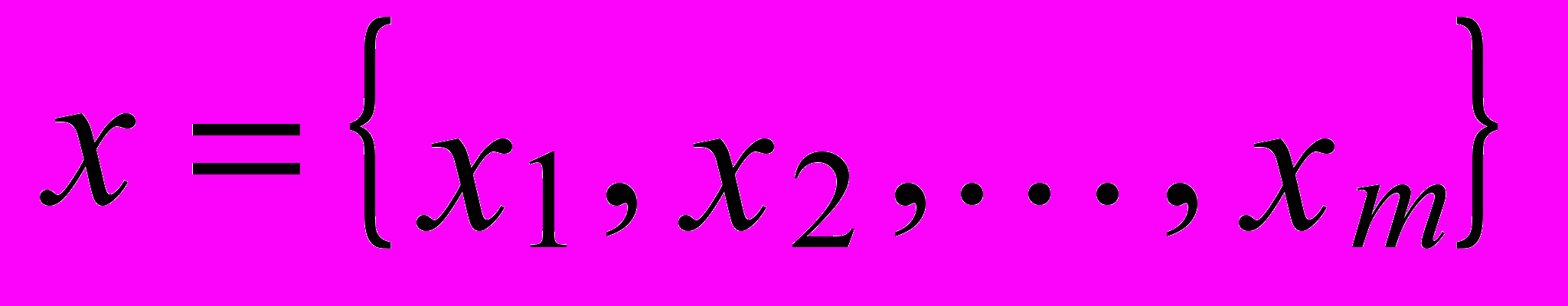2. Преобразование входных переменных в нечеткую форму – процедура фаззификации.

3. Цикл i:=1 to N do (где N – число шагов нечеткого вывода)

3.1. выполнить процедуру нечеткого логического вывода, с использованием соответствующих переменных и базы правил.

3.2. if i=N then goto 4. (дефаззификация результата)

else нечеткое множество y_i передать на вход процедуры нечеткого логического вывода следующего уровня (i:=i+1).

4. Дефаззификация.

Данный алгоритм обеспечил нам следующие преимущества:

1. Выполняется без фаззификации/дефаззификации промежуточных переменных, вследствие чего снижается вычислительная погрешность;
   
2. Использование в качестве базового алгоритма схемы Сугено помогает избежать увеличения нечеткости нечетких множеств;
   
3. Позволяет работать с иерархическими базами данных и знаний;
   
4. Помогает преодолеть «проклятие размерности» и позволяет описывать меньшим количеством правил зависимости в исходных данных.
   

Модель экологической безопасности

Структурная схема разрабатываемой экспертной системы представлена на рис. 2.



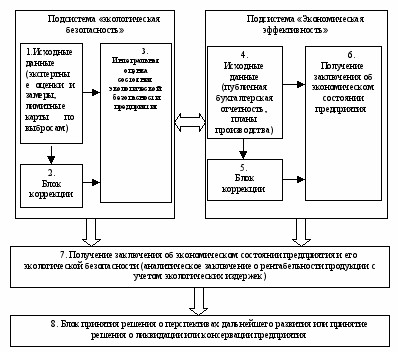
Рисунок 2. Структурная схема модели

Исходными данными для экспертной системы эколого-экономического анализа являются «бухгалтерский баланс» предприятия (форма №1), «отчет о прибылях и убытках» (форма №2), экспертные оценки ценности территории, на которой расположено предприятие, класс опасности предприятия, закрепленный нормативными документами, показатели выбросов и сбросов вредных веществ, данные по лимитам и нормативам для этих веществ по предприятию. Система описана набором из 14 лингвистических переменных, которые представляют собой аналитические показатели, полученные из исходных данных. На первом слое – 6 задач, на 2 -2, и на 3 – 1.

Рассмотрим подробнее одну из подзадач: EcoSafety-Terra. Она описана четырьмя лингвистическими переменными: BiologicValue, CulturalValue, HistoricValue, PeopleValue, которые могут принимать значения от 0 до 10. Для описания переменных введены три терма {«Low», «Medium», «High»}, описывающие значения этой переменной. Значение степеней принадлежности вычисляем по формуле: .

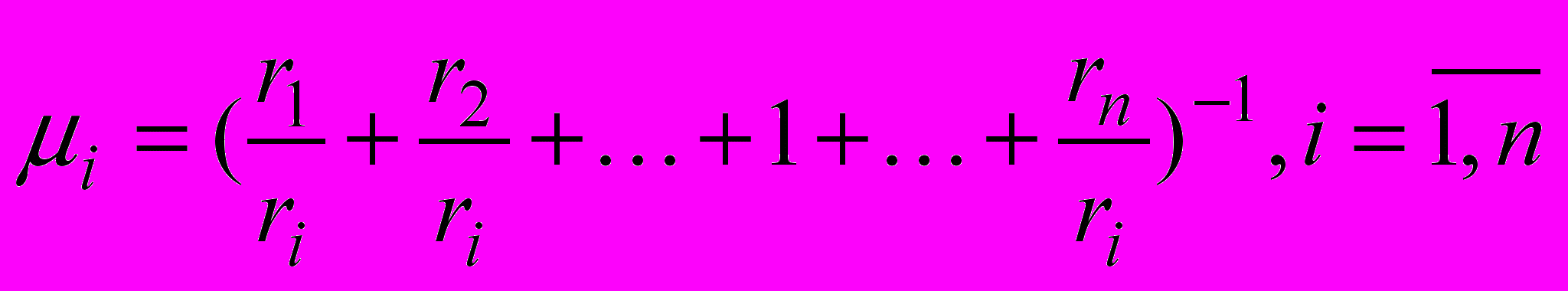Наилучшим образом отражать данные зависимости будут трапециевидные функции принадлежности (рис. 3).



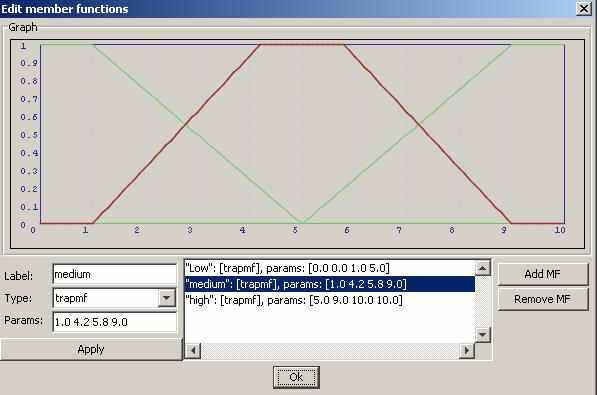
Рисунок 3. Функции принадлежности переменных EcoSafety-Terra

Математическая нечеткая модель оценки экологической безопасности будет выражаться следующими формулами:

Первый слой:

1.

2.

3.

4.

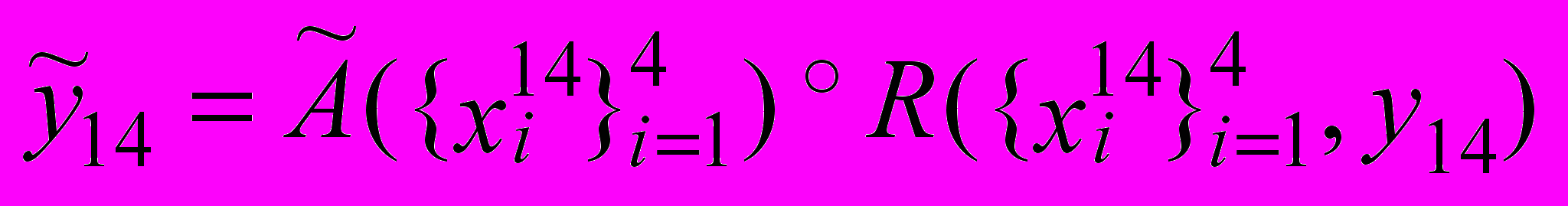
5.

6.

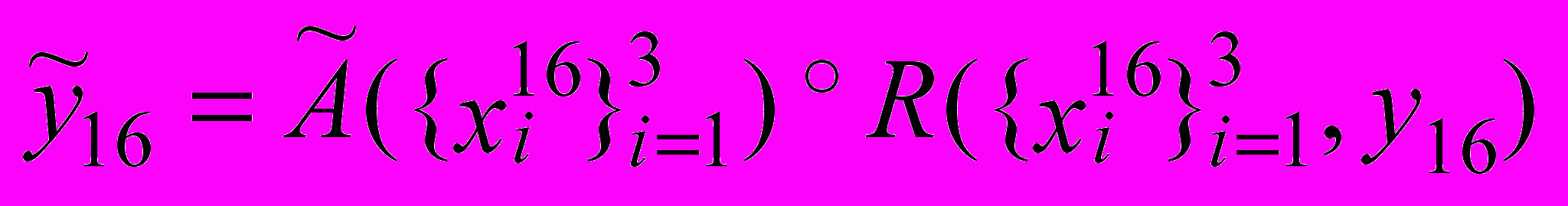
Не выделяя задачи, с помощью композиционного правила Заде получим:

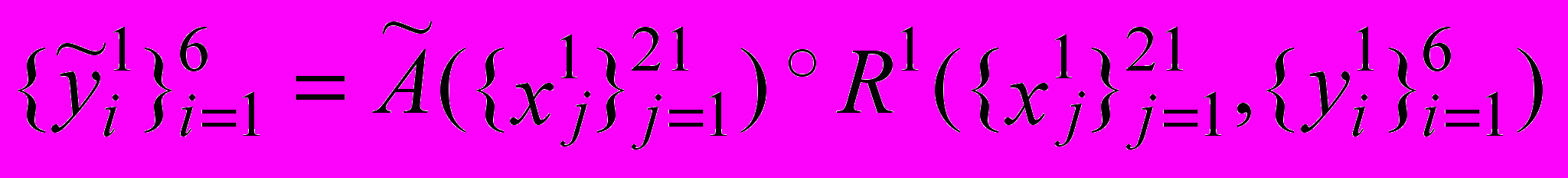(6).

Второй слой:

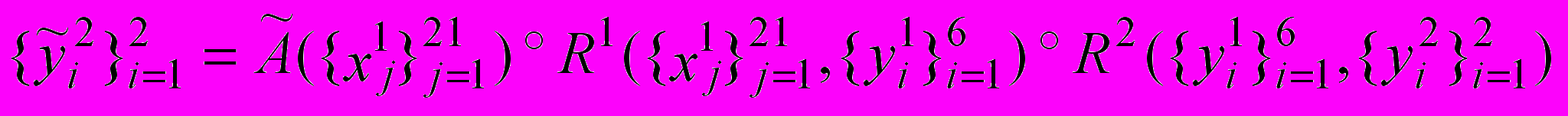(7).

Третий слой:

(8).

Для получения результата нечеткое множество (8) необходимо продефаззифицировать.

Практическая реализация

Широкое внедрение экспертных систем всегда сдерживалось целым рядом причин, в числе которых отсутствие достаточно удобного и мощного инструментария разработки прикладных систем и разнородность технических и операционных сред пользователей. Основным средством для создания переносимых приложений в настоящее время является язык Java. Поэтому для реализации экспертной системы было решено использовать следующее программное обеспечение: J2SE 6.0, Apache Derby 10.2.2.0, Hibernate 3.2.0, Swing / AWT

Рассмотрим общую UML – диаграмму нашего приложения (рис.4.).

Пакет JFuzzy - это управляющая часть, он является главным модулем программы и отвечает за выполнение расчетов по иерархическому нечеткому выводу.

JFuzzyTool – графический модуль, предоставляющий пользователю возможность создавать и редактировать иерархии нечеткого вывода при проектировании экспертных систем на его основе.

JFuzzyDB – модуль для работы с данными, используемый для расчетов в экспертной системе анализа эколого-экономического анализа предприятия, построенной на многошаговом нечетком логическом выводе.




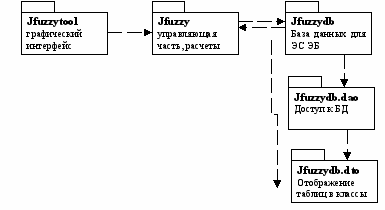
Рисунок 4. Взаимосвязь модулей программы


Организация проекта на базе объектно-ориентированного программирования позволила легко перейти от одношагового (стандартного) логического вывода к многошаговому (иерархическому), путем изменения поведения соответствующих классов в зависимости от шага вывода. Все задачи экспертной системы (class FuzzyTask) в программе разбиты на слои (class FuzzyLayer). Каждый шаг нечеткого вывода представлен экземпляром класса FuzzyTask, задающего набор входных переменных и правил нечеткого вывода. Также в зависимости от шага итерации необходимо знать, нужны ли процедуры фаззификации и дефаззификации переменных на данном шаге. Это проблема представления данных, и она была решена следующим образом: вместо бинарных файлов для хранения информации о нечетком вывода используется формат XML, позволяющий хранить иерархическую систему в виде древовидной структуры.

Сценарий работы с программой представлен на рис. 5. При этом особо следует отметить, что описанный программный продукт не только дает пользователю возможность пользоваться готовой экспертной системой, но и разрабатывать собственные.




Рисунок 5. Сценарий работы с JFuzzyTool 1.0 для создания нечетких экспертных систем


Заключение

В ходе исследования был разработан новый метод вычислительного интеллекта, и с его помощью успешно решена задача интеллектуального анализа состояния экологической безопасности на предприятии.

Список литературы

[Ярушкина, 2004] Ярушкина Н.Г. Основы теории нечетких и гибридных систем: учебное пособие.- М.: Финансы и статистика, 2004.- 320 с.: ил.