В. В. Губарев " " 20 г. Рабочая программа
| Вид материала | Рабочая программа |
- В. В. Губарев " " 20 г. Рабочая программа, 240.77kb.
- Кафедра Автономных Информационных и Управляющих Систем "утверждаю" Декан автф, 431.69kb.
- Учреждение Российской Академии наук Институт экономики ран москва, Новочеремушкинская, 148.35kb.
- Рабочая программа по дисциплине: Экономика недвижимости для специальности: Экспертиза, 293.4kb.
- Рабочая программа по дисциплине: Теоретические основы оценки собственности для специальности:, 226.61kb.
- Рабочая программа по дисциплине: Экономика недвижимости для специальности: Экономика, 293.45kb.
- Рабочая программа По истории 10 класс Пояснительная записка, 116.13kb.
- Рабочая программа учебной дисциплины ф тпу 1 -21/01, 102.93kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 утверждаю, 68.83kb.
- Петрович Гайдар «Горячий камень», 26.68kb.
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
“УТВЕРЖДАЮ”
Декан АВТФ
 В.В.Губарев
В.В.Губарев“___ ”______________20 г.
РАБОЧАЯ ПРОГРАММА
по дисциплине “Теория информации”
для студентов, обучающихся по направлению 075500
“Комплексное обеспечение информационной безопосности автономных систем”
Факультет автоматики и вычислительной техники
Кафедра автономные системы и информационная безопасность
Курс 3 Семестр 5
Лекции 34 час.
Лабораторные работы 17 час.
Самостоятельная работа 50 час.
Экзамен 5 семестр
Всего часов 101
2003 г.
Рабочая программа составлена на основании Государственного образовательного стандарта высшего профессионального образования по направлению 075500 “Комплексное обеспечение информационной безопасности автоматизированных систем” от 05.04.2000
Номер государственной регистрации 284 инф/сп
Дисциплин федерального компонента индекс _ЕН.Ф.06
Рабочая программа обсуждена на заседании кафедры АСИБ, протокол № 3
от “30” октября 2001 г.
Программу составил
к.т.н., доцент В.П. Ющенко
Заведующий кафедрой
д .т.н., В.Н. Лёгкий
Ответственный за основную
образовательную программу
Эксперт НМЦ
1.Принципы построения курса.
В основу курса “Теория информации ” положены следующие принципы:
- курс входит в число дисциплин федерального компонента;
- цель преподавания дисциплины «Теория информации» состоит в освоении студентами основ теории информации и теории кодирования сигналов как носителей информации. Дать студентам знания о потенциальных возможностях передачи и преобразования информации;
- Дисциплина должна быть фундаментом для последующих дисциплин: «Системы и сети передачи информации», «Технические средства и методы защиты информации» и др. Основное внимание уделяется изучению энтропии аналоговых, дискретных, марковских источников информации, исследованию различных видов кодов, разработке математической модели канала передачи информации;
- ядро курса составляет фундаментальная теория информации;
- для успешного изучения курса студенту необходимо знать основы теории вероятностей и математической статистки, основы информатики, основы дискретной математики, теорию радиотехнических цепей и сигналов;
- в курсе закрепляются такие общепредметные умения как классификация (задач теории информации, типов кодирования сигналов и систем передачи информации, условий их функционирования, методов расчета), оценивание (результатов расчета), моделирование ( процессов функционирования сложных систем с целью определения их показателей), абстрагирование (при выборе модели расчета показателей реальной системы);
- курс имеет практическую часть (лабораторные работы - 17 часов и расчетно-графическое задание - 17 часов). Студенты применяют теоретические положения для анализа конкретных систем. Часть заданий меняется, имея нестандартный проблемный характер;
- оценка знаний и умений студентов проводится с помощью итогового теста, который включает в себя 32 вопроса по основным проблемам курса.
2. ТРЕБОВАНИЯ государственного образовательного стандарта (ГОС) К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКА ПО СПЕЦИАЛЬНОСТИ 075500 – КОМПЛЕКСНОЕ ОБЕСПЕЧЕНИЕ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ АВТОМАТИЗИРОВАННЫХ СИСТЕМ.
Специальность утверждена приказами Минобразования России №2719 от 30.12.1997 г., № 686 от 2.03.2000 г. и №1010 от 6.04.2000 г.
Требования к профессиональной подготовленности специалиста.
Выпускник должен уметь решать задачи, соответствующие его квалификации, указанные в п.1.3 настоящего государственного образовательного стандарта.
Специалист по защите информации должен уметь:
- решать основные задачи на вычисление пределов функций, их дифференцирование и интегрирование, на разложение функций в ряды, включая оценку качества полученных решений прикладных задач; решать простые обыкновенные дифференциальных уравнения и линейные системы уравнений;
- оперировать с элементами числовых и конечных полей, колец, подстановками, многочленами, матрицами; решать системы уравнений над полями и кольцами вычетов;
- исследовать простейшие геометрические объекты по их уравнениям в различных системах координат; описывать строение основных классов геометрических групп;
- применять стандартные методы и модели к решению типовых теоретико-вероятностных задач и стандартных задач математической статистики; использовать стандартные статистические пакеты и давать содержательное объяснение получаемым результатам;
- работать на современных ПЭВМ на уровне пользователя под управлением основных операционных систем;
- применять на практике основные законы общей физики и оценивать численные порядки величин, характерных для различных разделов естествознания;
- использовать современные средства разработки программного обеспечения, включая современный пользовательский интерфейс, на языках высокого уровня и языках СУБД, библиотеки объектов и классов для решения задач создания и сопровождения автоматизированных систем;
- выявлять возможные способы нарушения информационной безопасности при работе автоматизированных систем обработки информации и использовать средства и возможности современных ЭВМ и их сетей, микропроцессоров, операционных систем, СУБД для проектирования и реализации средств обеспечения информационной безопасности;
- реализовывать основные структуры данных на языках программирования высокого уровня;
- эффективно программировать основные алгоритмы сортировки и поиска на языках программирования высокого уровня;
- выбирать оптимальные в конкретных условиях структуры данных и алгоритмы;
- анализировать основные механизмы, реализованные в современных операционных системах и СУБД, и модифицировать их для решения задач обеспечения информационной безопасности;
- проектировать базы данных и распределенные системы обработки информации, обладающие требуемыми характеристиками обеспечения безопасности данных;
- анализировать технологии обработки данных в распределенных системах с целью оптимизации их производительности и повышения надежности функционирования;
- в рамках задач обеспечения информационной безопасности решать вопросы использования радиоэлектронной аппаратуры и других технических средств;
- применять основные методы анализа радиоэлектронных систем, составляющих техническую базу комплексных систем обеспечения информационной безопасности;
- ставить задачи и интерпретировать результаты проведения специальных измерений с использованием технических средств контроля характеристик автоматизированных систем;
- применять типовые методы проектирования и оценки эффективности сложных систем в области своей деятельности, применять стандарты по оценке защищенности автоматизированных систем при их анализе и проектировании;
- применять действующую законодательную базу в области информационной безопасности для обеспечения необходимых действий профессиональной деятельности, применять правовые акты в области информационной безопасности и защиты государственной тайны в конкретной сфере деятельности, включая адекватные организационные меры;
- применять стандартные криптографические решения для защиты информации и квалифицированно оценивать их качество;
- используя современные методы и средства разрабатывать и оценивать модели и политику безопасности;
- реализовывать системы защиты информации в автоматизированных системах в соответствии со стандартами по оценке защищенных систем;
- практически решать задачи защиты программ и данных программно-аппаратными средствами и давать оценку качества предлагаемых решений;
- определять и измерять параметры опасных сигналов для технических каналов утечки информации и определять эффективность защиты от утечки информации;
- применять системный подход к обеспечению информационной безопасности в различных сферах деятельности, включая комплекс организационных мер, учитывающих особенности функционирования предприятия и решаемых им задач;
- проектировать и реализовывать комплексную систему защиты информации оценивать ее качество
3. Цели курса.
| Но-мер цели | Содержание цели | |
| Студент будет иметь представление: | ||
| 1 | о задачах, решаемых на базисе знаний теории информации. | |
| 2 | о различиях в подходах к решению вопросов передачи информации с наименьшими потерями по каналу связи. | |
| 3 | о возможных последствиях из–за несогласованности источника информации с пропускной способностью канала. | |
| 4 | О прикладных вопросах теории теории информации, интенсивно развиваемых в настоящее время применительно к IP телефонии, передаче изображения и звука по цифровым каналам. | |
| 5 | о вопросах помехоустойчивого кодирования, решаемых для конкретных систем. | |
| Студент будет знать: | ||
| 6 | объект курса (обеспечение информационной безопасности ее элементный состав), предмет курса (возможности источников информации и возможности информационного канала), задачи курса (выбор показателей количества информации и пропускной способности канала и методов их расчета.), место теории информации, как базовой дисциплины для других курсов. | |
| 7 | понятие количественной меры информации, КОЛИЧЕСТВЕННЫЕ ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ ИСТОЧНИКОВ СООБЩЕНИЙ И КАНАЛОВ. | |
| 8 | понятие условной энтропии и взаимной информации. | |
| 9 | понятие дискретного источника сообщений с памятью, понятие избыточности дискретного источника сообщений, понятие производительности источника дискретных сообщений и скорости передачи информации | |
| 10 | Теорему Шеннона для канала без шума | |
| 11 | Математическую модель дискретизированного сигнала и спектр дискретизированного сигнала. | |
| Студент будет уметь: | ||
| 12 | согласовать дискретный источник с дискретным каналом | |
| 13 | согласовать дискретный источник с дискретным каналом с шумом. | |
| 14 | построить помехоустойчивые коды, учитывая информационный предел избыточности | |
| 15 | выбирать, параметры квантования и дискретизации для непрерывного сообщения. | |
| 16 | Применять теорему Котельникова. | |
| 17 | оценить ошибки дискретизации и квантования | |
| | Оценить информацию в непрерывных сообщениях, то есть энтропию и -производительность источника непрерывных сообщений | |
| 18 | Определить пропускную способность непрерывного канала. | |
| 19 | Использовать информационный подход к оценке качества функционирования систем связи | |
4. Содержание курса
| Ссылки на цели курса | Часы | Темы лекционных занятий |
| 1,2,3,4 | 1 | Введение. Предмет и задачи курса. Математический аппарат теории информации |
| 7,8 | 4 | Энтропия. Количественная мера информации. Основные свойства энтропии. |
| 9 | 4 | Основные теоремы теории информации Аксиомы Хинчина и Фаддеева. |
| 8 | 4 | Условная энтропия. |
| 8,9 | 4 | Взаимная информация и её свойства. Источники информации; энтропия источников; дискретный источник без памяти.. |
| 10 | 4 | Теорема Шеннона об источниках. |
| 6,7,9 | 2 | Марковские и эргодические источники; информационная дивергенция; граница Симмонса. |
| 9,11,12, 13,14 | 4 | Оптимальное кодирование; префиксные коды; неравенство Крафта. |
| 13,14 | 2 | Линейные коды; параметры кодов и их границы ; корректирующие свойства кодов; циклические коды; БЧХ- коды; код Хемминга; сверточные коды. |
| 11 | 4 | Математическая модель канала связи; пропускная способность канала связи; прямая и обратная теоремы кодирования. . |
| 1…….19 | 1 | Применение теории информации для синтеза систем, обеспечивающих высокую достоверность приема информационных сигналов. |
5. ТЕМЫ ЛАБОРАТОРНЫЧ РАБОТ
| Ссылки на цели курса | Часы | Темы лабораторных занятий |
| 3,7,16 | 5 | Временные и спектральные характеристики дискретных сигналов |
| 3,6,7,8 | 4 | Исследование характеристик каналов передачи информации на моделях каналов. |
| 3,9,12 | 4 | Прохождение дискретной информации по каналам без шумов. |
| 3,10,13, 18 | 4 | Прохождение дискретной информации по каналам с шумами. |
6. КОНТРОЛЬНЫЙ ОПРОС
Контрольный опрос по теме № 1
1. Доказать формулу полной вероятности
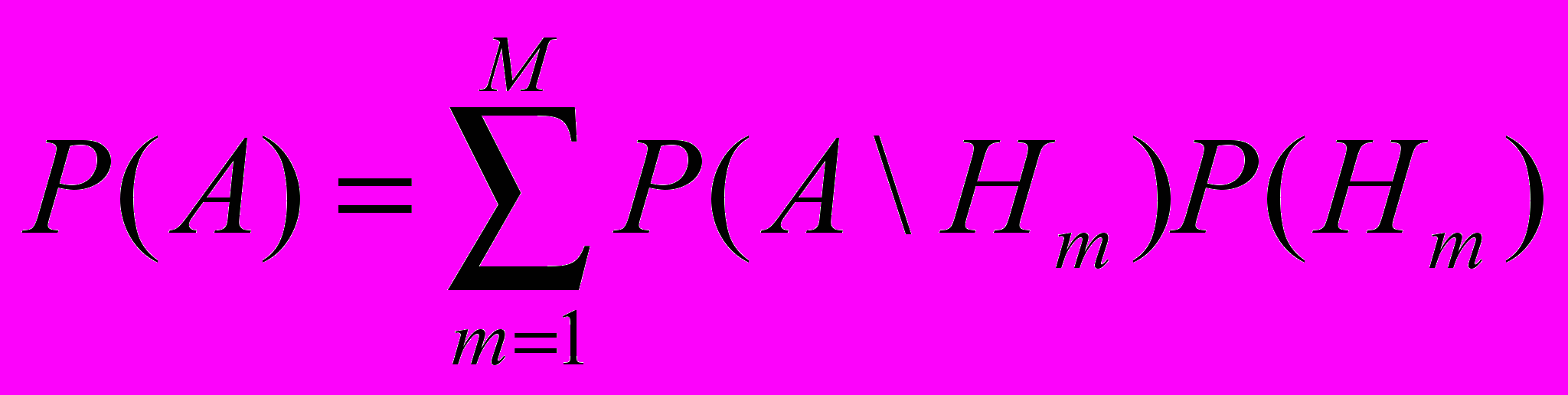
2. Доказать формулу апостериорной вероятности (формулу Байеса)
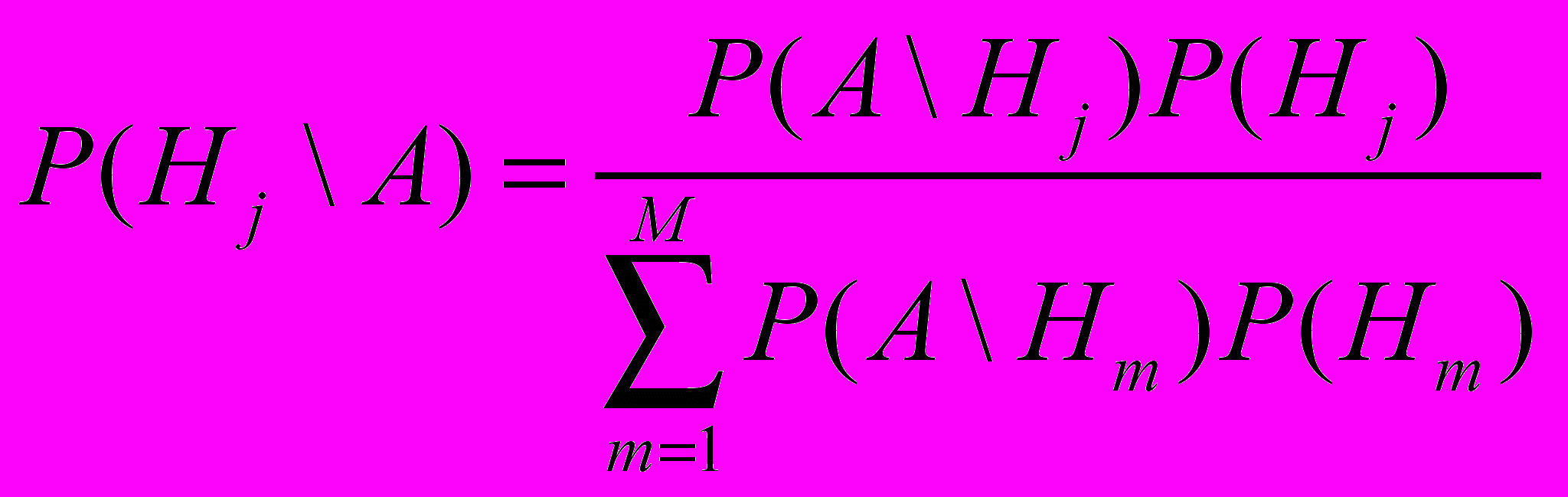
3. Доказать, что для любых случайных величин x и у
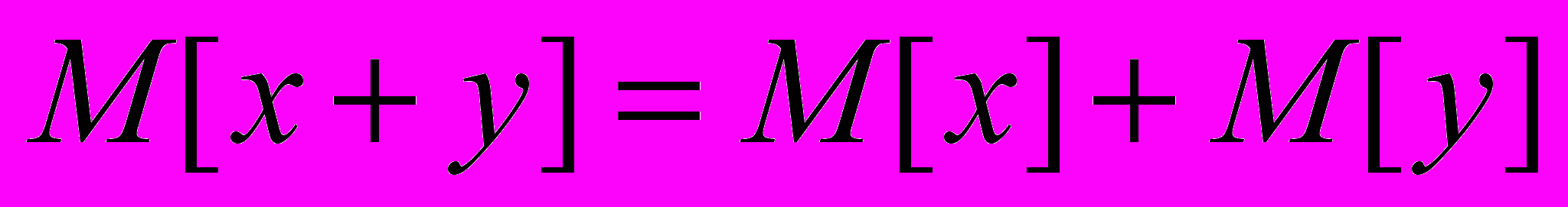
4. Доказать, что если с - константа, х - случайная величина, то
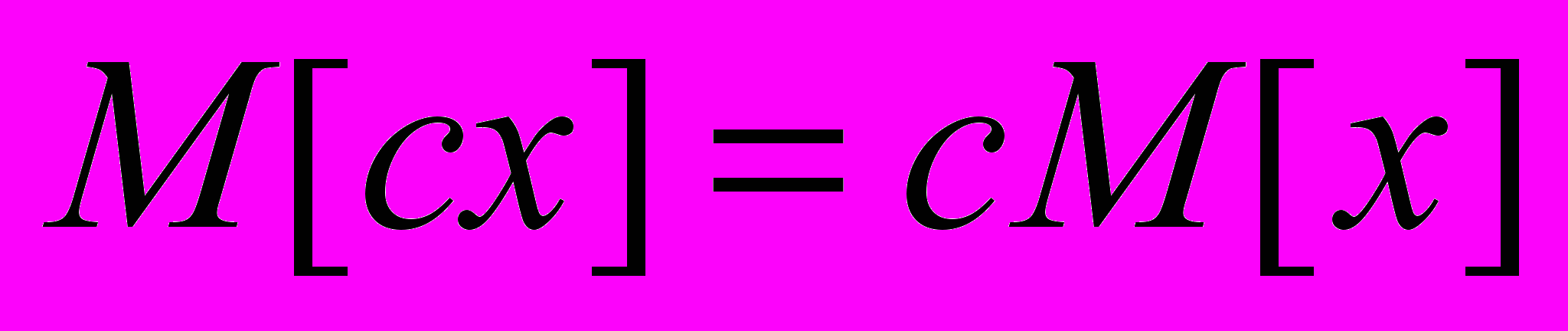
5. Доказать, что если х и у - независимые случайные величины, то
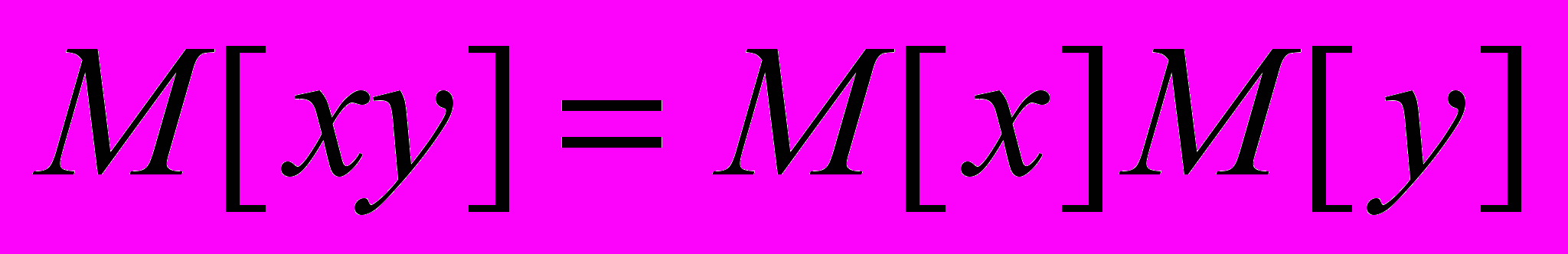
6. Доказать, что для некоррелированных случайных величин х и у
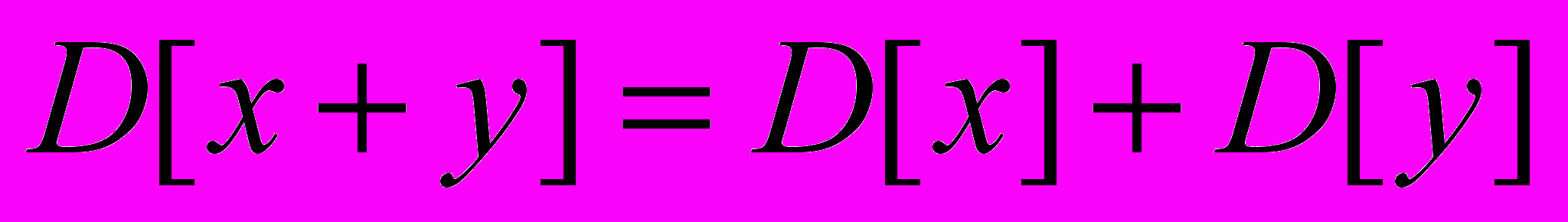 .
.7. Доказать, что если с - константа, х - случайная величина, то
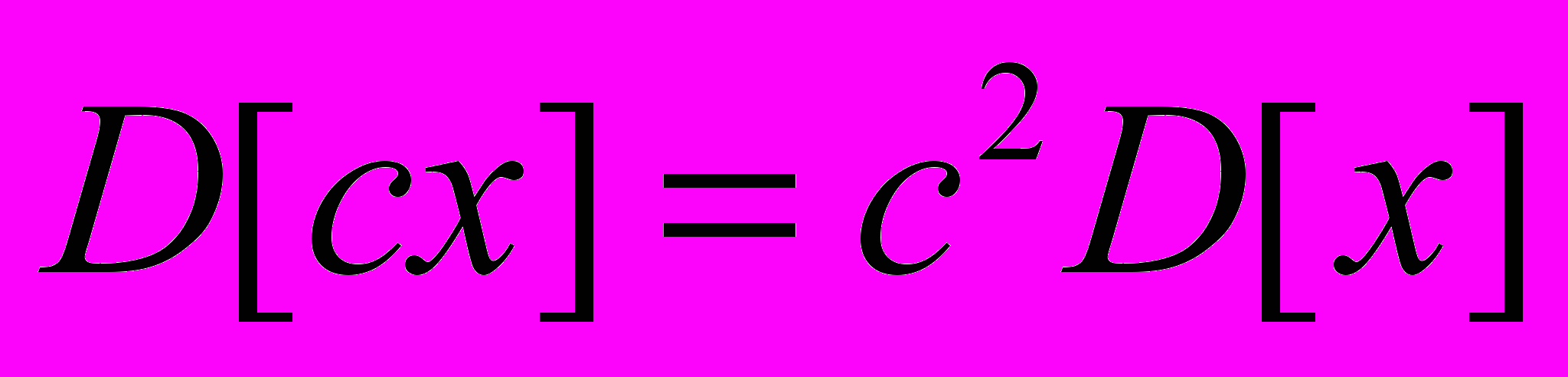
8. Доказать, что если с - константа, х - случайная величина, то D[c+A-]=D[.v].
9. Доказать, что если -х и у независимы то К(х, у) = 0, то есть из независимости случайных величин следует их некоррелированность
10. Доказать, что если
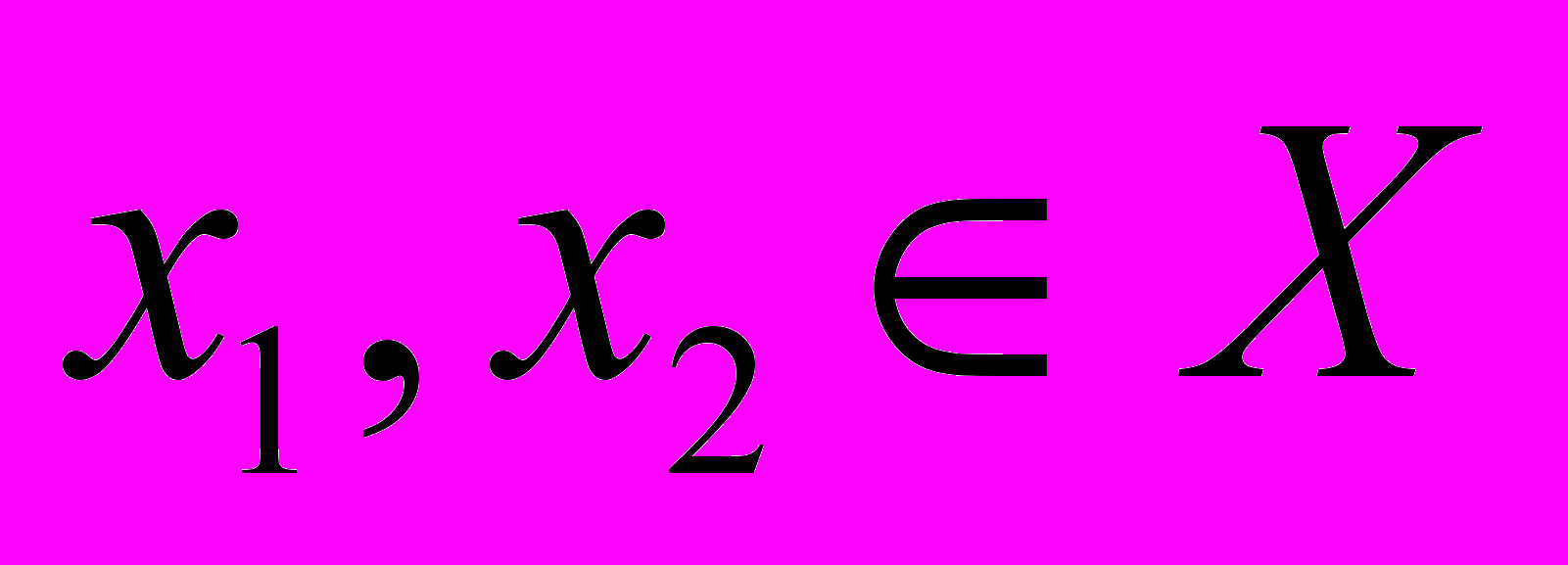 ,
, 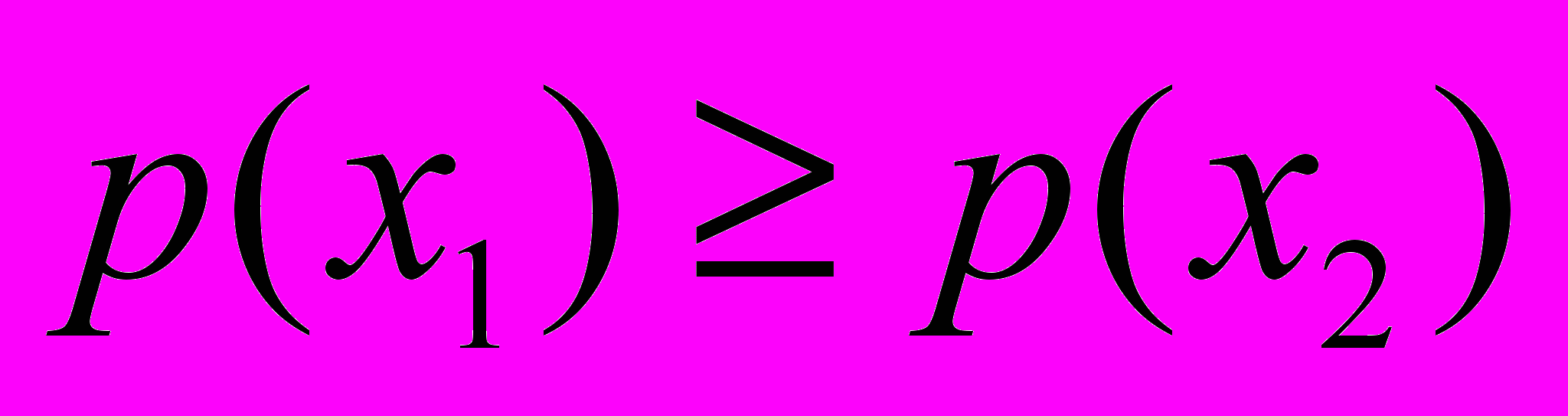 , то
, то 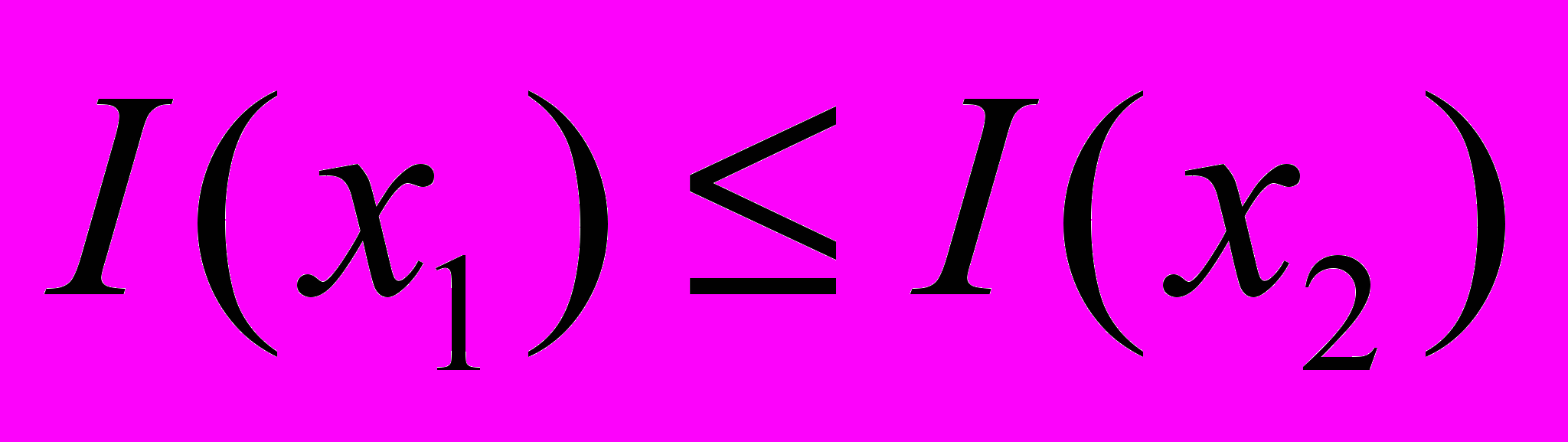
11. Доказать, что для независимых сообщений
 имеет место равенство
имеет место равенство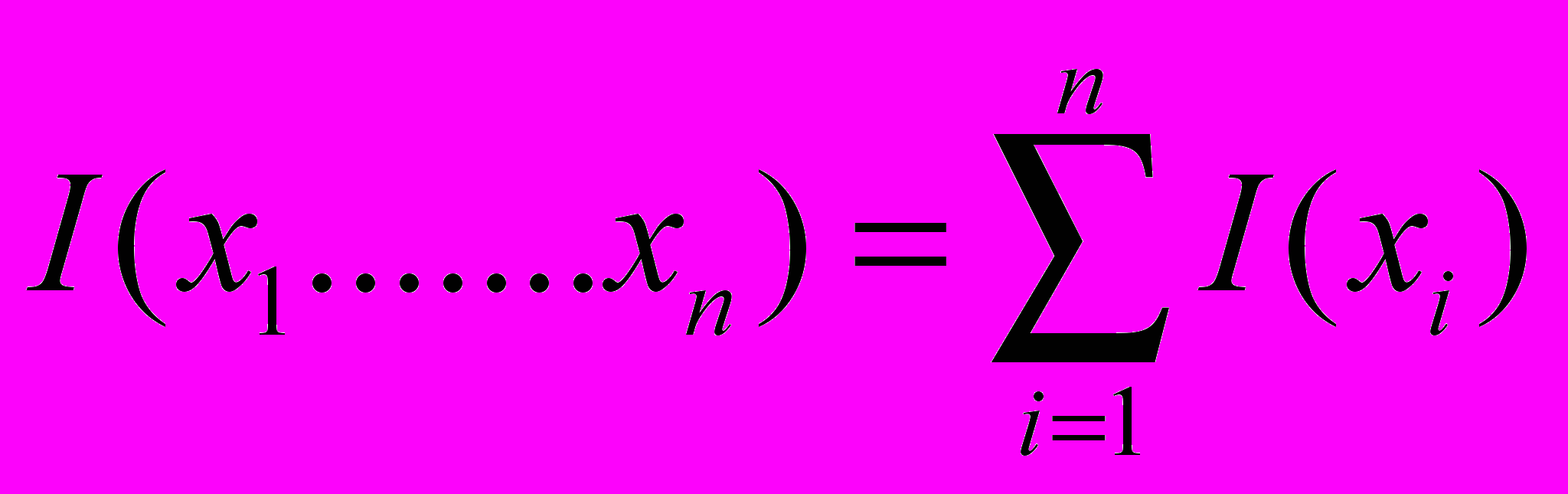
12. Доказать, что
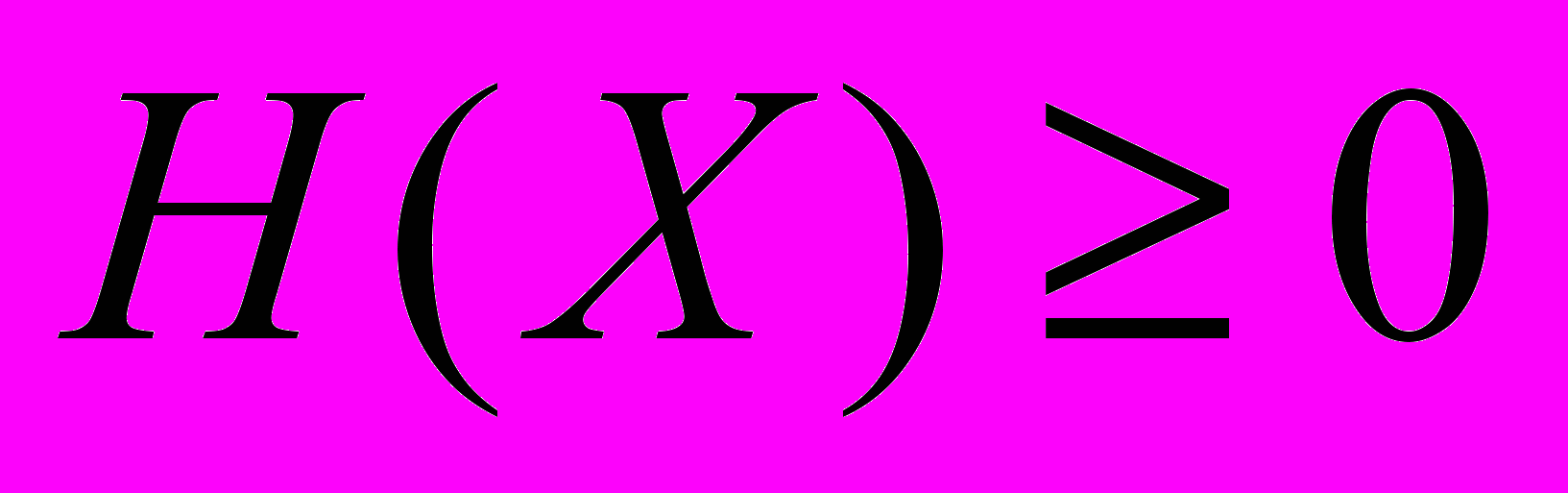
13. Доказать, что
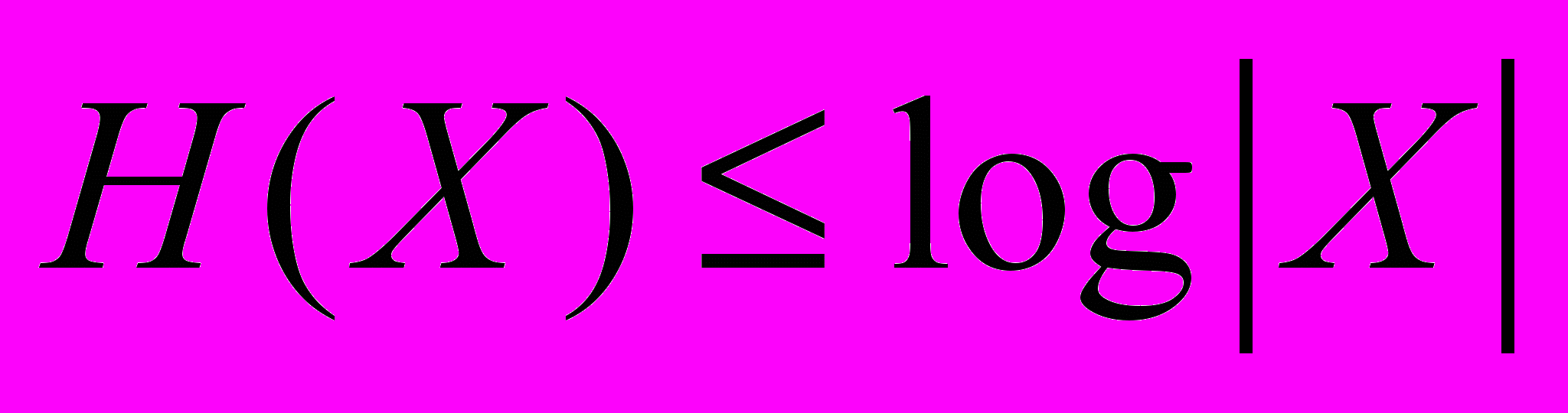 .
.14. Доказать, что
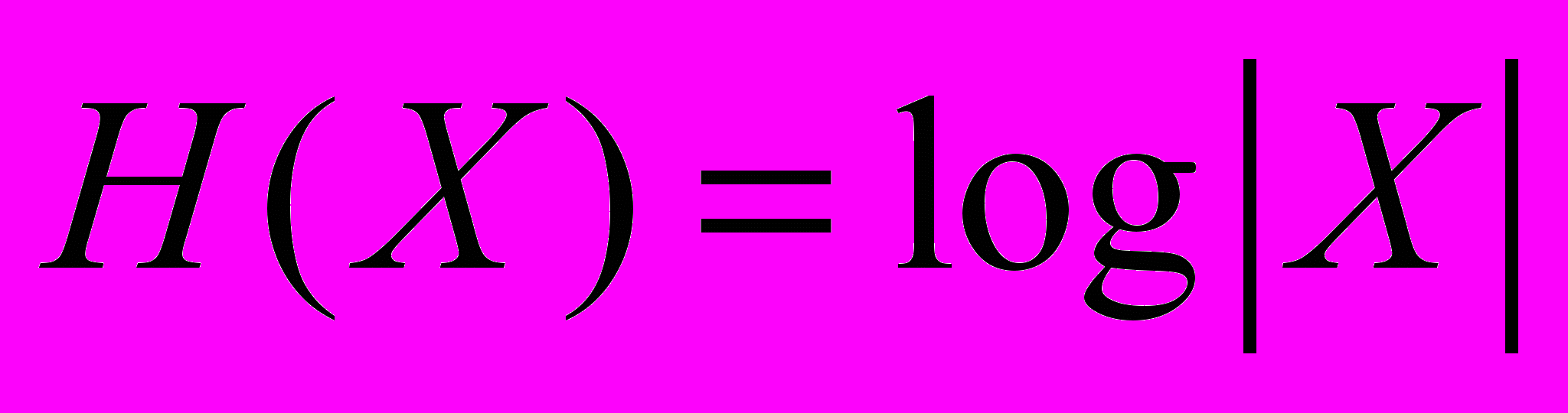 | в том и только в том случае, когда элементы ансамбля Х равновероятны.
| в том и только в том случае, когда элементы ансамбля Х равновероятны.15. Если для двух ансамблей Х и Y распределения вероятностей представляют собой одинаковые наборы чисел (отличаются только порядком следования элементов), то Н(Х)=Н(Y).
16. Если ансамбли Х и Y независимы, то
Н(ХУ)=Н(Х)+Н(Y).
17. Энтропия - выпуклая
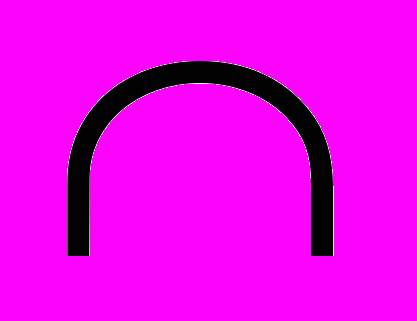 функция распределения вероятностей на элементах ансамбля X.
функция распределения вероятностей на элементах ансамбля X.18. Доказать, что
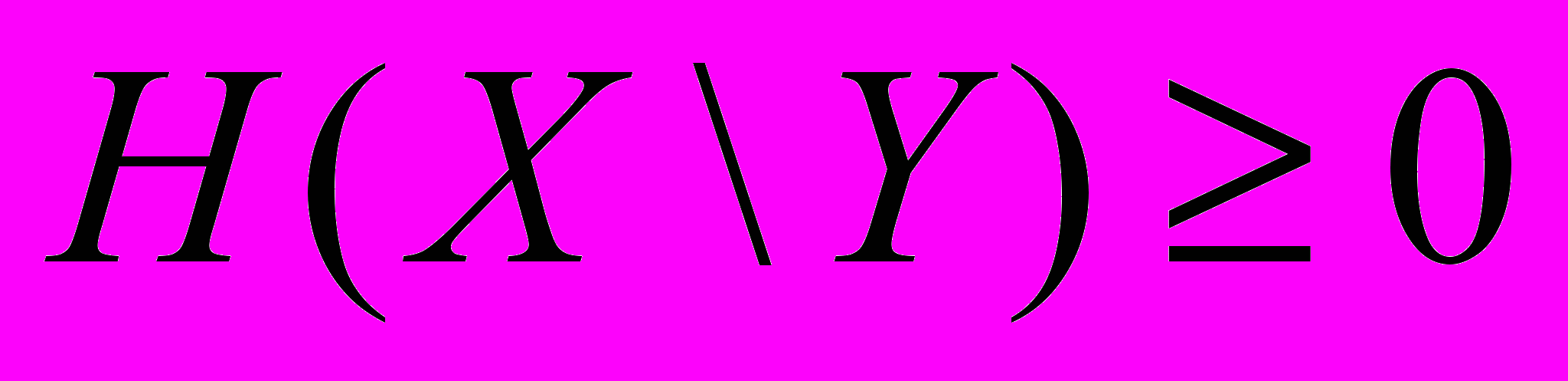
19. Доказать, что
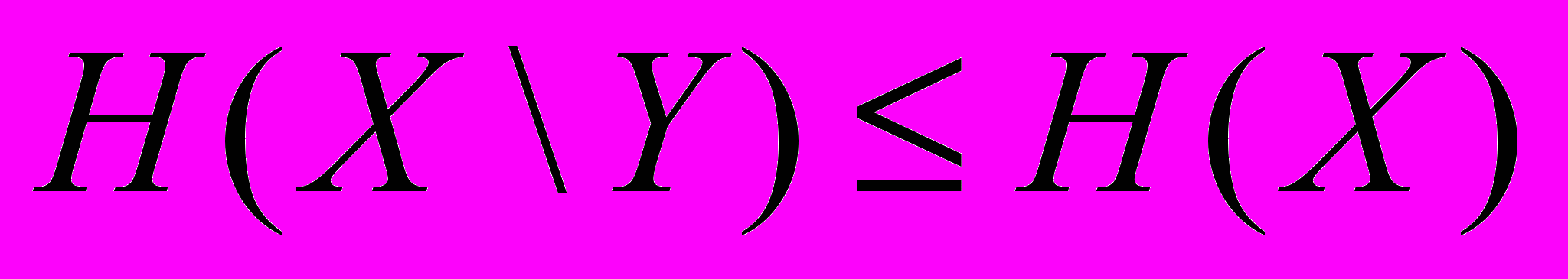 , причем равенство имеет место в том и только в том случае, когда ансамбли Х и У независимы.
, причем равенство имеет место в том и только в том случае, когда ансамбли Х и У независимы.20. Доказать, что
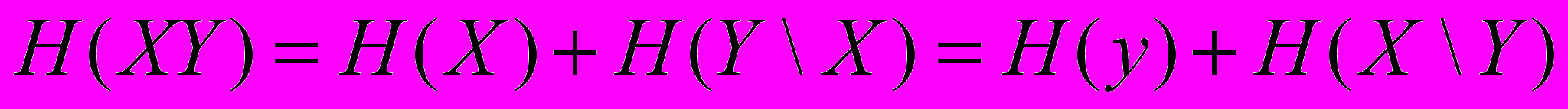
21. Доказать, что
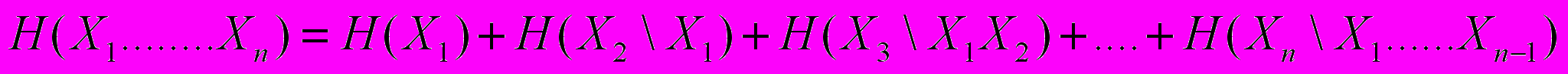
22. Доказать, что
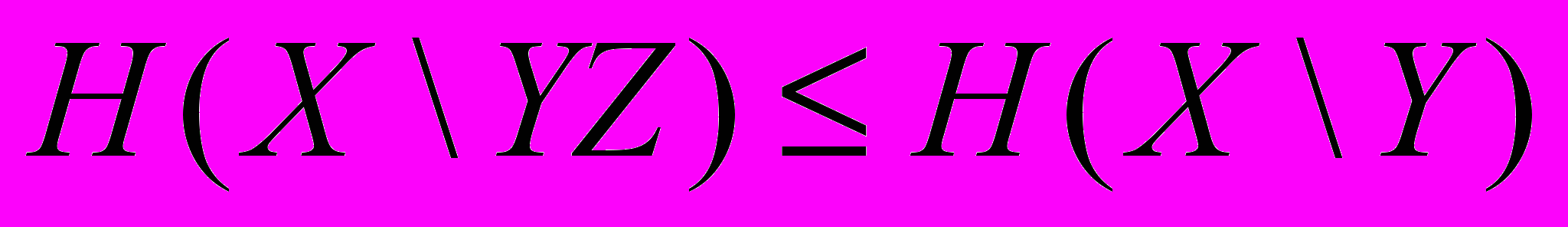
23. Доказать, что сумма выпуклых функций выпукла.
24. Доказать, что произведение выпуклой функции и положительной константы -выпуклая функция.
25. Доказать, что линейная комбинация выпуклых функций с неотрицательными коэффициентами - выпуклая функция.
26. Доказать, что h(p)=- 0 при р = 0.
27. Доказав что
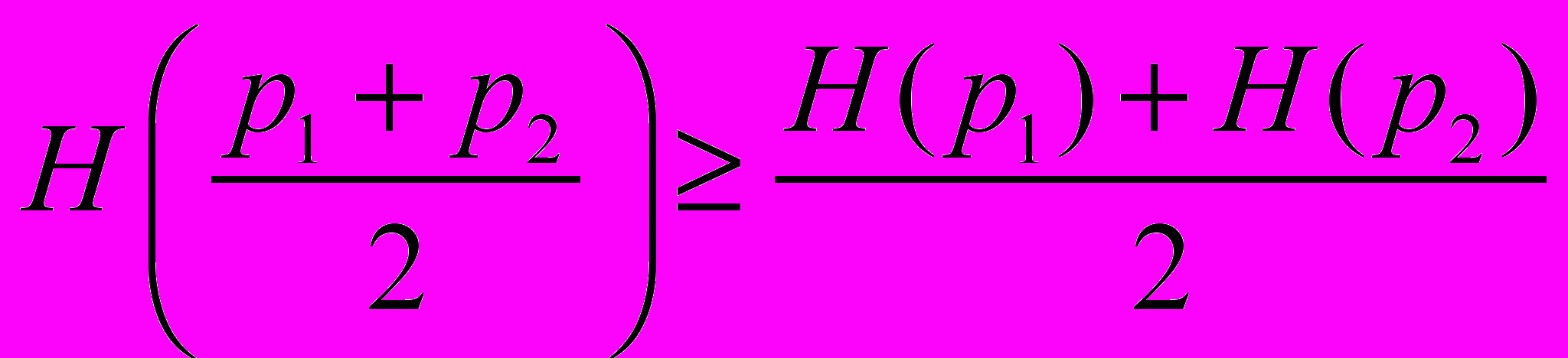
28. Доказать, что
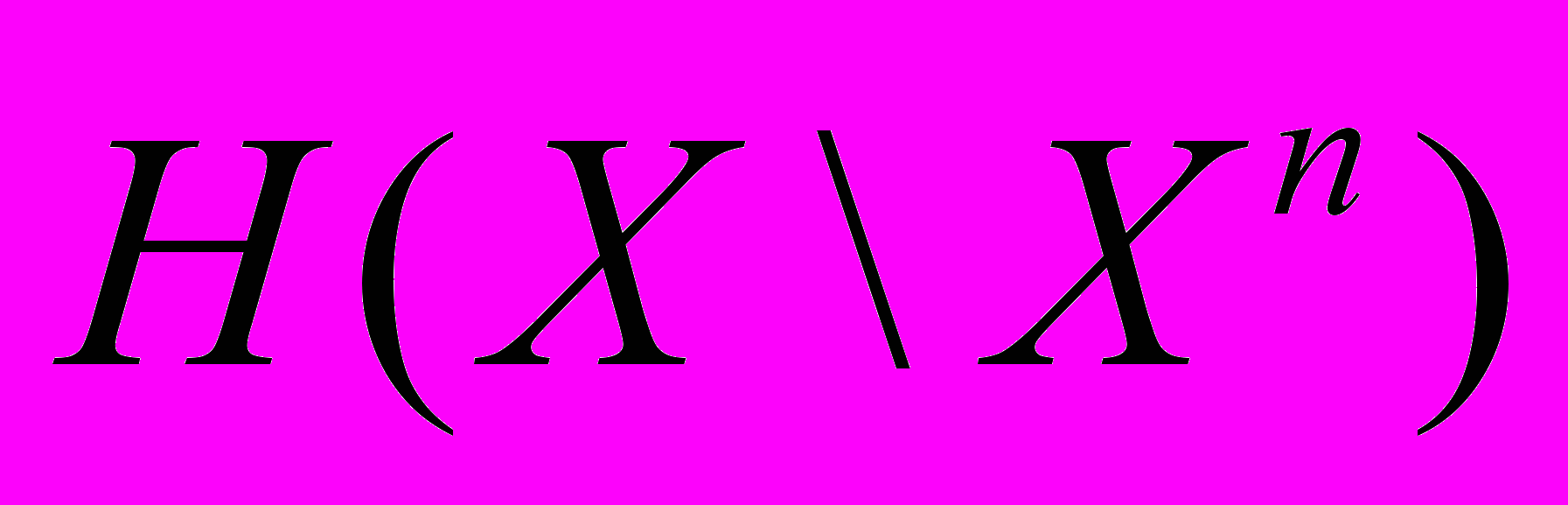 не возрастает с увеличением п.
не возрастает с увеличением п.29. Доказать, что
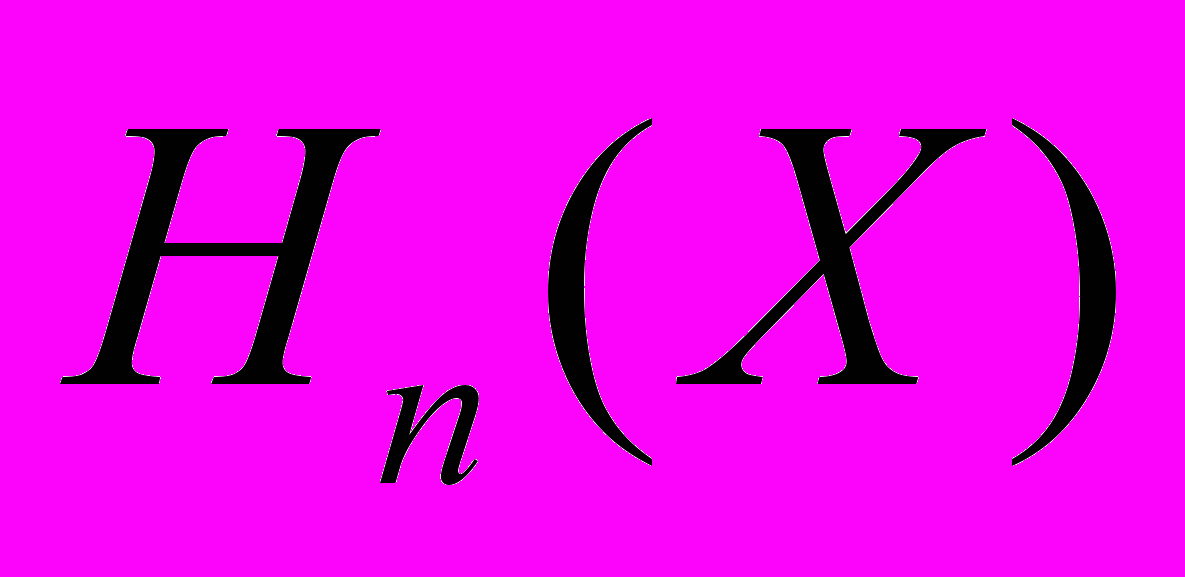 не возрастает с увеличением п.
не возрастает с увеличением п.30. Доказать, что
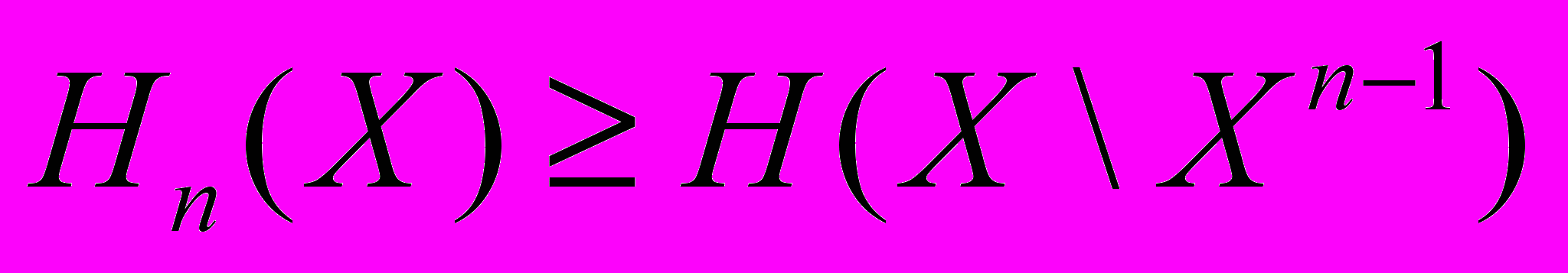
31. Доказать, что
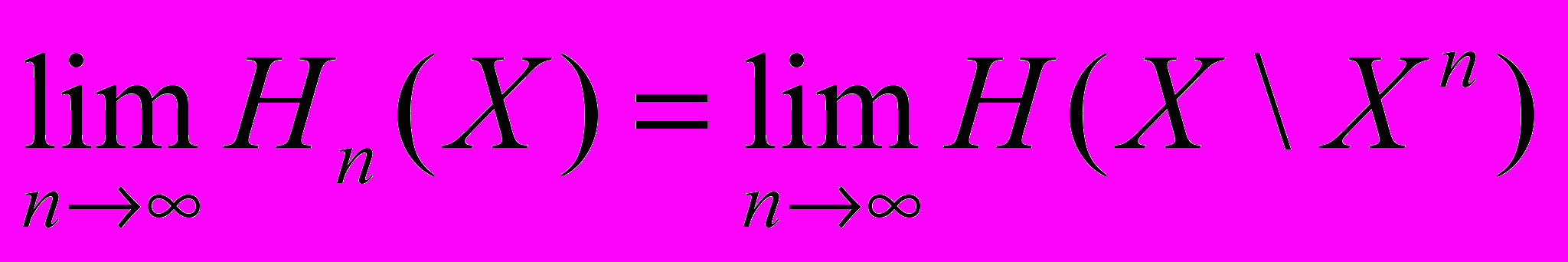
32. Доказать, что для дискретного постоянного источника
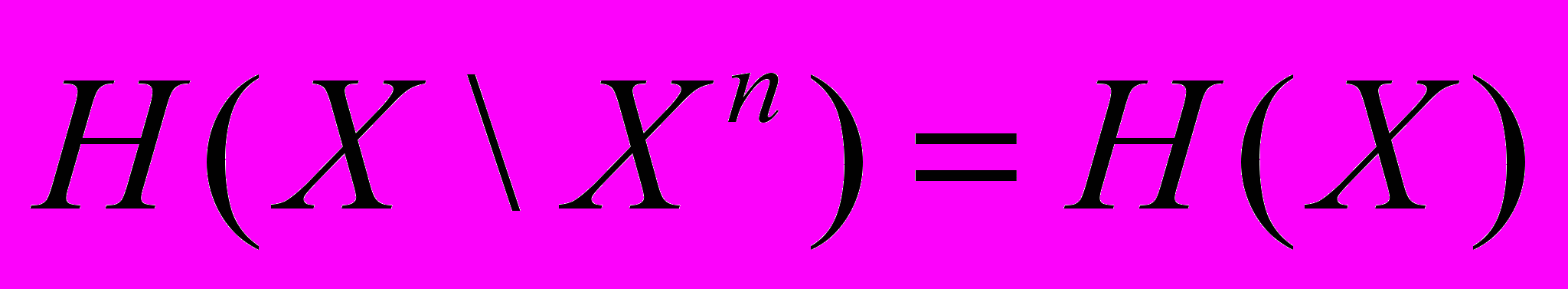
33. Для однородной стационарной цепи Маркова связности s доказать, что
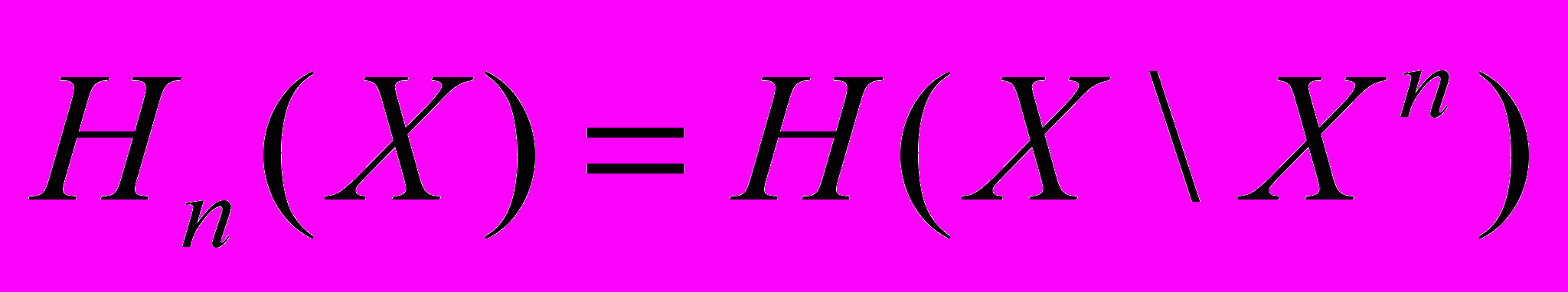
34. Доказать, что для неотрицательной случайной величины
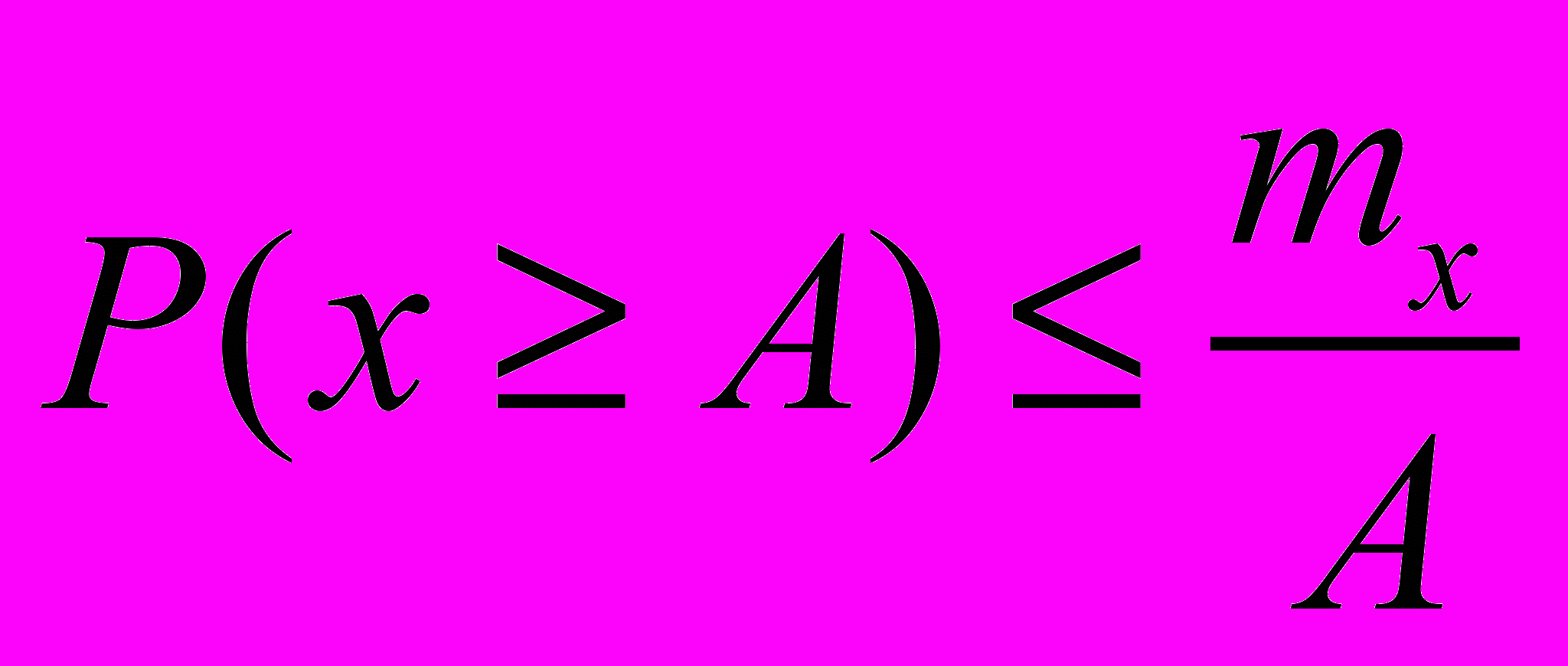
35. Доказать неравенство Чебышева
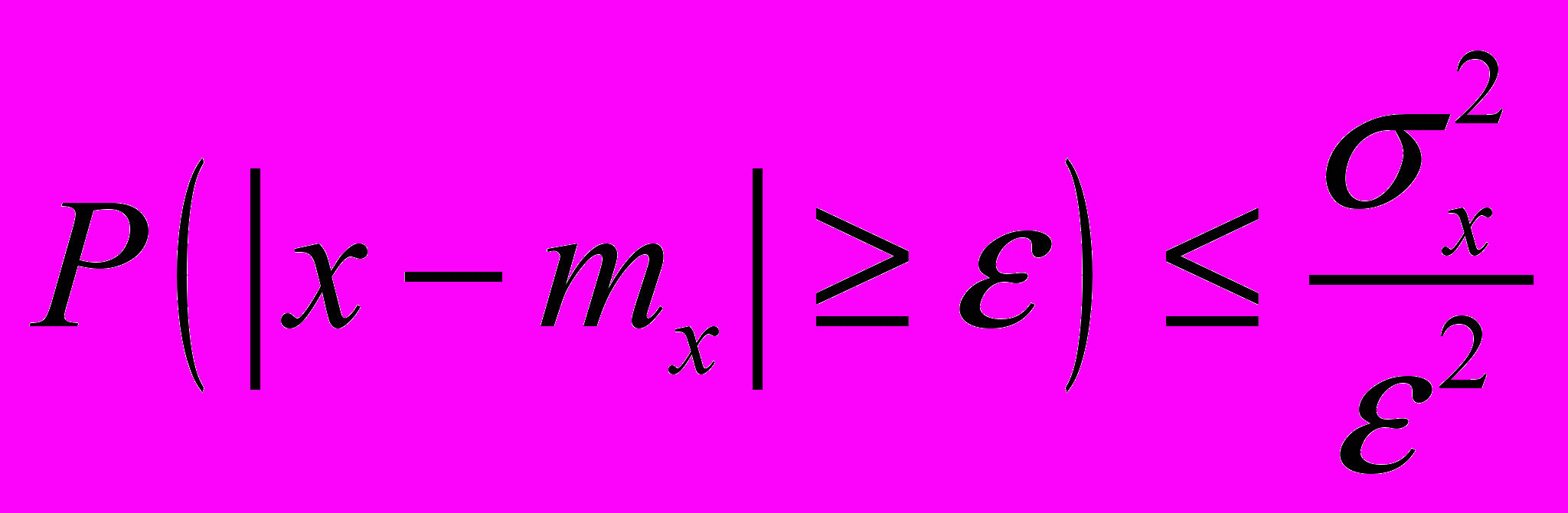
36. Доказать неравенство Чебышева для суммы независимых случайных величин
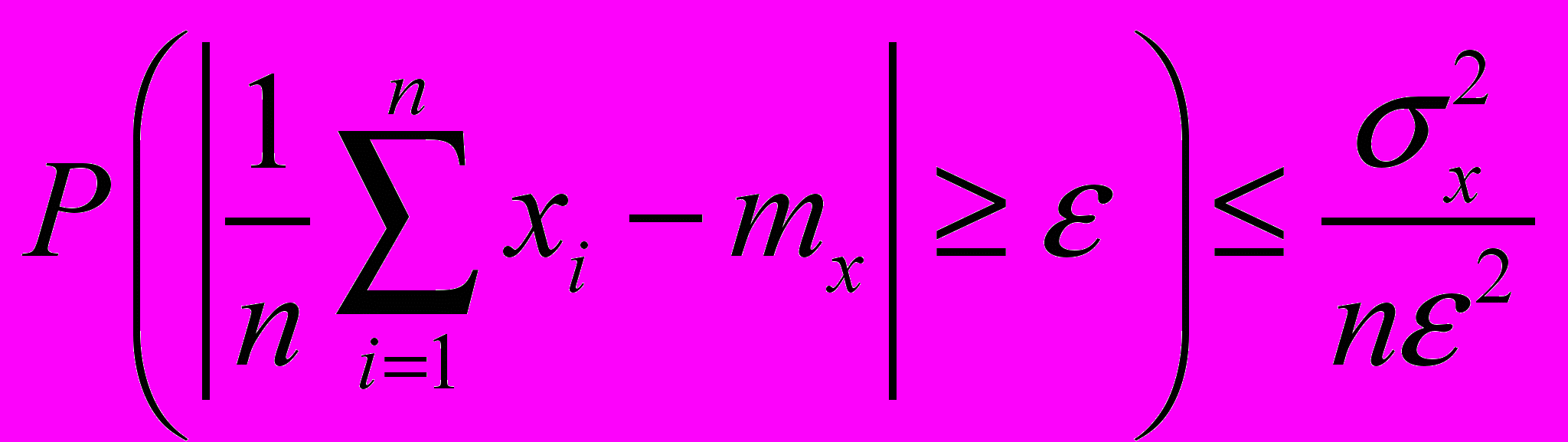
37. Дчя высоковероятного множества
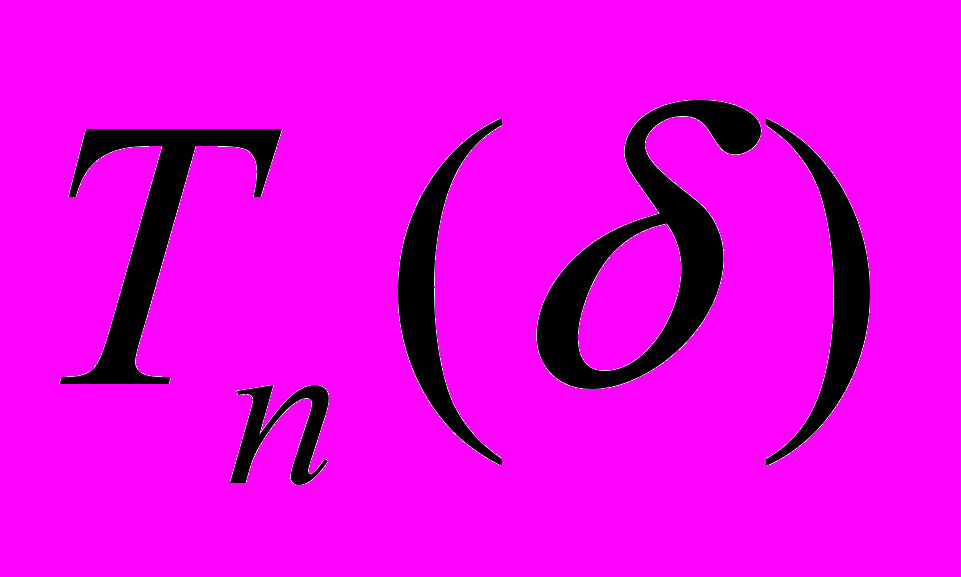 доказать, что
доказать, что 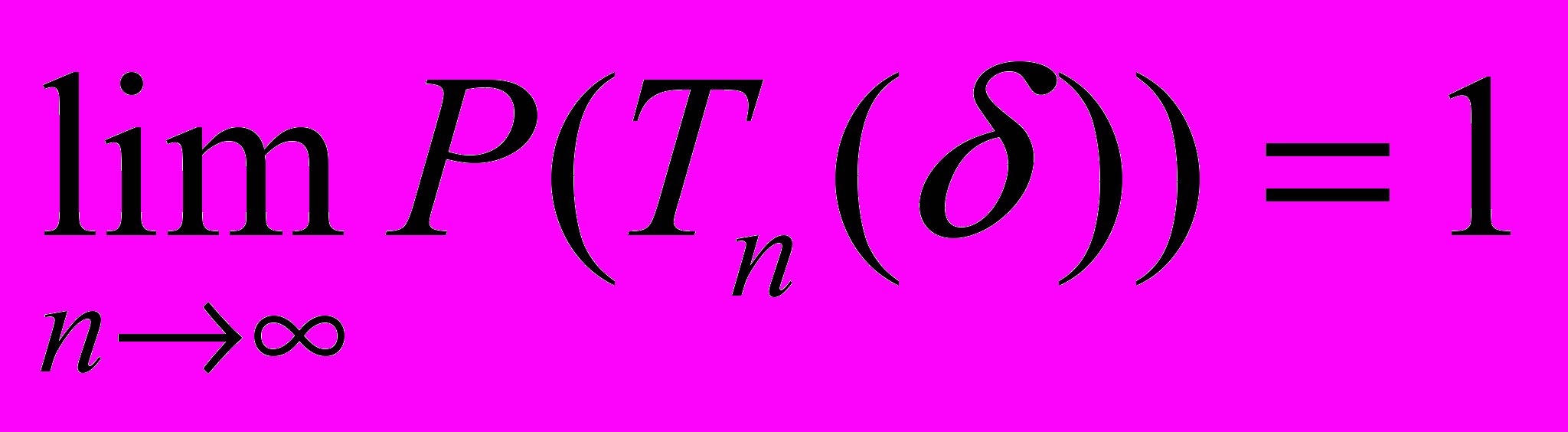
38. Для высоковероятного множества
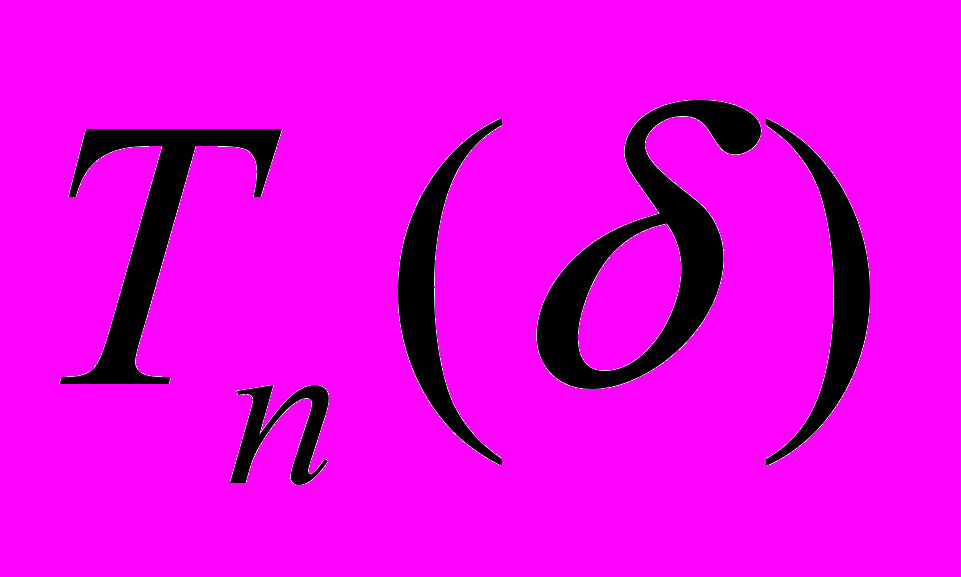 доказать, что
доказать, что 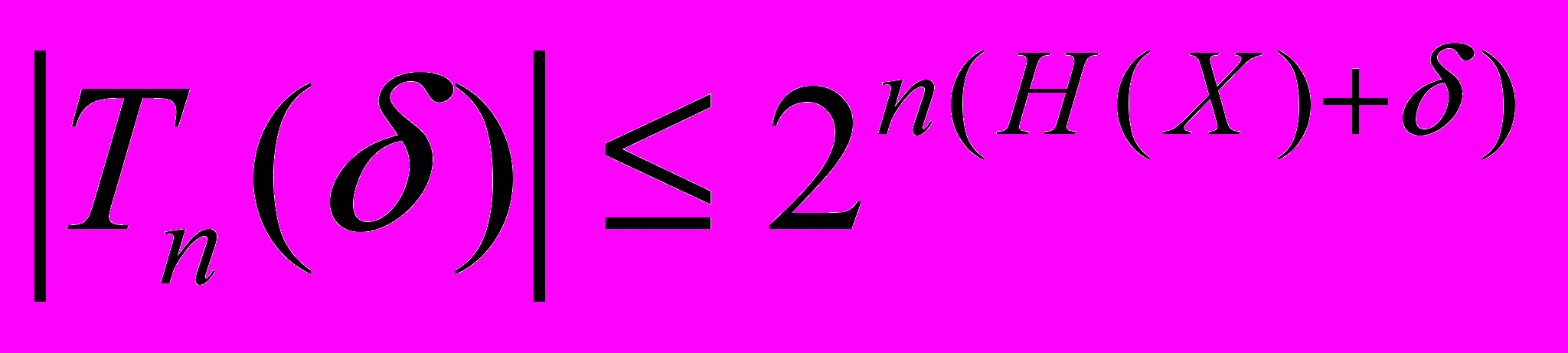
39. Для высоковероятного множества
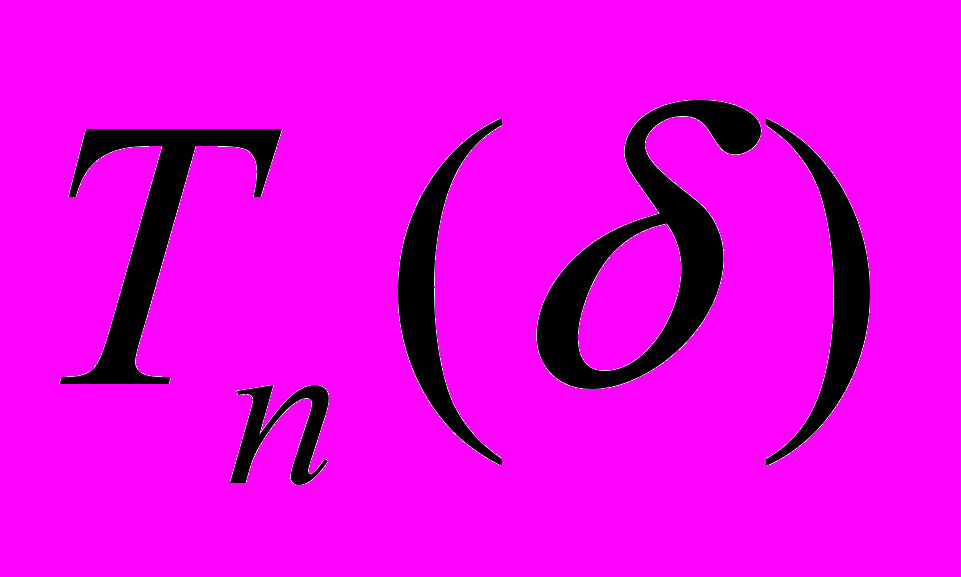 доказать, что
доказать, что 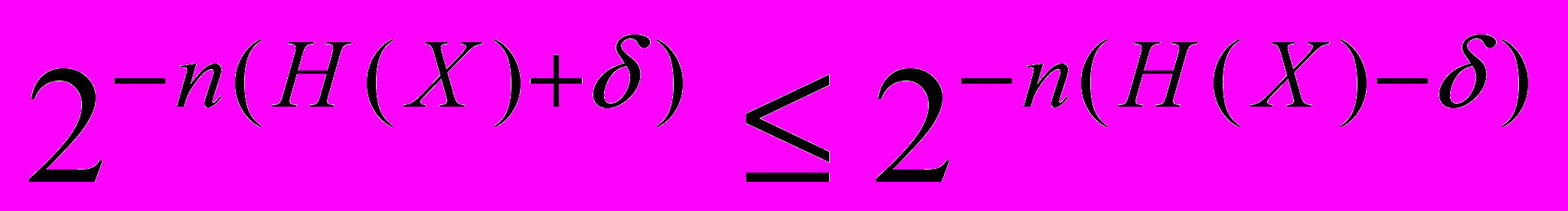 для любого
для любого 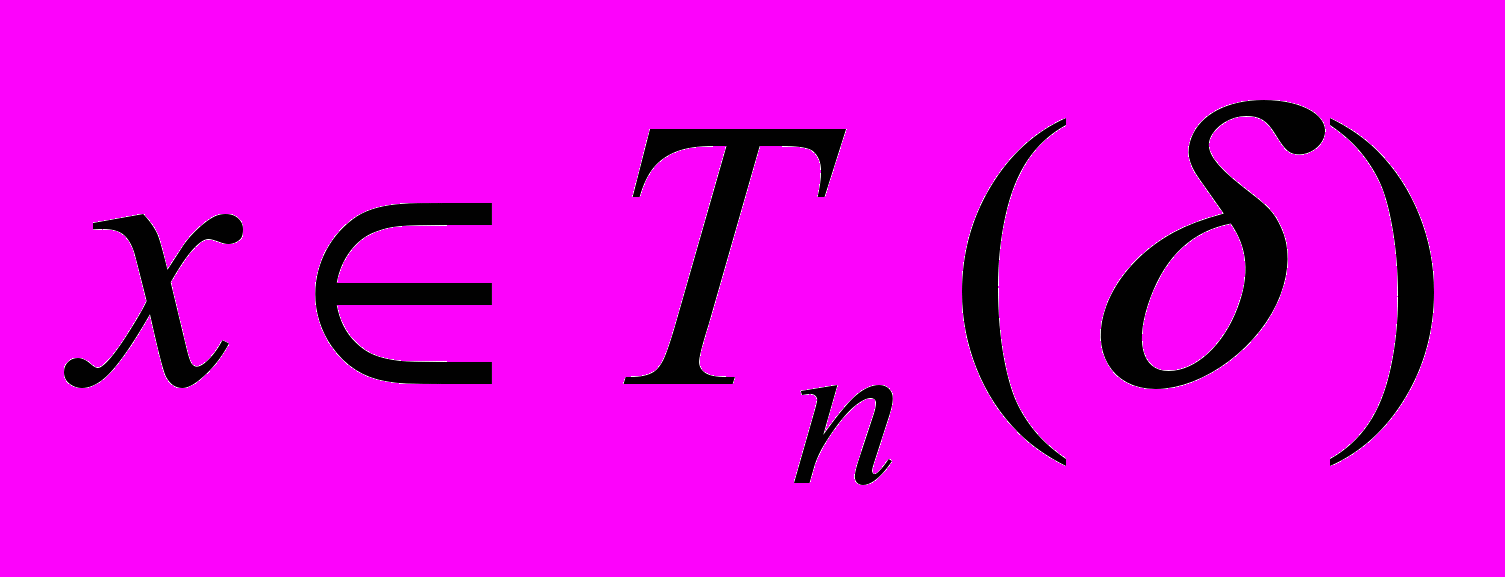
Контрольный опрос №2
1. Доказать неравенство I(X;Y)>0.
2. Доказать неравенство
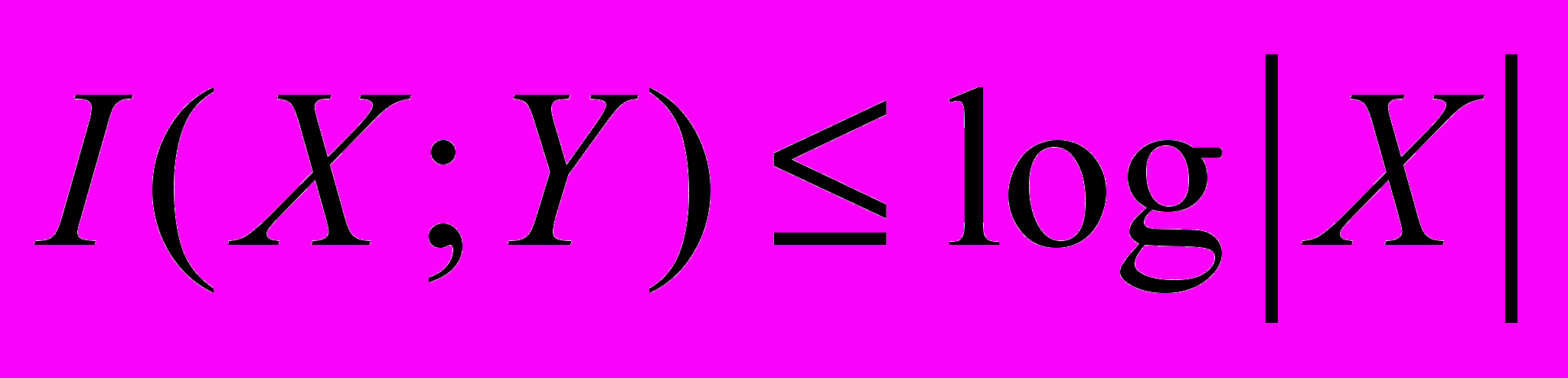
3. Доказать неравенство
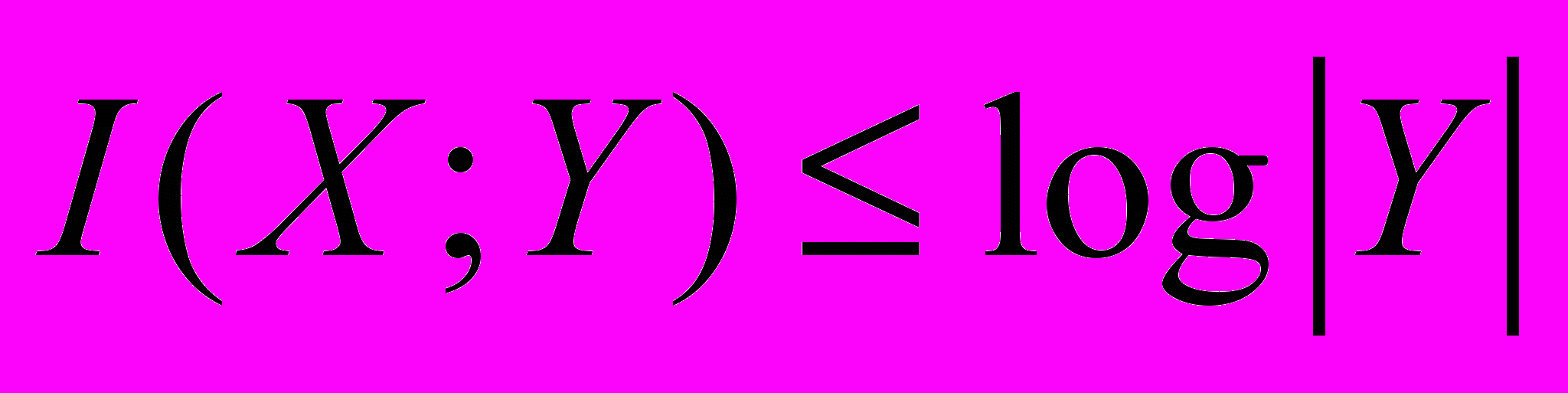 .
.4. Доказать тождество
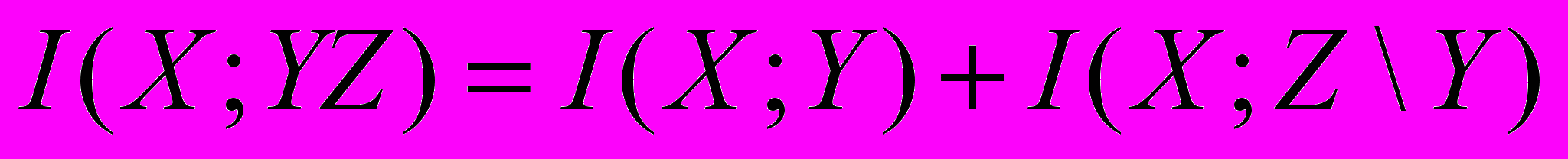
5. Доказать тождество I(X;YZ) = 1(X;Z)+1{Х;У \Z).
6. Доказать неравенство
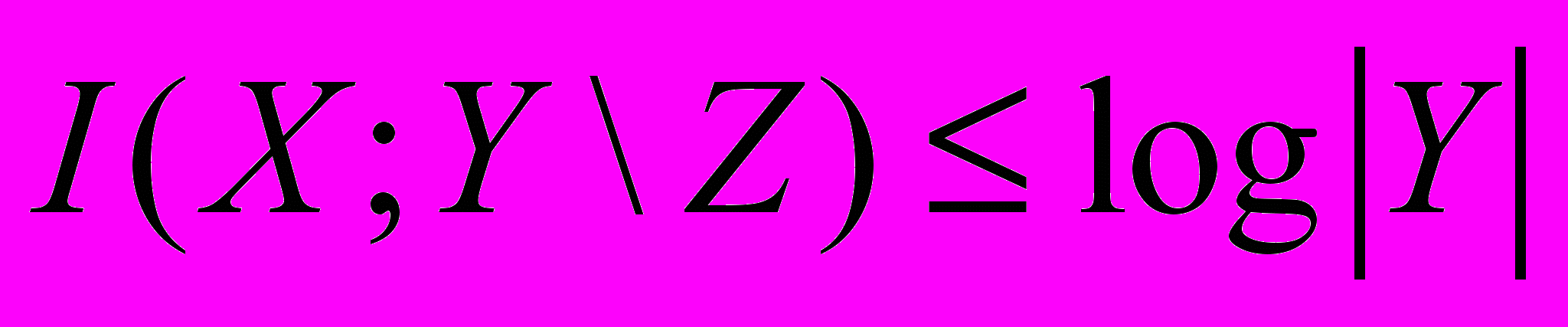
7. Доказать неравенство
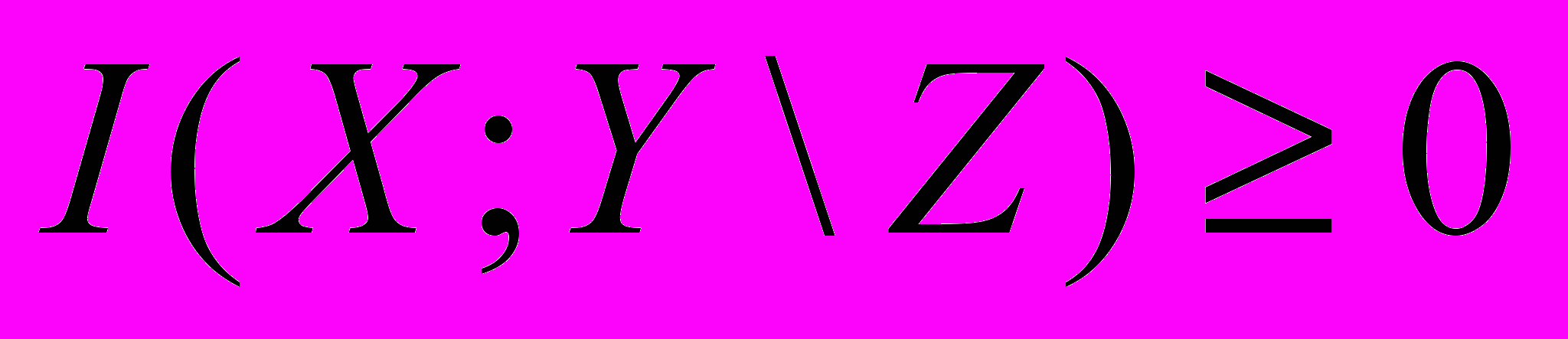
8. Доказать, что для дискретного постоянного канала
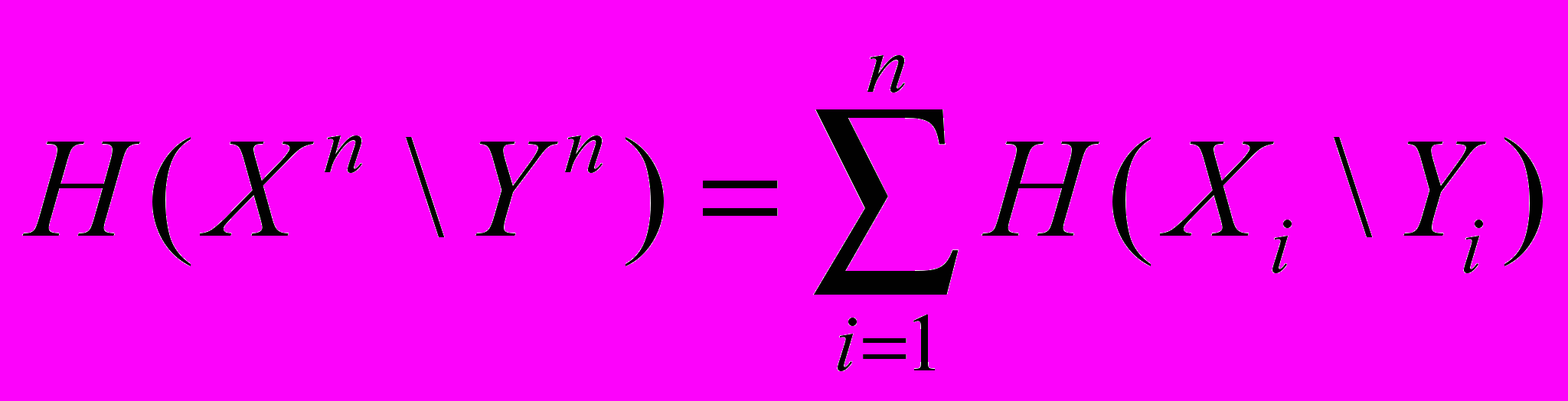
9. Доказать, что для дискретного постоянного канала при передаче последовательности независимых символов
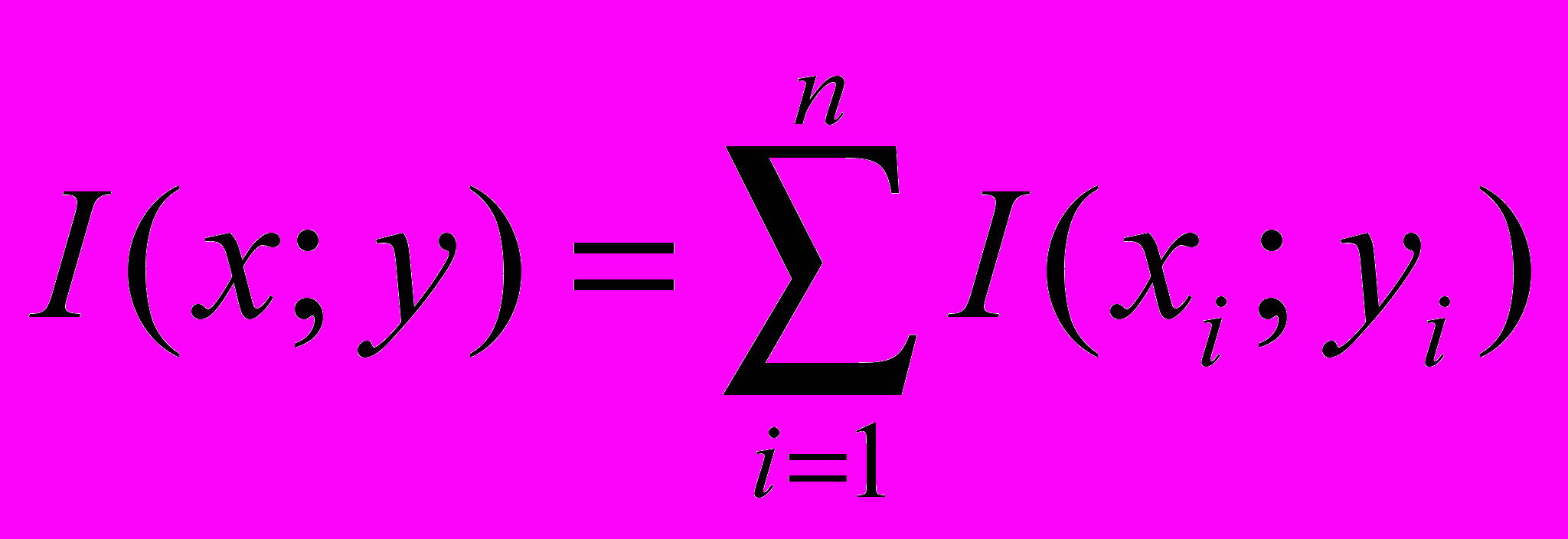
10. Доказать, что
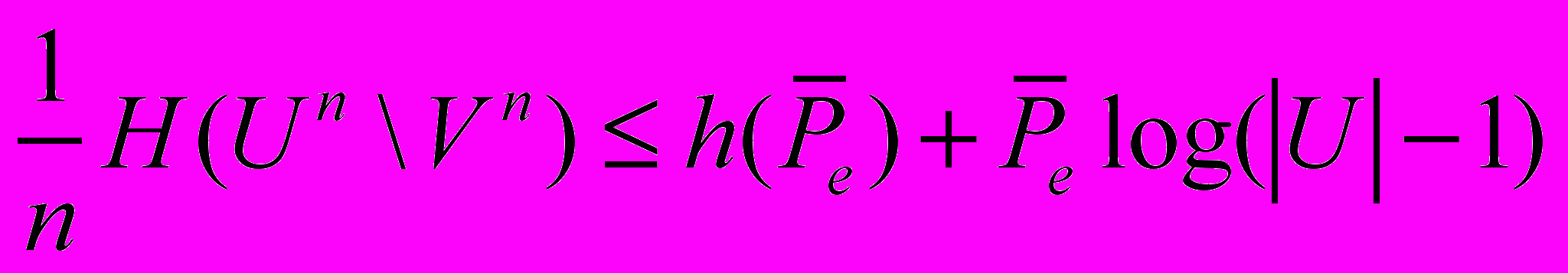
11. Доказать, что для дискретного стационарного канала
без памяти
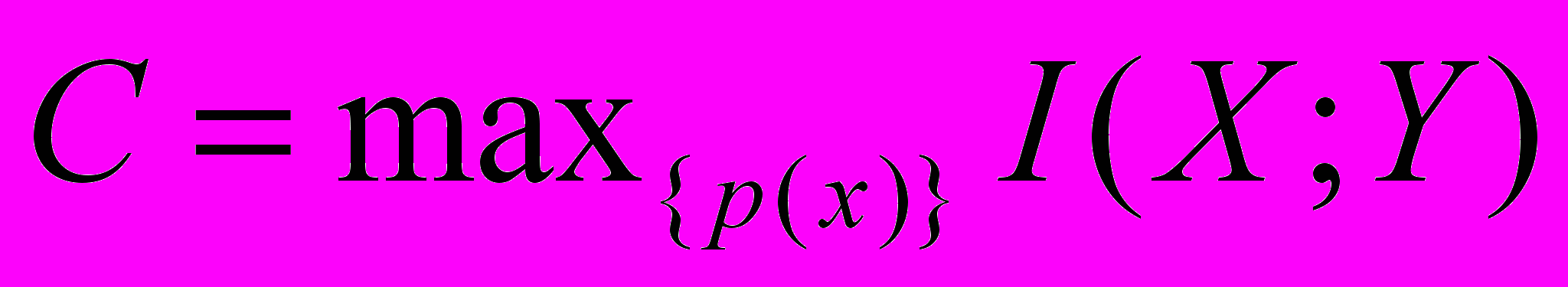
12. Для канала без памяти доказать, что из независимости символов на входе канала следует независимость символов на выходе канала.
13. Доказать, что
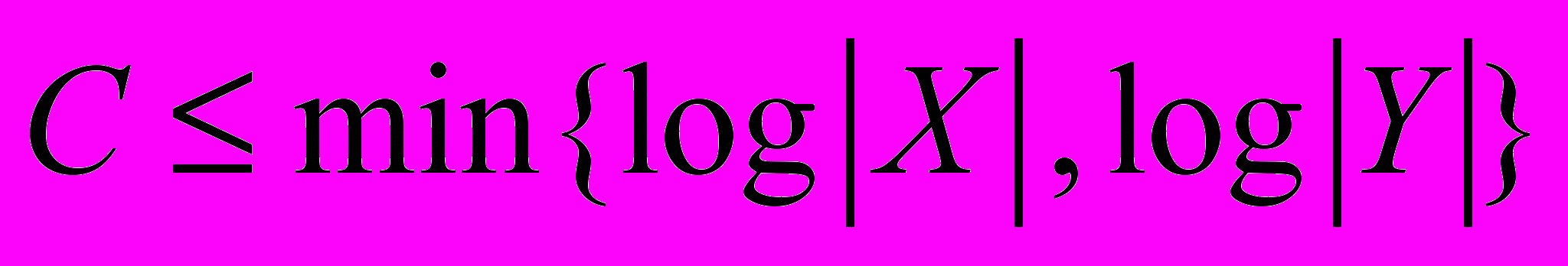
14. Для симметричного по входу канала доказать, что
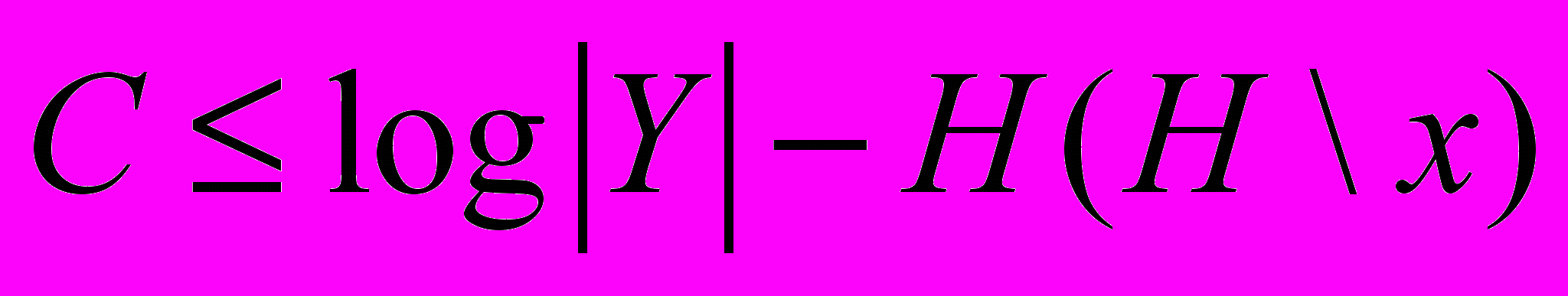
15. Для симметричного канала доказать, что при равновероятных символах на входе выходные символы равновероятны.
16. Для симметричного канала доказать, что
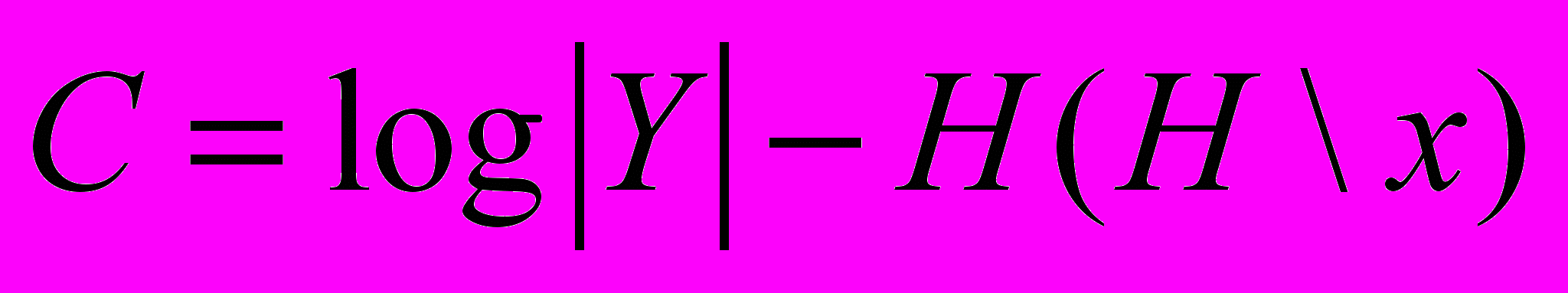
17. Вывести формулу для пропускной способности ДСК.
В таблице приведена рейтинговая система оценки работы студента по отдельным видам деятельности.
-
N
Вид деятельности
Максимальный рейтинг
Достаточный рейтинг для зачета
1
Результаты контрольных опросов
20
14
2
Лабораторные работы
20
13
-
Итого:
40
27
Для получения зачета необходимо набрать не менее 27 баллов.
6. Учебно-методические материалы.
6.1.Литература.
6.1.1.Основная литература.
- Б.Б. Самсонов, Е.М. Плохов, А.И. Филоненков, Т.В. Кречет "Теория информации и кодирования" Феникс 2002. г.
- Котоусов А.С. "Теория информации" 2003 г.
- Дмитриев В.И. Прикладная теория информации. М.: Высшая школа. 1989. 320с
- Коган И.М. Прикладная теория информации. М. Радио и связь. 1981.216с.
- Плтапов В.Н. "Теория информации, кодирование дискретных вероятностных источников".
- Лидовский В.В. "Теория информации"
- Блейхер Р. Теория и практика кодов, контролирующих ошибки— М.: Мир, 1986.
- Винер Н. Кибернетика— М.: Наука; 1983.
- Мастрюков Д. Алгоритмы сжатия информации //''Монитор" 7/93-6/94.
- Питерсон Р., Уэлдон Э. Коды, исправляющие ошибки— М.: Мир, 1976.
- Плотников В. Алгоритмическая реализация криптографического метода RSA //-•Монитор" 2/94.
- Чисар И., Кернер Я. Теория информации— М.: Мир; 1985.
- Шеннон К. Работы по теории •информации и кибернетики— М., Издательство иностранной литературы, 1.963.
- Введение в криптографию /Под общей редакцией В. В. Ящеыко.— М.: МПНМО: "ЧеРо", 2000.
- Марков А. А. Введение в теорию кодирования. М.; Наука. 1982.
- Питерсон У., Уалдон Э .Коды, исправляющие ошибки. М,: Мир, 1576
6.1.2.Дополнительная литература
- Биркгоф Г., Барти Т. Современная прикладная алгебра М.: Мир,
- КолмагоровА.Н. Три подхода к определению понятия "Количество информации"
- Колмогоров А. П. Теории информации и теория алгоритмов,. М.: Паука, 1987.
- Я.Кричевский Р. Г. Сжатие и поиск информации. М.: Радио и связь>, 1989.
- Яглом А. М., Яглом И. М. Вероятность и информация. М.: Паука, 1973.
- 1. С. Кульбак. Теория информации и статистика. М.: Наука.-1967.406 с.
- Водолазкий В. Коммерческие системы шифрования: основные алгоритмы и их реализация //"Монитор'' 6-8/92.
- Глушков В.М. Основы, безбумажной информатики — М.: Наука, 1987.
- Джордж Ф. Основы кибернетики—М,: Радио и Связь, 1984.
- Кенцл Т. Форматы файлов Internet — СПб; Питер, 1997.
- Нельсон М. Верификация файлов //"Журнал д-ра Добба" 1993.
- Нечаев В. И. Элементы криптографии••-- М.: Высшая школа, 1999.
- Яглом А., Яглом И. Вероятность и информация - М.: Наука, 1973.
- Аршинов М. ТТ., Садовский Л. Г. Коды и математика. М.: Наука, 1983.
- Горовкон А. А. Теория вероятностей, М.: Паука, 1976.
- Галлагер Р. Таория информации и надежная связь. М,: Советское радио, 1974,
- Гоппа. В. Д. Введение в алгебраическую теорию информации, М: Паука, 1995.
- Вентцель Е.С. Теория вероятностей. М.: 1964. 576 с.
- Хеминг Р.В. Теория кодирования и теория информации. -М.: Радио и связь, 1983
6.2.Перечень сборников задач и методических материалов.
- Кричевский Р. Г. Лекции по теории информации. Новосибирск: Издательство НГУ,1970.
- Кудряшов Б.Д. "Конспект лекций по теории информации"
7. КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ ЭКЗАМЕНОВ
1 Классификация кодов.
2. Средства представления детерминированных сигналов.
3. Представление сигналов с использованием в качестве базисных единичных импульсных функций.
4. Функция корреляции аналитического сигнала.
5. Вероятностные характеристики
6. Дискретные и непрерывные спектры.
7. Понятия дискретизации по времени и по уровню.
8. Методы дискретизации.
9. Критерии качества восстановления. Квантование сигналов.
10. Преобразование непрерывных сигналов в дискретные
11. Ошибки квантования. Шум квантования.
12.. Количественная мера информации.
13. Свойства энтропии.
14. Условная энтропия.
15.. Энтропия ансамблей.
16. Энтропия непрерывных источников информации
17.. Свойства дифференциальной энтропии.
18. Количество информации.
19. Среднее количество информации при наличии помех.
20.. Передача информации от непрерывного источника.
21. Основные свойства количества информации.
22. Эпсилон энтропия случайной величины.
23. Одномерные и многомерные распределения.
24. Скорость поступления информации.
25. Теорема Шеннона.
26. Канал связи. Пропускная способность.
27. Оптимальное кодирование;
28. Информационная дивергенция;
29. Неравенство Крафта;
30. Линейные коды; параметры кодов и их границы; корректирующие свойства кодов; циклические коды;
31. Сверточные коды;
32. Прямая и обратная теоремы кодирования.
8. ПРИМЕРЫ ЗАДАЧ, РЕШАЕМЫХ НА ЭКЗАМЕНЕ
1. Определить энтропию непрерывной случайной величины, подчиняющейся
а) нормальному закону распределения вероятностей с
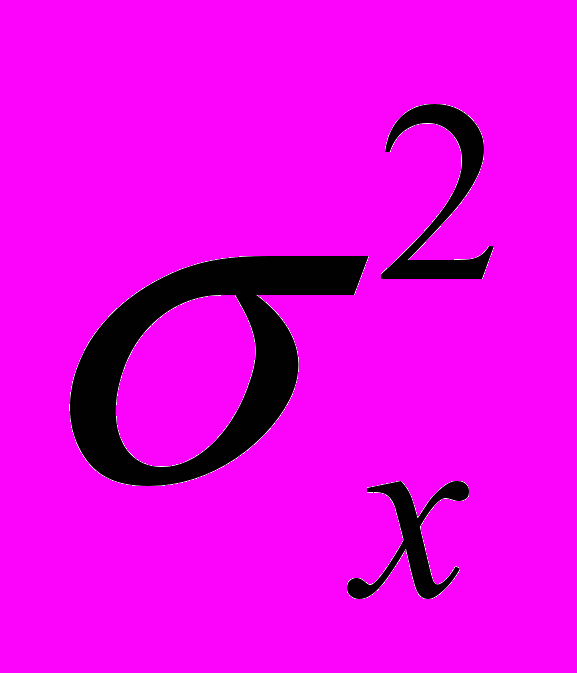
б) экспоненциальному закону
с)
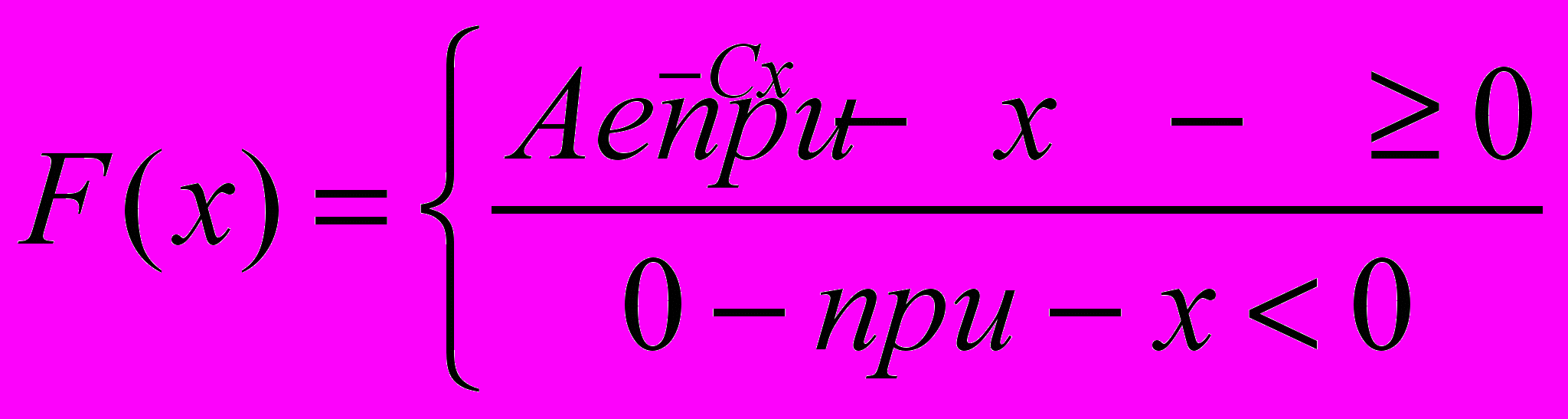 , A –Const, при
, A –Const, при 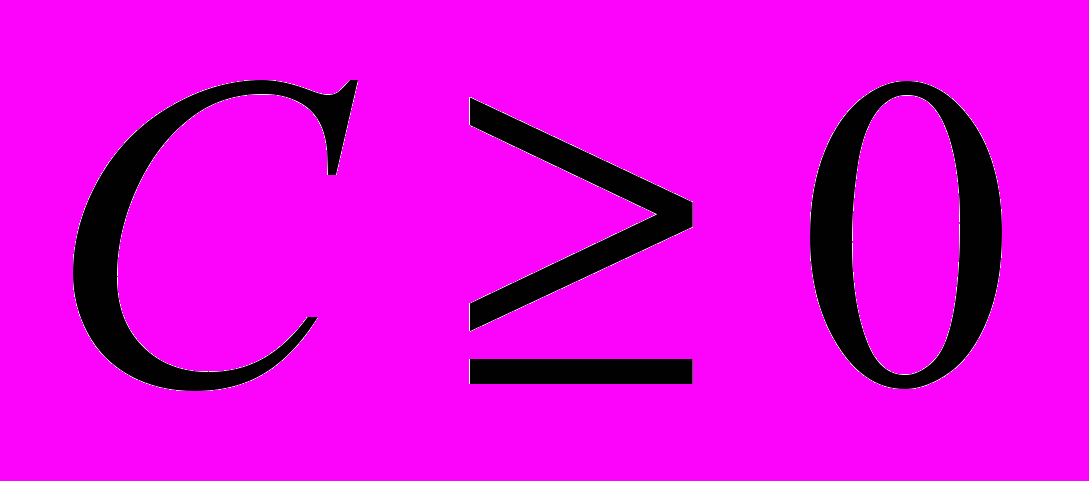
Ответ:
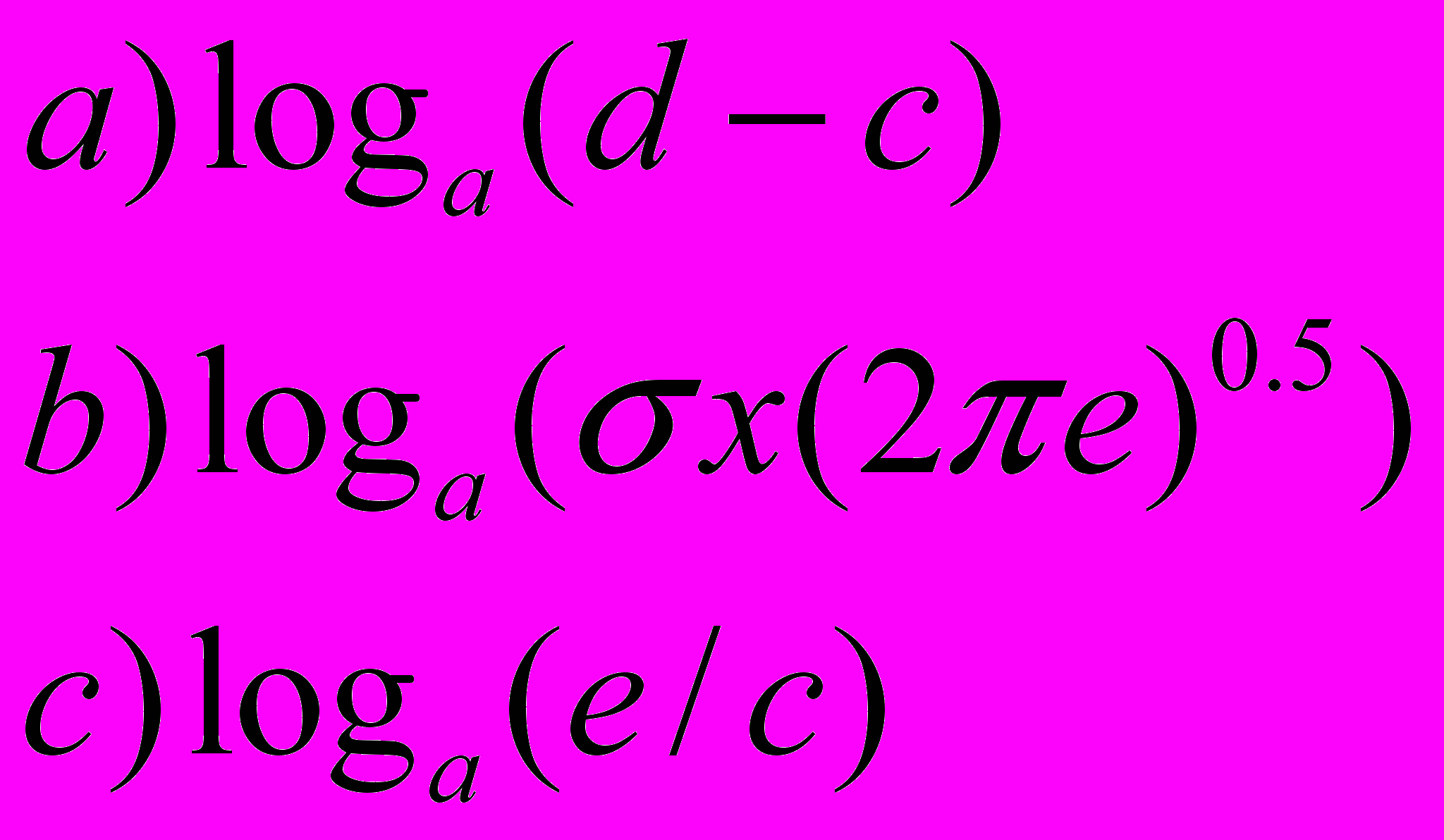
2.Найти энтропию случайной величины х, функция распределения которой


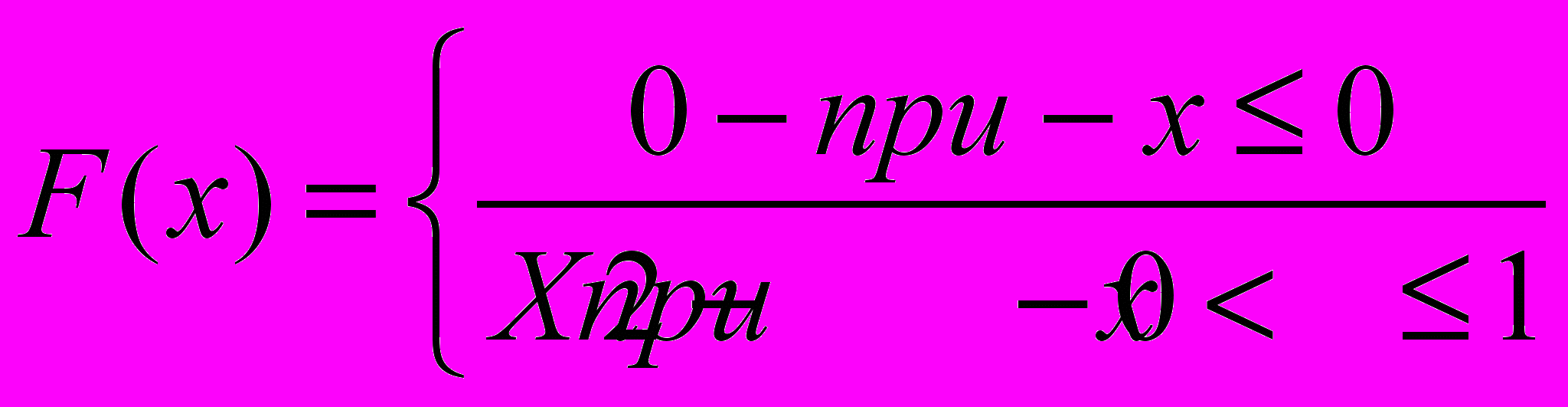
Ответ:
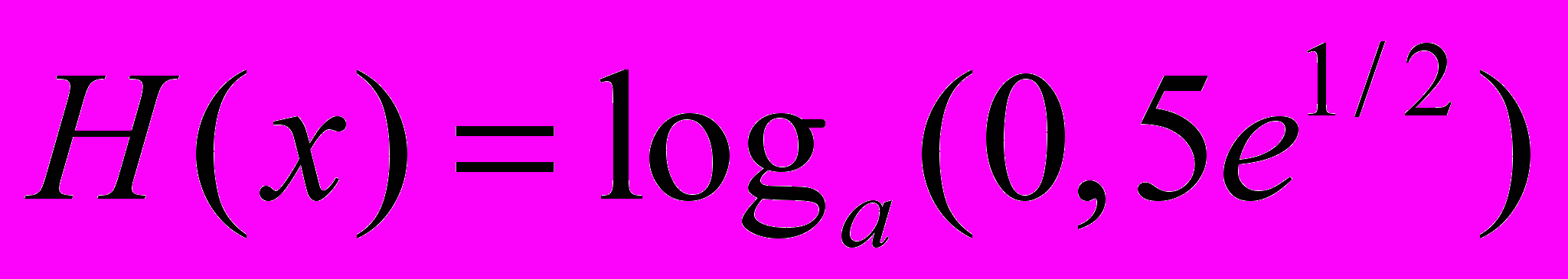
3. Определить энтропию системы, состояние которой описывается
непрерывной случайной величиной х с рядом распределений
| xi | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
| pi | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
