Анализ и разработка моделей систем передачи данных с гибридной решающей обратной связью

Вид материала

Содержание

Общая характеристика работы
Цель работы
Методы исследования
Научная новизна
Практическая ценность работы и внедрение её результатов
Структура и объем диссертации
Основные результаты, выносимые на защиту
Достоверность полученных результатов
Основное содержание работы
Во второй главе
В третьей главе
В четвёртой главе
Параметры кодов
В заключении
В приложении

Подобный материал:

На правах рукописи

Шапин Алексей Геннадьевич

АНАЛИЗ И РАЗРАБОТКА МОДЕЛЕЙ

СИСТЕМ ПЕРЕДАЧИ ДАННЫХ

С ГИБРИДНОЙ РЕШАЮЩЕЙ ОБРАТНОЙ СВЯЗЬЮ

Специальность 05.12.13 – Системы, сети и устройства телекоммуникаций

АВТОРЕФЕРАТ

диссертации на соискание учёной степени

кандидата технических наук

НОВОСИБИРСК – 2011

Работа выполнена в государственном образовательном учреждении высшего профессионального образования «Сибирский государственный университет телекоммуникаций и информатики» на кафедре передачи дискретных сообщений и метрологии

Научный руководитель - д.т.н., проф. Мелентьев О.Г.

Официальные оппоненты: - д.т.н., проф. Ярославцев А.Ф.

- к.т.н., проф. Астрецов Д.В.

Ведущая организация Институт вычислительной математики
и математической геофизики СО РАН

Защита состоится «1» июля 2011 г. в 10.00 часов на заседании диссертационного совета Д 219.005.01 при ГОУ ВПО «Сибирский государственный университет телекоммуникаций и информатики» по адресу: 630102, Новосибирск, Октябрьский район, ул. Кирова, 86, ауд. 625.

С диссертацией можно ознакомиться в читальном зале ГОУ ВПО «Сибирский государственный университет телекоммуникаций и информатики»

Автореферат разослан «____» мая 2011 г.

Ученый секретарь

диссертационного совета Д 219.005.01

доктор технических наук, профессор _____________ Г.В. Мамчев

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы исследования

Популярность услуг передачи данных за последние годы привела к увеличению требований к скоростям. Рост объёмов передаваемой информации в сетях передачи обуславливает необходимость разработки систем, наиболее эффективно использующих пропускную способность каналов. Интерес в данном случае представляют именно беспроводные каналы связи, имеющие нестационарный характер. В этих условиях использование гибридной решающей обратной связи (ГРОС) позволяет в значительной степени повысить качественные показатели систем передачи данных (СПД).

Системы передачи данных с ГРОС занимают промежуточное положение между системами с переспросом и системами с прямым исправлением ошибок, сочетая лучшее из этих двух подходов. Идея заключается в переспросе не только информационной последовательности, как это делается в классических системах, а ещё и последовательности проверочных элементов кода с высокой исправляющей способностью, что в ряде случаев позволяет снизить затраты на передачу одного бита информации и повысить производительность системы.

Впервые в 1965 году А.А. Харкевич в своей монографии обозначил перспективность использования обратной связи совместно с различными корректирующими кодами. Позже вопросами анализа систем с гибридной решающей обратной связью занимались Е. Высоцкий, О.Г. Мелентьев, Shu Lin, Michael Miller, Fulvio Babich, Robert Deng, Masao Kasahara, Samir Kallel и другие. Сегодня СПД
с ГРОС уже используются в стандарте UMTS и активно внедряются в другие стандарты мобильной связи, такие как 3GPP Long Term Evolution (LTE) и IEEE 802.16 (WiMAX).

В работах Shu Lin, Michael Miller, Philip Yu проанализированны системы
с ГРОС и блочным корректирующим кодом (БКК). Недостатком работ авторов является отсутствие методик, позволяющих оценивать вероятностно-временны́е характеристики (ВВХ) этих систем в случаях с ограниченным количеством попыток переспроса, так как в работах приведены математические выражения лишь для оценки границ вероятности остаточной ошибки только при бесконечно большом числе переспросов.

Maan Kousa и Mushfiqur Rahman в своей работе предложили использовать гибридную систему с каскадированием двух блочных кодов, но ни в одной из работ о системах с ГРОС не было предложено совместное использование блочных
и свёрточных корректирующих кодов в одной системе.

Joachim Hagenauer, Robert Deng и Samir Kallel занимались анализом гибридных систем с использованием свёрточных корректирующих кодов (СКК). Изучены методики адаптации скорости свёрточного кода к качеству канала
за счёт «выкалывания» и методики переспроса наименее «надёжных» бит, определяемых с помощью алгоритма апостериорной вероятности при декодировании. В работах этих авторов рассматривается снижение скорости свёрточного кода минимально до 1/2, но не предусмотрено снижение скорости свёрточного кода до 1/3 и ниже, что будет уместно для сильнозашумлённых каналов.

Цель работы: проведение анализа существующих систем с ГРОС, разработка новых систем с ГРОС, а также разработка математических и имитационных моделей систем передачи данных с ГРОС, позволяющих оценивать их ВВХ
при работе по дискретному каналу связи.

Методы исследования: В диссертации представлены результаты исследований, полученные с помощью аппарата теории вероятностей, имитационного
и математического моделирования сложных систем.

Научная новизна:

Впервые разработаны математические модели для оценки ВВХ систем ГРОС-БКК для дискретного канала при заданном числе переспросов.
Предложен метод повышения верности доставки в системах с ГРОС
и свёрточным корректирующим кодированием (ГРОС-СКК) путём адаптивного снижения скорости свёрточного кодирования от 1 до 1/3.
Предложена архитектура системы передачи с ГРОС, использующая свёрточное и блочное корректирующее кодирование (ГРОС-ККК), что позволяет до 50 % повысить верность доставки по сравнению с системами ГРОС-БКК.
Разработаны имитационные модели систем ГРОС-БКК, ГРОС-СКК
и ГРОС-ККК для дискретного канала, позволяющие получать ВВХ.

Практическая ценность работы и внедрение её результатов:

1. Разработанные в диссертации имитационные и математические модели СПД с ГРОС для оценки качественных характеристик этих систем использовались при разработке системных решений по стандарту беспроводного широкополосного доступа NG1 в ЗАО «Национальный институт радио и инфокоммуникационных технологий» (Акт внедрения от 6.12.2010 №77).

2. Разработанные в среде Simulink имитационные модели систем с ГРОС используются в лабораторно-практических занятиях посвященных моделированию СПД курса «Системы и сети передачи информации», а теоретический материал используется в лекциях о современных беспроводных системах в рамках курсов «Основы построения телекоммуникационных систем и сетей», «Основы передачи дискретных сообщений» (Акт внедрения от 4.05.2011 №499/11).

Апробация работы. Основные положения работы докладывались на следующих семинарах и конференциях:

Международная школа-семинар по электронным приборам и материалам «EDM» – Эрлагол, 2007, 2008;
Российская научно-техническая конференция «Информатика и проблемы телекоммуникации» – Новосибирск, 2008, 2009, 2010;
Международная конференция «INTERNANO» – Новосибирск, 2009.

Публикации: По теме диссертации опубликовано 9 работ. В число указанных публикаций входят 2 статьи из перечня ВАК ведущих научных журналов
и изданий.

Структура и объем диссертации: диссертационная работа состоит из введения, четырех глав, заключения и двух приложений. Содержит сто шестнадцать страниц, четыре таблицы, шестьдесят пять рисунков. Список литературы состоит из 57 наименований.

Основные результаты, выносимые на защиту:

Математические модели оценки ВВХ систем ГРОС БКК для дискретного канала.
Метод повышения верности доставки в системах ГРОС-СКК путём адаптивного снижения скорости свёрточного кодирования от 1 до 1/3 в нестационарных каналах связи.
Архитектура системы передачи с ГРОС-ККК.
Имитационные модели систем ГРОС-БКК, ГРОС-СКК и ГРОС-ККК для дискретного канала.
Результаты сравнения ВВХ рассмотренных в диссертации систем с ГРОС.

Достоверность полученных результатов обеспечена корректным применением методов теории вероятности, математической статистики, сравнением аналитических результатов с результатами имитационного моделирования
и с результатами, полученными другими авторами.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертации, сформулированы цель исследований, методы, научная новизна и практическая ценность результатов диссертации.

В первой главе рассматривается СПД с ГРОС и блочным корректирующим кодированием (БКК). Схема такой системы приведена на рис. 1.

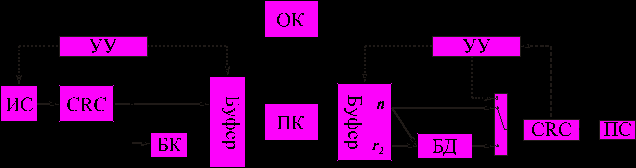
Рис. 1. Структура системы ГРОС-БКК

От источника сообщений (ИС) в CRC-кодер поступает последовательность длиной k, где к сообщению добавляется r₁ проверочных элементов, после чего n элементов (n=k+r₁) поступают в буфер и блочный кодер (БК). Последний вычисляет корректирующую группу – r₂ проверочных элементов блочного кода
с исправляющей способностью t_и , которые также записываются в буфер. Первоначально в прямой канал передаётся n элементный блок. Если на приёмной стороне CRC-декодер обнаруживает ошибку в блоке, то устройство управления (УУ) через обратный канал (ОК) запрашивает передачу r₂ элементной корректирующей группы. На приёмной стороне после исправления ошибок в блочном декодере (БД) информационный блок повторно проверяется на наличие ошибок. Если ошибки остаются, то в следующей попытке повторяется n элементный блок, т.е. при обнаружении ошибки CRC декодером передача n элементного информационного блока и r₂ элементной корректирующей группы чередуются.

При приёме любого блока на приёмной стороне происходит его запись
в буфер. В зависимости от ёмкости буферной памяти предлагаются три стратегии декодирования.

В стратегии ГРОС-БКК-1 при приёме n элементного информационного блока результаты прежних попыток для декодирования не используются, т.е. информационный блок, принятый с ошибкой в нечётной попытке, всегда исправляется корректирующей группой из следующей попытки. На рис. 2 приведён пример исправления информационных блоков за счёт принятых корректирующих групп (в скобках обозначены номера попыток передачи). Из рисунка видно, что принятые в чётных попытках r₂ элементные корректирующие группы используются только для исправления принятых в предыдущей попытке n элементных информационных блоков.

В стратегии ГРОС-БКК-2, при обнаружении ошибок в случае повторного приёма n элементного информационного блока, делается попытка исправления
с помощью r₂ элементной корректирующей группы, полученной ранее, а в случае неудачи – попытка исправить этот информационный блок корректирующей группой из следующей передачи (рис. 3).

В стратегии ГРОС-БКК-3 при получении n-элементного информационного блока с ошибками для их исправления используются все полученные ранее r₂ элементные корректирующие группы. Аналогично, при получении корректирующей группы делается попытка исправить все полученные ранее информационные блоки (рис. 4).


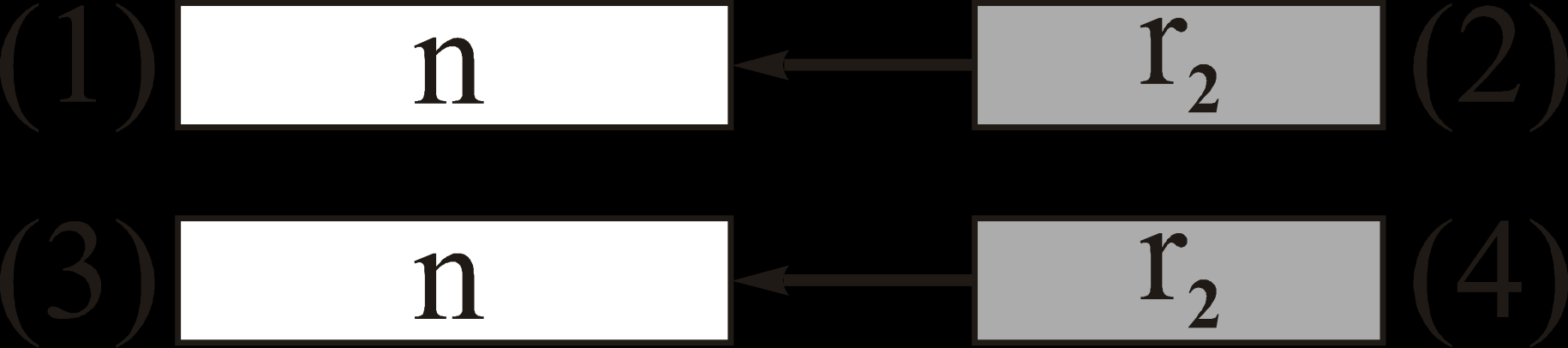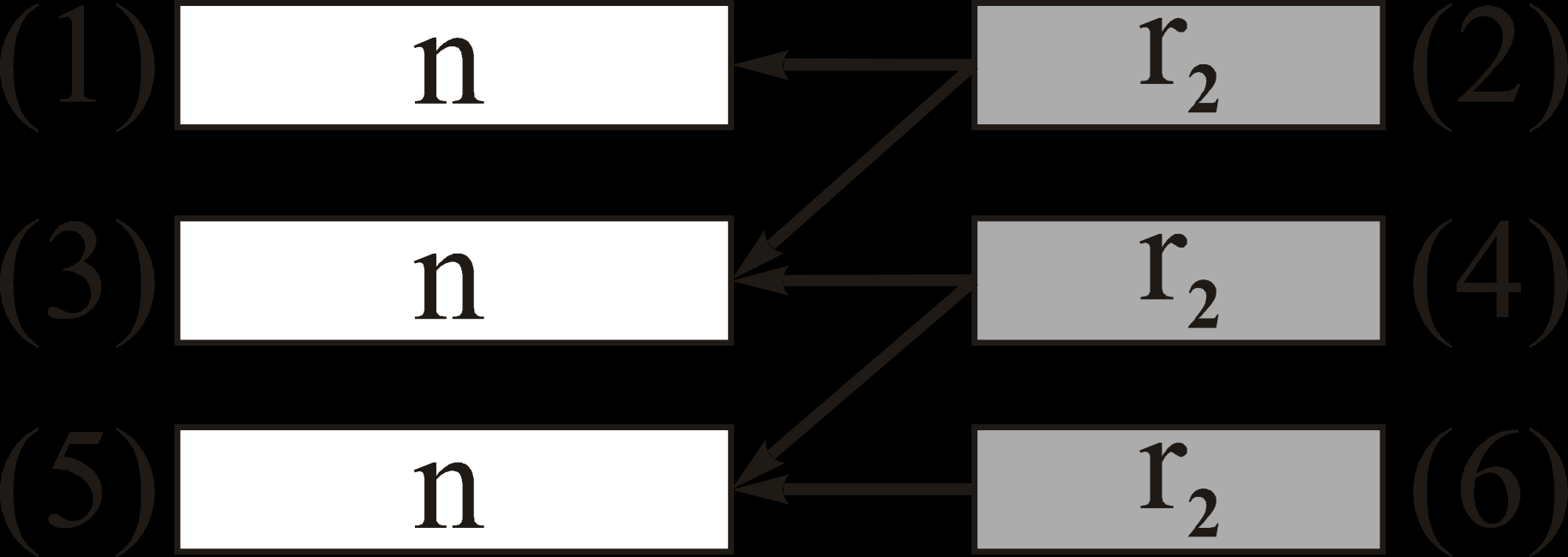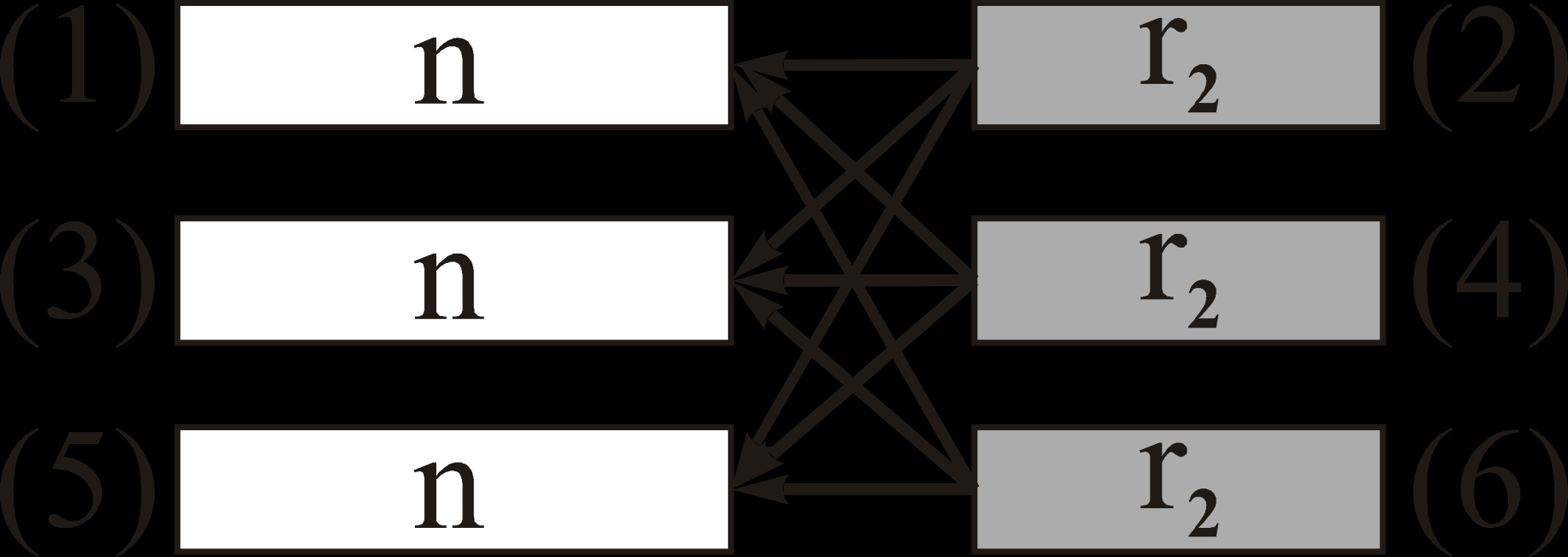Рис. 2. Пример для ГРОС БКК 1	Рис. 3. Пример для ГРОС БКК 2	Рис. 4. Пример для ГРОС БКК 3

В стратегии ГРОС-БКК-1 вероятность успешной доставки P_уд информационного блока в зависимости от номера переспроса L_m определяется следующими выражениями:

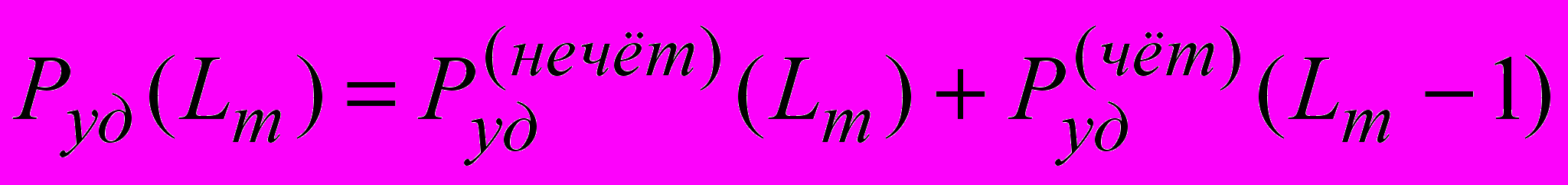(1)

при нечётном L_m и

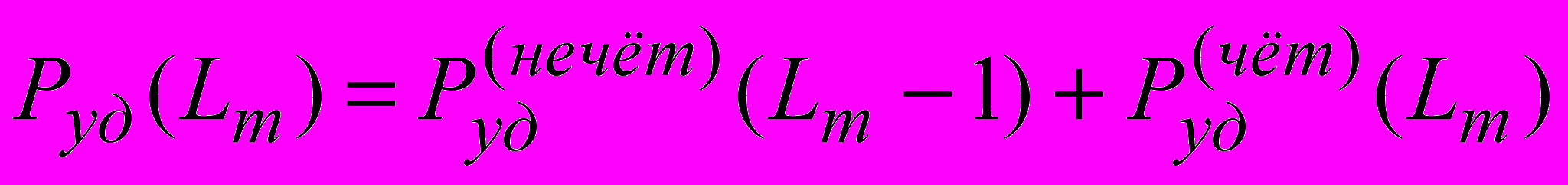(2)

при чётном L_m, где

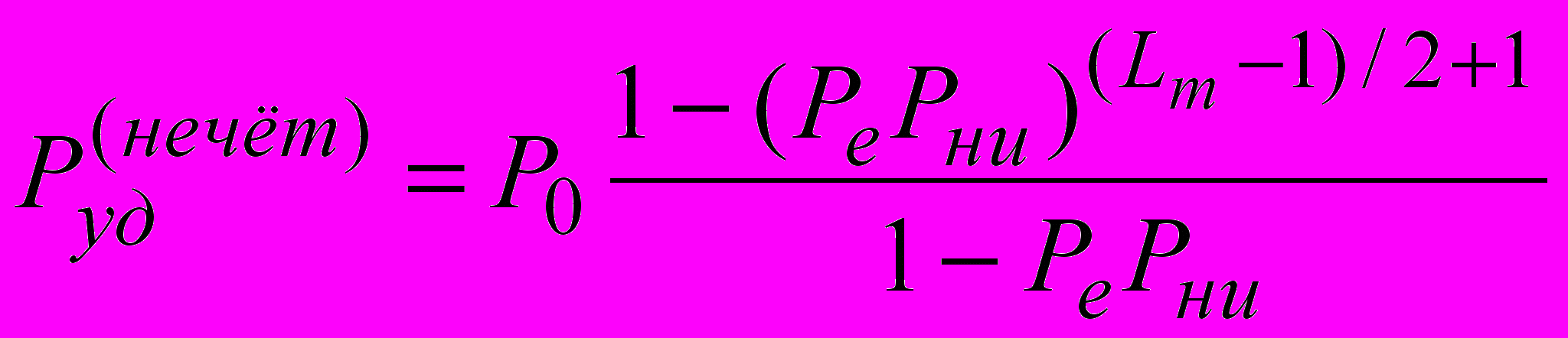, (3)

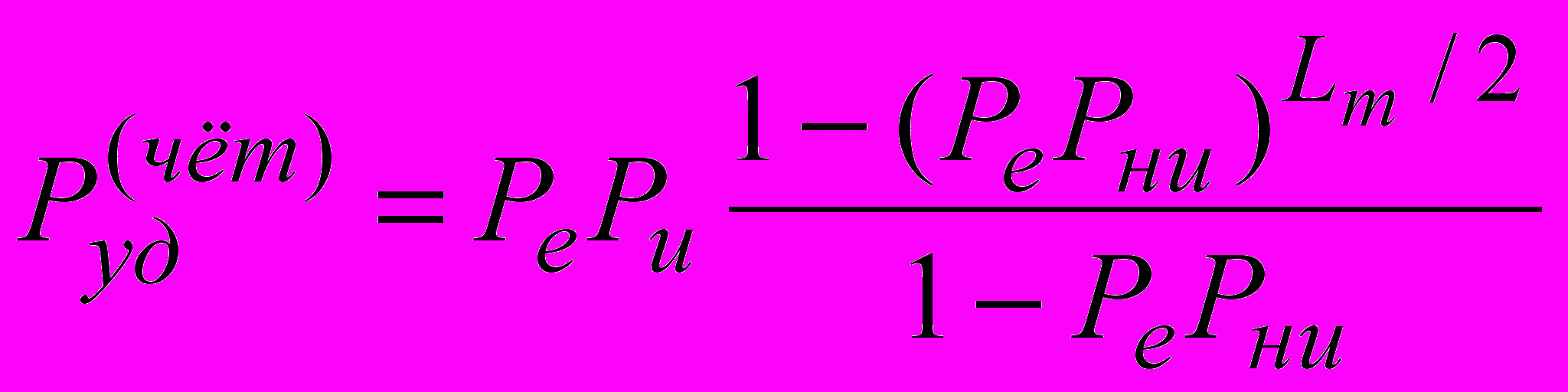. (4)

Здесь P_e – вероятность приёма блока с одной и более ошибками, P₀ – вероятность приёма блока без ошибок, P_и – вероятность исправления ошибок,
P_ни – вероятность того, что после исправления ошибки останутся.

В стратегии ГРОС-БКК-2 для расчёта вероятности успешной доставки информационного блока необходимо формировать матрицу «хороших» исходов G и «плохих» исходов B. Элементы матрицы G представляют собой вероятности правильного декодирования, если в попытке, соответствующей номеру строки, произошло x ошибок. Элементами матрицы B являются вероятности ошибочного декодирования, если в попытке, соответствующей номеру строки, произошло x ошибок. При этом вероятность возникновения x ошибок в информационном блоке длиной n обозначим a_х, а вероятность возникновения x ошибок в корректирующей группе длиной r₂ – b_х . Запишем общие выражения для элементов матриц.

Для нулевой строки G_0,0 = a₀, соответственно B_0,0 = 0.

При i [1...n]: B_0,i=a_i; G_0,i=0.

Нулевой элемент чётной ненулевой строки (l>0)

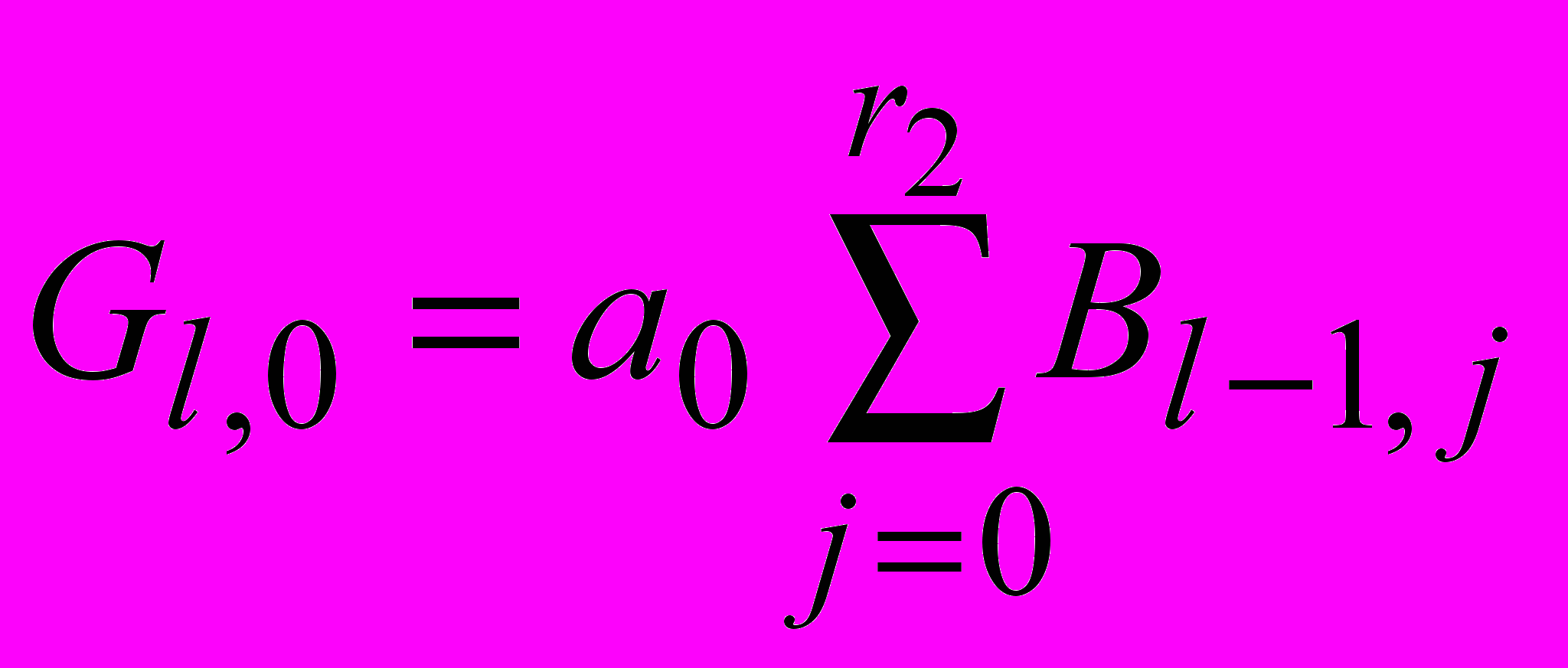, соответственно B_l_,0=0.

При i [1...t_и]:

;

.

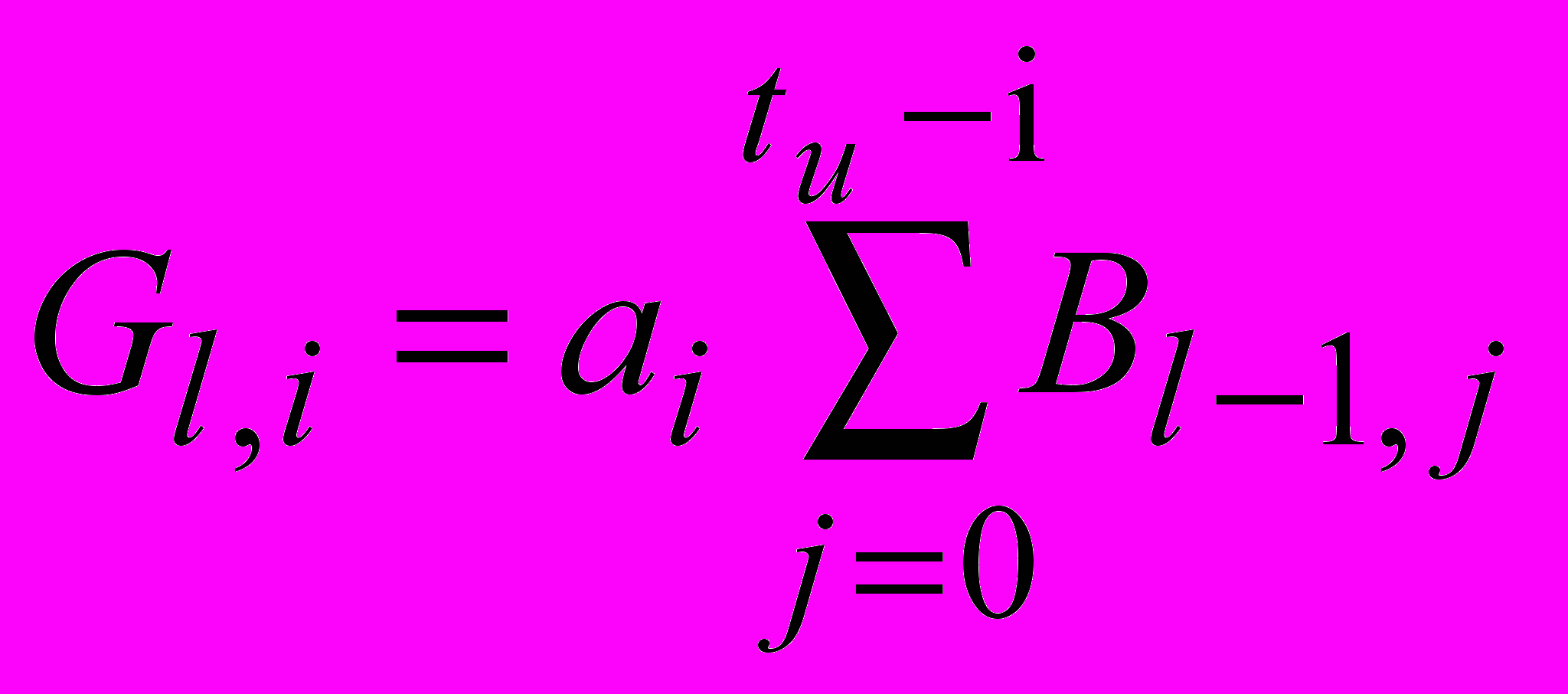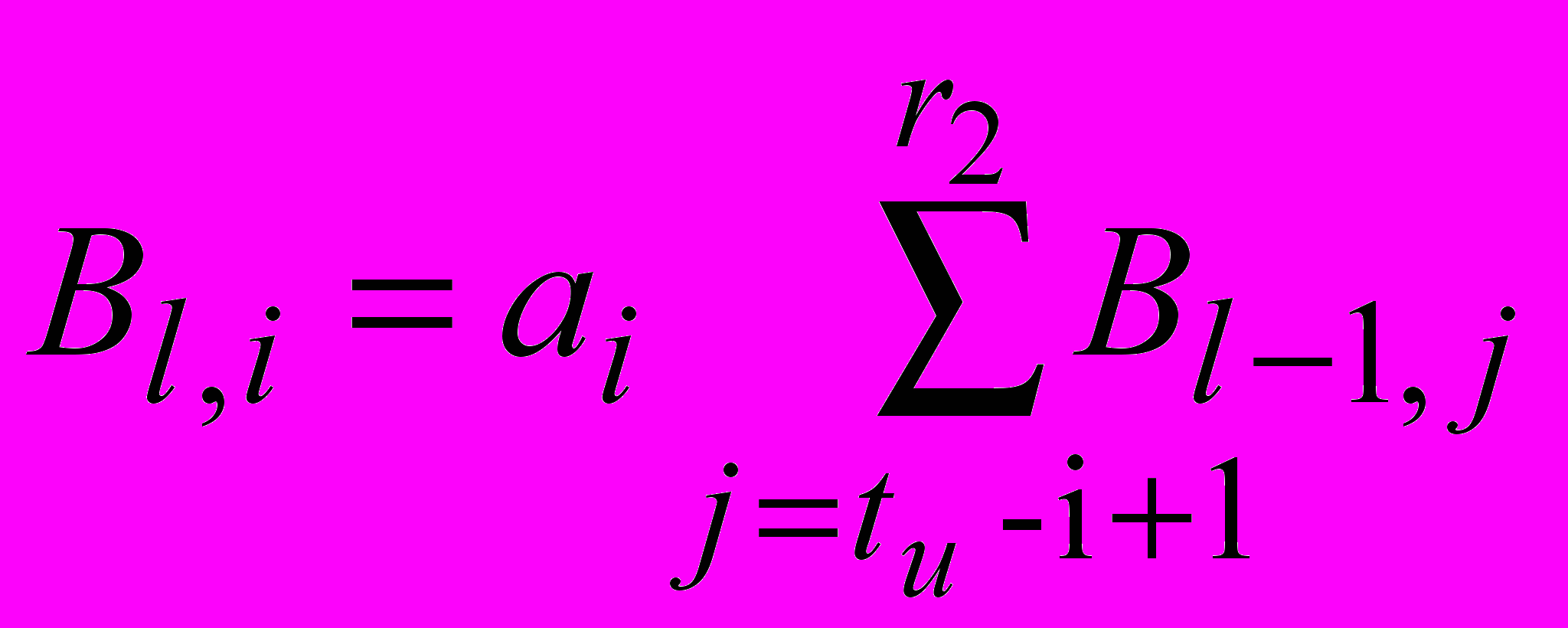Все элементы чётных строк матрицы G с индексами, больше t_и, равны нулю. Элементы матрицы В при i [t_и+1…n] равны

.

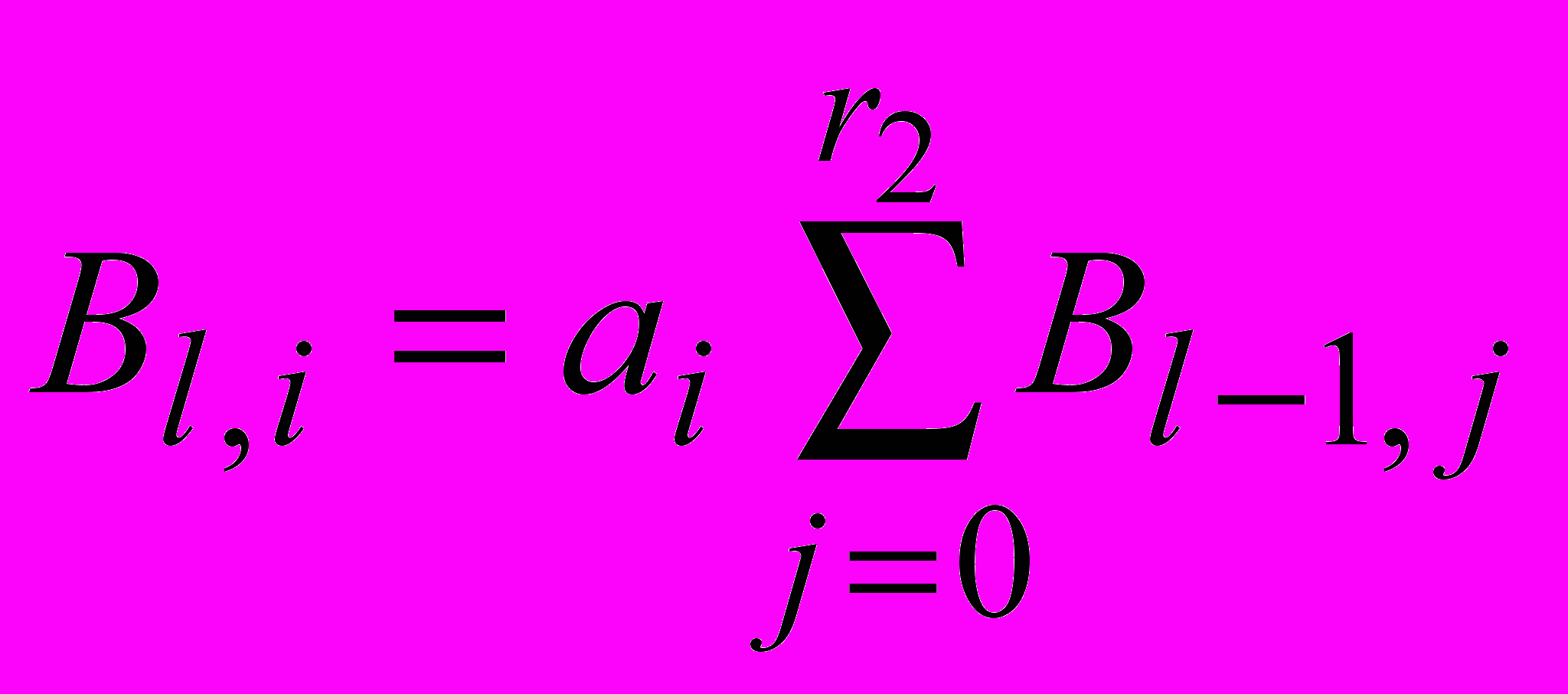Подобным образом формируются элементы нёчетных строк матриц. Следует отметить, что в данном случае отличными от нуля могут быть только первые (r₂+1) элементов каждой матрицы.

Для i [0...t_и–1]:

;

.

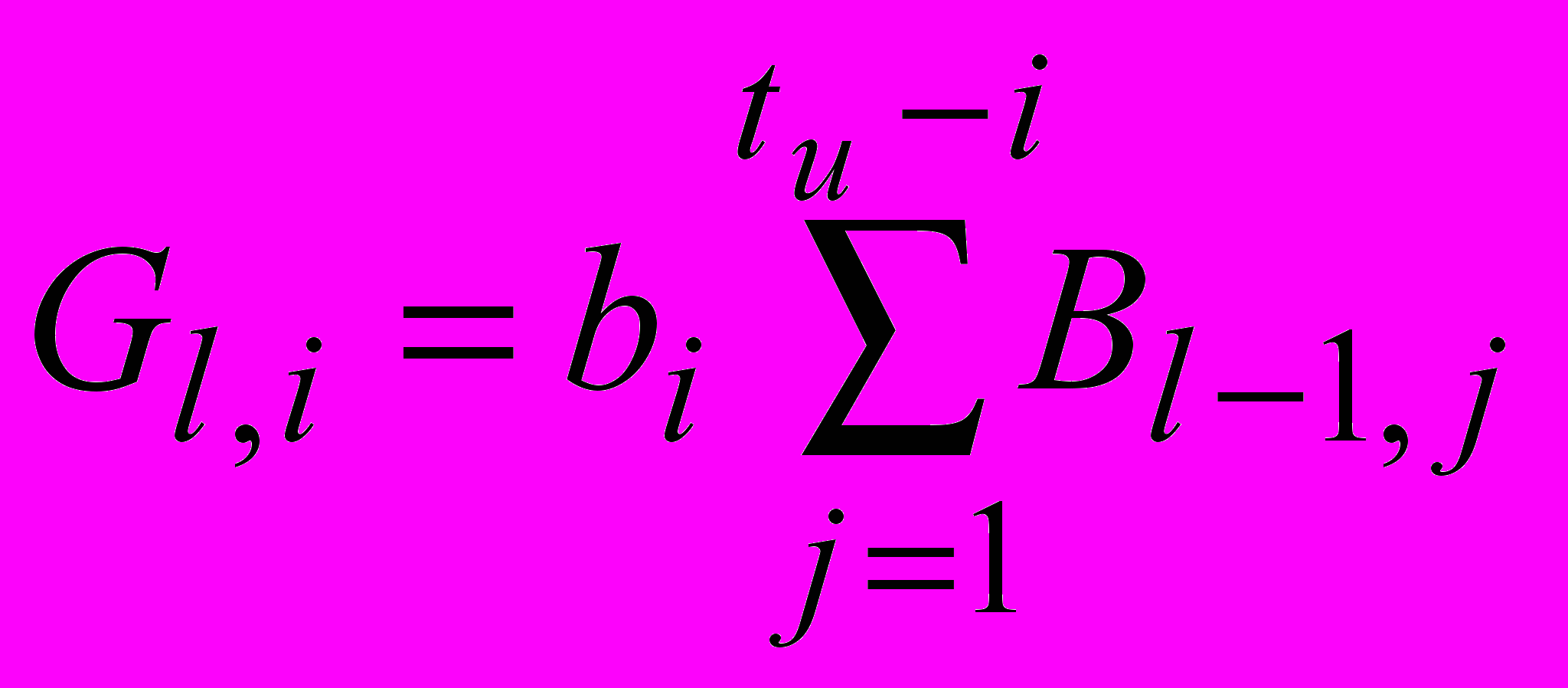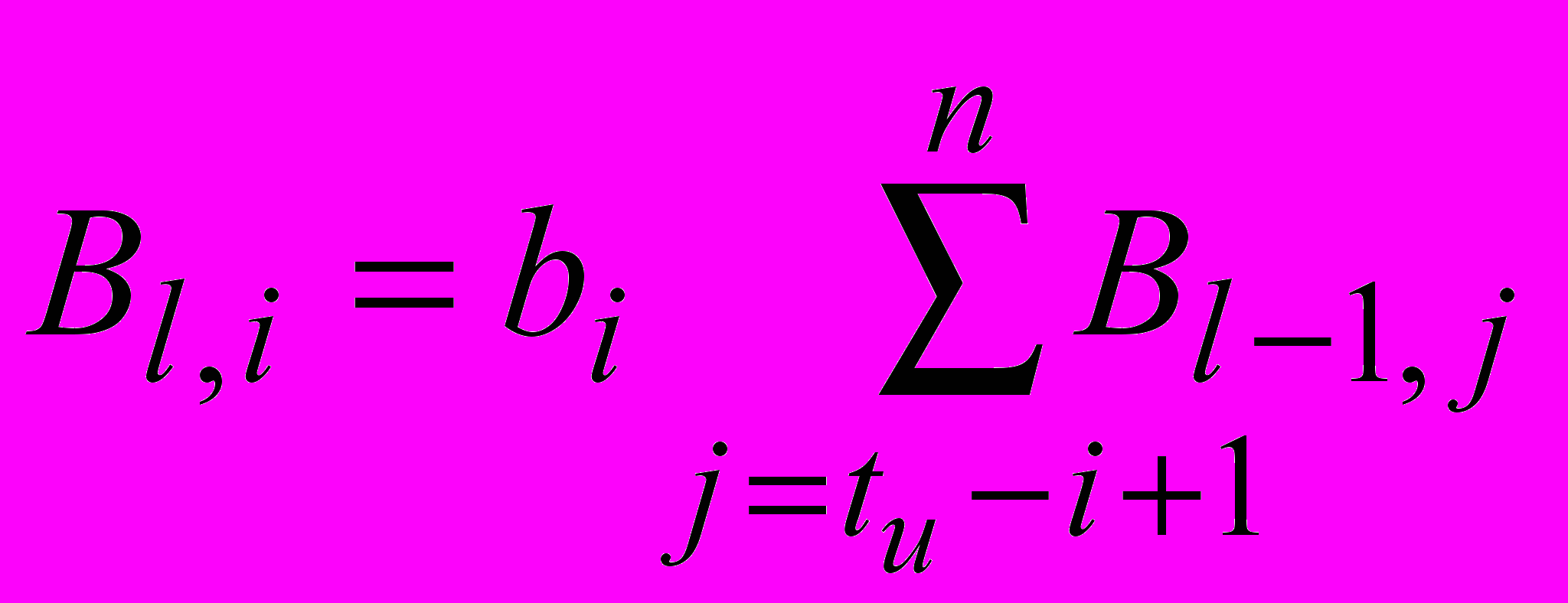Для i [t_и...r₂]:

;

.

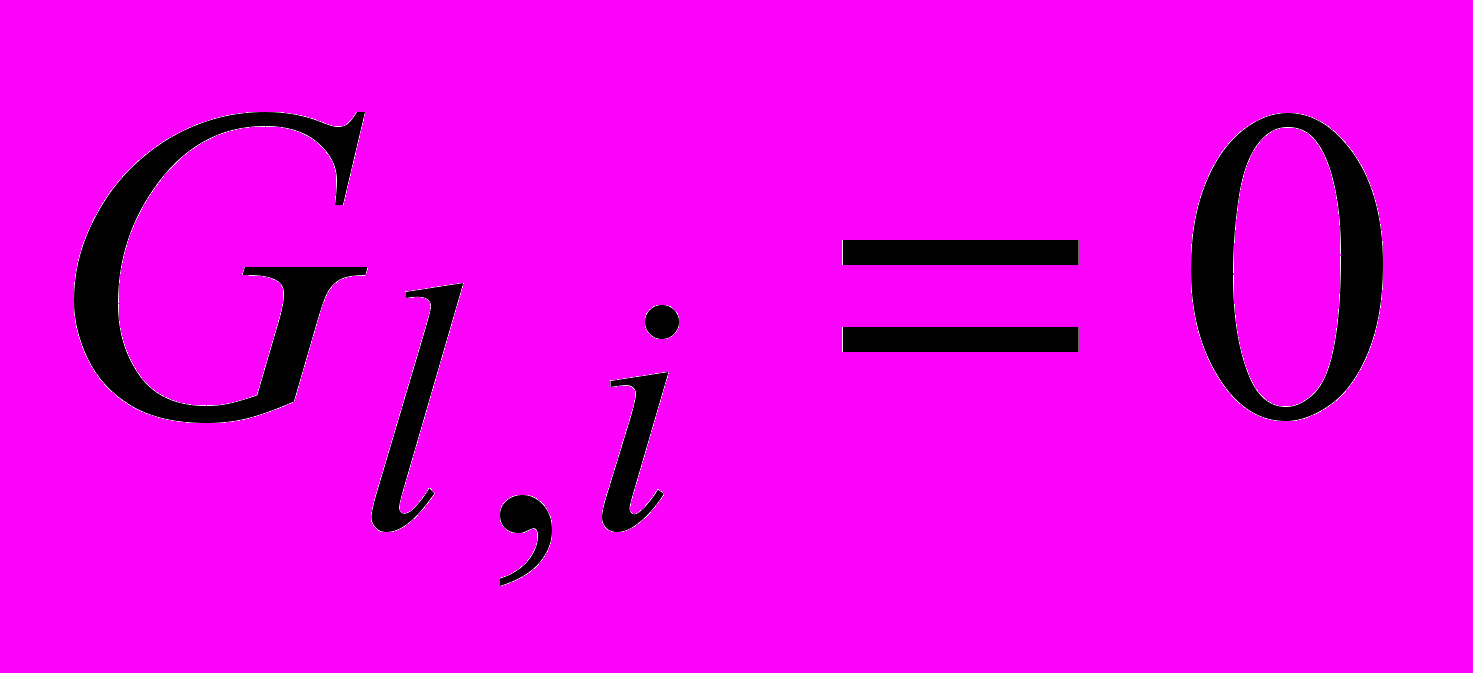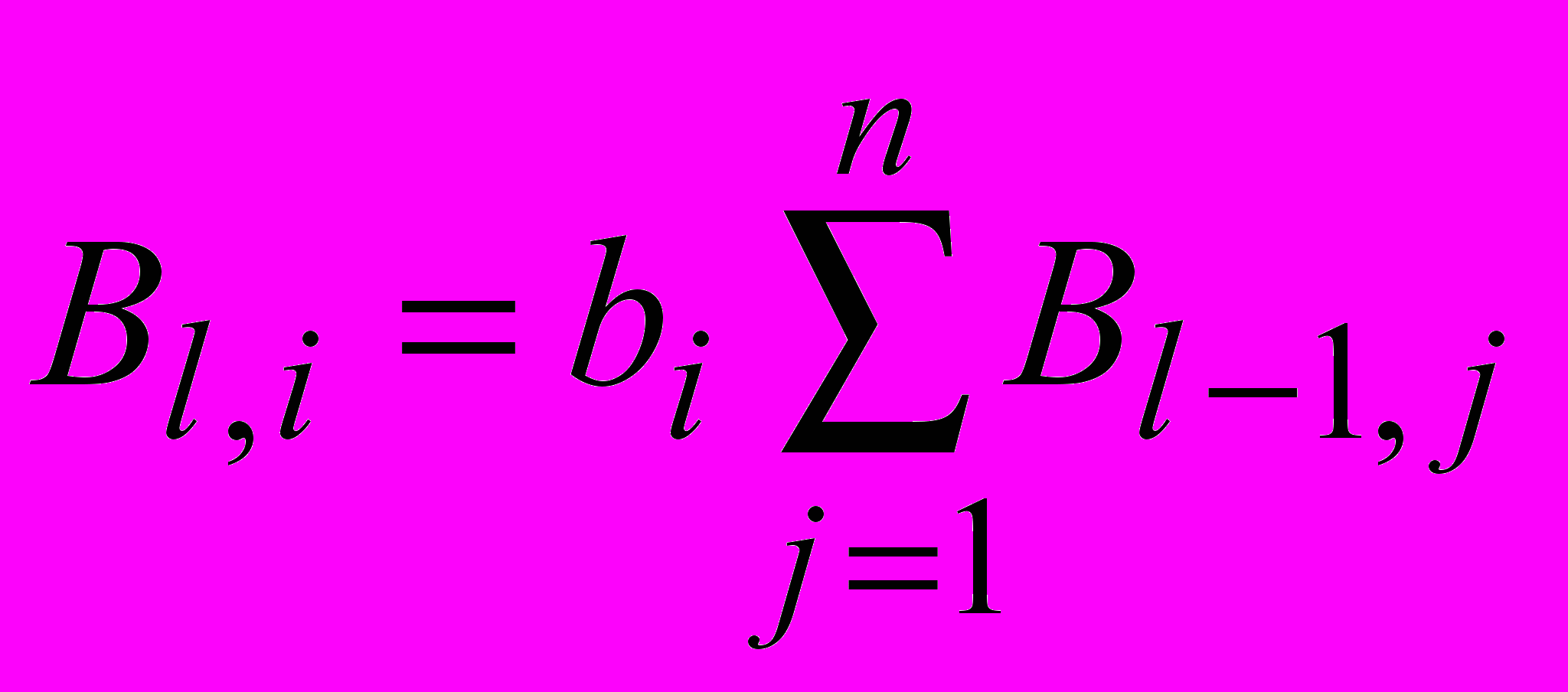Сумма элементов строки матрицы G является вероятностью правильного декодирования точно в текущей попытке. Сумма элементов строк с 0 по L_m есть вероятность успешной доставки за L_m попыток:

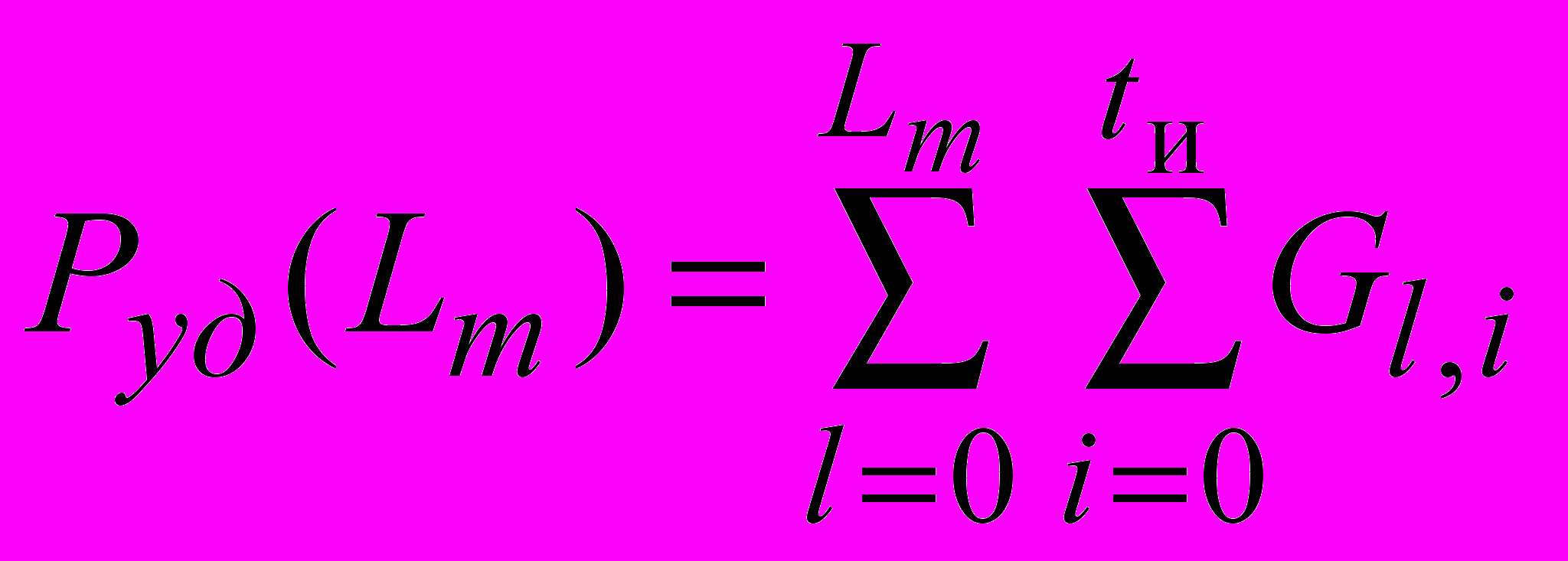. (5)

Для стратегии ГРОС-БКК-3 формирование матриц происходит более сложным способом, но для расчёта вероятности успешной доставки также
используется выражение 5. Формирование первых двух строк матриц B и G происходит способом, аналогичным ГРОС-БКК-2, т.к. в первой и второй попытках системы функционируют одинаково. Приведём общие выражения для элементов нечётных строк матриц:

, (6)

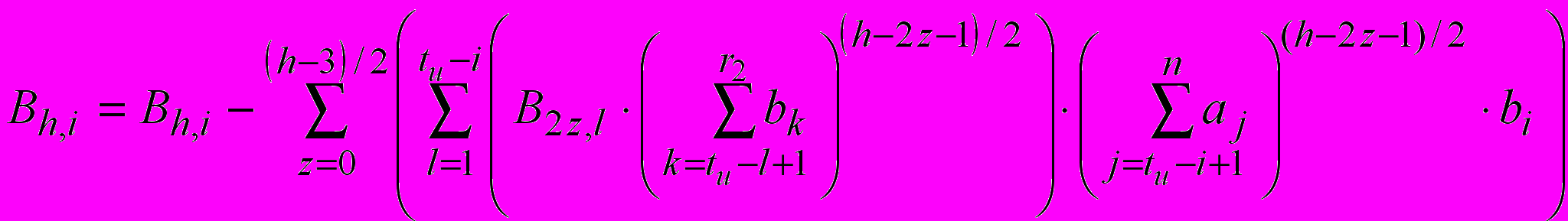, (7)

где h – номер попытки передачи от трёх и выше.

Для чётных строк матриц:

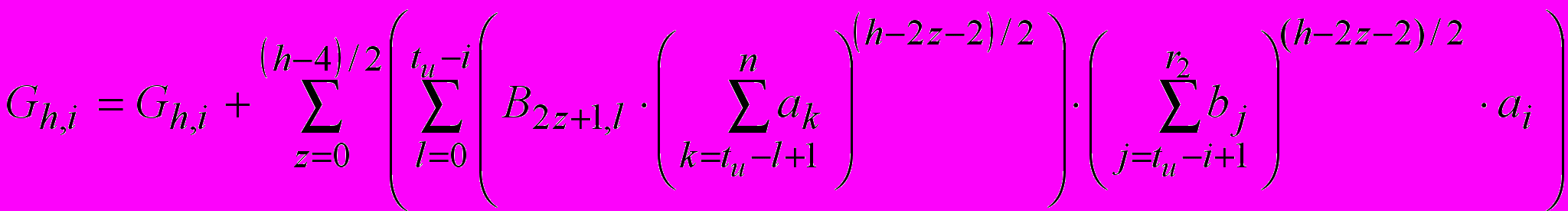, (8)

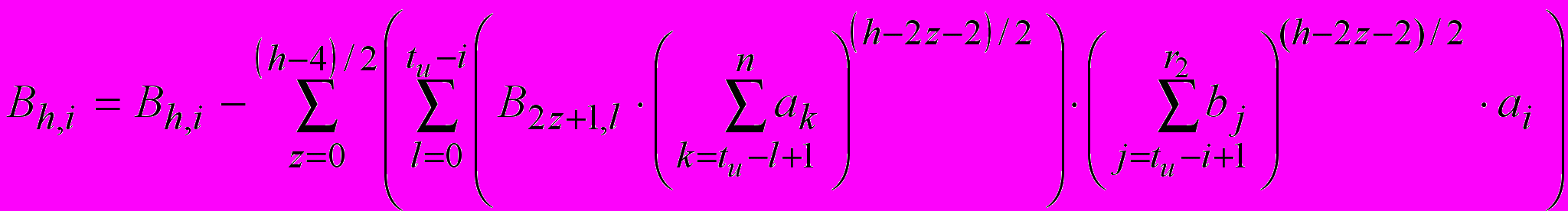, (9)

где h – номер попытки передачи от четырёх и выше.

Одним из показателей эффективности использования канала связи являются затраты двоичных элементов на передачу одной информационной последовательности длиной k элементов. В системе с гибридной ОС при вычислении затрат необходимо учитывать две длины блока n, r₂, а также вероятности обнаружения ошибок в блоке и их исправления. В зависимости от максимального числа переспросов L_m, разрешённых в системе, средние затраты в прямом канале могут быть вычислены по следующим рекурсивным формулам:

– при одной попытке Z_пр(1)=n; (10)

– при чётном значении L_m

Z_пр(L_m) = Z_пр(L_m– 1) + r₂(1 – P_уд(L_m– 1)); (11)

– при нечётном L_m ≥ 3

Z_пр(L_m) = Z_пр(L_m– 1) + n (1 – P_уд(L_m– 1)). (12)

Затраты в обратном канале вычисляются аналогично, но вместо длин n и r₂ подставляется длина квитанции в обратном канале n_ok.

При одной попытке Z_ок = n_ок. (13)

При остальных значениях L_m ≥ 2,

Z_ок(L_m) = Z_ок(L_m– 1) + n_ок (1 – P_уд(L_m– 1)). (14)

Суммарные затраты на передачу одного блока можно определить как сумму затрат в прямом и обратном каналах:

Z_(L_m) = Z_пр(L_m) + Z_ок(L_m). (15)

Относительная скорость определится выражением:

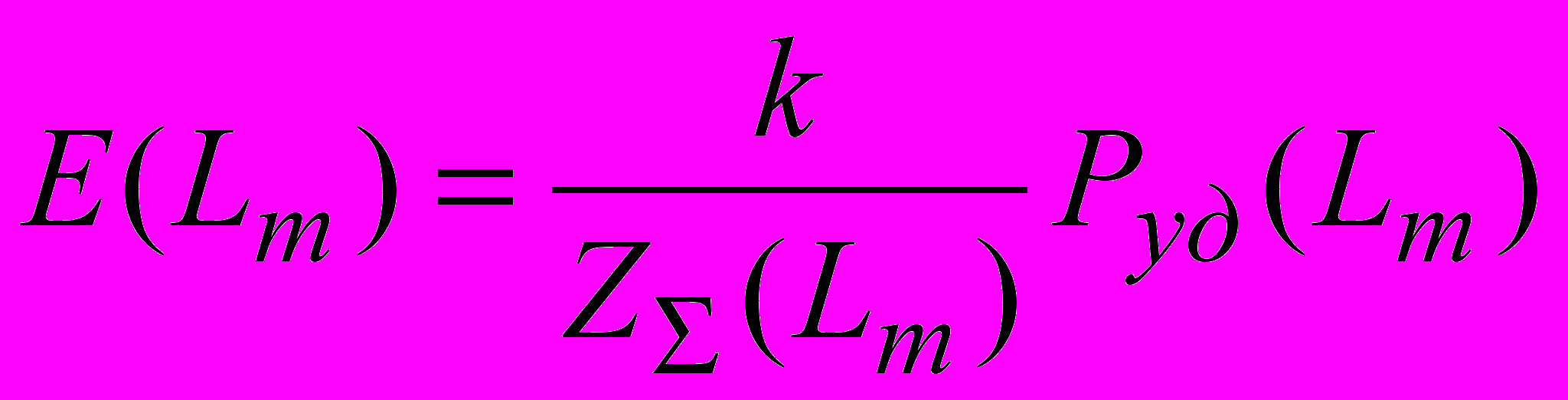. (16)

Имитационное моделирование

Кроме математических моделей для систем передачи данных ГРОС БКК 1, 2 и 3 в первой главе были разработаны алгоритмы имитационного моделирования в среде MathCAD. Алгоритмы используют границы Хемминга
для определения исправляющей и обнаруживающей способностей кодов, что является их недостатком. В связи с этим в среде Simulink были разработаны имитационные модели систем ГРОС-БКК-1 и ГРОС-БКК-2, использующие БЧХ
и CRC кодеки. Создание модели ГРОС-БКК-3 в Simulink невозможно, так как
с четвёртой попытки переспроса начинает возрастать число одновременно использующихся декодеров, что недопустимо в данной среде моделирования.

Для сравнения эффективности стратегий декодирования и дополнительной проверки корректности математических моделей было проведено математическое и имитационное моделирование в среде MathCAD и Simulink при следующих параметрах систем: n=223, r₂=32, t_и=4, r₁=16, n_ОК=64. В Simulink для исправления ошибок использовался циклический код БЧХ (223, 255), а для обнаружения – CRC 16. Были исследованы ВВХ для вероятности ошибки в дискретном канале от 0 до 0.05, но для наглядности графика (рис. 5) сравнение проведём с вероятностью ошибки p=0.018.

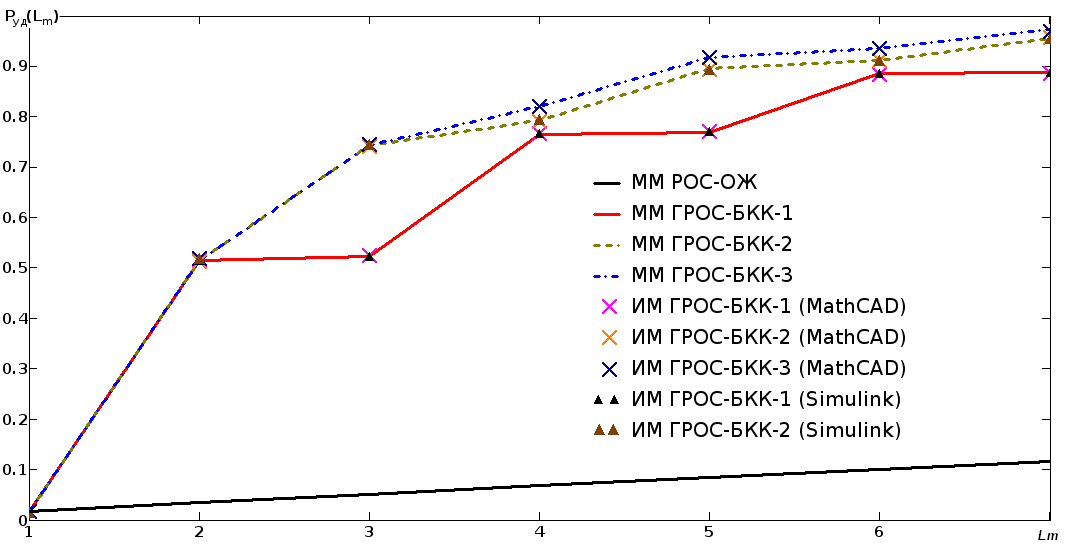Рис. 5. Зависимости вероятности успешной доставки от допустимого числа попыток. ММ — математическая модель, ИМ — имитационная модель

На рис. 5 приведены зависимости вероятности успешной доставки блока за L_m попыток для разных стратегий декодирования, полученные аналитически,
а также результаты имитационного моделирования. Результаты имитационного моделирования совпали с результатами, полученными по выражениям 1 — 9, что подтверждает их корректность. Относительная разница вероятности успешной доставки, полученной путём аналитического расчёта и имитационного моделирования, не превысила 1 % при объёме выборки 1 млн. блоков.

Как видно из рис. 5, начиная со второй попытки передачи, системы ГРОС БКК позволяют повысить вероятность успешной доставки блока в 14 и более раз по сравнению с классической системой, использующей решающую обратную связь (РОС). Стоит также отметить, что с ростом коэффициента ошибки
в канале выигрыш ГРОС-БКК по сравнению с классическими системами с РОС может достигать нескольких порядков.

Во второй главе рассматривается система с гибридной решающей обратной связью и свёрточным корректирующим кодированием (ГРОС-СКК, рис. 6). После кодирования в CRC кодере информационная последовательность вместе
с r₁ проверочными разрядами кода, обнаруживающего ошибки, образуют блок длиной n элементов. Перед свёрточным кодированием к блоку добавляется z «нулевых» элементов для возврата свёрточного кодера к нулевому состоянию. Затем блок поступает в свёрточный кодер (СК), скорость которого 1/3. Каждый входной элемент порождает три элемента на выходе кодера. Выходные элементы с каждого сумматора кодера записываются в три регистра буфера так, что первый регистр содержит первые элементы С₁, второй – вторые С₂, и, соответственно, третий – третьи С₃. Длина каждого блока по n+z элементов.

В соответствии с номером попытки передачи (l = 1, 2, 3), в перемежитель (ПМ) из буфера поступает блок С_l. После перемежения блок длиной n+z элементов передаётся по прямому каналу (ПК).

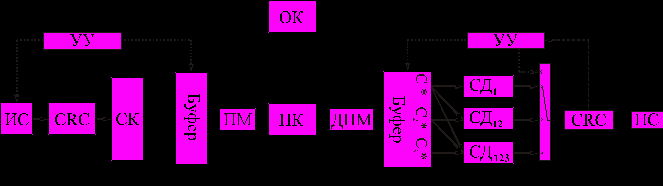
Рис. 6. Структура системы передачи данных ГРОС-СКК

На приёмной стороне блок поступает в деперемежитель (ДПМ), где восстанавливается исходный порядок следования элементов. Принятую и деперемежённую последовательность обозначим С_l*, где l – номер сумматора, с которого пришла последовательность. С_l* записывается в буфер. В зависимости от номера попытки передачи буфер выдает один блок в первый свёрточный декодер (СД₁)
(l = 1) либо выдаёт сразу два или три блока (l =2, 3) в декодеры СД₁₂ и СД₁₂₃ соответственно. Все СД декодируют полученную последовательность со скоростью 1/l и усекают блок до n элементов. CRC декодер проверяет блок на наличие ошибок и принимает решение о качестве декодирования.

Обнаружение ошибок в блоке инициирует передачу по обратному каналу (ОК) отрицательной квитанции. При получении первой отрицательной квитанции по ПК передаётся перемежённый блок С₂, а на приёме производится исправление ошибок СД₁₂ со скоростью 1/2. В случае повторного обнаружения ошибок перемежается и передается С₃, а ошибки исправляются СД₁₂₃ со скоростью 1/3. Если третья попытка оказывается неудачной, система возвращается к первой попытке или переходит к передаче следующего информационного блока.

Для описанной выше системы передачи ГРОС-СКК можно предложить три основных способа декодирования. Все они будут различаться количеством СД.

Первый способ – самый простой в реализации. Он основан на использовании трёх СД. В первой попытке приёма блок декодируется СД₁ со скоростью 1, используя принятую последовательность С₁*, во второй попытке последовательности С₁* и С₂* декодируются со скоростью 1/2 в СД₁₂, в третьей попытке последовательности С₁*, С₂* и С₃* декодируются со скоростью 1/3 в СД₁₂₃. Схема такой СПД приведена на рис. 9. Назовем такую систему ГРОС-СКК-1.

Второй способ требует для реализации пять СД. Декодеры СД₁, СД₁₂
и СД₁₂₃ работают так же, как в ГРОС-СКК-1. СД₂ включается в работу только во второй попытке, декодируя принятую последовательность С₂* со скоростью 1, СД₂₃ – только в третьей попытке, обрабатывая принятые С₂* и С₃* последовательности, декодируя их со скоростью 1/2. Такой подход позволит повысить вероятность успешного приёма блока для случая, когда в принятой С₁* последовательности содержится большое количество ошибок. Назовём такую стратегию ГРОС СКК 2. Система передачи при использовании такого способа отличается
от рис. 6 лишь схемой декодирования, которая приведена отдельно на рис. 7. Стоит также отметить, что, начиная со второй попытки, в стратегии ГРОС СКК 2 необходимо параллельно проверять на ошибки результаты декодирования двух СД. Это требует наличия в системе двух CRC-декодеров.

Третий способ – самый сложный в построении. В схеме используется семь СД (рис. 11). СД₁, СД₂, СД₁₂, СД₂₃ и СД₁₂₃ работают идентично пяти декодерам предыдущей схемы. СД₃ и СД₁₃ включаются в работу только при третьей попытке переспроса. СД₃ декодирует принятую С₃* последовательность со скоростью 1, СД₁₃ – со скоростью 1/2 (последовательности C₁* и C₃*). Таким образом, в предложенной схеме осуществляются все варианты декодирования принятых последовательностей. Назовём такую стратегию ГРОС-СКК-3. Такая система отличается от системы, представленной на рис. 6, только схемой декодирования, которая приведена отдельно на рис. 8. В третьей попытке в стратегии ГРОС СКК 3 целесообразно параллельно проверять на ошибки результаты декодирования четырёх СД, что требует наличия в системе четырёх CRC-декодеров.

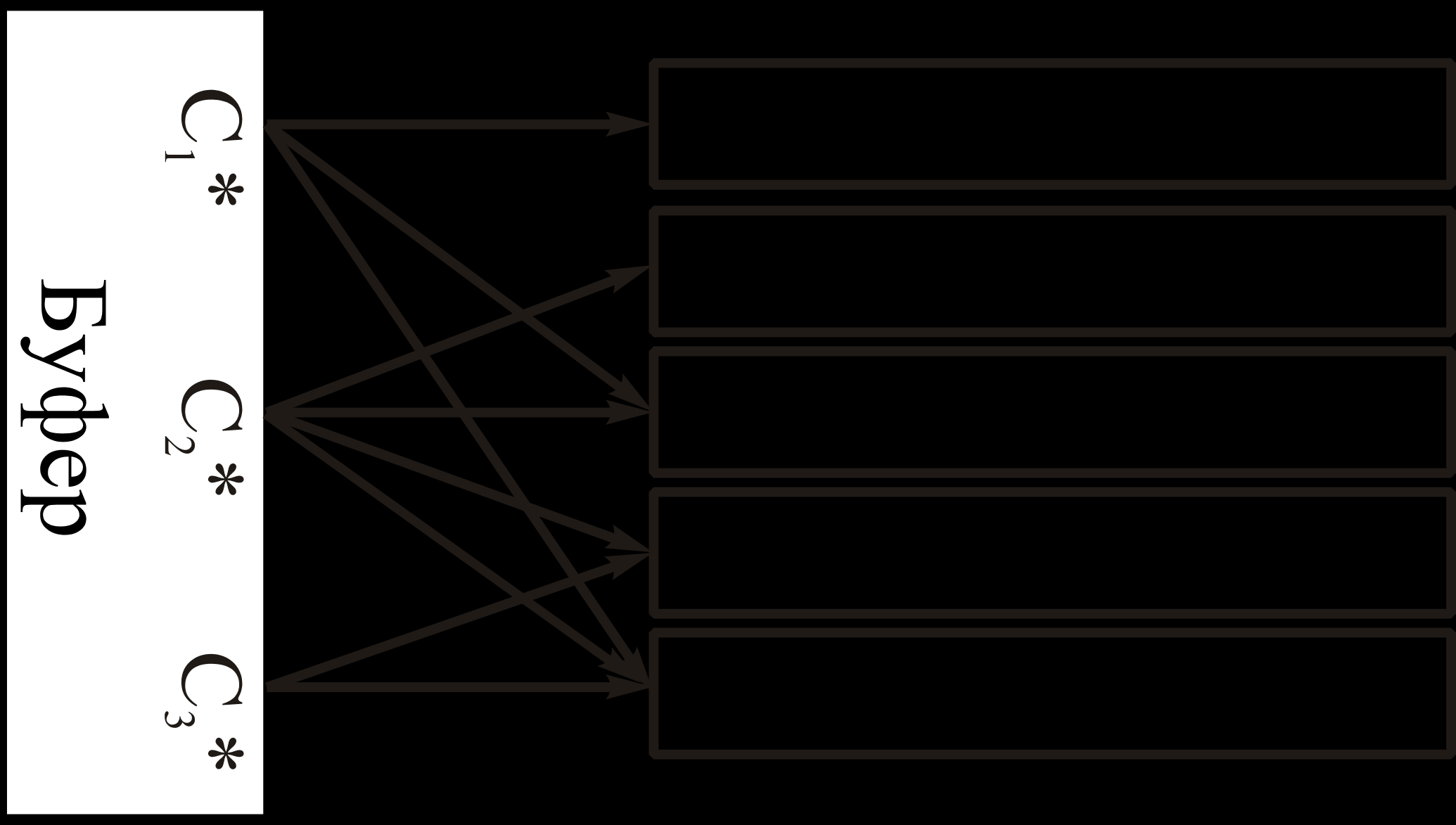Рис. 7. Схема декодирования
в ГРОС СКК 2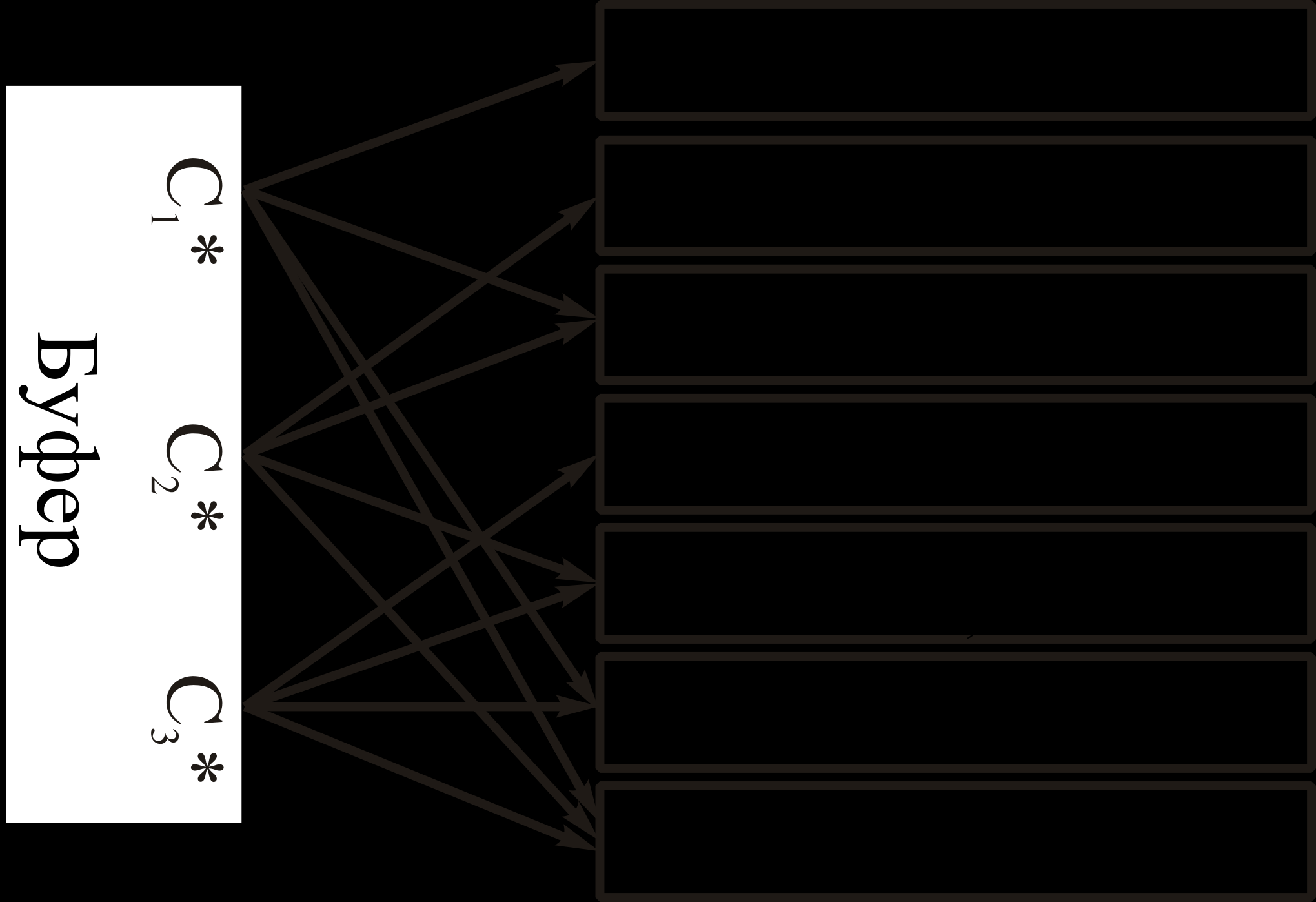

ис. 8. Схема декодирования
в ГРОС СКК 3

Поиск параметров свёрточного кодирования

После анализа вышеописанного принципа работы системы, ставилась задача поиска тройки полиномов, которые обеспечили бы максимальную помехоустойчивость системы. Для решения такой задачи необходимо было подобрать такие три полинома, парные сочетания которых давали бы максимальный выигрыш помехоустойчивости. Поиск лучших параметров свёрточного кодирования со скоростями 1/2 и 1/3 осуществлялся способом математического моделирования в системе Simulink. Для этого были созданы две модели: для скорости 1/2 и для скорости 1/3. Обе модели представляют собой упрощённую систему передачи без обратного канала, состоящую из источника сообщений, генератора CRC последовательности для проверки на ошибки, свёрточного кодера, канала
с независимыми ошибками, свёрточного декодера и детектора CRC. Стоит отдельно отметить, что перемежение в этом случае не применялось, т.к. группирование ошибок отсутствует. Основываясь на результатах имитационного моделирования, предложены три конфигурации свёрточного кодека для системы передачи с ГРОС-СКК (табл. 1).

Таблица 1. Лучшие конфигурации полиномов для системы ГРОС-СКК

Число ячеек регистра	1-ая попытка	2-ая попытка	3-яя попытка
5	(35)	(35, 23)	(35, 23, 27)
5	(37)	(37, 25)	(37, 33, 25)
7	(171)	(171, 133)	(171, 133, 165)

Имитационное моделирование. Для разработки имитационных моделей трёх стратегий системы ГРОС-СКК в среде MATLAB&Simulink создан свёрточный кодер и декодер Витерби, способный декодировать последовательности со скоростью 1, так как имеющиеся в Simulink готовые решения не позволяют производить такие операции. Блоки свёрточного кодека написаны на языке MATLAB в форме S функций второго уровня.

С помощью разработанных моделей проведено имитационное моделирование для стратегий декодирования системы ГРОС-СКК. Для моделирования были выбраны следующие параметры:

дискретный канал Гилберта P_gg = 0.995, P_bb = 0.93, вероятность ошибки в плохом состоянии p=1, средняя вероятность ошибки в канале P = 0.067;
свёрточный кодек: 5 ячеек регистра, полиномы (35, 23, 27), глубина декодирования – 15, включено дополнение нулями – «tail biting»;
длина информационной последовательности k = 300 бит;
проверка на ошибки: CRC-16;
объём выборки имитационного моделирования подбирался таким образом, чтобы доверительная вероятность была не менее 0.99.

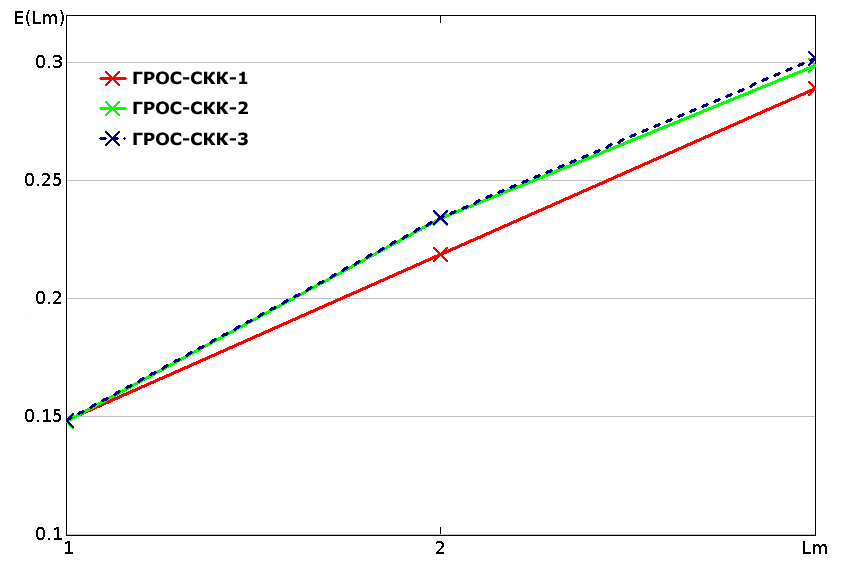
Рис. 9. Относительная скорость передачи после L_m попыток.

Сравнение стратегий декодирования ГРОС-СКК.

По результатам имитационного моделирования получены зависимости относительной скорости передачи после L_m попыток для трёх стратегий декодирования ГРОС-СКК. Как видно из полученного графика (рис. 9), стратегия ГРОС СКК 3 является наиболее выигрышной, но она является самой сложной по реализации и вычислительным затратам, так как использует больше свёрточных декодеров. Простейшая по реализации стратегия ГРОС-СКК-1 показывает худшие результаты. Стоит заметить, что различие показателей вероятности успешной доставки систем ГРОС-СКК-3 и ГРОС-СКК-2 наблюдается только лишь
в третьей попытке и для выбранных параметров системы составляет всего 1 %, поэтому в большинстве случаев достаточно применять ГРОС-СКК-2, так как эта система проще и требует меньше затрат элементной базы.

В третьей главе рассматриваются системы с гибридной решающей обратной связью и комбинированным корректирующим кодированием (ГРОС ККК). На рис. 10 представлена структурная схема одной из таких систем. Название системы обусловлено совмещением свёрточного и блочного кодирований.

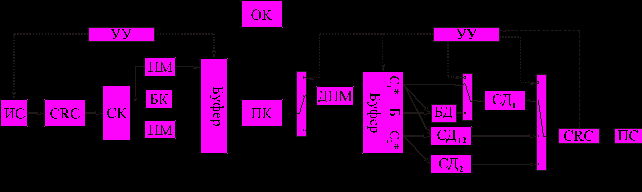
Рис. 10. Структура системы передачи данных ГРОС-ККК-1

Из ИС информационная последовательность поступает в CRC кодер, где кодируется кодом с высокой обнаруживающей способностью. Далее информационная последовательность вместе с проверочными элементами поступает на СК. В СК n-элементная последовательность кодируется со скоростью 1/2, а последовательности длиной n+z элементов с выхода каждого сумматора перемежаются
в ПМ, формируя последовательности C₁ и C₂ , которые записываются в буфер. Кроме того, последовательность из n+z с первого сумматора поступает в блочный кодер (БК), где кодируется блочным кодом с высокой исправляющей способностью (например, кодом БЧХ или Рида – Соломона), а получившиеся проверочные элементы r₂ записываются в буфер.

Сначала в ПК передаётся последовательность С₁ с первого сумматора свёрточного кодера. На приёмной стороне последовательность поступает на ДПМ и записывается в буфер. В СД₁ последовательность декодируется со скоростью свёрточного кода 1 и поступает в CRC декодер, где проверятся на ошибки.

Если в декодированной информационной последовательности были обнаружены ошибки, УУ приёма отсылает отрицательную квитанцию. УУ передачи, приняв отрицательную квитанцию, подаёт команду буферу, который отсылает последовательность r₂, содержащую проверочные элементы блочного кода. Стоит заметить, что эта последовательность не перемежается. На приёмной стороне результат объединения последовательности С₁* с r₂ декодируется в БД, а результат декодирования декодируется со скоростью 1 в СД₁, после чего проверяется
на ошибки.

При неудаче во второй попытке инициируется третья, в которой происходит передача последовательности C₂, которая проходит через ДПМ на приёмной стороне. Принятые последовательности С₁* и С₂* декодируются в СД₁₂ со скоростью 1/2, декодированная последовательность проверяется на ошибки в CRC декодере. Кроме того, последовательность С₂* декодируется отдельно в СД₂ со скоростью 1, после чего проверяется на ошибки. После этой попытки система переходит к обработке следующей информационной последовательности независимо от успеха либо неудачи. Назовём такую систему ГРОС-ККК-1.

Анализ взаиморасположения блочного и свёрточного кодов в системе ГРОС-ККК-1 позволяет сделать следующие выводы. При приёме последовательности С₁* с числом ошибок, превышающим исправляющую способность кода (t_и), передача r₂-элементной корректирующей группы в следующей попытке нецелесообразна, так как блочный код в этом случае только размножит ошибки. Наоборот, применение свёрточного кодирования во второй попытке позволит если не исправить, то уменьшить число ошибок в n элементной последовательности, которую впоследствии можно будет попытаться исправить блочным кодом. Исходя из этого предлагается система передачи ГРОС-ККК-2.

ГРОС ККК 2 (рис. 11) отличается от предыдущей тем, что n элементная последовательность кодируется параллельно в СК со скоростью 1/2 и в БК. Последовательности с выхода каждого сумматора СК перемежаются и записываются в буфер вместе с вычисленной в БК r₂-элементной корректирующей группой.
В первой попытке передаётся перемежённая последовательность С₁, во второй – перемежённая последовательность С₂, в третьей – корректирующая группа r₂.
На приёмной стороне в первой попытке принятая и деперемежённая последовательность С₁* декодируется со скоростью 1 в СД₁. Во второй – последовательности С₁* и С₂* декодируются со скоростью 1/2 в СД₁₂, а С₂* co скоростью 1 в СД₂. В третьей – результат декодирования СД₁₂ и r₂-элементная корректирующая группа декодируются в БД.

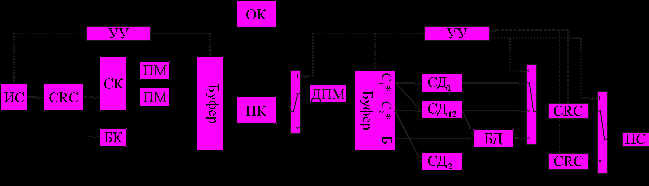
Рис. 11. Структура системы передачи данных ГРОС-ККК-2

Для того чтобы оценить ВВХ предложенных систем ГРОС-ККК, были созданы имитационные модели в среде Simulink.

В четвёртой главе производится сравнение всех рассмотренных систем передачи данных методом имитационного моделирования с помощью разработанных моделей в среде Simulink. Параметры моделируемых систем (табл. 2) подобраны таким образом, что r₂≈ n, что позволяет сравнивать системы по показателям вероятности успешной доставки. Кроме того, объём выборки имитационного моделирования подбирался таким образом, чтобы доверительная вероятность была не менее 0.99.

В качестве модели канала выбран дискретный канал с группирующимися ошибками, описываемый моделью Гилберта. Данный дискретный канал соответствует каналу с релеевскими замираниями, что типично для радиоканалов.

Имитационное моделирование СПД проводилось для двух случаев: типичного радиоканала и сильно зашумлённого радиоканала. Параметры канала Гилберта для типичного радиоканала: P_gg=0.995; P_bb=0.93; вероятность ошибки
в плохом состоянии p=0.5, что соответствует средней вероятности ошибки 0.0333. Параметры канала Гилберта для сильно зашумлённого радиоканала: P_gg=0.99; P_bb=0.93; вероятность ошибки в плохом состоянии p=0.8, что соответствует средней вероятности ошибки 0.1.

Объём выборки при моделировании составлял 1 миллион блоков.

Таблица 2. Параметры моделируемых систем

Система передачи	Длина ИП k, элементов	Параметры кодов
Система передачи	Длина ИП k, элементов	Свёрточного	Блочного	CRC
ГРОС БКК	243	--	БЧХ [259, 511], t = 30	CRC-16
ГРОС СКК (5)	243	Полиномы (35, 23, 27), z=4, глубина декодирования – 20z кодовых слов	--	CRC-16
ГРОС СКК (7)	243	Полиномы (171, 133, 165), z=6, глубина декодирования – 20z кодовых слов	--	CRC-16
ГРОС ККК 1 (5)	239	Полиномы (35, 23), z=4, глубина декодирования – 20z кодовых слов	БЧХ [259, 511]	CRC-16
ГРОС ККК 2 (5)	243	Полиномы (35, 23), z=4, глубина декодирования – 20z кодовых слов	БЧХ [259, 511]	CRC-16
ГРОС ККК 1 (7)	237	Полиномы (171, 133), z=6, глубина декодирования – 20z кодовых слов	БЧХ [259, 511]	CRC-16
ГРОС ККК 2 (7)	243	Полиномы (171, 133), z=6, глубина декодирования – 20z кодовых слов	БЧХ [259, 511]	CRC-16
РОС	243	--	--	CRC-16

На рис. 12 и 13 показаны результаты моделирования описанных в диссертации систем передачи данных с ГРОС и результаты теоретического расчёта для классической системы с решающей обратной связью (РОС). Гистограммы отображают зависимость вероятности успешной доставки информационной последовательности (P_уд) от количества попыток передачи (L_m).

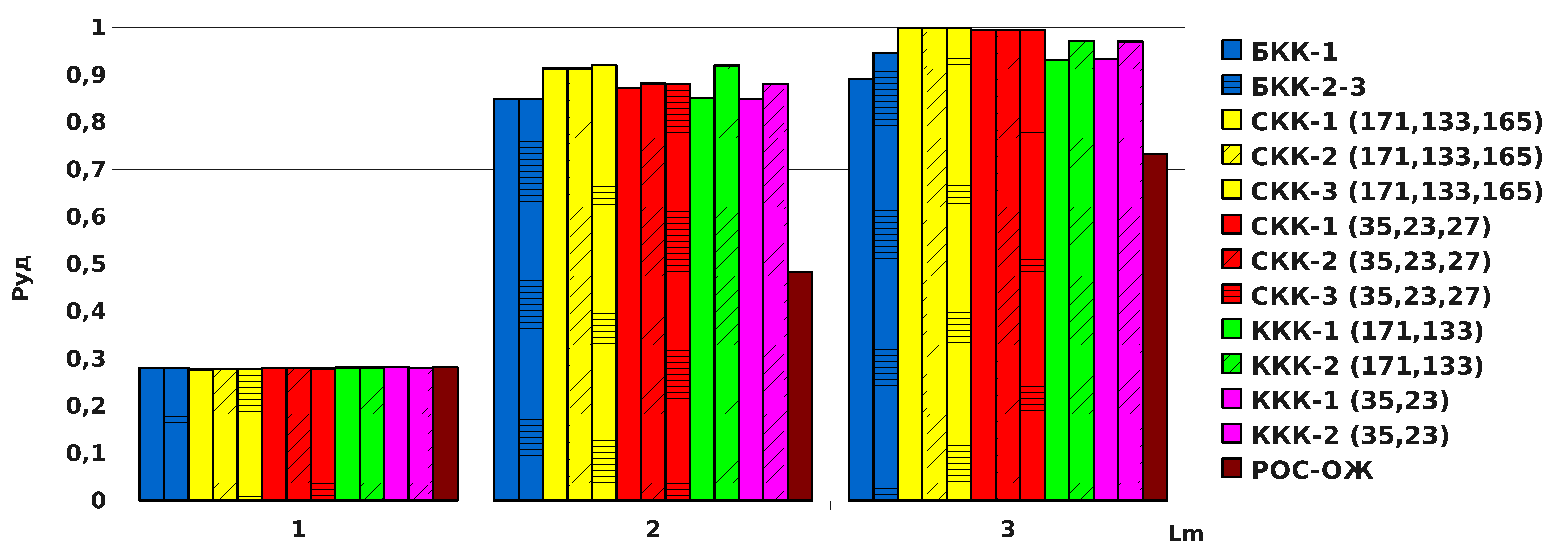
Рис. 12. Результаты моделирования для типичного радиоканала

Рис. 13. Результаты моделирования для сильно зашумлённого радиоканала

Анализ гистограмм (рис. 12 и 13) позволяет сделать следующие выводы.

В первой попытке все вероятности успешной доставки примерно равны, так как длины последовательностей в первой попытке практически для всех систем одинаковы, а исправление ошибок не производится.

По результатам второй попытки системы ГРОС-СКК-1 и ГРОС-ККК-1 имеют одинаковые показатели, так как в первых двух попытках их принцип работы одинаков. Однако во второй и третьей попытке лучшие показатели имеют системы ГРОС СКК (171, 133, 165). Их средний выигрыш по сравнению с другими системами в сильно зашумлённом радиоканале составляет 26 % после второй
и 52 % после третьей попытки.

Выигрыш ГРОС-ККК-2 по сравнению со средними показателями систем ГРОС-БКК составляет 8 % во второй и 5 % в третьей попытке для типичного радиоканала, 50 % во второй и 32 % в третьей попытке для сильно зашумлённого.

Средний выигрыш гибридных систем в сильно зашумлённом радиоканале после третьей попытки по сравнению с классической системой с РОС составляет 57 % для ГРОС-БКК, 196 % для ГРОС СКК (35, 23, 27), 228 % для ГРОС СКК (171, 133, 165), 86 % для ГРОС ККК (171, 133) и 84 % для ГРОС-ККК (35, 23).

Таким образом, системы с ГРОС позволяют в разы повысить верность доставки и эффективность использования канала в сравнении с классической системой с решающей обратной связью.

В заключении сформулированы основные результаты работы, которые состоят в следующем:

Предложены три схемы декодирования для ГРОС-БКК.
Разработаны математические модели для оценки ВВХ систем ГРОС БКК.
Разработаны алгоритмы имитационного моделирования систем ГРОС-БКК в среде MathCAD, позволяющие производить оценку ВВХ систем, используя границы Хемминга.
Разработаны модели систем передачи ГРОС-БКК-1 и ГРОС-БКК-2 в среде Simulink, использующие корректирующий код БЧХ и обнаруживающий ошибки CRC код.
Предложены альтернативные варианты систем ГРОС-БКК и произведено сравнение их ВВХ с классическими стратегиями.
Предложены три схемы декодирования для систем ГРОС-СКК.
Для систем ГРОС-СКК с кодовым ограничением 4 и 6 произведён подбор трёх полиномов, парные сочетания которых дают максимальный выигрыш помехоустойчивости.
В среде Simulink разработаны кодер и декодер Витерби, поддерживающие скорость кода 1, необходимую для систем ГРОС-СКК.
Предложена архитектура систем передачи данных с ГРОС, в которой используется комбинирование свёрточного и блочного кодирований, ГРОС ККК.
В среде Simulink разработаны имитационные модели систем ГРОС-ККК и ГРОС-СКК для дискретного канала, позволяющие получать ВВХ систем.
Проведено моделирование и сравнение ВВХ рассмотренных систем
с ГРОС на различных уровнях зашумлённости канала. Приведены оценки выигрышей одних систем относительно других.

В приложении приведены листинги программ, разработанных в средах MATLAB&Simulink и MathCAD.

Список работ автора по теме диссертации:

Мелентьев О.Г., Шапин А.Г., Оценка эффективности модифицированных алгоритмов декодирования в системах передачи данных с гибридной обратной связью. «Электросвязь», № 8, Москва: 2008, стр. 51-53.
Krasheninnikov P., Karpilev M., Shapin A. Sharing Hopping and Interleaving Processes in Channels, Described by Simplified Fritchman Model. International Workshop and Tutorial on Electron Devices and Materials, Novosibirsk, 2007,
pp. 199-200.
Shapin A. Model building data transmission system HARQ-CCC in environment Simulink. International Workshop and Tutorial on Electron Devices and Materials, Novosibirsk, 2008, pp. 170-172.
Шапин А.Г. Разработка универсального свёрточного кодека для скорости 1/n в среде моделирования Simulink. Информатика и проблемы телекоммуникаций, Материалы конференции РНТК, Том 1, Новосибирск 2008, стр. 271-274.
Шапин А.Г. Поиск лучших параметров свёрточного кодирования для систем ГРОС-СКК // Информатика и проблемы телекоммуникаций: Материалы конференции РНТК, Том 1. – Новосибирск, 2009. – стр. 220 222.
Мелентьев О.Г, Шапин А.Г. Универсальный свёрточный кодек для моделирования гибридных систем передачи данных // Надёжность функционирования и проблемы информационной безопасности телекоммуникационных систем железнодорожного транспорта: Межвуз. тематич. сб. науч. тр. ОГУПС. – Омск, 2009. – стр. 36-40.
Шапин А.Г. Результаты моделирования систем передачи данных с гибридной обратной связью и различными типами корректирующего кодирования, «Электросвязь», № 2, Москва: 2010, стр. 44-47
Shapin A., Modeling HARQ System with convolution and block codes // Modern Problems of Nanoelectronics, Micro- and Nanosystem Technologies, INTERNANO 2009, pp. 65-66.
Клейко Д.В., Лямин Н.В., Шапин А.Г., «Математическая модель широко-вещательной системы с гибридной обратной связью и адаптивным исправлением ошибок» // Современные проблемы технических наук: Сборник тезисов докладов Новосибирской межвузовской конференции «Интеллектуальный потенциал Сибири». - Новосибирск, 2010.

Подписано в печать 06.05.2011,

Формат бумаги 60х84/16, отпечатано на ризографе, шрифт №10,

идз. л. 1,0 заказ №28, тираж 100. СибГУТИ

6

30102, Новосибирск, ул. Кирова, 86

Blog

Анализ и разработка моделей систем передачи данных с гибридной решающей обратной связью

Содержание