Пятая подобие и моделирование процессов конвективного теплообмена

Вид материала

Документы

Содержание N характеризует возможность передачи теплоты от одного теплоносителя другому в данном теп-лообменном аппарате. Физический смысл F и при этом заданы k, W

Подобный материал:

• М. А. Моисеенко моделирование процессов теплообмена в дисковом тормозе скоростного, 125.47kb.
• Интенсификация конвективного теплообмена в промышленных циклонных секционных нагревательных, 634.11kb.
• Д. Б. Сполдинг 1 и В. И. Артёмов, 482.05kb.
• Численное моделирование и разработка комплекса программ исследования теплообмена, 466.89kb.
• Лекция Моделирование физических процессов, 111.71kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Лекции по дисциплине «Социальное моделирование и программирование», 44.69kb.
• Закономерности теплообмена и диагностика загрязнений термоанемометрической нити, 95.5kb.
• Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
• Вторая Международная научная конференция моделирование нелинейных процессов и систем, 145.53kb.

§ 67. Использование безразмерных характеристик для расчета теплообменных аппаратов

Переменные величины, входящие в уравнения тепло­вого баланса и теплопередачи (температуры горячего и холодного теплоносителей, их полные теплоемкости массового расхода, коэффициент теплопередачи) могут быть сгруппированы в безразмерные параметры (ха­рактеристики), обладающие определенным физическим смыслом. Некоторые из этих характеристик уже встре­чались при изучении теплового расчета теплообменни­ков, основанного на совместном решении уравнений теплового баланса и теплопередачи.

Эффективность (КПД) теплообменника определяет­ся выражением:



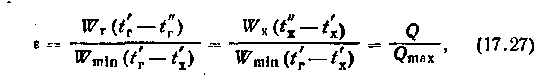
где W_min — наименьшая из величин W_г и W_x.

Эффективность  выражает соотношение между фактически переданным количеством 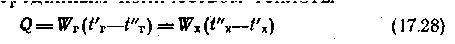теплоты

и максимально возможным количеством теплоты Q_maх, переданным в идеальном противоточном теплообменнике с бесконечно большой площадью поверхности теплооб­мена;

при W_хг:



при W_гx:

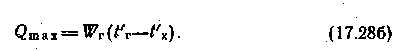
При заданных рабочих параметрах t'_г, t'_x, W_г, W_x величина  полностью определяет условия теплообмена между теплоносителями. Так, если W_г=W_min, то величи­на = (t'_г—t"_г)l(t'_г—t'_x) может трактоваться как темпе­ратурный КПД процесса охлаждения горячей жидкости, а при W_х— W_min величина =(t"_x—t'_x)/(t'_г—t'_x) харак­теризует эффективность процесса нагревания холодной жидкости.

Следующий безразмерный параметр — число единиц переноса теплоты N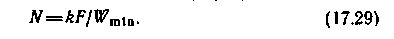определяется по формуле

Величина N характеризует возможность передачи теплоты от одного теплоносителя другому в данном теп-лообменном аппарате.

Физический смысл величины N, а также ее взаимо­связь с эффективностью  характеризуются кривыми, по­казанными на рис. 17.6. Очевидно, что для заданного со­отношения полных теплоемкостей при малых N низка и эффективность  теплообменника. При увеличении пара­метра N эффективность  повышается и приближается к пределу, определяемому схемой движения теплоносите­лей. Зная величину N, включающую в себя площадь по­верхности теплообмена F и коэффициент теплопередачи k [см. формулу (17.29)], моожно оценить степень повы­шения величины  с учетом капитальных затрат, массы и объема аппарата для заданной площади поверхности теплообмена, а также затрат энергии на преодоление гидравлического сопротивления при повышении коэффи­циента теплопередачи.

Если пренебречь термическим сопротивлением стенки, то формула (17.11а), определяющая полное термическое сопротивление теплопередаче, может быть преобразова­на в следующее выражение:

где L — рабочая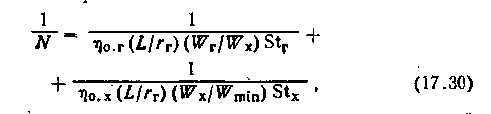длина поверхности нагрева; r_г — гидравлический

радиус, определяемый с учетом площади свободного сечения f_c по формуле r_г=f_сL/F; St_г и St_x — числа Стентона, рассчитываемые по определяющим температурам холодного и горячего теплоносите­лей.

Третья безразмерная характеристика W_min/W_max— отношение полных теплоемкостей массовых расходов теплоносителей. Перечисленные безразмерные парамет­ры могут быть связаны в единое уравнение для каждой из возможных схем движения потоков теплоносите­лей, т. е.

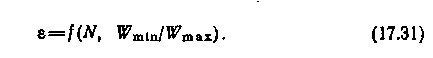
Рассмотрим противоточный теплообменник, темпера­турные условия в котором схематически представлены на рис. 17.3. Предположим, что для него W_г/W_х<1, т. е. W_г= W_min. Исходя из теплового баланса, получаем:



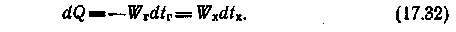
или

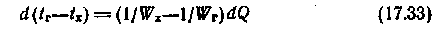
Очевидно, что можно построить так называемую «ра­бочую» линию, выражающую зависимость t_г от t_x для случая W_x/W_г= const. Эта «рабочая» линия нанесена на рис. 17.7. Ее наклон определяется отношением dt_г/dt_x— =W_х/W_г=m₀=const>1. При t_г = t_x существует равно­весие между двумя потоками теплоносителей; линия, вы­ражающая это равновесие, также представлена на рис. 17.7, она проходит через начало координат.

Из определения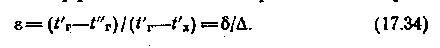эффективности и из рис. 17.7 следует:

Решая совместно уравнения (17.33) и (17.1), полу­чаем

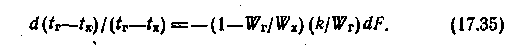
Интегрирование этого выражения в пределах темпе­ратур входа и выхода горячей жидкости приводит к сле­дующему уравнению:



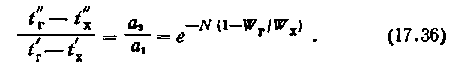
В соответствии с рис. 17.7 можно получить равенства:



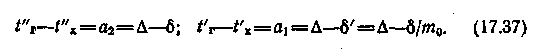
Такимобразом,

Решая совместно уравнения (17.36) и (17.38), получаем окончательно



По этому уравнению построен график на рис. 17.6.

Анализ зависимости =f(N) для противоточного теп­лообменника приведен выше. Следует добавить, что меньшее соотношение полных теплоемкостей теплоноси­телей позволяет получить большую эффективность при заданном значении N.

На практике встречаются два предельных вида урав­нения (17.39). Если в процессе передачи теплоты одна из жидкостей остается при постоянной температуре (ки­пение или конденсация), то ее полная теплоемкость бес­конечно велика, т. е. W_min/W_max= 0 и при этом



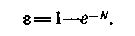
Если W_x=W_г, т. е. W_min/W_max= 1, то уравнение (17.39) принимает вид: =N/(1+N).

Если при расчете теплообменника требуется опреде­лить необходимую площадь поверхности теплообмена F и при этом заданы k, W_x, W_г, конечные температуры и характер относительного движения потоков, то применя­ют схему расчета с использованием зависимости г = —f(N); в общем виде схема расчета приведена ниже.

По известным конечным температурам вычисляют эффективность , а также отношение W_min/W_max. Ис­пользуя зависимости для заданной схемы движения по­токов, по величине W_min/W_max определяют N. Площадь поверхности теплообмена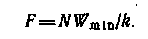F находят по формуле

При указанной формулировке задачи использование среднелогарифмической разности температур также не вызывает сложностей и трудоемкость расчета примерно такая же, как и при расчете по методу безразмерных характеристик.

В случае поверочного расчета теплообменника (см. § 64), когда необходимо определить температуры тепло­носителей на выходе из аппарата при заданных F, k, W_г, W_x, t'_г, t'_x, схема расчета по методу безразмерных харак­теристик будет выглядеть так. Используя исходные дан­ные, вычисляют N и отношение W_min/W_max. Далее по из­вестным N и W_min/W_max для данной схемы движения по­токов определяют величину . Тепловую мощность аппа­рата рассчитывают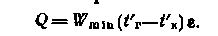по выражению

Значения конечных температур теплоносителей опре­деляют из уравнений:



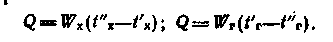
Метод безразмерных характеристик позволяет опре­делить эффективность работы теплообменных аппаратов различных типов. При этом появляется возможность учесть влияние различных факторов на эффективность работы аппарата: схемы движения теплоносителей, чис­ла ходов в перекрестноточных теплообменниках, а также наличия перемешивания теплоносителя (или течения его по отдельным параллельным каналам). Кроме того, этот метод позволяет установить, что перемешивание тепло­носителя с меньшей полной теплоемкостью массового расхода приводит к более высокой эффективности ра­боты теплообменника, а также оценить влияние отноше­ния полных теплоемкостей массового расхода теплоно­сителей на характеристики теплообменника-