Geum.ru

М. А. Моисеенко моделирование процессов теплообмена в дисковом тормозе скоростного вагона

Вид материалаДокументы

Содержание


Список литературы
Подобный материал:

Вестник Брянского государственного технического университета. 2011. № 4(32)

УДК 621.81.004.1:624.04


М. А. Моисеенко


МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ТЕПЛООБМЕНА В ДИСКОВОМ ТОРМОЗЕ СКОРОСТНОГО ВАГОНА


Представлены результаты численного моделирования теплового состояния деталей дискового тормоза скоростного вагона, полученные путём решения уравнения нестационарной теплопроводности в движущейся среде методом расщепления по физическим процессам. Показано доминирующее влияние конвективного переноса тепла на характер распределения температур в деталях тормоза.


Ключевые слова: численное моделирование, фрикционное торможение, дисковый тормоз, процессы теплообмена, конвективный перенос тепла.


Математическое моделирование представляет собой один из наиболее эффективных инструментов анализа теплового и напряжённо-деформированного состояний деталей фрикционных тормозов железнодорожного подвижного состава во время их проектирования и доводки. На сегодняшний день наибольшую сложность при построении расчётных схем этих деталей представляет моделирование процессов теплообмена в зоне фрикционного контакта. При упрощённом подходе к решению этой проблемы предполагается, что пульсирующий тепловой поток, возникающий из-за неполного перекрытия деталей, образующих пару трения, можно заменить постоянным, усредненным за время одного оборота тепловым потоком [1; 2]. При таком усреднении нарушаются подобия [3]. Недостоверность получаемых результатов делает модели, построенные на указанном допущении, непригодными для расчётов ответственных узлов трения.

Способ построения моделей, адекватно описывающих процессы теплообмена при сухом трении, был предложен Х. Блоком в 1937 г. [4] и состоит в использовании уравнения нестационарной теплопроводности в движущейся среде [5]:

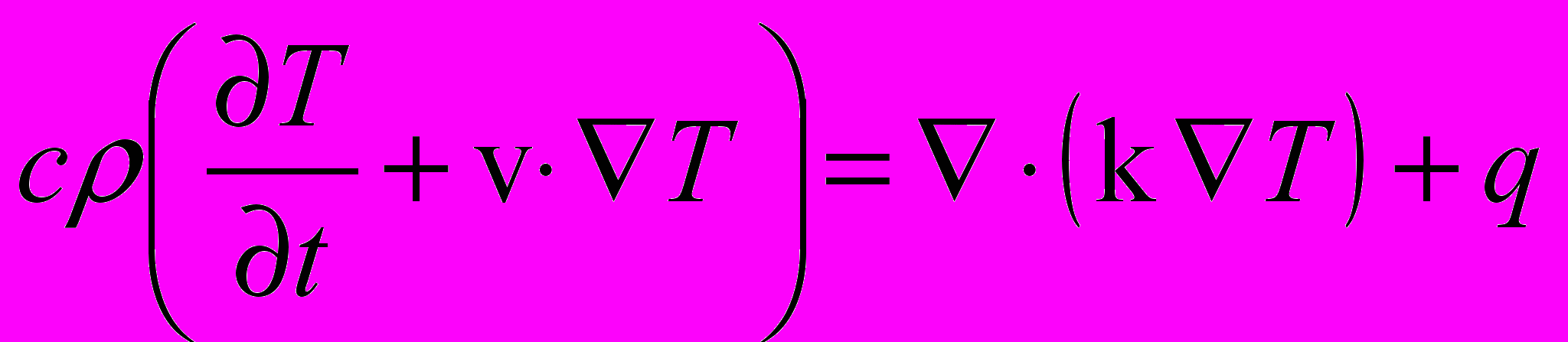, (1)

где c, ρ и k- теплоёмкость, плотность и теплопроводность материала среды соответственно; v- скорость движения среды; q- источник тепла; – оператор Гамильтона.

Наличие в уравнении (1) конвективного члена 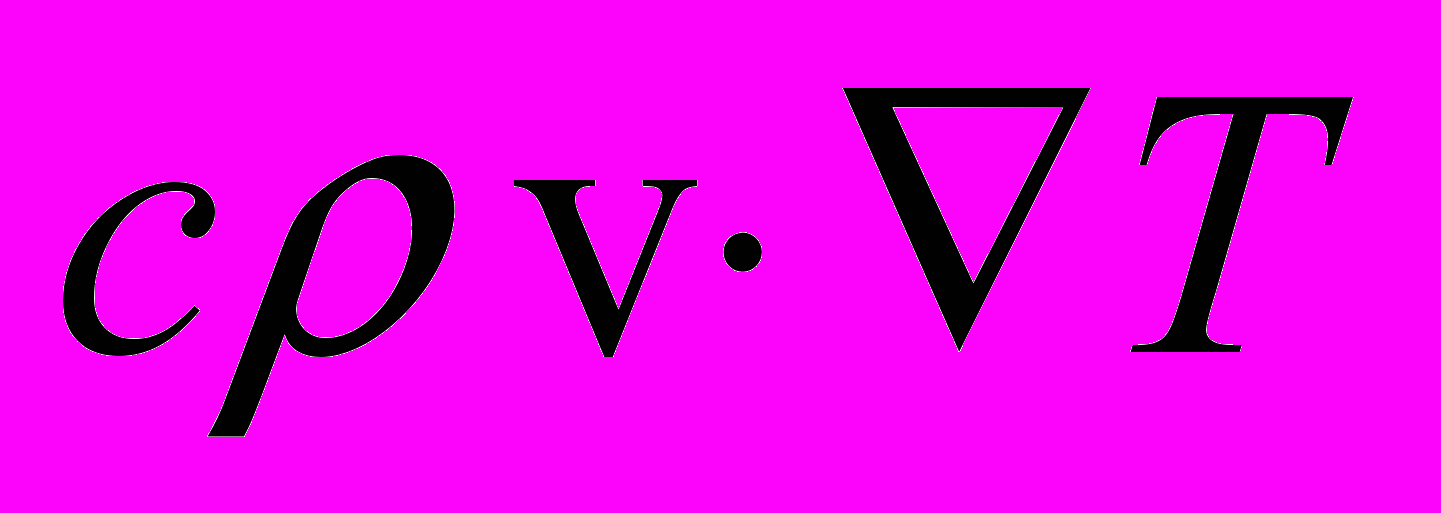позволяет учесть влияние скорости относительного движения тел, образующих пару трения, на распределение тепла, выделяющегося в зоне фрикционного контакта. По мнению Г. Берри и Д. Барбера [6], это открывает путь к изучению природы контактных явлений при скольжении.

В работах зарубежных авторов уравнение (1) широко используется для моделирования таких явлений, возникающих при фрикционном торможении, как термоупругая нестабильность (Thermoelastic Instability Phenomenon) [7] и появление на поверхностях трения деталей тормоза зон (пятен) с аномально высокой температурой (hot-spots) [8]. В указанных работах для получения решения уравнения (1) используются стабилизированные схемы галёркинского типа, среди которых предпочтение отдаётся методу Streamline Upwind Petrov-Galerkin (SUPG). Практическое использование этого метода связано с большими затратами на вычисление стабилизирующих членов и со сложностью выбора оптимального значения параметра стабилизации [9]. При внешнем трении твёрдых тел задача транспорта тепла решается относительно просто [10]. В этом случае хорошей альтернативой методу SUPG могут стать методы расщепления [11].

В настоящем исследовании для решения уравнения (1) использовался метод расщепления по физическим процессам [12]. Описание этого метода упрощается при использовании операторной записи уравнения (1):

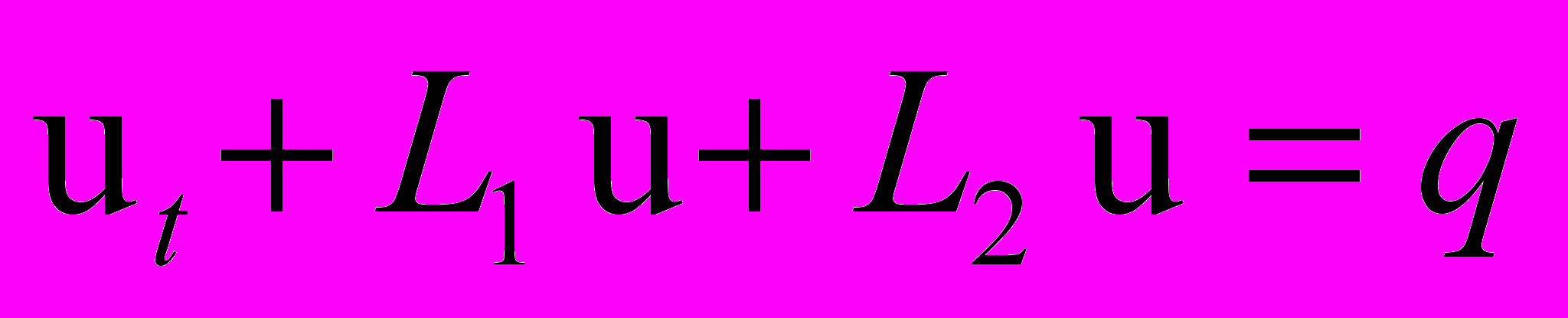, (2)

где ;; ; .

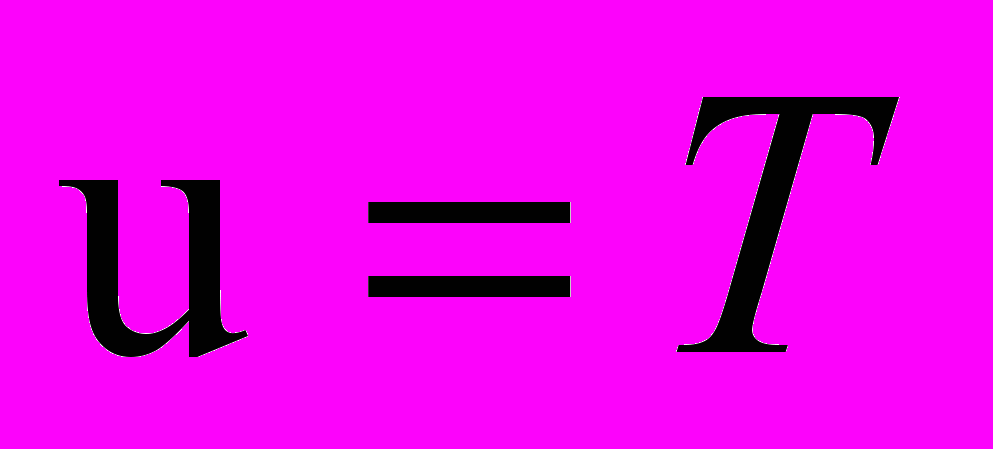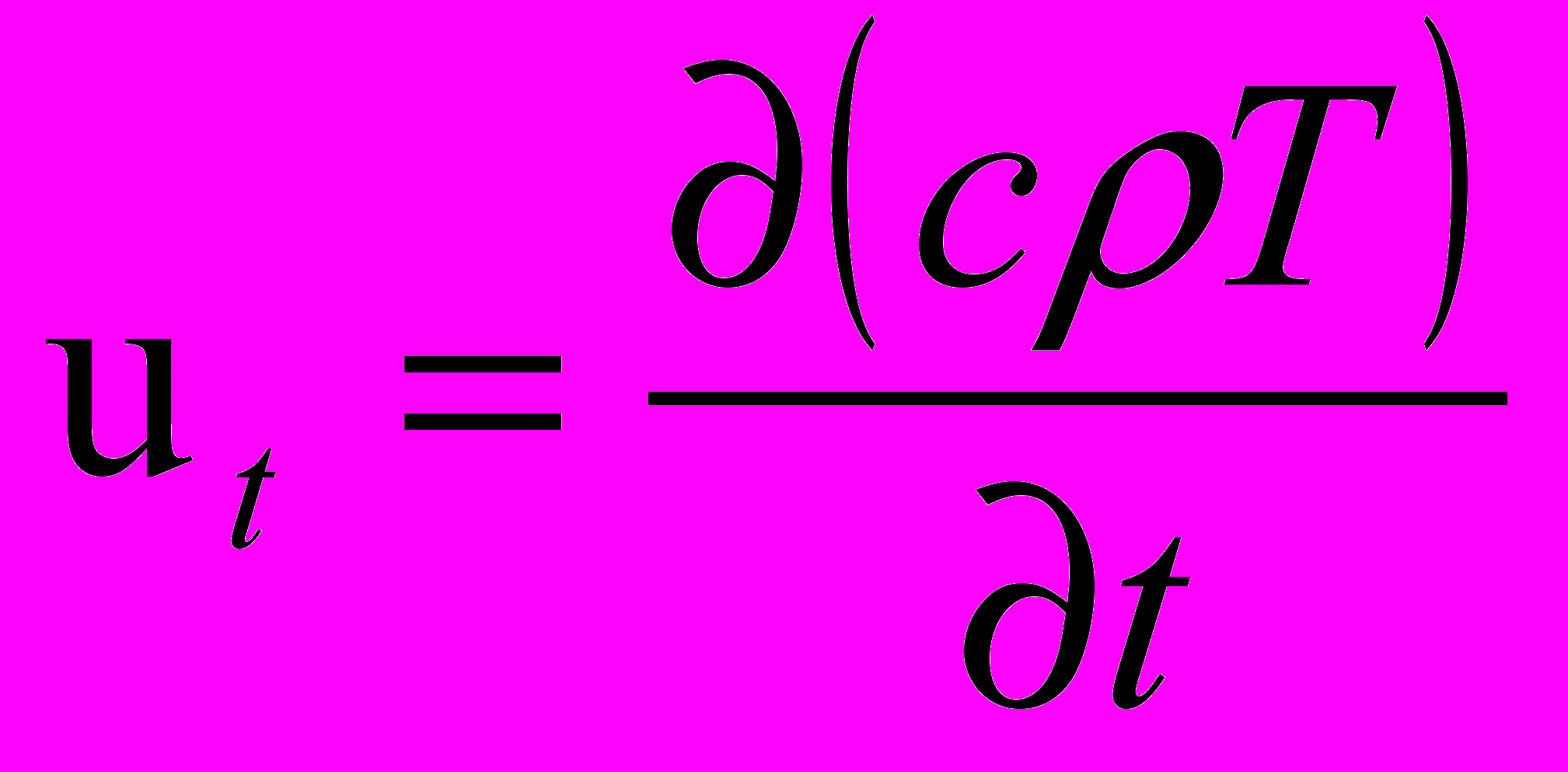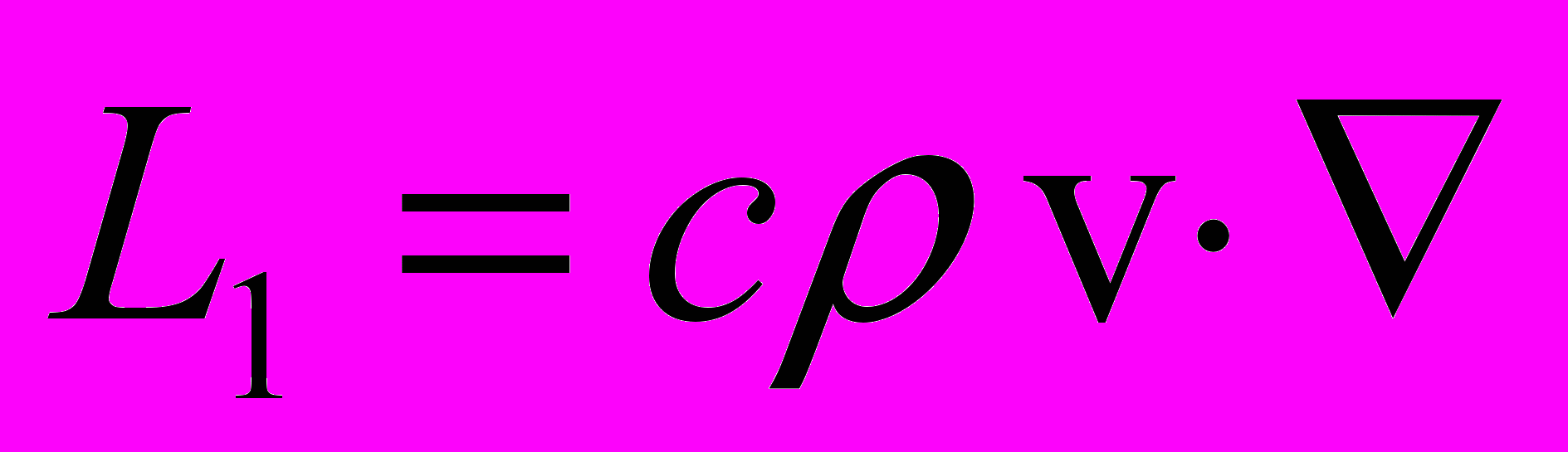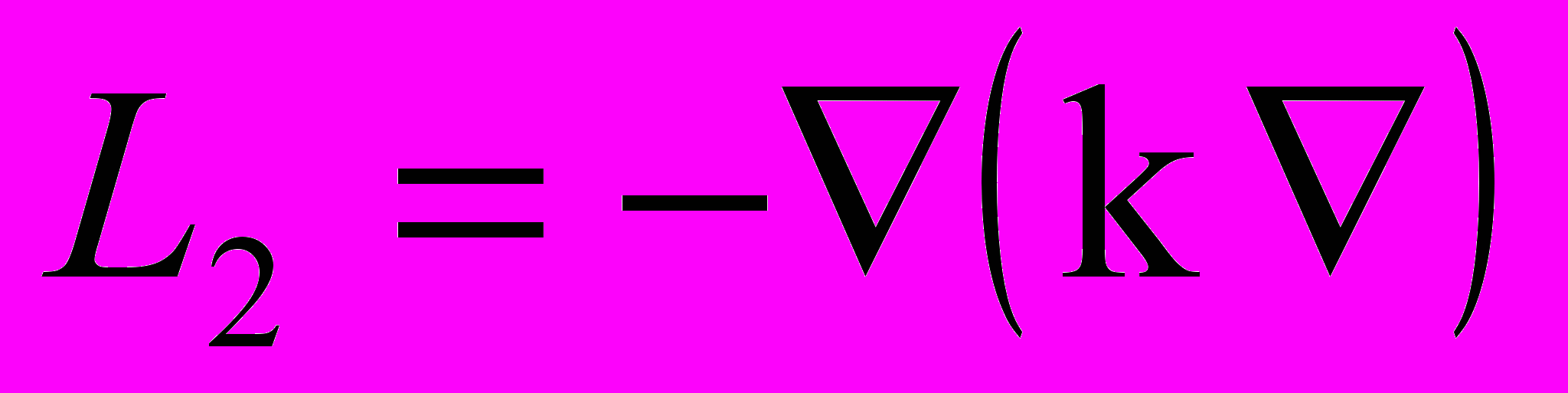Алгоритм решения уравнения (2) состоит в последовательном выполнении следующих шагов:

Шаг 1: vt + L1v = 0; v(tn) = un. (3)

Шаг 2: wt + L2w = q; w(tn) = vn+1. (4)

Шаг 3: un+1= wn+1.

На шаге 1 решается гиперболическое уравнение (3), описывающее конвективный перенос тепла (без теплообмена между частицами тела (среды)). На шаге 2 решается уравнение нестационарной теплопроводности в неподвижной среде (без конвективного члена) (4), которое описывает процессы теплопроводности (диссипации тепла) в теле (среде). Переход на новый временной слой происходит на шаге 3.

Для твёрдого тела решение задачи (3) тривиально. Оно сводится к нахождению значений температур в узлах сетки, смещенных в положение, которое они занимали на предыдущем шаге по времени. Для равномерной сетки эта процедура описана в [10]. Для нерегулярных сеток со сложной топологией решение этой задачи сводится к геометрическому поиску и решению системы нелинейных уравнений для каждого узла конечноэлементной сетки.

Для получения дискретного аналога задачи (4) использовался метод частичной дискретизации [13], в котором дискретизация по пространству и по времени осуществляется разными методами. В настоящем исследовании для дискретизации по пространству использовался метод конечных элементов (МКЭ). Результатом конечноэлементной дискретизации уравнения (4) является система обыкновенных дифференциальных уравнений:

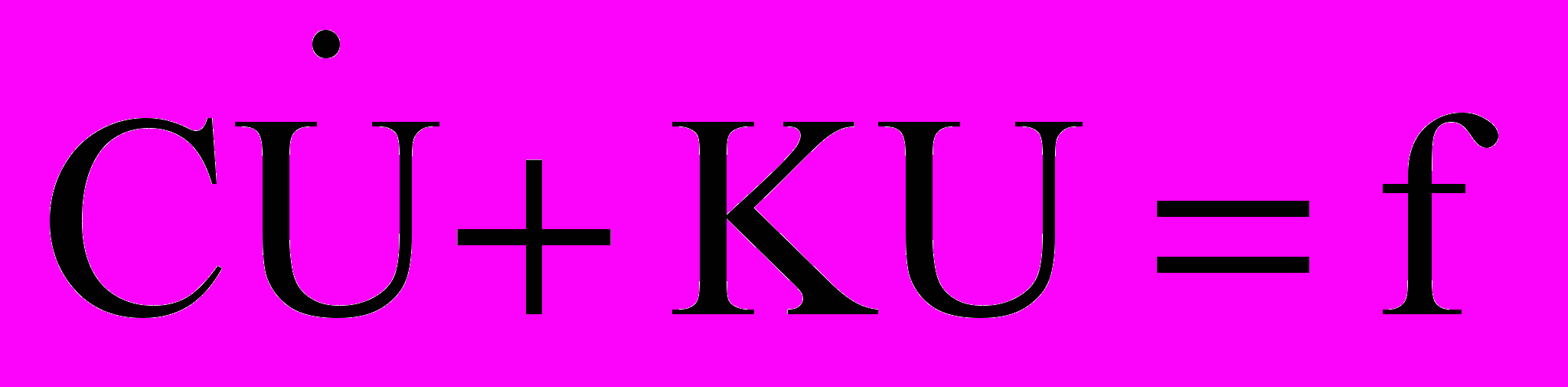, (5)

где С - глобальная матрица теплоёмкости; U - вектор узловых температур; K - глобальная матрица теплопроводности; f - глобальный вектор тепловых сил.

Для решения системы (5) использовались неявные многостадийные методы Рунге-Кутты 2-го [14] и 3-го [15] порядков точности. Эти методы были разработаны для решения задачи нестационарной теплопроводности с быстро меняющимися граничными условиями. Необходимость их использования вызвана высокой жёсткостью системы (5).

Для реализации рассмотренных методов был разработан специализированный комплекс программ. Он был использован для анализа полей температур и напряжений, возникающих в деталях дискового тормоза скоростного вагона Тверского вагоностроительного завода при экстренном торможении со скорости 160 км/ч. Время торможения до полной остановки принималось равным 52 с. Движение вагона считалось равномерно-замедлен­ным.

Конструкция тормоза показана на рис. 1. Тормозной диск 1 выполнен из жаропрочной стали 20Х13. Толщина диска - 40 мм, наружный диаметр - 620 мм, внутренний – 340 мм. С помощью разрезных втулок он крепится к ступице, насаженной на ось колесной пары. При торможении к торцевым поверхностям диска с обеих сторон с помощью клещевого механизма, воздействующего на башмак 2, прижимаются накладки 3. Материал накладок – износостойкая металлокерамика «Челябинск-8». Коэффициент трения для такой пары составляет 0,25 и мало зависит от скорости.

З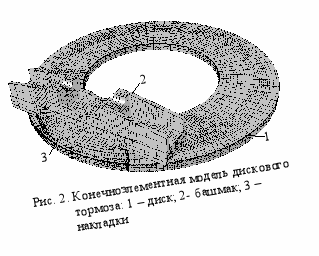еркальная симметрия конструкции этого тормоза позволяет ограничить область исследования одной из симметричных его половин (рис. 2). Указанная область была разбита на 24644 переходных конечных элемента сирендипова семейства шестигранных призм [16]. Чтобы учесть высокую неравномерность температурных полей, возникающих в деталях тормоза, их конечноэлементные сетки сгущались у поверхностей трения. Так, по толщине диска тормоза размер элементов менялся от 6 до 0,6 мм, а порядок их функций формы увеличивался со 2-го до 3-го (hp-схемы МКЭ). Для лучшей аппроксимации градиентов температуры промежуточные узлы на рёбрах кубических элементов были смещены по следующему принципу: чем ближе узел к поверхности трения, тем больше его смещение к ней (r- схемы МКЭ). В разработанной автором реализации МКЭ переходные элементы могут иметь от 0 до 2 промежуточных узлов на рёбрах [17]. Это позволяет управлять точностью аппроксимации исследуемой функции путём добавления или удаления промежуточных узлов на рёбрах элементов. Таким способом удалось достичь хорошей точности решения на оптимизированной сетке, имеющей 117836 узлов.

При моделировании температурных полей в деталях фрикционного тормоза возникают две фундаментальные проблемы: проблема определения количества тепла, выделяющегося в зоне фрикционного контакта, и проблема распределения этого тепла между деталями, образующими пару трения.

Интенсивность тепловыделения в зоне фрикционного контакта q можно вычислить по формуле

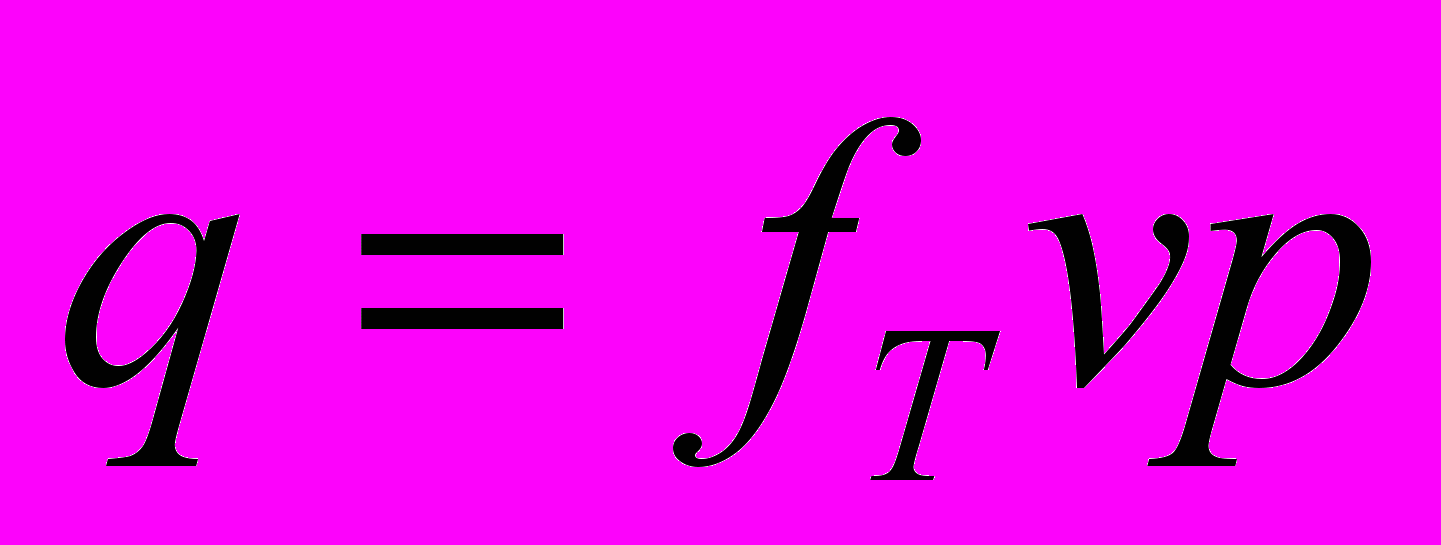, (6)

где fT – коэффициент трения; v – скорость движения состава; p – контактные давления.

Для определения контактных давлений использовался модифицированный метод Дирихле-Неймана [18], который позволяет решать задачи механического контакта с учётом трения. Расчёт выполнялся при силе нажатия на башмак 21 кН. Сложность расчёта состояла в том, что при торможении детали тормоза нагреваются и изменяют свою форму. Это, в свою очередь, приводит к перераспределению давлений между диском и накладками. По этой причине расчёт контактных давлений приходится повторять заново через несколько шагов по времени.

Вторая проблема более серьёзная. Она связана с определением пропорций, в соответствии с которыми следует распределять тепло, выделяющееся при трении, между деталями тормоза. Одно из решений этой проблемы вытекает из результатов, полученных И. В. Крагельским.

В 1939 г. И. В. Крагельский в основополагающей работе «О трении несмазанных поверхностей» [19] сформулировал основные особенности сухого трения. Он показал, что взаимодействие тел при трении сосредоточивается в некотором объёме материала, наделённом упруговязкими свойствами. Этот объём был назван «третьим телом». Чтобы реализовать модель «третьего тела», достаточно между диском и накладками ввести слой контактных элементов, объёмное тепловыделение в которых определяется по формуле (6). Таким образом удаётся решить проблему распределения тепла при внешнем трении, которая долгие годы остаётся камнем преткновения при моделировании температурных полей в деталях фрикционных тормозов.

Для неохлаждаемых дисковых тормозов теплоотдача в окружающую среду незначительна. Для её моделирования использовались граничные условия 3-го рода. Температура окружающей среды принималась равной нулю; коэффициент теплоотдачи выбирался по методике, описанной в работе [20]. Температура деталей тормоза в начале торможения считалась равной температуре окружающей среды. Шаг по времени составлял 2,1·10-4 с. Его значение выбиралось из условия устойчивости вычислительного процесса, которое требует, чтобы шага по времени и размеры элементов были согласованы [21]. Чтобы ослабить требования к размерам элементов, у поверхностей трения были размещены сингулярные кубические элементы.

В 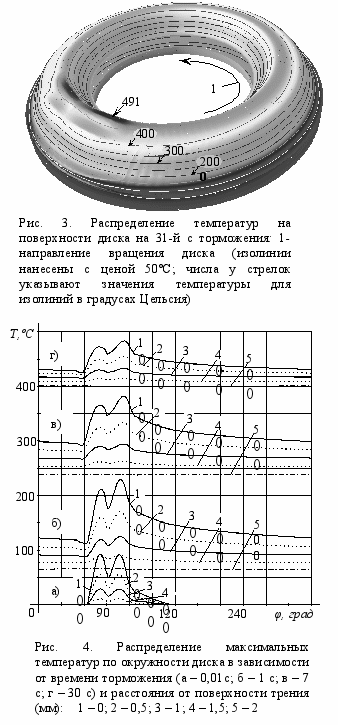результате проведённой серии расчётов было установлено, что максимум температуры в сопряжении «накладка-диск» тормоза достигает 491ºС на 31-й с торможения (рис. 3). В дальнейшем он снижается до 392ºС в конце торможения. Координаты точки, в которой температуры достигают максимума, постоянно меняются. В начале торможения он соответствует положению максимума контактных давлений, который из-за опрокидывающего момента смещен в направлении набегающего края башмака. Но уже через несколько миллисекунд он перемещается на 159 мм в направлении сбегающего края башмака, а затем медленно мигрирует в радиальном направлении. В результате миграции радиус точки поверхности диска уменьшается с 251 мм на 1-й с торможения до 202 мм на 40-й с, а затем на 50-й с вновь увеличивается до 223 мм. Такой характер изменения максимума температуры объясняется двумя факторами: сносом тепла от места его подвода в направлении вращения диска, что вызывает окружное смещение максимума температуры, и более быстрым прогревом внутренней части диска. Последний фактор и вызывает радиальные смещения максимума температуры.

Динамика изменения максимальных температур на поверхности диска по окружности и на разных глубинах в его теле показана на рис. 4. Очевидно, что пульсации температур возникают только в поверхностных слоях диска. На глубине 2 мм они полностью отсутствуют. Амплитуда колебаний температуры на поверхности диска достигает 46ºС на 1-й с торможения и затем постепенно уменьшается. Колебания температуры в несколько десятков градусов вызывают колебания интенсивности напряжений с амплитудой в сотни мегапаскалей (рис. 5, 6).

Поле температурных напряжений характеризуется более высокими темпами перестройки. Уже на 1-й с торможения уровень интенсивности напряжений достигает 681 МПа, а на 7-й с он проходит свой максимум 902 МПа. По мере прогрева деталей тормоза уровень интенсивности температурных напряжений начинает снижаться. В конце торможения он опускается до 372 МПа.

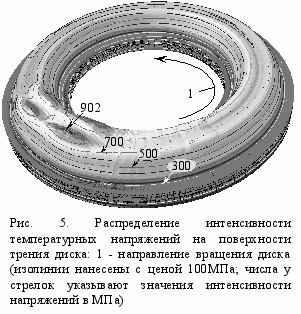
Н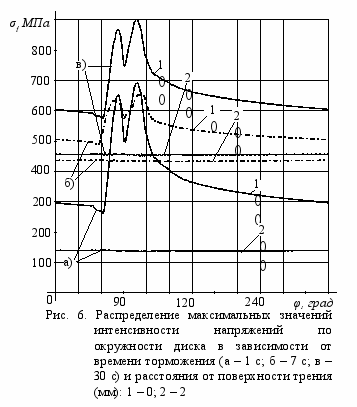ебольшие по величине растягивающие напряжения возникают на внешнем радиусе диска. На 7-й с их значение составляет 350 МПа. В остальной части диска напряжения сжимающие; в радиальном направлении они составляют 798 МПа, а в осевом - 940 МПа. Амплитуда колебаний интенсивности напряжений достигает 162 МПа при среднем значении 739 МПа. Высокий уровень напряжений в диске тормоза указывает на опасность образования трещин. Их причиной могут стать, с одной стороны, остаточные напряжения, вызванные сжимающими напряжениями, уровень которых превышает предел текучести стали 20Х13, а с другой – высокочастотные колебания их значений.

Из-за сложного характера теплового и механического нагружения прогнозирование долговечности и надежности диска тормоза представляет собой достаточно трудоёмкую задачу. Однако уже на основе представленных данных можно сделать вывод о том, что многих проблем в рассматриваемой конструкции тормоза можно было бы избежать, если бы для изготовления диска был использован материал с более высокой теплопроводностью. На сегодняшний день это наиболее эффективный способ уменьшить амплитуду колебаний температуры и напряжений в поверхностных слоях диска тормоза.


СПИСОК ЛИТЕРАТУРЫ
  1. Першин, В. К. Моделирование тепловых режимов при фрикционном взаимодействии колеса и тормозной колодки/ В. К. Першин, Л. А. Фишбейн // Транспорт Урала. - 2005. - №1(4). - C. 34-42.
  2. Титарёв, Д. В. Нестационарные температурные поля и напряжения в дисках тормозов железнодорожного подвижного состава / Д. В.Титарёв, В. И. Сакало // Транспорт Урала. - 2007. - №4(15). – С. 74-79.
  3. Щедров, В. С. Температурное поле фрикционной пары как основной параметр моделирования при испытании на трение и износ / В. С. Щедров, А. В. Чичинадзе, Г. И. Трояновская // Методы испытания на изнашивание. Труды совещания, состоявшегося 7-10 декабря 1960 года. - М.: Изд-во АН СССР, 1962. - С. 140-151.
  4. Крагельский, И. В. Развитие науки о трении. Сухое трение / И. В. Крагельский, В. С. Щедров. – М.: Изд-во АН СССР, 1956. – 237 с.
  5. Самарский, А. А. Вычислительная теплопередача / А. А. Самарский, П. Н. Вабищевич. – М. : Едиториал УРСС, 2003. - 784 с.
  6. Берри, Г. Распределение тепла, выделяемого при трении, - путь к изучению природы контактных явлений при скольжении/ Г. Берри, Д. Барбер // Труды американского общества инженеров - механиков. Серия «Проблемы трения и смазки». – 1984. - №3. – С. 83-96.
  7. Eltoukhy, M. Braking Process in Automobiles: Investigation of the Thermoelastic Instability Phenomenon / M. Eltoukhy, S. Asfour  // Department of Industrial Engineering, College of Engineering, University of Miami USA. – ссылка скрыта
  8. Chan, W. Analysis of Heat Dissipation in Mechanical Braking Systems/ W. Chan // Department of Mechanical and Aerospace Engineering University of California, San Diego. - MAE 221A - Heat Transfer, December 7, 2007. – 12 p. – ссылка скрыта
  9. Ольшанский, М. А. Равномерные по параметру многосеточные и итерационные методы: дис. ... д-ра физ.-мат. наук / М. А. Ольшанский. - М.: МГУ, 2006. - 284 с.
  10. Старостин, И. П. Численное решение задачи теплопроводности в парах трения с малым коэффициентом перекрытия / И. П. Старостин// Математическое моделирование. - 2005.- Т. 17. - № 7. - С. 23-30.
  11. Mapчук, Г. И. Методы расщепления / Г. И. Mapчук. - М.: Наука, 1988. – 264 c.
  12. Donea, J. Finite Element Methods for Flow Problems / J. Donea, A. Huerta. – Wiley, 2003. – 350 p.
  13. Зенкевич, О. Конечные элементы и аппроксимация / О. Зенкевич, К. Морган. – М.: Мир, 1986. – 318 с.
  14. Исполов, Ю. Г. Конечноэлементный анализ нестационарных полей температур в деталях ГТУ /  Ю. Г. Исполов, Н. Н. Шабров // Проблемы прочности. – 1989. - №12. - С. 82-87.
  15. Исполов, Ю. Г. Построение методов и организация алгоритмов численного интегрирования нестационарной задачи теплопроводности/ Ю. Г. Исполов , Е. А. Постоялкина, Н. Н. Шабров// Электронный журнал. Дифференциальные управнения и процессы управления. - 2002.- №2. - 25 c. -ru/journal/pdf/2002/vol2/j087.pdf
  16. Корнеев, В. Г. Схемы метода конечных элементов высоких порядков точности / В. Г. Корнеев. – Л.: Изд-во Ленингр. ун-та, 1977. – 208 с.
  17. Моисеенко, М. А. Решение задачи термоупругости с использованием переходных конечных элементов высокой точности / М. А. Моисеенко, Г. А. Неклюдова // Материалы XII Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред». Избранные доклады. – М.: Изд-во МАИ, 2006. – С. 121-124.
  18. Krause, R. H. A Dirichlet-Neumann Type Algorithm for Contact Problems with Friction / R. H. Krause, B. I. Wohlmuth // Computing and Visualization in Science. - 2002. - Vol. 5. - No 3. - P. 139-148.
  19. Крагельский,  И. В. О трении несмазанных поверхностей / И. В. Крагельский // Всесоюзная конференция по трению и износу в машинах.- M.: Изд-во АН СССР, 1939. - Т. I. - С. 543-561.
  20. Сакало, В. И. Контактные задачи железнодорожного транспорта /  В. И.Сакало,  В. С. Коссов. – М.: Машиностроение, 2004. – 496 с.
  21. Шимкович, Д. Г. Расчет конструкций в MSC.VisualNastran for Windows / Д. Г. Шимкович. - М.: ДМК Пресс, 2004. - 704 с.


Материал поступил в редколлегию 27.10.11.