Моделирование нелинейной системы управления мобильными объектами в среде Matlab
| Вид материала | Документы |
СодержаниеNCD Blockse |
- П. П. Порешин московский инженерно-физический институт (государственный университет), 23.75kb.
- Моделирование системы управления стеклоочистителем на базе нечеткого контроллера, 16.79kb.
- Математическое моделирование системы управления для управляемого выпрямителя на igbt-транзисторах, 26.76kb.
- Моделирование автоматизированной системы контроля и управления технологическими объектами, 35.31kb.
- Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
- Математическая модель тиристорного асинхронного электропривода в среде matlab, 183.43kb.
- Типография Издательства Мордовского университета 430000, Саранск, ул. Советская,, 365.09kb.
- Тема диссертационной работы, 45.86kb.
- Лабораторная работа на тему "Решение оду и систем оду в среде Simulink", 27.38kb.
- При выполнении сложных расчетных заданий в курсе теории автоматического управления, 83.98kb.
Моделирование нелинейной системы управления
мобильными объектами в среде Matlab
Шарипбаев А.А. д.т.н., профессор, заведующий кафедрой "Вычислительная техника" ЕНУ им Л.Н.Гумилева,
Атанов С.К., к.т.н, доцент кафедры «Компьютерные системы» КазАТУ им. С.Сейфуллина
Управление мобильными объектами с помощью любой инерциальной системы может рассматриваться как взаимодействие двух процессов: решения навигационной задачи и решения задачи стабилизации. Рассмотрим эту проблему на примере летательного аппарата, где данные задачи наиболее актуальны в связи с возможностью их автономной работы и высокими скоростями движения. Первая задача заключается в определении требуемой траектории летательного аппарата и в вычислении фактической траектории, вторая — в управлении аппаратом для поддержания требуемого курса с заданной точностью [1]. Так на рис 1. приведена типичная схема бесплатформенной системы управления космическим аппаратом для выхода на геостационарную орбиту. Подобный механизм используется для управления крылатыми ракетами. С бортовой цифровой вычислительной машиной 1 соединены три группы датчиков, условно обозначенных через Д1 , Д2 и Д3.
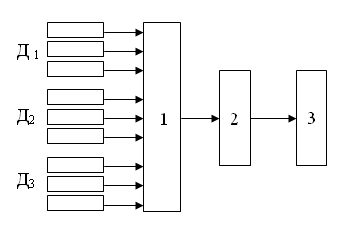
Рис. 1 - Схема бесплатформенной системы управления ориентацией:
1 – бортовая цифровая вычислительная машина;
2 – блок согласования;
3-исполнительные органы
Вырабатываемые в машине сигналы управления преобразуются должным образом в блоке согласования 2, после чего поступают на исполнительные органы системы ориентации 3. Воздействуя на динамику ракеты (в зависимости от работы исполнительных органов, изменяется его угловое движение, и на входе вычислительной машины появляются измененные сигналы датчиков системы ориентации). На приведенной схеме все датчики условно разбиты на три группы в зависимости от основной задачи, выполняемой ими в полете.
При этом задача системы стабилизации — обеспечить управление рулями и тягой таким образом, чтобы выполнить задаваемую программу полета с требуемой точностью. Ее структурная схема показана на рис. 2.
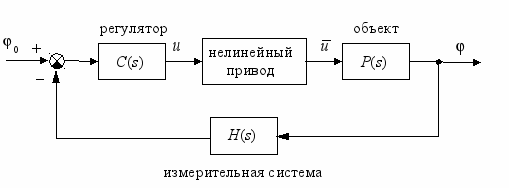
Рис 2.Структурная схема системы стабилизации ракеты на курсе
Линейная математическая модель, описывающая движение аппарата, имеет вид[2]:
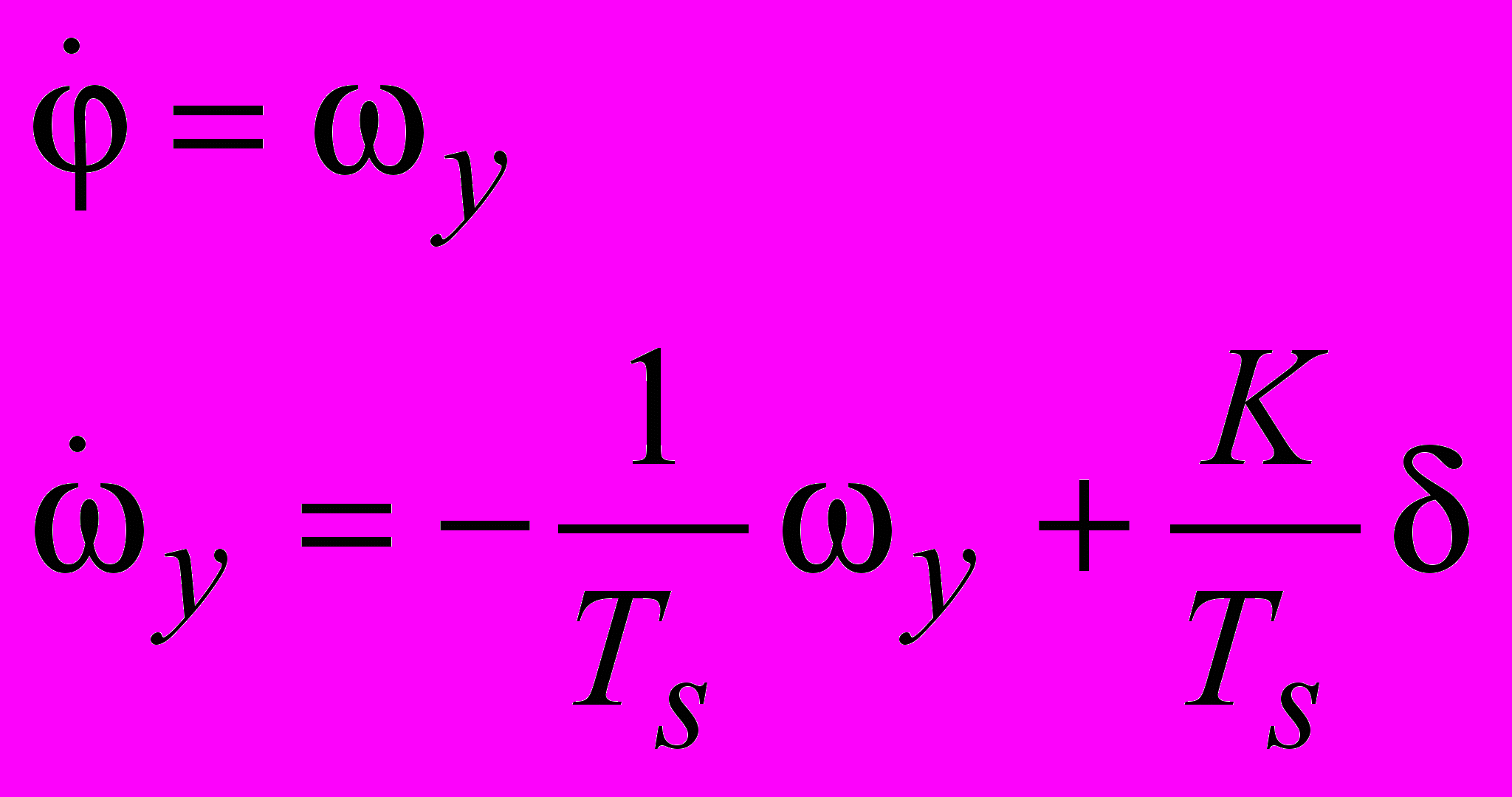
где
 – угол рыскания (угол отклонения от заданного курса),
– угол рыскания (угол отклонения от заданного курса), 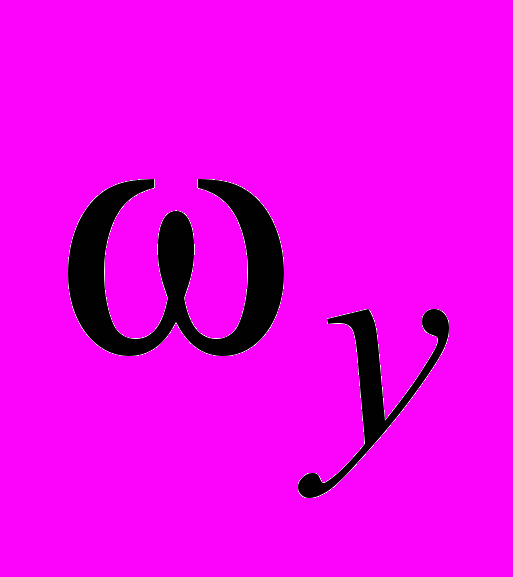 – угловая скорость вращения вокруг вертикальной оси,
– угловая скорость вращения вокруг вертикальной оси, 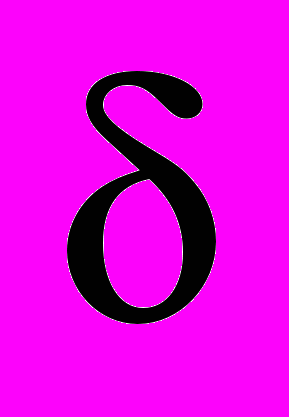 – угол поворота вертикального руля относительно положения равновесия,
– угол поворота вертикального руля относительно положения равновесия, 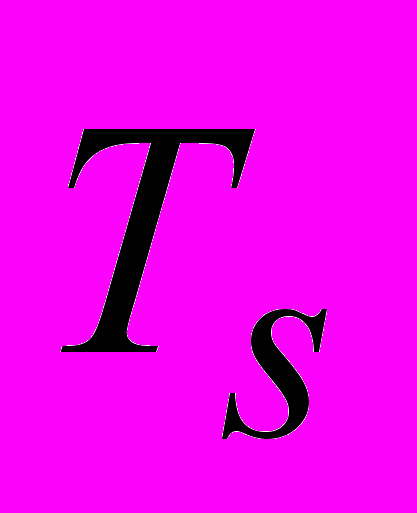 – постоянная времени,
– постоянная времени, 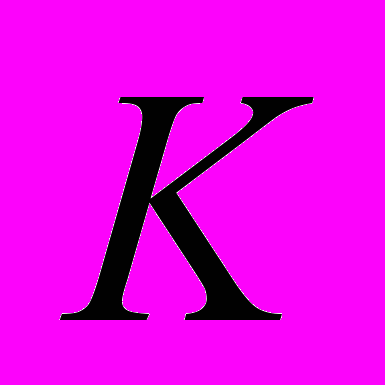 – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота тяги руля к углу рыскания запишется в виде
– постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота тяги руля к углу рыскания запишется в виде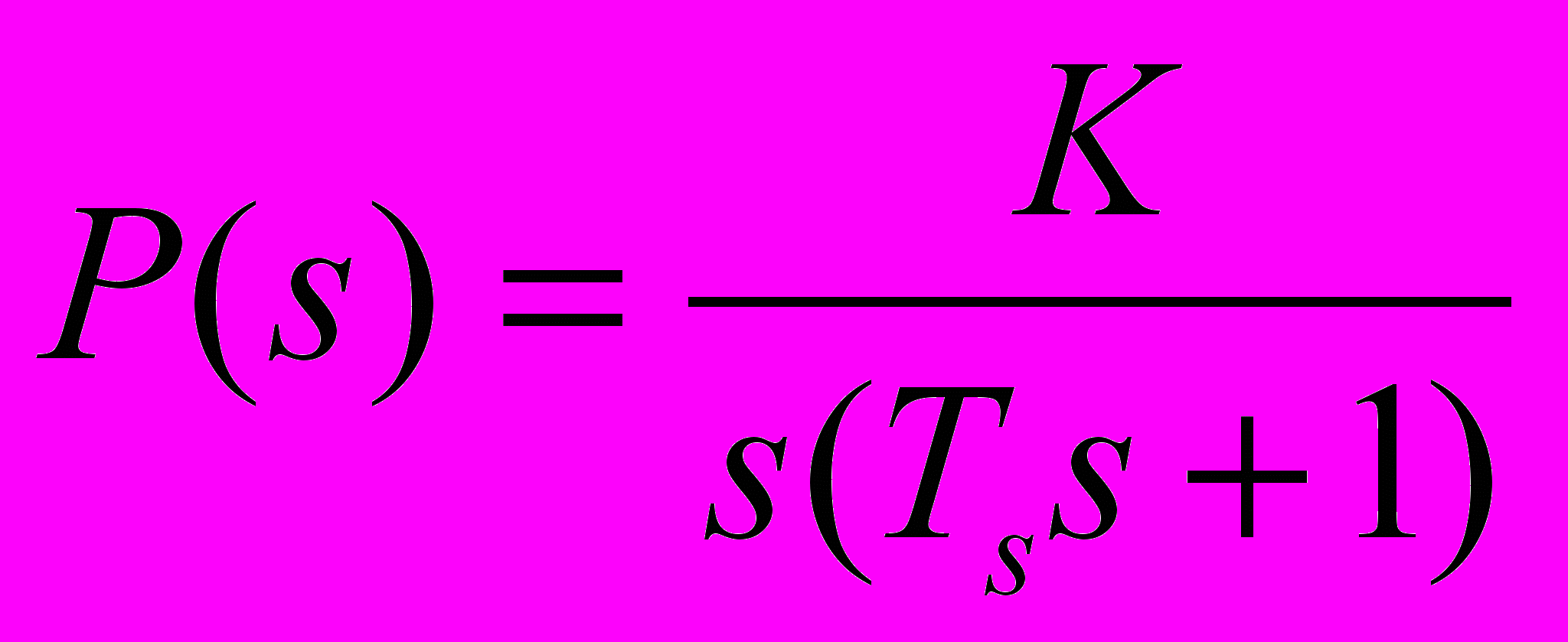 .
.Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
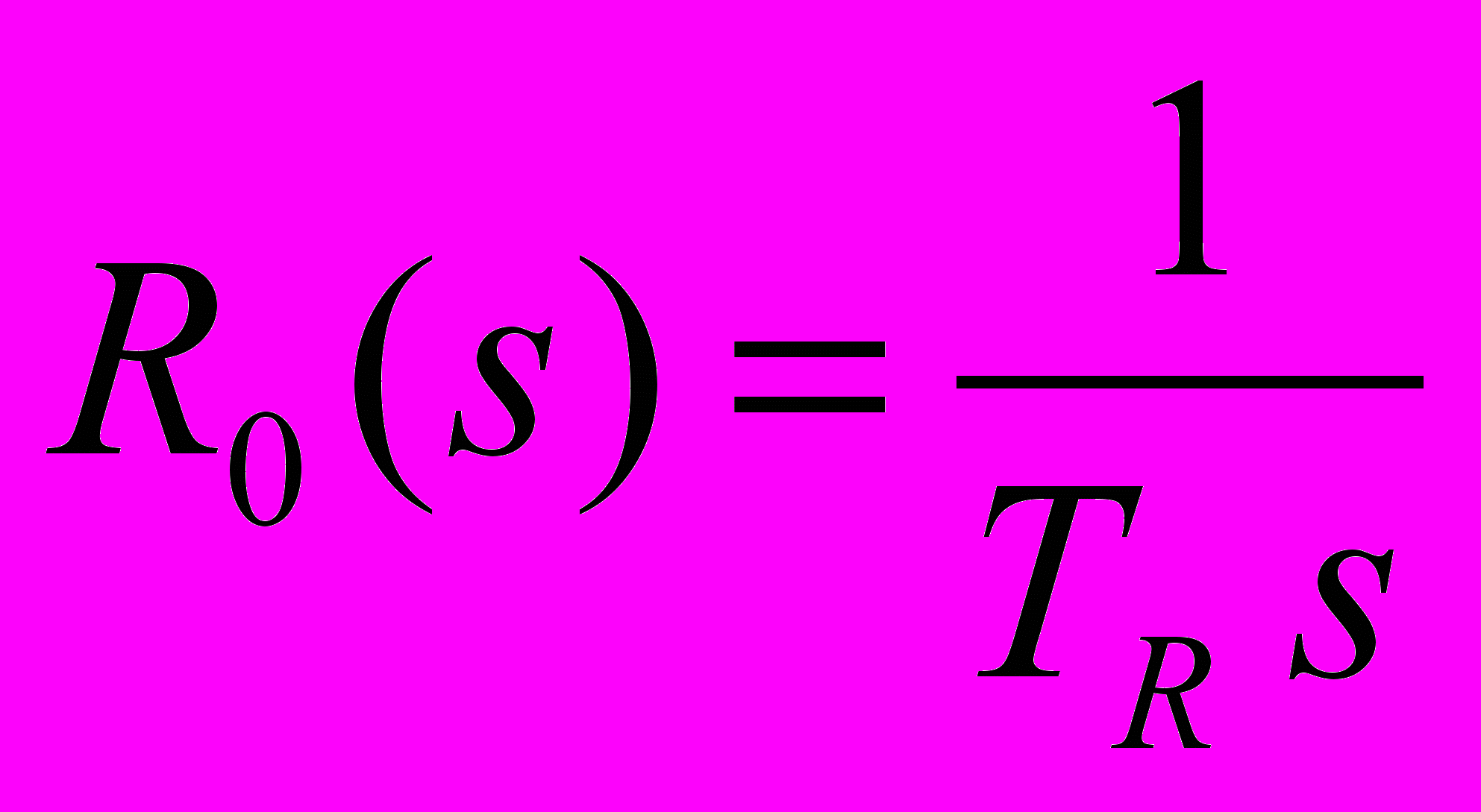 ,
, охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
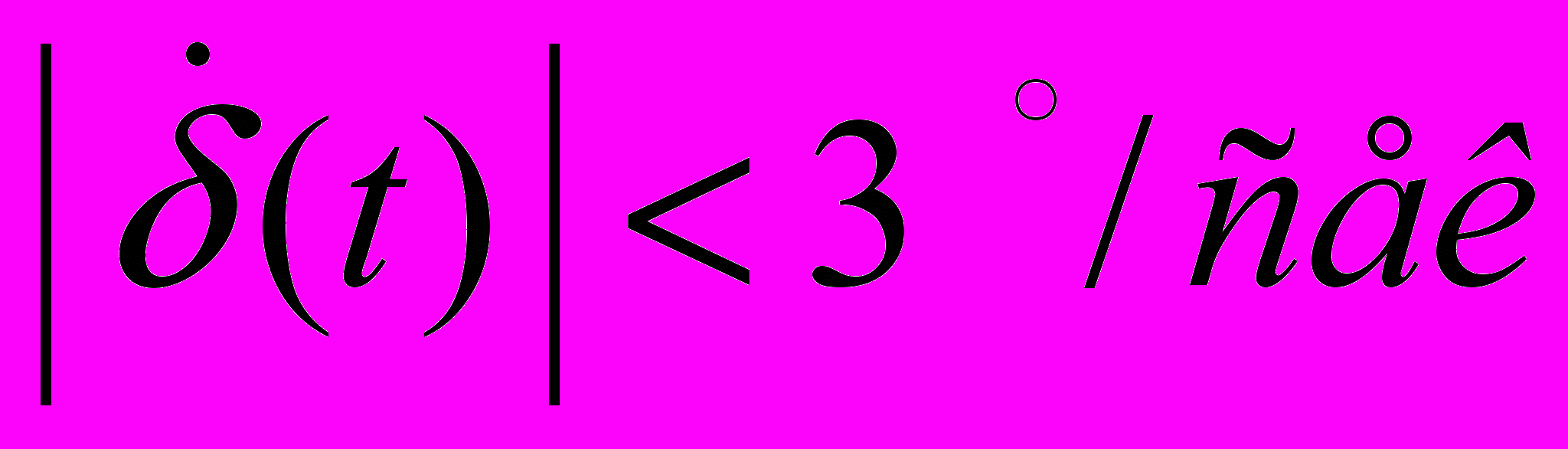 ,
, 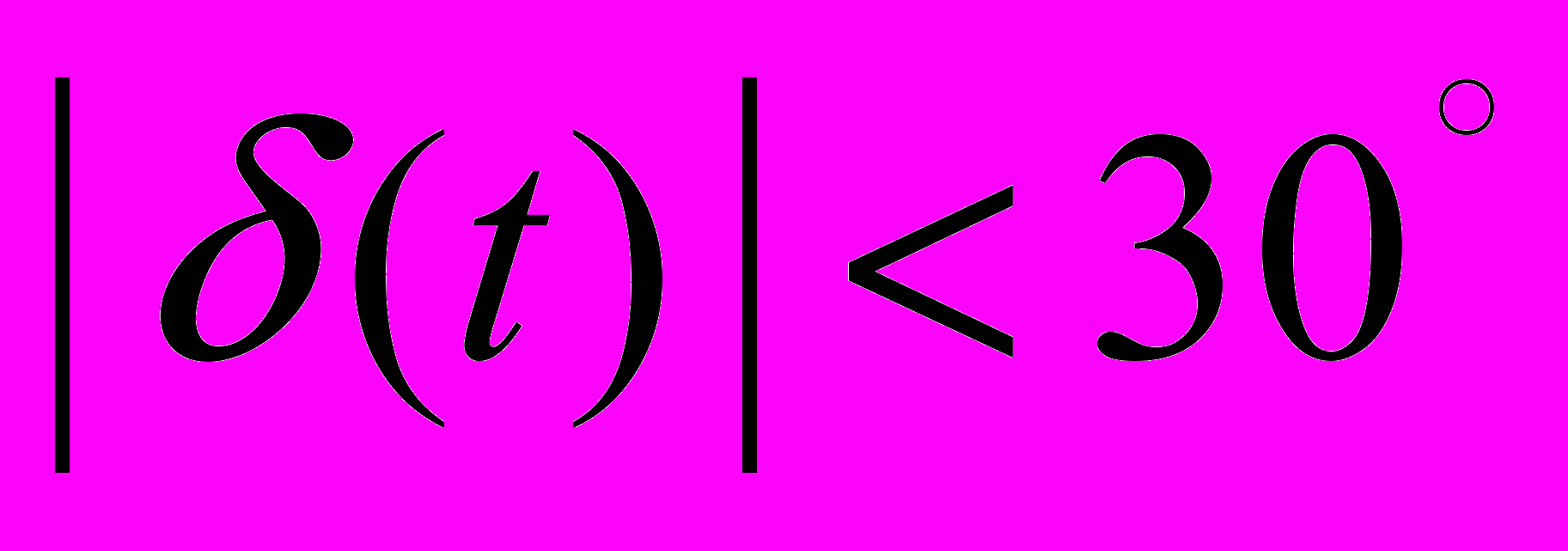 .
.Для измерения угла рыскания используется GPRS-навигатор, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией [2]:
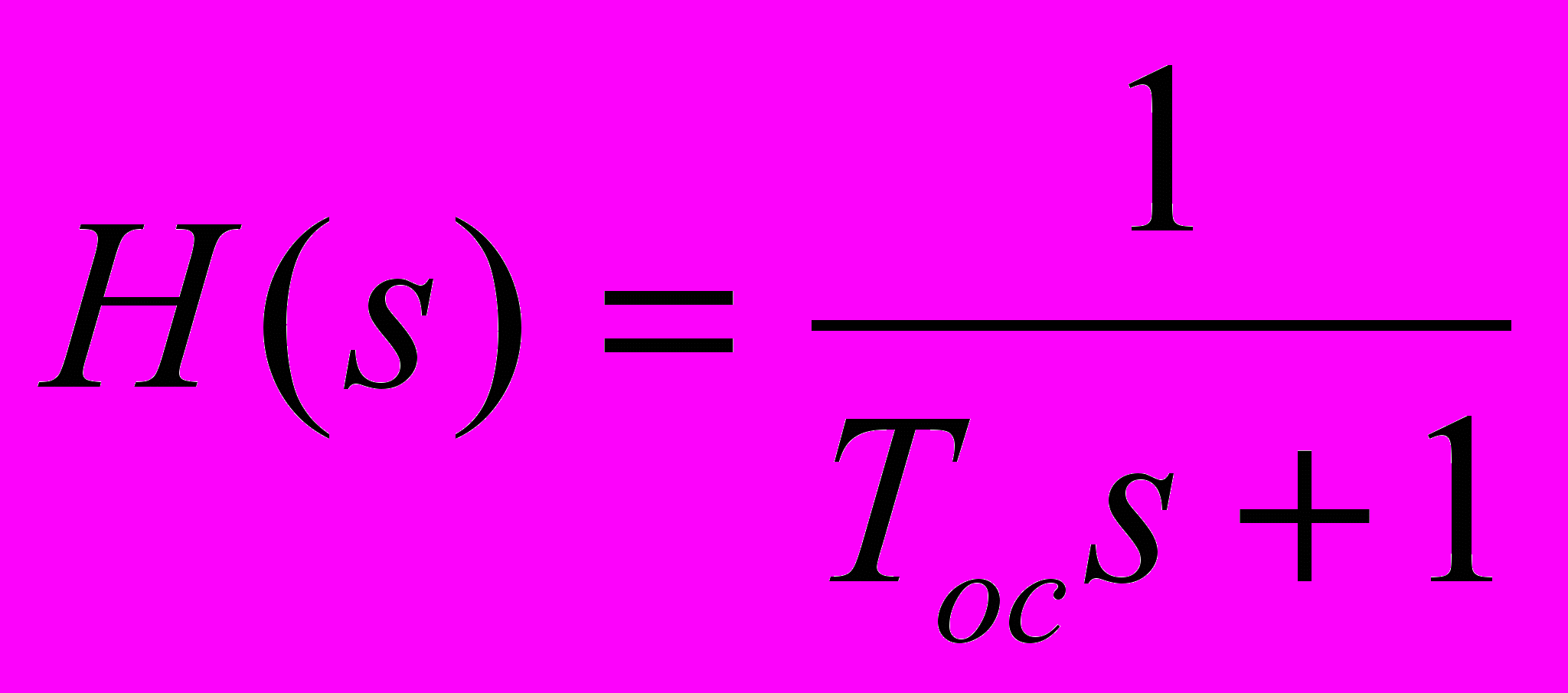 ,
,В качестве управляющего устройства рассмотрим ПИД-регулятор с передаточной функцией для конкретного примера из[3]:
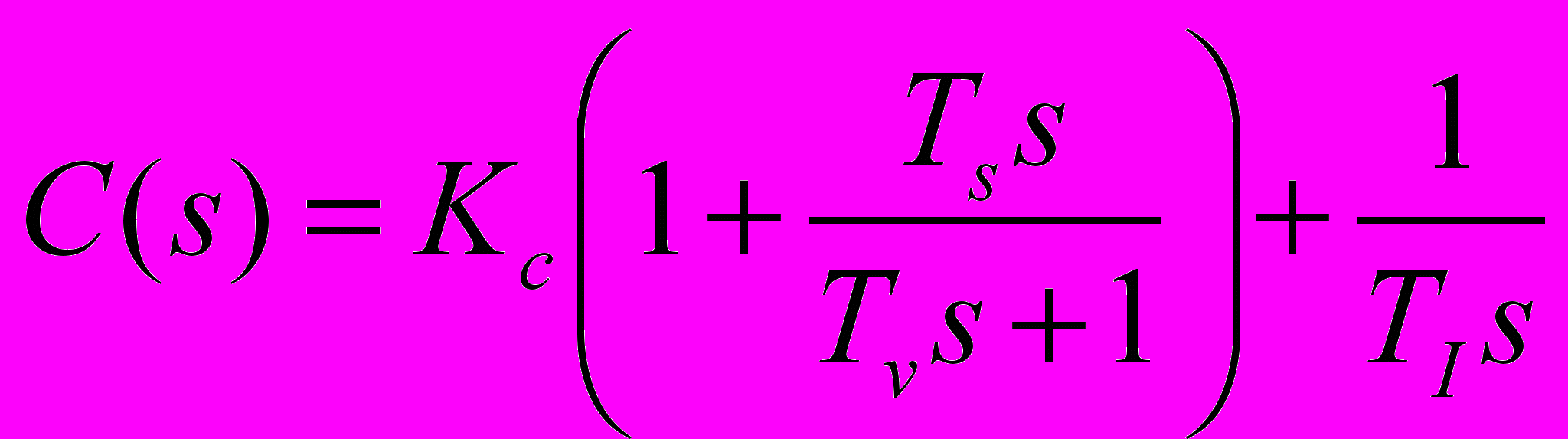 , где
, где 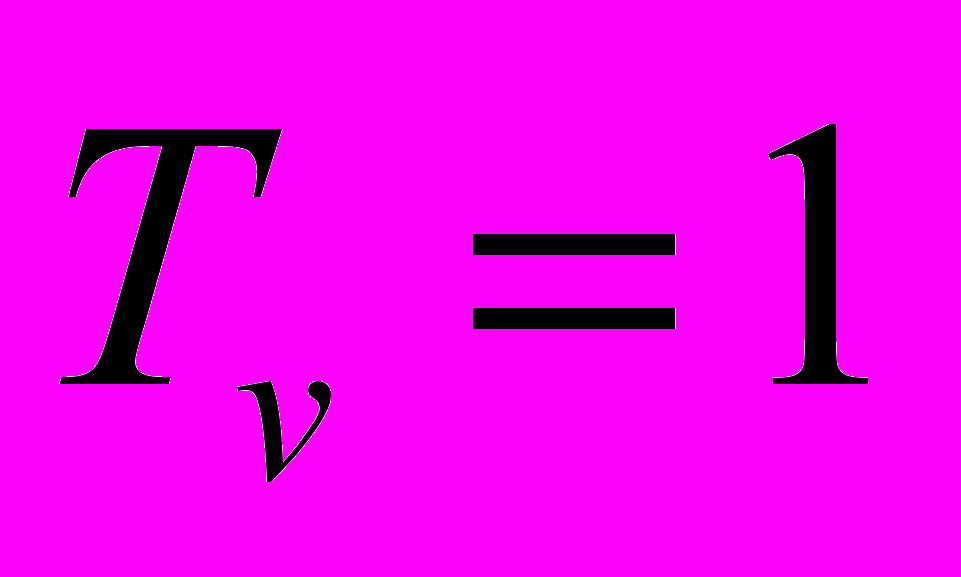 сек и
сек и 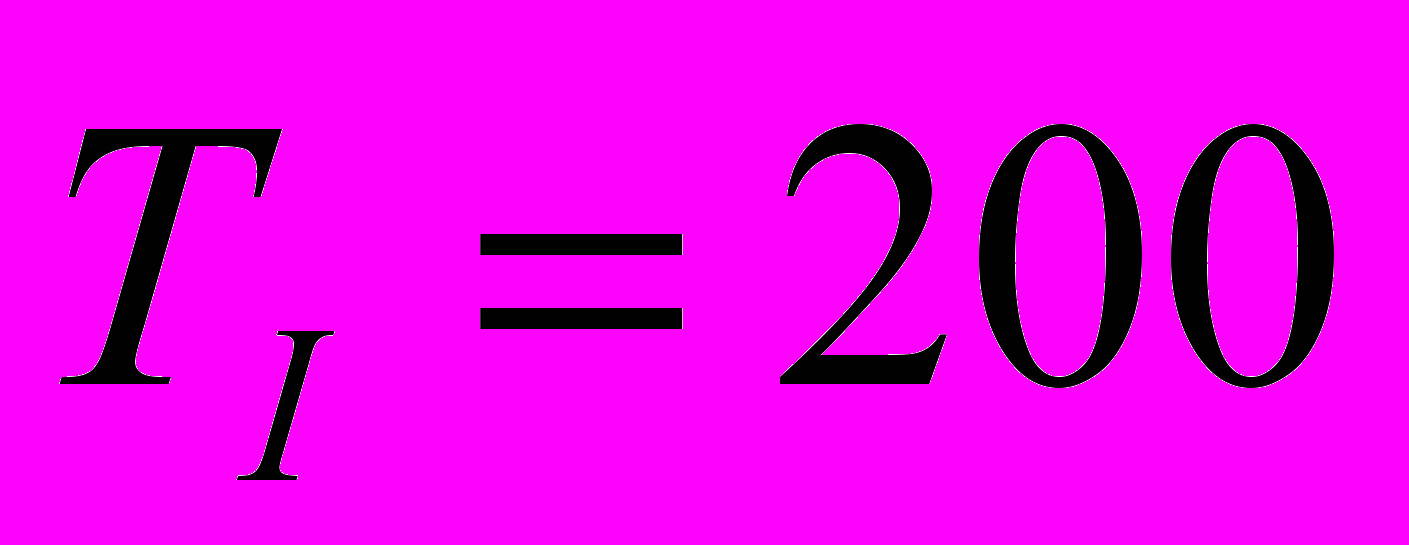 сек.
сек. Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используем схему с внутренней нелинейной обратной связью, охватывающей интегратор в составе регулятора.
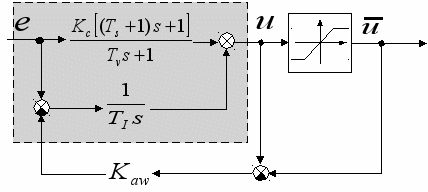
Базовый регулятор, построенный по линейной модели, выделен серым фоном. Сигнал
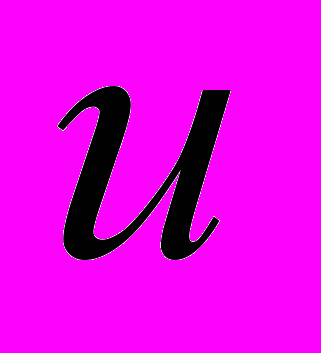 на его выходе представляет собой желаемый угол перекладки руля. Для блока нелинейной коррекции типа «насыщение» выбираются пределы, равные ограничениям на угол перекладки руля.
на его выходе представляет собой желаемый угол перекладки руля. Для блока нелинейной коррекции типа «насыщение» выбираются пределы, равные ограничениям на угол перекладки руля. Если насыщения нет, разность сигналов
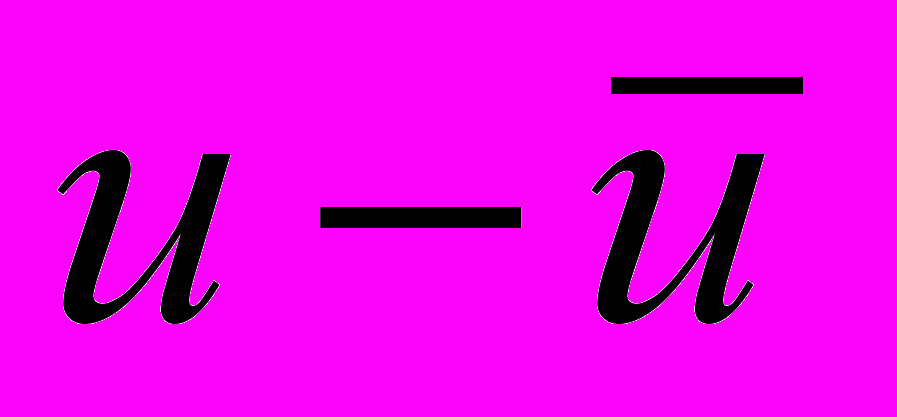 равна нулю, и обратная связь не работает; используется закон управления, синтезированный для линейной системы. Если сигнал
равна нулю, и обратная связь не работает; используется закон управления, синтезированный для линейной системы. Если сигнал 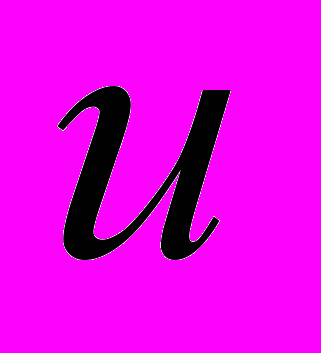 превышает допустимые пределы, разность
превышает допустимые пределы, разность 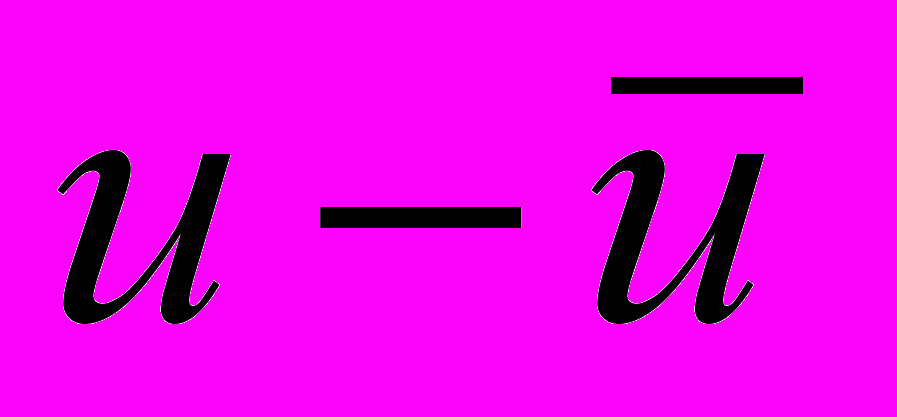 подается (со знаком «минус») на вход интегратора через усилитель. Таким образом, при насыщении сигнал на входе интегратора ослабляется тем сильнее, чем больше разность между желаемым и допустимым углами перекладки. Такой метод коррекции получил в литературе название anti-windup (противодействие «наматыванию»).
подается (со знаком «минус») на вход интегратора через усилитель. Таким образом, при насыщении сигнал на входе интегратора ослабляется тем сильнее, чем больше разность между желаемым и допустимым углами перекладки. Такой метод коррекции получил в литературе название anti-windup (противодействие «наматыванию»).Для выбора оптимального значение коэффициента
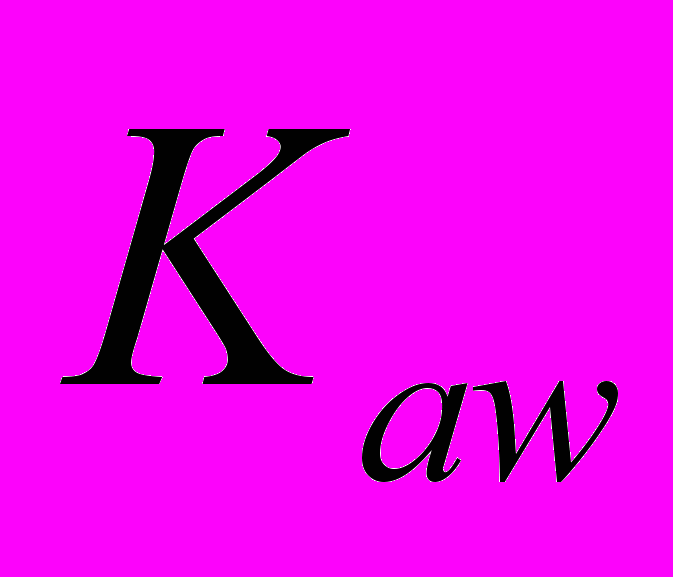 использована процедура численной оптимизации пакета NCD Blockset.
использована процедура численной оптимизации пакета NCD Blockset. Движение судна описывается линейной математической моделью в виде передаточной функции и для конкретного частного случая примет вид:
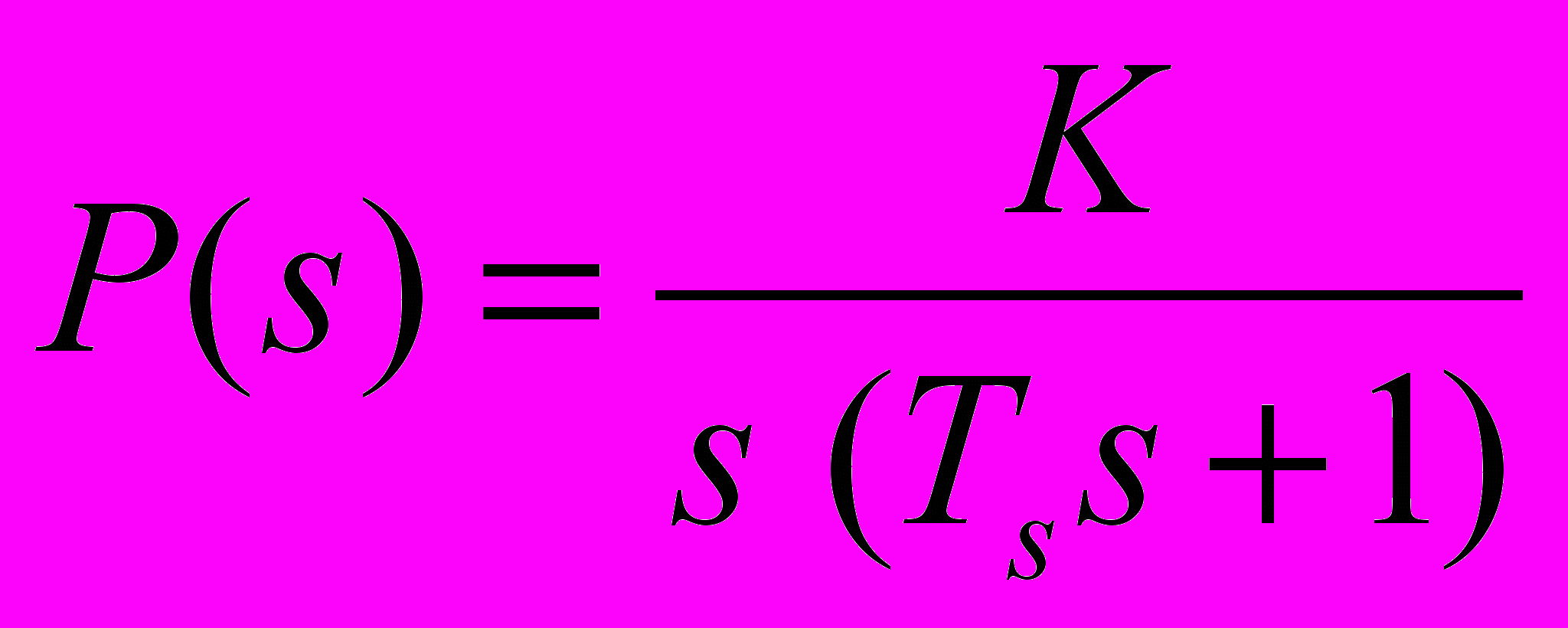 , где
, где 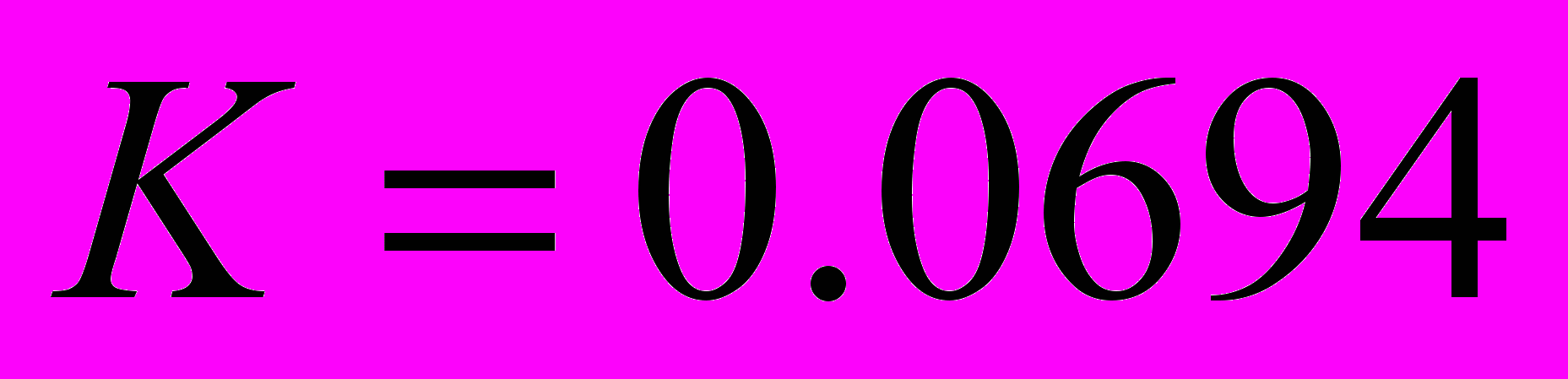 рад/сек,
рад/сек, 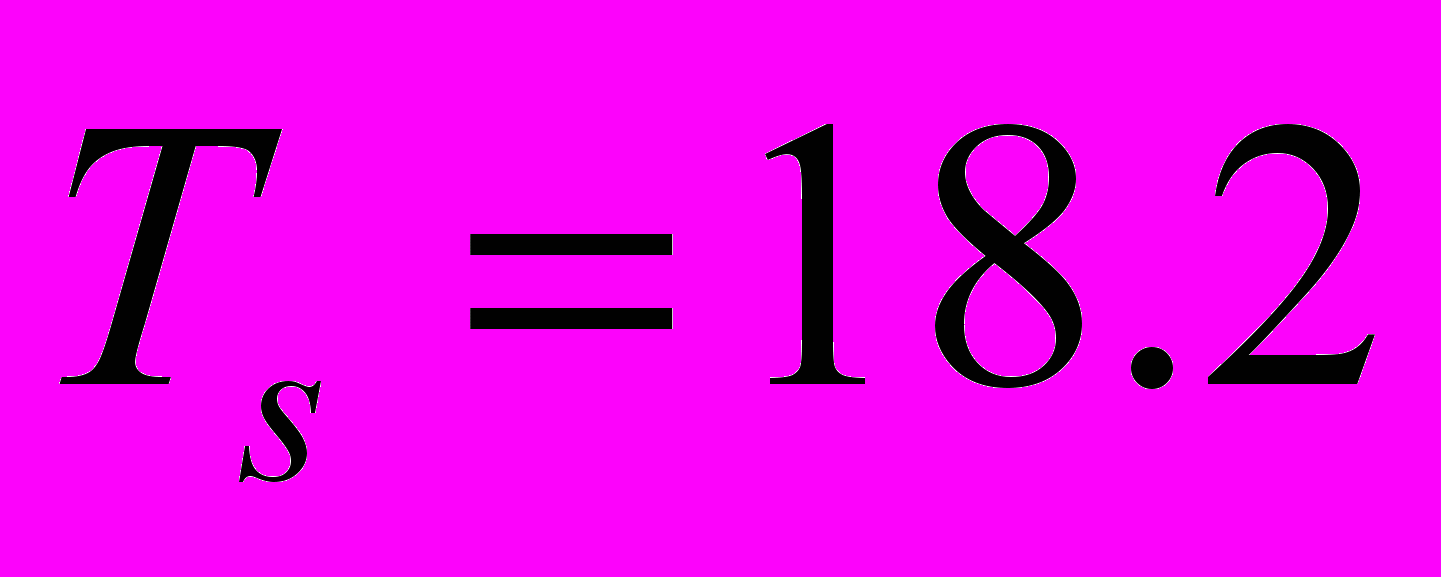 сек,
сек, Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
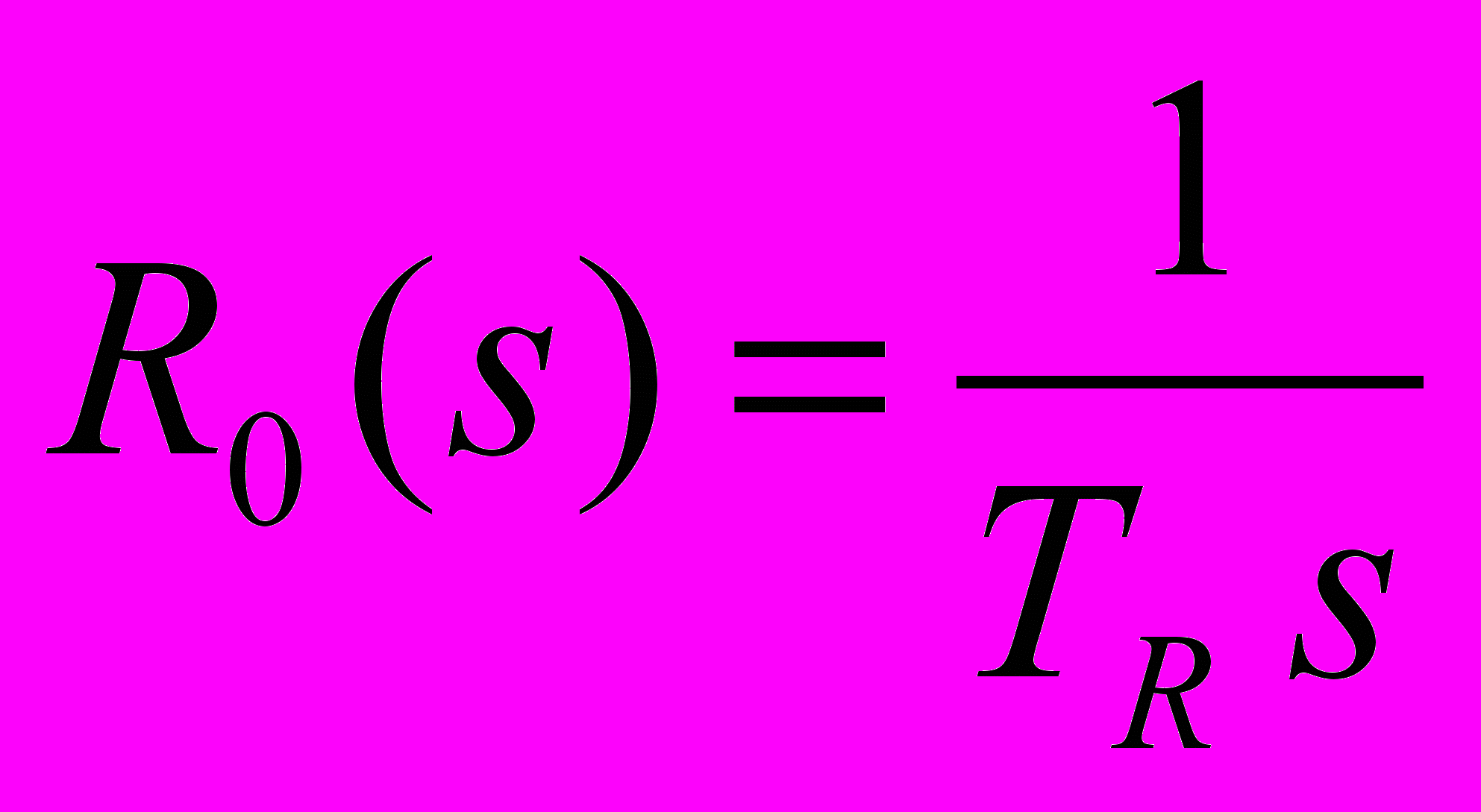 ,
, 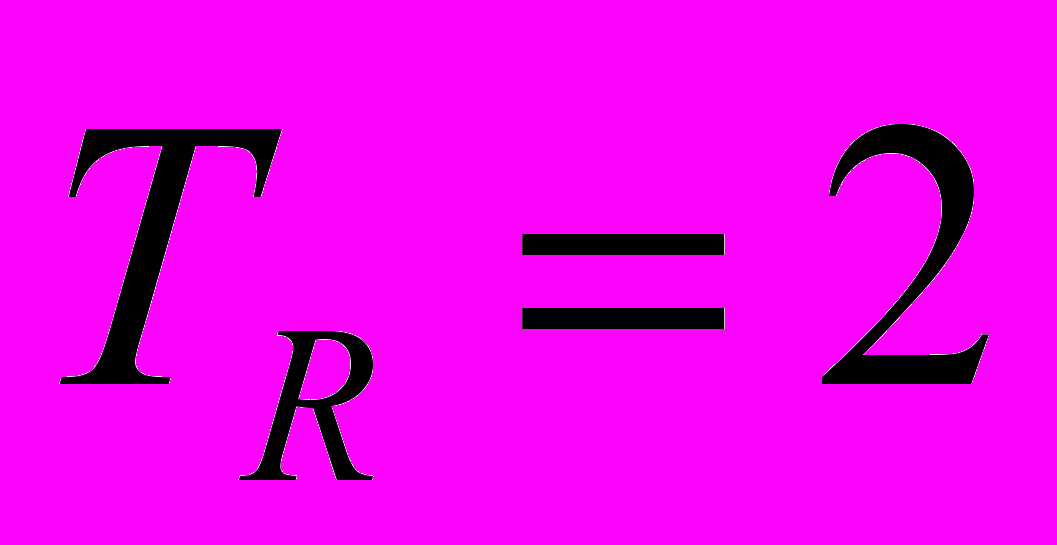 сек,
сек, охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки наложим нелинейные ограничения
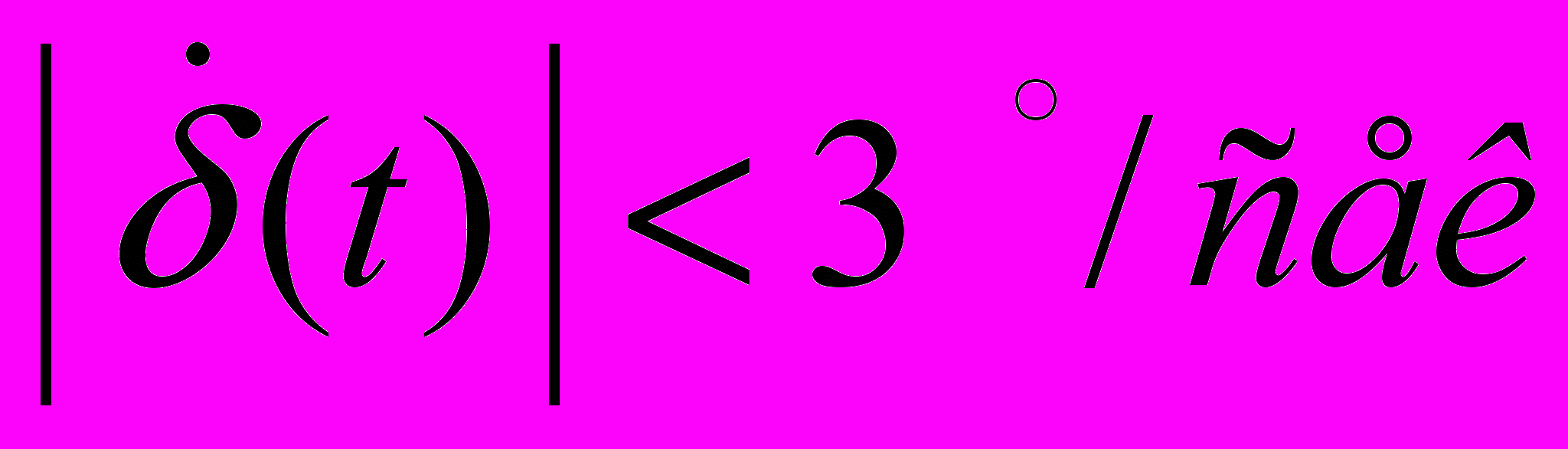 ,
, 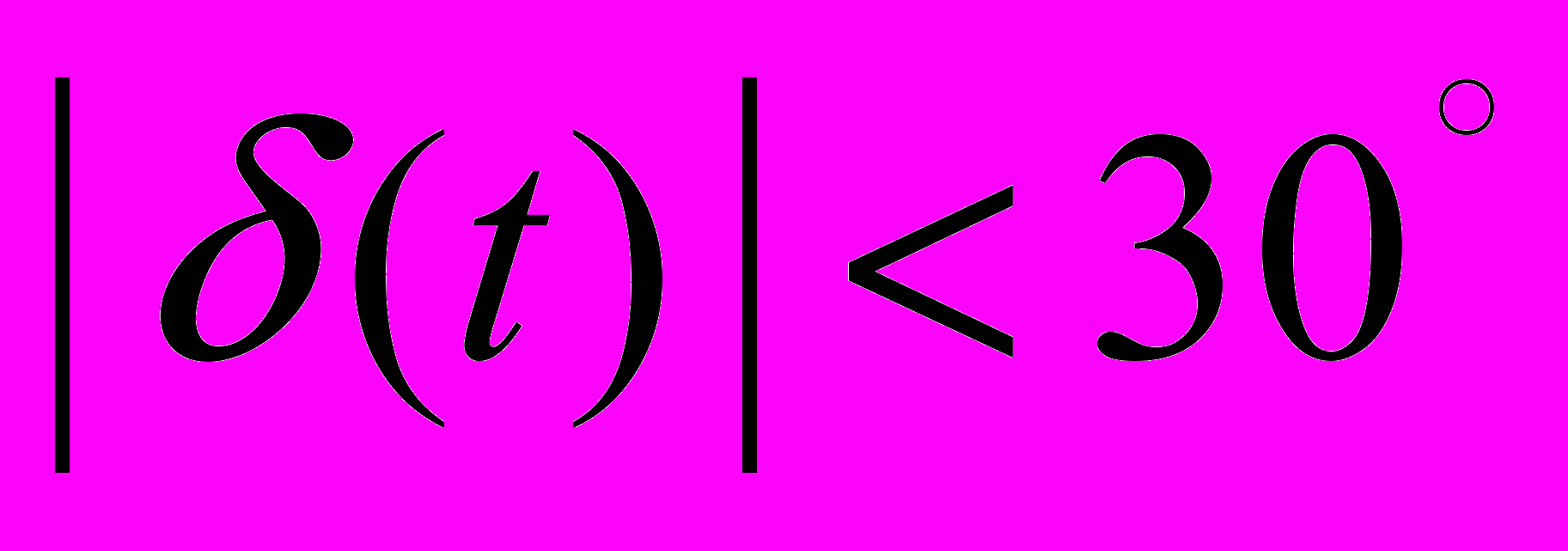 .
.Измерительное устройство (гирокомпас, GPRS-навигатор или иное) моделируется как апериодическое звено с передаточной функцией
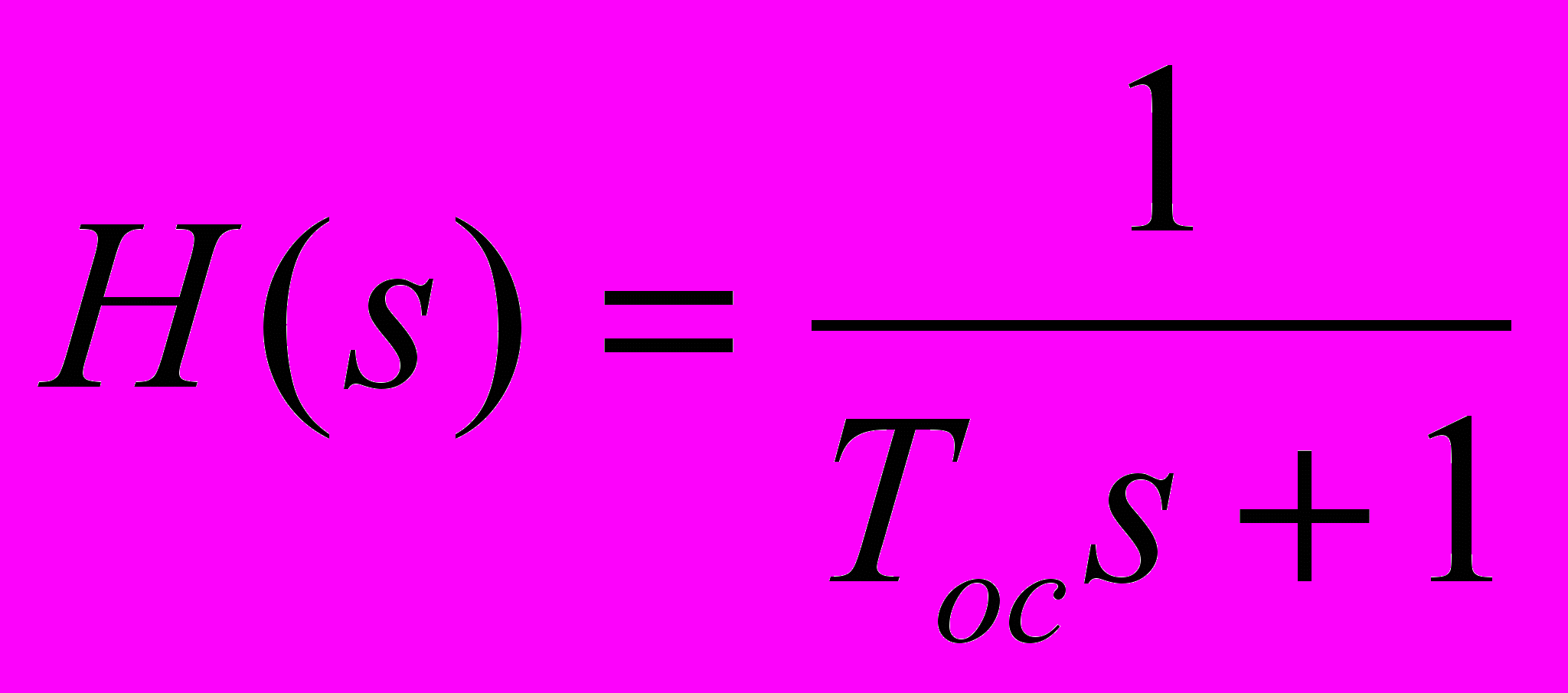 ,
, 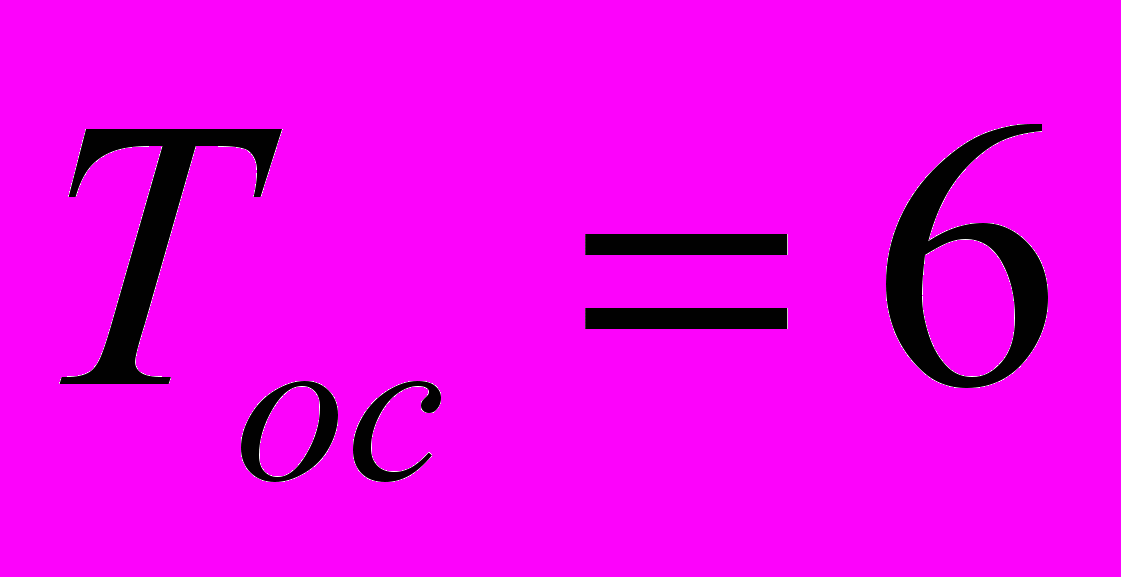 сек,
сек,В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
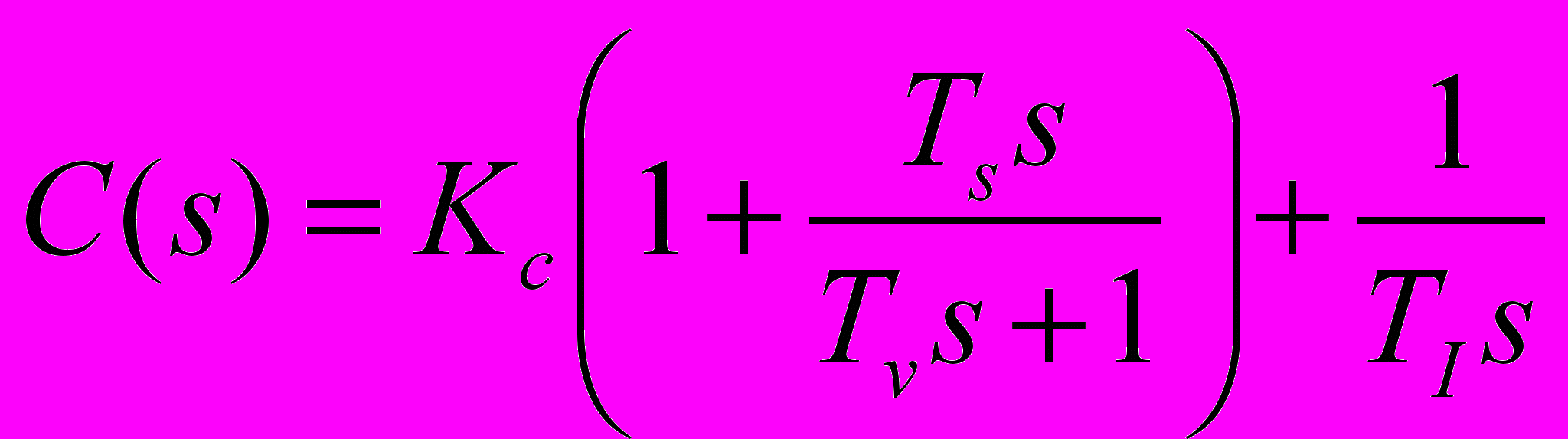 ,
, где
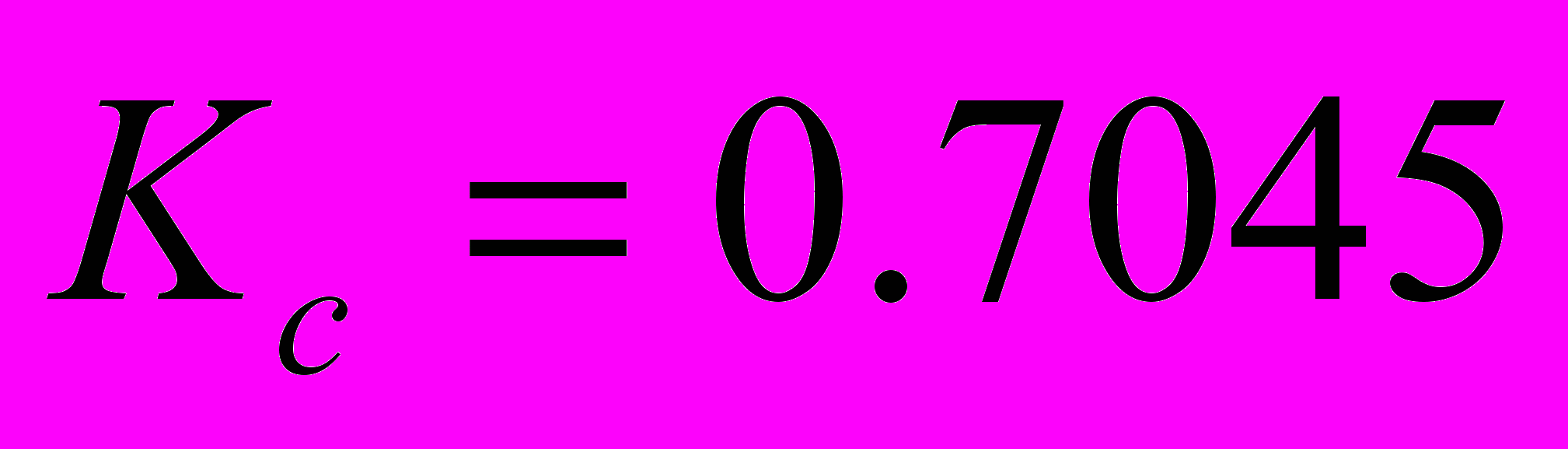 ,
, 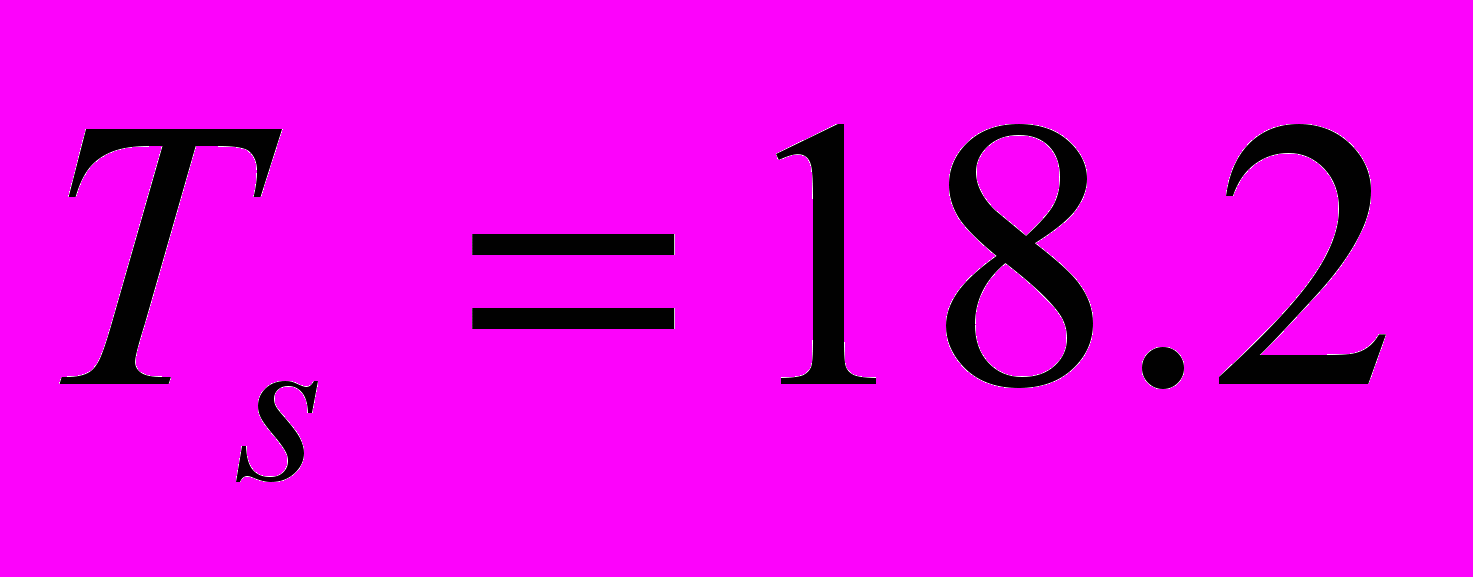 сек,
сек, 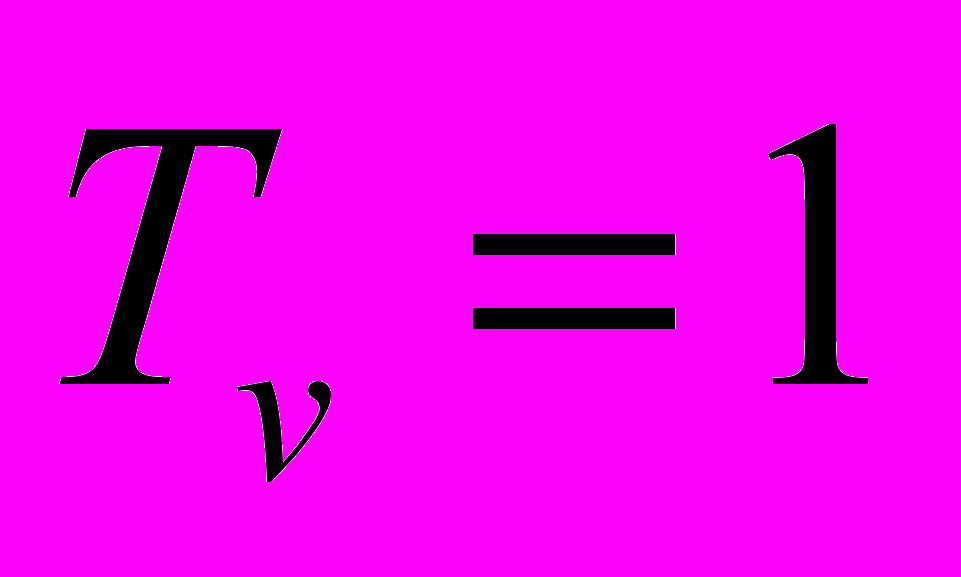 сек,
сек, 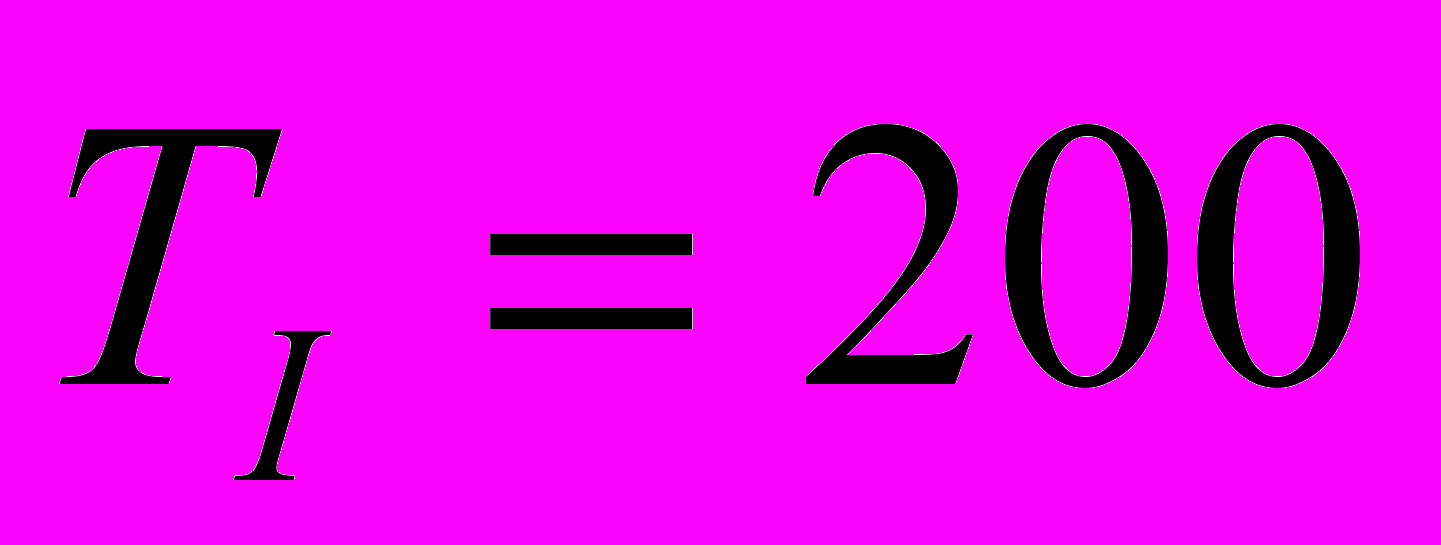 сек,
сек,Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используем схему с нелинейной обратной связью, охватывающей интегратор в составе регулятора. В ходе моделирования рассчитаем оптимальное значение коэффициента усиления в обратной связи с помощью пакета NCD Blockset [3].
В этом случае блок компенсации насыщения будет иметь вид:
- подсистема «Регулятор»
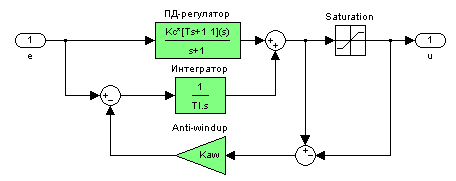
- пределы для блока Saturation
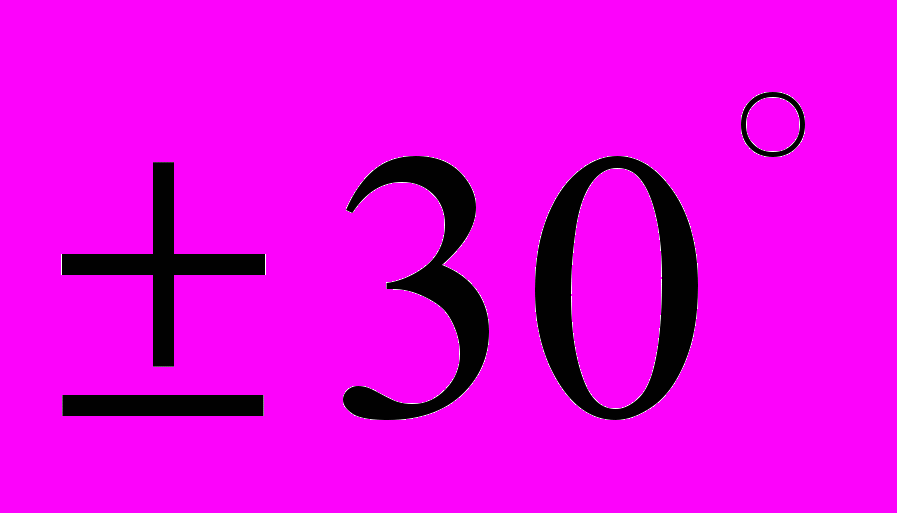

- номинальное значения
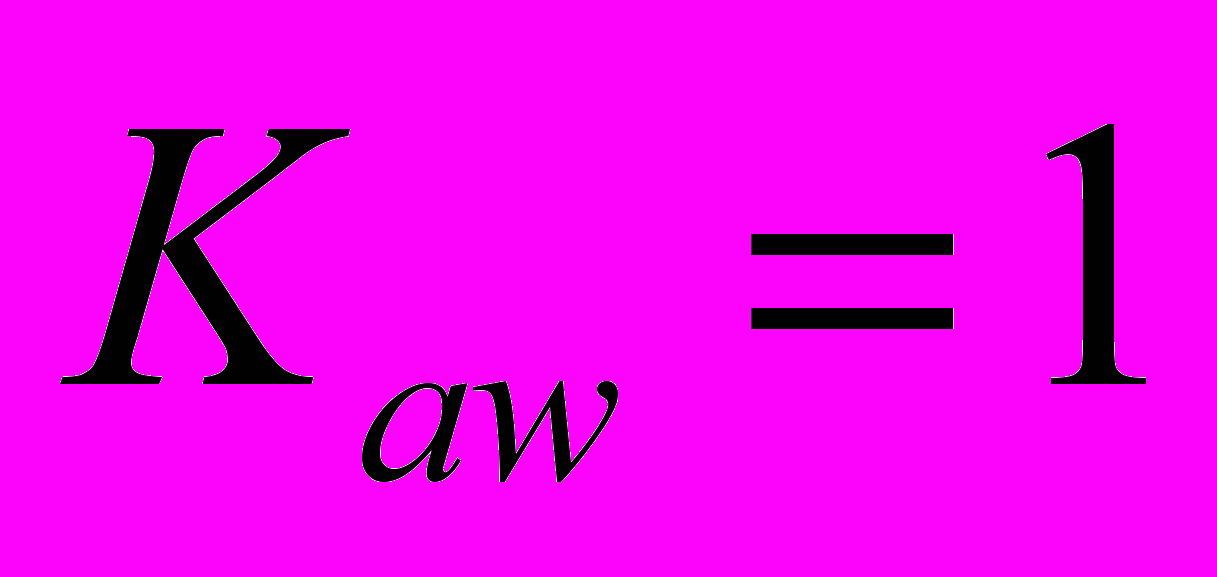

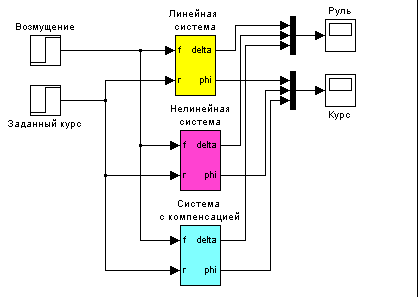
- модель для сравнения трех типов систем
- переходные процессы при
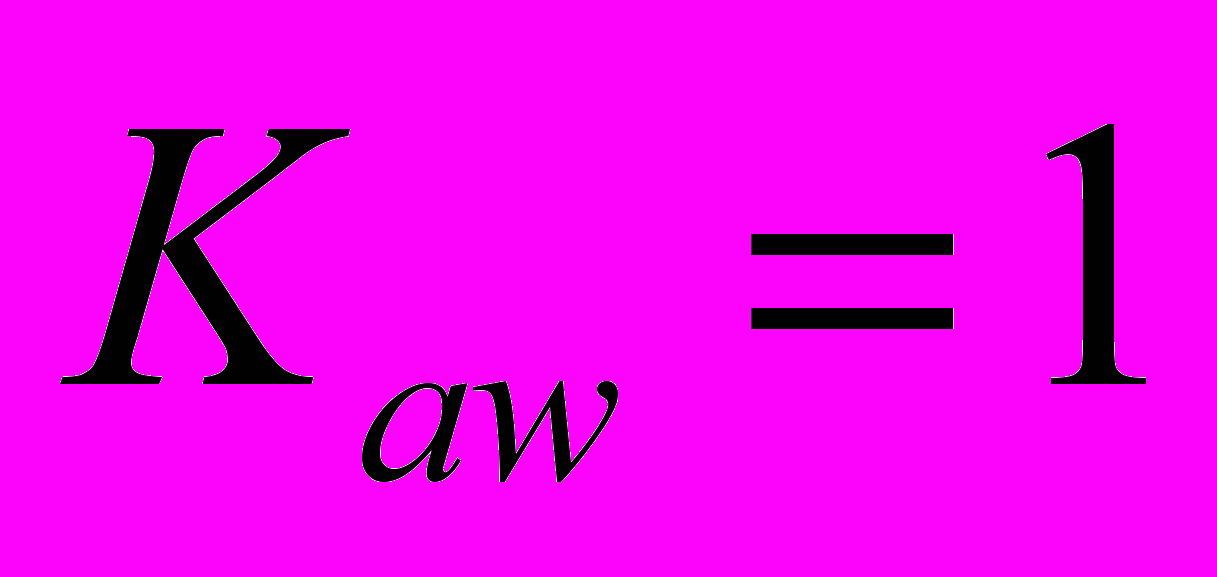
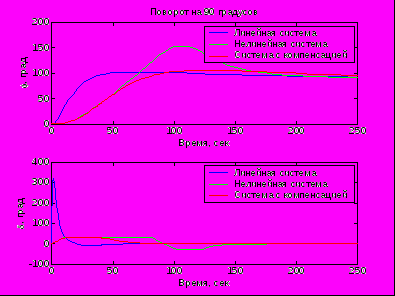
При введении компенсации насыщения интегрирующего звена видим устойчивое и оптимальное управление при заданном изменении курса.
Проведем анализ оптимальной системы управления
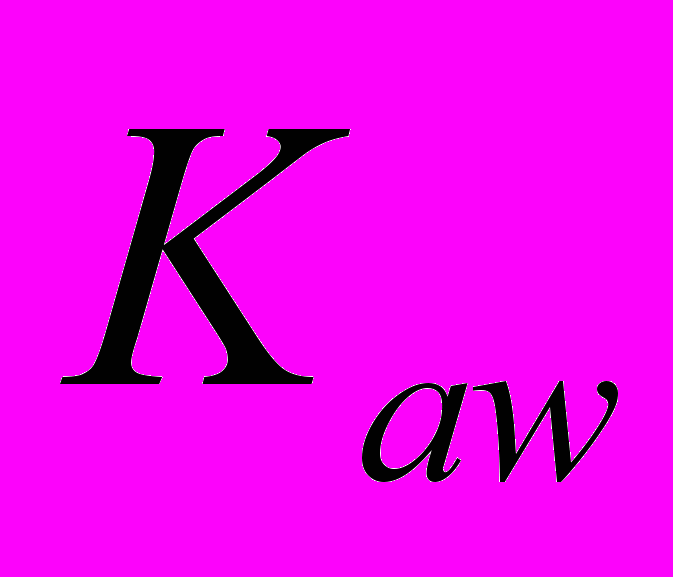 в экстремальных условиях.
в экстремальных условиях. 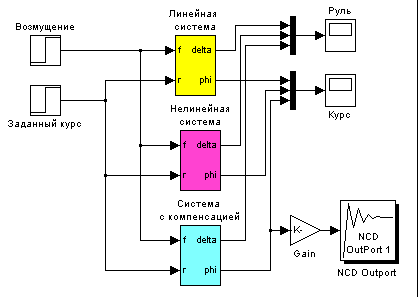
- переходные процессы при
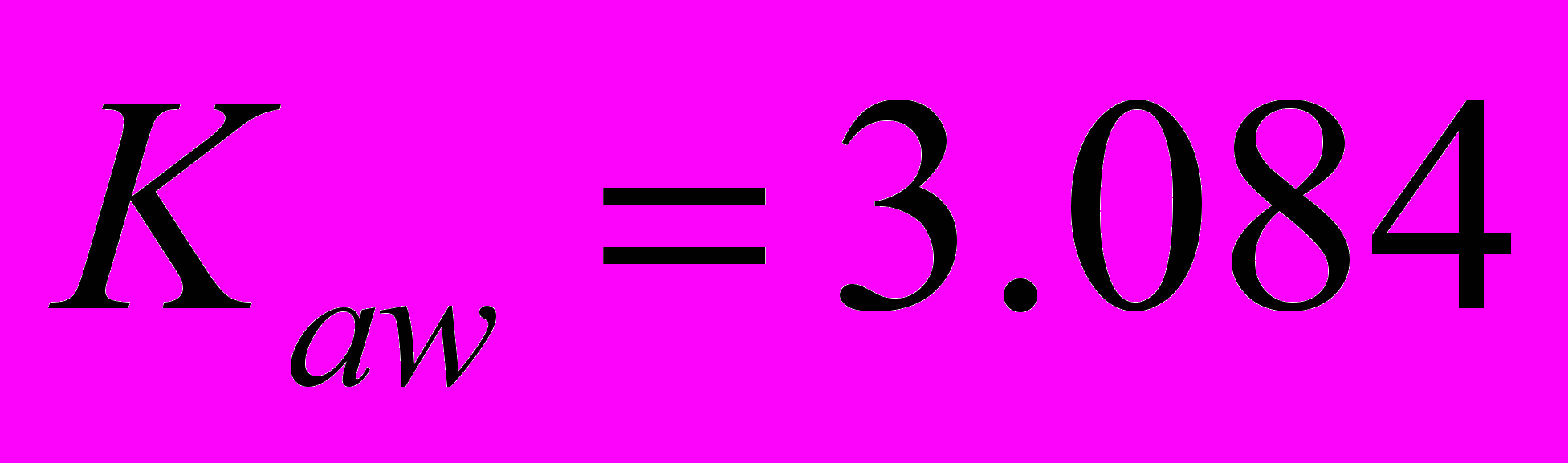 (поворот на 90 градусов)
(поворот на 90 градусов)
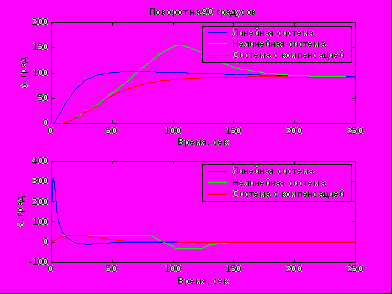
- перерегулирование
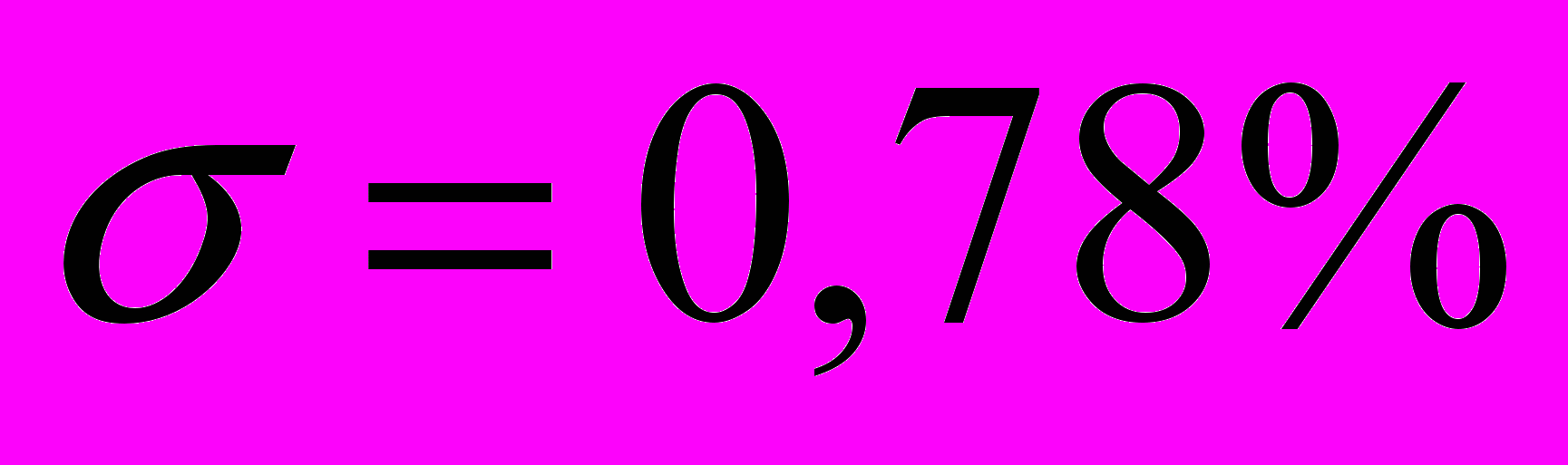 , время переходного процесса
, время переходного процесса 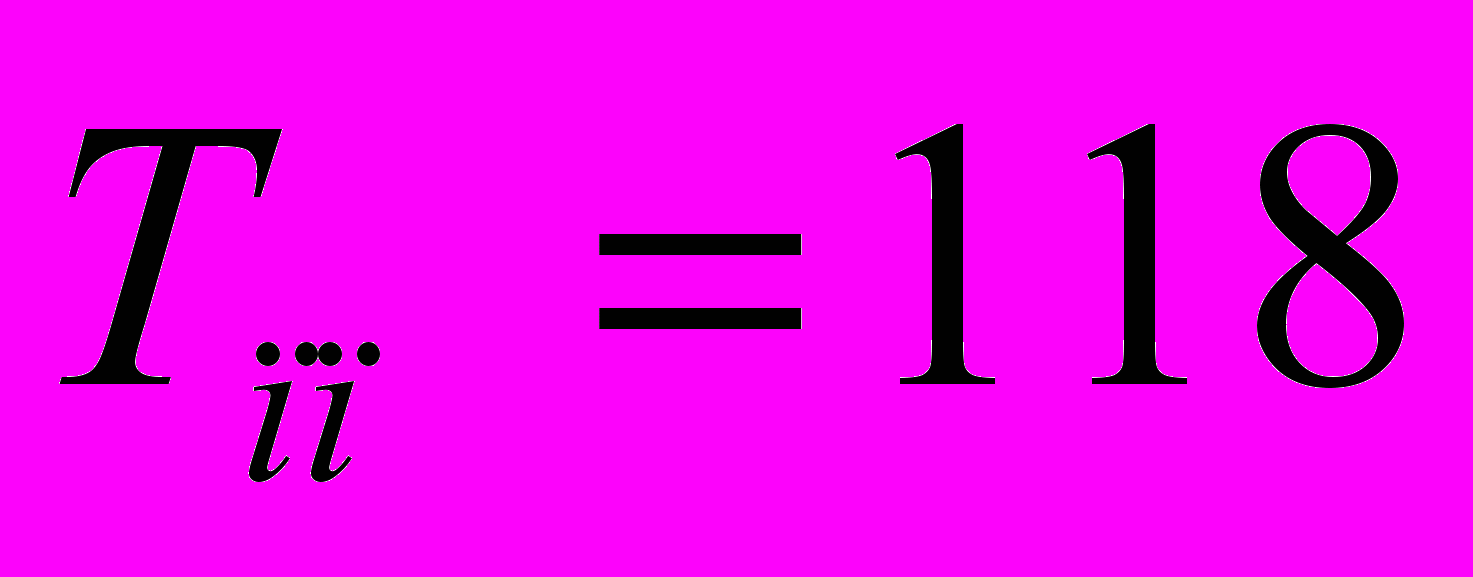 сек.
сек.
- переходные процессы при повороте на 30 градусов
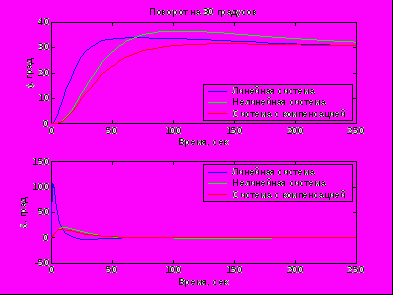
- перерегулирование
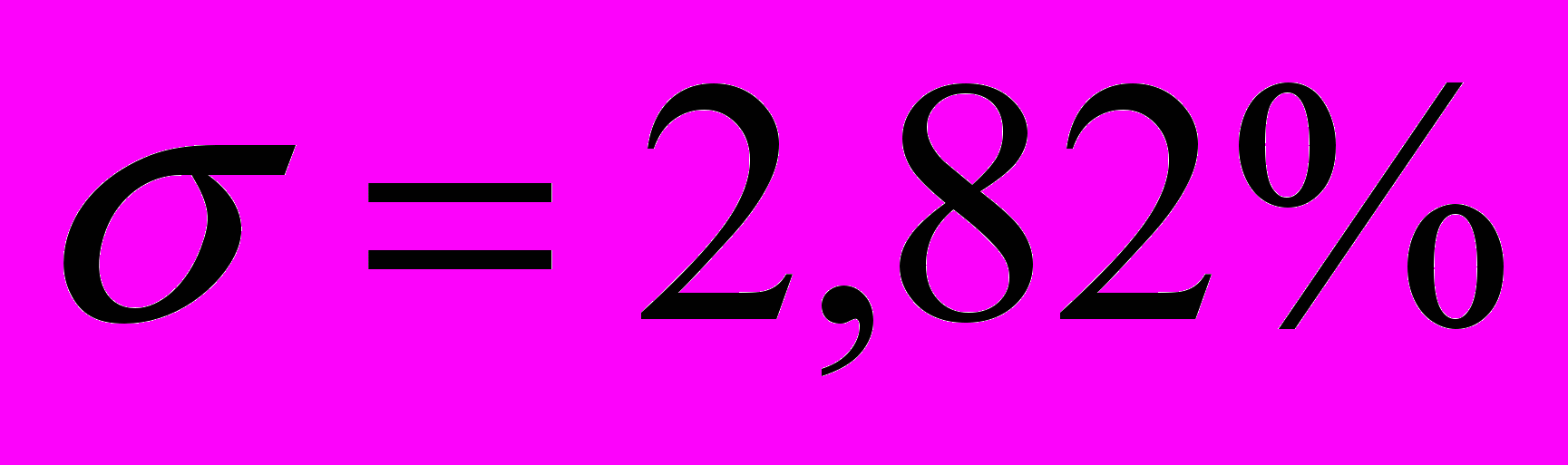 , время переходного процесса
, время переходного процесса 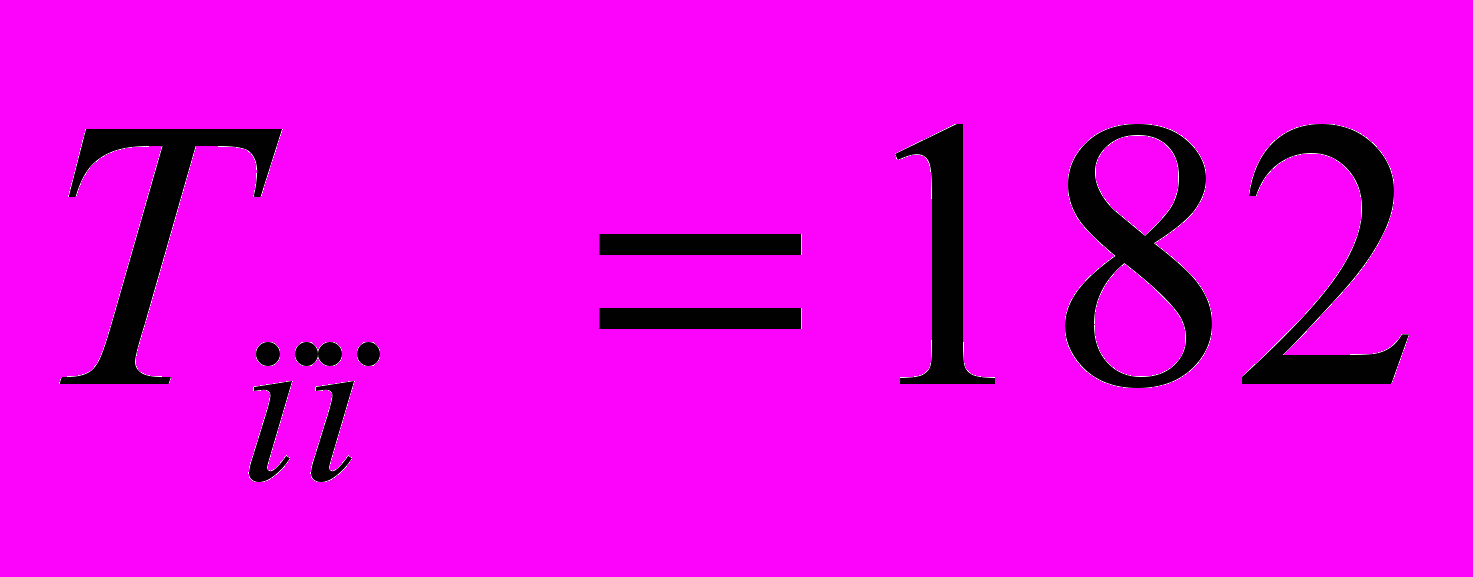 сек.
сек.
Таким образом, применение оптимальной компенсации позволило выйти на заданный курс полета на 20-40 % быстрее линейной системы и нелинейной системой управления даже в экстремальных условиях полета, а также избежать перерегулирования, что могло на высоких скоростях полета привести к турбулентности и потери управляемости ракеты.
Литература
1. Киреев Н.Г. Системы управления беспилотных летательных аппаратов. – К.: УМК ВО, 1993. – 160 с.
2. Пельпор Д.С. Гироскопические системы ориентации и стабилизации. Справочное пособие. - М.: Машиностроение, 1982, 165 с.
3. Потемкин В. Г. MATLAB 6: среда проектирования инженерных приложений.—
М.:Диалог–МИФИ, 2003.— 448с.
