Geum.ru

Тема диссертационной работы

Вид материалаДокументы

Содержание


Объект исследования
Цифровые регуляторы
К - коэффициент передачи, Т
U(k) вычесть сигнал U(k-1)
Подобный материал:
Автор: Тулупова Т.В.

Тема диссертационной работы: Разработка комплекса лабораторных работ по дисциплине « Основы теории управления» в среде Matlab.


Основное направление исследования: исследование методик моделирования систем автоматического регулирования с применением среды моделирования Matlab.

Для проведения исследования организуется вычислительный эксперимент, который позволяет сравнить различные подходы к моделированию систем автоматического регулирования с помощью Matlab.

Предмет исследования: моделирование систем автоматического регулирования в среде Matlab.

Объект исследования: синтез и анализ САР при использовании непрерывного и цифрового регулятора в среде моделирования Matlab.


ПИД - регуляторы

Классическая схема управления с единичной отрицательной обратной связью показана на рис. 1.



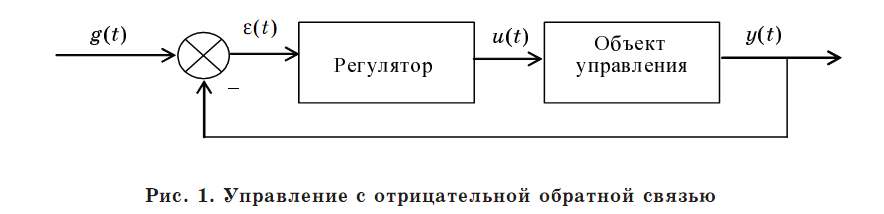
Назначение регулятора системы заключается в коррекции динамических свойств объекта управления с помощью управляющего сигнала u(t) так, чтобы реальный выходной сигнал y(t) как можно меньше отличался от желаемого выходного сигнала g(t). Регулятор вырабатывает управление, используя ошибку регулирования e(t) = g(t) – y(t).

Для оценки динамических свойств системы часто рассматривается реакция на единичное ступенчатое воздействие. Переходный процесс должен отвечать заданным показателям качества, к которым относятся время переходного процесса, перерегулирование и колебательность. Могут быть также использованы интегральные оценки качества переходного процесса.

ПИД - регуляторы (ПИД – пропорционально – интегродифференциальный) получили самое широкое распространение при управлении производственными и технологическими процессами. Основное уравнение ПИД регулятора имеет следующий вид:



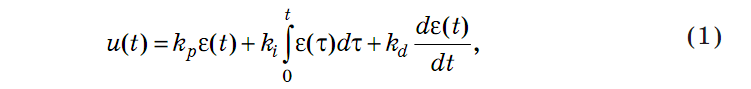
где kp, ki, kd – константы, выбираемые в процессе проектирования. С их помощью удается обеспечить соизмеримость отдельных слагаемых формулы (1).

Дифференциальная составляющая в формуле (1) позволяет повысить быстродействие регулятора, предсказывая будущее поведение процесса.

Интегральная составляющая в формуле (1) призвана ликвидировать статические ошибки управления, поскольку интеграл даже от малой ошибки может быть значительной величиной, вызывающей реакцию регулятора.

Хотя ПИД - регулятор представляет собой систему второго порядка, его можно успешно применять для управления процессами, имеющими более высокий порядок. Это вызвано возможностью аппроксимации многих систем высокого порядка системами второго порядка.

На практике часто используются упрощенные версии ПИД регулятора – П-, И-, ПД- и ПИ-регуляторы, описываемые соответственно формулами:



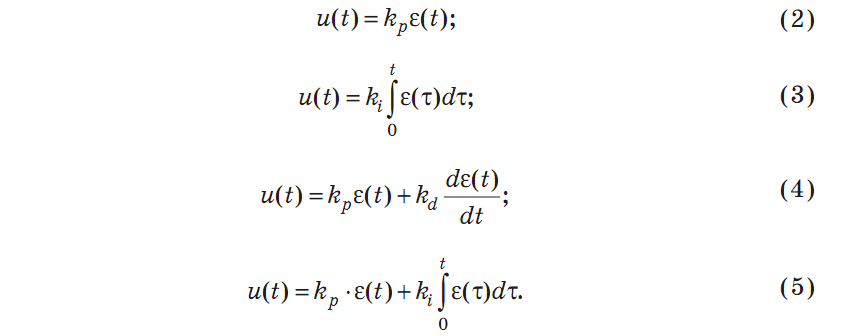
При большом значении коэффициента усиления П. - и ПИ - регуляторы ведут себя как двухпозиционное реле.

Существует инженерный подход к синтезу ПИД - регуляторов – методика Зиглера - Николса, которая предполагает следующие шаги:

1. Коэффициенты kd и ki устанавливаются равными нулю, а коэффициент kp увеличивается до тех пор, пока система не потеряет устойчивость.

2. Предельное значение kp обозначается как ku, а период автоколебаний как pu.

3. Значения коэффициентов ПИД регулятора рассчитываются по следующим формулам:

kp = 0,6ku;

ki = 1,2(ku/pu);

kd = 3kupu/40

В аналоговых промышленных ПИД - регуляторах коэффициенты настраиваются вручную.

Следует заметить, что коэффициент K, от которого строится корневой годограф, соответствует, по сути, П - регулятору. Процесс построения корневого годографа нескорректированной системы можно рассматривать как одновременный синтез этой системы с использованием П - регулятора .


Цифровые регуляторы

       В системах автоматического регулирования управляющее устройство является регулятором, реализующим закон регулирования, который устанавливает зависимость между управляющим воздействием U и ошибкой (рассогласованием) , т.е. U=f( ).

      В непрерывных системах широко используются пропорционально-интегрально-дифференциальные (ПИД) регуляторы, которые представляются следующим идеализированным уравнением:



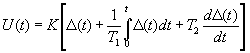
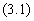
      где К - коэффициент передачи, Т1 - постоянная интегрирования, Т2 - постоянная дифференцирования.

      Для малых периодов дискретизации Т это уравнение может быть преобразовано в разностное с помощью дискретизации, которая представляет замену производной разностью первого порядка, а интеграл суммой. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников или трапеций. При использовании метода прямоугольников уравнение (3.l) в дискретной форме записывается в следующем виде:



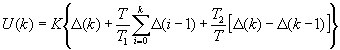
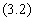
      В результате получим нерекуррентный алгоритм управления, в котором для вычисления суммы необходимо помнить все предыдущие значения сигнала ошибки  (k). Поскольку каждый раз значение управляющего сигнала U(k) вычисляется заново, этот алгоритм получил название позиционного.

      Для реализации программ закона регулирования на ЭВМ более удобным является рекуррентный алгоритм. Этот алгоритм характеризуется тем, что для вычисления текущего значения управляющего сигнала U(k) используемся его предыдущее значение U(k-1) и поправочный коэффициент.

      Для формирования рекуррентного алгоритма необходимо из сигнала U(k) вычесть сигнал U(k-1). Сигнал U(k-1) описывается следующим уравнением:



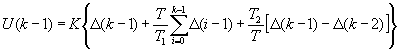
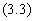
      В результате вычитания из уравнения (3.2) уравнения (3.3) получим









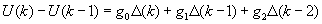
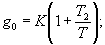
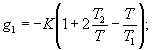
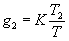
      В результате вычисляется только текущее приращение управляющего сигнала U(k)-U(k-1), и поэтому данный алгоритм называется скоростным.

      Если для аппроксимации непрерывного интеграла использован метод трапеций, то из уравнения (3.1) получим следующее разностное уравнение:



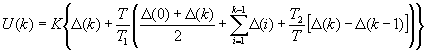
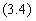
      Произведя вычитание из уравнения (3.4) соответствующего уравнения для U(k-1) получим второе рекуррентное соотношение:









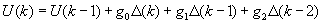
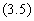
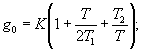
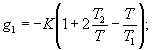
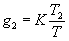
      Для малых периодов дискретизации Т коэффициенты g0, g1, g2       вычисляются с использованием параметров К, Т1 и Т2 аналогового ПИД-регулятора.