1. Основные понятия теории моделирования

Вид материала

Документы

Содержание 1. Основные понятия теории моделирования 1.1. Термины Адекватность модели объекту Классификацию моделей Вычислительная техника Цифровой (дискретный) сигнал Полная модель 1.4. Имитационное моделирование 2. Стохастическое моделирование 2.1.Основные понятия Дискретной случайной величиной Непрерывной случайной величиной Функцией распределения случайной величины Х Математическим ожиданием случайной величины Х Математическим ожиданием непрерывной случайной величины Х Мода и медиана случайной величины Медианой Md случайной величины x Геометрическая медиана Дисперсия и среднеквадратическое отклонение Дисперсией случайной величины Моменты случайной величины Начальным моментом К-го порядка случайной величины x ... Полное содержание

Подобный материал:

• Вопросы вступительного экзамена в магистратуру по специальности, 24.96kb.
• Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
• 1. Введение. Основные понятия моделирования Общая характеристика проблем моделирования., 38.29kb.
• Календарно-тематический план учебная дисциплина: «Математика», 40.92kb.
• Темы лекций. Неделя I: Предмет, объект, методы корпоративного управления. Основные, 54.05kb.
• Основные понятия темы и проверочные знания, 43.12kb.
• Лекция: Анализ и моделирование функциональной области внедрения ис: Основные понятия, 234.94kb.
• Основные понятия, природа и механизмы воспитания основные понятия теории и практики, 734.54kb.
• Логистика запасов основные понятия теории управления запасами, 166.21kb.
• 1 Основные понятия и показатели теории надежности, 163.45kb.

Моделирование систем Основные понятия теории моделирования; классификация видов моделирования; имитационные модели информационных процессов; математические методы моделирования информационных процессов и систем; планирование имитационных экспериментов с моделями; формализация и алгоритмизация информационных процессов; концептуальные модели информационных систем; логическая структура моделей; построение моделирующих алгоритмов; статистическое моделирование на ЭВМ; оценка точности и достоверности результатов моделирования; инструментальные средства; языки моделирования; анализ и интерпретация результатов моделирования на ЭВМ; имитационное моделирование информационных систем и сетей.

1. Основные понятия теории моделирования

1.1. Термины

Объект - все то, на что направлена человеческая деятельность.

Гипотеза - предсказание о свойствах объекта основанное на неполных данных.

Аналогия - суждение о каком-либо частном сходстве объектов. Аналогия связывает гипотезу с экспериментом.

Модель - объект-заместитель объекта, обеспечивающий изучение некоторых свойств оригинала. Модель обеспечивает наглядность исследования объекта- оригинала.

Модель - логическая схема, упрощающая рассуждения и логические построения, позволяющие проводить эксперименты, и уточняющая природу явлений.

Моделирование - замещение одного объекта другим с целью получения информации о важнейших свойствах объекта - оригинала с помощью объекта-модели (далее по тексту для упрощения заменяем объект-оригинал на объект, объект-модель на модель).

Адекватность модели объекту - совпадение результатов моделирования и результатов экспериментов с объектом.

При моделировании сложных объектов (систем) рассматривают: макромоделирование - моделирование системы в целом на уровне подсистем; микромоделирование - моделирование систем или подсистем на уровне элементов.

Модель и моделирование – это универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания объекта, процесса, явления (через модели и моделирование). Модели и моделирование объединяют специалистов различных областей, работающих над решением межпредметных проблем, независимо от того, где эта модель и результаты моделирования будут применены. Модель – это некоторое представление или описание оригинала (объекта, процесса, явления), которое при определенных предложениях, гипотезах о поведении оригинала позволяет замещать оригинал для его лучшего изучения, исследования, описания его свойств. Пример. Рассматривая физическое тело, брошенное с высоты h и падающее свободно в течение t времени, можно записать соотношение: h = gt2/2 . Это физико-математическая модель системы (математическая модель физической системы) пути при свободном падении тела. При построении этой модели приняты следующие гипотезы: 1) падение происходит в вакууме (то есть коэффициент сопротивления воздуха равен нулю); 2) ветра нет; 3) масса тела неизменна; 4) тело движется с одинаковым постоянным ускорением g в любой точке. Слово "модель" (лат. modelium) означает "мера", "способ", "сходство с какой-то вещью". Проблема моделирования состоит из трех взаимосвязанных задач: построение новой (или адаптация известной) модели; исследование модели (разработка метода исследования или адаптация, применение известного); использование (на практике или теоретически) модели. Схема построения модели М системы S с входными сигналами X и выходными сигналами Y изображена на рис. 13.1.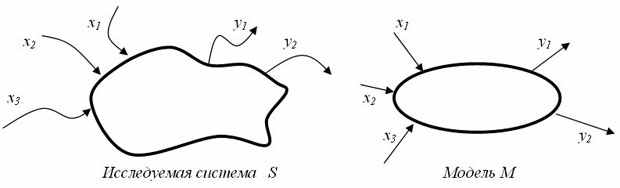

Рис. 13.1.  Схема построения модели

Если на вход М поступают сигналы из X и на входе появляются сигналы из Y, то задан закон, правило f функционирования модели, системы.

Классификацию моделей проводят по различным критериям.

Модель – статическая, если среди параметров описания модели нет (явно) временного параметра.

Модель – динамическая, если среди параметров модели явно выделен временной параметр.

Модель – дискретная, если описывает поведение оригинала лишь дискретно, например, в дискретные моменты времени (для динамической модели).

Модель – непрерывная, если описывает поведение оригинала на всем промежутке времени.

Модель – детерминированная, если для каждой допустимой совокупности входных параметров она позволяет определять однозначно набор выходных параметров; в противном случае – модель недетерминированная, стохастическая (вероятностная).

Модель – функциональная, если представима системой функциональных соотношений (например, уравнений).

Модель – теоретико-множественная, если представима некоторыми множествами и отношениями их и их элементов.

Модель – логическая, если представима предикатами, логическими функциями и отношениями.

Модель – инфрмационно-логическая, если она представима информацией о составных элементах, подмоделях, а также логическими отношениями между ними.

Модель – игровая, если она описывает, реализует некоторую игровую ситуацию между элементами (объектами и субъектами игры).

Модель – алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование, развитие. Введение такого, на первый взгляд, непривычного типа моделей (действительно, кажется, что любая модель может быть представлена алгоритмом ее исследования), на наш взгляд, вполне обосновано, так как не все модели могут быть исследованы или реализованы алгоритмически.

Модель – графовая, если она представима графом (отношениями вершин и соединяющих их ребер) или графами и отношениями между ними.

Модель – иерархическая (древовидная), если она представима иерархической структурой (деревом).

Модель – языковая, лингвистическая, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой. Иногда такие модели называют вербальными, синтаксическими и т.п.

Модель – визуальная, если она позволяет визуализировать отношения и связи моделируемой системы, особенно в динамике.

Модель – натурная, если она есть материальная копия оригинала.

Модель – геометрическая, если она представима геометрическими образами и отношениями между ними.

Модель – имитационная, если она построена для испытания или изучения, проигрывания возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.

Есть и другие типы моделей.

Пример. Модель F = am – статическая модель движения тела по наклонной плоскости. Динамическая модель типа закона Ньютона: F(t) = a(t)m(t) или, еще более точно и лучше, F(t)=s''(t)m(t). Если рассматривать только t = 0.1, 0.2, …, 1 (с), то модель S_t = gt²/2 или числовая последовательность S₀ = 0, S₁ = 0.01g/2, S₂ = 0.04g, …, S₁₀ = g/2 может служить дискретной моделью движения свободно падающего тела. Модель S = gt²/2, 0 < t < 10 непрерывна на промежутке времени (0;10).

Пусть модель экономической системы производства товаров двух видов 1 и 2, соответственно, в количестве x₁ и x₂ единиц и стоимостью каждой единицы товара a₁ и a₂ на предприятии описана в виде соотношения a₁x₁ + a₂x₂ = S , где S – общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, определяя общую стоимость S в зависимости от тех или иных значений объемов производимых товаров. Приведенные выше физические модели – детерминированные.

Если в модели S= gt²/2, 0 < t < 10 мы учтем случайный параметр – порыв ветра с силой p при падении тела, например, просто так: S(p) = g(p)t²/2, 0 < t < 10 , то мы получим стохастическую модель (уже не свободного!) падения. Это – также функциональная модель.

Для множеств X = {Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна} опишем отношения Y: "Николай – супруг Елены", "Екатерина – супруга Петра", "Татьяна – дочь Николая и Елены", "Михаил – сын Петра и Екатерины". Тогда множества X и Y могут служить теоретико-множественной моделью двух семей.


Тип модели зависит от связей и отношений его подсистем и элементов, окружения, а не от его физической природы.

Пример. Математические описания (модели) динамики эпидемии инфекционной болезни, радиоактивного распада, усвоения второго иностранного языка, выпуска изделий производственного предприятия и т.д. являются одинаковыми с точки зрения их описания, хотя процессы различны.

Основные свойства любой модели:

• целенаправленность;
  
• конечность;
  
• упрощенность;
  
• приблизительность;
  
• адекватность;
  
• информативность;
  
• полнота;
  
• замкнутость и др.
  

Жизненный цикл моделируемой системы:

• сбор информации;
  
• проектирование;
  
• построение;
  
• исследование;
  
• оценка;
  
• модификация.
  

Наука моделирования состоит в разделении процесса моделирования (системы, модели) на этапы (подсистемы, подмодели), детальном изучении каждого этапа, взаимоотношений, связей, отношений между ними и затем эффективного описания их с максимально возможной степенью формализации и адекватности.

Приведем примеры применения математического, компьютерного моделирования в различных областях:

• энергетика: управление ядерными реакторами, моделирование термоядерных процессов, прогнозирование энергетических процессов, управление энергоресурсами и т.д.;
  
• экономика: моделирование, прогнозирование экономических и социально-экономических процессов, межбанковские расчеты, автоматизация работ и т.д.;
  
• космонавтика: расчет траекторий и управления полетом космических аппаратов, моделирование конструкций летательных аппаратов, обработка спутниковой информации и т.д.;
  
• медицина: моделирование, прогнозирование эпидемий, инфекционных процессов, управление процессом лечения, диагностика болезней и выработка оптимальных стратегий лечения и т.д.;
  
• производство: управление техническими и технологическими процессами и системами, ресурсами (запасами), планирование, прогнозирование оптимальных процессов производства и т.д.;
  
• экология: моделирование загрязнения экологических систем, прогноз причинно-следственных связей в экологической системе, откликов системы на те или иные воздействия экологических факторов и т.д.;
  
• образование: моделирование междисциплинарных связей и систем, стратегий и тактик обучения и т.д.;
  
• военное дело: моделирование и прогнозирование военных конфликтов, боевых ситуаций, управления войсками, обеспечение армий и т.д.;
  
• политика: моделирование и прогнозирование политических ситуаций, поведения коалиций различного характера и т.д.;
  
• социология, общественные науки: моделирование и прогнозирование поведения социологических групп и процессов, общественного поведения и влияния, принятие решений и т.д.;
  
• СМИ: моделирование и прогнозирование эффекта от воздействия тех или иных сообщений на группы людей, социальные слои и др.;
  
• туризм: моделирование и прогнозирование потока туристов, развития инфраструктуры туризма и др.;
  
• проектирование: моделирование, проектирование различных систем, разработка оптимальных проектов, автоматизация управления процессом проектирования и т.д.
  

Современное моделирование сложных процессов и явлений невозможно без компьютера, без компьютерного моделирования.

Компьютерное моделирование – основа представления (актуализации) знаний как в компьютере, так и с помощью компьютера и с использованием любой информации, которую можно актуализировать с помощью ЭВМ.

Разновидность компьютерного моделирования – вычислительный эксперимент, осуществляемый экспериментатором над исследуемой системой или процессом с помощью орудия эксперимента – компьютера, компьютерной технологии. Вычислительный эксперимент позволяет находить новые закономерности, проверять гипотезы, визуализировать события и т.д.

Компьютерное моделирование от начала и до завершения проходит следующие этапы.

1. Постановка задачи.
   
2. Предмодельный анализ.
   
3. Анализ задачи.
   
4. Исследование модели.
   
5. Программирование, проектирование программы.
   
6. Тестирование и отладка.
   
7. Оценка моделирования.
   
8. Документирование.
   
9. Сопровождение.
   
10. Использование (применение) модели.
    

1.2. Средства моделирования

Аналитический метод - вычисление параметров модели по аналитическим зависимостям.

Имитационный метод - вычисление параметров модели по логической схеме совокупности аналитических зависимостей.

Вычислительная техника - основное средство реализации методов моделирования.

Аналоговый (непрерывный) сигнал может принимать произвольные значения в произвольные моменты времени.

Цифровой (дискретный) сигнал может принимать значения только из определенного набора значений в определенные моменты времени.


1.3. Классификация моделей

Модели могут быть относительно полными и неполными. Теория подобия утверждает, что абсолютное подобие может иметь место лишь при замене объекта точно таким же. Но тогда теряется смысл моделирования.

Полная модель характеризует все основные свойства объекта во времени и в пространстве.

Неполная модель характеризует ограниченную часть свойств объекта.

Систематизация моделей приведена в таблице 2.

Таблица 2 - Модели систем

Модели систем
Детерминированная	Стохастическая
Статическая	Динамическая
Цифровая (Дискретная)	Аналоговая (Непрерывная)
Мысленная	Реальная
Наглядная Символьная Математическая	Натуральная Искусственная

1.4. Имитационное моделирование

При конструировании модели любого физического объекта в начале разрабатывается его физическая модель, в которой описывается принцип действия. Затем разрабатывается математическая модель, в которой устанавливаются количественные зависимости между входными и выходными параметрами объекта. На основе математической модели разрабатывается вычислительная модель, представляющая собой программу для ЭВМ. Имея вычислительную модель, можно проводить вычислительный эксперимент - исследование характеристик объекта путём многократного выполнения программы вычислительной модели при разных исходных данных.

Если движение и преобразование информации в рамках вычислительной модели имитирует физические процессы в объекте моделирования, то вычислительный эксперимент называется имитационным моделированием.



Итерационный процесс разработки моделирования отражён на рисунке. Если результаты вычислительного эксперимента радикально не согласуются с результатами физического эксперимента, то выдвигается новая гипотеза физической модели. Если результаты вычислительного эксперимента согласуются с результатами физического эксперимента, но погрешность превышает допустимые нормы, то корректируется математическая модель. Если же процесс моделирования недостаточно робастный и требует от пользователя много трудовых затрат, а от ЭВМ - больших ресурсов, то требуется корректировка вычислительной модели.

При работе с моделью проектировщик задает как входные воздействия, так и внутренние параметры системы, определяющие преобразовательные свойства последней.

Процесс анализа некоторой системы с помощью вычислительной модели показан на рисунке 3.

Математически этот процесс можно представить в виде выражения: Y =F{X}

где Х - вектор входных воздействий, т. е. набор числовых значений различных параметров сигналов, поступающих на вход системы;

Y - вектор отклика системы, т.е. набор числовых значений, характеризующих реакцию системы на заданные входные воздействия;

F - обобщённый оператор, характеризующий процессы преобразования информации в модели.

2. Стохастическое моделирование

2.1.Основные понятия

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение (но только одно), причем заранее, до опыта, неизвестно какое именно.

Дискретной случайной величиной называется такая величина, число возможных значений которой либо конечное, либо бесконечное счетное множество (множество, элементы которого могут быть занумерованы).

Непрерывной случайной величиной называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал (конечный или бесконечный) числовой оси.

Функцией распределения случайной величины Х называется задание вероятности неравенства Х < х, рассматриваемой как функция аргумента х:

F(x) = P(X < x)

Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х + dx к длине этого участка dx, когда х стремится к нулю, называется плотностью распределения случайной величины в точке х и обозначается f(x)

f(x) = F '(x)

Кривая, изображающая плотность распределения f(x) случайной величины, называется кривой распределения


2.1.1. Параметры случайной величины

Основное назначение числовых характеристик случайной величины состоит в том, чтобы в сжатой форме выразить наиболее существенные особенности того или иного распределения.

Математическим ожиданием случайной величины Х называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.




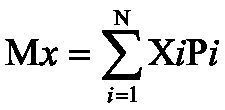
Так как произведение dx * f(x) приближенно равно вероятности попадания случайной величины Х на элементарный участок dx, то сумма произведений xf(x)DX, сопоставленная по аналогии с определением математического ожидания для дискретной случайной величины, приближенно равна математическому ожиданию непрерывной случайной величины Х. Переходя к пределу в сумме при стремлению к нулю длины наибольшего из частичных отрезков dx, получим определенный интеграл.

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежит отрезку [a, b], называют определенный интеграл




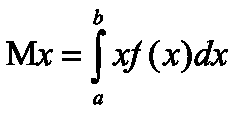
Если возможные значения непрерывной случайной величины Х, принадлежат всей оси Ох, то математическое ожидание определяется интегралом




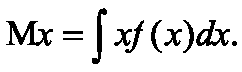
Мода и медиана случайной величины

Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода есть такое значение случайной величины, при котором плотность распределения имеет максимум, т.е. f(M0) = max

Если кривая распределения имеет два или несколько максимумов, то распределение называется двухмодальным или многомодальным.

Иногда встречаются распределения, которые имеют минимум, но не имеет максимум. Такие распределения называют антимодальными.

Медианой Md случайной величины x называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.

P(x < Md) = P(x > Md)

Геометрическая медиана - это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Каждая их этих площадей равна 0.5, так как вся площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке Md:

F(Md) = P(x < Md) = 0.5

Если распределение одномодально и симметрично, то все три характеристики положения случайной величины - математическое ожидание, мода и медиана - совпадают.

Дисперсия и среднеквадратическое отклонение

Основными характеристиками рассеивания случайной величины является дисперсия и среднеквадратическое отклонение. При определении указанных характеристик используется разность между случайной величиной Х и ее математическим ожиданием Мх, т.е. x - Мх. Эта разность называется центрированной случайной величиной, соответствующей величине x

Дисперсией случайной величины называется математическое ожидание квадрата отклонения величины от её математического ожидания, то есть:

Dx = M[(x - Mx)²] или Dx = M[x]²

для дискретной случайной величины дисперсия выражается суммой




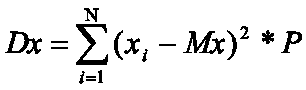
А для непрерывной - интегралом




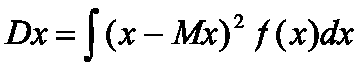
Для большего удобства желательно иметь параметр, по размерности совпадающую c размерностью случайной величины. Таким параметром является среднее квадратическое отклонение случайной величины, которое представляет собой положительный квадратный корень из ее дисперсии




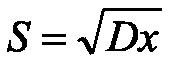
Моменты случайной величины

Обобщением основных числовых характеристик случайных величин является понятие моментов случайной величин. Различают моменты двух видов: начальные и центральные.

Начальным моментом К-го порядка случайной величины x называют математическое ожидание величины x, т. е.




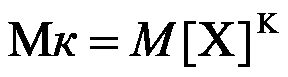
Следовательно, для дискретной случайной величины начальный момент выражается суммой




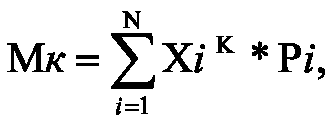
а для непрерывной - интегралом




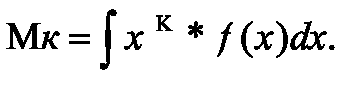
Из начальных моментов случайной величины особое значение имеет момент первого порядка, который представляет собой не что иное, как математическое ожидание случайной величины.

Центральным моментом к-го порядка случайной величины Х называют математическое ожидание величины (X - Мх).

Uk=M[(X - Mx)]

Для дискретной случайной величины центральный момент выражается суммой:




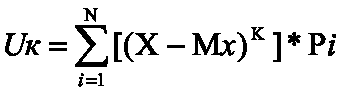
Для непрерывной - интегралом:




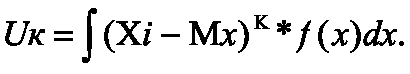
Среди центральных моментов случайной величины особое значение имеет центральный момент второго порядка, который представляет не что иное, как дисперсию случайной величины. Третий случайный момент U3 служит характеристикой асимметрии ("скошенности") распределения. Если случайная величина Х распределена симметрично относительно своего математического ожидания, то третий центральный момент равен нулю: U3 =0. Величина a, равная отношению U3 к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.




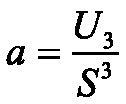
При а>0 кривая распределения имеет положительную асимметрию, при а < 0 - отрицательную







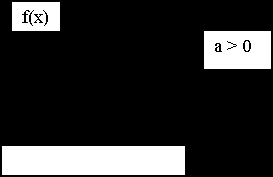
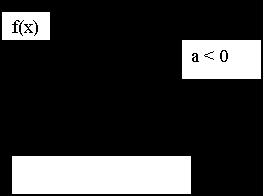
Четвертый центральный момент U4 служит для характеристики островершинности или плосковершинности распределения. Это свойство распределения называется эксцессом. Эксцессом случайной величины x называется величина




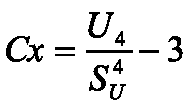
Здесь число 3 вычитается из отношения 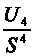потому, что для наиболее распространенного нормального закона распределения это отношение равно трем.

Кривая нормального распределения, для которого эксцесс равен нулю, принята за эталон, с которым сравниваются другие распределения. Кривые более островершинные имеют положительный эксцесс, кривые более плосковершинные




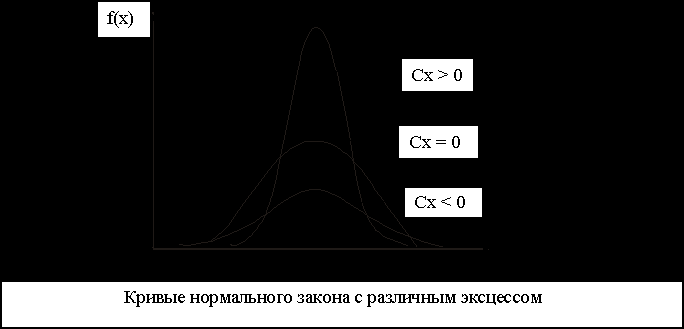
2.1.2. Равномерное распределение

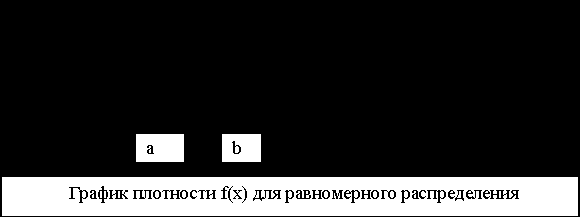
Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его - равна нулю. Так как площадь, ограниченная кривой распределения, равна единице то плотность равномерного распре деления на интервале (а, b), как высота прямоугольника с основанием (b - а), равна




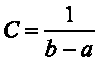
И, следовательно, плотность распределения f(x) имеет вид:

0 при x < a

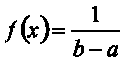при a < x

0 при x > b

Функция распределения F(x) для равномерного распределения:

0 при x < a

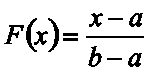при a < x

0 при x > b

Математическое ожидание




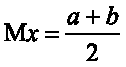
Дисперсия




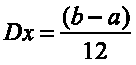
Среднеквадратической отклонение




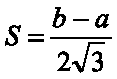
График плотности f(x) для равномерного распределения изображен на рисунке.




2.1.3. Нормальное распределение

Среди распределений непрерывных случайных величин центральное место занимает нормальный закон (закон Гаусса)




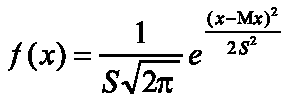
где Мх и S - параметры нормального распределения, которые являются математическим ожиданием и средне-квадратическим отклонением соответственно. Функция распределения случайной величины, имеющей нормальное распределение, имеет вид:




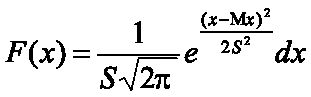
Основная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.

График плотности вероятности нормального распределения называется нормальной кривой (кривая Гаусса).

Отметим некоторые свойства нормальной кривой:

- Кривая распределения симметрична относительно ординаты, проходящей через точку Мх.

- Кривая имеет один максимум при Х=Мх, равный

- При 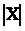ветви кривой асимптотически приближаются к оси Оx.

- Изменение математического ожидания Мх при S = const приводит к смещению кривой распределения вдоль оси Ox. При этом кривая распределения сохраняет свой вид.

При изменении средне-квадратического отклонения S и Мх = const кривая распределения изменяет свой вид. На рисунке кривая I соответствует случаю S = 2.5, для кривой II - S = 1, а для III - S = 0.4.

2.1.4. Метод Монте-Карло

Для моделирования объектов, содержащих случайные параметры, используется метод статистических испытаний (метод Монте-Карло). Этот метод позволяет на основе аналитического описания объекта моделировать поведение выходной характеристики с учетом случайного изменения входных и внутренних параметров. Для этого с помощью генератора случайных чисел задаются значения входных параметров для первого испытания, и вычисляется значение выходного параметра. Затем задаются значения входных параметров для второго испытания, и вычисляется соответствующее значение выходного параметры, и т.д. В результате получается совокупность случайных значений выходного параметра. С помощью статистического анализа оценивается закон распределения этой совокупности и его параметры. Такая задача называется прямой. Более важной является обратная задача: определение требований к значениям входных параметров по заданным требованиям к значениям выходного параметра. Практически обратная задача решается многократным повторением прямой задачи. При этом значения параметров распределений входных параметров изменяются до тех пор, пока параметры выходного распределения не будут удовлетворять заданным требованиям.

2.2. Моделирование случайных чисел

Под моделированием случайной величины x принято понимать процесс получения на ЭВМ её выборочных значений x1,...xn. Проблема получения на ЭВМ равномерно распределённых случайных величин может быть решена различными способами:

- ввод таблиц равномерно распределённых случайных чисел в память ЭВМ.

- использование специального приспособления к ЭВМ - "датчика" случайных чисел, формирующего случайные величины путём физического моделирования некоторых случайных процессов (излучения радиоактивных источников, шумов электронных ламп и др.).

- использование псевдослучайных (квазислучайных) последовательностей, реализуемых программным генератором случайных чисел. Псевдослучайные равномерно распределенные случайные числа получаются в ЭВМ программным способом с помощью некоторого рекуррентного соотношения. При этом каждое последующее число x1+1 образуется из предыдущего путём применения некоторого алгоритма, состоящего из арифметических и логических операций. Такая последовательность чисел удовлетворяет известным критериям случайности, хотя входящие в эту последовательность числа зависимы между собой. Одним из недостатков этого метода является периодичность образованных программным способом псевдослучайных чисел, но для ряда задач, не требующих большого количества случайных чисел, длина периода является достаточной.


2.2.1. Оценки параметров моделируемых последовательностей случайных чисел

Под выборкой при генерации случайных чисел будем понимать последовательность псевдослучайных чисел, полученную при N обращении к генератору случайных чисел. В таблице 4 приведены обозначения параметров выборки для выборочных значений.

Таблица 4 - Параметры выборки для выборочных значений

Параметр	Обозначение	Определение
Выборочные данные	Xi, где i = 1, ... N	Наблюденные значения случайной величины
Объем выборки	N	Количество случайных чисел в выборке
Выборочное среднее	x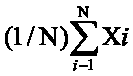
Выборочная дисперсия	S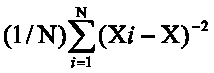

Но для того, чтобы оценка имела практическую ценность, она должна обладать следующими свойствами:

Несмещенность - математическое ожидание оценки должно совпадать с математическим ожиданием распределения.

Состоятельность - при достаточно большой выборке со сколь угодно большой достоверностью отклонение оценки от истинного значения характеристики должно быть меньше любой наперед заданной величины.

Эффективность - дисперсия оценки должна быть минимальной.

В таблице 5 приведены оценки моментов случайной величины.

Таблица 5 - Оценка моментов случайной величины

Момент	Обозначение	Оценка момента
Mk - математическое ожидание	M1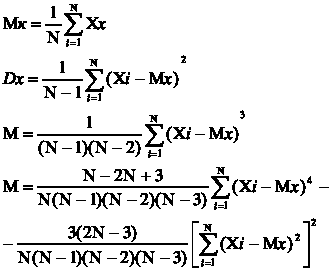
Dx - S - дисперсия	М2
Третий центральный момент	М3
Четвертый центральный момент	М4

2.2.2. Критерии согласия

Критерий хи-квадрат.

Мера расхождения статистического и теоретического закона распределения для критерия хи-квадрат определяется формулой;




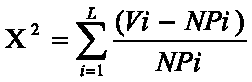
где: L - количество интервалов;

Vi - количество выборочных объектов в 1-м интервале:

Pi - вероятность попадания случайной величины в 1-й интервал, вычисленная для теоретического закона распределения;

N - объем выборки.

Критерий Колмагорова.

Мера расхождения статистического и теоретического затонов расхождения для критерия Колмогорова определяется формулой:




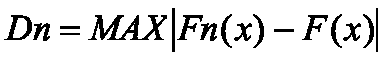
Fn(x) - эмпирическая функция распределения, равная (N -объем выборки,

Vx - количество объектов в выборке, не превышающих величины х);

F(x) = P(X < x) - теоретическая функция распределения.

2.3.1. Создание программного датчика случайных чисел

Для создания датчика запрашиваются коэффициенты рекуррентной формулы:

- множитель А, приращение С, модуль М.

Для генерации датчиком равномерной последовательности случайных чисел требуется ввести:

- объем выборки N,

- целое нечетное число, с которого начинается генерация равномерной последовательности случайных чисел Ix .

Для генерации последовательности случайных чисел, распределенных по нормальному закону, получаемой на основе последовательности случайных чисел, распределенных по равномерному закону, требуется ввести:

- математическое ожидание Мх,

- среднеквадратическое отклонение S.

В результате выполнения программы получаем выходные данные:

- таблица случайных чисел, если N <=10;

- оценки параметров: математическое ожидание, дисперсия, третий центральный момент и эксцесс;

- количество периодов в каждой последовательности;

- мера расхождения для критерия хи-квадрат: Х*Х;

- мера расхождения для критерия Колмогорова К+;

- гистограммы.

2.3.2. Метод Монте-Карло

Определяется закон распределения функций случайных величин методом Монте-Карло. Для этого генерируются три последовательности, закон распределения каждой из которых задается специальным признаком вида последовательности (1 - равномерный, 2 - нормальный). Числа выходной последовательности вычисляются по формуле:

(D*X1+E*X2)+P*X3

где Х1, Х2, Х3 - три сгенерированные последовательности случайных чисел

D, E, F -коэффициенты вводимые в диалоге.

Перед выполнением запрашиваются входные данные:

- вид последовательности;

- математическое ожидание (номинал);

- среднеквадратическое отклонение;

- целое нечетное число;

- объем выборки.

В результате вычислительной модели необходимо получить выходные данные:

- оценки математического ожидания трех последовательностей,

- ожидаемое номинальное значение полученной последовательности,

- оценка математического ожидания полученной последовательности,

- мера расхождения для критерия хи-квадрат Х*К,

- мера расхождения для критерия Колмогорова К+,

- гистограмма полученных последовательностей.

Для построения гистограммы в вычислительной модели весь диапазон исследуемой последовательности делится на 20 интервалов. Частота попадания случайных чисел в эти интервалы используется также для вычисления критерия Х*К и критерия Колмогорова.

При доверительной вероятности 0.02 < Р < 0,98 и числе степеней свободы 20 из таблицы Х*Х - распределения находим , что значения критерия Х*К, при которых гипотеза о соответствии распределения полученной последовательности о гипотетической принимается, лежат в пределах 9 < Х*Х < 35.

Для критерия Колмогорова допустимыми считаются значения, лежащие в интервале 0.5 < К+ < 1.5.

3. Оптимизация

3.1. Основные понятия

Оптимизация - поиск наилучшего решения с учетом ограничений.

Для оптимизации ищется целевая функция. Эта функция конструируется искусственно на основе уравнений, описывающих объект оптимизации. Целевая функция обычно имеет много аргументов: φ=f (х1, х2, ..., х n).

Чтобы найти оптимальное значение, перебирают значение аргументов хi пошагово до тех пор, пока значение φ станет удовлетворять условиям оптимума. Даже количество аргументов не более трех, "тупой" перебор может потребить очень много времени.

Поэтому разработаны десятки методов оптимизации:

- первый строгий математический метод предложил в 1840г. венгерский математик Коши - МСС - метод скорейшего спуска. При формулировании задач оптимизации обычно стараются ее свести к поиску минимума. МСС относится к классу градиентных методов.

Градиент - вектор, указывающий на направление максимального возрастания функции.

Антиградиент - вектор, указывающий на направление максимального убывания функции. Чтобы повернуть вектор на 180⁰, достаточно изменить все знаки у градиентов на противоположные (т.е. х (-1)).

Для иллюстрации поиска экстремума в процессе оптимизации функций двух переменных используют линии равного уровня (ЛРУ). Если задаться постоянным значением φ и так подбирать значения хi чтобы значение φ было равным заданному значению, то геометрическое место точек φ составит линию равного уровня.




В зависимости от целевой функции линий равного уровня могут характеризоваться следующими географическими понятиями:

Долина - когда соседние линии равного уровня изменяется очень слабо в широком диапазоне аргументов.

Возвышенность - когда соседние линии равного уровня представляют собой замкнутые линии и значение φ возрастает от внешних линий к внутренним.

Впадина - когда соседние линии равного уровня представляют собой замкнутые линии, и значение φ убывает от внешних линий к внутренним.




Седловина - локальный минимум, в центре которого векторы указывают на возрастание функции, но вскоре направление вектора резко изменяется вверх или вниз.

МСС - простейший метод оптимизации, пригодный для сложных систем. Работа метода хорошо иллюстрируется с помощью линий равного уровня (ЛРУ).

Порядок поиска оптимума:

- выбирается исходная точка в виде значений параметров целевой функции:

φ=f (х1, х2, ..., х n).

- ищется градиент;

- движемся в направлении антиградиента с заданным шагом;

- на каждом шаге проверяем выполнение условия движения, оно такое: φi < φi-1 ( текущее значение φ должно быть меньше предыдущего).

- если условие движения нарушается, то процесс останавливается, иначе, движение продолжается;

- при нарушении условий движения уточняется одномерный минимум и ищется новый градиент;

- условие останова:

а) значение φ меньше заданного;

б) разность значений соседних φ меньше заданной;

в) количество шагов превышает допустимое.

- если после останова минимума не удовлетворяет требованиям, то либо ищется другая исходная точка и процесс повторяется, либо выбирается другой метод оптимизации.


3.2. Пример конструирования целевой функции

Допустим, объект оптимизации описывается следующей системой уравнений:

х² + у² = 1

х + у = 1

Графически эту систему можно представить как окружность и секущая прямая



Для детального рассмотрения рисунка щелкнуть по нему мышкой.

Задача: найти минимальное расстояние между точками прямой и окружности.

В данном случае имеется два минимума. Последовательность конструирования целевой функции:

1. приводим систему уравнений к нулевому виду:

х² + у² - 1 = 0

х + у -1 = 0

2. складываем два уравнения:

1 ур. + 2 ур. = 0

3. для усиления чувствительности к изменению аргументов обе части уравнения можно возвести в квадрат:

(1 ур.)² + (2 ур.)² = 0

4. Целевую функцию представим в виде:

φ = (х² + у² - 1)² + (х + у - 1)²;

Численный поиск минимума

Составляется компьютерная программа, в которой значение х и у изменяется с заданным шагом в диапазоне +- 2. На каждом шаге вычисляется значение φ, с помощью плоттера рисуется картина ЛРУ.

Таким способом были построены ЛРУ еще для двух следующих целевых функций:

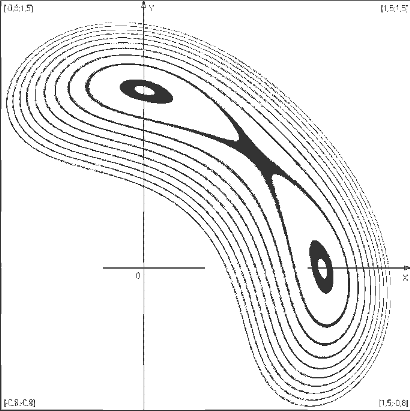
φ = 100(x²-y)²+(1-x)²





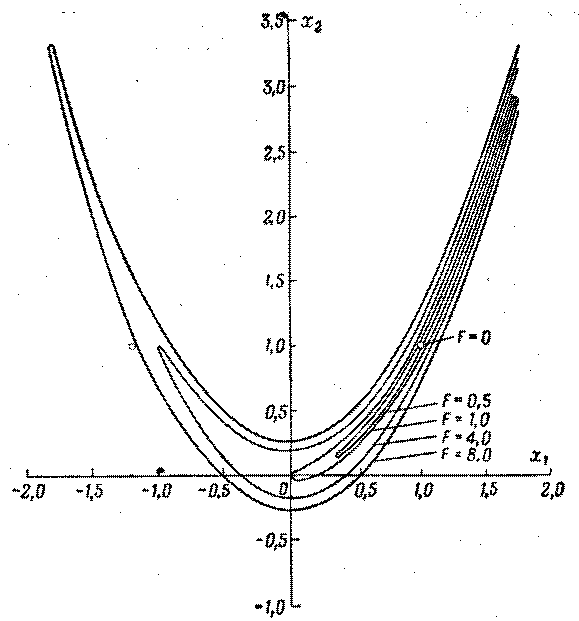
φ = (x-y)²+((x+y-10)/3)²





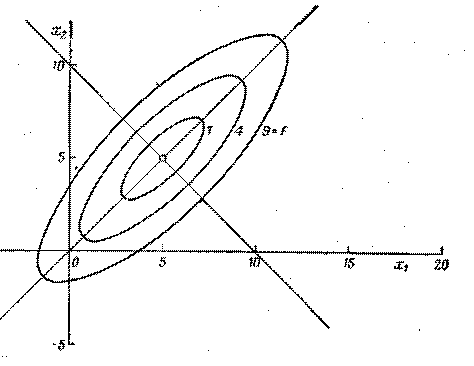
3.3. Многомерный и одномерный поиск

МСС представляет собой многомерный поиск, т.к. минимум ищется на разных направлениях. Когда минимум ищется только в одном направлении для уточнения направления следующего уровня - одномерный поиск.

Одномерный поиск

Для многомерного поиска разработаны десятки методов, для одного поиска около 1 десятка методов. Рассмотрим одномерное приближение.

Метод последовательных приближений




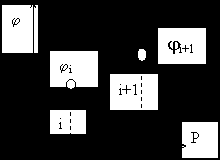
P - длина шага оптимизации;

φ - значение целевой функции

1. при нарушении условий движения (φi+1 > φi) движение останавливается

2. Возвращается на 1 шаг назад.

3. Делим длину шага на R где R = 3-10

4. Возобновляем движение с новым шагом.

5. При нарушении условий движения все повторяется, и т.д.

Условия останова:

- Значение j < заданного

- Разность между соседними значениями j < заданной

- Длина шага < заданной

- Кол-во шагов превышает заданное.

Любое из этих условий приводит к останову.

Метод золотого сечения

Если возьмем пропорцию:

x₁/x = x₂/x₁ = 0.618-m_o







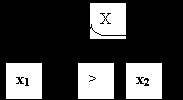
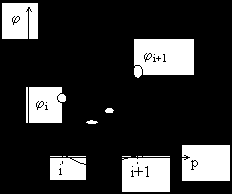
Такое соотношение называется золотой пропорцией.

1. При нарушении условий движения последний шаг делим в отношении золотой пропорции слева на право.

2. Этот же отрезок делим в золотой пропорции справа на лево. В результате получим 2 новые точки

3. Сравниваем значения j в новых точках.

4. Выбираем отрезок, которому соответствует меньшее из этих двух j.

5. Полученный отрезок делим в отношении золотой пропорции слева направо, и т.д.

Условия останова те же, что и в предыдущем случае.

Метод параболической аппроксимации (МПА)





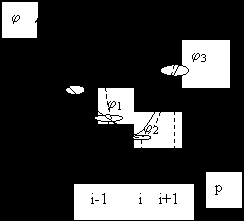
При нарушении условий значения j в последних 3-х точках подставляется в формулу решения системы 3-х уравнений для параболы. Это решение позволяет находить координаты минимума параболы, проходящий через 3 последние точки.

Сравнение методов одномерного поиска

МПП более прост (движемся, делим), но требует много шагов (м.б. 10 и 100 шагов).

МЗС позволяет найти min за 3-4 шага.

МПА более сложен, но позволяет найти min за 1 шаг. Но МПА обладает методической погрешностью, поскольку парабола отличается от истинной кривой; обычно эта погрешность невелика. В пакетах программ для расчета оптики обычно используется в качестве метода многомерного поиска демнорированый МСС, а в качестве метода одномерного поиска - МПА.