Аннотация ном научно-образовательный материал «вм моделирование временных рядов в среде eviews»

Вид материала

Практикум

Содержание По информационным критериям (наименьшее значение статистики) выбираем модель ARIMA(1,1,0)

Подобный материал:

• Модификация программного комплекса ас дрм для обработки временных рядов в технике, 125.29kb.
• Программа дисциплины Анализ финансово-экономических временных рядов для направления, 76.91kb.
• Пояснительная записка: Требования к студентам: необходимо знание курсов «Математического, 78.04kb.
• Пояснительная записка: Требования к студентам: необходимо знание курсов «Математического, 49.13kb.
• Программа дисциплины Нелинейные модели временных рядов для направления 521600 Экономика, 66.64kb.
• Статистика временных рядов, 19.49kb.
• Рабочая программа дисциплины экономический анализ временных рядов цели и задачи изучения, 118.03kb.
• Научно-образовательный материал (ном), 77.59kb.
• Современный интеллектуальный анализ нечетких временных рядов, 141.75kb.
• Применение методов математической оптимизации в электроэнергетике Научно-образовательный, 20.69kb.

АННОТАЦИЯ НОМ

Научно-образовательный материал « ВМ Моделирование временных рядов в среде EViews»

Н.А.Сливина

nslivina@mail.ru

Кафедра высшей математики МЭИ(ТУ)

Почти в каждой области знания встречаются явления, которые важно изучать в развитии во времени и в пространстве – данные типа временных рядов. Данные типа временных рядов широко используются в различных областях человеческой деятельности. В экономике это данные финансовых рынков, макроэкономические показатели; в метеорологии — температура, объёмы осадков и т.п.; в медицине — данные о заболеваемости, о результатах использования лечебных процедур, препаратов, динамика различных показателей жизнедеятельности пациентов (давление, пульс, сигналы нервной системы), в технике и технологии – параметры технологических процессов, сигналы различной природы

Практически всегда в закономерное течение процесса вмешивается случайность – в виде случайных импульсов, помех, случайных ошибок. Поэтому изучение временных рядов – раздел прикладной статистики – важная часть современного образования инженеров, экономистов, работников сферы управления.

Поскольку в стандартном курсе математической статистики нет задач прикладной статистики, описанный практикум «ВМ Моделирование временных рядов в среде EViews» может быть эффективно использован в системе повышения квалификации, в системе дополнительного образования.

Практикум ориентирован на использование популярного эконометрического пакета EViews, который широко используется как в научных, так и в учебных целях. Практикум содержит две лабораторные работы: Лабораторная работа 1 «Моделирование и анализ простейших одномерных временных рядов» и Лабораторная работа 2 «Построение ARIMA-моделей. Исследование стохастической природы тренда».

Каждая лабораторная работа содержит краткое теоретическое введение, содержащее используемые при анализе временных рядов понятия, формулы, описание статистик и т.п.

Например. Справочные теоретические сведения (фрагмент описания)

Временной ряд представляет собой совокупность наблюдений случайной величины в различные моменты времени. Его рассматривают как выборку из последовательности случайных величин , где 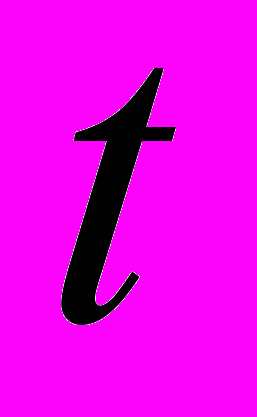принимает целые значения из промежутка .

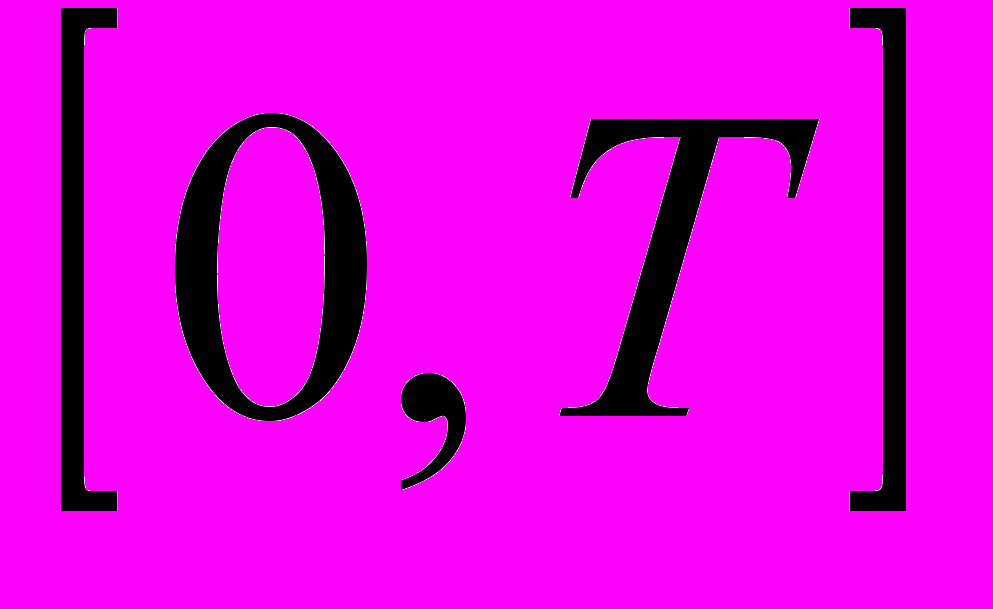Процесс авторегрессии скользящего среднего процесс ARMA(p, q):



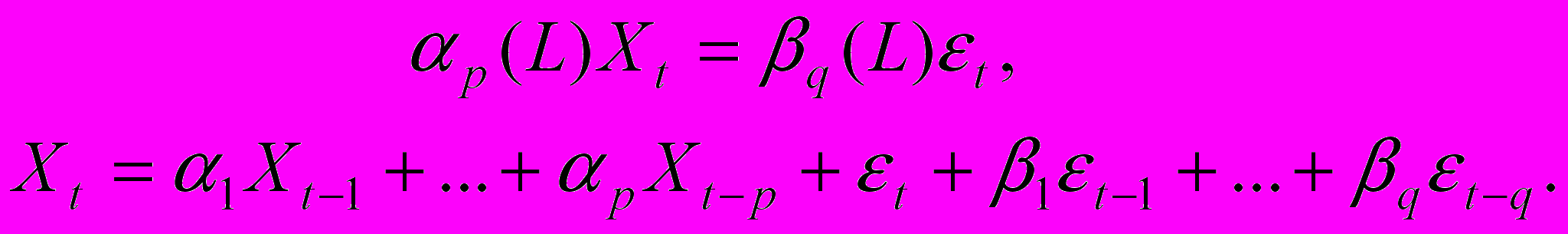
Понятно, что стационарность процесса ARMA(p, q) определяется его AR частью AR(p), т.е. условия стационарности те же, что и у AR(p). Если процесс ARMA стационарный, то он имеет представление MA (∞) и конечное представление AR (p).

Каждая работа состоит из нескольких заданий, каждое задание посвящено решению простейшей задачи (генерирование временного ряда с заданными свойствами, построение графика, исследование стационарности, статистических характеристик ряда и т.п.).

В тексте описания к лабораторной работе формулируется задача и даны все необходимые указания о способе решения поставленной задачи на компьютере для обучающегося, который не владеет навыками работы в среде EViews, а также описание и интерпретация результатов вычислений.

Например. Создание рабочего файла EViews для моделирования и исследования временных рядов (фрагмент описания)

Создадим рабочий файл EViews недатированных данных для исследования временных рядов, содержащих 150 наблюдений и сохраним его на Рабочем столе в папке Временные ряды его с именем Time Series 1:





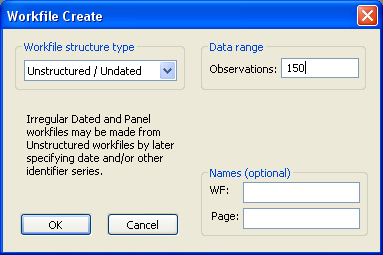
Моделирование процессов ARIMA(p,d,q) Оцениваем модель ARIMA(1,1,0), вводим в командной строке ls d(arima_1_1_0) c d(arima_1_1_0(-1))



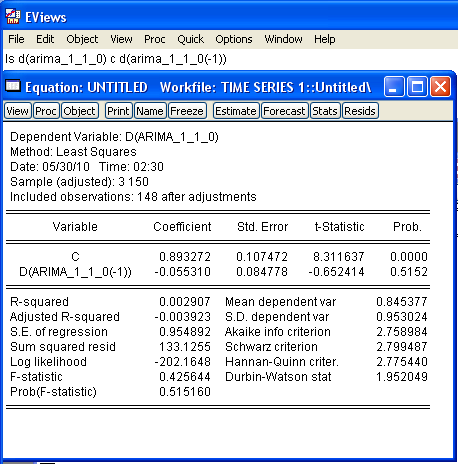
По информационным критериям (наименьшее значение статистики) выбираем модель ARIMA(1,1,0):



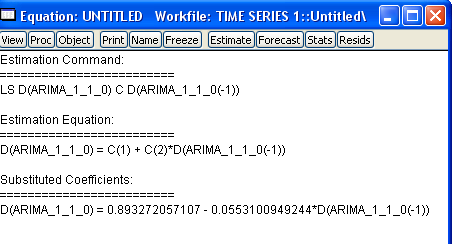
В каждой работе сформулированы задания для самостоятельного исследования, цель которых – закрепить навыки исследования временных рядов и работы в среде EViews, приобретённые в процессе выполнения работы.

Например. Задания для самостоятельной работы (фрагмент)

Сгенерируйте нестационарный случайный процесс 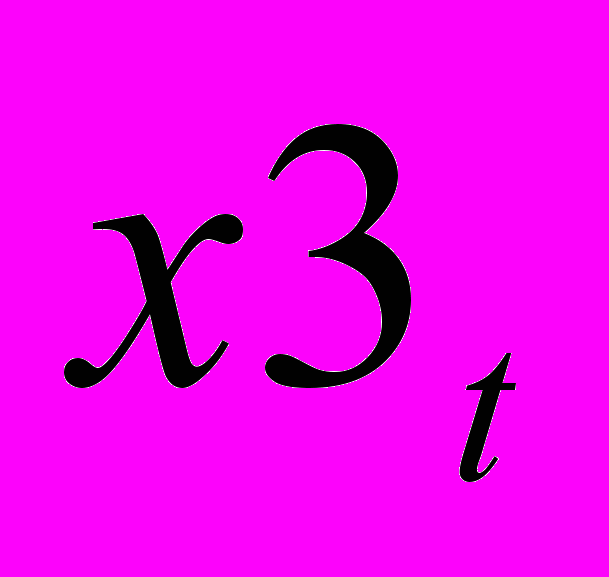− ARIMA(2,1,0) с константой много меньшей единицы. Исследуйте его стационарность и стационарность его первых разностей. Постройте для него модели ARIMA(2,1,1), ARIMA(2,1,0), ARIMA(1,1,1), ARIMA(1,1,0). Выберите и исследуйте лучшую из них. Исследуйте стохастическую природу тренда ряда .

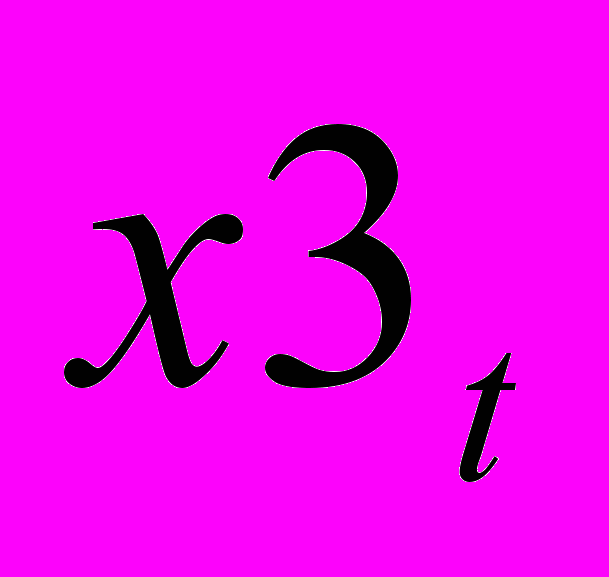Для успешной работы с практикумом обучающемуся достаточно владеть основными сведениями из теории вероятностей и математической статистики (в рамках стандартного курса для инженерных и экономических вузов) и простейшими приёмами работы за компьютером в среде Windows.

Лабораторный практикум предназначен для самостоятельной работы или для работы в компьютерном классе. При работе в классе полезным представляется совместное сравнение и обсуждение полученных результатов. Предполагается, что обучающийся, следуя приведенному описанию, последовательно самостоятельно выполняет задания работы, а затем выполняет самостоятельные исследования, сформулированные в задании.