Учебное пособие по курсу " Электроника и микроэлектроника" для студентов, обучающихся по направлению "Электроника и микроэлектроника"
| Вид материала | Учебное пособие |
- Программа вступительного экзамена в магистратуру по направлению 210100. 68 Электроника, 78.21kb.
- Рабочая учебная программа факультет №1 Неорганической химии и технологии Кафедра неорганической, 94.02kb.
- Рабочая программа учебной дисциплины материалы и элементы электронной техники ооп 210100, 296.57kb.
- Программа государственного экзамена по направлению подготовки дипломированных специалистов, 83.37kb.
- Рабочая учебная программа по дисциплине: электротехника и электроника (Теоретические, 407.78kb.
- Курсовая работа по курсу: "Микроэлектроника и функциональная электроника" Допущено, 311.14kb.
- Рабочая программа учебной дисциплины ф эфф 1-21/01 Государственное образовательное, 130.14kb.
- 210100. 62 – Электроника и микроэлектроника, 24.24kb.
- Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию, 202.38kb.
- Программа вступительных испытаний в магистратуру кафедры «Проектирование и конструирование, 138.26kb.
УДК
621.38
В - 751
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
М.Д.Воробьев
ПОЛУПРОВОДНИКОВЫЕ АКТИВНЫЕ ЭЛЕМЕНТЫ
С б о р н и к з а д а ч, в о п р о с о в
и з а д а н и й н а м о д е л и р о в а н и е
учебное пособие
по курсу
“Электроника и микроэлектроника”
для студентов, обучающихся по направлению
“Электроника и микроэлектроника”
Москва Издательство МЭИ 2000
УДК
621-38
В - 751
УДК: 621.382 (075.8)
Утверждено учебным управлением МЭИ в качестве учебного пособия для студентов
Подготовлено на кафедре “Электронные приборы”
Воробьев М.Д. Полупроводниковые активные элементы. Сборник задач, вопросов и заданий на моделирование. Учебное пособие по курсу "Электроника и микроэлектроника" для студентов, обучающихся по направлению “Электроника и микроэлектроника”. M.: Изд-во МЭИ, 2000. 36 с.
ISB N5-7046-0622-9.
Приведены задачи и вопросы по основным разделам курса – полупроводниковые диоды на основе p-n перехода, биполярные и полевые транзисторы. По каждому разделу предлагаются задания на компьютерное моделирование основных характеристик диодов и транзисторов в сочетании с методическими указаниями по их выполнению и тестовыми аналитическими расчетами.
Предназначено для студентов 2-го курса, обучающихся по направлениям 200300 и 552500.
Введение
Предлагаемые в настоящем сборнике задачи, вопросы и задания отражают содержание курса “Электроника и микроэлектроника” по разделу “Полупроводниковые активные элементы” (диоды на основе p-n перехода, биполярные и полевые транзисторы). Каждому из указанных разделов предшествует краткое изложение теории, содержащее необходимые для выполнения заданий основные расчетные соотношения. Следует иметь ввиду, что упрощенный в ряде случаев характер изложения материала, как показывает многолетний опыт автора, вполне оправдан при изучении студентами II курса дисциплины “Электроника и микроэлектроника”, так как позволяет сконцентрировать внимание на наиболее существенных физических явлениях, характеристиках и параметрах полупроводниковых активных элементов. Вместе с тем необходимо помнить, что теоретические разделы сборника ни в коей мере не могут рассматриваться как сокращенное учебное пособие в отрыве от конспекта лекций и рекомендуемой литературы.
Одной из главных особенностей сборника являются задания на моделирование статических характеристик с использованием современных программных средств, что позволяет за короткий период времени получить представление об основных закономерностях изучаемых объектов в более широком плане по сравнению с лабораторным практикумом. Для того чтобы облегчить и сделать более эффективными усилия, направленные на освоение программных средств моделирования, каждое задание снабжено методическими указаниями по его выполнению. Существенным дополнением к заданиям на моделирование служат выполняемые вручную аналитические расчеты, в результате чего появляется возможность быстро и наглядно убедиться в корректности проведенных расчетов.
Перечень заданий на моделирование, предлагаемый в сборнике, может быть значительно расширен и должен рассматриваться лишь как база для накопления опыта по проведению занятий с использованием компьютерного моделирования. Очевидно, что наличие достаточно обширных библиотек активных элементов позволяет индивидуализировать задания и придать им в ряде случаев исследовательский характер.
Методические указания также следует рассматривать лишь как рекомендации. После приобретения минимальных навыков работы с программными средствами, как правило, появляется желание предложить свои собственные пути выполнения заданий, что заслуживает одобрения и поощрения.
1.Электронно-дырочный переход и диоды на его основе
1.1.Основные характеристики p-n перехода и диодов
Вольт-амперная характеристика (ВАХ) p-n перехода описывается уравнением
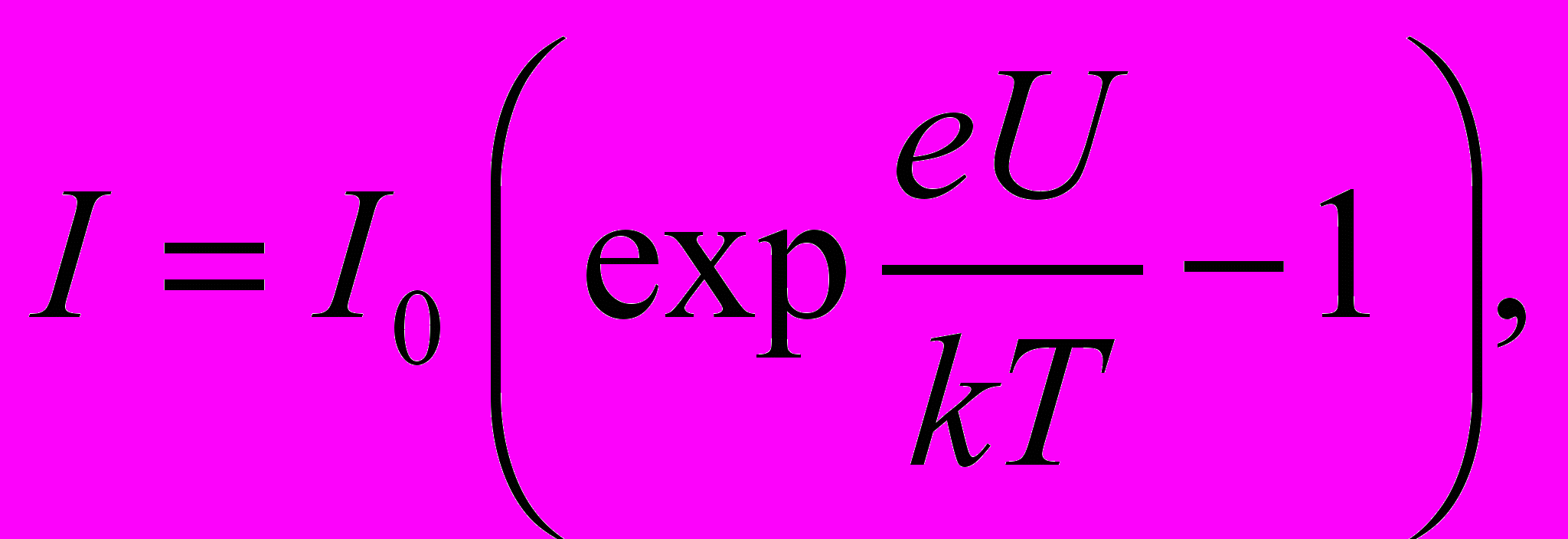(1.1)где e – заряд электрона; k – постоянная Больцмана; U – приложенное напряжение; T – абсолютная температура; I0 – тепловой ток.
Тепловой ток зависит от температуры и определяется свойствами полупроводникового материала, из которого изготовлен p-n переход:
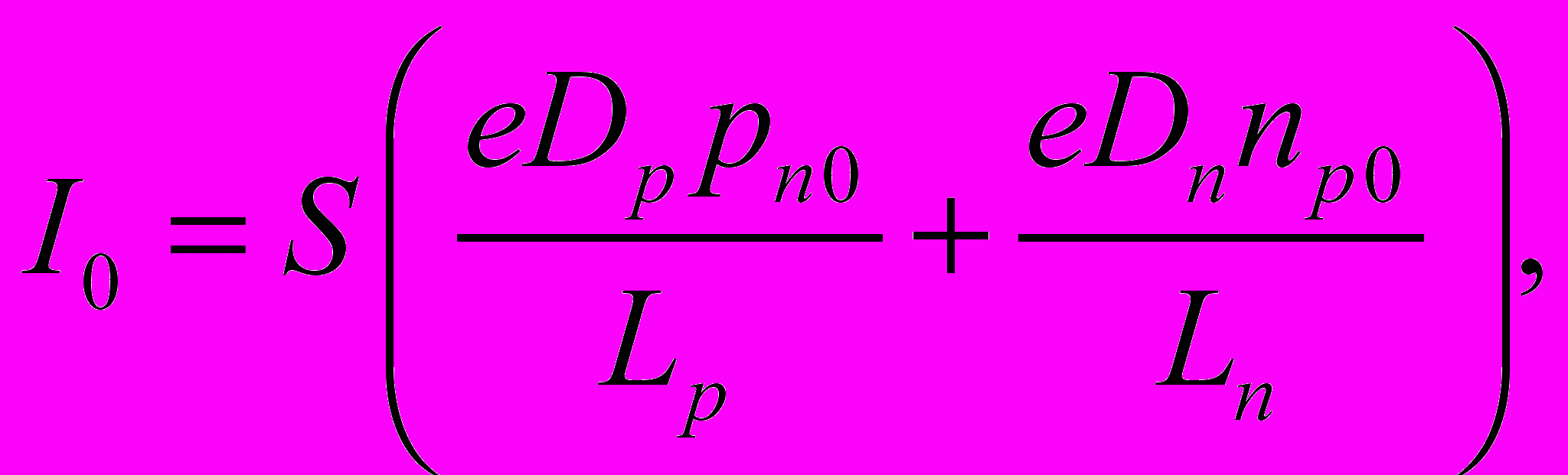(1.2)где S – площадь перехода; Dp,n – коэффициенты диффузии неосновных носителей заряда – соответственно дырок в n-области перехода и электронов в p-области перехода; pn0 и np0 – концентрации неосновных носителей заря да; Lp,n – диффузионные длины неосновных носителей заряда.
Диффузионная длина и коэффициент диффузии связаны соотношением:
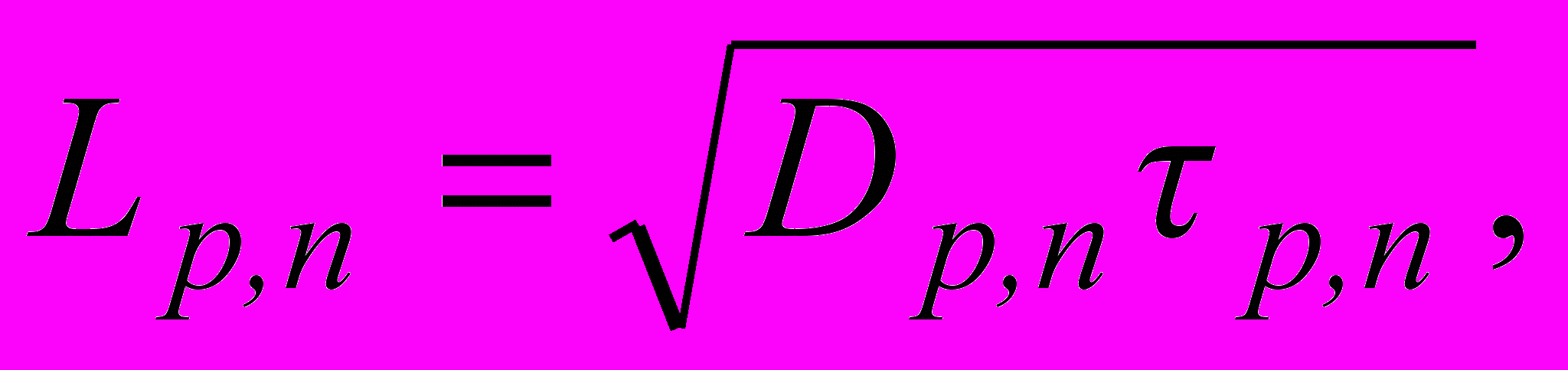(1.3)где p,n – время жизни соответственно дырок и электронов.
Согласно соотношению Эйнштейна, коэффициенты диффузии связаны с подвижностью носителей заряда
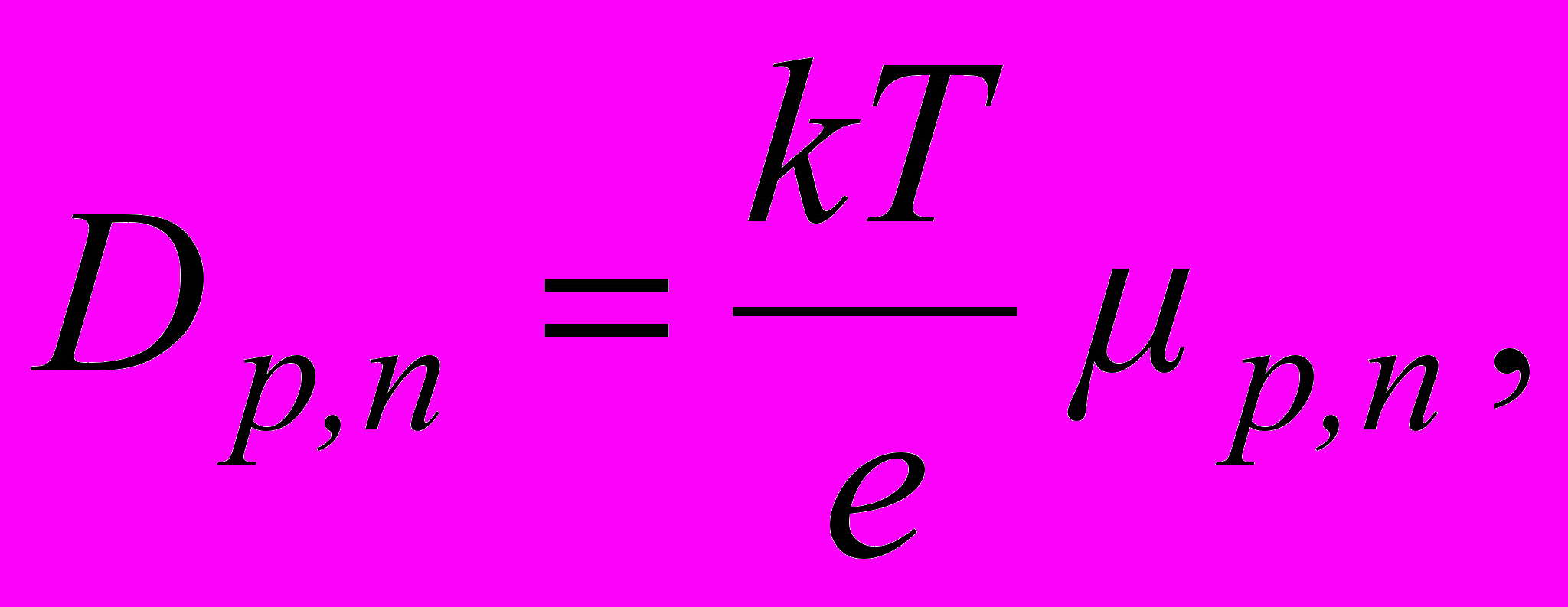(1.4)где p,n – подвижность дырок и электронов соответственно.
Для диапазона температур, в котором обычно эксплуатируются полупроводниковые приборы, концентрация неосновных носителей заряда определяется соотношениями:
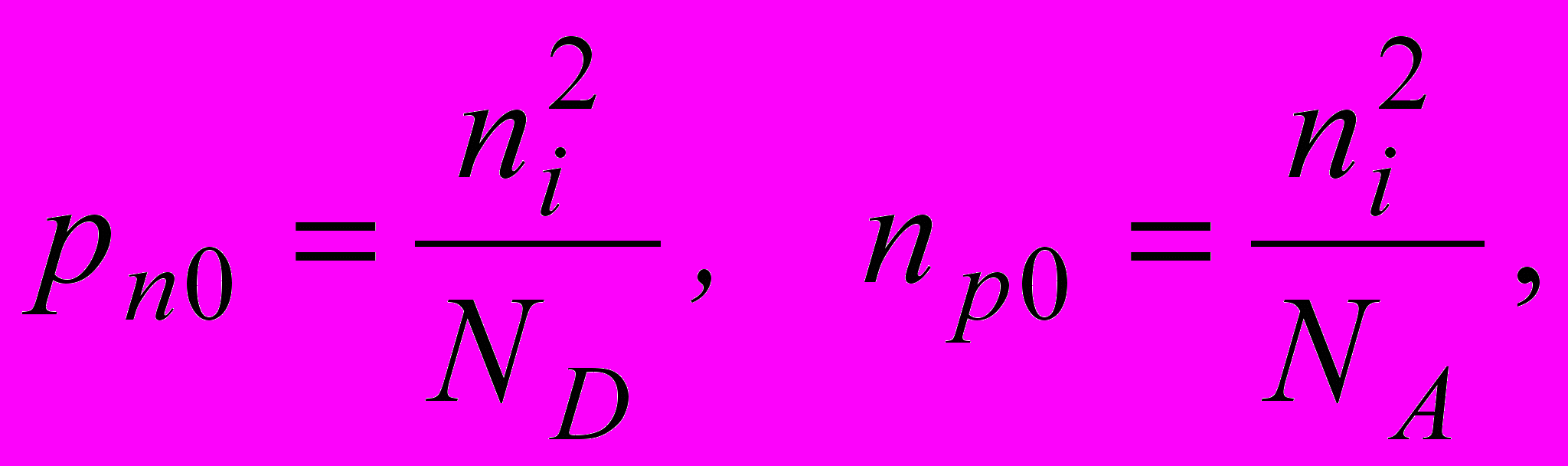(1.5)где ni – концентрация собственных носителей в полупроводнике; ND,A – концентрации примесей соответственно в n и p-областях перехода.
Величина ni является одной из важнейших характеристик полупроводникового материала, она определяет концентрацию свободных носителей заряда (электронов и дырок) в собственном (беспримесном) полупроводнике. Обычно значения ni приводятся в справочных данных для полупроводниковых материалов (как правило, при T=300 K). Для ni характерна сильно выраженная температурная зависимость, которая определяется соотношением
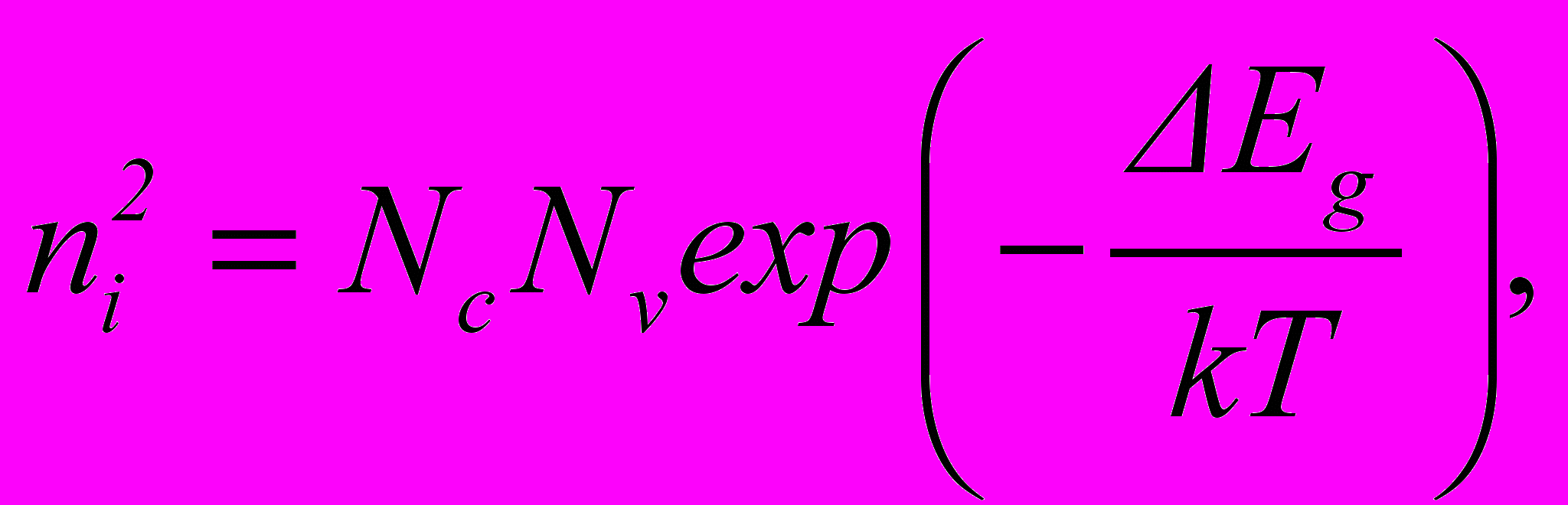(1.6)где Eg – ширина запрещенной зоны полупроводника; Nc,v – эффективные плотности состояний в зоне проводимости и валентной зоне полупроводника соответственно. Все указанные величины приводятся в справочных данных для полупроводникового материала. Температурная зависимость для Eg выражено очень слабо и ею при решении задач практически можно пренебречь; для Nc,v температурная зависимость может быть описана соотношением
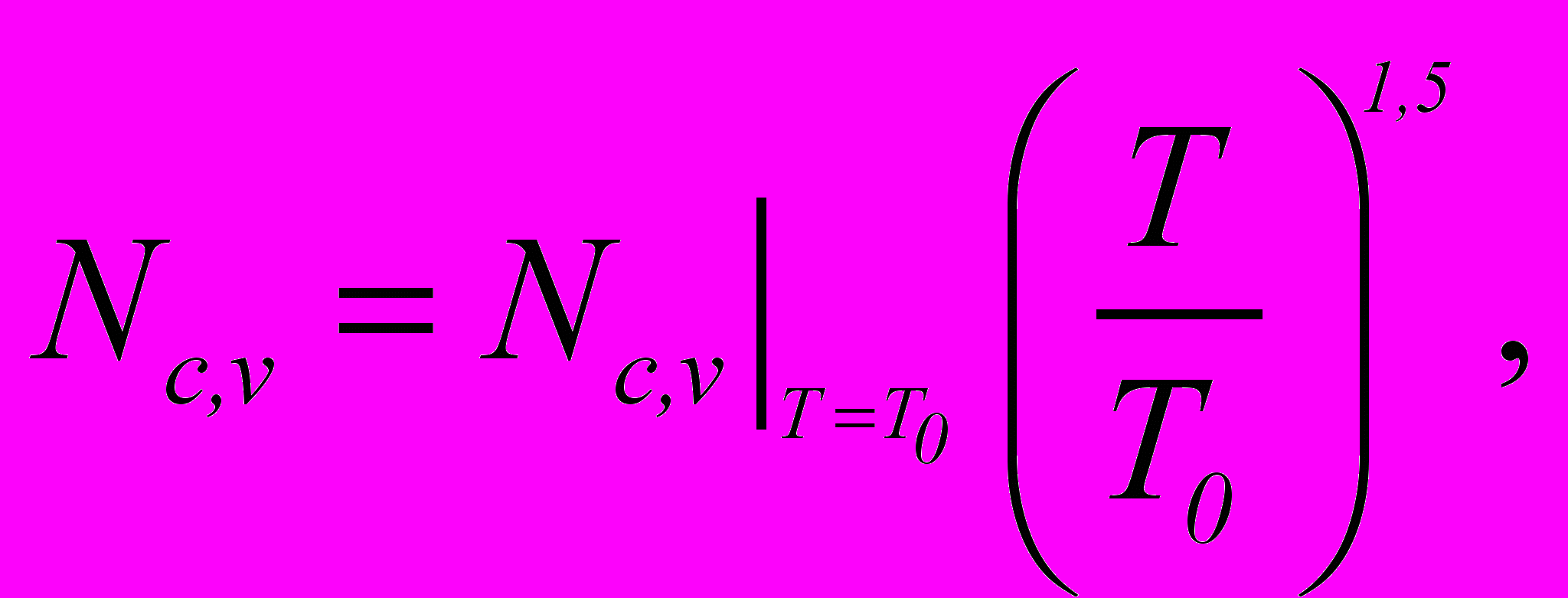(1.7)где T0 – температура, для которой в справочных данных указано значение эффективной плотности состояний (обычно T0=300 K).
Поскольку величины Dp,n и Lp,n слабо зависят от температуры, то из (1.2), (1.5) – (1.7) следует, что температурная зависимость теплового тока I0 определяется в основном соотношением (1.6) или, в первом приближении, экспоненциальным множителем в этом соотношении. Очевидно также, что ток I c увеличением температуры возрастает, так как уменьшение экспоненциальной компоненты в (1.1) будет компенсироваться гораздо большим возрастанием экспоненты в (1.6). Это происходит вследствие того, что множитель при 1/T в показателе для первой экспоненты по абсолютной величине всегда будет меньше соответствующего множителя в показателе для второй экспоненты, поскольку принципиальным условием существования p-n перехода является сохранение неравенства
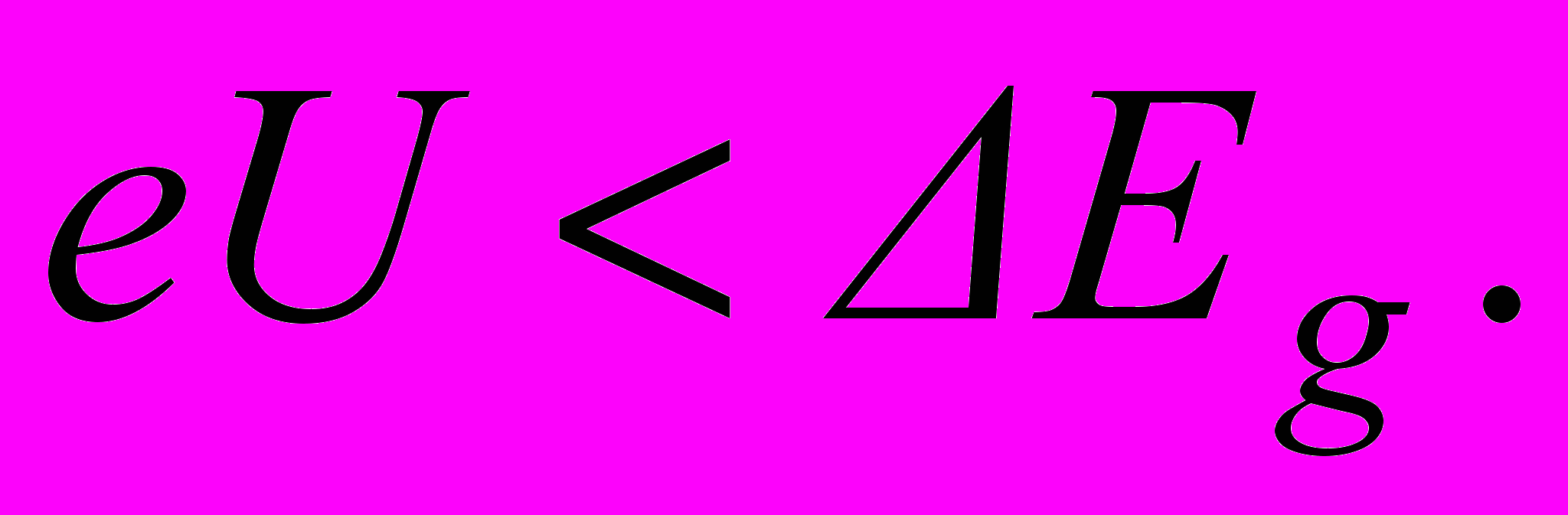
Реальный p-n переход, используемый при изготовлении диодов, всегда является несимметричным, т.е. концентрация примесей в одной из областей всегда намного выше, чем в другой. Область с наивысшей концентрацией примеси называют эмиттером, с наименьшей – базой. С учетом того, что NA>>ND или ND>>NA, согласно (1.5) аналогичные соотношения существуют и между концентрациями неосновных носителей заряда (pn0>>np0 или np0>>pn0). При расчете теплового тока по (1.2) такие неравенства позволяют пренебречь одним из слагаемых, поскольку различие между величинами Dp и Dn, а также между Lp и Ln невелико.
Ввиду того, что сопротивление базы Rб существенно превышает сопротивление эмиттера и может составлять значительную величину, в уравнение (1.1) должны быть внесены коррективы:
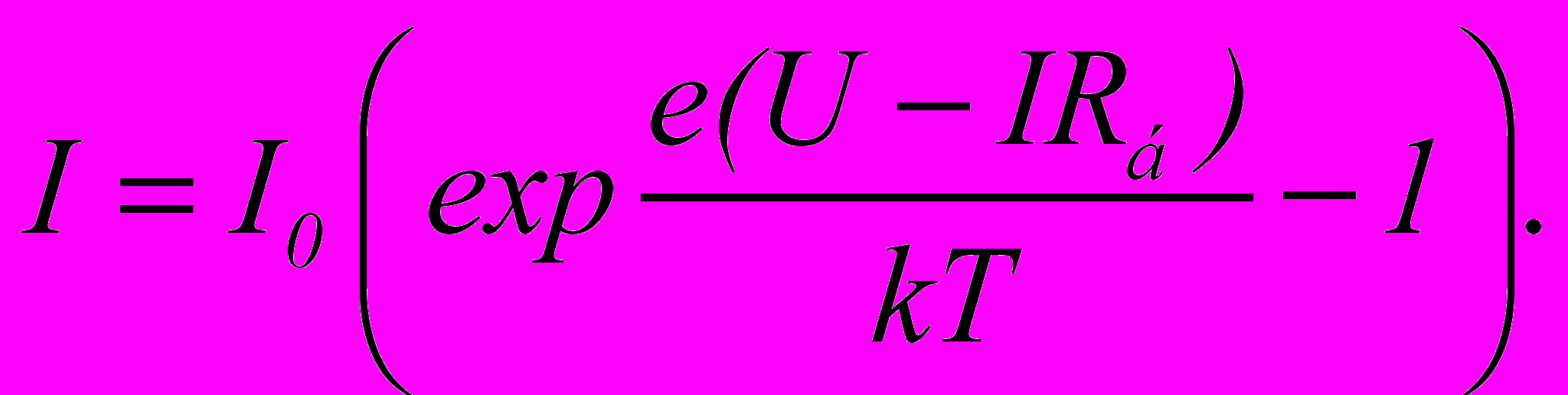(1.8)Очевидно, что при заданном напряжении ток в (1.8) может быть определен только при использовании численных методов, однако для упрощения расчетов целесообразно находить напряжение при заданном токе:
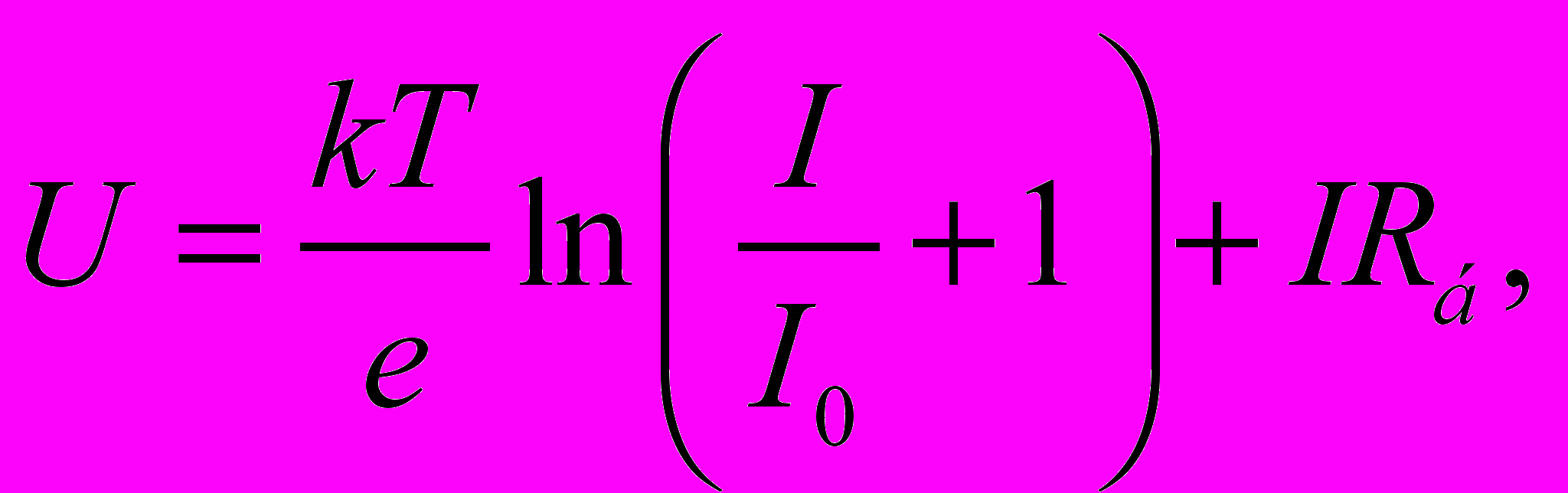(1.9)причем первое слагаемое соответствует напряжению на p-n переходе, а второе – падению напряжения на сопротивлении базы.
Сопротивление Rб нетрудно рассчитать, если известны его размеры, а также удельная проводимость материала , определяемая концентрацией основных носителей заряда (приблизительно равной концентрации легирующей примеси), и их подвижностью:
(1.10)Для простоты в предлагаемых ниже задачах следует считать, что p-n переход плоский, а протяженность базы, определяющая сопротивление, равна ее толщине.
Другим фактором, приводящим к отличию ВАХ реального диода от (1.1), являются процессы генерации – рекомбинации в области пространственного заряда p-n перехода. Наиболее существенное влияние эти процессы оказывают на ВАХ диодов, изготовленных на основе кремния. При обратном смещении диода ток генерации нелинейно возрастает по мере увеличения абсолютного значения напряжения и может значительно превысить тепловой ток. При небольших прямых смещениях наличие тока рекомбинации может привести к заметному превышению тока над рассчитанным значением согласно (1.1) или (1.8).
Реальная ВАХ диода может отличаться от (1.1) или (1.8) из-за существования токов утечки с приблизительно линейным их изменением в зависимости от напряжения. Влияние этих токов вследствие малых значений проявляется лишь при обратных смещениях.
При больших прямых токах ход ВАХ по сравнению с (1.1) или (1.8) искажается вследствие эффектов высокого уровня инжекции – модуляции сопротивления базы, снижения коэффициента инжекции, изменения L, и др.
Перечисленными факторами (процессами генерации – рекомбинации, эффектами высокого уровня инжекции и, если это не оговаривается специально, токами утечки) в процессе решения предлагаемых задач следует пренебречь.
К числу важнейших параметров диода, используемых при схемотехнических расчетах, относятся дифференциальные или малосигнальные параметры, определяющие связь малых изменений электрических величин в цепи диода. Одним из таких параметров является дифференциальное сопротивление rдиф или обратная ему величина – дифференциальная проводимость (крутизна):
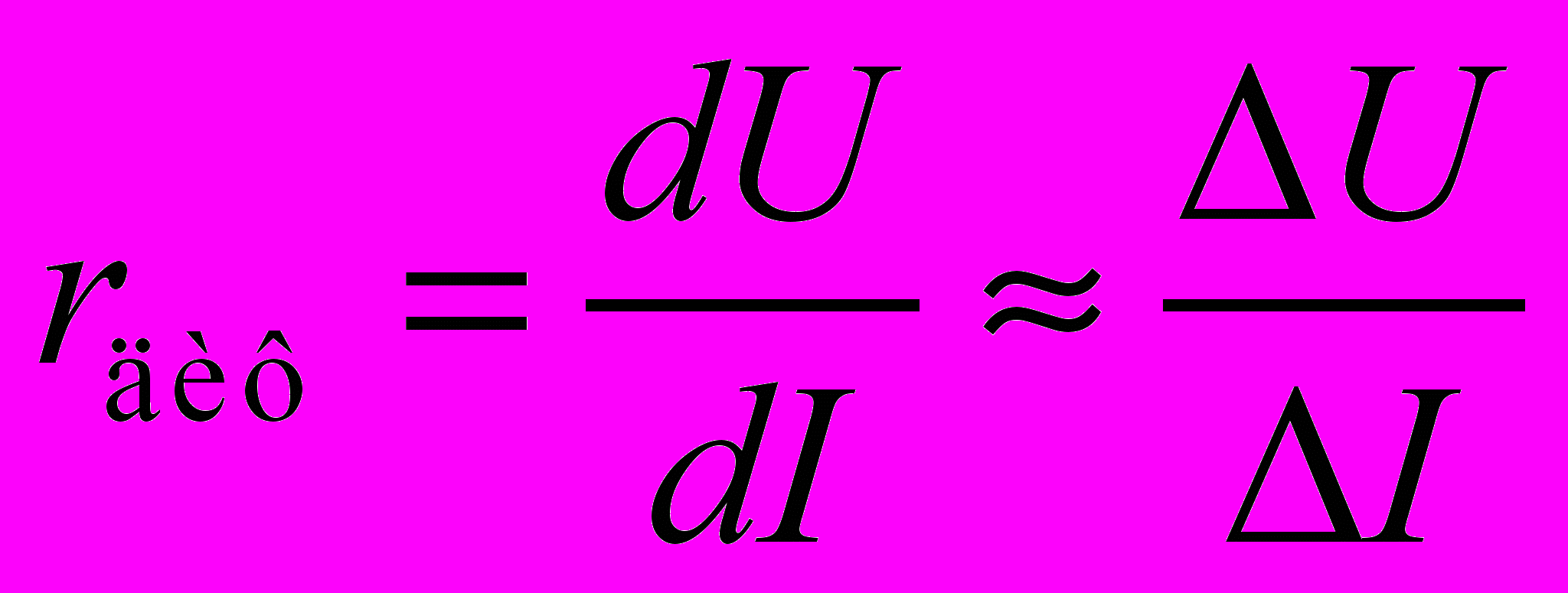(1.11)Поскольку диод является нелинейным элементом, rдиф имеет смысл только в том случае, если оно соответствует известному постоянному напряжению или постоянному току, определяющим режим работы диода (т.е. рабочую точку).
К числу дифференциальных параметров относится емкость p-n перехода
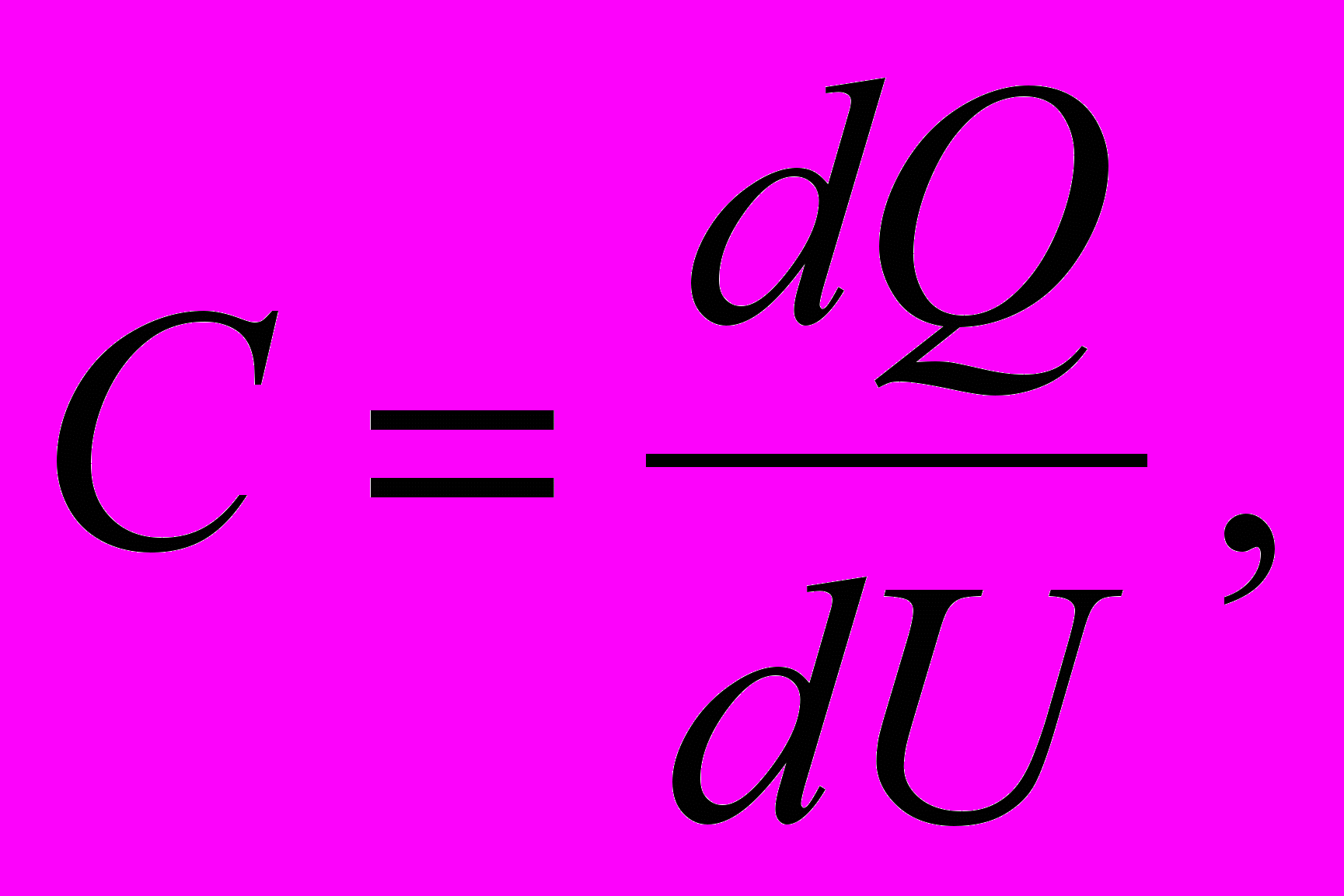(1.12)где Q – заряд, который может быть связанным или накопленным.
Связанный заряд обусловлен ионизированными атомами примеси, расположенными по обе стороны от металлургической границы перехода, причем
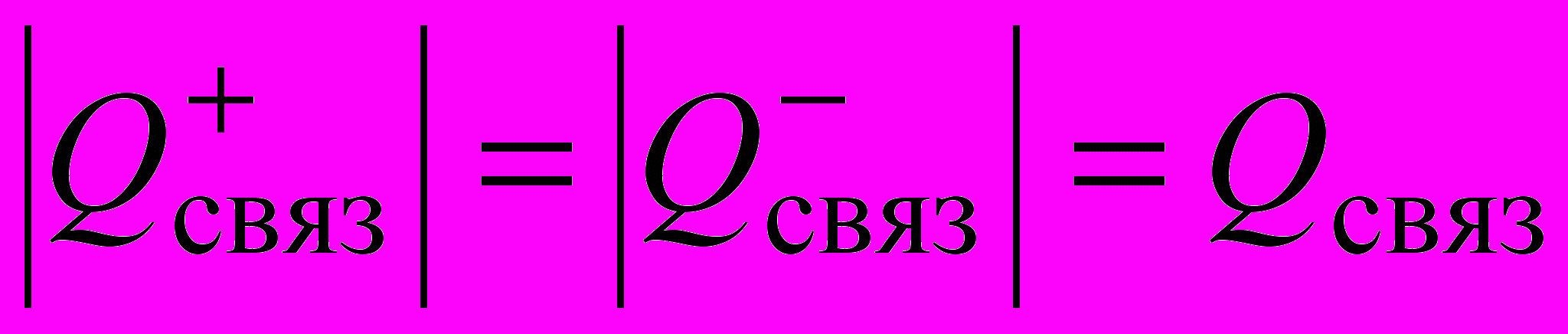. Изменение приложенного к переходу напряжения влечет за собой изменение ширины перехода lp-n и Qсвяз. Связь между этими величинами позволяет рассчитать емкость, называемую барьерной:
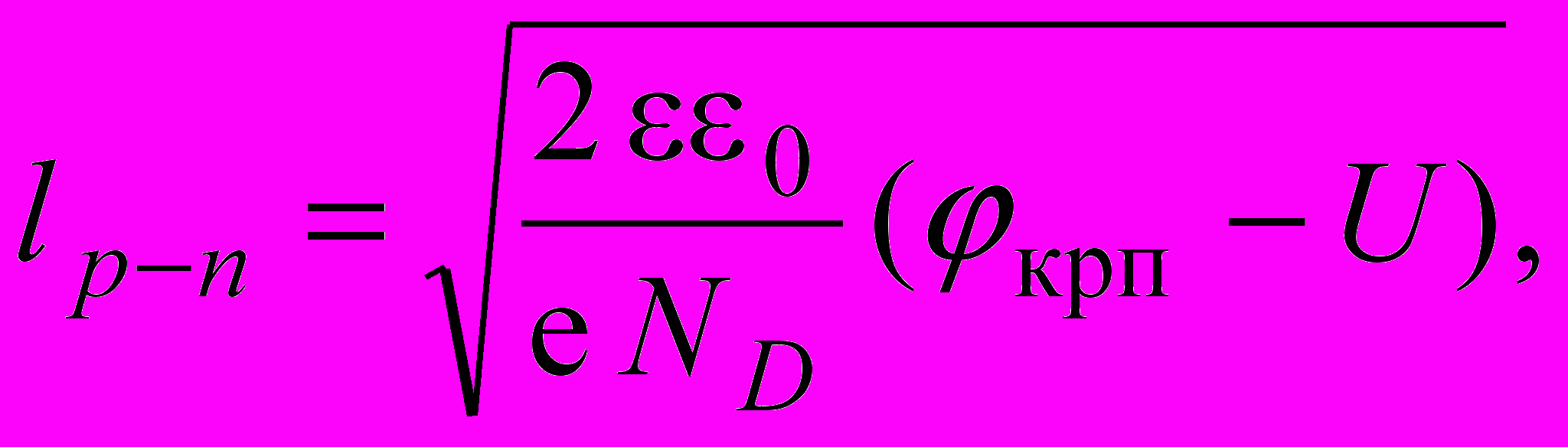(1.13)
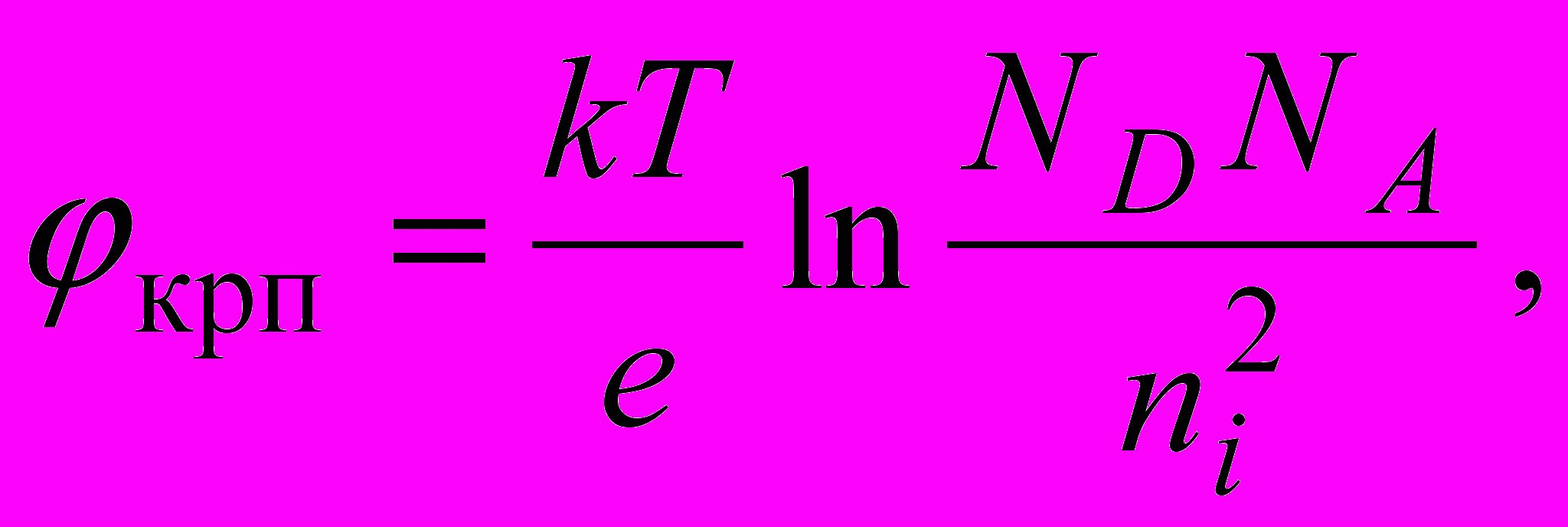(1.14)
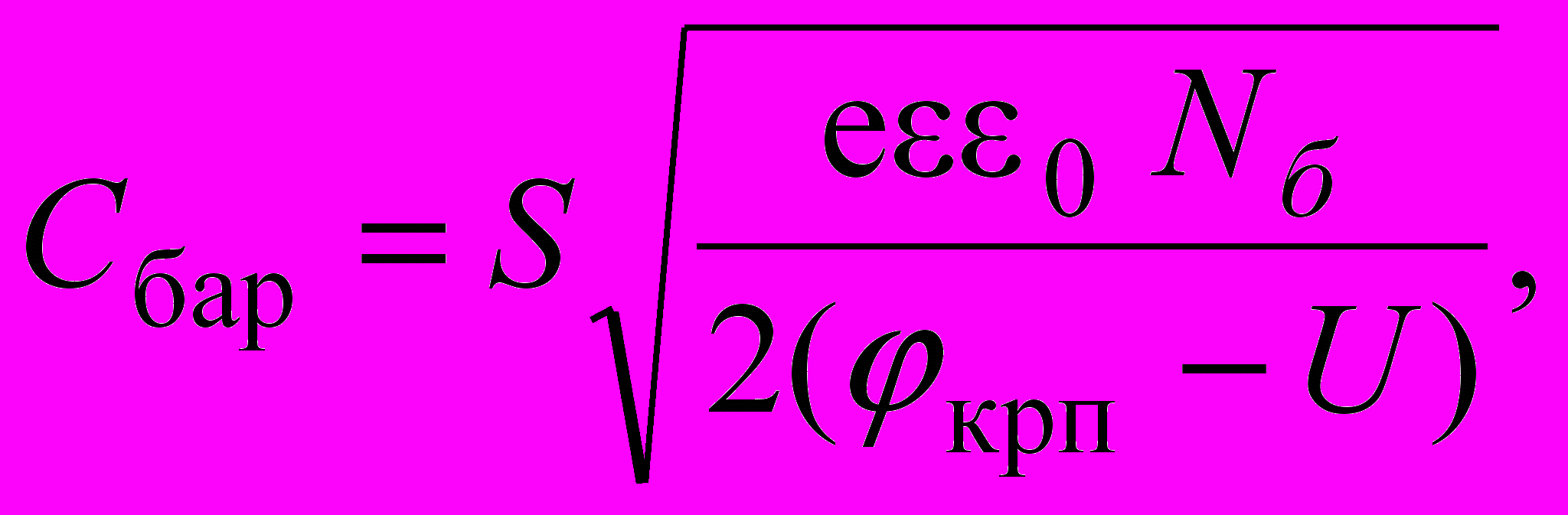(1.15)где 0 – энергетическая постоянная; - относительная диэлектрическая постоянная полупроводникового материала; крп - контактная разность потенциалов; Nб – концентрация примесей в базе. Соотношения (1.13) и (1.15) соответствуют несимметричному p-n переходу, для которого NA>>ND=Nб или ND>>NA=Nб.
Помимо связанного, при изменении приложенного напряжения может изменяться накопленный заряд Qнак. Существование последнего для несимметричного перехода обусловлено непрерывной инжекцией подвижных носителей из эмиттера в базу. В результате возникает неравновесный заряд инжектированных носителей, вместе с которым в базе сосредотачивается дополнительный заряд основных носителей, что в целом обеспечивает ее электронейтральность:
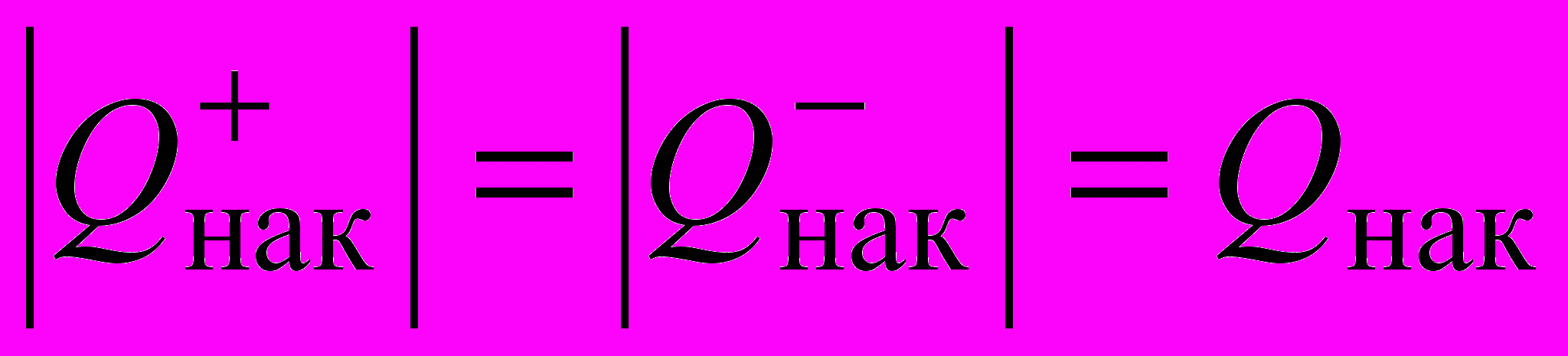. Увеличение прямого напряжения приводит к возрастанию числа инжектированных носителей, т.е. Qнак, что соответствует существованию емкости, называемой диффузионной. Для несимметричного перехода 
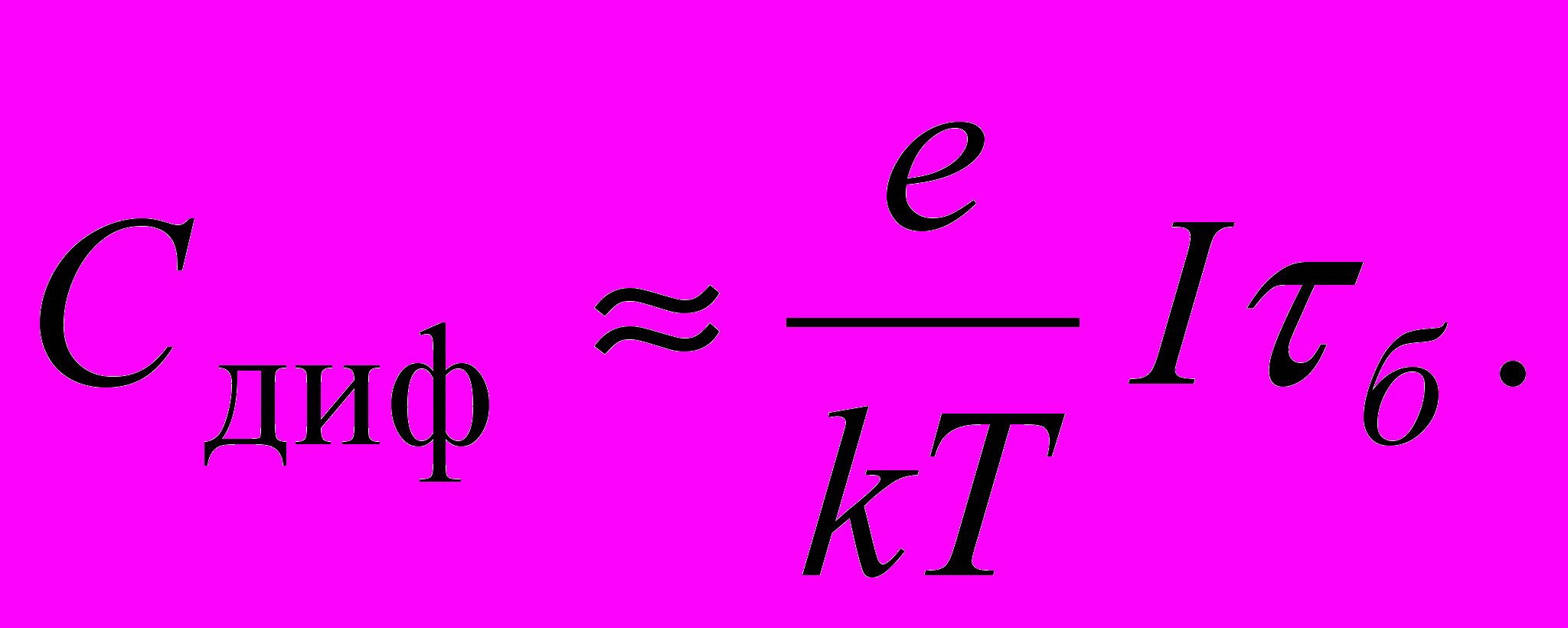(1.16)Обе компоненты емкости существуют независимо друг от друга и поэтому при расчетах суммарной емкости могут складываться. Очевидно, что при обратных смещениях перехода диффузионная емкость практически отсутствует.