Человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 1011 нейронов участвуют в 1015 передающих связях, имеющих длину метр и более

Вид материала

Документы

Содержание История исследований в области нейронных сетей 1970–1976 гг. Активные разработки в области персептронов в СССР (основные заказчики – военные ведомства). Биологические нейронные сети Искусственные нейронные сети. Основные черты и свойства Параллельность обработки и реализуемость НС Тирания межсоединений. Трехмерность структуры Сложность программирования. Место нейронных сетей среди других методов решения задач Классификация образов. Аппроксимация функций. Память, адресуемая по содержанию. Основные положения теории искусственных нейронных сетей.

Подобный материал:

• Человеческий мозг нечто более совершенное, чем самые дерзкие мечты инженеров и даже, 31.38kb.
• Динамическое планирование поведения робота на основе сети «интеллектуальных» нейронов, 172.49kb.
• Лекция 2 Лекция «Нейронные сети» Начнем с определения: Искусственные нейронные сети, 131.57kb.
• Г. Г. Райкунов генеральный директор фгуп центра, 22.38kb.
• Тема 14 Физиология головного мозга Часть V новая кора больших полушарий, 155.96kb.
• Реферат по курсу «Анатомия центральной нервной системы» Тема: «Строение нейрона и нервного, 92kb.
• «стратегии развития инновационной экономики», 60.08kb.
• Лекция 2 Нервная ткань, 135.19kb.
• Марианский желоб глубокий желоб на дне океана на границе между Филиппинским морем, 24.56kb.
• Программа дисциплины опд. Ф. 01. 2 «технологии в связях с общественностью» Цели и задачи, 359.81kb.

Введение

Нервная система человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 1011 нейронов участвуют в 1015 передающих связях, имеющих длину метр и более.

Наш мозг - это своего рода великолепный компьютер. Он способен с невероятной быстротой интерпретировать неточную информацию, поступающую от органов чувств: различает шепот в шумной комнате, лицо в полутемном переулке, улавливает скрытый смысл слов. Самое удивительное то, что мозг умеет обучаться самостоятельно, он умеет без каких-либо явных указаний создавать внутренние представления, благодаря которым и проявляет перечисленные способности. Пока мы многое не знаем о том, каким образом мозг обучается обрабатывать информацию, поэтому в настоящее время существует множество теорий и гипотез на этот счет. А на основе уже полученных знаний предпринимаются попытки создания моделей нервной системы, в частности, с использованием искусственных нейронных сетей (ИНС). Поскольку наши знания о нейронах далеко неполны, модели могут быть лишь грубым приближением к реальным нейронным сетям (НС), и еще слишком рано говорить о создании искусственного мозга сравнимого с человеческим. В настоящее время он еле дотягивает до уровня нервных систем улиток и дождевых червей, но уже сейчас нейронные сети часто выполняют функции бывшие ранее исключительно прерогативой человека, проводят сложные вычисления, позволяют следить за процессами, для которых отсутствуют какие-либо аналитические зависимости.

История исследований в области нейронных сетей

В истории исследований в области нейронных сетей, как и в истории любой другой науки, были свои успехи и неудачи. Кроме того, здесь постоянно сказывается психологический фактор, проявляющийся в неспособности человека описать словами то, как он думает.

Основной областью исследований по искусственному интеллекту в 60-е ­– 80-е годы были экспертные системы. Однако, скоро стало ясно, что они, хотя и приносят пользу в некоторых областях, но не охватывают ключевые аспекты работы человеческого мозга. Согласно одной из точек зрения, причина этого состоит в том, что они не в состоянии воспроизвести структуру мозга. Чтобы создать искусственный интеллект, необходимо построить систему с похожей архитектурой.

Первой попыткой создания и исследования искусственных нейронных сетей считается работа Дж. Маккалока (J. McCulloch) и У. Питтса (W. Pitts) "Логическое исчисление идей, относящихся к нервной деятельности" (1943 г.), в которой была построена модель нейрона, и сформулированы основные принципы построения ИНС. Хотя эта работа была лишь первым этапом, многие идеи, описанные в ней, остаются актуальными и на сегодняшний день.

1949 г. Д. Хебб (D. Hebb) высказал идеи о характере соединений нейронов мозга и их взаимодействии. Впервые предложил правила обучения нейронной сети.

Огромный вклад в нейронауку внесла детекторная теория. Ее основоположником считается Дж. Маккалок, который с группой своих сотрудников в 1959 году опубликовал статью под названием "О чем глаза лягушки говорят мозгу лягушки", где впервые было введено понятие нейрона-детектора. Работа заинтересовала многих исследователей, наиболее успешные из которых - Д. Хьюбел (D. Hubel) и Т. Визель (T. Wiesel), объединив гистохимические и нейрофизиологические методы, показали, распределенный и параллельный характер хранения и обработки информации в биологических нейронных сетях.

Большим прорывом в области нейроинтеллекта стало создание американским нейрофизиологом Френком Розенблатом (F. Rosenblatt) в 1962 г. модели однослойной нейронной сети, названной персептроном. Она была использована для такого широкого класса задач, как предсказание погоды, анализ электрокардиограмм и искусственное зрение. Первые успехи вызвали всплеск оптимизма и послужили стимулом для продолжения исследований. Однако вскоре выяснилось, что созданные сети не способны решать некоторые задачи, существенно не отличающиеся от тех, которые они решали успешно.

Позднее (1969 г.) Марвин Минский, используя точные математические методы, строго доказал ряд теорем, показав, что используемые однослойные сети теоретически не способны решить многие простые задачи, например, реализовать логическую функцию "Исключающее ИЛИ". Безупречность доказательств Минского, подкрепленная его авторитетом в ученых кругах, явилась одной из причин задержки развития нейроинтеллекта почти на два десятилетия. Однако ряд наиболее настойчивых ученых, таких как Кохонен, Гроссберг, Андерсон продолжили исследования, постепенно создавая теоретические основы для построения и применения искусственных нейронных сетей. Как выяснилось, Минский был слишком пессимистичен в своих прогнозах и многие из задач, описанных им как не решаемые, сейчас решаются нейронными сетями с использованием стандартных процедур.

В 70-е годы было предложено много интересных разработок, таких, например, как когнитон, способный с высокой достоверностью распознавать достаточно сложные образы (например, иероглифы) независимо от поворота и масштаба изображения. Автором когнитона является японский ученый К. Фукушима (K. Fukushima).

1970–1976 гг. Активные разработки в области персептронов в СССР (основные заказчики – военные ведомства).

В 1982 году американский биофизик Дж. Хопфилд (J. Hopfield) предложил оригинальную модель нейронной сети, названную его именем. Позднее было разработано ряд эффективных алгоритмов: сеть встречного потока (R. Hecht-Neilsen), двунаправленная ассоциативная память (B. Kosko) и другие.

1985 г. Появление первых коммерческих нейрокомпьютеров (НК), например, Mark III фирмы TRW (США).

1987 г. Начало широкомасштабных разработок в области ИНС и НК в США, Японии и Западной Европе.

1989 г. Разработки и исследования в области ИНС и НК ведутся практически всеми крупными электротехническими фирмами. НК – один из самых динамичных секторов рынка (за два года объем продаж вырос в пять раз).

1990 г. Активизация советских исследовательских организаций в области ИНС и НК. Общее число фирм достигает трехсот.

1991 г. Годовой оборот продаж на рынке ИНС и НК 140 млн. долларов.

1992 г. Проводятся десятки международных конференций и форумов по ИНС; более 20-ти специализированных периодических научных изданий.

1996 г. Число международных конференций по ИНС достигло ста.

1997 г. Годовой объем продаж на рынке ИНС и НК более 2 млрд. долларов, а ежегодный прирост составил 50%.

2000 г. Переход на субмикронные и нанотехнологии, а также успехи молекулярной и биомолекулярной технологии приводят к принципиально новым архитектурным и технологическим решениям по созданию НК.

Глубокое изучение ИНС требует знания нейрофизиологии, науки о познании, психологии, физики (стат. механики), теории управления, теории вычислений, проблем искусственного интеллекта, статистики/математики, распознавания образов, компьютерного зрения, параллельных вычислений и аппаратных средств (цифровых и аналоговых). С другой стороны, ИНС стимулируют эти дисциплины, обеспечивая их новыми инструментами и представлениями.

Биологические нейронные сети

Существенную роль в теории НС занимают биофизические проблемы. Для построения адекватной математической модели необходимо детально изучить работу биологических нервных клеток и сетей с точки зрения химии, физики, теории информации и синергетики. Должны быть известны ответы на следующие основные вопросы:

1. Как работает нервная клетка – биологический нейрон? Необходимо иметь математическую модель, адекватно описывающую информационные процессы в нейроне. Какие свойства нейрона важны при моделировании, а какие – нет?
   
2. Как передается информация через соединения между нейронами – синапсы? Как меняется проводимость синапса в зависимости от проходящих по нему сигналов?
   
3. По каким законам нейроны связаны друг с другом в сеть? Откуда нервная клетка знает, с какими соседями должно быть установлено соединение?
   
4. Как биологические нейронные сети обучаются решать задачи? Как выбираются параметры сети, чтобы давать правильные выходные сигналы? Какой выходной сигнал считается «правильным», а какой – ошибочным?
   

Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 1). Она состоит из тела клетки (cell body), или сомы (soma), и двух типов внешних древоподобных ветвей: аксона (axon) и дендритов (dendrites). Тело клетки включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль аксона (передатчик), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся синапсы (synapses).



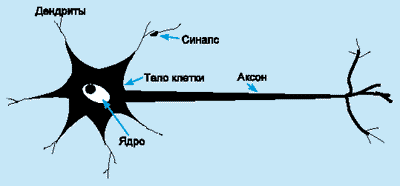
Рис. 1. Схема биологического нейрона.

Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека.

Кора головного мозга человека является протяженной, образованной нейронами поверхностью толщиной от 2 до 3 мм с площадью около 2200 см², что вдвое превышает площадь поверхности стандартной клавиатуры. Кора головного мозга содержит около 1011 нейронов, что приблизительно равно числу звезд Млечного пути. Каждый нейрон связан с 103 – 104 другими нейронами. В целом мозг человека содержит приблизительно от 1014 до 1015 взаимосвязей.

Нейроны взаимодействуют посредством короткой серии импульсов, как правило, продолжительностью несколько мс. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем самые быстродействующие переключательные электронные схемы. Тем не менее, сложные решения по восприятию информации, как, например, распознавание лица, человек принимает за несколько сотен мс. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько мс. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг "запускает" параллельные программы, содержащие около 100 шагов. Это известно как правило ста шагов. Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень маленьким (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами. Этим объясняется такое название, как коннекционистская модель, применяемое к ИНС.

Архитектура биологической нейронной системы совершенно не похожа на архитектуру машины фон Неймана:

	Машина фон Неймана	Биологическая нейронная система
Процессор	Сложный	Простой
	Высокоскоростной	Низкоскоростной
	Один или несколько	Большое количество
Память	Отделена от процессора	Интегрирована в процессор
	Локализована	Распределенная
	Адресация не по содержанию	Адресация по содержанию
Вычисления	Централизованные	Распределенные
	Последовательные	Параллельные
	Хранимые программы	Самообучение
Надежность	Высокая уязвимость	Живучесть
Специализация	Численные и символьные oперации	Проблемы восприятия
Среда функционирования	Строго определенная	Плохо определенная
	Строго ограниченная	Без ограничений

Важнейшие свойства биологических нейросетей:

1. Параллельность обработки информации. Каждый нейрон формирует свой выход только на основе своих входов и собственного внутреннего состояния под воздействием общих механиз­мов регуляции нервной системы.

2. Способность к полной обработке информации. Все известные человеку задачи решаются нейронными сетями. К этой группе свойств относятся ассоциативность (сеть может восстана­вливать полный образ по его части), способность к классификации, обобщению, абстрагиро­ванию и множество других. Они до конца не систематизированы.

3. Самоорганизация. В процессе работы биологические НС самостоятельно, под воздействием внешней среды, обучаются решению разнообразных задач. Неизвестно никаких принципиаль­ных ограничений на сложность задач, решаемых биологическими нейронными сетями. Нерв­ная система сама формирует алгоритмы своей деятельности, уточняя и усложняя их в течение жизни. Человек пока не сумел создать систем, обладающих самоорганизацией и самоусложне­нием. Это свойство НС рождает множество вопросов. Ведь каждая замкнутая система в про­цессе развития упрощается, деградирует. Следовательно, подвод энергии к нейронной сети имеет принципиальное значение. Почему же среди всех диссипативных (рассеивающих энер­гию) нелинейных динамических систем только у живых существ, и, в частности, биологичес­ких нейросетей проявляется способность к усложнению? Какое принципиальное условие упущено человеком в попытках создать самоусложняющиеся системы?

4. Биологические НС являются аналоговыми системами. Информация поступает в сеть по боль­шому количеству каналов и кодируется по пространственному принципу: вид информации определяется номером нервного волокна, по которому она передается. Амплитуда входного воздействия кодируется плотностью нервных импульсов, передаваемых по волокну.

5. Надежность. Биологические НС обладают фантастической надежностью: выход из строя даже 10% нейронов в нервной системе не прерывает ее работы. По сравнению с последовательными ЭВМ, основанными на принципах фон-Неймана, где сбой одной ячейки памяти или одного узла в аппаратуре приводит к краху системы.

Искусственные нейронные сети. Основные черты и свойства


Искусственные нейронные сети (НС) – совокупность моделей биологических нейронных сетей. Представляют собой сеть элементов – искусственных нейронов – связанных между собой синаптическими соединениями. Сеть обрабатывает входную информацию и в процессе изменения своего состояния во времени формирует совокупность выходных сигналов.

Работа сети состоит в преобразовании входных сигналов во времени, в результате чего меняется внутреннее состояние сети и формируются выходные воздействия. Обычно НС оперирует цифро­выми, а не символьными величинами.

Искусственные нейронные сети – набор математических и алгоритмических методов для реше­ния широкого круга задач.

Большинство моделей НС требуют обучения. В общем случае, обучение – такой выбор парамет­ров сети, при котором сеть лучше всего справляется с поставленной проблемой. Обучение – это задача многомерной оптимизации, и для ее решения существует множество алгоритмов.

Выделим характерные черты искусственных нейросетей как универсаль­ного инструмента для решения задач:

1. НС дают возможность лучше понять организацию нервной системы человека и животных на средних уровнях: память, обработка сенсорной информации, моторика.

2. НС – эффективное средство обработки информации:

а) гибкая модель для нелинейной аппроксимации многомерных функций;

б) средство прогнозирования во времени для процессов, зависящих от многих переменных;

в) классификатор по многим признакам, дающий разбиение входного пространства на области;

г) средство распознавания образов;

д) инструмент для поиска по ассоциациям;

г) модель для поиска закономерностей в массивах данных.

3. НС свободны от ограничений обычных компьютеров благодаря параллельной обработке и сильной связанности нейронов.

4. В перспективе НС должны помочь понять принципы, на которых построены высшие функции нервной системы: сознание, эмоции, мышление.

Современные искусственные НС по сложности и "интеллекту" приближаются к нервной системе таракана, но уже сейчас демонстрируют ценные свойства:

1. Обучаемость. Выбрав одну из моделей НС, создав сеть и выполнив алгоритм обучения, мы можем обучить сеть решению задачи, которая ей по силам. Нет никаких гарантий, что это удастся сделать при выбранных сети, алгоритме и задаче, но если все сделано правильно, то обучение бывает успешным.

2. Способность к обобщению. После обучения сеть становится нечувствительной к малым изме­нениям входных сигналов (шуму или вариациям входных образов) и дает правильный резуль­тат на выходе.

3. Способность к абстрагированию. Если предъявить сети несколько искаженных вариантов входного образа, то сеть сама может создать на выходе идеальный образ, с которым она никог­да не встречалась.


Параллельность обработки и реализуемость НС


Быстродействие современных ЭВМ составляет около 100 Мflops (flops - операция с плавающей запятой в секунду). В мозгу содержится примерно 1011 нейронов. Время прохождения одного нер­вного импульса около 1 мс, и можно считать, что производительность одного нейрона порядка 10 flops. Эквивалентное быстродействие мозга составит 1011 * 10 = 1012 flops. Если рассмотреть зада­чи, решаемые мозгом, и подсчитать требуемое количество операций для их решения на обычных ЭВМ, то получим оценку быстродействия до 1012..1014 flops. Разница в производительности меж­ду обычной ЭВМ и мозгом — 4..6 порядков! Чем это объясняется?

Во многом этот выигрыш обусловлен параллельностью обработки информации в мозге. Следова­тельно, для повышения производительности ЭВМ необходимо перейти от принципов фон-Нейма­на к параллельной обработке информации. Тем не менее, параллельные компьютеры пока не полу­чили распространения по нескольким причинам:

1. Тирания межсоединений. Каждый процессор в параллельной системе связан с большим коли­чеством других. Количество связей занимает намного больший объем, чем сами процессоры. Такая плотность связей не реализуется в обычных интегральных схемах.

2. Трехмерность структуры связей между процессорами. Существуют различные типы связности процессоров в параллельной системе. Обычно требуются трехмерные связи. Технологически такие связи тоже пока невыполнимы.

3. Сложность программирования. Пока не создано единых способов программирования парал­лельных ЭВМ и средств для написания программ.

Несмотря на перспективность параллельных ЭВМ и, в частности, нейронных сетей, для их созда­ния нет элементной базы. Поэтому, вместо моделирования НС на параллельных машинах, большая часть исследований проводится двумя способами:

1) моделирование НС на обычных последовательных ЭВМ (программное исполнение);

2) создание специализированных нейроплат и нейропроцессоров для ускорения работы ЭВМ с нейронными сетями (аппаратное исполнение). Аппаратная реализация нейронной сети может быть выполнена на нейрочипах (микросхемах, содержащих фрагменты нейронных сетей), на СБИС-пластинах или оптоэлектронным способом. Нейрокомпьютером называют вычислительную систему, архитектура которой ориентирована на выполнение операций, заданных структурой нейронной сети. Нейрокомпьютеры принято относить к шестому поколению вычислительных систем.

Первый способ дает проигрыш в быстродействии даже по сравнению с обычной ЭВМ, а второй способ не позволяет переходить от одной модели нейросети к другой, т.к. модель определяется ис­пользуемой нейроплатой или нейропроцессором, и требуется сменить нейропроцессор, чтобы сме­нить модель.

Попытки использовать оптические, химические, биологические и другие технологии для созда­ния НС, несмотря на перспективность, пока не имеют практического применения.


Место нейронных сетей среди других методов решения задач


Нейронные сети превосходят последовательные машины в решении тех же задач, в которых ма­шину превосходит человек. Задачи, требующие большого объема вычислений или высокой точно­сти лучше выполняются обычной ЭВМ.

К задачам, успешно решаемым НС на данном этапе их развития относятся:

– распознавание зрительных, слуховых образов; огромная область применения: от распознава­ния текста и целей на экране радара до систем голосового управления;

– ассоциативный поиск информации и создание ассоциативных моделей; синтез речи по тексту; форми­рование естественного языка;

– формирование моделей и различных нелинейных и трудно описываемых математически сис­тем, прогнозирование развития этих систем во времени: применение на производстве; прогнозирование развития циклонов и других природных про­цессов, прогнозирование изменений курсов валют и других финансовых процессов;

– системы управления и регулирования с предсказанием; управление роботами (например, машиной при парковке), другими слож­ными устройствами;

– разнообразные конечные автоматы: системы массового обслуживания и коммутации, телекоммуникационные системы;

– принятие решений и диагностика, исключающие логический вывод; особенно в областях, где отсутствуют четкие математические модели: в медицине, криминалистике, финансовой сфере.

Уникальное свойство нейросетей – универсальность. Хотя почти для всех перечисленных задач существуют эффективные математические методы решения и несмотря на то, что НС проигрывают специализированным методам для конкретных задач, благодаря универсальности и перспективно­сти для решения глобальных задач, например, построения ИИ и моделирования процесса мышле­ния, они являются важным направлением исследования, требующим тщательного изучения.

Представим некоторые проблемы, решаемые в контексте ИНС и представляющие интерес для ученых и инженеров.

Классификация образов. Задача состоит в указании принадлежности входного образа (например, речевого сигнала или рукописного символа), представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови.

Кластеризация/категоризация. При решении задачи кластеризации, которая известна также как классификация образов "без учителя", отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения знаний, сжатия данных и исследования свойств данных.

Аппроксимация функций. Предположим, что имеется обучающая выборка ((x₁,y₁), (x₂,y₂)..., (x_n,y_n)) (пары данных вход-выход), которая генерируется неизвестной функцией (x), искаженной шумом. Задача аппроксимации состоит в нахождении оценки неизвестной функции (x). Аппроксимация функций необходима при решении многочисленных инженерных и научных задач моделирования.

Предсказание/прогноз. Пусть заданы n дискретных отсчетов {y(t₁), y(t₂)..., y(t_n)} в последовательные моменты времени t₁, t₂,..., t_n . Задача состоит в предсказании значения y(t_n+1) в некоторый будущий момент времени t_n+1. Предсказание/прогноз имеют значительное влияние на принятие решений в бизнесе, науке и технике. Предсказание цен на фондовой бирже и прогноз погоды являются типичными приложениями техники предсказания/прогноза.

Оптимизация. Многочисленные проблемы в математике, статистике, технике, науке, медицине и экономике могут рассматриваться как проблемы оптимизации. Задачей алгоритма оптимизации является нахождение такого решения, которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию. Задача коммивояжера, относящаяся к классу NP-полных, является классическим примером задачи оптимизации.

Память, адресуемая по содержанию. В модели вычислений фон Неймана обращение к памяти доступно только посредством адреса, который не зависит от содержания памяти. Более того, если допущена ошибка в вычислении адреса, то может быть найдена совершенно иная информация. Ассоциативная память, или память, адресуемая по содержанию, доступна по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному входу или искаженному содержанию. Ассоциативная память чрезвычайно желательна при создании мультимедийных информационных баз данных.

Управление. Рассмотрим динамическую систему, заданную совокупностью {u(t), y(t)}, где u(t) является входным управляющим воздействием, а y(t) - выходом системы в момент времени t. В системах управления с эталонной моделью целью управления является расчет такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой эталонной моделью. Примером является оптимальное управление двигателем.


Основные положения теории искусственных нейронных сетей.


Широкий круг задач, решаемый ИНС, не позволяет в настоящее время создавать универсальные, мощные сети, вынуждая разрабатывать специализированные ИНС, функционирующие по различным алгоритмам.

В дальнейшем речь пойдет в основном о программном типе ИНС.

Несмотря на существенные различия, отдельные типы ИНС обладают несколькими общими чертами.

Во-первых, основу каждой ИНС составляют относительно простые, в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Далее под нейроном будет подразумеваться искусственный нейрон, то есть ячейка ИНС.

Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид нейрона приведен на рисунке 2.




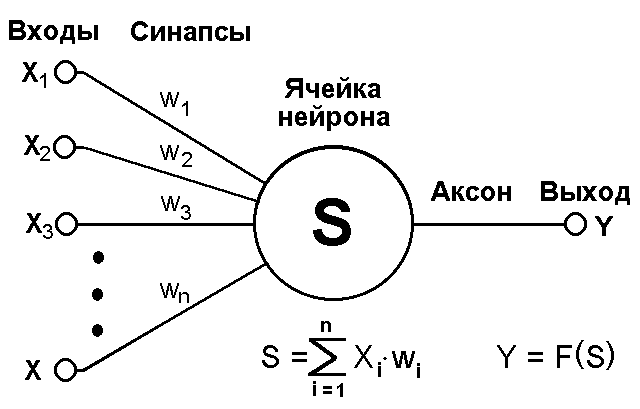
Рис.2 Искусственный нейрон




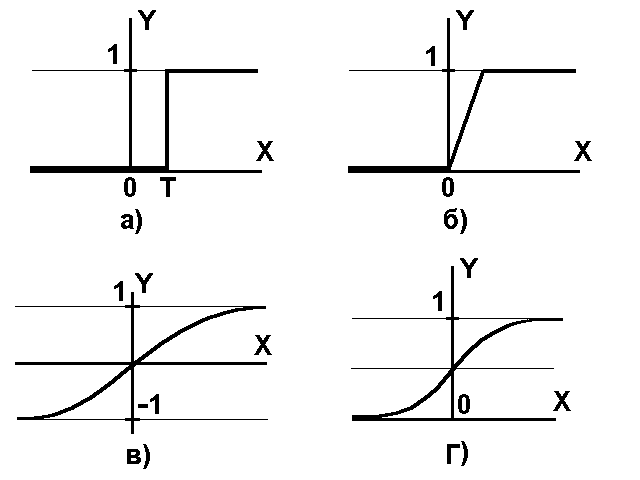
Рис.3 а) функция единичного скач­ка; б) линейный порог (гис­те­ре­зис); в) сигмоид – гипербо­ли­ческий тангенс; г) сигмоид – фор­мула (3)



Каждый синапс характеризуется величиной синаптической связи или ее весом w_i, который по физическому смыслу эквивалентен электрической проводимости.

Текущее состояние нейрона определяется, как взвешенная сумма его входов:

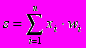(1)

Выход нейрона есть функция его состояния:

y = f(s) (2)

Нелинейная функция f называется активационной и может иметь различный вид, как показано на рисунке 3. Одной из наиболее распространеных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

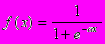(3)

При уменьшении  сигмоид становится более пологим, в пределе при =0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении  сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции – простое выражение для ее производной, применение которого будет рассмотрено в дальнейшем.

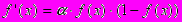(4)

Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.

Возвращаясь к общим чертам, присущим всем ИНС, отметим, во-вторых, принцип параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев, а также, в некоторых конфигурациях, и нейронов одного слоя между собой, причем обработка взаимодействия всех нейронов ведется послойно.

В качестве примера простейшей ИНС рассмотрим трехней­ронный перцептрон (рис.4), то есть такую сеть, нейроны которой имеют активационную функцию в виде единичного скачка^* . На n входов поступают некие сигналы, проходящие по синапсам на 3 нейрона, образующие единственный слой этой ИНС и выдающие три выходных сигнала:




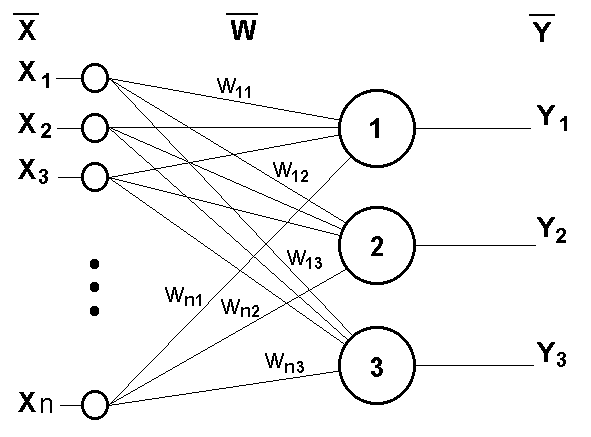
Рис.4 Однослойный перцептрон
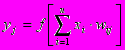, j=1...3 (5)

Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент w_ij задает величину i-ой синаптической связи j-ого нейрона. Таким образом, процесс, происходящий в ИНС, может быть записан в матричной форме:

Y=F(XW) (6)

где X и Y – соответственно входной и выходной сигнальные векторы, F( V) – активационная функция, применяемая поэлементно к компонентам вектора V.

Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется ИНС. Чем сложнее ИНС, тем масштабнее задачи, подвластные ей.

Выбор структуры ИНС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные, на сегодняшний день, конфигурации. Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать сложную проблему синтеза новой конфигурации. При этом он руководствуется несколькими основополагающими принципами: возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев; введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети; сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов – возбуждающих, тромозящих и др.) также способствует усилению мощи ИНС. Вопрос о необходимых и достаточных свойствах сети для решения того или иного рода задач представляет собой целое направление нейрокомпьютерной науки. Так как проблема синтеза ИНС сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбора.

Очевидно, что процесс функционирования ИНС, то есть сущность действий, которые она способна выполнять, зависит от величин синаптических связей, поэтому, задавшись определенной структурой ИНС, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех переменных весовых коэффициентов (некоторые синаптические связи могут быть постоянными).

Этот этап называется обучением ИНС, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время эксплуатации. На этапе обучения кроме параметра качества подбора весов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.

Обучение ИНС может вестись с учителем или без него. В первом случае сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей. Во втором случае выходы ИНС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.

Существует великое множество различных алгоритмов обучения, которые однако делятся на два больших класса: детерминистские и стохастические. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором – она производится на основе действий, подчиняющихся некоторому случайному процессу.

Развивая дальше вопрос о возможной классификации ИНС, важно отметить существование бинарных и аналоговых сетей. Первые из них оперируют с двоичными сигналами, и выход каждого нейрона может принимать только два значения: логический ноль ("заторможенное" состояние) и логическая единица ("возбужденное" состояние). К этому классу сетей относится и рассмотренный выше перцептрон, так как выходы его нейронов, формируемые функцией единичного скачка, равны либо 0, либо 1. В аналоговых сетях выходные значения нейронов спо­соб­ны принимать непрерывные значения, что могло бы иметь место после замены активационной функции нейронов перцептрона на сигмоид.

Еще одна классификация делит ИНС на синхронные и асинхронные. В первом случае в каждый момент времени свое состояние меняет лишь один нейрон. Во втором – состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в ИНС задается итерационным выполнением однотипных действий над нейронами. Далее будут рассматриваться только синхронные ИНС.




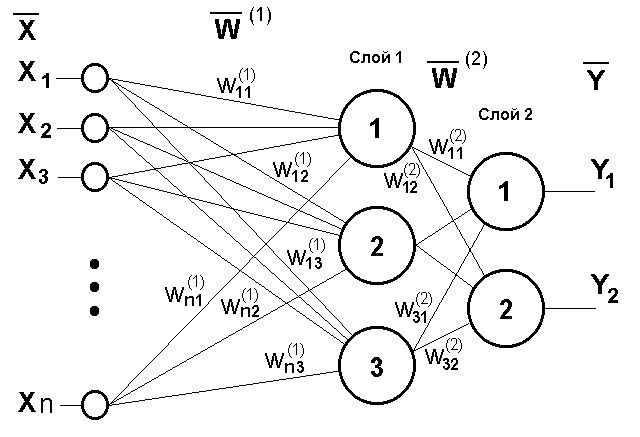
Рис.5 Двухслойный перцептрон
Сети также можно классифицировать по числу слоев. Слой - это совокупность нейронов с единым входным сигналом. Внешние входные сигналы подаются на входы нейронов первого слоя, а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько промежуточных (скрытых) слоев. Вход нейронной сети можно рассматривать как выход "нулевого слоя" вырожденных нейронов. Связи от выходов нейронов некоторого слоя m к входам нейронов следующего слоя (m+1) называются последовательными. На рисунке 5 представлен двухслойный перцептрон, полученный из перцептрона с рисунка 3 путем добавления второго слоя, состоящего из двух нейронов. Здесь уместно отметить важную роль нелинейности активационной функции, так как, если бы она не обладала данным свойством или не входила в алгоритм работы каждого нейрона, результат функционирования любой p-слойной ИНС с весовыми матрицами W⁽ⁱ⁾, i=1,2,...p для каждого слоя i сводился бы к перемножению входного вектора сигналов X на матрицу

W^()=W⁽¹⁾W⁽²⁾ ...W^(p) (7)

то есть фактически такая p-слойная ИНС эквивалентна однослойной ИНС с весовой матрицей единственного слоя W^():

Y=XW^() (8)

Продолжая разговор о нелинейности, можно отметить, что она иногда вводится и в синаптические связи. Большинство известных на сегодняшний день ИНС используют для нахождения взвешенной суммы входов нейрона формулу (1), однако в некоторых приложениях ИНС полезно ввести другую запись, например:

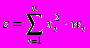(9)

или даже

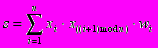(10)

Вопрос в том, чтобы разработчик ИНС четко понимал, для чего он это делает, какими ценными свойствами он тем самым дополнительно наделяет нейрон, и каких лишает. Введение такого рода нелинейности, вообще говоря, увеличивает вычислительную мощь сети, то есть позволяет из меньшего числа нейронов с "нелинейными" синапсами сконструировать ИНС, выполняющую работу обычной ИНС с большим числом стандартных нейронов и более сложной конфигурации.

Можно различать ИНС по архитектуре следующим образом:

• полносвязные сети (рис. 6-а),
  
• многослойные сети (рис. 6-б),
  
• слабосвязные сети (нейронные сети с локальными связями) (рис.6-в).
  

В слабосвязных сетях нейроны располагаются в узлах прямоугольной решетки. Каждый нейрон связан с четырьмя или восемью своими ближайшими соседями.

В полносвязной сети каждый нейрон связан со всеми остальными (на входы каждого нейрона подаются выходные сигналы остальных нейронов).

Если нейроны каждого слоя сети имеют единую функцию активации, то такую нейронную сеть будем называть однородной.



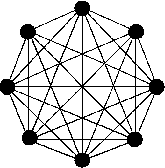
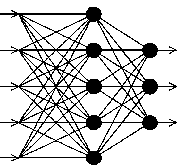
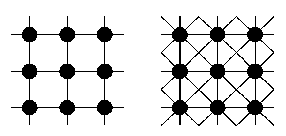
Рис. 6. Архитектуры нейронных сетей: а) полносвязная сеть, б) многослойная сеть с последовательными связями, в) слабосвязные сети

Многообразие существующих структур ИНС позволяет отыскать и другие критерии для их классификации, но они выходят за рамки данной лекции.

Теперь рассмотрим один нюанс, преднамеренно опущенный ранее. Из рисунка функции единичного скачка видно, что пороговое значение T, в общем случае, может принимать произвольное значение. Более того, оно должно принимать некое произвольное, неизвестное заранее значение, которое подбирается на стадии обучения вместе с весовыми коэффициентами. То же самое относится и к центральной точке сигмоидной зависимости, которая может сдвигаться вправо или влево по оси X, а также и ко всем другим активационным функциям. Это, однако, не отражено в формуле (1), которая должна была бы выглядеть так:

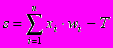(11)

Дело в том, что такое смещение обычно вводится путем добавления к слою нейронов еще одного входа, возбуждающего дополнительный синапс каждого из нейронов, значение которого всегда равняется 1. Присвоим этому входу номер 0. Тогда

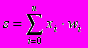(12)

где w₀ = –T, x₀ = 1.

Очевидно, что различие формул (1) и (12) состоит лишь в способе нумерации входов.




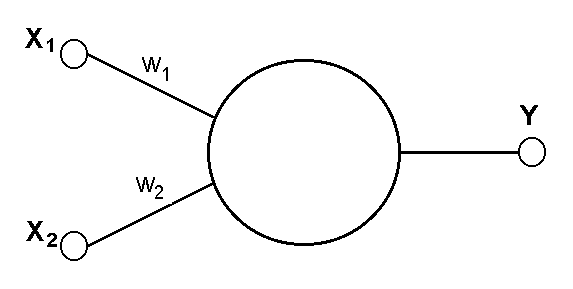
Рис.7 Однонейронный перцептрон
Из всех активационных функций, изображенных на рисунке 2, одна выделяется особо. Это гиперболический тангенс, зависимость которого симметрична относительно оси X и лежит в диапазоне [-1,1]. Забегая вперед, скажем, что выбор области возможных значений выходов нейронов во многом зависит от конкретного типа ИНС и является вопросом реализации, так как манипуляции с ней влияют на различные показатели эффективности сети, зачастую не изменяя общую логику ее работы. Пример, иллюстрирующий данный аспект, будет представлен после перехода от общего описания к конкретным типам ИНС.

Какие задачи может решать ИНС? Грубо говоря, работа всех сетей сводится к классификации (обоб­щению) входных сигналов, принадлежащих n-мерному гипер­про­странству, по некоторому числу классов. С матема­ти­ческой точ­ки зрения это происходит путем разбиения гипер­про­странства ги­пер­плоскостями (запись для случая однослой­ного пер­цеп­тро­на)

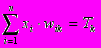, k=1...m (13)

Каждая полученная область является областью определения отдельного класса. Число таких классов для одной ИНС перцептронного типа не превышает 2^m, где m – число выходов сети. Однако не все из них могут быть разделимы данной ИНС.

Например, однослойный перцептрон, состоящий из одного нейрона с дву­мя входами, представленный на рисунке 7, не способен разделить плос­кость (двумерное гиперпространоство) на две полуплоскости так, чтобы осу­ще­ствить классификацию входных сигналов по классам A и B.

Уравнение сети для этого случая

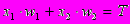(14)

является уравнением прямой (одномерной гиперплоскости), которая ни при каких условиях не может разделить плоскость так, чтобы точки из множества входных сигналов, принадлежащие разным классам, оказались по разные стороны от прямой (см. рисунок 8).




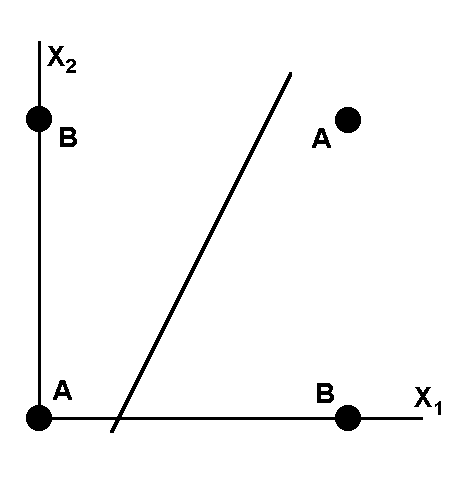
Рис.8 Визуальное представление работы ИНС с рисунка 5
Можно заметить, что данное разбиение на классы реали­зу­ет логическую функцию исключающего ИЛИ для входных сигналов. Невозможность реализа­ции однослойным перцептроном этой функции получила название проблемы исключающего ИЛИ.

Функции, которые не реализуются однослойной сетью, называ­ют­ся линейно неразделимыми. Решение задач, подпадающих под это ог­ра­ничение, заключается в применении 2-х и более слойных сетей или се­тей с нелинейными синапсами, однако и тогда существует вероят­ность, что корректное разделение некоторых входных сигналов на классы невозможно.

Наконец, мы можем более подробно рассмотреть вопрос обучения ИНС, для начала – на примере перцептрона с рисунка 3.

Рассмотрим алгоритм обучения с учителем.

1. Проинициализировать элементы весовой матрицы (обычно небольшими случайными значениями).

2. Подать на входы один из входных векторов, которые сеть должна научиться различать, и вычислить ее выход.

3. Если выход правильный, перейти на шаг 4.

Иначе вычислить разницу между идеальным и полученным значениями выхода:



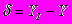
Модифицировать веса в соответствии с формулой:



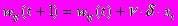
где t и t+1 – номера соответственно текущей и следующей итераций;  – коэффициент скорости обучения, 0<Ј1; i – номер входа; j – номер нейрона в слое.

Очевидно, что если Y_I > Y весовые коэффициенты будут увеличены и тем самым уменьшат ошибку. В противном случае они будут уменьшены, и Y тоже уменьшится, приближаясь к Y_I.

4. Цикл с шага 2, пока сеть не перестанет ошибаться.

На втором шаге на разных итерациях поочередно в случайном порядке предъявляются все возможные входные вектора. К сожалению, нельзя заранее определить число итераций, которые потребуется выполнить, а в некоторых случаях и гарантировать полный успех. Этот вопрос будет косвенно затронут в дальнейшем.