Задача Формирование оптимального портфеля ценных бумаг по модели Марковица Цель работы: Получить практические навыки и умения формирования портфелей ценных бумаг

Вид материала

Задача

Содержание Задача 2. Формирование оптимального портфеля ценных бумаг по модели Тобина. Сделать выводы по работе. Варианты заданий

Подобный материал:

• Формирование портфеля ценных бумаг Принципы формирования портфеля ценных бумаг, 181.91kb.
• Учебная программа по курсу «управление портфелем ценных бумаг» Специальность, 48.16kb.
• Информационные системы мониторинга портфеля ценных бумаг, 52.96kb.
• Контрольная работа по предмету: рынок ценных бумаг на тему: Портфели ценных бумаг, 175.08kb.
• Воропаева блок1 вопрос18 Понятие портфеля ценных бумаг. Виды ценных бумаг, являющиеся, 152.5kb.
• Решение задачи формирования оптимального портфеля основано на двух группах предположений:, 31.2kb.
• Рабочей программы дисциплины Рынок ценных бумаг по направлению подготовки 080100 Экономика, 16.9kb.
• Темы курсовых работ по курсу «Инвестиционный анализ»        Базовые модели формирования, 13.67kb.
• Методические указания к курсовой работе по дисциплине: «Оценка стоимости ценных бумаг», 96.67kb.
• Сообщение о сведениях, которые могут оказать существенное влияние на стоимость ценных, 27.95kb.

Задача 2. Формирование оптимального портфеля ценных бумаг по модели Тобина.

Порядок выполнения задачи.

1. В соответствии с вариантом задания получить данные по эффективности безрисковых бумаг 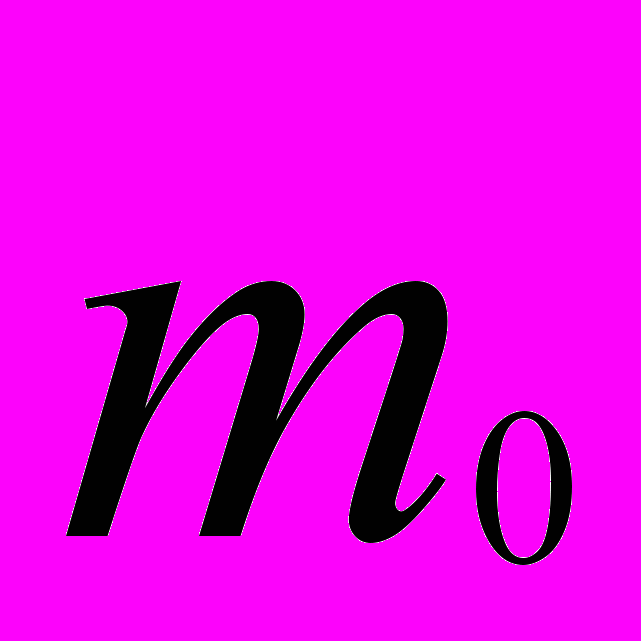и допустимому риску портфеля .
   
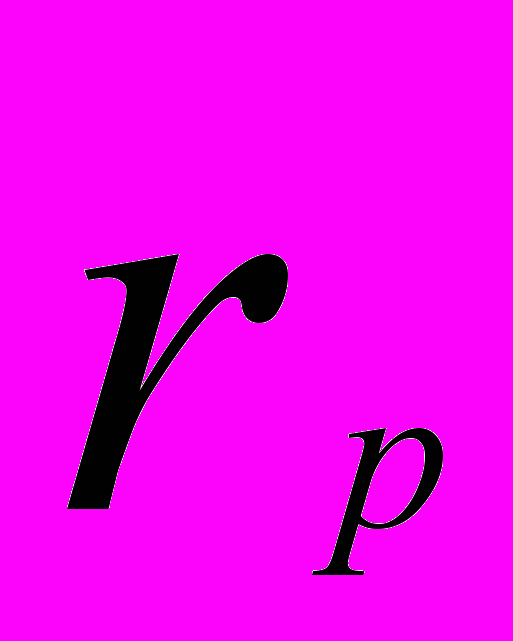2. Данные по эффективности рисковых бумаг 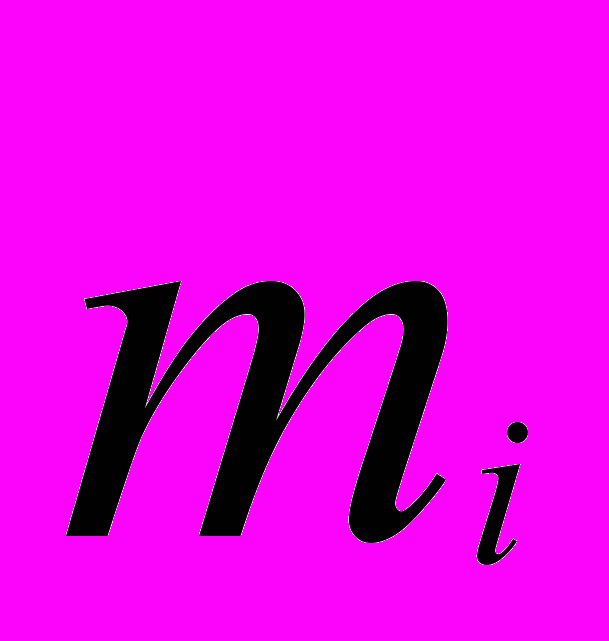и необходимые результаты расчетов взять из предыдущей задачи.
   
3. Составить математическую модель портфеля Тобина минимального риска (1) и решить ее.
   
4. Составить математическую модель портфеля Тобина максимальной доходности и решить ее. При численном решении использовать метод сопряженных градиентов или Ньютона. Для вычислений можно использовать ЭВМ.
   
5. Сделать выводы по работе.
   

Краткие теоретические сведения.


Портфель Тобина минимального риска

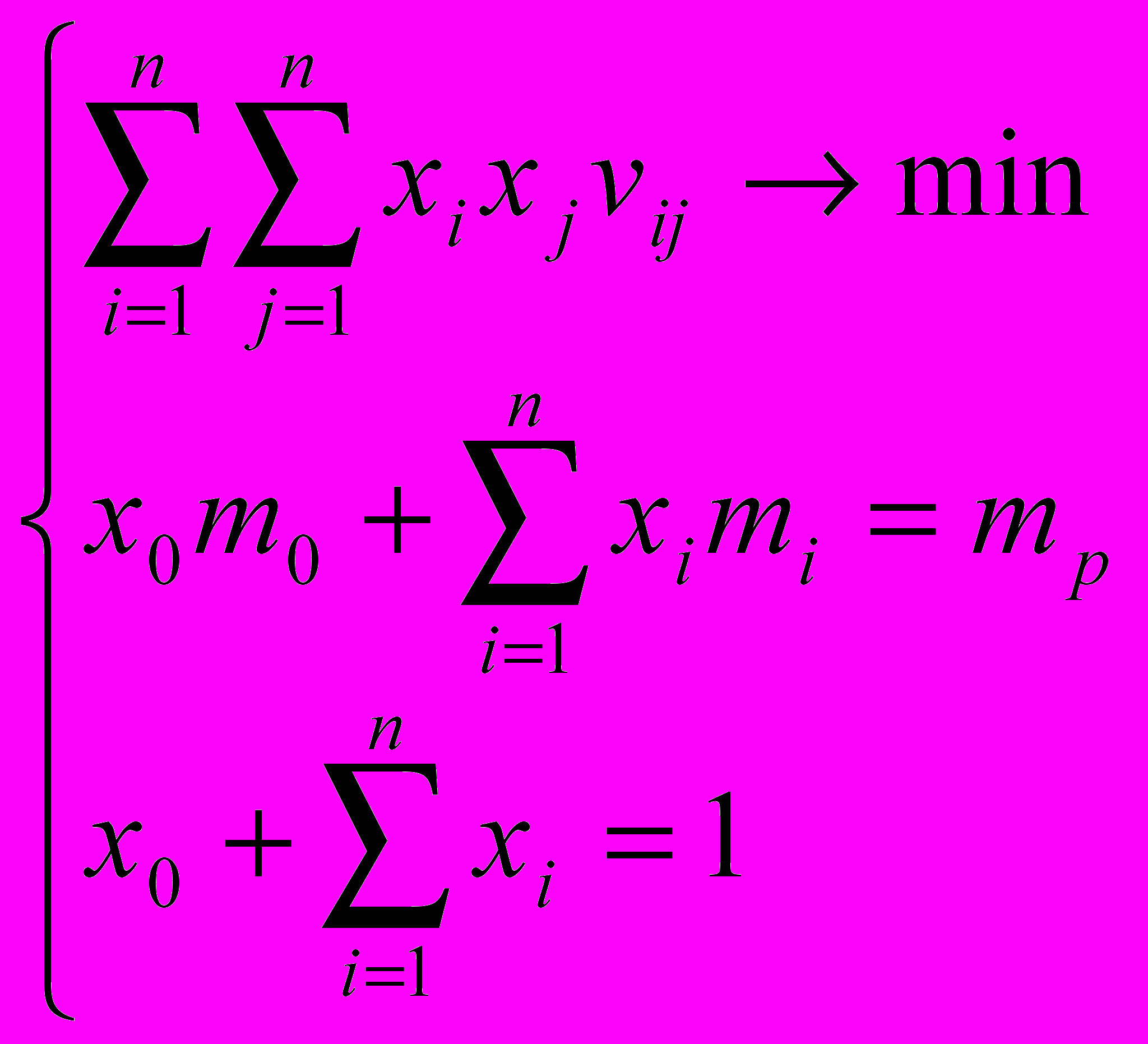(1)

где m₀ – эффективность безрисковых бумаг;

x₀ – доля капитала вложенная в безрисковые бумаги;

x_i,x_j - доля капитала вложенная в ценные бумаги i-го и j–го видов;

m_i – математическое ожидание (среднее арифметическое) доходности i - й ценной бумаги;

v_ij – корреляционный момент между эффективностью бумаг i-го и j –го видов;


Портфель Тобина максимальной эффективности

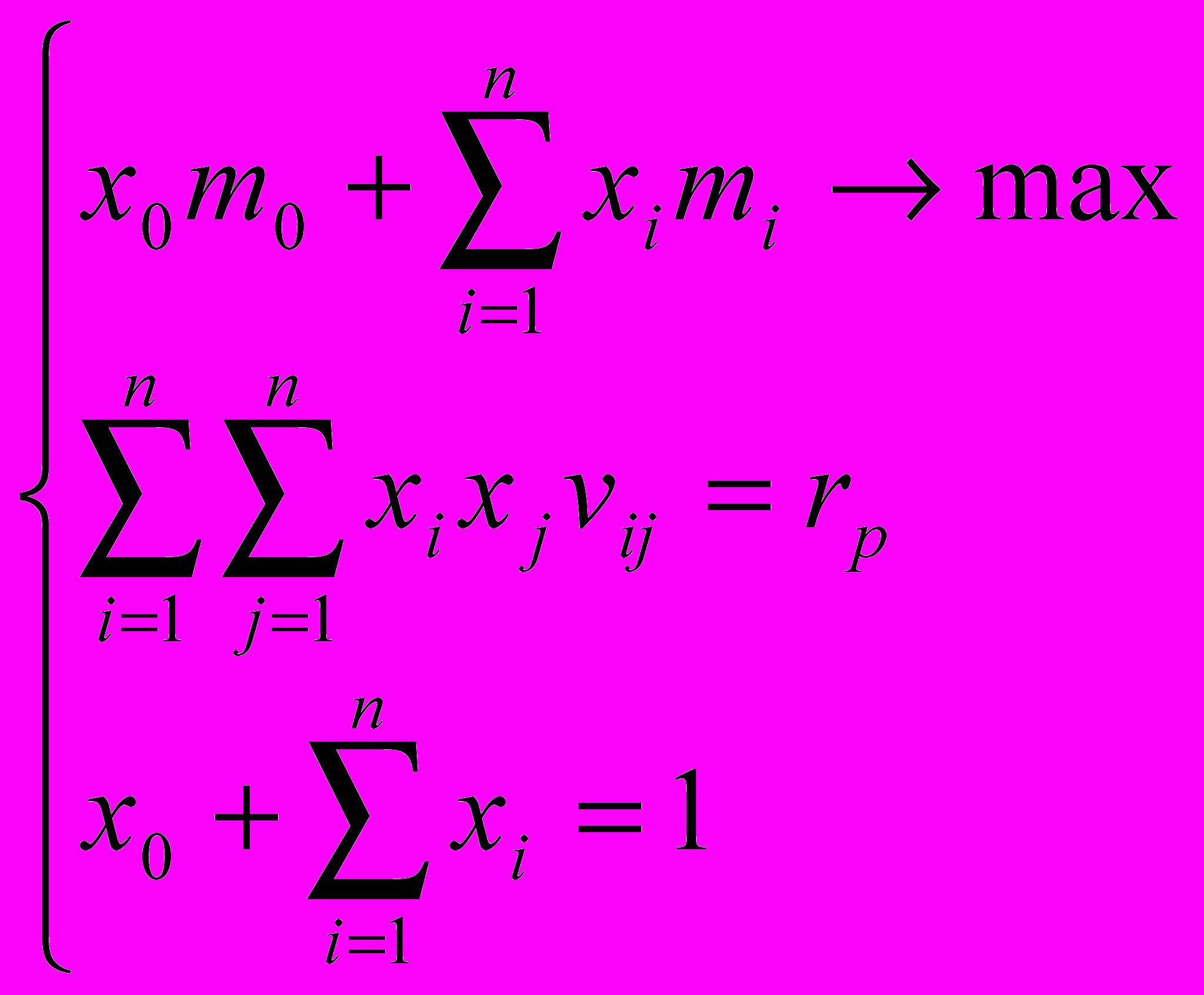(2)


где r_p – риск портфеля


Расчетные формулы аналогичны формулам задачи составления оптимального портфеля ценных бумаг Марковица.


Варианты заданий

№ варианта	m0	rp	mp	№ варианта	m0	rp	X0
1	10	0,3	13,5	16	9	0,05	12,2
2	10	0,3	13,3	17	9	0,05	12,2
3	10	0,3	12,55	18	9	0,05	12,2
4	10	0,3	12,55	19	9	0,05	12,2
5	10	1	12,55	20	9	0,05	12,2
6	10	0,5	12,7	21	9	0,05
7	10	0,04	12,7	22	9	0,088	12,8
8	10	0,04	12,7	23	9	0,09	12,8
9	10	0,04	12,7	24	9	0,12	12,8
10	10	0,04	12,7	25	9	0,1	12
11	8	0,05	12,7	26	9	0,05	12
12	8	0,05	12,7	27	9	0,05	12,3
13	8	0,09	12,5	28	9	0,12	12,2
14	8	0,05	12,5	29	8	0,1	12
15	9	0,05	12,2	30	8	0,1	12