Розділ I. Деякі загальні особливості розвитку математики XIX сторіччя
| Вид материала | Документы |
- Реферат до складання заліку з інформатики, 234.53kb.
- Відомості Верховної Ради (ввр), 2003, №52, ст. 377 ) Розділ I загальні положення стаття, 540.31kb.
- Розділ 4 Актуальні питання менеджменту та маркетингу, 193.82kb.
- Рекомендації для покращення пам'яті та уваги молодших школярів Загальні висновки, 737.37kb.
- Урок ХХІ сторіччя" Загальні положення Положення ґрунтується на Законах України "Про, 109.62kb.
- 1 Загальні положення колізійного регулювання приватно-правових відносин з іноземним, 274.19kb.
- Зміст розділ І. Загальні положення, 725.88kb.
- Розділ 7 облік виробничих витрат, 659.47kb.
- Розділ І. Загальні положення 29 розділ, 10361.92kb.
- Розділ 1, 933.83kb.
ВСТУП…………………………………………………………………………..……2
РОЗДІЛ I. Деякі загальні особливості розвитку математики XIX сторіччя……………………………………………………………………………….3
РОЗДІЛ ІІ. Розвиток алгебри у контексті інших математичних дисциплін у ХІХ столітті……………………………………………………………………….5
2.1 Арифметичні обчислення……………………………………………….5
2.2 Символічне обчислення. Комплексні величини……………………….6
2.3 Комбінаторика. Визначники……………………………………………7
2.4 Теорія чисел…………………………………………………………...…8
2.5 Числові рівняння. Загальна теорія рівнянь і груп……………………..9
ВИСНОВКИ………………………………………………………………….…….12
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ…………………………………... ..13
ВСТУП
В сучасному світі спостерігається тенденція намагання широко розкрити і показати розвиненість і складність духовного життя нашого періоду, хоча б у головних його проявах. Кожній людини, яка цікавиться математикою зрозуміло, що при даному обзорі культурних факторів сучасності, наша наука не може залишитися осторонь, а навпаки відіграє в цьому процесі одну з найголовніших ролей. Тому знання її становлення і розвитку є певними факторами ідентифікування освіченої людини.
Враховуючи той факт, що в математиці, вся наука побудована на певних основних принципах, які включені у закони. Ця структура виділяє її серед інших витворів людського розуму. Дійсно, людина, яка бажає глибоко в неї проникнути, повинна самостійно пройти весь шлях її розвитку; неможливо оволодіти хоча б одним математичним поняттям, якщо не встановити для себе все попередні поняття і всі взаємовідносини між ними, котрі привели до утворення цього поняття, як і не можливо оволодіти досконало цим поняттям, не знаючи всі етапи його історичного відкриття та становлення. Враховуючи очевидно говорити про актуальність вивчення історії математики.
Актуальність вивчення розвитку математики саме XIX сторіччя обумовлено як основною тенденцією вивчення її історії загалом , так і актуальністю вивчення цього періоду в якості такого, котрий знаменується початком реалізації таких перетворень, які стали головною причиною приведення математики до сучасного стану.
Метою моєї роботи є загальний огляд розвитку математики у XIX столітті, детальний огляд перетворень у алгебрі , котрі стали головною причиною приведення її до сучасного стану, а загалом і усієї математики. Для досягнення мети слід виконати наступні завдання:
1) Опрацювати літературу за обраної теми;
2) Дослідити основні тенденції розвитку математики у ХІХ столітті;
3) Дослідити розвиток алгебри у контексті інших математичних дисциплін.
РОЗДІЛ I. Деякі загальні особливості розвитку математики XIX сторіччя.
В історії математики XIX в. знаменує початок нового періоду, що держав (згідно з періодизацією А. Н. Колмогорова) назва періоду сучасної математики. Поняття сучасної математики, так само як і виділення відповідного періоду її розвитку, зрозуміло, трохи невиразно. Воно, очевидно, не може бути іншим, так як розвиток науки постійно міняє вистави про з сучасності її головних теоретичних ідей і практичних досягнень. Автори багатьох підручників з історії математики домовилися включати в період сучасної математики такий відрізок часу, початок якого відзначений здійсненням у математиці таких перетворень, які послужили головною причиною приведення її до сучасному стану.
Характерні риси нового періоду розвитку математики з великою визначеністю стали з'являтися в самому початку XIX в. Загалом мається на увазі роботи Абеля й Галуа про можливість розв'язання алгебраїчних рівнянь у радикалах. Вони висунули на перше місце в алгебрі ряд досить абстрактних загальних понять, серед яких перше місце безумовне належало поняттю групи. Створення й розвиток теорії Галуа й теорії груп зробився однією з головних завдань нової алгебри. Відкриття в 20- 30 роках XIX в. Лобачевским, а також Я. Больяі й Гауссом основних фактів неевклідової гіперболічної геометрії, а в 60- 70х роках - відшукання їх інтерпретацій викликали в системі геометричних наук утворень воістину революційного характеру. Значення останніх полягало не тільки в зміні особи геометрії; воно вийшло за межі цієї області математики, а потім і за межі математики взагалі.
Загальний прорив розвитку зумовлено діяльністю ще багатьох вчених таких як, Карл - Фрідріх Гаусс, О. Коші, Вейерштрассе, Діріхлє,Морган, Дж. Сільвестр,Г.Шерк, Гессель, Карл Густаво Якобі, Ц. Леонеллі, Є.Генчель, Ф. Клєйном. Цей список можна довго продовжувати.
Поряд з розвитком апарата класичного математичного аналізу і його додатків з нього виділилися самостійні математичні дисципліни. Насамперед , ця величезні області диференціальних рівнянь, а також теорій функцій дійсної й відповідно комплексної змінної.
Відзначені вище явища не вичерпують усієї картини розвитку математики в XIX сторіччі. Вони приведені в якості головних аспектів, що визначають ліній цього розвитку. Відзначимо ще три характерні риси, що мають загальний для більшості математичних наук характер.
По-перше, розширення змісту предмета математики. Воно обумовлене тим, що у всіх математичних науках відбувався процес узагальнення основних понять, заміни одних понять іншими, більш загальними. Велика кількість завдань виникала також усередині математики в результаті внутрішніх логічних потреб розвитку теорії.
Серед досліджень, що виникли в результаті запитів математичної теорії, було в ті часи особливо багато таких, які відбивають посилення уваги до обґрунтування математики. Це є другою характерною рисою математики XIX в. Спроби обґрунтування математики в цілому або окремих її частин настільки ж численні, як і я минулому, XVIII, сторіччі. Але вони прийняли тепер інший напрямок. У них проводився критичний перегляд результат-вихідних понять (визначень) і тверджень (аксіом).
Третьою характерною рисою розвитку математики в XIX в. є значне розширення області додатків, в основному обумовлене збільшенням можливостей апарата математичного аналізу.
РОЗДІЛ II. Розвиток алгебри у контексті інших математичних дисциплін у ХІХ столітті.
Сучасна алгебра - надзвичайно широка й розгалужена галузь математики. Вона поєднує велике число самостійних наукових дисциплін. Їхнім загальним предметом є алгебраїчні операції, що представляють собою абстракції, що далеко йдуть, операцій елементарної алгебри. Ці операції визначаються в різноманітних множинах. Алгебра взаємодіє із іншими областями математики, беручи участь в утворі нових, "прикордонних", дисциплін (топологічна алгебра, теорія груп і алгебр Лі й т.п. ) .Будемо розглядати розвиток алгебри у контексті розвитку математики вцілому,виключаючи тільки розвиток геометрії.
3.1 Арифметичні обчислення….
В області обчислення як такого протягом усього розглянутого періоду були зроблені лише невеликі успіхи. Назвемо Лагранжа, який ввів у своїх лекціях з елементарної математики новий спосіб віднімання і приділяв особливу увага скороченому множенню й діленню. Фур'є в "Аналізі певних рівнянь" , 1831) вжив своєрідний спосіб ділення. Гаус був одним із самих талановитих старанних обчислювачів усіх часів і його методи розрахунку багато в чому послужили зразком. Так, його манера додавати й віднімати з ліва направо числа, які стоять одні під іншими стала вже звичкою для більшості астрономів. Він був прихильником більшої точності скорочення десяткових дробів у таблицях. В "Арифметичних дослідженнях" Гаус не тільки розвинув повну теорію періодичних дробів, але й опублікував повну таблицю періодів для всіх простих чисел і ступенів простих чисел до 100; особисто для себе він продовжив її навіть до 1 000. У справі обчислення великої таблиці простих чисел велика заслуга належить гамбурзькому обчислювачу Ц. Дазе, який в 1844 році обчислив також число П с 200 знаками.
Великі успіхи зробила і методика обчислення. В письмовому обчисленні з’явився так званий австралійський метод віднімання і ділення. Були уточнені і доступно оброблені методи скороченого множення і ділення. Великого розвитку досягла комерційна арифметика, яка складає основу сучасних банківських розрахунків.
3.2 Символічне обчислення. Комплексні величини…..
Символічне обчислення розвивалося настільки поступово, що ніхто не замислювався над тим, що воно потребує певного пояснення. Правила знаків і інші подібні положення були введено індуктивно. В цілому над обґрунтуванням алгебри почали мислити на початку ХІХ столітті. Так, Сервуа ввів вирази «комутативний» і «дистрибутивний», до яких Гамільтон додав вираз «асоціативний». Слід відмітити, що Дункан Грегорі – британський математик, який перший спробував заснувати «символічну алгебру». А піонером у розповсюдженні ідей символічної алгебри щодо обчислення комплексних величин був ірландець У.Р Гамільтон. Свої погляди на алгебру як «науку о про чистий час», тобто науку об одному тільки порядку наступності, і свою теорію комплексних чисел, він виклав у своїх роботах. Пізніше Морган розвив цю думку у книзі «Тригонометрия и двойная алгебра» (Лондон,1849р). Завдяки цим роботам комплексні величини були строго введені не тільки геометрично, але й алгебраїчно.
Проблему обчислення з комплексними величинами складали у випадку довільних степенем і логарифмів, внаслідок безкінечності цих операцій в комплексній області. Займався даною проблемою Мартін Ом, виклавши результати свої праці у другому томі «Опыт совершенно последовательной системы математики». Також він друкував багато своїх праць у Берліні о логарифмах. Проте у нього ще булла відсутнє поняття «головного значення функції», яке ввів Коші у «Курсі алгебраїчного аналізу». З геометричної точки зору багато робіт, починаючи з Весселя являли собою зачатки векторного обчислення, яке надбало великого значення тільки в новий час.
3.3 Комбінаторика. Визначники….
К початку ХІХ століття школа комбінаториків знаходилася ще у повному розквіті сил. Доведенням цього є багато робіт вчених таких як, ельзасець Крамп, який вводить у своїй праці знак n!, венський професор А.Еттінгсхаузена, який вперше ввів позначення
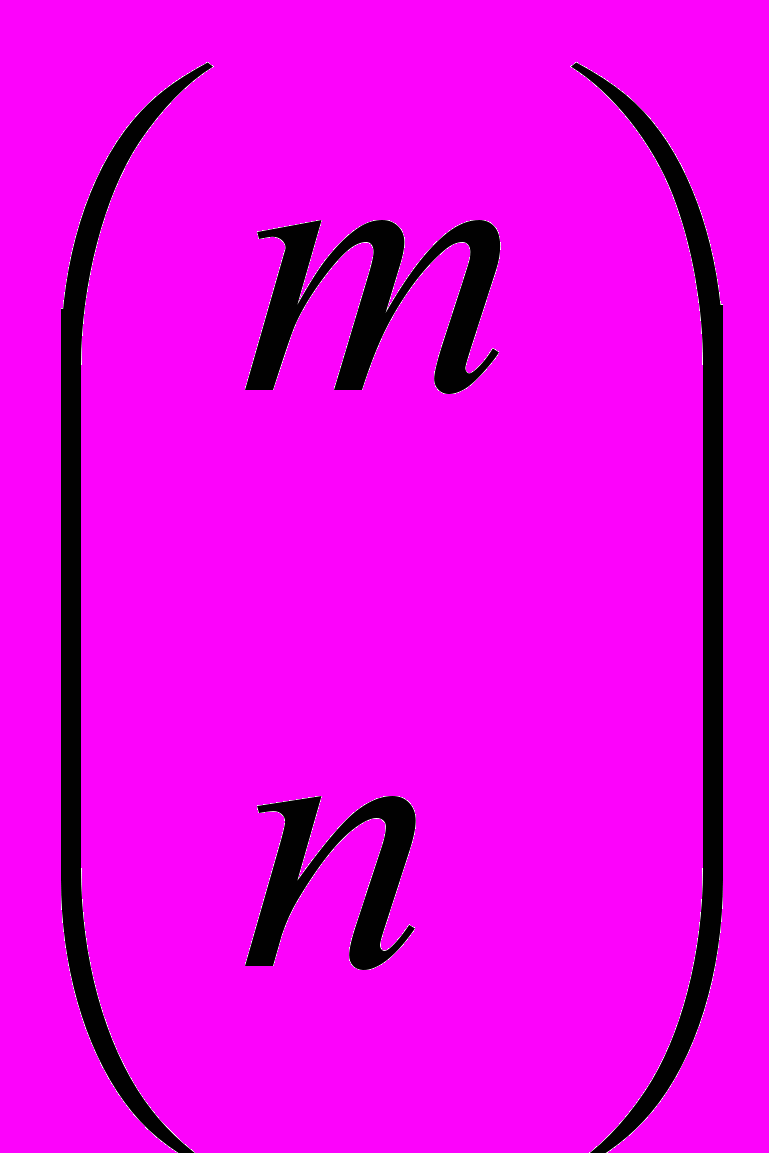. З частних робіт слідує відмітити комбінаторну задачу о 15 учненицях Кіркмана, яка булла пов’язана з загальною проблемою тріад. Відмітемо також теорему Ферма про те, що кожне ціле додатне число може представлено у вигляді сумми n-угольних чисел, яку в загальному вигляді довів Коші. Достатньо добрі роботи з комбінаторики в цей період дали Г.Шерк і Гессель.Розвивалася достатньо швидко теорія визначників.
Коши знайшов уже всі головні властивості визначників, вчасності, теорему множення, причому він спирався на поняття знакозмінної функції. Коши вживав і термін «детермінант», хоча на завжди. Це слово вперще було введено Гауссом у «Арифметических исследованиях» для позначення дискримінанту квадратичної форми. В Англії вивченням цієї галузі математики було розпочато Артуром Келлі, котрий ввів поняття косих і косо-симметричних визначників. Квадратна схема з вертикальними рисками теж походить від нього(а подвійні індекси від Якобі). Біне і Коші розповсюдили теорему множення і на матриці. Якобі вказав, що якщо число строк m більше числа стовбців n , то добуток двух таких матриць дорівнює нулю. Додамо ще те, ортогональне перетворення загальної квадратичних форм у суму квадратів було глибоко вивчено Коші та Якобі . Загалом невелике введення в теорію визначників написав англієць У. Споттисвуд. Але першим справжнім курсом слід вважати «Теорию определителей» Ф.Бріоксі.
Ця терія підготувала грунт для розвитку у другій половині такої дисципліни як алгебраїчна теорія форм і інваріантів, вивченням якої займалися Сільвестр і Келі.
3.4 Теорія чисел….
Перш за все слід відмітити фундаментальну працю Гауса «Арифметическое исследование»(1801). Так, Гаус створив поняття порівняння і перш за все досліджував порівняння першої та другої степені. З останніми були пов’язані теорія квадратичних лишків і закон взаємності, який Гаус не тільки відкрив самостійно, але і доповнив двома доказами. Цей закон також був центральним у книзі Лежандра «Опыт теории чесел». Гаусс також ввів поняття індекса за допомогою якого розв’язав двучлене порівняння
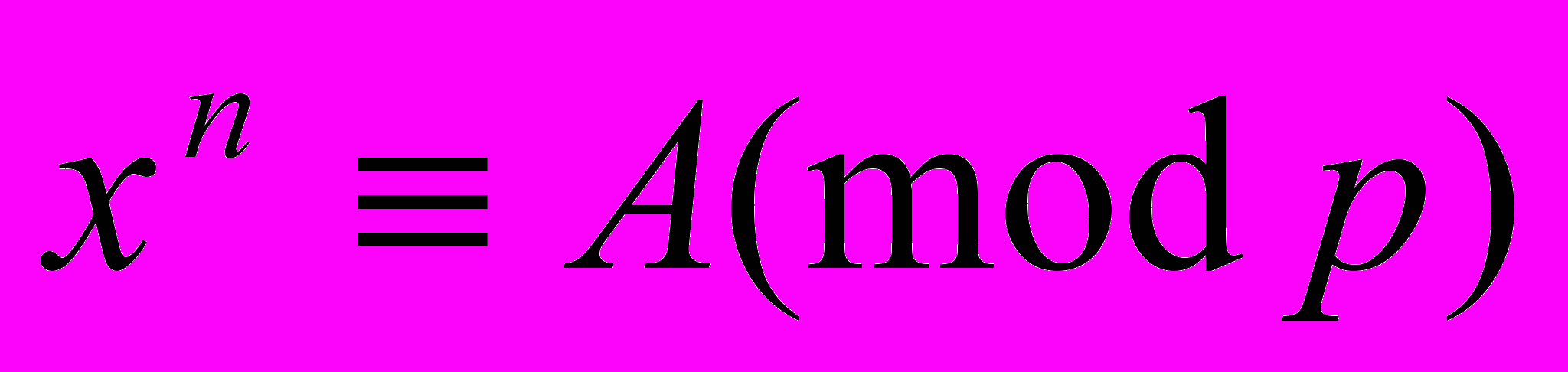. Він дав прямий метод його рішення. Заново створив арифметичну теорію форм, в якій докладно зайнявся бінарними квадратичними формами. Ця теорія також дозволила створити новий метод рішення рівняння Ферма 
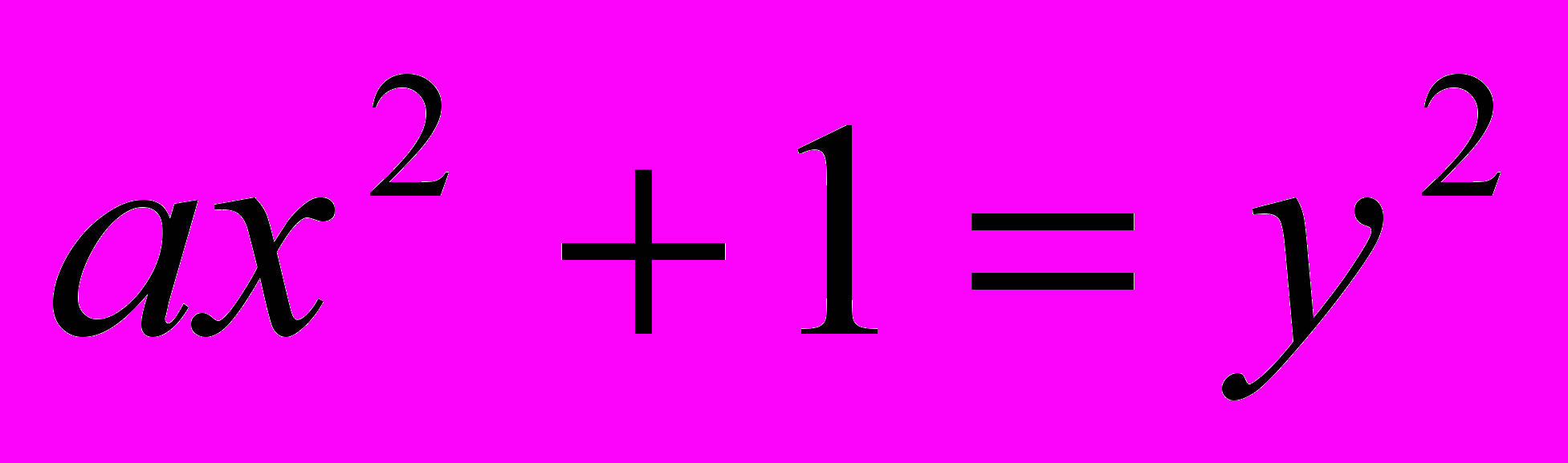. Спираючись на свої нові методи, Гаус зміг повністю розібрати теорію періодичних десятинних дробів. Крім того він виклав свою геометричну теорію комплексних чисел. В цих працях Гауса приховувалися перші зачатки теорії числових полей, яка розвивалася у другій половині ХІХ століття із дослідження Лежен-Діріхлє і Куммера.Одним с послідовників Гауса був Якобі. Він знайшов закон взаємності для кубічних лишків. Публікував праці пов’язані з кватернарними формами, теорію яких також розробляв Ліувілль. Якобі створив теорію еліптичних функцій,яка привела його до різних теорем про представлення чисел у вигляді суми квадратів.
Коши також вніс певний вклад у теорію чисел. Він перший вивчив загальне невизначене тернарне кубічне рівняння і розробив теореми про невизначені тернарні квадратичні рівняння і про порівняння з однаковим модулем і загальним рішенням. Рядами, які були установлені Дж.Фарєєм , Коші також займався. В цьому ж напрямку працювали Ф.Ейзенштейн, Смит та Ерміг.
Послідовник Гауса, Діріхлє довів справедливість великої теореми Ферам для
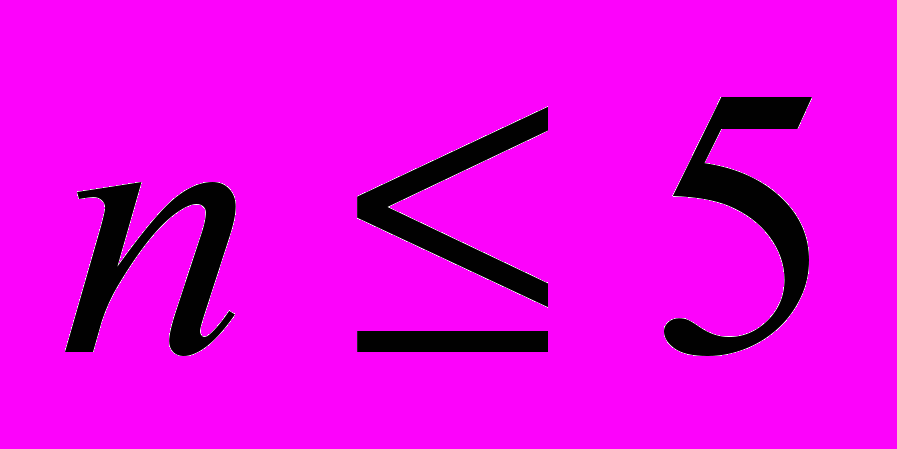. Також він довів, що всяка арифметична прогресія при деяких умовах містить безкінечну множину простих чисел.Багато з вчених доклали зусиль у розвиток теорії чисел. Це Куммер,який запропонував Діріхлє мнімо повний доказ теореми Ферма, Чєбишев, котрий вивчав закон розподілу простих чисел, Лєбег і Галуа,які вивчади зв’язки між неперервними періодичними дробами та інші.
3.5 Числові рівняння. Загальна теорія рівнянь і груп.
Чисельним рішенням рівнянь вищих степенів займався Ж.Фур’є. Розробив теорему о кількості дійсних коренів між двома даними границями.
Пізніше цю теорему замінила більш загальна теорема женевця Ж.Ш.Штурмана.
Пізніше Коші розповсюдив цю теорему і на комплексні корені.
П. Руффіні в одній із своїх робіт дав спосіб наближеного рішення рівняння будь-якої степені, опублікував багато праць в яких розробив метод рішення загальних алгебраїчних рівнянь. Своєрідний спосіб розробив бельгієць Ж.Данделен, наслідуючи швейцарця К.Греффе. Він одночасно знаходив всі дійсні і мнимі корені, без попереднього їх числа і розташування. Деякі окремі випадки роздивився астроном Енкє. Також Данделен звернув особливу увагу на рішення тричленних рівнянь, теорію яких розвили потім Гаус і Дж. Беллавітіс, які застосували тут логарифми сум,вперше відкриті Ц.Леонеллі. Гаус потім видав п’ятизначні таблиці цих логарифмів, відмітивши їх творця.
Сучасна теорія рівнянь веде свій початок від ідеї складати рівняння для таких функцій коренів початкового рівняння, котрі при любій перестановці коренів мають певне число значень. Для
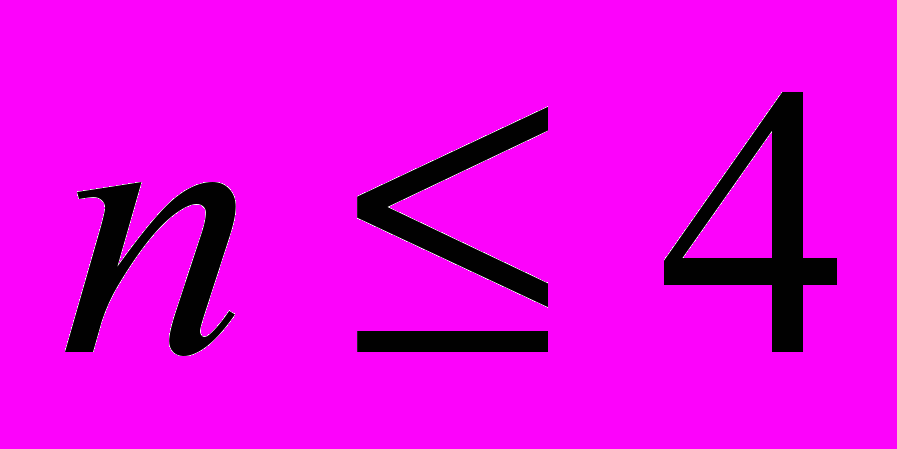отримувалась,таким чином,резольвента нижчої степені. Лагранж уже застосовував при цьому теорему про те, що як ми говоримо, порядок підгрупи є дільник порядку групи. Доказ її дав тільки П.Аббаті. Робота над рівняннями четвертої степені продовжувалася. Перетворення рівняння п’ятої степені до тричленної форми, яке було дане Брінгом залишилося невідомим. Між цим молодий норвежець Н.Г.Абель у 1826 році довів неможливість рішення цієї задачі. Абель також знайшов ще більш глибокі теореми, наприклад, що не приведене рішення простої степені завжди має розв’язок у радикалах, якщо для всякої пари коренів один виражається раціонально через інший. Це є необхідною умовою, такі рівняння називають абелевими.
Засновником теоретико - групового метода дослідження рівнянь є Е. Галуа, який у 1832 році загинув на дуелі через історію кохання. Розуміючи значення своїх відкриттів в останню ніч свого життя написав лист своєму товаришу, в якому виклав свій науковий заповіт. Галуа ввів термін «група». Він вказав для кожного рівняння групу підстановок, по якій можна взнати найбільш суттєві властивості рівнянь.Він розрізняв прості і складені группи і ввів клас кінцевих груп, які були названі «конгруенцгрупами». Він також зробив вклад у теорію так званих медулярних рівнянь. Вперше зв’язано виклав його теорію Е.Бетті. Засновником теорії кінцевих груп можна вважати Коші. Він також застосував багато термінів, наприклад, «транзитивний», «транспозиція», визначив групу як систему спряжених підстановок. Він довів теорему Галуа про те, що кожна група, порядок якої ділиться на просте число р, містить хоча б одну підгрупу порядку р.
Келі виразив дискримінант цілої алгебраїчної функції через суми степенем коренів, та виділив більш абстрактне поняття групи.
Жергон розробив теорію лінійних рівнянь з багатьма невідомими. Загальним випадком займалися Якобі, який виразив рішення за допомогою визначених інтегралів, Коші, який виразив рішення за допомогою коренів із одиниці.
К.Жордан у 1870 р у своїх працях узагальнив результати теорії кінцевих груп у застосуванні к теорії чисел, теорії функцій і алгебраїчної геометрії. К кінцю ХІХ ст. теорія груп та рівнянь оформилася і досягла виского рівня.
ВИСНОВКИ
Дослідивши літературу з обраної теми, розглянувши основні тенденції розвитку математики у ХІХ столітті, основні досягнення розвитку алгебри цього ж періоду приходимо до висновків,що в процесі роботи з багатої й різноманітної історії алгебри XIX ст. виділено порівняно невелику область формування деяких основних понять алгебри і математики взагалі. Це зроблене тому, те в виділенні деяких алгебраїчних об'єктів - групи, поля, а пізніше кільця й структури – і у створенні відповідних теорій - відбивається головний зміст змін, які відбулися в алгебрі протягом XIX - початку XX в. Ці зміни визначили основні напрямки розвитку алгебри в першій половині XX в.
Таким чином, ХІХ століття є необхідним етапом розвитку математики, що привів її до сучасного вигляду, зумовив головні завдання і напрямки подальшого її розвитку ХХ століття, заклавши тим самим фундамент для розвитку нової математики.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ:
1. Вилейтнер Г. История математики от Декарта до середины XIX столетия. [Текст]/ А.П. Юшкевич - М.: ГИФМЛ, 1960. - 468 с.
2. Клейн Ф. Лекции о развитии математики в XIX столетии. Часть I. [Текст]/ [Текст]/ Р.Курант,О.Нейгебауерон.- М.–Л., ГОНТИ, 1937 — 432 с.
3. Рыбников К.А. История математики. ( В 2-х томах ) [Текст]/Л.А. Сорокина. -М.: Изд-во Моск. Университета. т.1 - 1960, 191с.; т.2 - 1963, 336с.
4.
Алгебра. Історія. [Електронний ресурс] - Режим доступу: o.ua/algebra.php5. История математики. На стыке алгебры, анализа и геометрии. [Електронний ресурс] - Режим доступу: u/category/na-styke-algebry-analiza-i-geometrii-kompleksnye-chisla
6. История математики. Ряды непрерывных функций и равномерная сходимость. [Електронний ресурс] - u/16-ryady-nepreryvnyx-funkcij-i-ravnomernaya-sxodimost.php
7. Алгебра. Исторический очерк. [Електронний ресурс] - ссылка скрыта
8. Алгебра. Из истории. [Електронний ресурс] - ссылка скрыта
9. Математика XIX века. (Математическая логика. Алгебра. Теория чисел. Теория вероятностей.) Под редакцией А. Н. Колмогорова и А. П. Юшкевича (рецензия) [Електронний ресурс] -et.ru/php/archive.phtml?wshow=paper&jrnid=rm&paperid=3190&option_lang=rus
10. Математика. Из истории идей. [Електронний ресурс] -gov.ua/Vernadsky/e-texts/archive/ideas.php
11. Наука и образование первой половины 19 века. [Електронний ресурс] - ссылка скрыта