Воснові всіх числових множин лежить натуральний ряд чисел. Елементи натурального ряду відображають найпростіші кількісні співвідношення
| Вид материала | Документы |
- Створити текстовий документ як можна ближче до зразка, 15.72kb.
- Абрамкина Надежда Юрьевна Студентка 23 группы числовые последовательности реферат, 183.55kb.
- Вопросы к гак по методике преподавания начального курса математики, 23.01kb.
- Азарян О. М. Ефективне функціонування споживчого ринку: параметри та умови, 85.75kb.
- Гимназия 1543, 8-в класс Листик 1, 13 марта 2010, 12.71kb.
- Диференціальне числення функції однієї змінної, 18.73kb.
- Вопросы к экзамену по курсу «Вычислительные системы, сети и телекоммуникации», 51.75kb.
- Вопросы к экзамену по курсу " ЭВМ и периферийные устройства" для групп К2-121, -122,, 75.03kb.
- Конспект лекцій зміст: Тема Систематизація видів світових цін, 6766.89kb.
- О. В. Мосин ядерные реакции и их использование в биологических исследованиях, 342.97kb.
Еволюція поняття числа.
В основі всіх числових множин лежить натуральний ряд чисел. Елементи натурального ряду відображають найпростіші кількісні співвідношення.
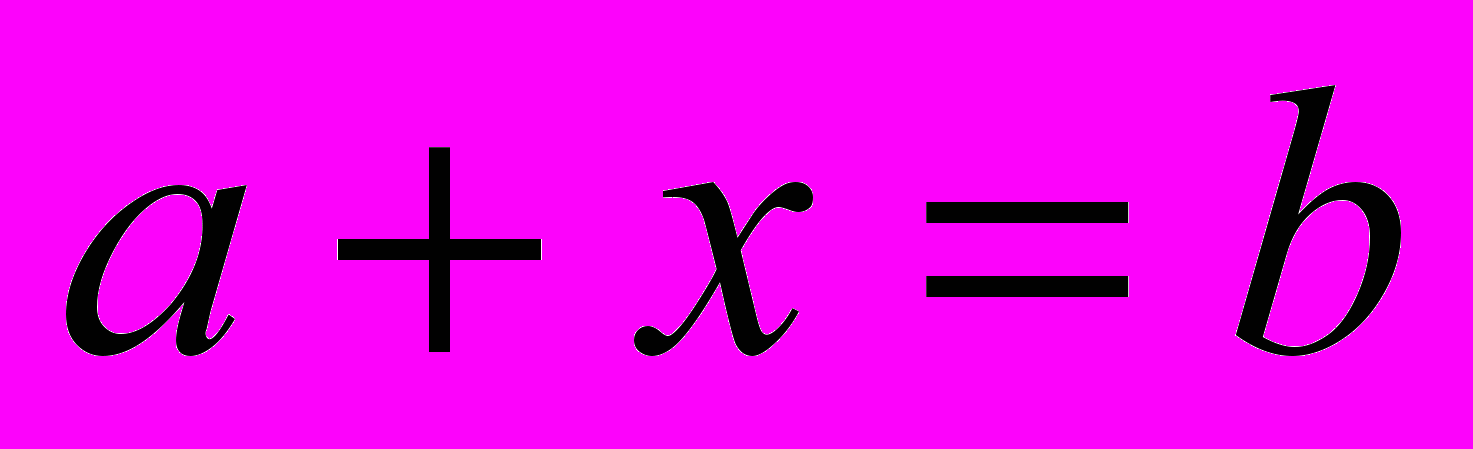
 , це рівняння має розв’язок в натуральних числах при
, це рівняння має розв’язок в натуральних числах при 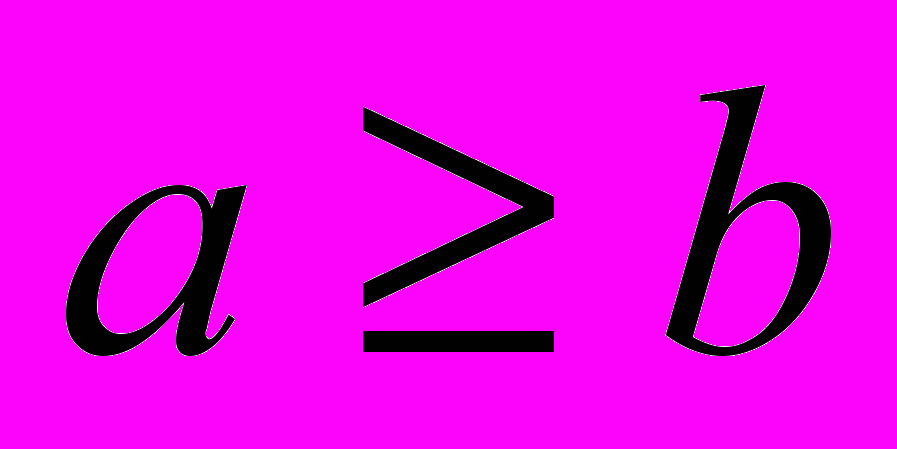 , тому для отримання розв’язку при будь-яких
, тому для отримання розв’язку при будь-яких 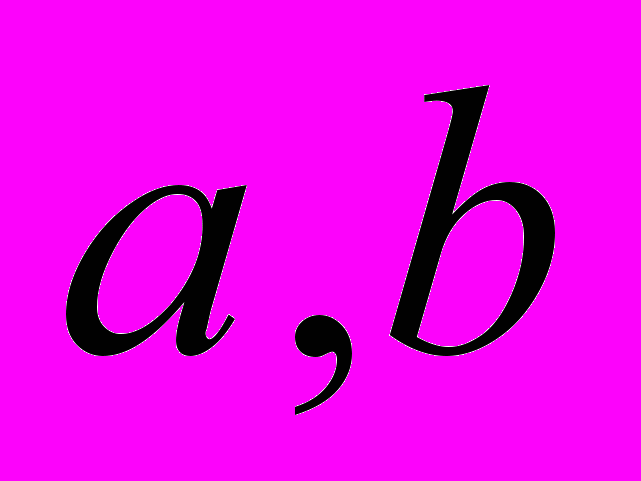 були введені від’ємні числа та
були введені від’ємні числа та  , які з натуральним рядом утворили множину
, які з натуральним рядом утворили множину  . В цій множині рівняння
. В цій множині рівняння 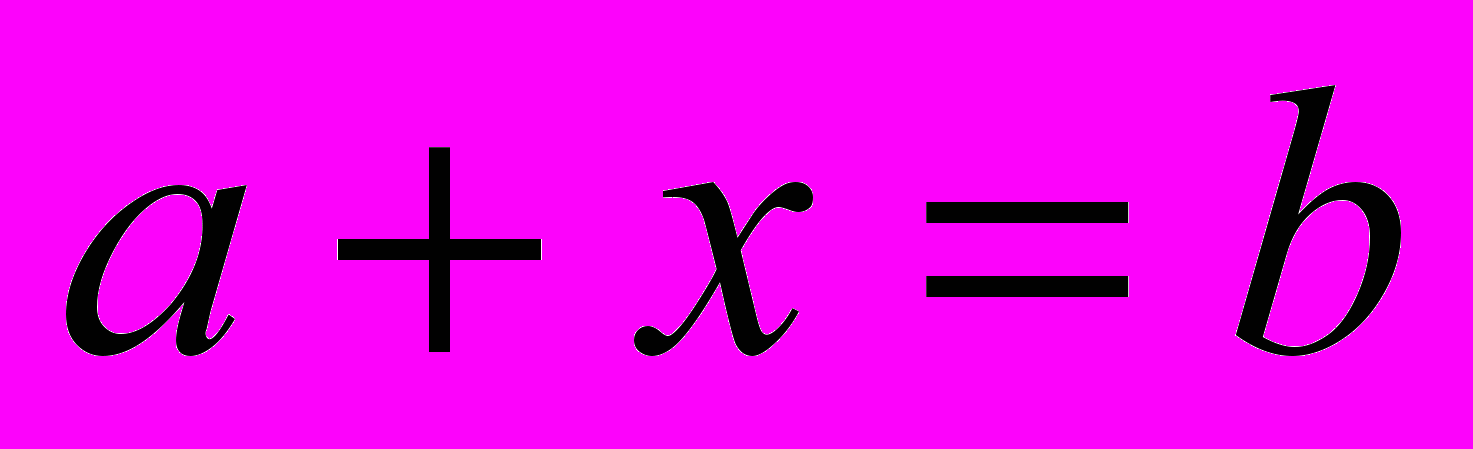 має розв’язок при будь-яких цілих числах
має розв’язок при будь-яких цілих числах 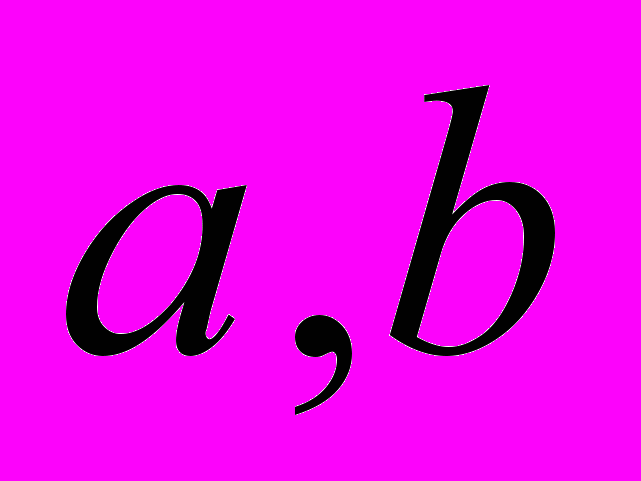 .
.Розглянемо інше рівняння
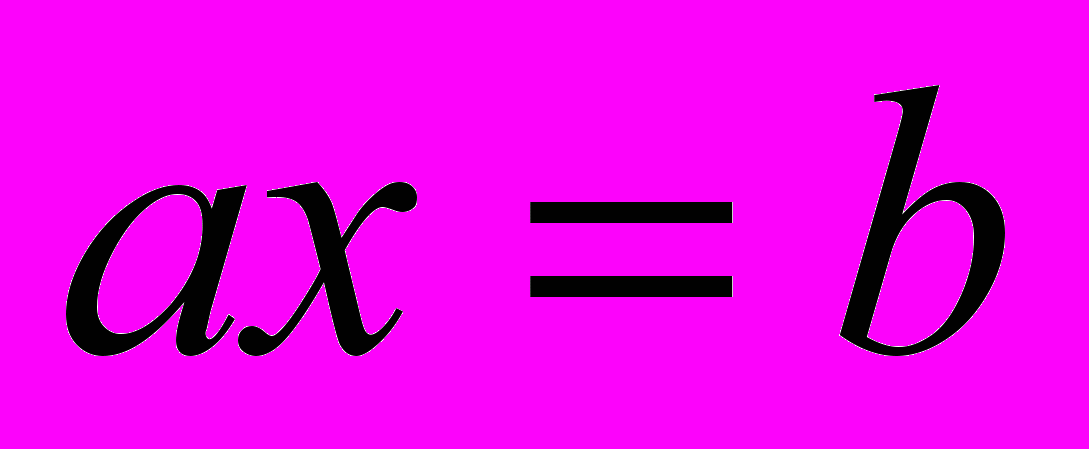 при
при 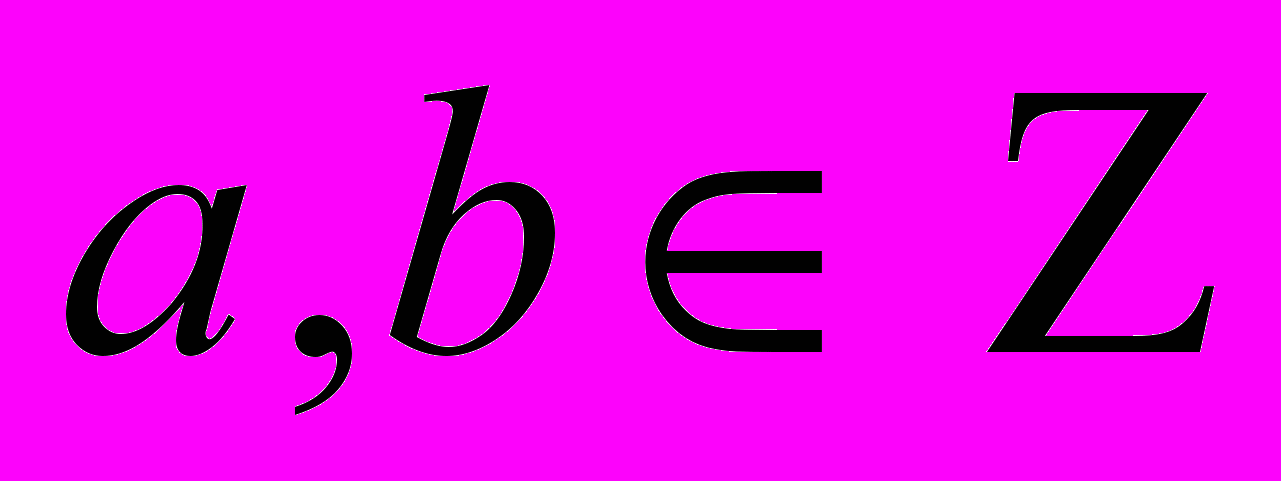 і
і  . Це рівняння не має розв’язків в цілих числах якщо
. Це рівняння не має розв’язків в цілих числах якщо 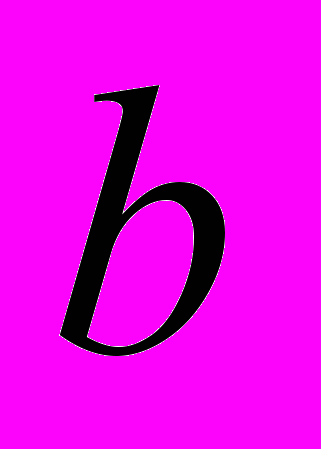 не ділиться на
не ділиться на  . Тому , щоб одержати розв’язок рівняння при будь-яких цілих
. Тому , щоб одержати розв’язок рівняння при будь-яких цілих 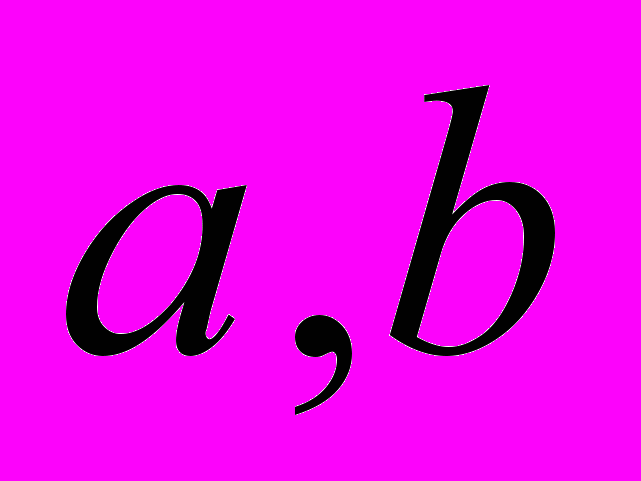
 введені раціональні чисельні множини.
введені раціональні чисельні множини.Розглянемо квадрат зі стороною рівною 1. Відомо, що діагональ квадрата в такому випадку рівна
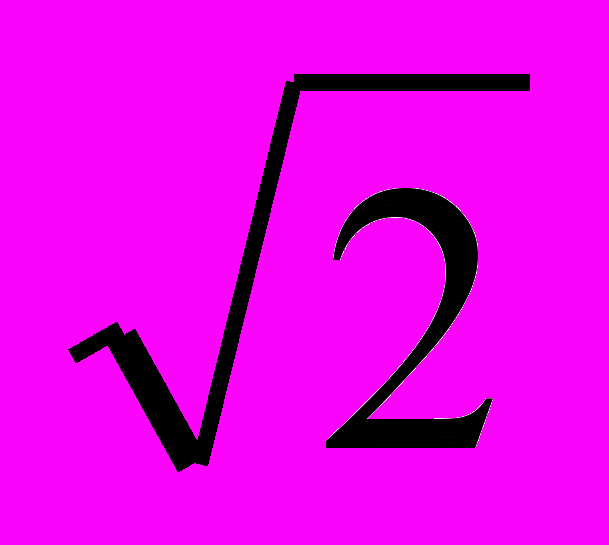 Покажемо, що
Покажемо, що 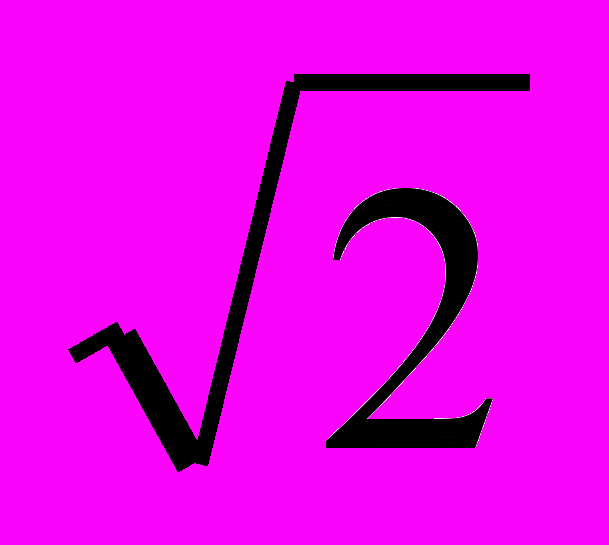 не є раціональним числом.
не є раціональним числом. Припустимо супротивне.
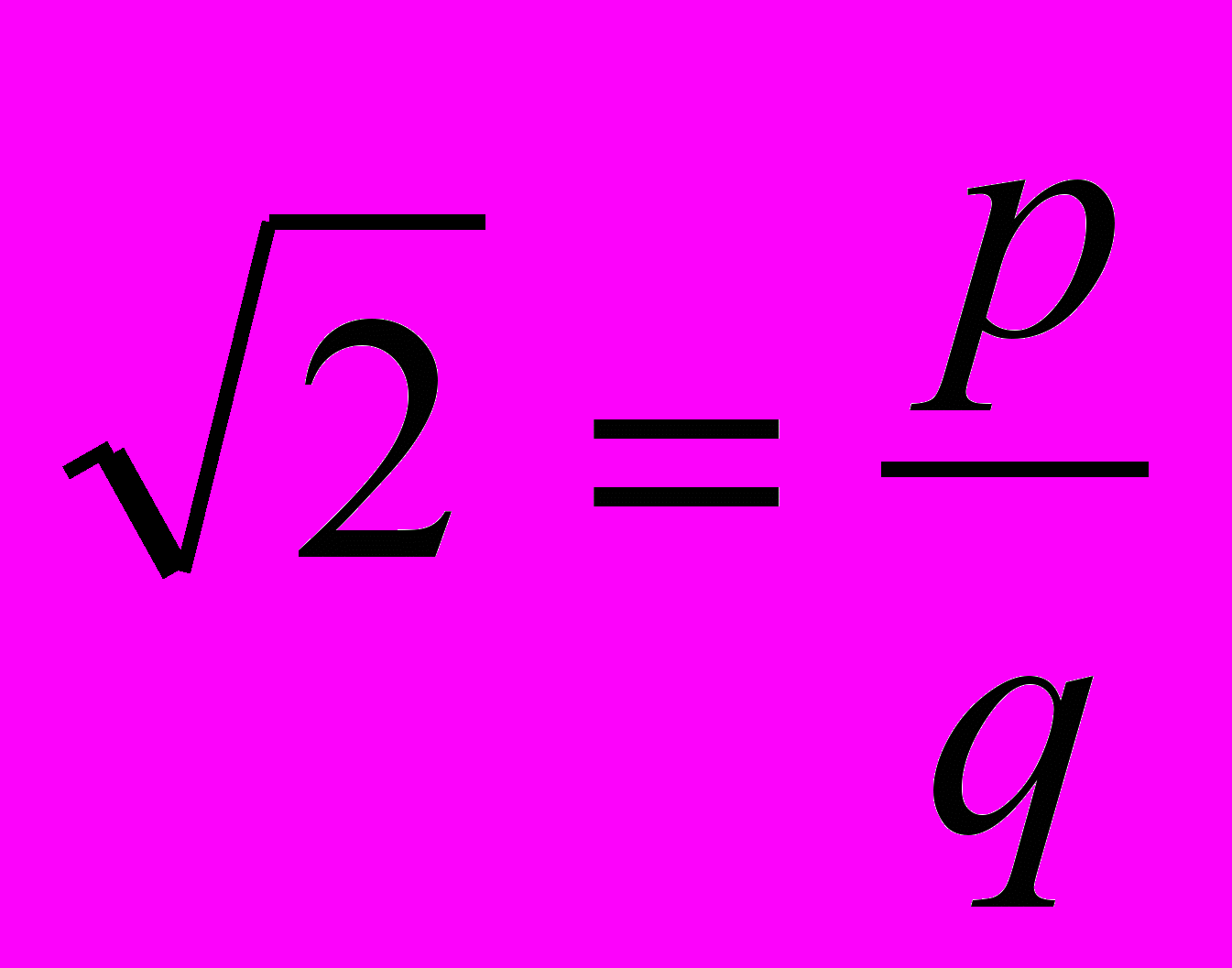
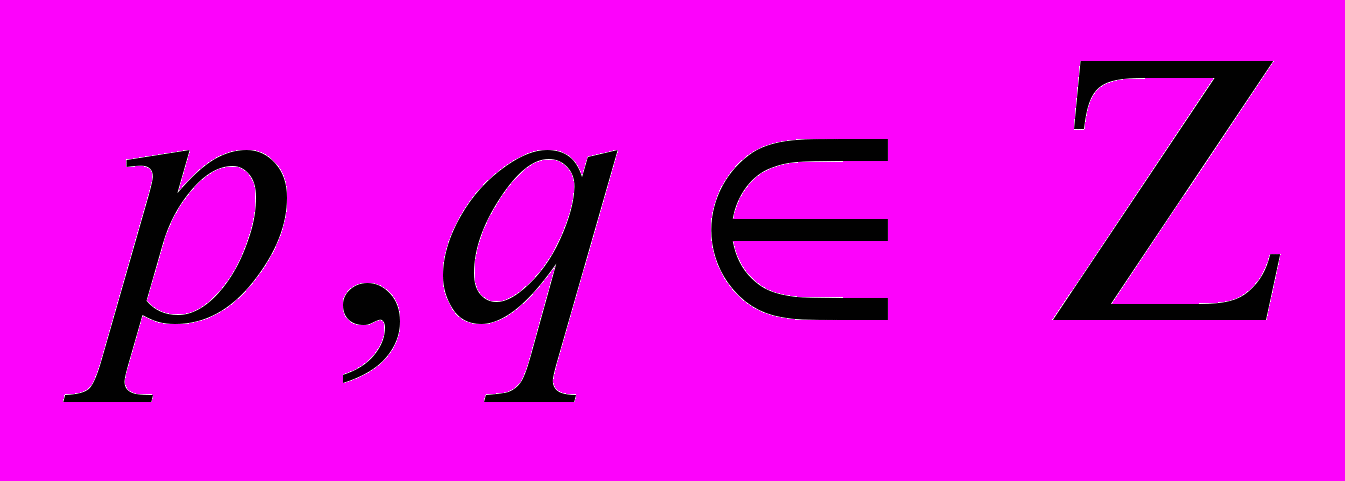 і
і 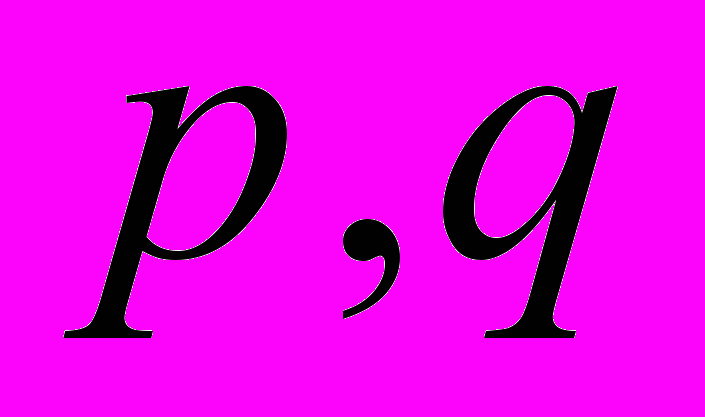 - взаємнопрості, тоді
- взаємнопрості, тоді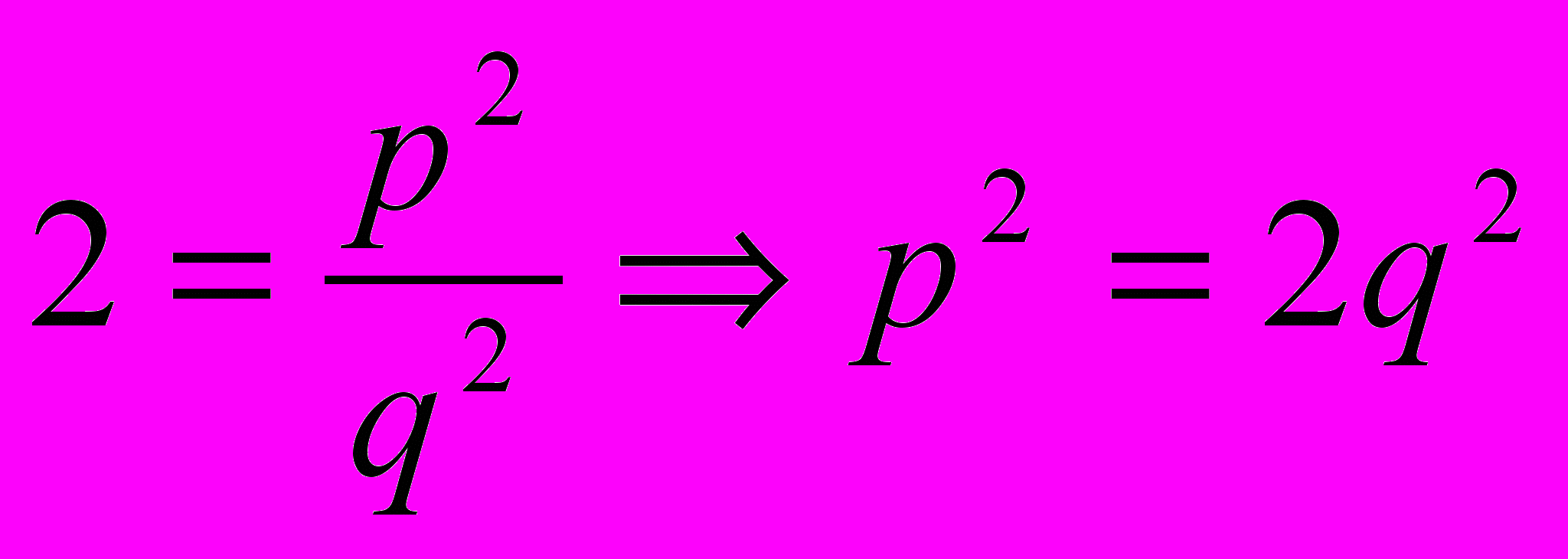

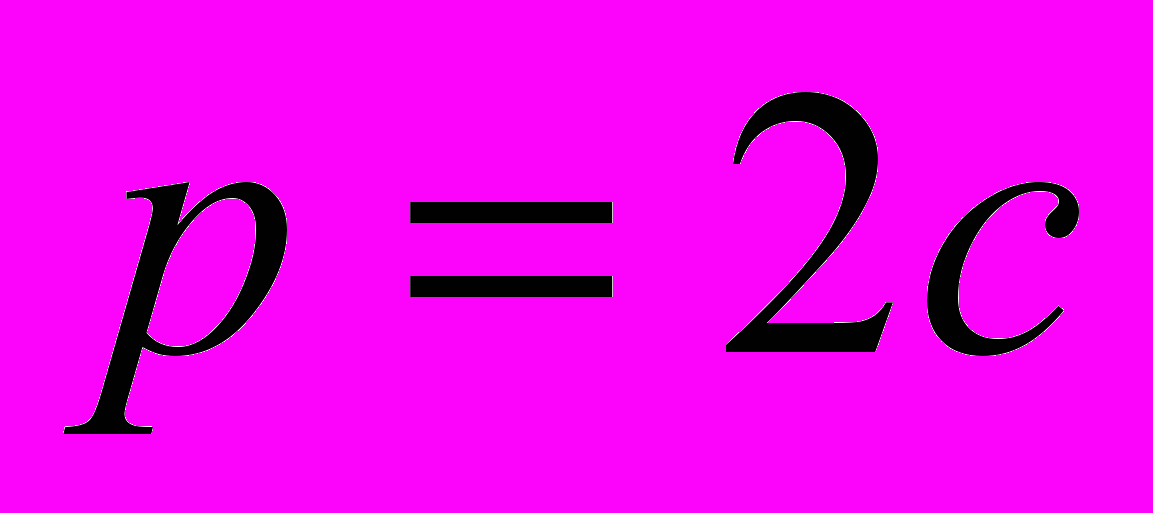 , де
, де 

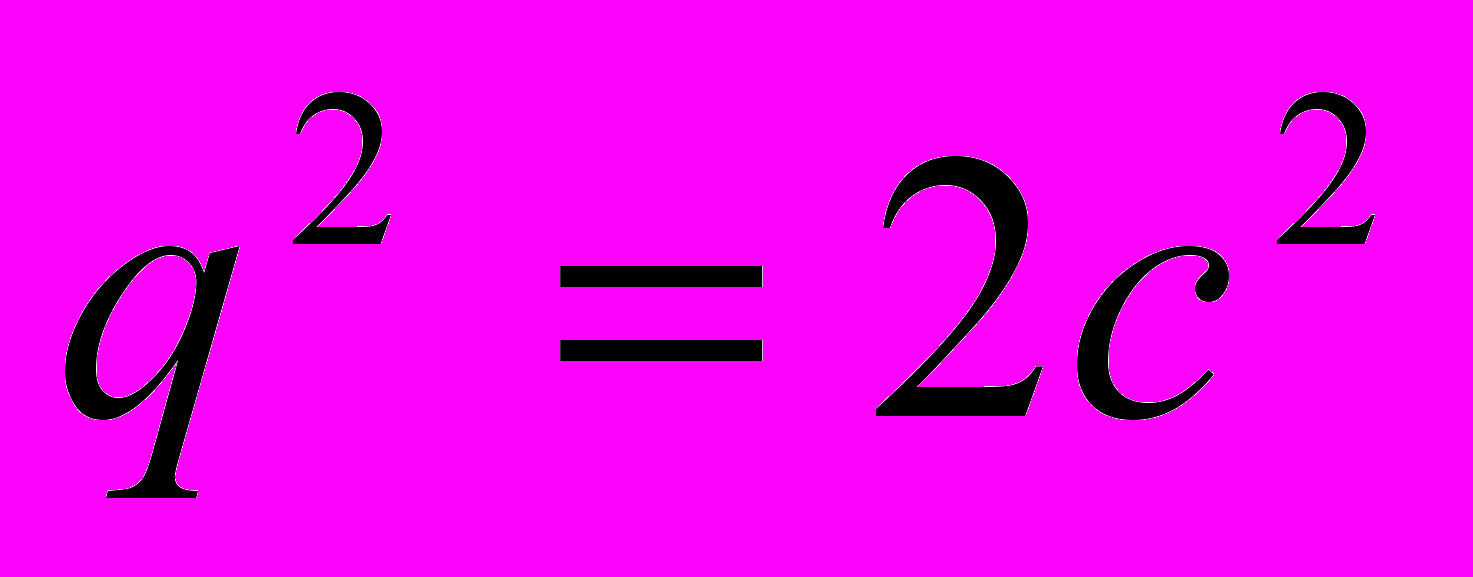
 тобто
тобто 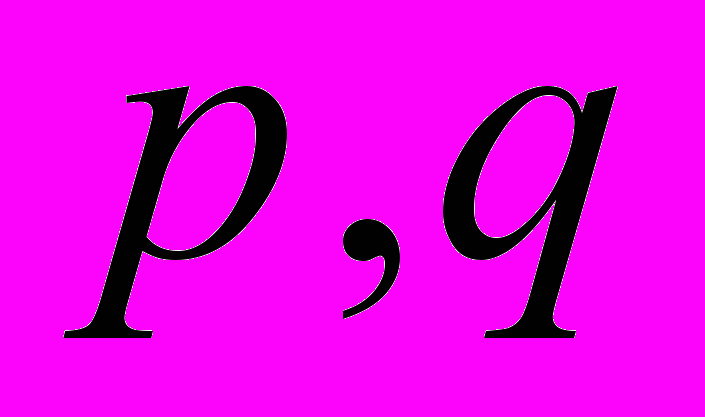 мають спільний дільник
мають спільний дільник 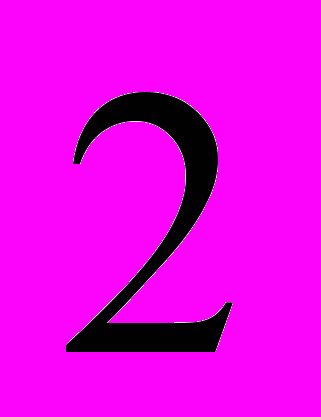 , ця суперечність доводить твердження.
, ця суперечність доводить твердження.Для того щоб одержувати довжини відрізків було введено розширення множини раціональних чисел – множина дійсних чисел. Кожне дійсне не раціональне число можна записати у вигляді нескінченного періодичного десяткового дробу.
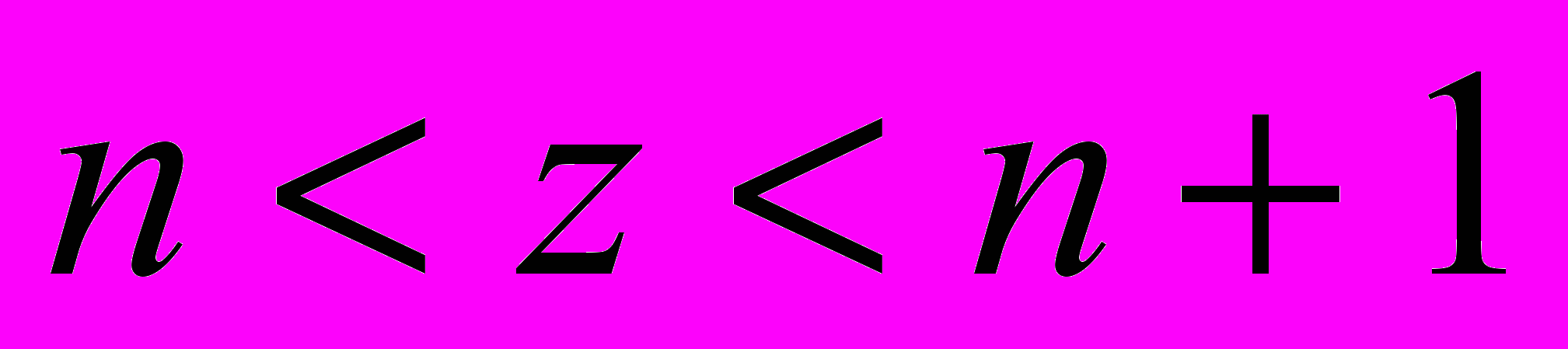 , де
, де  . Відрізок
. Відрізок  ділимо на 10 різних частин, за
ділимо на 10 різних частин, за 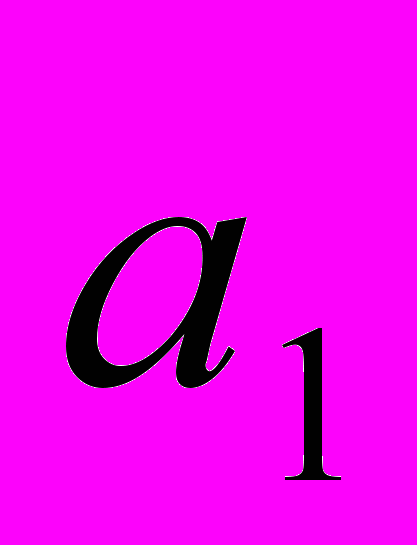 беремо число, яке на 1 менше за номер відрізка на якому знаходиться число
беремо число, яке на 1 менше за номер відрізка на якому знаходиться число  . Аналогічно цей відрізок ділиться на 10 рівних частин і за
. Аналогічно цей відрізок ділиться на 10 рівних частин і за 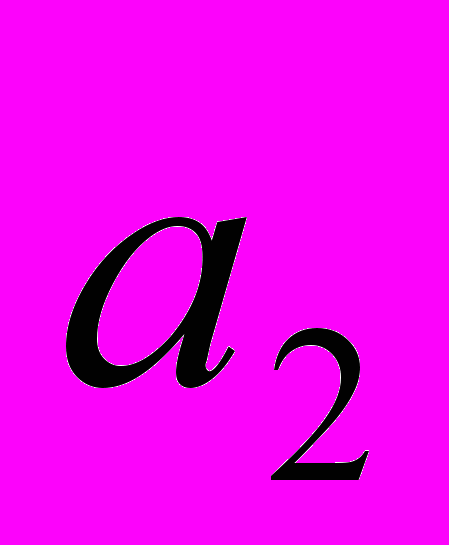 беремо число за номером відрізка на якому знаходиться число
беремо число за номером відрізка на якому знаходиться число  . Одержимо наступне
. Одержимо наступне 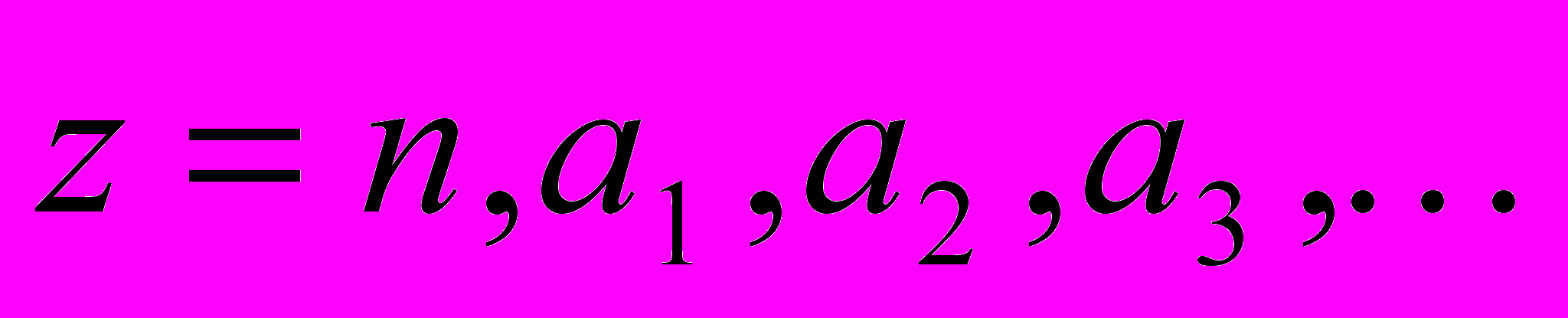 Розглянемо рівнняння
Розглянемо рівнняння 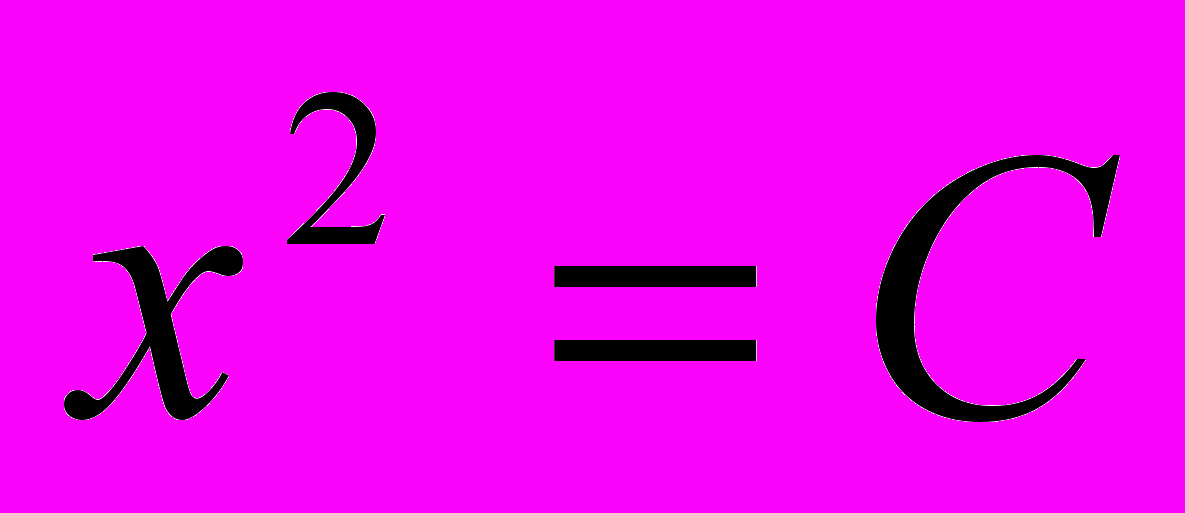 , де
, де  . Це ріняння має розв’язок в дійсних числах тільки якщо
. Це ріняння має розв’язок в дійсних числах тільки якщо 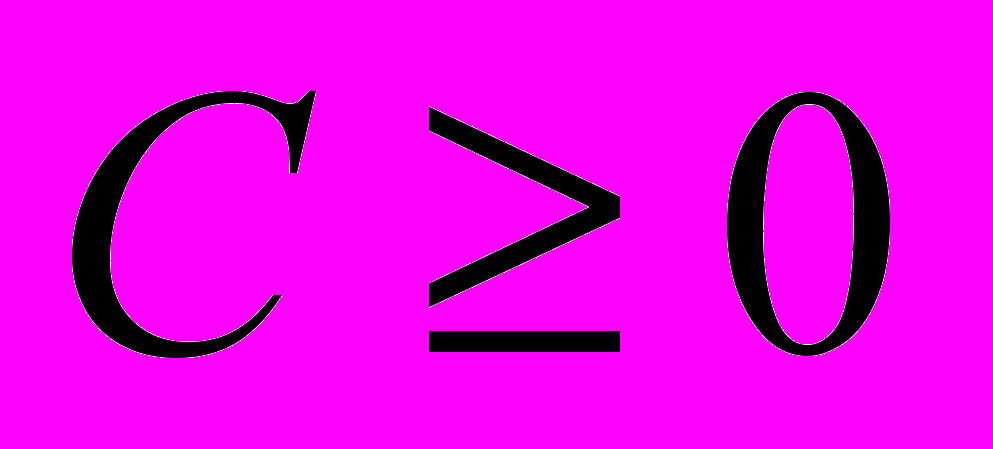 . Щоб одержати розв’язки цього рівняння при будь-яких
. Щоб одержати розв’язки цього рівняння при будь-яких  необхідно ввести розширення поля дійсних чисел, а саме поле комплексних чисел. В цій множині рівняння
необхідно ввести розширення поля дійсних чисел, а саме поле комплексних чисел. В цій множині рівняння 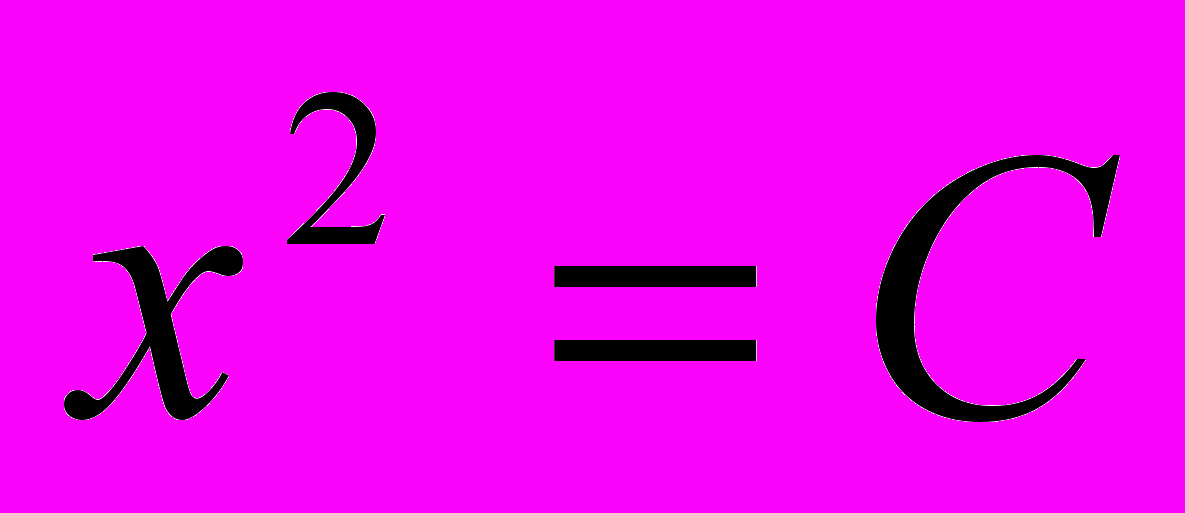 має розв’язки при будь-яких комплексних
має розв’язки при будь-яких комплексних  .
. Якщо
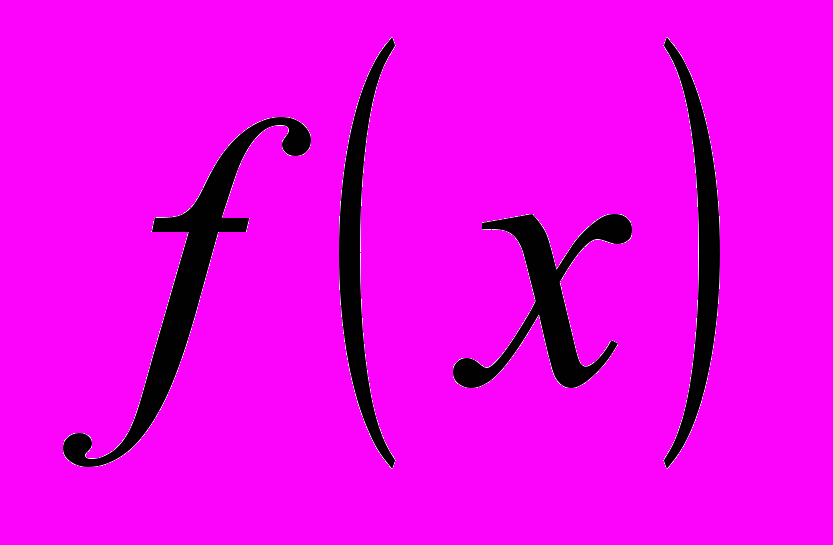 - деякий многочлен з комплексними коефіцієнтами то рівняння
- деякий многочлен з комплексними коефіцієнтами то рівняння  завжди має корінь в полі комплексних чисел (Основна теорема алгебри).
завжди має корінь в полі комплексних чисел (Основна теорема алгебри).Комплексні числа
Розглянемо рівняння
 , це ріняння має розв’язок в множині комплексних чисел, його позначимо через
, це ріняння має розв’язок в множині комплексних чисел, його позначимо через 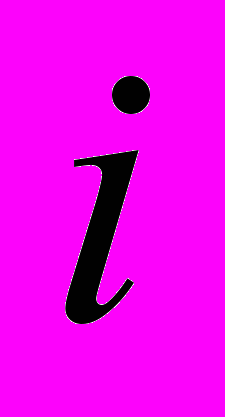 . Тоді
. Тоді 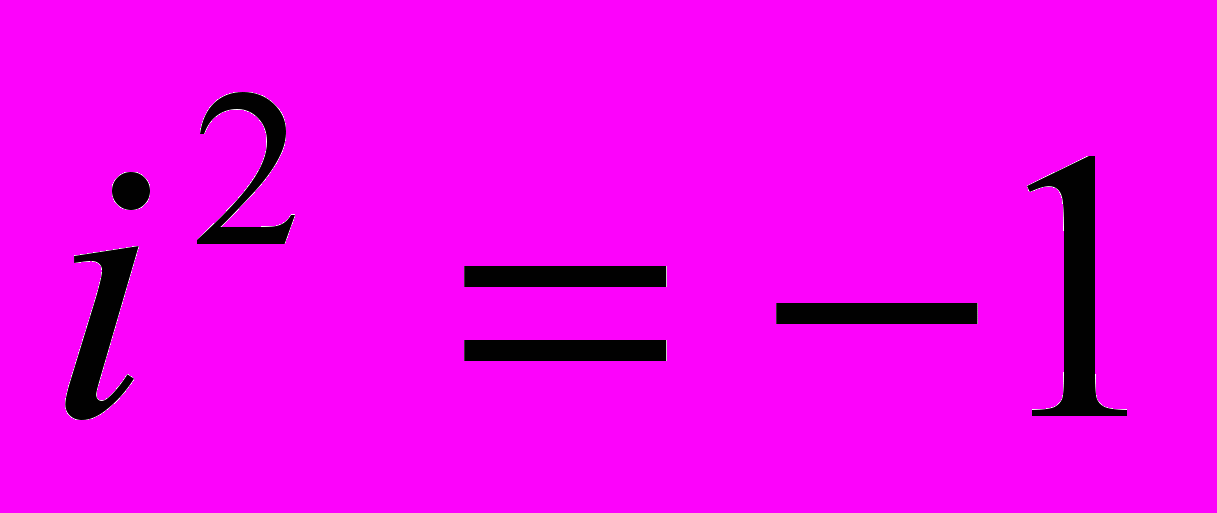 . Множина
. Множина  - розширення множини дійсних чисел
- розширення множини дійсних чисел 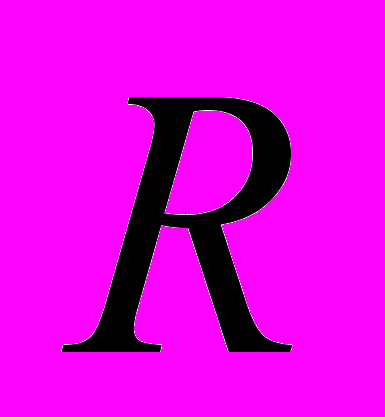 , тому
, тому  . Для елементів множини
. Для елементів множини  введемо арифметичні операції:
введемо арифметичні операції:
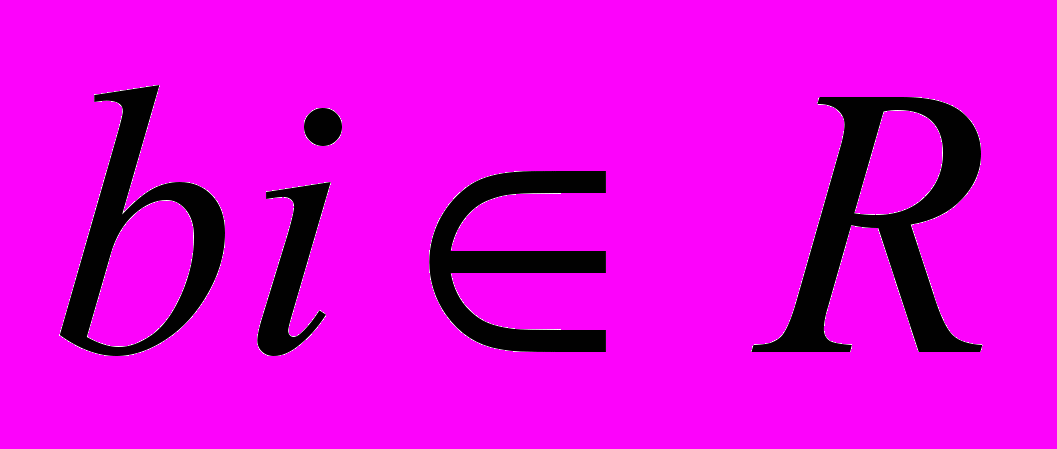
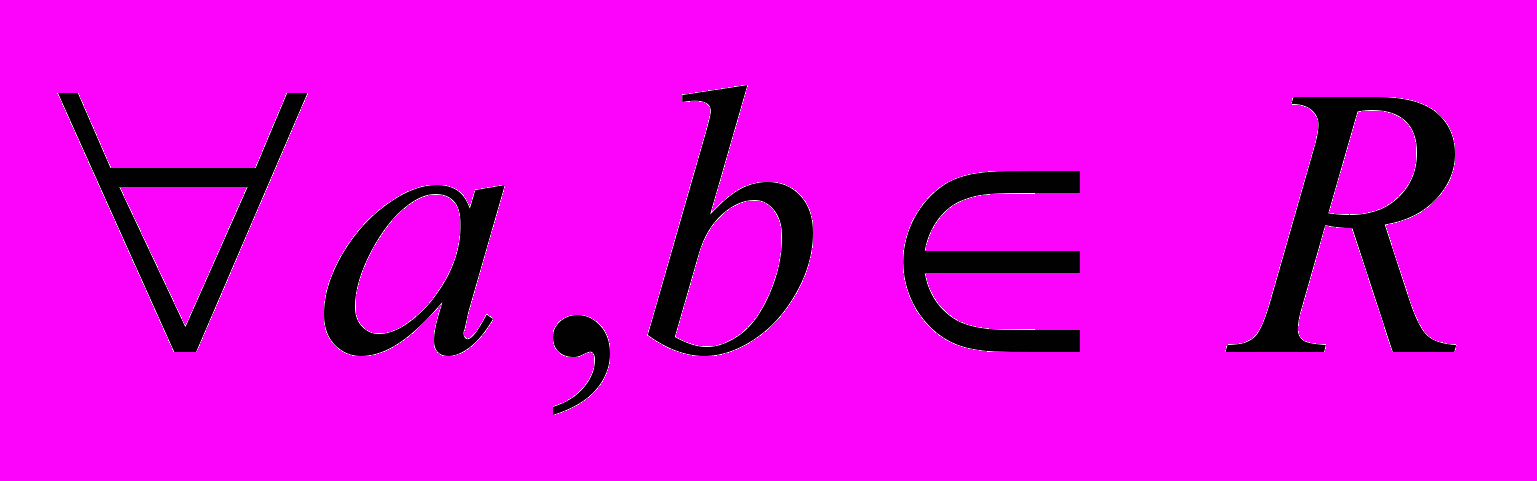
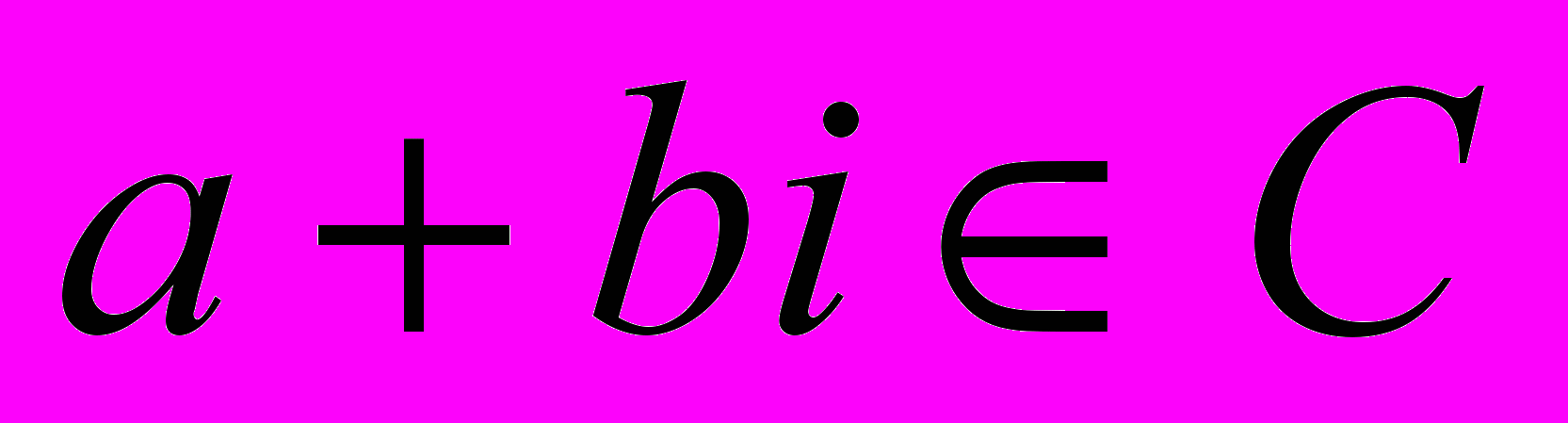 . Ці числа
. Ці числа  складові множини
складові множини  .
. Комплексним числом називається число вигляду
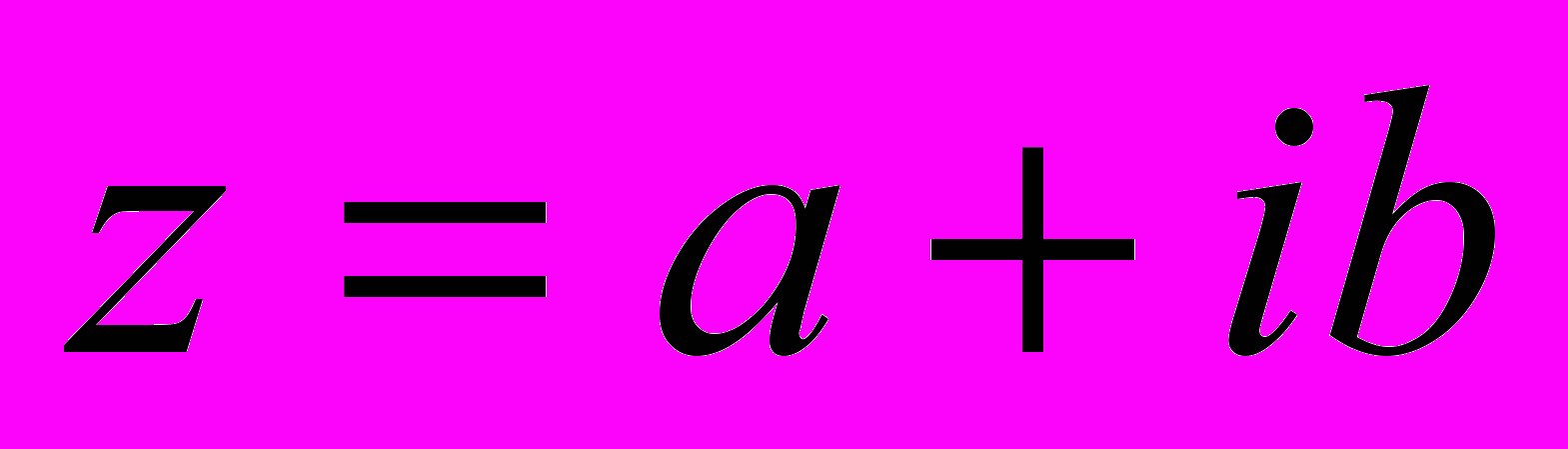 , де
, де 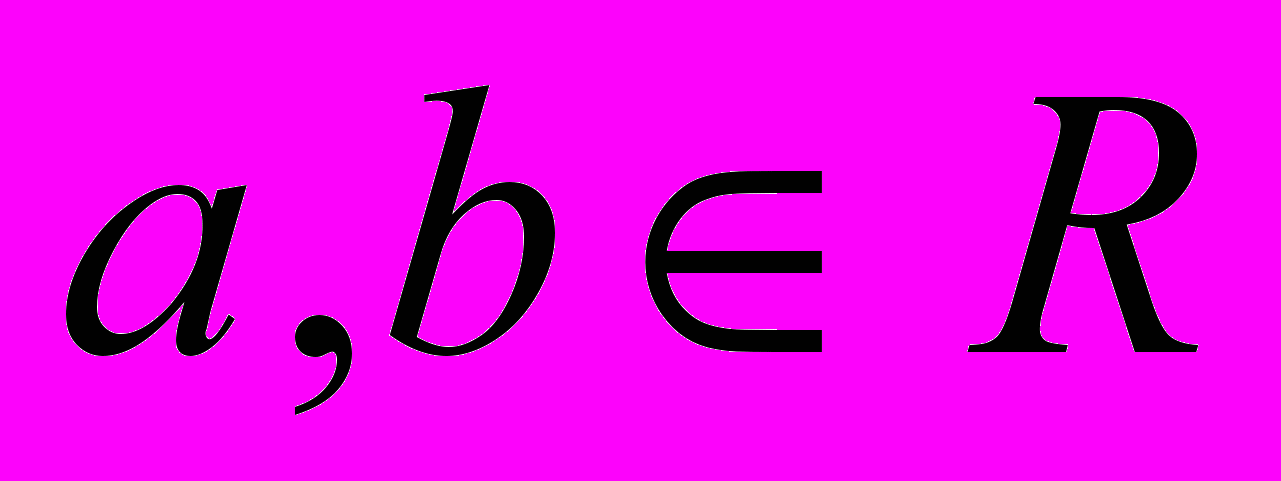 . Якщо
. Якщо 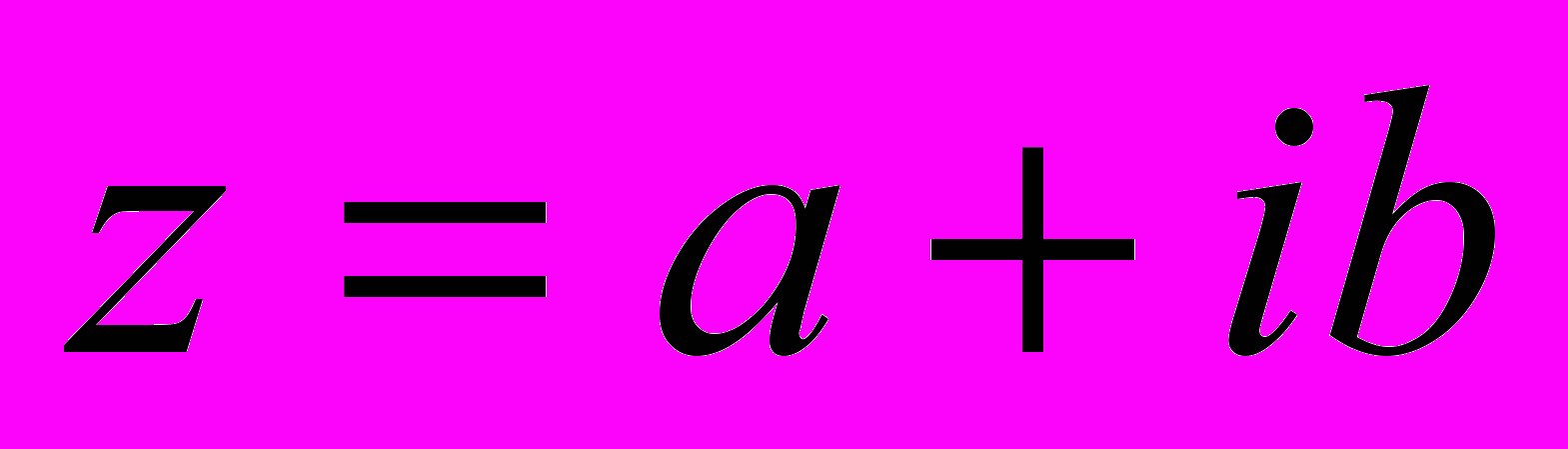 то
то  - дійсна частина
- дійсна частина  , а
, а 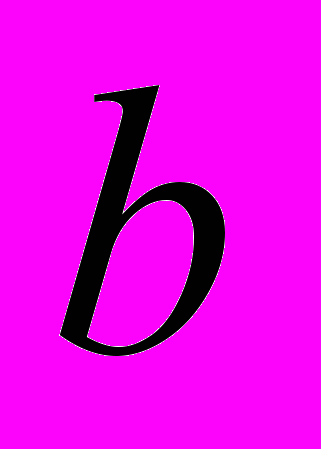 - уявна частина комплексного числа
- уявна частина комплексного числа  . Якщо
. Якщо 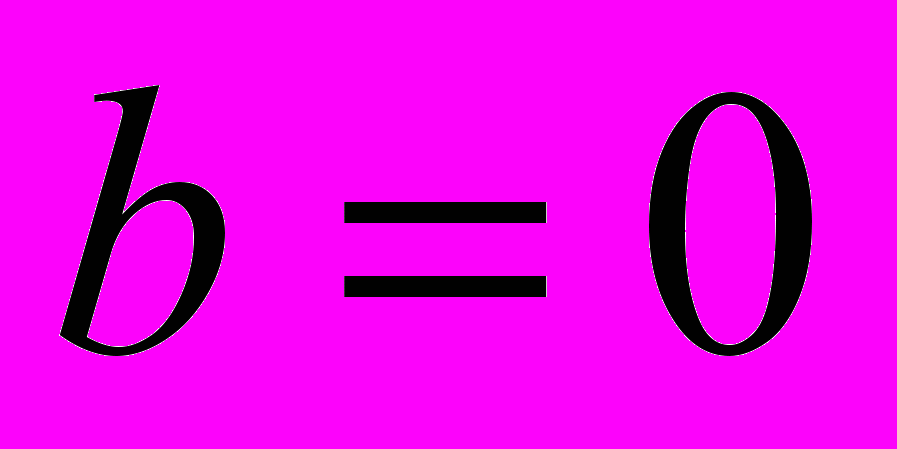 одержимо, що
одержимо, що  , дійсне число, якщо
, дійсне число, якщо 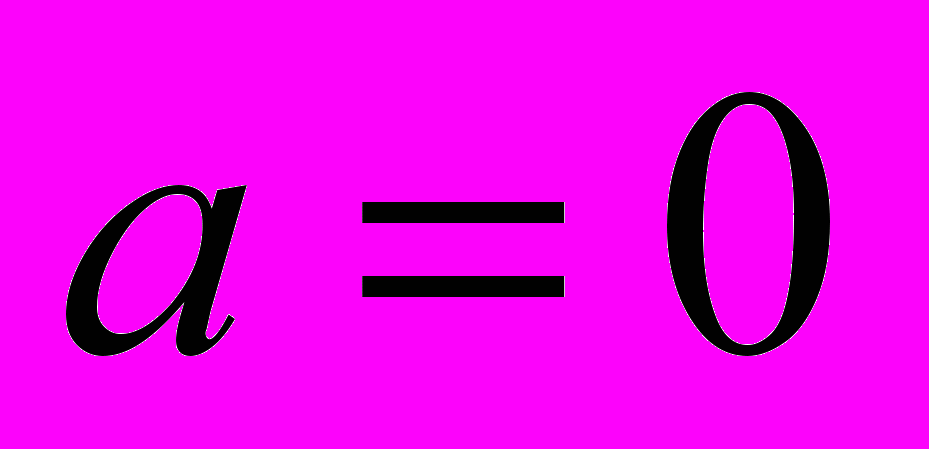 , то
, то 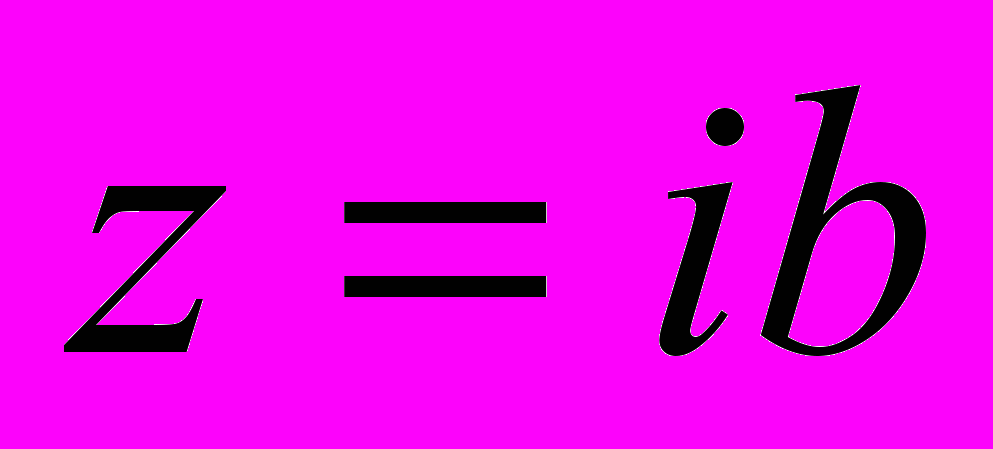 - чисто уявне комплексне число.
- чисто уявне комплексне число. Числа
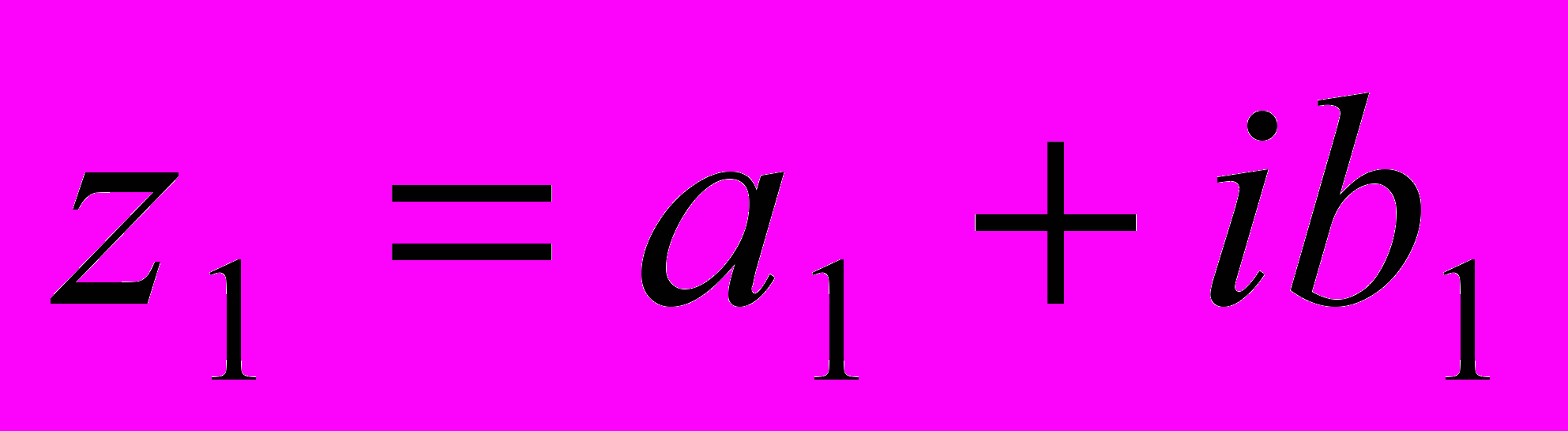 і
і 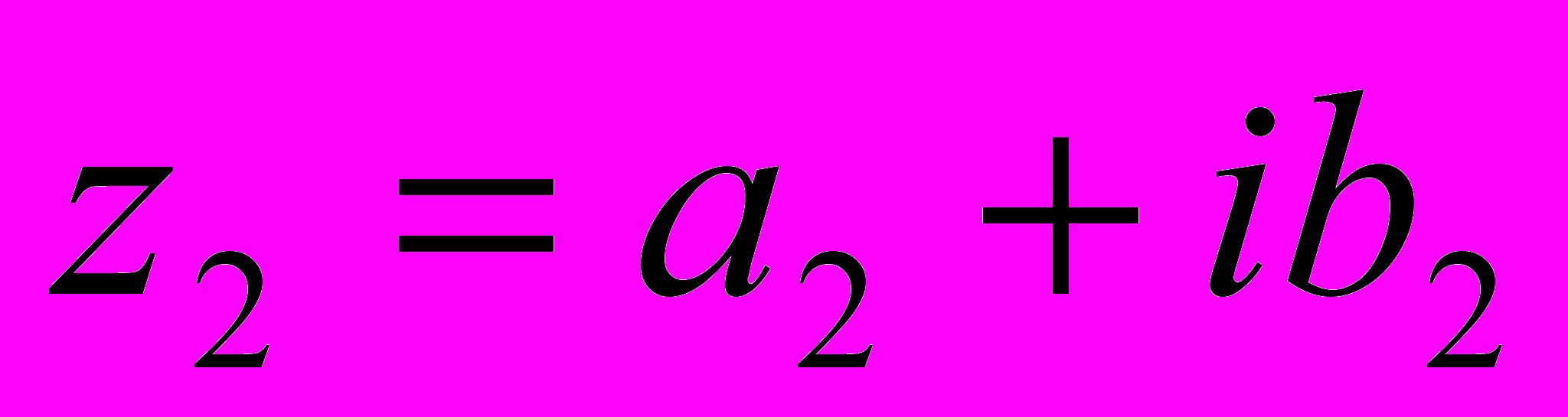 вважєють рівними якщо рівні їх дійсні та уявні частини, тобто
вважєють рівними якщо рівні їх дійсні та уявні частини, тобто 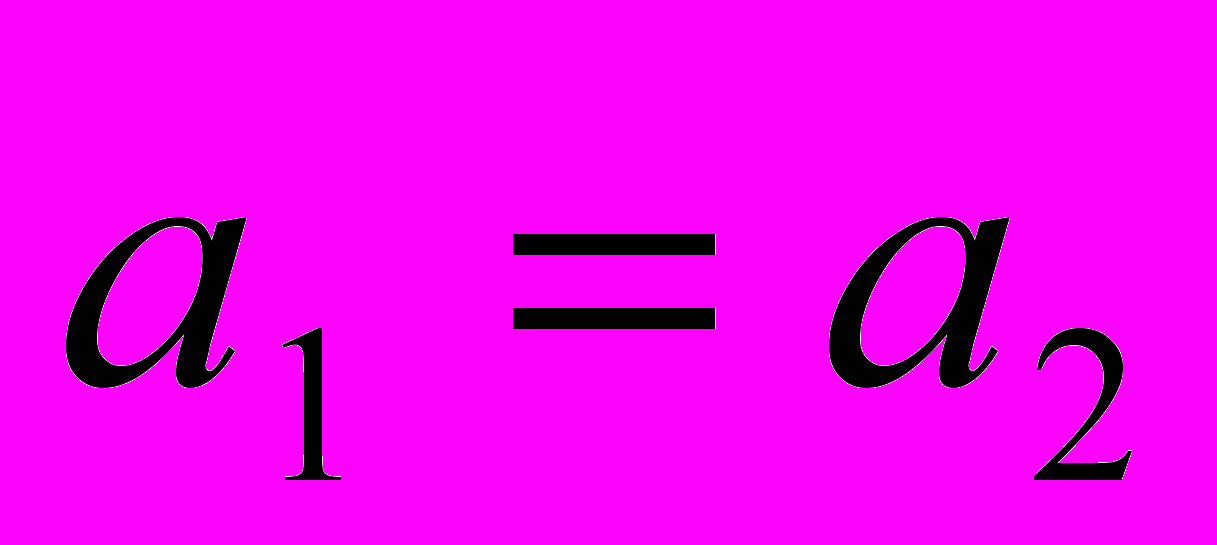 ,
, 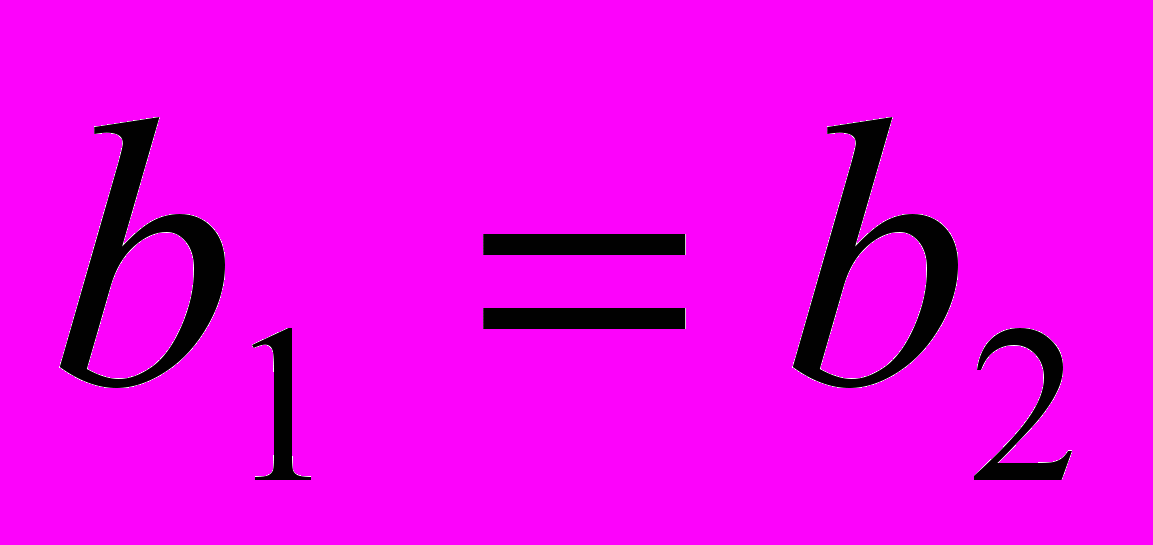 .
. Нехай
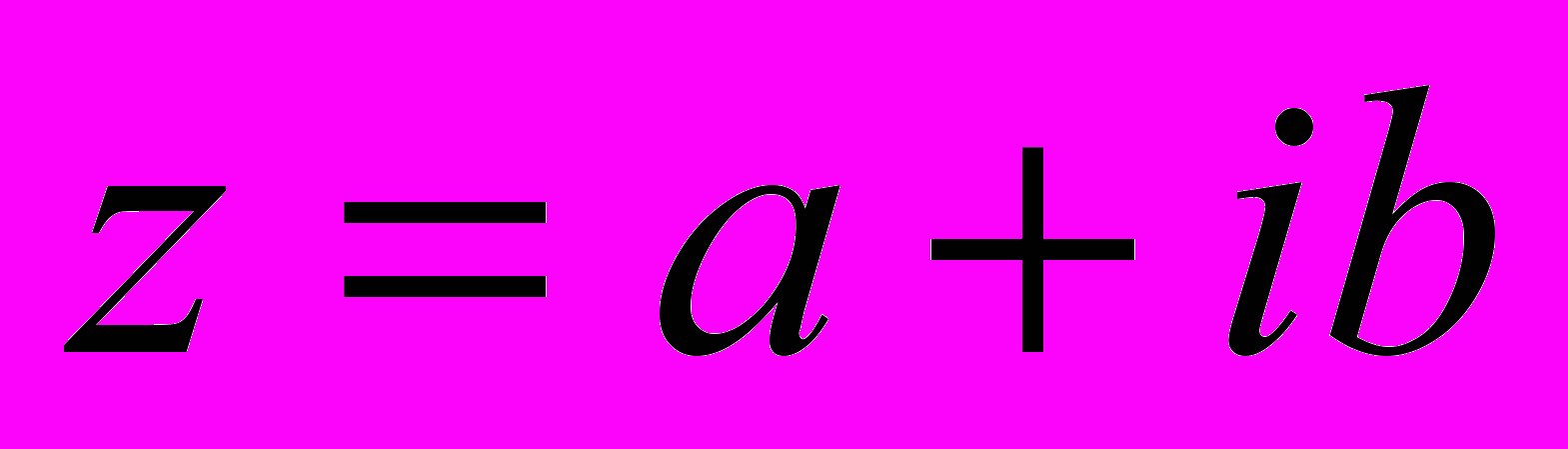 комплексне число, тоді комплексноспряженим до нього назвемо число
комплексне число, тоді комплексноспряженим до нього назвемо число 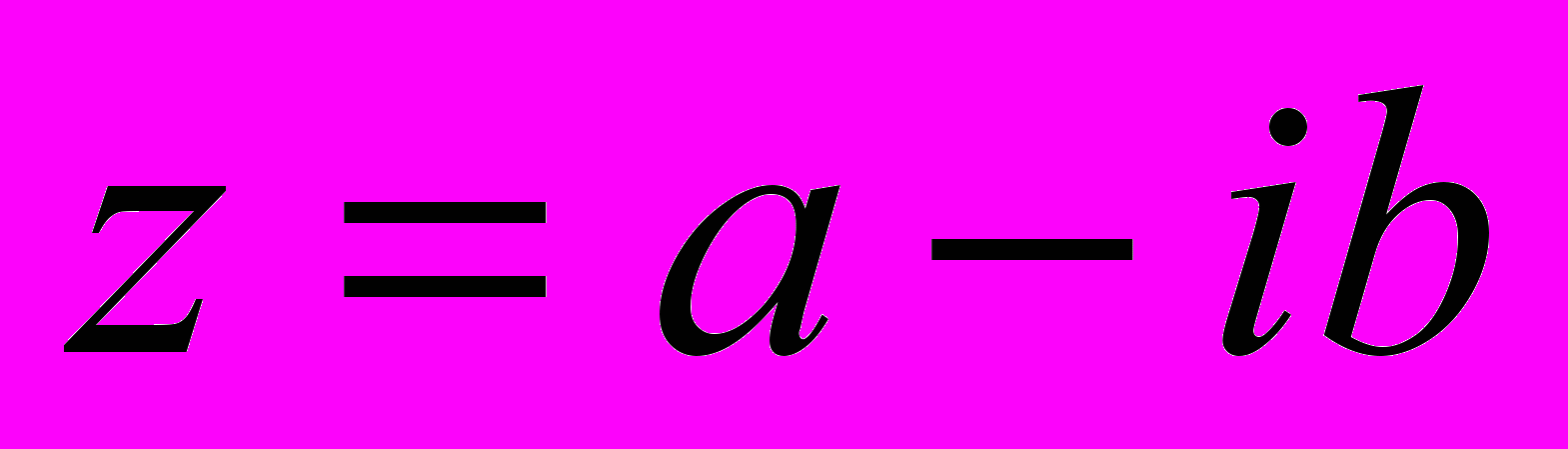 .
.
