Абрамкина Надежда Юрьевна Студентка 23 группы числовые последовательности реферат

Вид материала

Реферат

Содержание I. Числовые последовательности. 1.2 Способы задания числовых последовательностей. Развитие учения о прогрессиях. 3.1 Арифметическая прогрессия. 3.1.2 Понятие арифметической прогрессии. 3.1.3 Формула суммы n-первых членов арифметической прогрессии. 3.2 Геометрические прогрессии. 3.2.2 Понятие геометрической прогрессии. 3.2.3 Формула суммы n-первых членов геометрической прогрессии.

Подобный материал:

• План: Вступительное слово Шалашная В. М., преподаватель; Философские идеи П. Я. Чаадаева, 352.23kb.
• Филиппова Надежда Анатольевна, студентка 1 курса 02001 группы «электронный определитель, 34.3kb.
• Владимирова Наталья Анатольевна Студентка 23 группы уравнения и неравенства в школьном, 176.4kb.
• Реферат подготовила студентка 11 «И» группы Грицкевич, 344.24kb.
• Груздева Елена Юрьевна 08. 12. 2011 11: 30 14: 30 Каб. 217 «Банковские операции» Паутова, 18.59kb.
• Отчет по преддипломной практике студентка группы, 60.68kb.
• Шилокшина Софья Владимировна Студентка 4 курса 402 группы Специальность «Информатика», 337.33kb.
• Автор: Одинцова Надежда Юрьевна, воспитатель мдоу №27 г. Оренбурга Представлено: Колисниченко, 686.94kb.
• Студентка группы Б5-04Ю, 190.57kb.
• Задачи урока: обучающие : вывести формулы для вычисления суммы вклада по простому, 93.27kb.

управление образования и науки белгородской области


Валуйский педагогический колледж


Школьное отделение


Предметно-цикловая комиссия физико-математических дисциплин


Абрамкина Надежда Юрьевна

Студентка 23 группы


чИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ


РЕФЕРАТ

По специальности 05020152 – преподавание математики в основной школе


Квалификация – учитель математики основной школы


Научный руководитель:

Преподаватель

Е.И. Старокожева


Валуйки, 2007


Содержание.


Введение………………………………………………………………………3

1. Числовые последовательности.
   

1. Понятие числовых последовательностей……………………………….5
   

1.2 Способы задания числовых последовательностей……………………..6

II. Развитие учения о прогрессиях……………………………………………...7

III. Прогрессии.

2.1. Арифметические прогрессии

2.1.1. Арифметические прогрессии в древности………………………….9

2.1.2 Понятие арифметических прогрессий……………………………...11

2.1.3 Формула суммы n-первых членов арифметической прогрессии…13

2.2 Геометрические прогрессии.

2.2.1 Геометрические прогрессии в древности…………………………..14

2.2.2 Понятие геометрической прогрессии………………………………15

2.2.3 Формула суммы n-первых членов геометрической прогрессии….17

Заключение……………………………………………………………………..18

Список литературы……………………………………………………………..19


Введение.

В настоящее время числовые последовательности рассматриваются как частные случаи функции. Числовая после­довательность есть функция натурального аргумента. (Так, на­пример, арифметическая прогрессия является линейной функцией натурального аргумента, а геометрическая прогрессия — показа­тельной функцией натурального аргумента.)

Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:

1. 
   1, 2, 3, 4, 5, … - последовательность натуральных чисел.
   
2. 2, 4, 6, 8, 10,… - последовательность чётных чисел.
   
3. 1, 3, 5, 7, 9,… - последовательность нечётных чисел.
   
4. 1, 4, 9, 16, 25,… - последовательность квадратов натуральных чисел.
   
5. 2, 3, 5, 7, 11… - последовательность простых чисел.
   
6. 1, ½, 1 /3, ¼, 1 /5,… - последовательность чисел обратных натуральным.
   

Число членов каждого из этих рядов бесконечно; первые пять последовательностей — монотонно возрастающие, последняя — мо­нотонно убывающая. Все перечисленные последовательности, кроме 5-й, являются заданными ввиду того, что для каждой из них извес­тен общий член, т. е. правило получения члена с любым номером. Для последовательности простых чисел общий член неизвестен, однако еще в III в. до н. э. александрийский ученый Эратосфен указал способ (правда, очень громоздкий) получения n-го ее члена. Этот способ был назван «решетом Эратосфена».

Идея предела последовательности восходит к V—IV вв. до н. э. Прогрессии — частные виды числовых последовательностей — встречаются в памятниках II тысячелетия до н. э.

В своей работе я попытаюсь рассмотреть основные понятия, связанные с числовыми последовательностями, их применение на практике. Расскажу о возникновении термина «прогрессия», (откуда он пошёл, что обозначал), о развитии учения о прогрессиях и т.д.


^ I. Числовые последовательности.

1. Понятие числовых последовательностей.
   

Числовая последовательность – это занумерованное числовое множество.

Будем выписывать в порядке возрастания положительные чётные числа. Первое такое число равно 2, второе – 4, третье – 6, четвёртое – 8 и т.д. таким образом мы получим последовательность:

2; 4; 6; 8; 10 ….

Очевидно, что на пятом месте в этой последовательности будет число 10, на десятом число – 20, на сотом число – 200. вообще для любого натурального числа n можно указать соответствующее ему положительное чётное число; оно равно 2n.

Рассмотрим ещё одну последовательность. Будем выписывать в порядке убывания правильные дроби с числителем, равным 1:

; ; ; ; ; … .

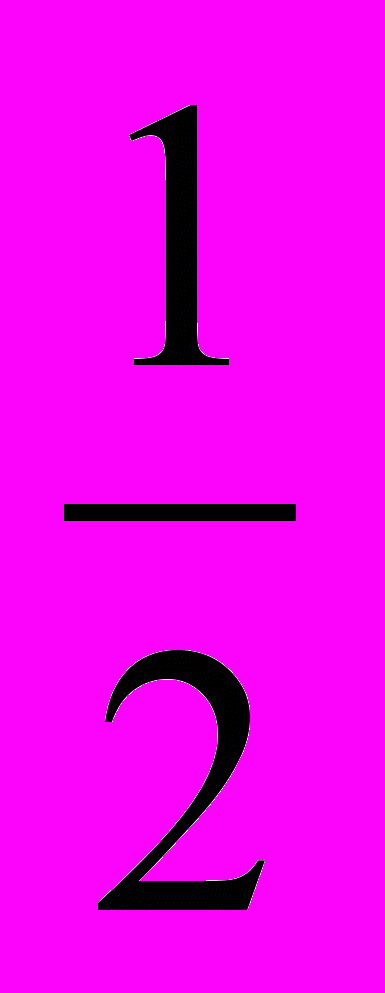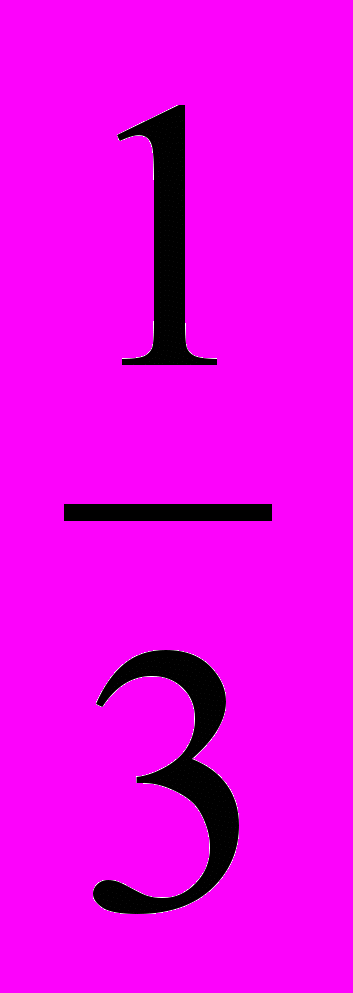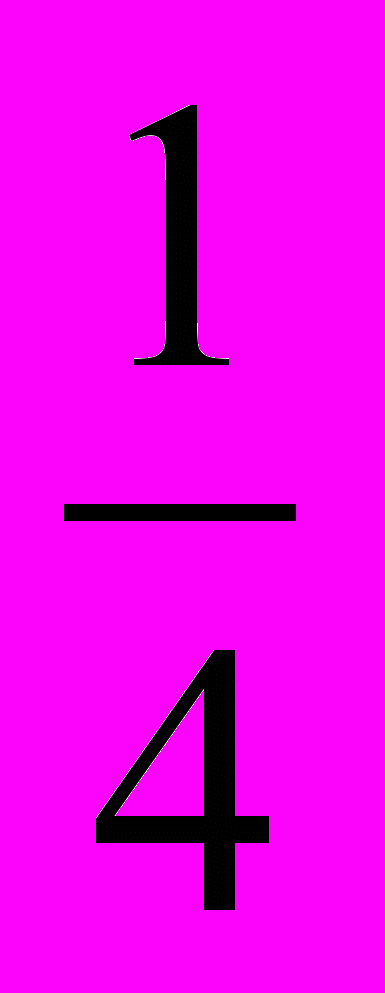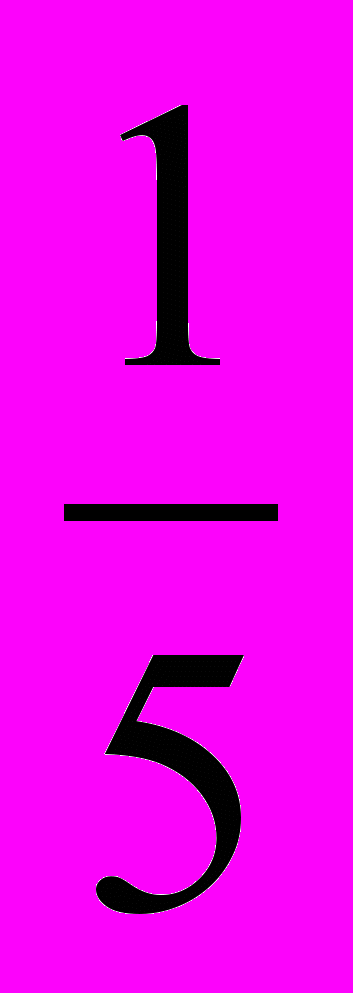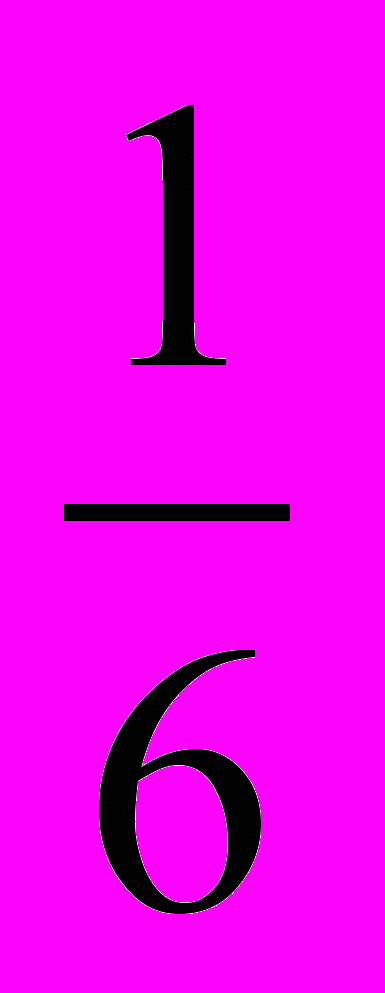Для любого натурального числа n мы можем указать соответствующую ему дробь; она равна 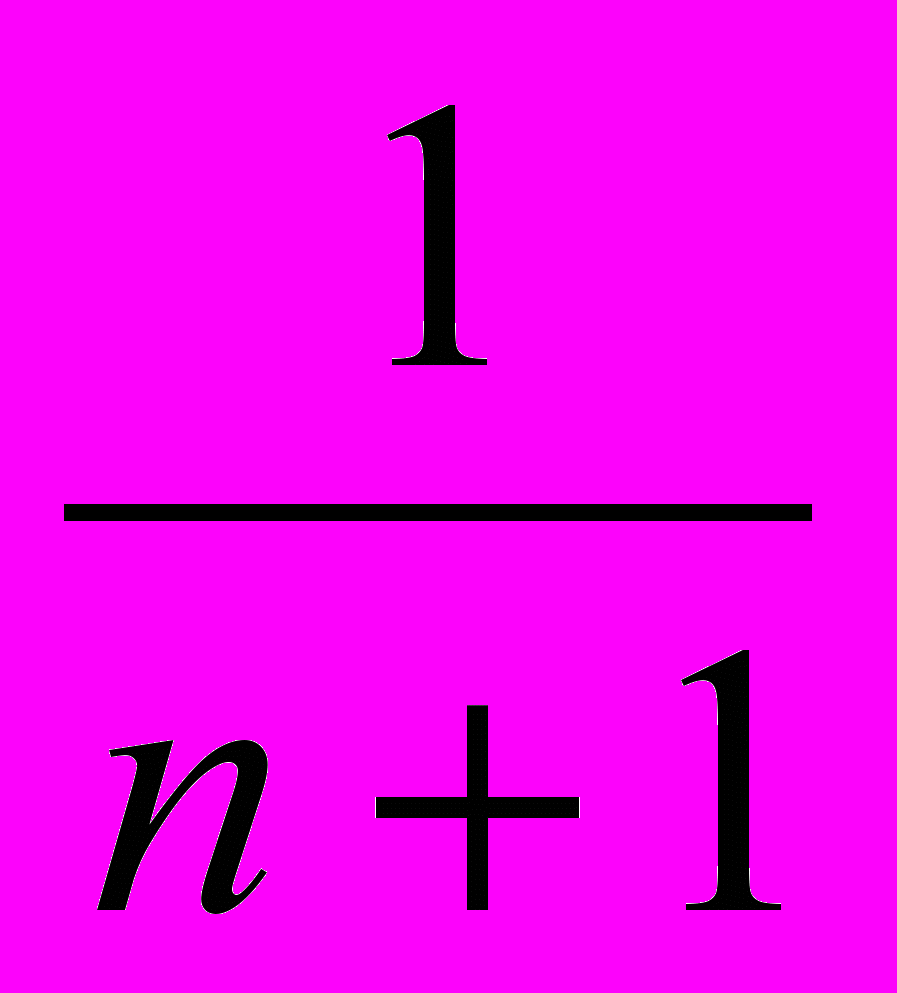. Так, на шестом месте должна стоять дробь 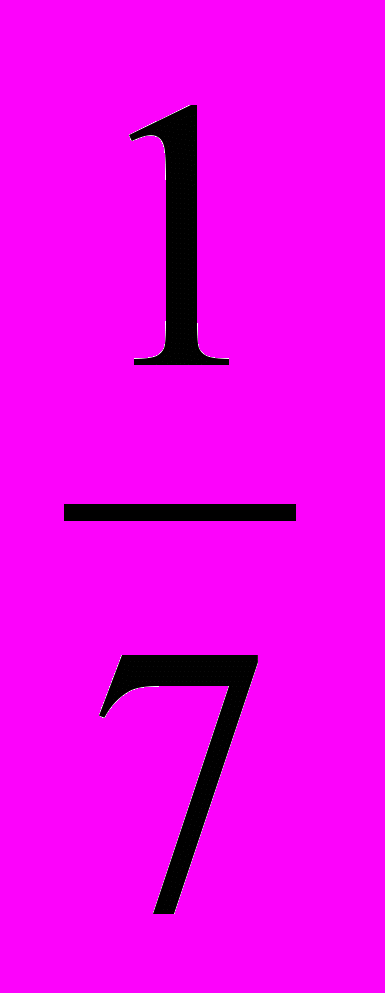, на тридцатом - 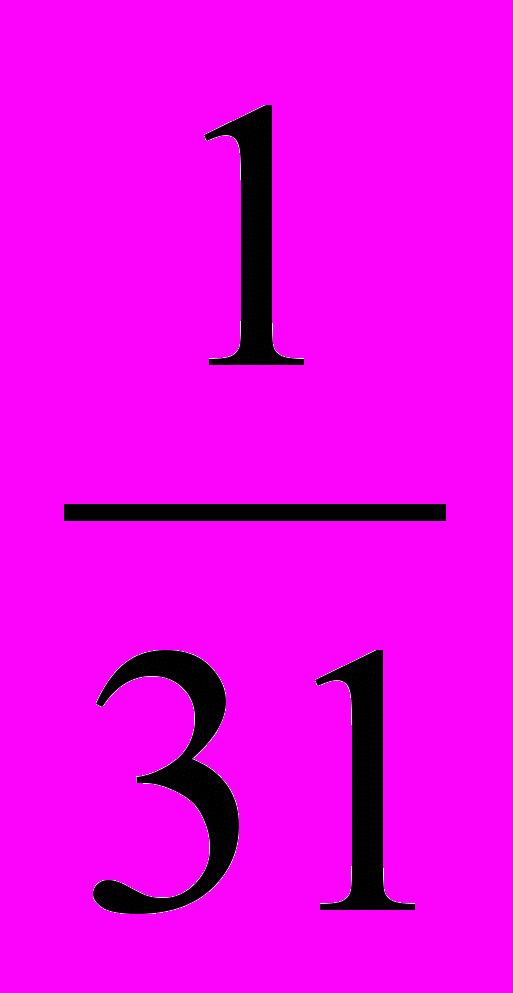, на тысячном – дробь .

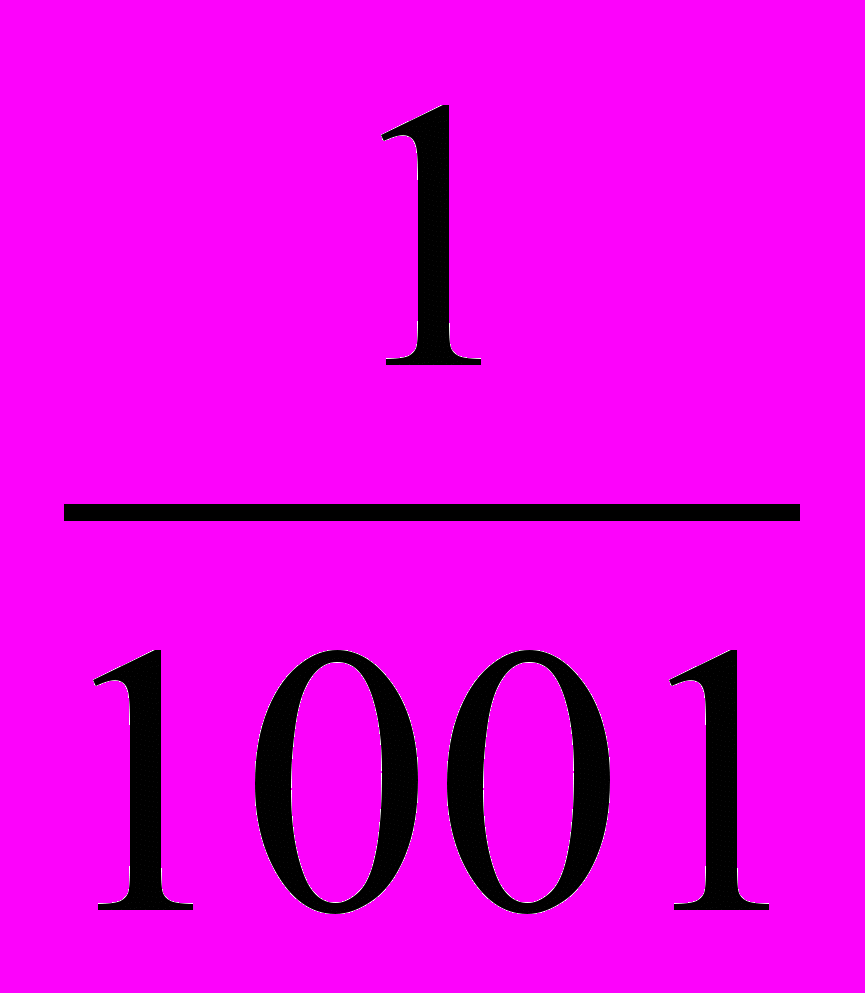Числа образующие последовательность, называют соответственно первым, вторым, третьим, четвёртым и т.д. членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена.

Например: 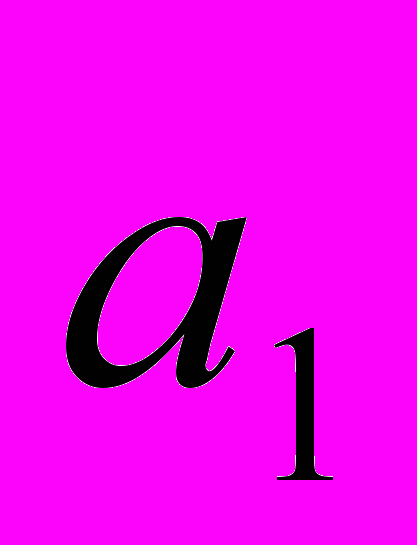, , 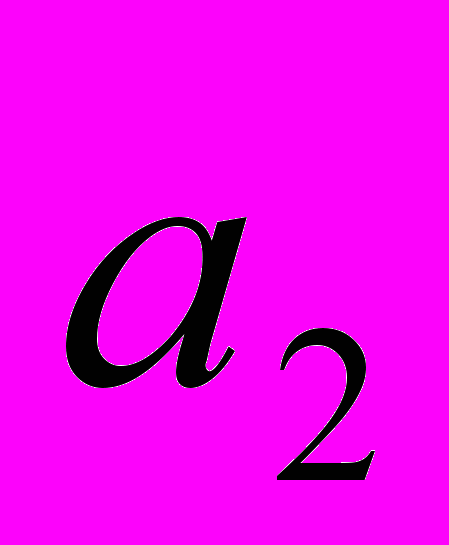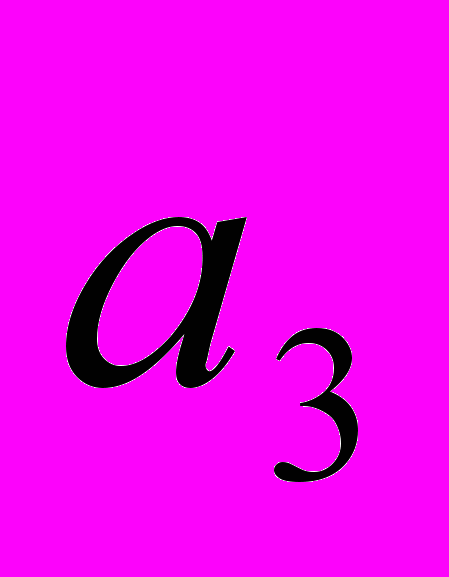и т.д. вообще член последовательности с номером n, или, как говорят, n-й член последовательности, обозначают 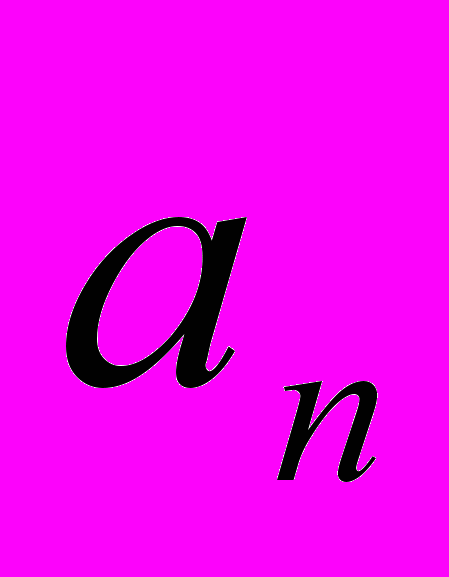. Саму же последовательность обозначают ().

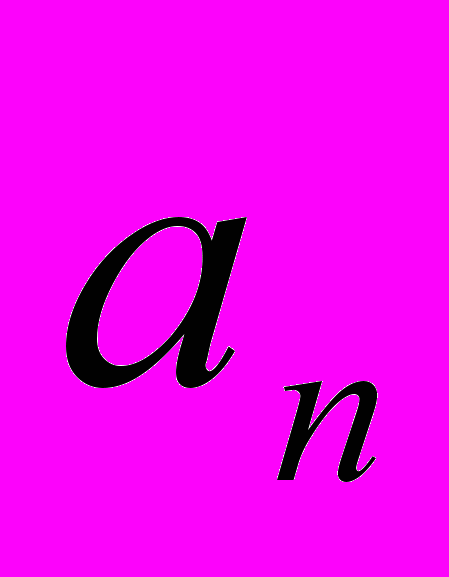Последовательность может содержать, как бесконечное число членов, так и конечное. В этом случае её называют конечной.

Например: последовательность двухзначных чисел.

10; 11; 12; 13; …; 98; 99


^ 1.2 Способы задания числовых последовательностей.


Последовательности можно задавать несколькими способами. Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.

Наиболее часто последовательность задают с помощью формулы n-го члена последовательности.

Например: последовательность положительных чётных членов 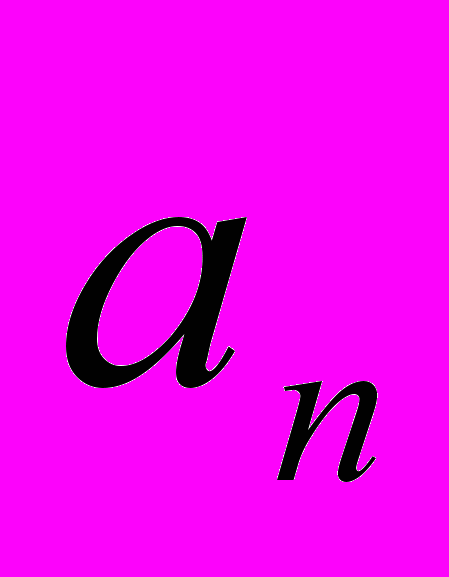=2n.

Последовательность правильных дробей: =.

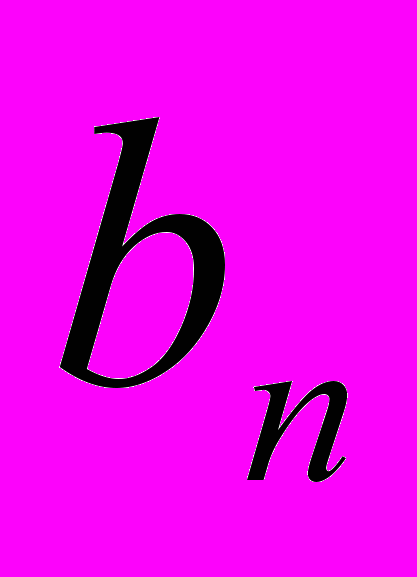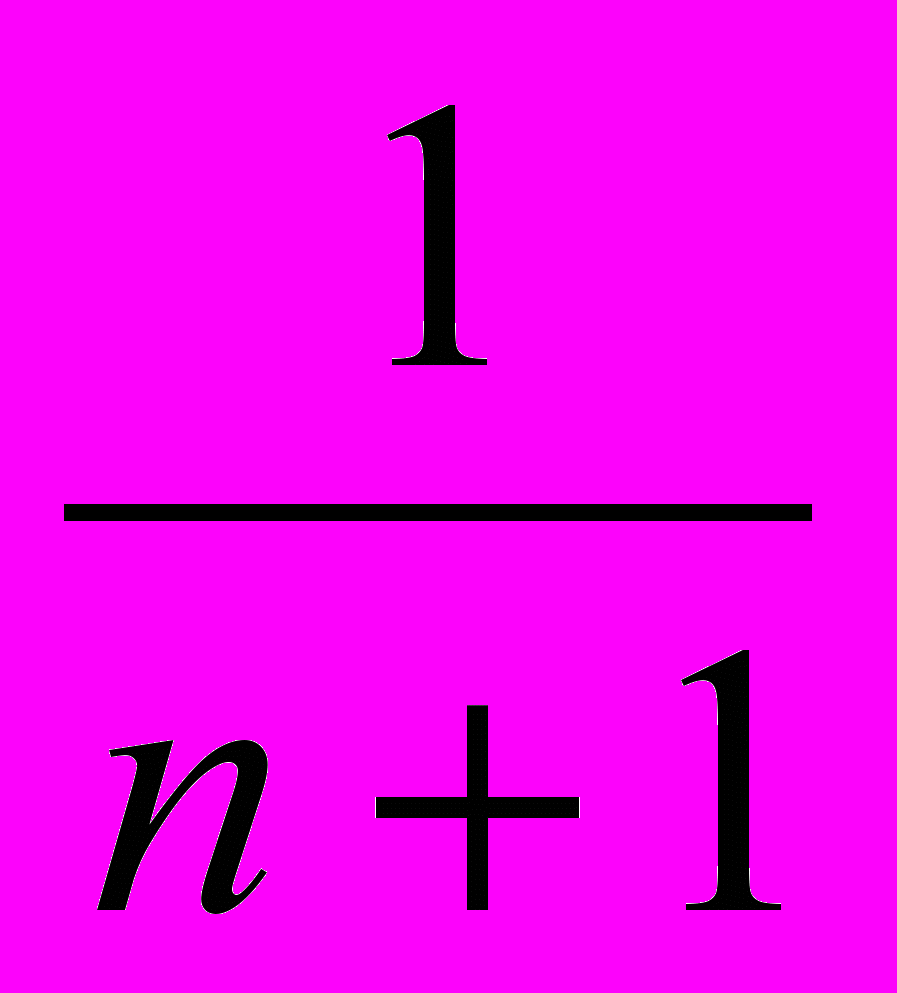Рассмотрим ещё один пример: пусть последовательность задана формулой: 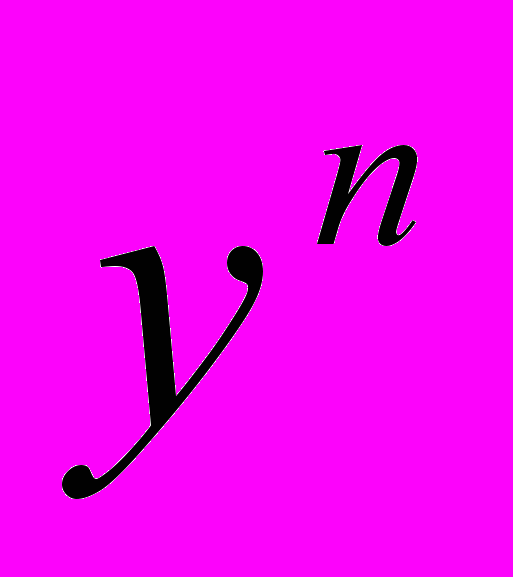=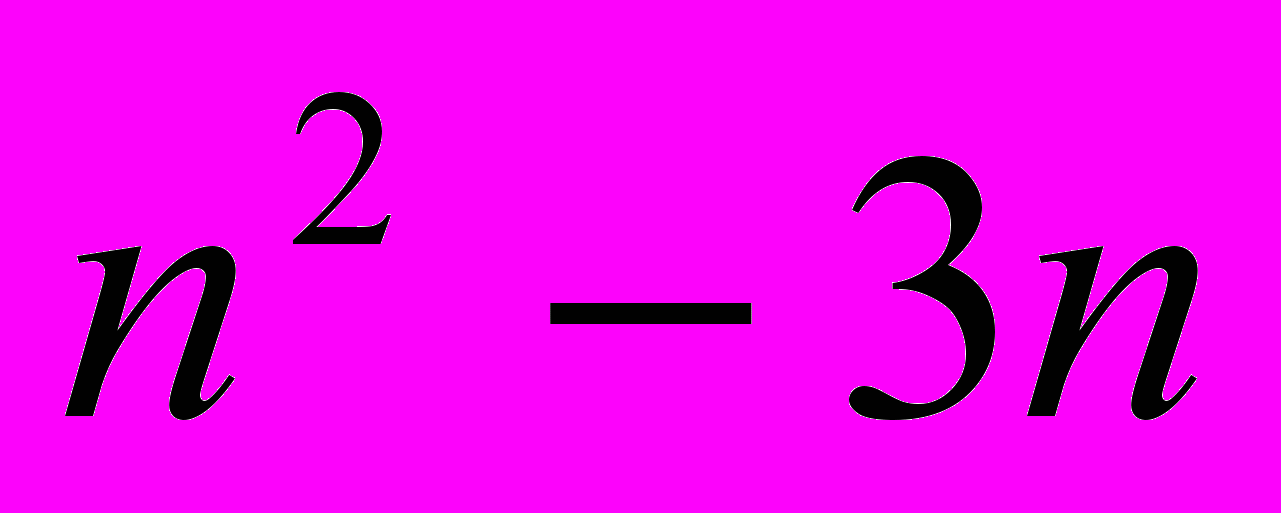. Подставляем вместо n натуральные числа 1, 2, 3, 4, 5, и т.д., получаем:

…

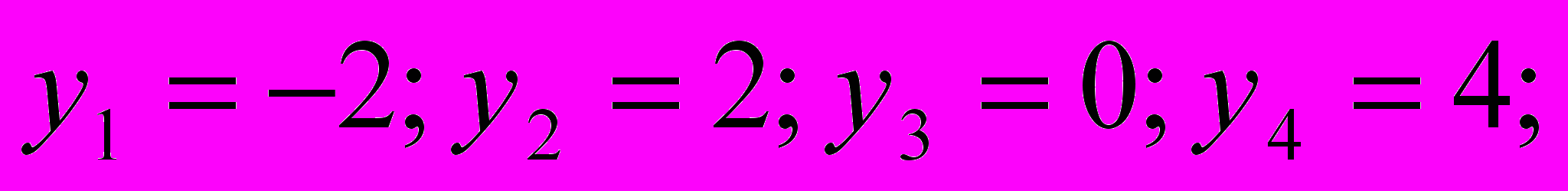Рассмотрим ещё один способ задания последовательности.

Пример: Пусть первый член последовательности (а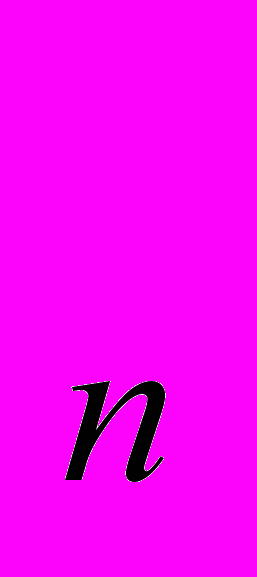) равен 10, а каждый следующий равен квадрату предыдущего, т.е. а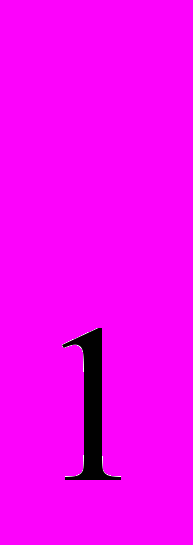=10, а=.

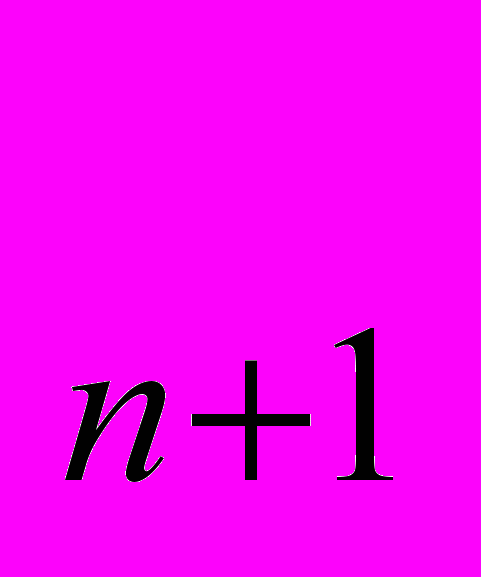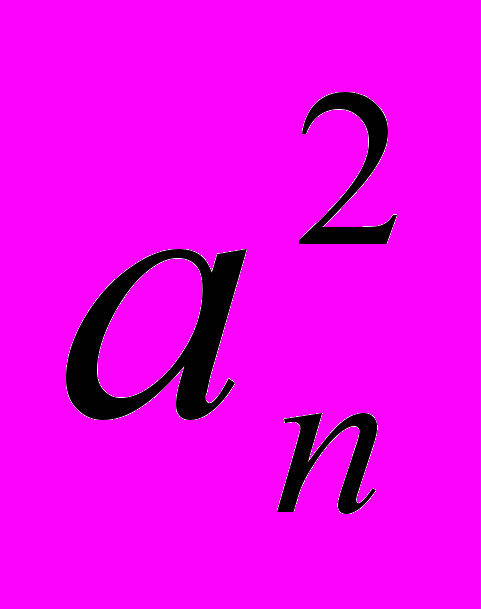С помощью формулы а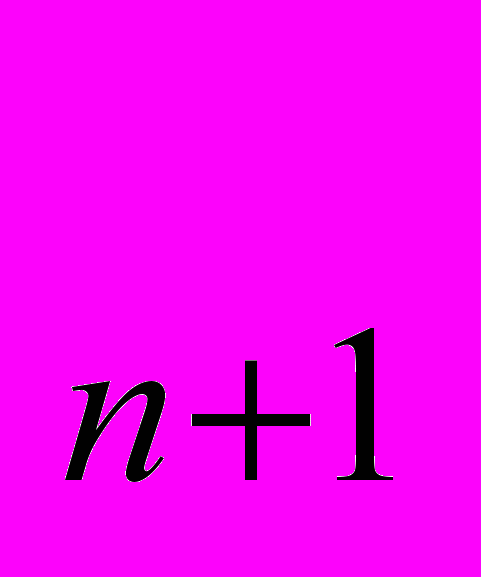= 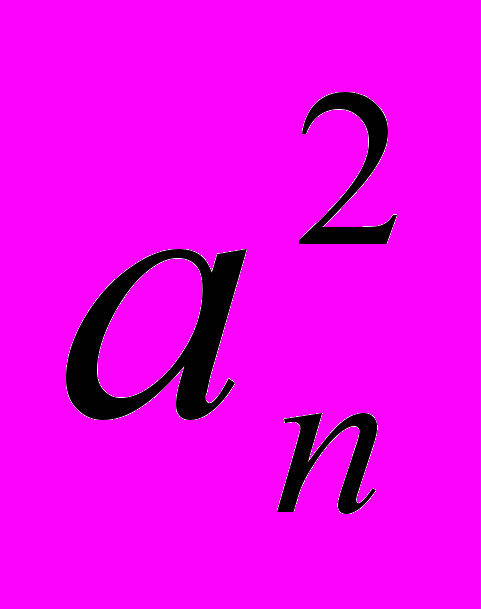можно по известному первому члену вычислить второй, затем третий и т.д.

Формулу выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro – возвращаться).

Так же числовую последовательность можно задать простым перечислением её членов.


^ Развитие учения о прогрессиях.


Слово прогрессия латинского происхождения (progressio), буквально означает «движение вперёд» (как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VIвв.), первоначально под прогрессией понимали всякую числовую последовательность, построенную по закону, позволяющему неограниченно продолжать её в одном направлении, например последовательность натуральных чисел, их квадратов и кубов. В конце средних веков и в начале нового времени этот термин перестаёт быть общеупотребительным. В XVII веке, например, Дж. Грегори употребляет вместо прогрессии термин «ряд», а другой видный английский математик, Дж. Валлис, применяет для бесконечных рядов термин «бесконечные прогрессии».

В настоящее время мы рассматриваем прогрессии как частные случаи числовых последовательностей.

Возможно, что древние вавилоняне и другие народы той далёкой эпохи имели некоторые общие приёмы решения задач, которые дошли до нас. Однако об этих приёмах мало что известно.

Теоретические сведения связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции.

Уже в V в. до н.э. греки знали следующие прогрессии и их суммы:

1. 
   1+2+3+…+n= ,
   
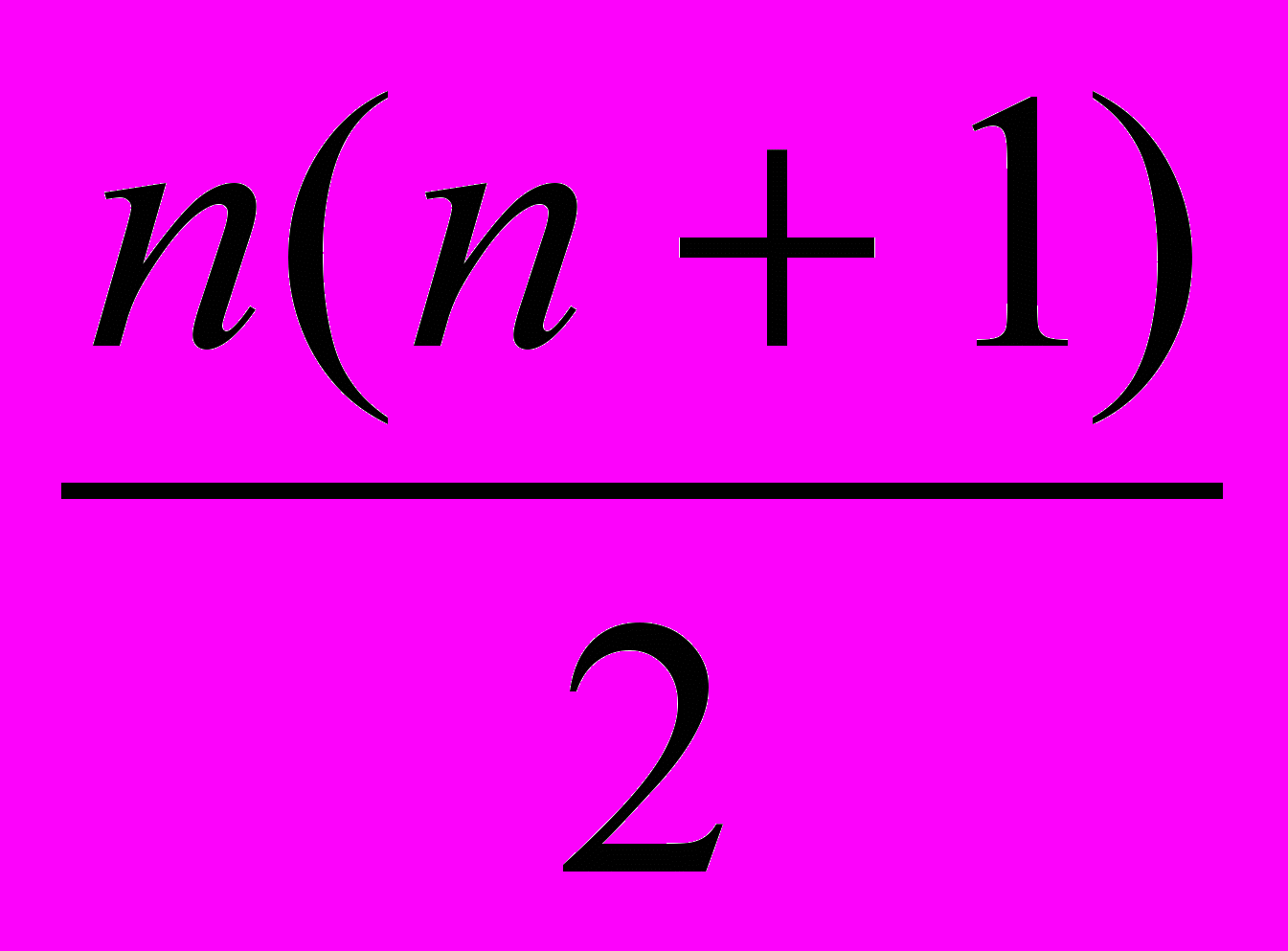2. 2+4+6+…+2n=n(n+1),
   
3. 1+3+6+…+(2n+1)=(n+1)² и др.
   

В «Псаммите» Архимед впервые сопоставляет арифметическую и геометрическую прогрессии:

1,2,3,4,5,………………..

10,10²,10³,10⁴,10⁵,………….

И указывает на связь между ними, например:

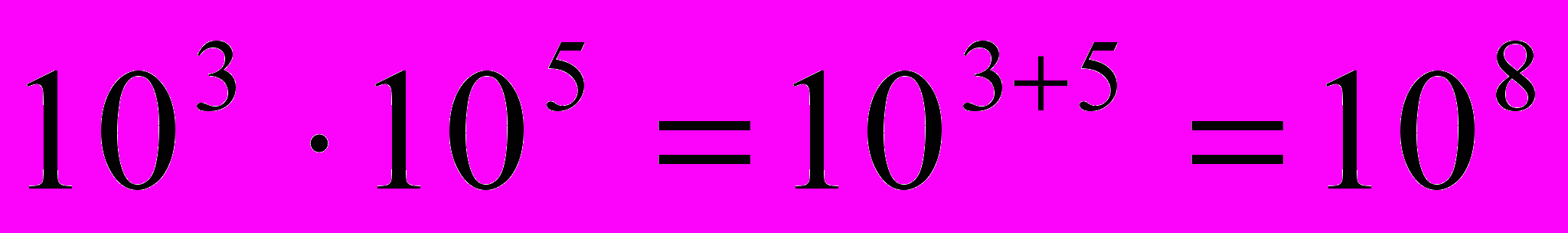, т.е. для умножения двух членов геометрической прогрессии достаточно сложить соответствующие члены арифметической прогрессии и взять полученную сумму в качестве показателя 10.

У греков теория геометрических прогрессий была связана с так называемой непрерывной геометрической пропорцией:

a:b = b:a, в котором числа a, b, c образуют геометрическую прогрессию со знаменателем .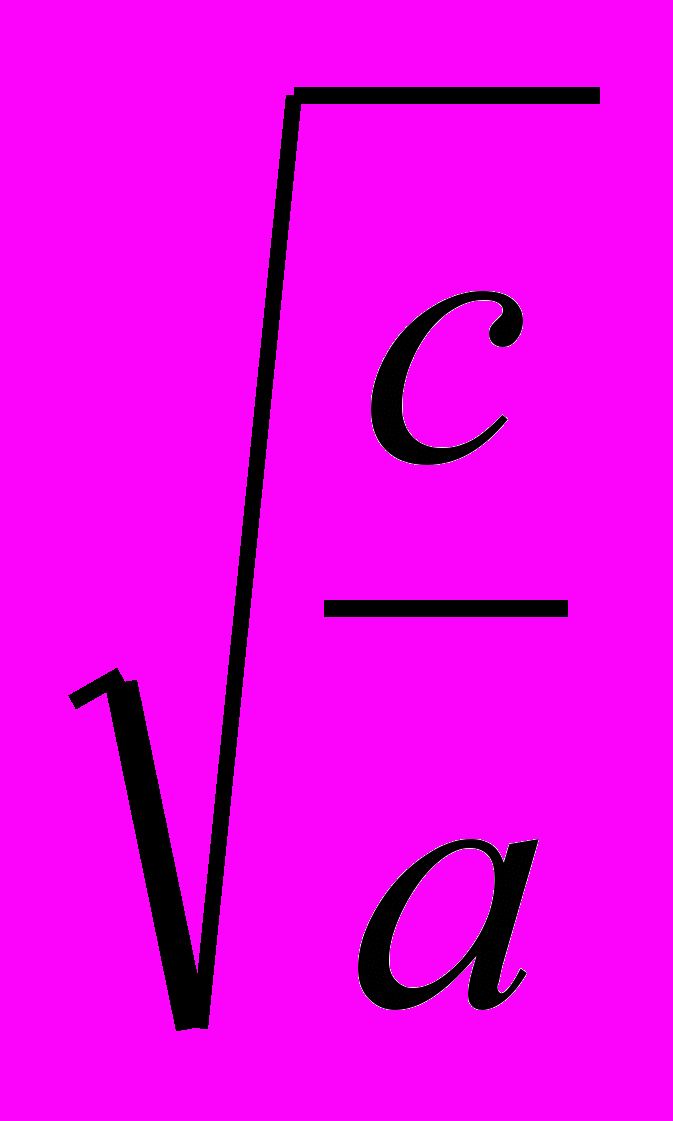

Прогрессии рассматривались как бы продолжением пропорций, вот почему эпитеты арифметическая и геометрическая были перенесены от пропорций к прогрессиям.

Такой взгляд на прогрессии сохранился и у многих математиков XVII и даже XVIIIв. Именно так следует объяснить тот факт, что символ встречающийся у Барроу, а затем и у других английских учёных того времени для обозначения непрерывной геометрической пропорции, стал обозначать в английских и французских учебниках XVIII века геометрическую прогрессию. По аналогии так стали обозначать и арифметическую прогрессию.

В «Началах» Евклида есть теорема, которая по существу эквивалентна знакомой нам формуле суммы геометрической прогрессии:

S_n = (lq-a)/q-1

Одно из доказательств Архимеда, изложенное в его произведении «Квадратура параболы», сводится опять таки по существу к суммированию бесконечно убывающей геометрической прогрессии.


Для решения некоторых задач из геометрии и механики Архимед вывел формулу суммы квадратов натуральных чисел, хотя её пользовались и до него.

1² + 2² +3² + ... + n² = 1/6n(n+1)(2n+1)

Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским учёным. Так, Ариабхатта (Vв.) знал формулы для общего члена, суммы арифметической прогрессии и др., Магавира (IXв) пользовался формулой: 1² + 2² +3² + ... + n² = 1/6n(n+1)(2n+1). И другими более сложными рядами. Однако правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в «Книге абака» (1202) Леонардо Пизанского. В «Науке о числах» (1484) Н. Шюке, как и Архимед, сопоставляет арифметическую прогрессию с геометрической и даёт общее правило для суммирования любой бесконечно малой убывающей геометрической прогрессии. Формула для суммирования бесконечно убывающей прогрессии была известна П. Ферма и другим математикам XVII века.


III Прогрессии.

^ 3.1 Арифметическая прогрессия.


3.1.1 Арифметические прогрессии в древности.

В клинописных табличках вавилонян, как и в египетских па­пирусах, относящихся ко II тысячелетию до н.э., встречаются при­меры арифметических и геометрических прогрессий.

Вот одна вавилонская задача, в которой используется ариф­метическая прогрессия.

Задача: «10 братьев, 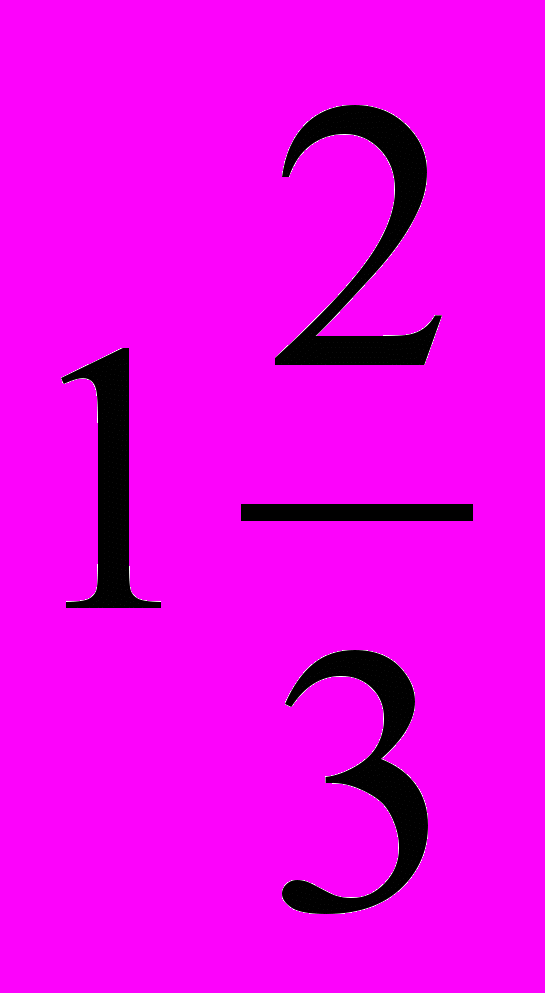мины серебра. Брат над братом поднимается, на сколько поднимается, не знаю. Доля восьмого 6 шекелей. Брат над братом — на сколько он выше?»

Итак, 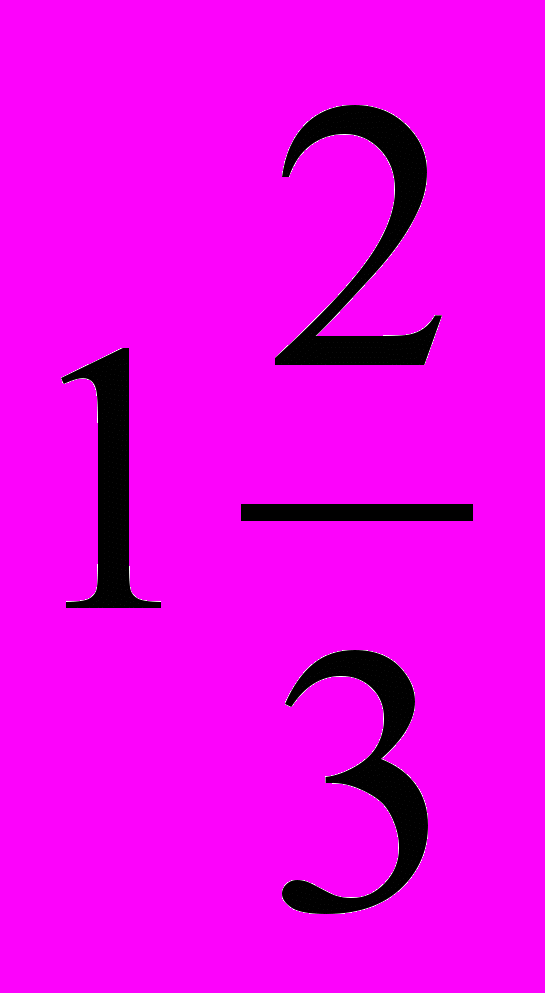мины (мина равна 60 шекелям) серебра требуется разделить между 10 братьями так, чтобы доли братьев составляли арифметическую прогрессию. Требуется найти разность прогрес­сии, зная, что восьмой брат получает б шекелей.

Вавилонский автор, не имевший в своем распоряжении ни сов­ременной символики, ни готовых формул, вынужден придержи­ваться строго арифметических рассуждений. Идея его решения следующая. Он начинает с нахождения средней арифметической (средней доли), деля 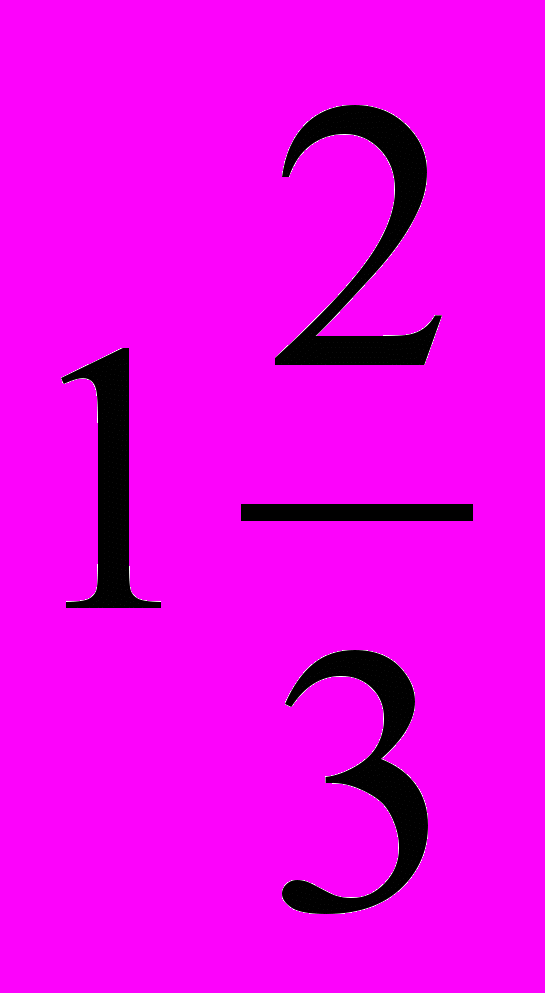мины на 10 и получая 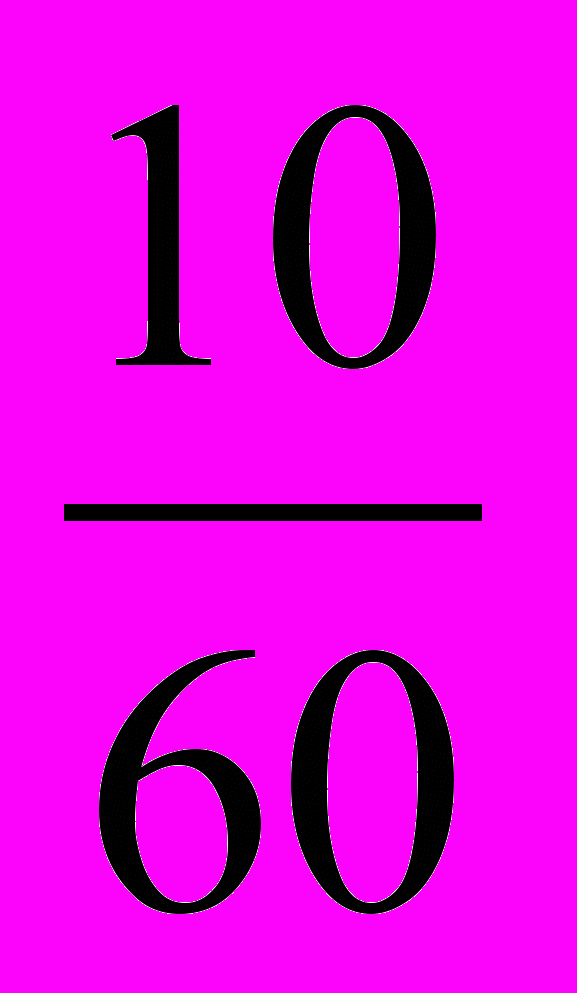мины, ее умножает затем на два. Итак, удвоенная средняя доля есть 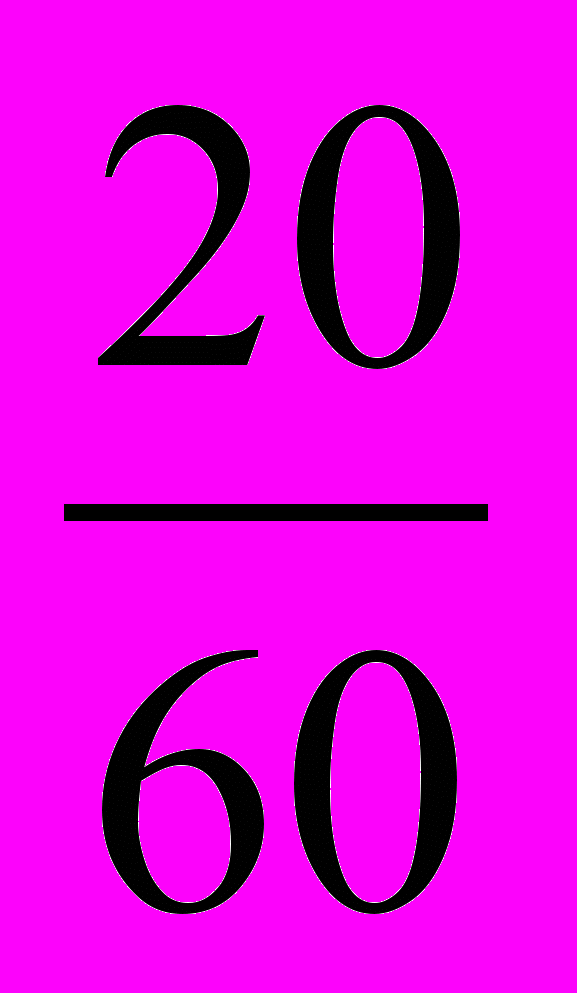мины. Это и есть сумма долей третьего и восьмого братьев, имея в виду, что первого от третьего, как и восьмого от десятого отделяют 2 ступени (интервала). Третьего же от восьмого отделяют 5 ступеней, а разность между их долями составляет 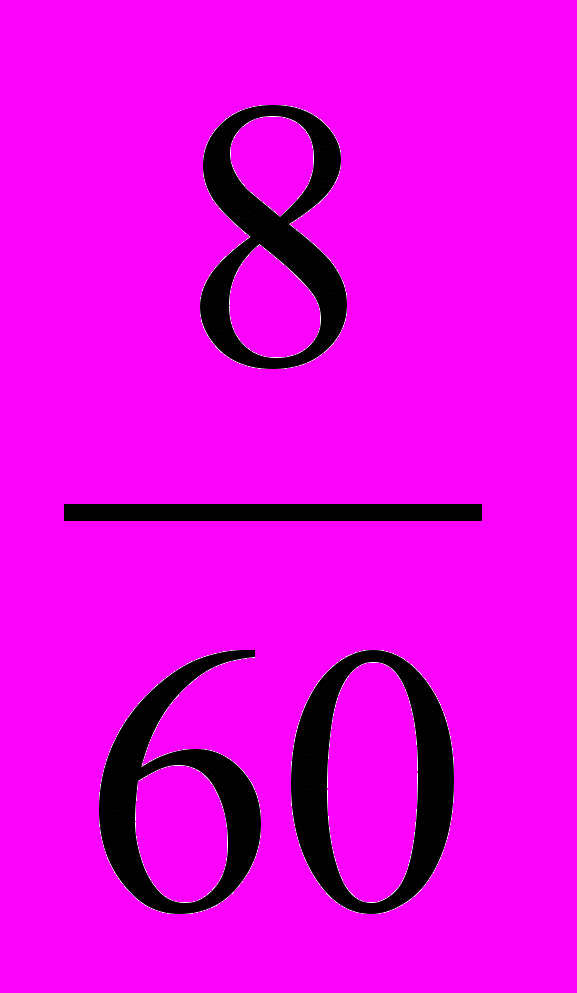мины. Отсюда

и находится значение одной ступени, т. е. разность прогрессии,

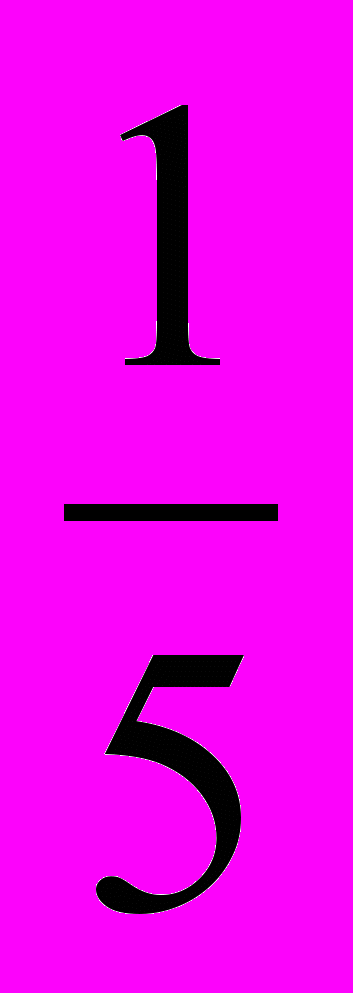от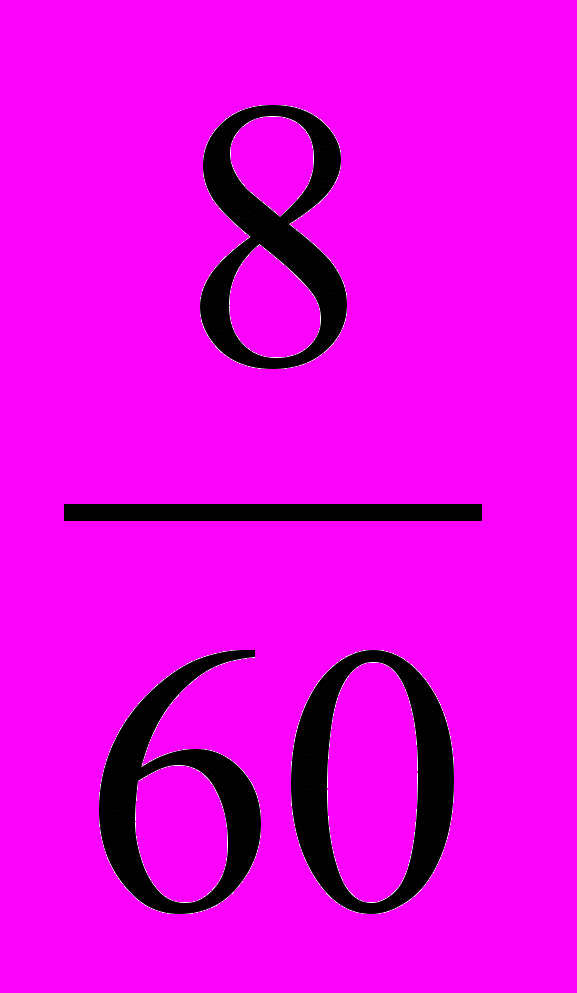 мины, или 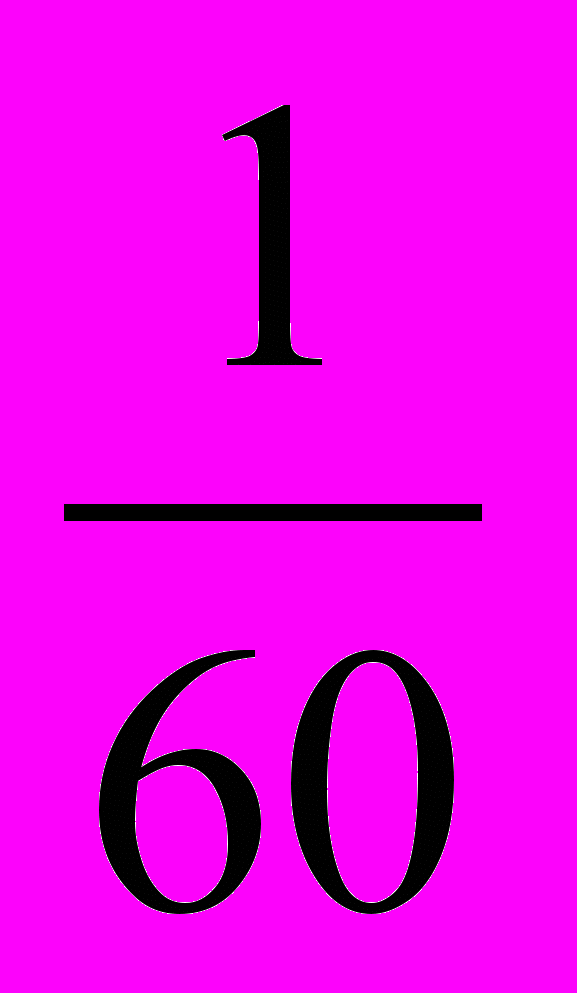+ 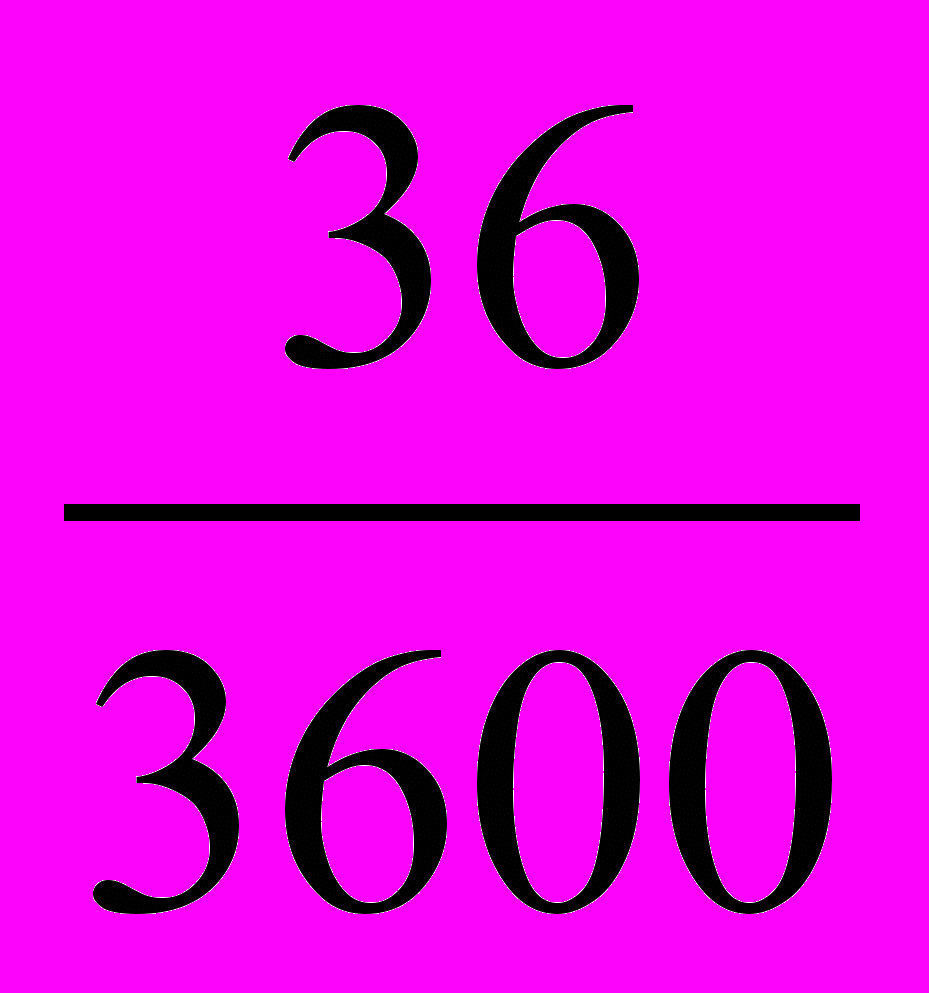мины.

А вот египетская задача из папируса Ахмеса.

Задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками, разность же между каждым человеком и его соседом равна 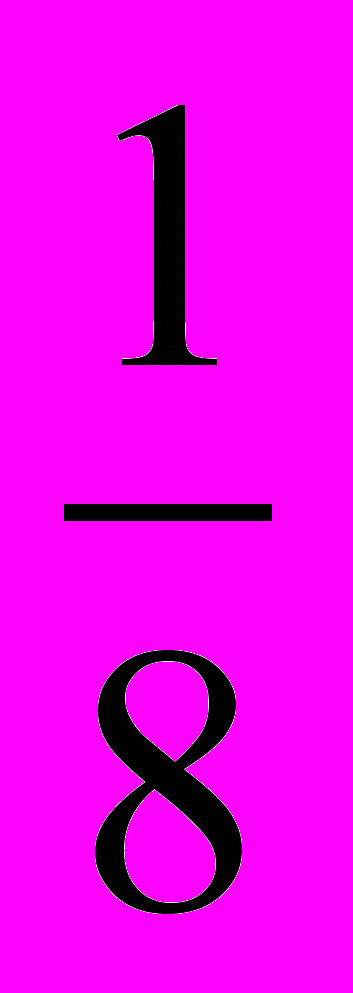меры».

При решении этой и других аналогичных задач египтяне, ви­димо, пользовались правилом, которое можно записать в совре­еной символике так:

.

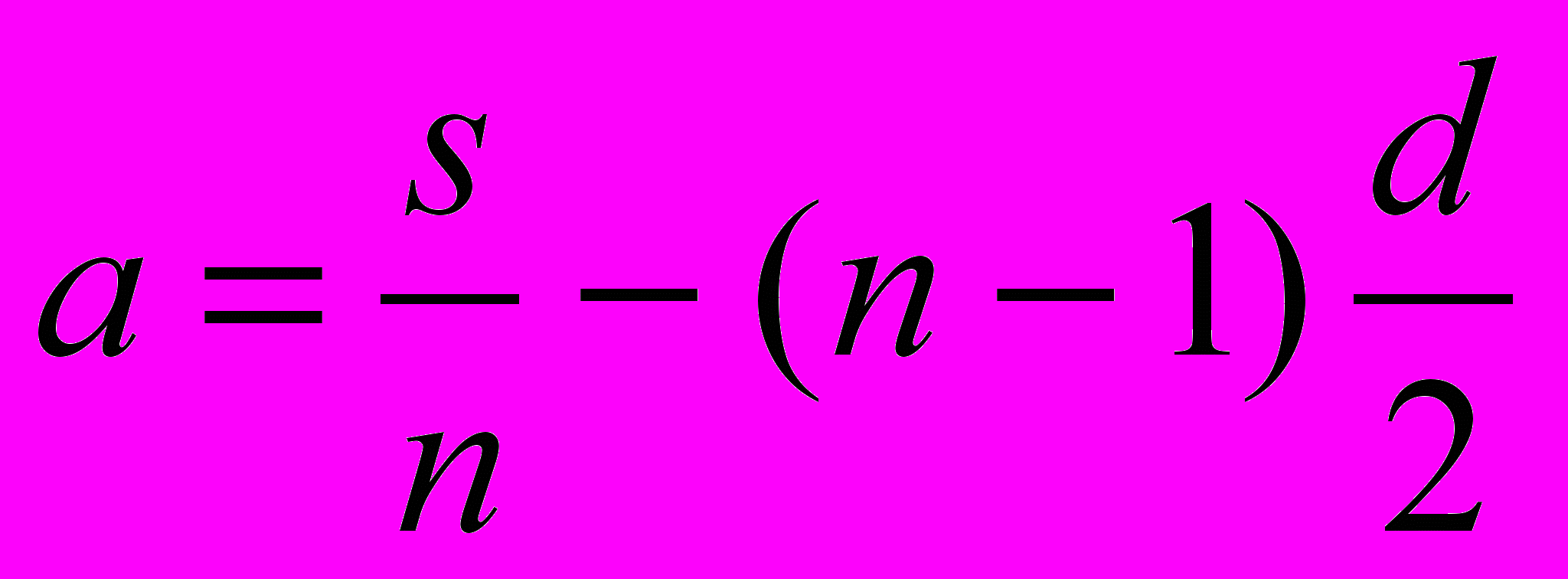Оно эквивалентно нашей формуле.

.

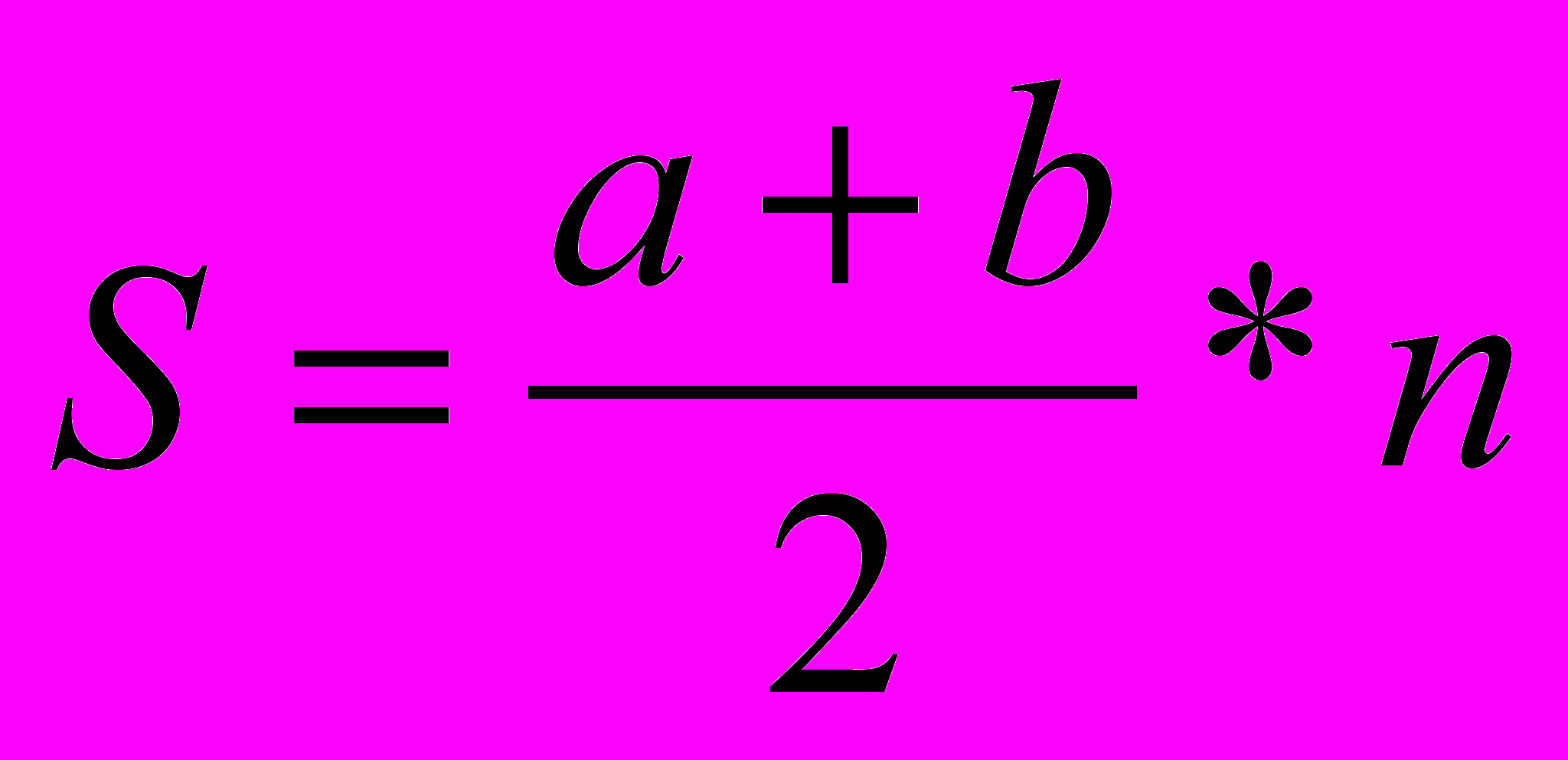Происхождение этого правила не установлено: оно, вероятно, эмпирического характера.

Задачи на арифметические (и геометрические) прогрессии имеется и в древнекитайском тракте «Математика в девяти книгах», в котором нет, однако, указаний на применение какой-либо формулы суммирования.

Первые из дошедших до нас задач на прогрессии связаны с запросами хозяйственной жизни и общественной практики, как, например, распределение продуктов, деление наследства и т.д.


^ 3.1.2 Понятие арифметической прогрессии.


Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

Рассмотрим последовательность натуральных чисел, которые при делении на четыре дают в остатке 1:

1; 5; 9; 13; 17; 21 …

Каждый её член, начиная со второго, получается прибавлением к предыдущему члену числа 4. эта последовательность является примером арифметической прогрессии.

Иначе говоря, последовательность () – арифметическая прогрессия, если для любого натурального n выполняется условие.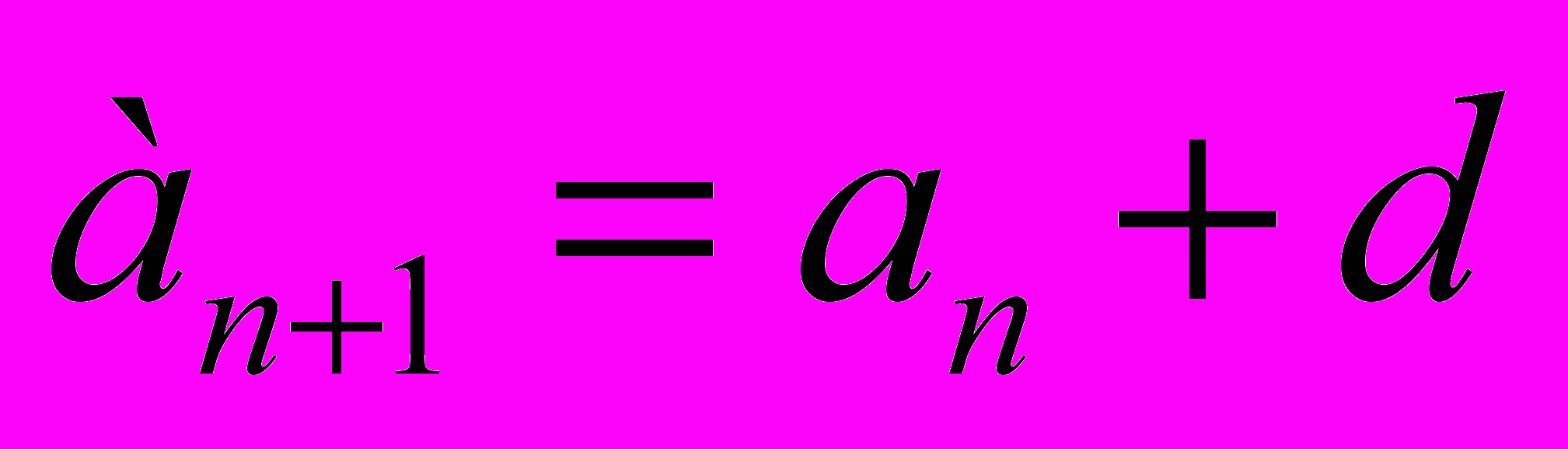

, где d некоторое число.

Из определения арифметической прогрессии следует, что разность между любым её членом, начиная со второго, и предыдущим членом равна d, т.е. при любом натуральном n верно равенство

.

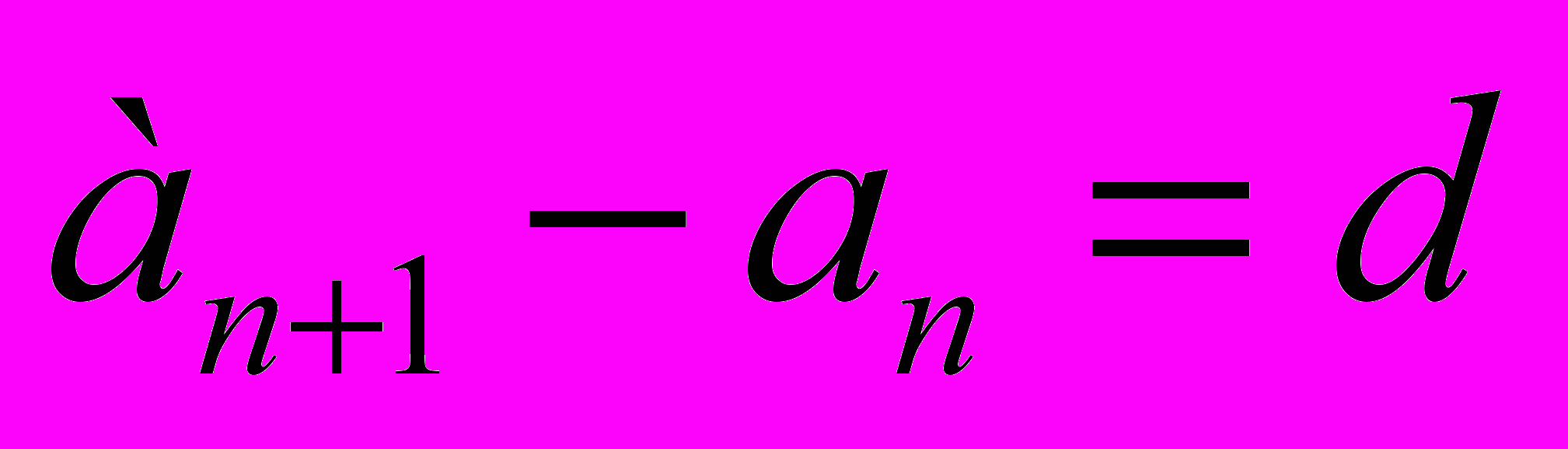Число d называют разностью арифметической прогрессии.

Чтобы задать арифметическую прогрессию достаточно указать её первый член и разность.

Например: если а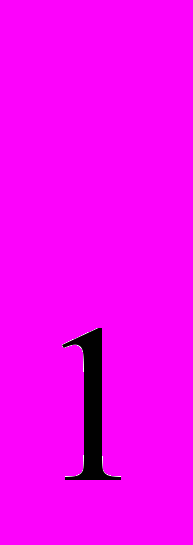=1 и d=1, то получим арифметическую прогрессию

1; 2; 3; 4; 5; …,

члены которой – последовательные натуральные числа.

Если разность арифметической прогрессии – положительное число, то такая прогрессия является возрастающей; если это отрицательное число, то такая прогрессия называется убывающей. Если разность арифметической прогрессии равна нулю, то все её члены равны между собой и прогрессия является постоянной последовательностью.

Зная первый член и разность арифметической прогрессии, можно найти любой её член, вычисляя последовательно второй, третий, четвёртый и т.д. члены. Однако для нахождения члена прогрессии с большим номером такой способ не удобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.

По определению арифметической прогрессии:



,



.

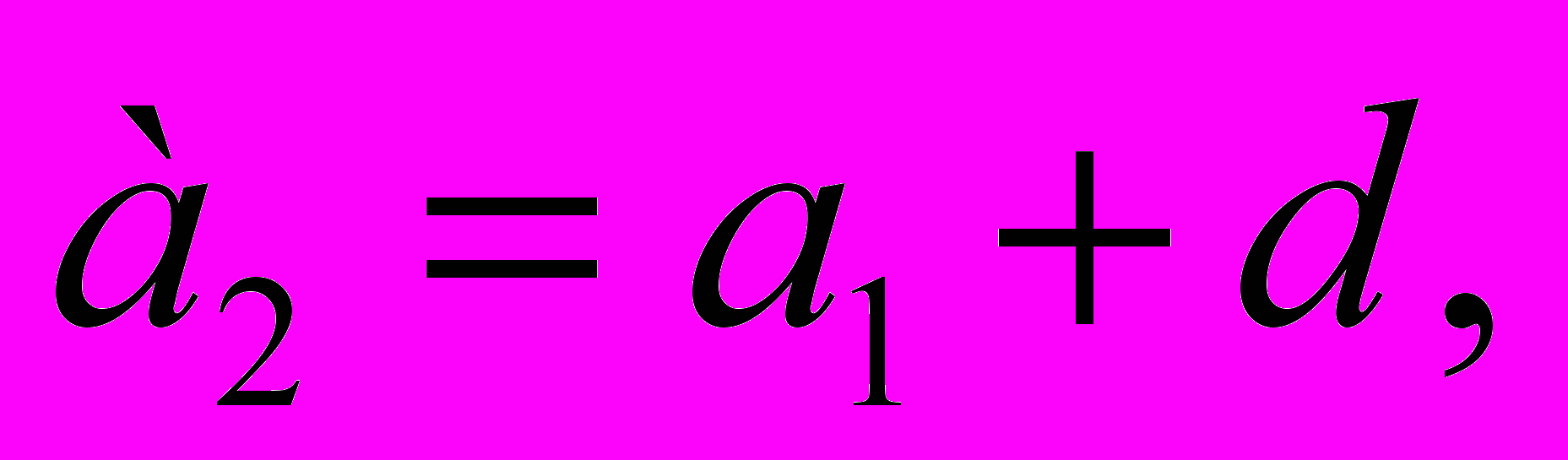
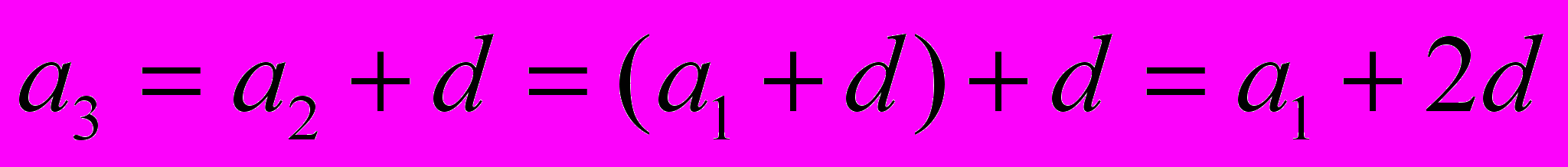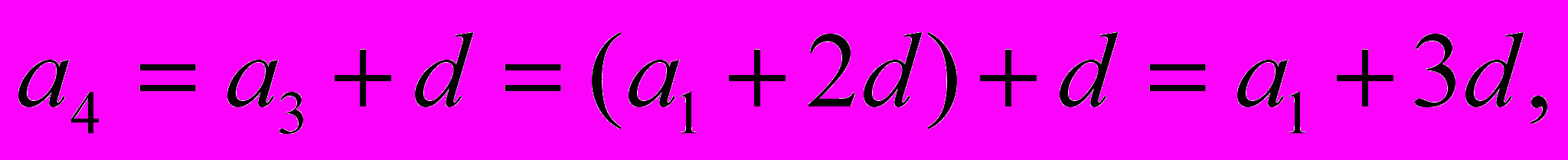
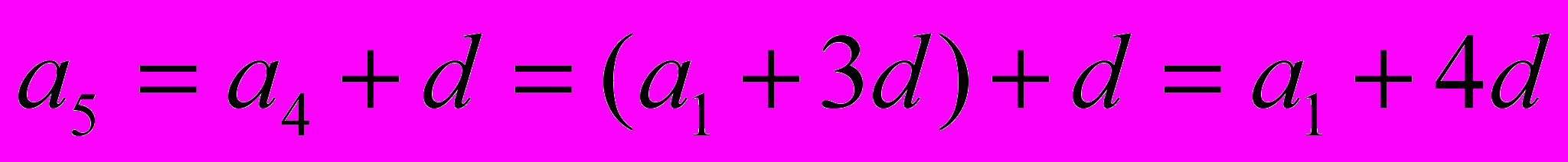Точно так же находим, что 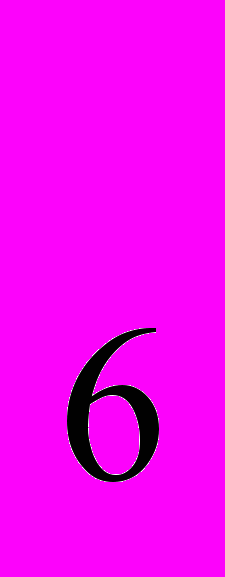а=а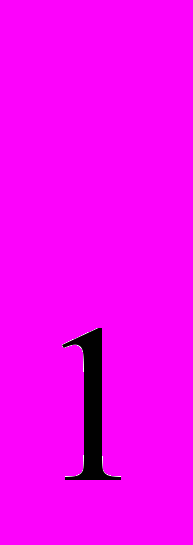+5d, и вообще, чтобы найти а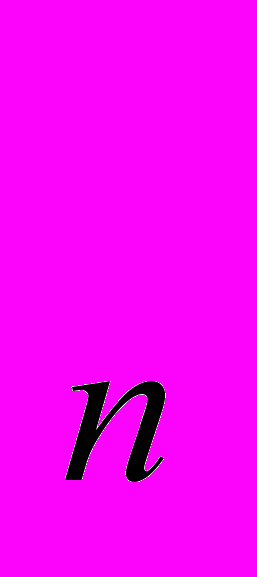, нужно к а 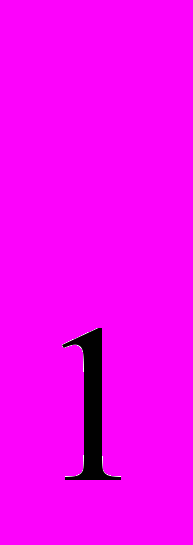прибавить (n-1)d, т.е.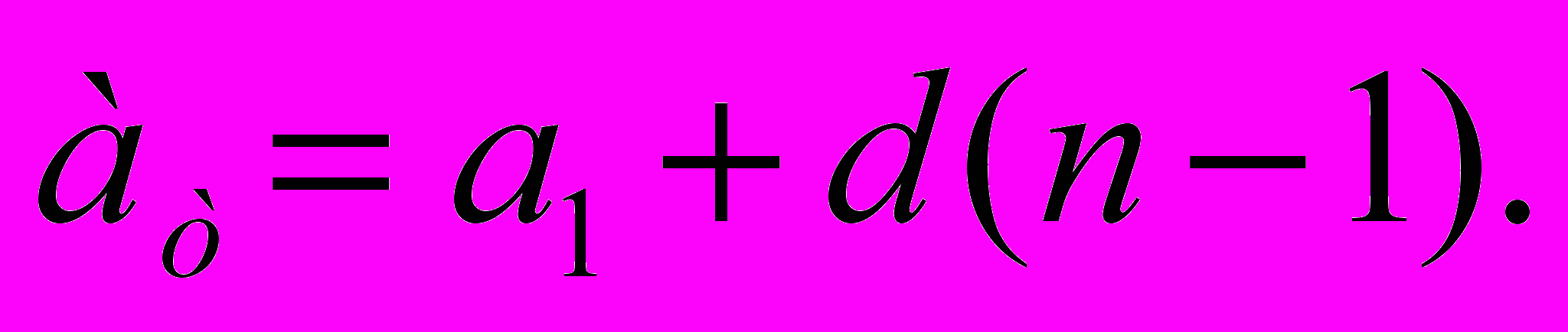



мы получим формулу n-го члена арифметической прогрессии.

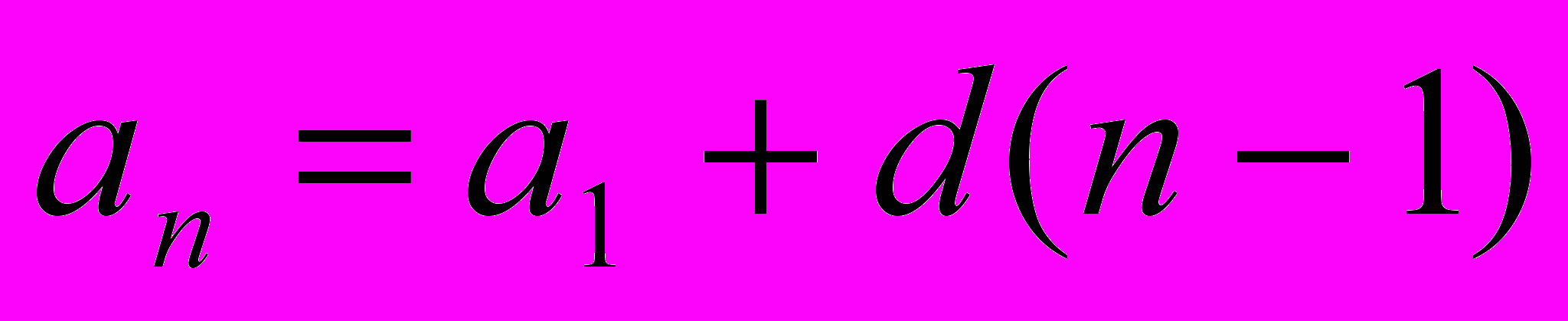
Формулу n-го члена арифметической прогрессии можно записать иначе: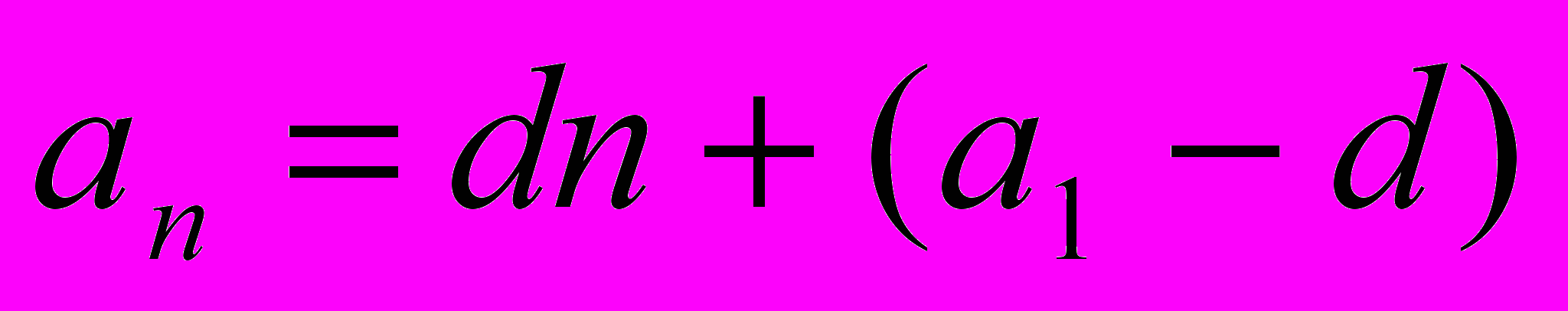

.

Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида 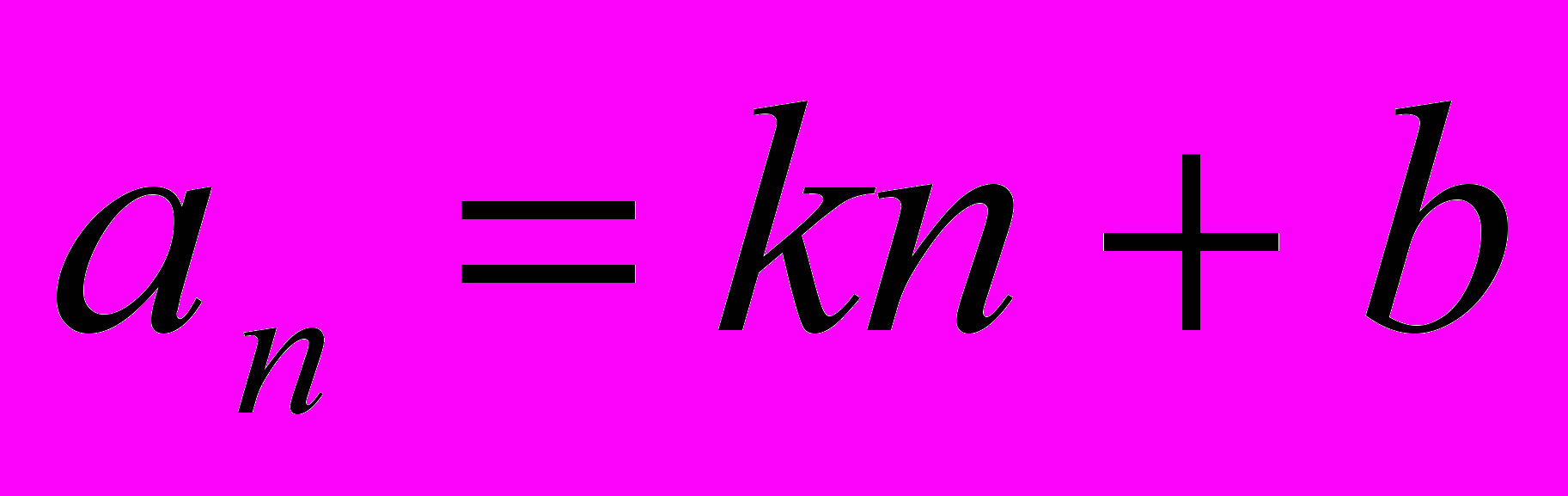, где k и b – некоторые числа.

При любом n справедливо равенство 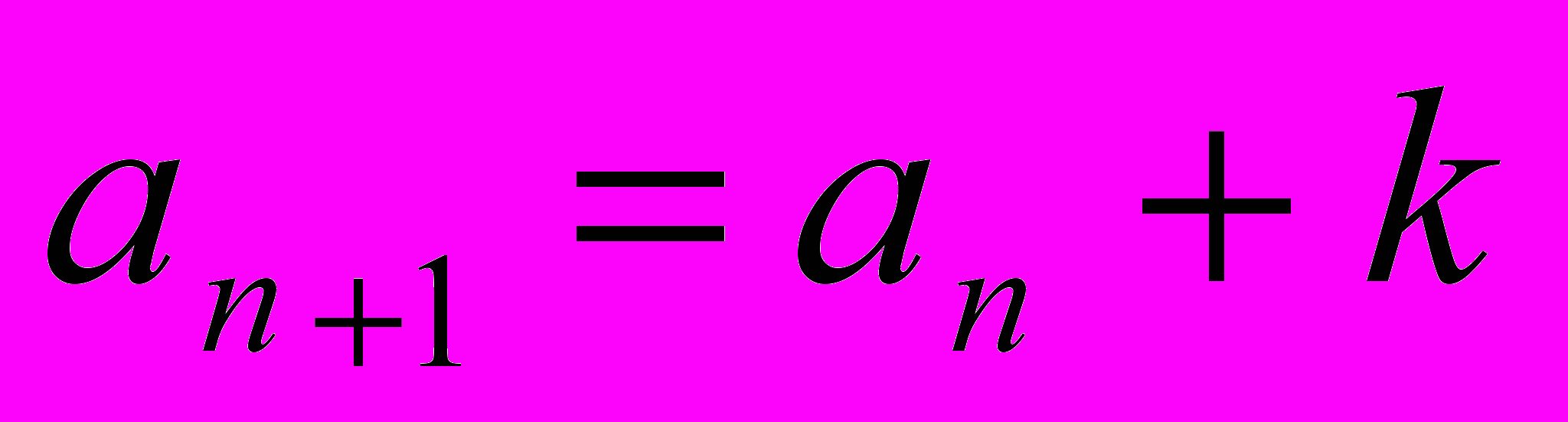, и по определению последовательность (а_n) является арифметической прогрессией, причём разность этой прогрессии равна k.


^ 3.1.3 Формула суммы n-первых членов арифметической прогрессии.


Обозначим сумму n- первых членов арифметической прогрессии (а_n) через S_n и запишем эту суму дважды, расположив в первом случае слагаемые в порядке возрастания их номеров, а во втором случае в порядке убывания:


,

.


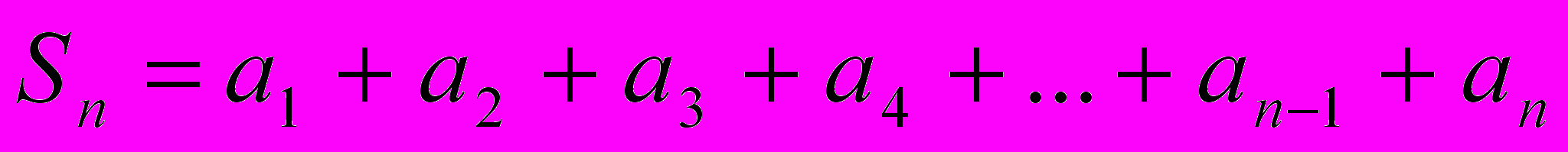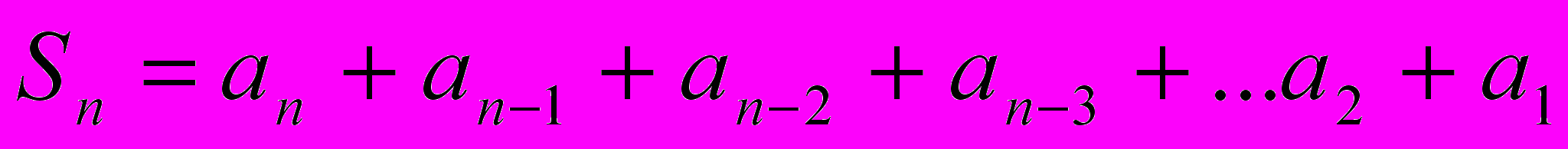Сумма каждой пары членов прогрессии, расположенных друг под другом, равна а₁+а_n. Действительно,




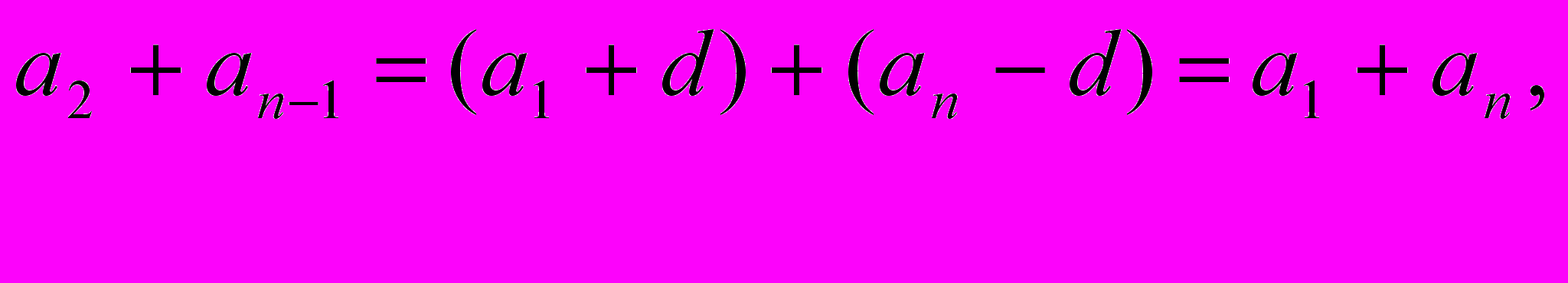
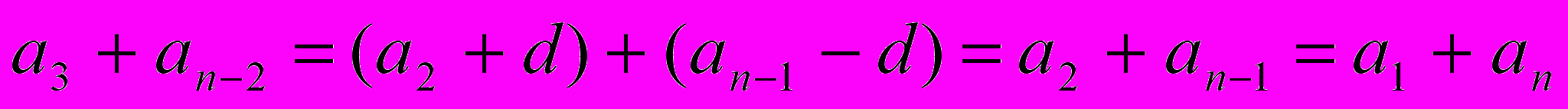и т.д.


число таких пар равно n. Поэтому, сложив почленно равенства, получим:

.

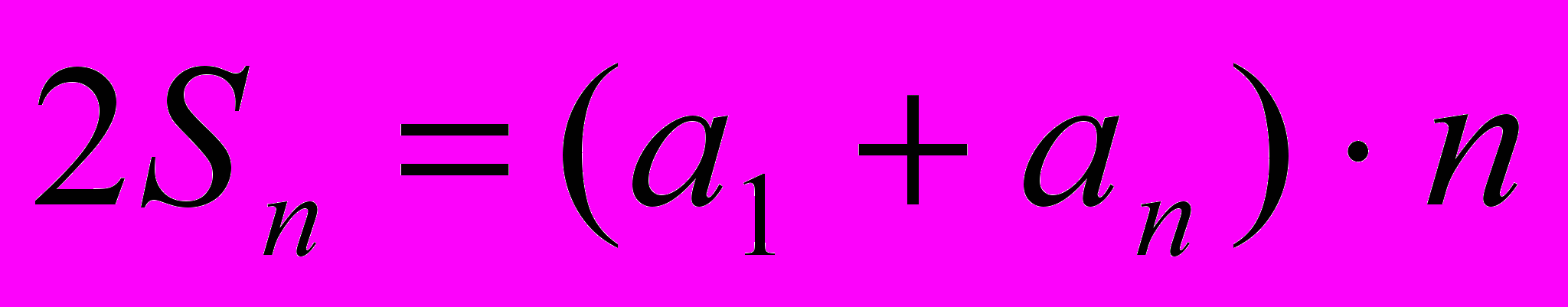Разделив обе части последнего равенства на 2, получим формулу суммы и первых членов арифметической прогрессии:


.


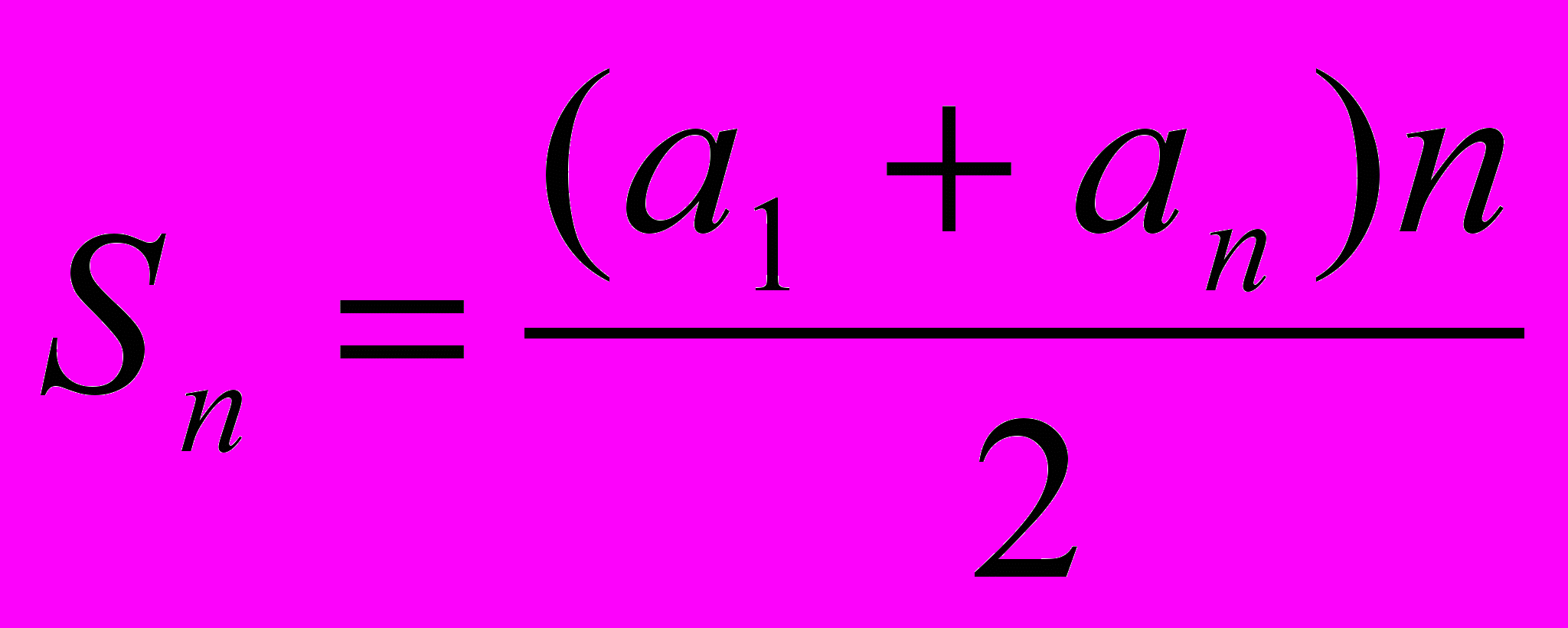^ 3.2 Геометрические прогрессии.


3.2.1 Геометрические прогрессии в древности.

В папирусе Ахмеса содержится задача, в которой требуется найти сумму n членов геометрической прогрессии, зная первый её член и знаменатель.

Из одной клинописной таблички можно заключить, что, наблюдая луну от новолуния до полнолуния, вавилоняне пришли к такому выводу: в первые пять дней после новолуния рост освещения лунного диска совершается по закону геометрической прогрессии со знаменателем 2. в другой более поздней табличке речь идёт о суммировании геометрической прогрессии:

1+2+2²+…+2⁹. решение и ответ S=512+(512-1), данные в табличке наводят на мысль, что автор пользовался формулой.


S_n=2ⁿ+(2ⁿ-1),


Однако о том, как он дошёл до нее никому не известно.

Издавна большой популярностью пользуется следующая задача легенда, которая относится к началу нашей эры.

«Индийский царь Шерам позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку. Сета, издеваясь над царём, потребовал за первую клетку шахматной доски 1 пшеничное зерно, за вторую – 2 зерна, за третью – 4 и т.д. оказалось, что царь не был в состоянии выполнить это «скромное» желание Сеты».

В этой задачи речь идёт о суммировании геометрической прогрессии 1, 2, 2², 2³, … 2⁶³. Её сумма равна:


2⁶⁴-1=18 446 744 073 709 551 615.

Такое количество зёрен пшеницы можно собрать лишь с урожая планеты, поверхность которой примерно в 2000 раз больше поверхности Земли.

Любопытно отметить, что в задачах на геометрические прогрессии китайской «Математики в девяти книгах» знаменатель равен 2. Формул суммирования здесь нет. По содержанию некоторые китайские задачи трактуют о растущей или убывающей производительности труда ткачих. Примеры арифметических и геометрических прогрессий имеются и в индийских «сиддхантах».

Суммированием геометрических прогрессий и составлением соответствующих , не всегда отвечающих практическим нуждам задач занимались многие любители математики на протяжении древних и средних веков.

В древнерусском юридическом сборнике «Русская правда» содержаться выкладке о приплоде от скота и пчёл за известный промежуток времени. О количестве зерна, собранного с определённого участка земли и т.д. в некоторых из них вычисляется сумма геометрической прогрессии со знаменателем 2. Эти задачи, по видимому, не имели хозяйственного или юридического значения, а как и в других странах являлись результатом развития интереса любителей математики к математическому содержанию подобных задач; однако впервые задачи на прогрессии возникли из наблюдений за явлениями природы из исследования общественно-экономических явлений, к которым применим закон арифметической или геометрической прогрессии.


^ 3.2.2 Понятие геометрической прогрессии.


Геометрической прогрессией называется последовательность отличных от нуля чисел. Каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Рассмотрим последовательность, членами которой являются числа 2 с натуральными показателями:

2, 2², 2³, 2⁴, 2⁵, ……

Каждый член этой последовательности начиная со второго, получается умножением предыдущего член ан а2. эта последовательность является примером геометрической прогрессии.

Иначе говоря, последовательность b_n – геометрическая прогрессия, если для любого натурального n выполняются условия: b_n не равно нулю и b_n+1=b_n·q, где q – некоторое число. Обозначим, например, через (b_n) последовательность натуральных степеней числа 2. в этом случае для любого натурального n верно равенство b_n+1 = b_n·2; здесь q=2.

Из определения геометрической прогрессии следует, что отношение любого её члена, начиная со второго, к предыдущему члену равно q, т.е. при любом натуральном n верно равенство:

b_n+1/b_n = q.

Число q называют знаменателем геометрической прогрессии. Понятно, что знаменатель геометрической прогрессии всегда отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.

Например:

Если b₁=1 и q=0,1, то получим геометрическую прогрессию

1; 0,1; 0,01; 0,001; 0,0001; 0,00001 … .

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой её член:


b₂ = b₁q,

b₃ = b₂q = (b₁q)q = b₁q²,

b₄ = b₃q = (b₁q²)q = b₁q³,

b₅ = b₄q = (b₁q³)q = b¹q⁴.


Из этого следует: чтобы найти b_n, мы должны b₁ умножить на q^n-1, т.е.


b_n = b₁ q^n-1.


^ 3.2.3 Формула суммы n-первых членов геометрической прогрессии.


Выведем формулу суммы n первых членов произвольной геометрической прогрессии.

Пусть дана геометрическая прогрессия (b_n). Обозначим сумму n первых членов её через S_n.:

S_n = b₁ + b₂ + b₃ + ... + b_n-1 + b_n. (1)

Умножим обе части этого равенства на q:

S_nq = b₁q + b₂q + b₃q + ... + b_n-1q + b_nq.

Учитывая, что b₁q = b₂, b₂q = b₃, b₃q = b₄, ..., b_n-1q = b_n, получим :

S_nq = b₂ + b₃ + b₄ + ... + b_n + b_nq. (2)

Вычтем почленно из равенства (2) равенство (1) и приведём подобные члены:

S_nq – S_n = (b₂ + b₃ + ... + b_n + b_nq) – (b₁ + b₂ +... + b_n-1 + b_n) = b_nq – b₁,

S_n(q – 1) = b_nq – b₁.

Отсюда следует, что при q не равном 1:

S_n = (b_nq – b₁)/(q-1).

Мы получили формулу n первых членов геометрической прогрессии, в которой q не равно 1, если q равно 1, то все члены прогрессии равны первому её члену.

При решении задач удобно пользоваться формулой суммы n первых членов геометрической прогрессии, записанной в другом виде:

S_n = (b₁(qⁿ – 1))/(q-1).


Заключение.

Изучением числовых последовательностей занимались многие ученые на протяжении многих веков. Они являются одним из ключевых понятий математики. В своей работе я постаралась отразить основные понятия связанные с числовыми последовательностями, способы их задания, рассмотрела некоторые из них. Отдельно были рассмотрены прогрессии (арифметическая и геометрическая), рассказано о истории их возникновения, о основных понятиях связанных с ними.


Список используемой литературы.

1. 
   Алгебра. 9 класс. С.А. Теляковский, Москва, «Просвещение» 1990г.
   
2. Большой справочник школьника. Москва, «Дрофа» 2001г.
   
3. Повторяем и систематизируем школьный курс алгебры и начала анализа. В.С. Крамор, Москва «Просвещение» 1990г.
   
4. «История математики», Глейзер.
   
5. «Математика в школе» Ж. 2002г.
   

Перейти к оглавлению