Исследование программных методов реализации операций в конечных алгебраических структурах

Вид материала

Содержание

Общая характеристика работы
Целью диссертации
Методы исследования.
Научная новизна
Достоверность научных результатов
Практическая значимость полученных результатов.
Реализация результатов.
Апробация полученных результатов
Структура и объем работы.
Основное содержание работы
Рис. 1. Пример последовательной программы для умножения 64-разрядных бинарных многочленов
Рис. 2. Пример цепочек действий для последовательной программы на рисунке 1
Основные результаты работы
Список работ, опубликованных по теме диссертации

Подобный материал:

На правах рукописи

Жебет Сергей Юрьевич

Исследование программных методов реализации операций в конечных алгебраических структурах

Специальность: 05.13.11 – Математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

Москва 2009

Работа выполнена на кафедре Математического моделирования Московского энергетического института (технического университета).

Научный руководитель: доктор технических наук, профессор

Фролов Александр Борисович.

Официальные оппоненты: доктор технических наук, профессор

Фальк Вадим Николаевич,

кандидат физико-математических наук, доцент

Часовских Анатолий Александрович.

Ведущая организация: Федеральное государственное унитарное предприятие “НИИ “Квант”.

Защита состоится «26» июня 2009 г. В 14:00 в ауд. М-704 на заседании диссертационного совета Д 212.157.01 при Московском энергетическом институте (техническом университете) по адресу: 111250, Москва, Красноказарменная ул., д.17.

С диссертацией можно ознакомиться в библиотеке Московского энергетического института (технического университета).

Отзывы в двух экземплярах, заверенные печатью организации, просьба отправлять по адресу: 111250, Москва, Красноказарменная ул., д.14, Ученый совет МЭИ (ТУ).

Автореферат разослан «___» мая 2009 г.

Ученый секретарь

диссертационного совета Д 212.157.01

кандидат технических наук, доцент Фомина М.В.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Операции в конечных алгебраических структурах − кольцах, полях, группах, реализуемые в виде методов алгебраических библиотек, составляют вычислительную базу современных информационных технологий. Эффективность и надежность их реализации предопределяет соответствующие свойства таких информационных систем как системы цифровой обработки сигналов и криптографические протоколы. Вопросам эффективной реализации алгебраических операций посвящено значительное количество, как теоретических работ, так и работ практической направленности. В 1962 г. был опубликован метод умножения Карацубы^¹, как первый в понижении асимптотической оценки сложности целочисленного умножения. Затем был обоснован метод Шоенхаге-Штрассена^², понизивший эту оценку в еще большей степени. Однако понижение асимптотической сложности не всегда сопровождается понижением практической сложности, под которой мы понимаем число операций или время, затрачиваемые для выполнения операции при заданных размерностях операндов.

Несмотря на сравнительно малую асимптотическую сложность изученных в теории методов, часто при программной реализации в оценке практической сложности получается довольно большая мультипликативная константа. Это существенно ограничивает целесообразность их применения на практике и делает актуальным исследование других, в том числе обладающих большей асимптотической сложностью методов, которые дают лучшие оценки производительности по времени для наиболее часто используемых в современных информационных системах размерностей операндов.

Не случайно на рубеже тысячелетий появились новые интерпретации давно известного метода сдвигов и сложений для реализации умножения^³, а также новые методы деления и инвертирования в конечных полях^⁴, имеющие лучшую производительность, чем асимптотически оптимальные методы в диапазоне размерностей современных криптографических протоколов.

Следует также отметить, что асимптотические оценки сложности схемной и программной реализации методов одинаковы и не учитывают той специфики последней, что производительность программы зависит от взаимного расположения операндов, а также от вспомогательных действий, связанных с организацией вычислений по программе (условных переходов, циклов). Чтобы сократить объем таких действий была предложена программная реализация метода Карацубы в виде декомпозиционной схемы, имеющей структуру ^⁵.

Для получения объективных оснований выбора того или иного метода при реализации конкретной информационной системы необходимы разработка и сравнительный анализ новых и известных методов (включая их комбинирование) программной реализации алгебраических операций в тех или иных диапазонах размерностей операндов, чему и посвящена тема настоящей диссертации. Актуальность этой тематики проявляется и в бурном развитии эллиптической криптографии, где появились новые криптографические протоколы, не имеющие аналогов в классе протоколов, основанных на свойствах мультипликативной группы^⁶.

Целью диссертации является повышение эффективности программной реализации арифметических операций в конечных алгебраических структурах.

При этом ставились следующие задачи:

систематизация и программная реализация типичных алгоритмов в конечных алгебраических структурах;
разработка способов сравнения и оценки методов программной реализации алгебраических операций;
разработка методов автоматической генерации последовательных программ умножения;
сравнительный анализ и обоснование выбора методов программной реализации умножения в конечных полях;
сравнительный анализ и обоснование выбора методов программной реализации производных операций (возведения в степень, инвертирования и деления) в конечных полях;
сравнительный анализ методов программной реализации операций сложения и скалярного умножения в группе точек эллиптической кривой на основе рекомендуемых в диссертации методов умножения и деления в конечных полях.

Полученные в диссертации научные результаты:

Обоснована целесообразность комбинирования метода умножения путем сдвигов и сложений (вспомогательного метода) и метода Карацубы с уточнением порога перехода к вспомогательному методу умножения для комбинированных методов, построенных с использованием рекурсивной, циклической и последовательной реализации метода Карацубы.
Разработан метод автоматического синтеза последовательных программ умножения многочленов, обеспечивающий локализацию адресов, и способ автоматической верификации результата такого синтеза.
Разработан метод аналитического сравнения производительности последовательных программ умножения.
Определены наилучшие условия применения последовательных программ умножения по методу А. Карацубы в процессе умножения многочленов высоких степеней над полями различных характеристик и показано существенно большее быстродействие последовательных программ по сравнению с рекурсивными.
Выявлены области рекомендуемого применения методов при умножении многочленов высоких степеней над полями различных характеристик.
На основе сравнительного анализа эффективности алгоритмов скалярного умножения на эллиптических кривых с использованием аффинной и проективной систем представления операндов подтверждено, что существенное преимущество проективной системы сохраняется и в условиях применения наиболее эффективных алгоритмов умножения, инвертирования и деления в конечных полях.

Методы исследования. Поставленные задачи решались с использованием методов дискретной математики, линейной алгебры, теории вычислительной сложности алгоритмов. При разработке программного обеспечения использовались методы объектно-ориентированного программирования и техники оптимизации программного обеспечения.

Научная новизна:

Проведено уточнение порога перехода для комбинированных методов, построенных с использованием рекурсивной, циклической и последовательной реализации метода Карацубы.
Предложен метод автоматического подтверждения правильности синтезируемых различными способами программ умножения.
Предложены аналитический метод оценки сложности и метод автоматического синтеза последовательных программ умножения по методу Карацубы, обеспечивающий локализацию адресов.
Подтверждена эффективность применения проективных координат при вычислениях в группе точек эллиптической кривой в условиях применения наиболее эффективных методов умножения и деления в конечных полях.

Достоверность научных результатов подтверждается соответствием теоретических выкладок и результатов экспериментов, а также сопоставлением полученных результатов с результатами, приведенными в отечественной и зарубежной научной литературе.

Практическая значимость полученных результатов. Применение предложенного метода автоматической проверки правильности синтезированных программ умножения позволит повысить качество разрабатываемого программного обеспечения и снизить временные затраты на его разработку и тестирование за счет формальной проверки 100% исходного кода еще до компиляции.

Полученные аналитическим и экспериментальным путями оценки и интервалы оптимальности методов умножения представляют практический интерес при программировании новых производных алгоритмов, использующих базовые операции.

Применение в алгоритмах на эллиптических кривых предложенных модификаций алгоритмов умножения многочленов для полей с порождающим многочленом степени больше 256 позволило сократить время выполнения операции умножения точки эллиптической кривой на константу на 5-15% в зависимости от типа кривой и порядка поля, в котором производились вычисления.

Реализация результатов. Работа выполнялась в соответствии с проектом РФФИ 08-01-00632-a и заданием по разработке программного средства «Алгебраический процессор» инновационной образовательной программы. Разработанные программные средства использованы в МЭИ (ТУ) при создании электронного образовательного ресурса «Алгебраический процессор»^⁷. Результаты внедрены в виде математического и методологического обеспечения лабораторной работы «Сравнительный анализ временных характеристик алгоритмов операций в конечных группах, кольцах и полях» электронного образовательного ресурса «Алгебраический процессор», и используются в лабораторном практикуме по дисциплине «Криптографические методы и средства защиты информации», что подтверждено актами об использовании.

Апробация полученных результатов осуществлена при их обсуждении на одиннадцатой, двенадцатой, четырнадцатой и пятнадцатой международной научно-технической конференции студентов и аспирантов «Радиоэлектроника, электротехника и энергетика», Москва 2005, 2006, 2008, 2009; девятой, десятой и одиннадцатой Московской Международной телекоммуникационной конференции студентов и молодых ученых «Молодежь и наука», Москва 2006, 2007, 2009.

Публикации. Основные результаты, полученные при выполнении диссертационной работы, опубликованы в 10 печатных изданиях, включая 3 статьи в журнале из Перечня ВАК.

Структура и объем работы. Работа состоит из введения, 4 глав, заключения, списка использованной литературы, содержащей 86 наименований, и приложений. Основной текст занимает 146 машинописных страниц, в том числе 31 рисунок и 33 таблицы. Полный объем диссертации (с приложениями) составляет 149 страниц.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертации, ее научная новизна и практическая значимость, сформулирована цель работы и приведено краткое содержание диссертации по главам.

В первой главе приводятся базовые определения и понятия, описывается современное состояние проблемы, и рассматриваются известные алгоритмы выполнения арифметических операций в конечных кольцах и полях.

При этом приводятся алгоритмы:

Четыре вариации классического алгоритма умножения методом сдвигов и сложений.
Алгоритм умножения с использованием рекурсивной реализации метода Карацубы.
Три комбинированных метода умножения (с использованием метода Карацубы и классического метода).
Два алгоритма приведения по модулю.
Алгоритм возведения в степень.
Четыре алгоритма инвертирования в поле в стандартном базисе.
Три алгоритма деления многочленов в поле в стандартном базисе.

Для каждого класса программ приводятся сравнительные таблицы времени выполнения и даются рекомендации по использованию одного из методов класса в зависимости от размера входных данных.

Для комбинированных методов умножения дополнительно приводится обоснование асимптотической оценки и производится экспериментальный выбор оптимальной базы рекурсии. Если представить количество разрядов в каждом многочлене множителе в виде 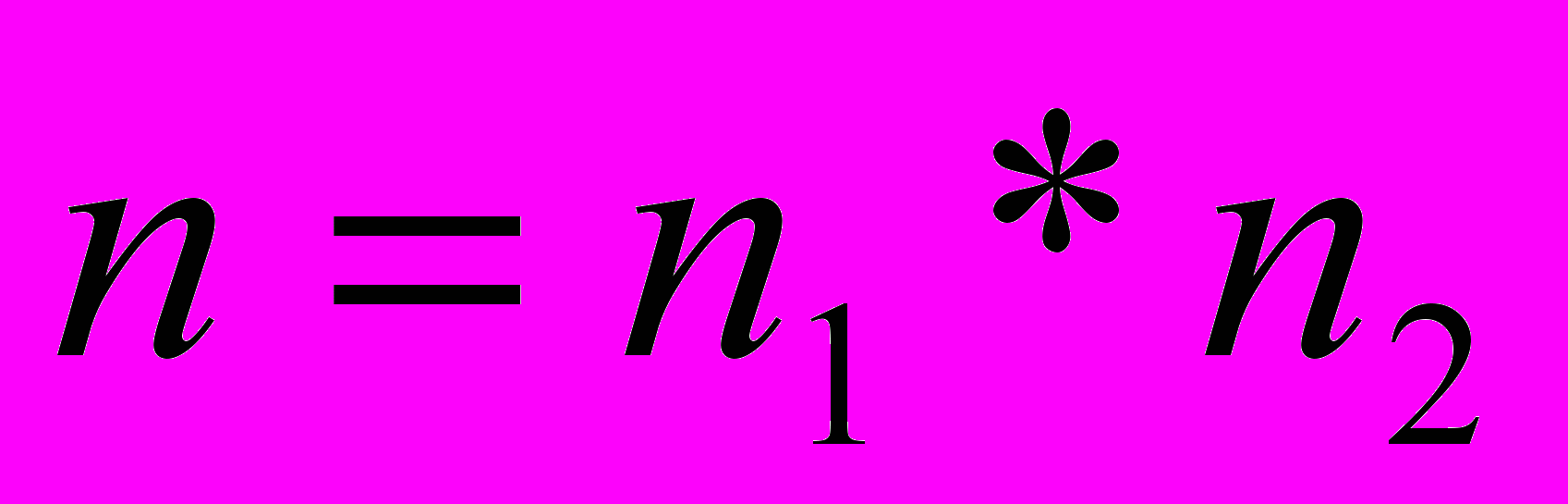, где n₂ – база рекурсии по методу Карацубы (количество разрядов в каждом многочлене – операнде, при котором производится переход от метода Карацубы к одному из вспомогательных методов), то глубина рекурсии по методу Карацубы определяется как log₂(n₁), при этом будет верно утверждение 1.

Утверждение 1. Для комбинированного метода умножения асимптотическая сложность определяется как

_.

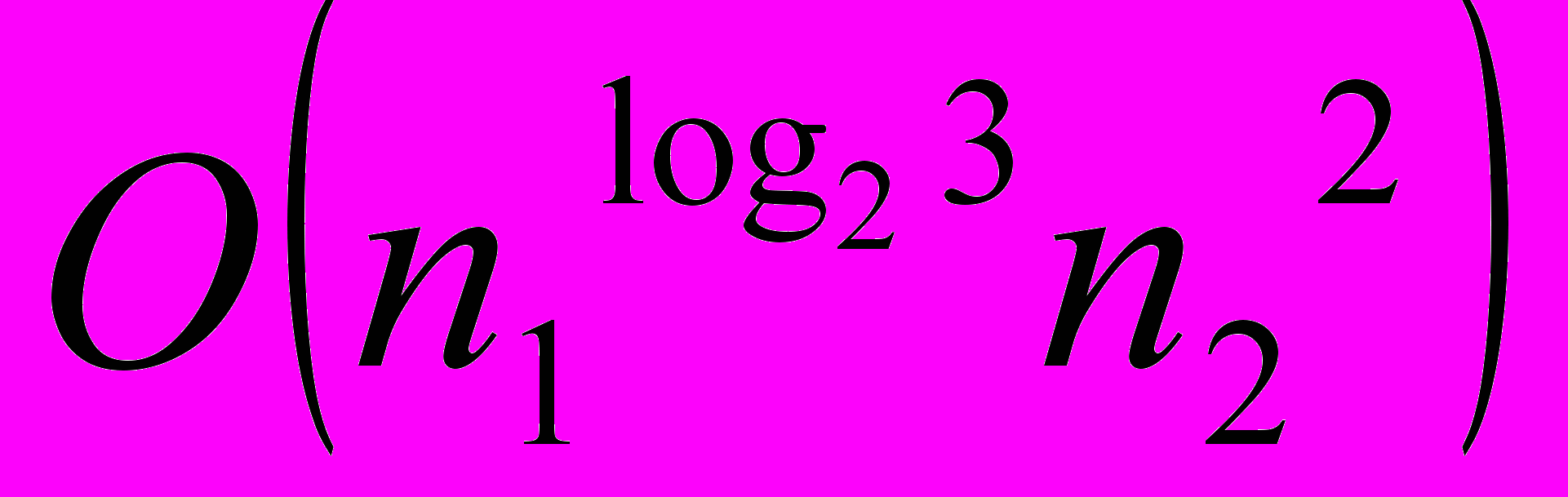В заключении к главе 1 производится обобщение полученных результатов и дается постановка задачи по исследованию других возможных реализаций метода Карацубы и комбинированных методов.

Во второй главе в сопоставлении с рекурсивной реализацией метода Карацубы изучаются последовательные программы. При этом описывается два способа автоматического построения последовательных программ умножения и метод их верификации. Для последовательных программ, построенных по комбинированному методу, приводится способ выбора оптимального параметра перехода – аналога базы рекурсии для комбинированных методов с рекурсивной реализацией.

Идея схемной реализации метода Карацубы была предложена и обоснована в 1999-2006 г.г. в работах А.А. Болотова, С.Б. Гашкова, А.Б. Фролова и А.А. Часовских. Она заключается в том, что предварительное сложение и умножение фрагментов многочленов, как и последующая сборка этих результатов, осуществляется схемой без циклов. Автоматизация построения таких схем была рассмотрена в работах М.И. Фомичева и А.Б. Дроздова в 2001-2002 г.г. В обеих работах на основе аналитического исследования метода строятся таблицы операций и адресов операндов, а затем из таких таблиц извлекается схема. Однако такой метод построения схем не учитывает необходимость оптимизации по объему занимаемой памяти и по размещению в ней результатов промежуточных вычислений. В нашем случае под последовательной программой понимается последовательность элементарных арифметических действий и операций присваивания. Последовательная программа характеризуется размером этой последовательности, объемом используемой памяти и степенью локализации адресаций. По этим параметрам последовательные программы можно оптимизировать. Пример последовательной программы приведен на рисунке 1. В программе делается предположение, что множители располагаются последовательно, начиная с единичного адреса, а после выполнения программы результат записывается на место сомножителей.

Mem[5]=Mem[1];

Mem[5]=Mem[2];

Mem[6]=Mem[4];

Mem[6]=Mem[3];

Mem[7]=Mul(Mem[1],Mem[3],2);

Mem[3]=Mul(Mem[2],Mem[4],2);

Mem[5]=Mul(Mem[5],Mem[6],2);

Mem[6]=Mem[8];

Mem[5]=Mem[7];

Mem[6]=Mem[4];

Mem[5]=Mem[3];

Mem[3]=Mem[6];

Mem[8]=Mem[5];

Mem[1]=Mem[7];

Mem[2]=Mem[8];

Рис. 1. Пример последовательной программы для умножения 64-разрядных бинарных многочленов

Важной особенностью таких последовательных программ является независимость хода выполнения от исходных данных. Эта особенность позволяет путем несложных преобразований, для каждого разряда многочлена – результата умножения, получить цепочку арифметических действий над разрядами операндов, производимых в процессе выполнения последовательной программы и приводящих к получению именно этого разряда результата. Пример такой цепочки для последовательной программы на рисунке 1, приведен на рисунке 2.

Mem[1]=(A[0])*(B[0])[0]

Mem[2]=(A[0])*(B[0])[1]+(A[0]+A[1])*(B[1]+B[0])[0]+(A[0])*(B[0])[0]+(A[1])*(B[1])[0]

Mem[3]=(A[1])*(B[1])[0]+(A[0]+A[1])*(B[1]+B[0])[1]+(A[0])*(B[0])[1]+(A[1])*(B[1])[1]

Mem[4]=(A[1])*(B[1])[1]

Рис. 2. Пример цепочек действий для последовательной программы на рисунке 1

Такие цепочки не зависят от способов адресации, порядка выполнения не связанных между собой операций и задают математическую суть программы. Значит, в случае эквивалентности, двух программ, будут порождаться одинаковые цепочки действий по формированию разрядов результата умножения. Верно и обратное: в случае равенства цепочек действий программы эквивалентны.

Одним из способов автоматического построения последовательных программ умножения является использование аналитически выведенных формул и таблиц распределения адресов операндов в элементарных операциях.

Идея второго способа автоматического построения последовательного алгоритма заключается в использовании уже разработанной и проверенной рекурсивной программы умножения. В коде такой программы каждая операция выполнения элементарного действия заменяется операцией сохранения наименования действия и адресов операндов. Затем ищется минимальный адрес операнда и принимается за нулевой адрес рабочего массива последовательной программы, соответствующая поправка вносится во все адреса операндов. При данном подходе необходимо обоснование корректности получаемой в результате программы, поскольку сам подход содержит неочевидные преобразования.

Последовательные программы, получаемые в результате реализации описанных выше подходов, принадлежат одному классу, при этом отличаются только способами адресации элементов и методами распределения памяти для хранения промежуточных результатов. Поэтому для доказательства их эквивалентности можно использовать метод сравнения цепочек действий. Таким образом, автоматизация проверки заключается в том, что при выбранных максимально возможных степенях сомножителей, задающих область применимости программ, автоматически синтезируются две последовательные программы с использованием первого подхода без оптимизации и второго подхода с оптимизацией. Затем из каждой программы извлекаются цепочки действий по формированию базовых слов результата умножения. Формальными преобразованиями производится автоматическое приведение цепочек к единому виду и их сравнение. При положительном заключении о равенстве цепочек формируется заключение о первичной корректности обеих синтезированных программ. Последующий этап компиляции, выполнения программ и сравнения результатов с эталонными значениями позволяет сделать окончательные выводы о корректности синтезированных программ.

В получаемых описанным выше методом последовательных программ умножения, можно выделить набор типовых операций, количество которых подчинено уточненной оценке:

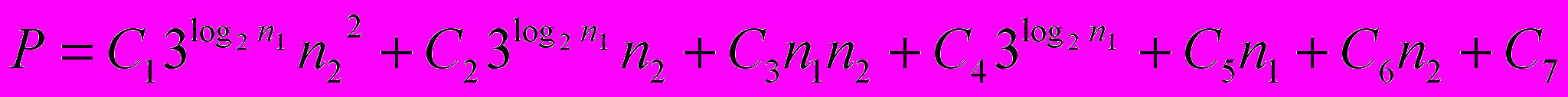(1)

Здесь n₁, n₂ – параметры алгоритма, причем 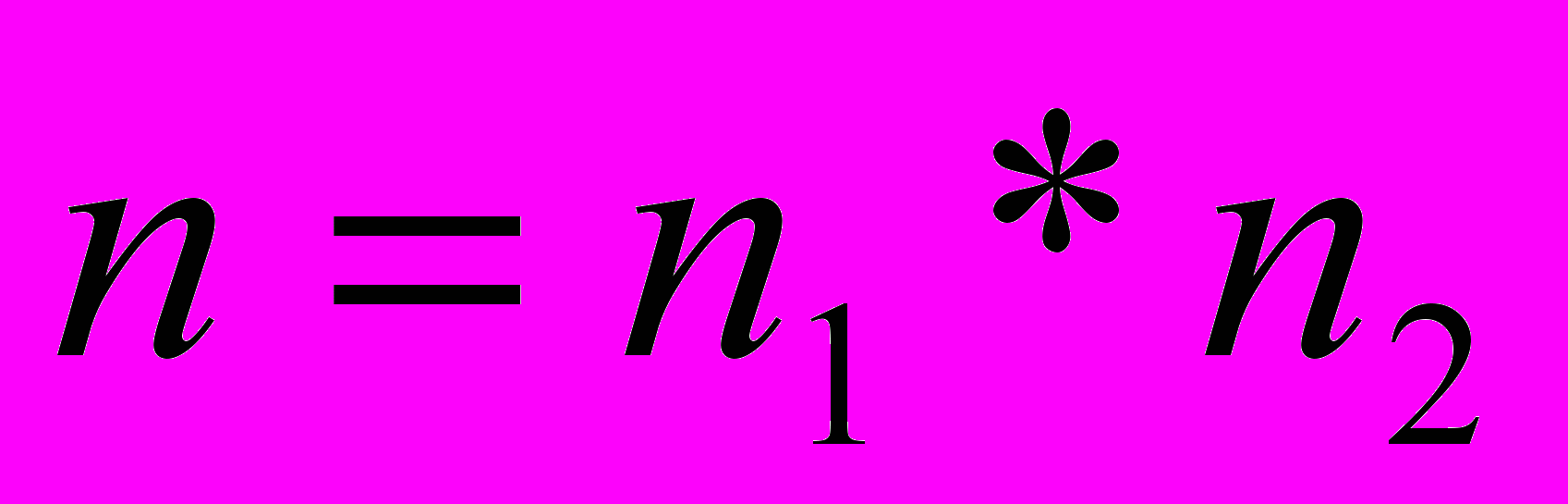– количество разрядов в многочленах – операндах. Эта формула едина для всех комбинированных методов, построенных на основе метода Карацубы и одной из реализаций метода сдвигов и сложений. Таким образом, задача получения оценки для конкретного комбинированного метода сводится к задаче определения постоянных С₁,…,С₇. Что делается путем построения семи последовательных программ и решением системы линейных уравнений относительно С₁,…,С₇. Например, соответствующая система уравнений для последовательных программ, построенных по комбинированному методу, использующему метод сдвигов и сложений с таблицей умножения, имеет вид:

а ее решение:

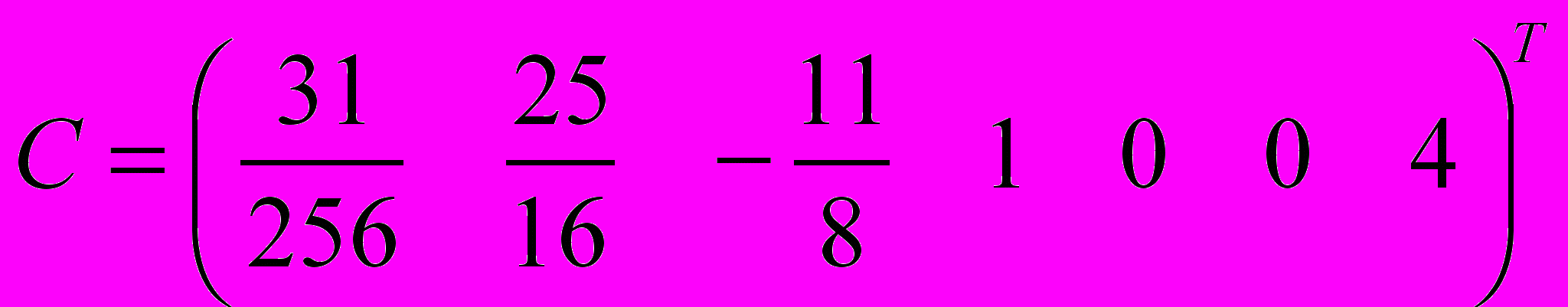
задает коэффициенты в функции (1).

В итоге были получены следующие оценки:

для последовательных программ, построенных по комбинированному методу, использующему метод сдвигов и сложений с таблицей (формула (2));
для последовательных программ, построенных по комбинированному методу, использующему метод сдвигов и сложений с условными переходами (формула (3));
для последовательных программ, построенных по методу Карацубы, использующему таблицу умножения для многочленов степени не выше 7 (формула (4));

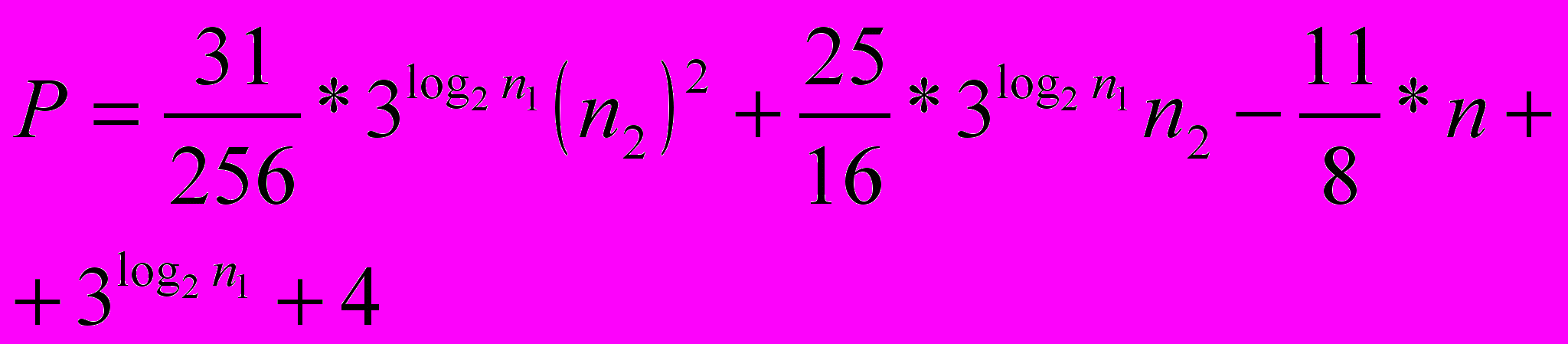
	(2)
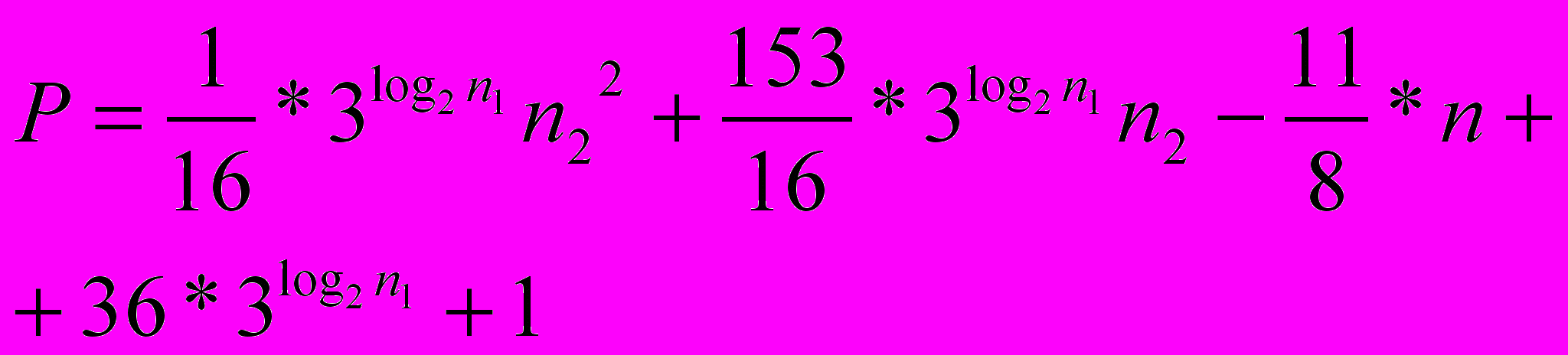
	(3)
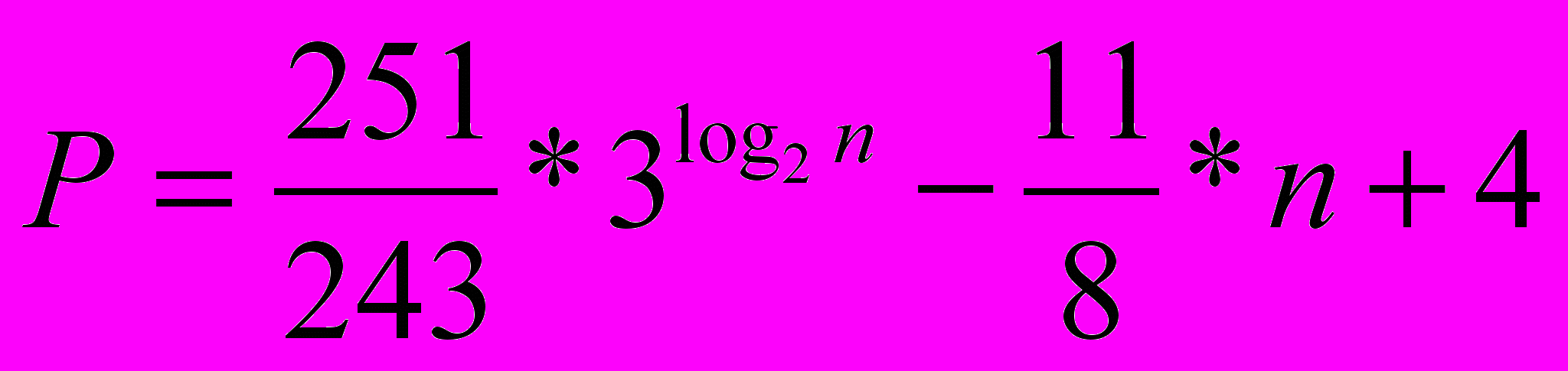
	(4)

Далее с использованием формул (2) и (3) функции сложности табулируются, и по таблицам определяется оптимальный параметр перехода для последовательных программ, построенных по комбинированным алгоритмам.

В итоге было получено, что:

для последовательных программ, построенных по комбинированному методу, использующему метод сдвигов и сложений с таблицей оптимальный параметр перехода равен 32;
для последовательных программ, построенных по комбинированному методу, использующему метод сдвигов и сложений с условными переходами оптимальный параметр перехода равен 256;

Преимущество использования последовательных программ, построенных по комбинированным методам, перед рекурсивной реализацией метода Карацубы, комбинированных методов и классических алгоритмов при достаточно больших степенях умножаемых многочленов видно из табл. 1, полученной экспериментально^⁸.

Табл. 1.

Результаты измерения времени выполнения операции умножения в GF(2ⁿ) в микросекундах различными методами при задании оптимального параметра для каждого метода.

Метод	n<64	n<128	n<256	n<512	n<1024
Сдвигов и сложений с таблицей умножения	0,6	1,7	4,1	15	69
Метод сдвигов и сложений с использованием условных переходов	0,7	1,4	3,2	9,7	29
Метод сдвигов и сложений с использованием таблицы определения единичных разрядов	0,7	1,2	2,9	8,4	26
Метод Карацубы с таблицей умножения	1,5	4	12	35	130
Комбинированный метод с таблицей умножения (оптимальный параметр 256)	0,9	2	4	12	35
Комбинированный метод с использованием условных переходов (оптимальный параметр 512)	1	1,7	3,5	9,5	32
Комбинированный метод с таблицей определения единичных разрядов (оптимальный параметр 512)	0,9	1,4	3	9	25,5
Последовательный алгоритм по методу Карацубы с таблицей умножения	6,2	6,8	7,7	12	30
Последовательный алгоритм по комбинированному методу с таблицей умножения (оптимальный параметр 32)	6,1	6,7	7,2	8,3	12
Последовательный алгоритм по комбинированному методу с условными переходами (оптимальный параметр 256)	6,5	6,8	7,3	9,0	24

Для обобщения данных результатов на поля большой характеристики GF(pⁿ), где 2l – количество бинарных разрядов, которые необходимы для представления одного элемента поля GF(p); m – количество бинарных разрядов в машинном слове; k – количество элементов поля GF(p), которые могут быть расположены в одном машинном слове. Тогда k=m/l.

При программировании операций умножения над такими полями, в качестве одного из вариантов реализации, можно использовать табулирование операций сложения и вычитания, для реализации которых в GF(2ⁿ) использовались операции «исключающего или» (XOR), то есть каждая операция «исключающего или» заменяется операциями адресации по таблицам сложения и вычитания над GF(pⁿ). Дополнительно с увеличением характеристики поля, последовательная программа неявно усложняется вследствие увеличения количества бинарных разрядов, которые отводятся на один элемент векторного представления элемента поля GF(pⁿ). Повторением вычислений констант, описанных выше, было получено, что функция сложности в последовательной программе умножения многочленов над полем GF(3ⁿ) имеет вид:

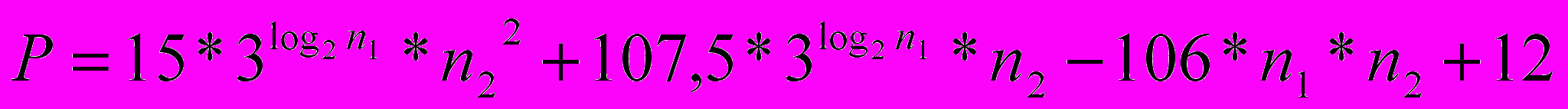
А оптимальный параметр перехода для такого метода будет равен 64.

Так как в указанной последовательной программе вместо всех арифметических операций использовались адресации по таблице, то для дальнейшего увеличения характеристики поля не требуется изменение алгоритма, достаточно лишь заменить таблицы выполнения элементарных арифметических действий. Иначе, если обозначить S(n,p) - последовательную программу умножения многочленов степени n над полем GF(pⁿ), то при условии использования таблиц операций с 8 разрядными словами и p251, получим S(n,2)=S((n/8)*8/(log₂(p)),p).

Полученная таким образом функция, позволяет оценить сложность последовательной программы для любого значения параметра n и p251. А ограничение p251 определяется физическим ограничением машинной памяти на использование таблиц выполнения элементарных арифметических действий, как максимальное простое число, меньшее 256. Преимущество последовательных программ перед рекурсивным и классическим алгоритмом в полях большой характеристики видно из табл. 2.

Табл. 2.

Сравнительная таблица для операции умножения в GF(pⁿ) различными методами в микросекундах.

Метод	GF(pⁿ), n/l<64	GF(pⁿ), 64≤n/l <128	GF(pⁿ), 128≤n/l <256	GF(pⁿ), 256≤n/l <512	GF(pⁿ), 512≤n/l<1024
Сдвигов и сложений с таблицей умножения	0,7	1,9	5	19	80
Метод Карацубы	1,9	5	13	45	150
Комбинированный метод (параметр перехода 64)	-	2	4,1	13	37
Последовательный алгоритм по комбинированному методу (параметр перехода 64)	-	7,0	7,5	9,7	18

В третьей главе производится сравнение методов умножения по времени выполнения для колец многочленов и приводятся идеи оптимизации алгоритма за счет локализации промежуточных результатов вычислений.

Непосредственная реализация рекурсивного метода Карацубы, при увеличении степени умножаемых многочленов, влечет за собой значительное увеличение объема оперативной памяти, необходимое для хранения промежуточных результатов, что в свою очередь увеличивает время, необходимое на выполнение операции умножения. Для минимизации затрат по памяти в работе предлагается модификация метода Карацубы, которая заключается во введении дополнительных операций по перемещению результатов вычисления таким образом, чтобы на каждом шаге метода перемножаемые многочлены располагались в оперативной памяти непосредственно друг за другом. Такое расположение позволяет записывать промежуточные результаты умножения многочленов меньшего порядка на место операндов, что исключает дублирование информации и позволяет более рационально использовать память за счет незначительного увеличения количества операций в алгоритме. В главе 3 также показывается, что количество дополнительных операций перемещения битов может быть вычислено по формуле:

.

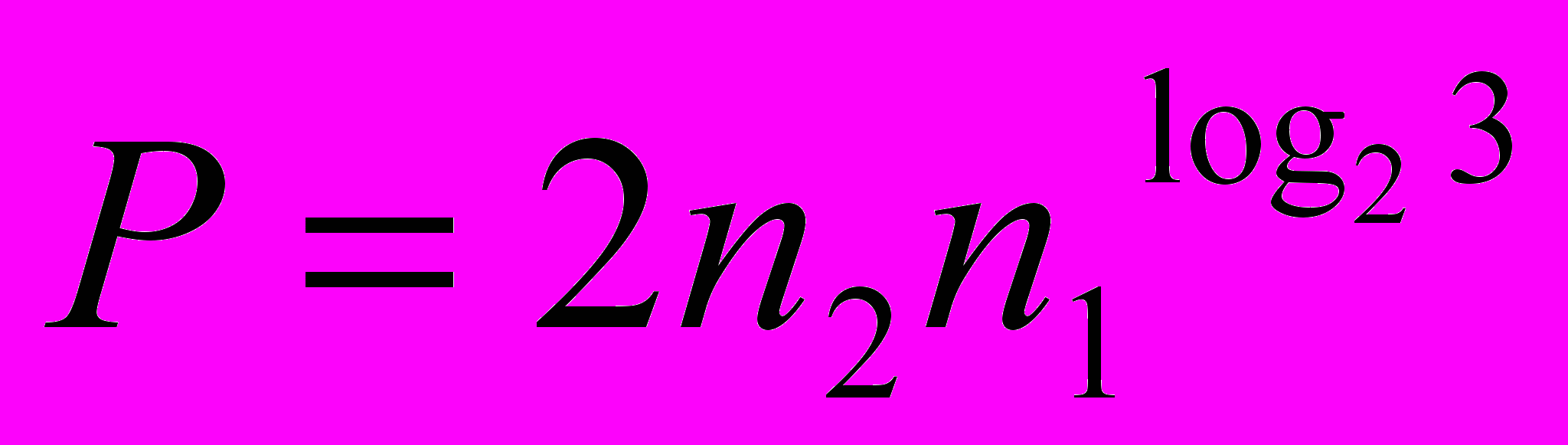Так как данная модификация алгоритма не предполагает внесения изменений в арифметическую суть метода, то для проверки корректности последовательной программы умножения, построенной по модифицированному методу, используется способ сравнения цепочек арифметических действий, описанный в главе 2. Дополнительно в главе 3 рассматривается и сравнивается с другими методами циклическая реализация комбинированного метода, эффективное построение которой становится возможным после упорядочивания хранения результатов промежуточных вычислений в памяти.

Из табл. 3 и 4, построенных по результатам экспериментов, видно, что наибольший выигрыш по скорости при достаточно больших степенях операндов дает последовательная реализация модифицированного алгоритма Карацубы, совмещенного с методом сдвигов и сложений с параметром перехода равным 32 для бинарных многочленов и 64 для обобщенного случая.

Табл. 3.

Результаты измерения времени выполнения операции умножения в GF(2ⁿ) различными методами при задании оптимального параметра для каждого метода, время приводится в микросекундах.

Метод	n≤64	n≤128	n≤256	n≤512	n≤1024
Сдвигов и сложений с таблицей умножения	0,6	1,7	4,1	15	69
Метод сдвигов и сложений с использованием таблицы определения единичных разрядов	0,7	1,2	2,9	8,4	26

Продолжение табл. 3.

Метод Карацубы с таблицей умножения (рекурсивная реализация)	1,5	4	12	35	130
Метод Карацубы с локализацией адресов и таблицей умножения (рекурсивная реализация)	1,4	3,9	11,7	34	127
Метод Карацубы с локализацией адресов и таблицей умножения (циклическая реализация)	1,4	3,8	11,5	33	125
Комбинированный метод с таблицей умножения (рекурсивная реализация, оптимальный параметр 256)	0,9	2	4	12	35
Комбинированный метод с локализацией адресов и таблицей умножения (рекурсивная реализация, оптимальный параметр 256)	0,9	2	4	12	34
Комбинированный метод Карацубы с локализацией адресов и таблицей умножения (циклическая реализация, оптимальный параметр 256)	0,9	2	4	10	31
Последовательный алгоритм по комбинированному методу с таблицей умножения (оптимальный параметр 32)	6,1	6,7	7,2	8,3	12
Последовательный алгоритм с локализацией адресов по комбинированному методу с таблицей умножения (оптимальный параметр 32)	6,1	6,6	7	7,9	11

Табл. 4.

Сравнительная таблица для операции умножения в GF(pⁿ) различными методами в микросекундах.

Метод	GF(pⁿ), n/l<64	GF(pⁿ), 64≤n/l <128	GF(pⁿ), 128≤n/l <256	GF(pⁿ), 256≤n/l <512	GF(pⁿ), 512≤n/l <1024
Сдвигов и сложений с таблицей умножения	0,7	1,9	5	19	80
Метод Карацубы (рекурсивная реализация)	1,9	5	13	45	150
Метод Карацубы с локализацией адресов (рекурсивная реализация)	1,7	5	12	44	145

Продолжение табл. 4.

Метод Карацубы с локализацией адресов (циклическая реализация)	1,7	5	12	43	142
Комбинированный метод (рекурсивная реализация, параметр перехода 64)	-	2,0	4,1	13	37
Комбинированный метод с локализацией адресов (рекурсивная реализация, параметр перехода 64)	-	2,0	4,0	12	35
Комбинированный метод с локализацией адресов (циклическая реализация, параметр перехода 64)	-	1,9	3,9	11	32
Последовательный алгоритм по комбинированному методу (параметр перехода 64)	-	7,0	7,5	9,7	18
Последовательный алгоритм по комбинированному методу с локализацией адресов (параметр перехода 64)	-	7,0	7,3	9,4	17

В четвертой главе проводится сравнительный анализ эффективности алгоритмов сложения точек эллиптической кривой и умножения точки кривой на константу с использованием аффинной и проективной систем представления операндов и усовершенствованных алгоритмов умножения, инвертирования и деления в конечных полях. Указанные алгоритмы рассматриваются как для суперсингулярных, так и для несуперсингулярных эллиптических кривых. Результаты экспериментов подтверждают рекомендации по применению проективных координат для выполнения операций в группе точек суперсингулярной и несуперсингулярной эллиптических кривых. Хотя использование ускоренного расширенного алгоритма Евклида существенно сокращает время деления в диапазоне степеней, характерных для криптографического применения, этого оказывается недостаточно для отказа от применения проективных координат, позволяющих сократить число выполнений делений за счет увеличения общего числа операций умножения. При этом применение оптимизированной в главах 2 и 3 операции умножения многочленов для выполнения операций над точками эллиптической кривой позволило сократить время умножения точки на константу на 5-15% в зависимости от типа кривой и порядка многочлена, образующего поле, в котором производятся вычисления.

В заключении даны выводы по результатам исследования.

В Приложениях приведены копии актов об использовании результатов диссертации.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

Обоснована целесообразность комбинирования метода умножения путем сдвигов и сложений и метода Карацубы.
Разработан метод автоматического синтеза последовательных программ умножения многочленов и метод аналитического сравнения производительности последовательных программ умножения.
Определены наилучшие условия применения последовательных программ умножения по методу А. Карацубы в процессе умножения многочленов высоких степеней над полями различных характеристик.
Выявлены области рекомендуемого применения методов при умножении многочленов высоких степеней над полями различных характеристик.
Проведен сравнительный анализ эффективности алгоритмов умножения точки эллиптической кривой на константу с использованием аффинной и проективной систем представления операндов и усовершенствованных алгоритмов умножения, инвертирования и деления в конечных полях.
Экспериментально подтверждены рекомендации по применению проективных координат в операциях умножения точки эллиптической кривой на константу.

СПИСОК РАБОТ, ОПУБЛИКОВАННЫХ ПО ТЕМЕ ДИССЕРТАЦИИ

Жебет С.Ю. Сравнительный анализ алгоритмов умножения бинарных многочленов в полиномиальном базисе // Вестник МЭИ, №6, 2006, Москва, Издательство МЭИ, с. 52-61.
Жебет С.Ю. Сравнительный анализ алгоритмов умножения многочленов над полями большой характеристики // Вестник МЭИ, №6, 2007, Москва, Издательство МЭИ, с. 84-90.
Жебет С.Ю., Фролов А.Б. Автоматический синтез программ умножения многочленов над конечным полем // Вестник МЭИ, №6, 2008, Москва, Издательство МЭИ, с. 59-71.
Жебет С.Ю., рук. Фролов А.Б., д.т.н., проф. Автоматизация проверки программ умножения в кольцах многочленов над конечными полями // Радиоэлектроника, электротехника и энергетика. Тезисы докладов 15 Международной научно-технической конференции студентов и аспирантов в 3-х т. – М.: Издательство МЭИ, 2009, Т.1, с. 256-257.
Жебет С.Ю., рук. Фролов А.Б., д.т.н., проф. Автоматизация программирования операции умножения в кольцах многочленов над конечными полями // 12-я Московская международная телекоммуникационная конференция студентов и молодых ученых "Молодежь и наука" .mephi.ru/reports.asp?rid=612
Жебет С.Ю., рук. Фролов А.Б., д.т.н., проф. Анализ автоматически сгенерированных схем умножения полиномов по методу Карацубы // Радиоэлектроника, электротехника и энергетика. Тезисы докладов 12 Международной научно-технической конференции студентов и аспирантов в 3-х т. – М.: Издательство МЭИ, 2006, Т.1, с. 360-361.
Жебет С.Ю., рук. Фролов А.Б., д.т.н., проф. Об одном методе оценки сложности алгоритма умножения многочленов над полем большой характеристики // Радиоэлектроника, электротехника и энергетика. Тезисы докладов 14 Международной научно-технической конференции студентов и аспирантов в 3-х т. – М.: Издательство МЭИ, 2008, Т.1, с. 395-396.
Жебет С.Ю., рук. Фролов А.Б., д.т.н., проф. Об одном методе уточнения оценки сложности алгоритма (на примере алгоритма умножения в кольце многочленов) // Научная сессия МИФИ-2007. Конференция «Молодежь и наука». Сборник научных трудов. В 17 томах. – М.: МИФИ, 2007, т.16, с. 110-111.
Жебет С.Ю., рук. Фролов А.Б., д.т.н., проф. Применение методов Фурье и Карацубы для оптимизации операции умножения полиномов // Радиоэлектроника, электротехника и энергетика. Тезисы докладов 11 Международной научно-технической конференции студентов и аспирантов в 3-х т.– М.: Издательство МЭИ, 2005, Т.1, с. 303.
Фролов А.Б., Гашков С.Б., Белова А.Ю., Морозов С.В., Жебет С.Ю., Щуров И.И. Программное средство "Алгебраический процессор"// В кн. Информатизация инженерного образования: электронные образовательные ресурсы МЭИ. Выпуск 3 / сост.: Ю.В.Арбузов, Т.И.Болдырева, А.И.Евсеев и др.; под общ. ред. С.И.Маслова. – М.: Издательский дом МЭИ, 2008. С.271-274.

Подписано в печать Зак. Тир. П.л.

Полиграфический центр МЭИ (ТУ)

Красноказарменная ул., д13

1 Карацуба А.А., Офман Ю.П. Умножение многозначных чисел на автоматах // ДАН СССР. Т. 145 №2. 1962 с. 293-294.

2 Schönhage A., Strassen V. Schnelle Multiplikation grosser Zahlen. // Computing №7 1971 p.281-292.

3 Lopez J., Dahab R. High Speed Multiplication in GF(2^m) // Proceedings of Indocrypt 2000, LNCS 1977. Springer, 2000. P.203-212.

4 Schroeppel R., Orman H., Malley S’O., Spatschek O. Fast Key exchange with elliptic curve systems // CRYPTO 95, Lecture Notes in Computer Science. 1995 № 963. P. 43-56

5 Болотов А.А., Гашков С.Б., Фролов А.Б., Часовских А.А. О методах имплементации арифметических операций в криптографических системах // Известия РАН. Теория и системы управления. 2002 №1 с 86-96.

6 А.А. Болотов, С.Б. Гашков, А.Б. Фролов. Элементарное введение в эллиптическую криптографию. Протоколы криптографии на эллиптических кривых.  М.: Комкнига, 2006.

7 Фролов А.Б. Алгебраический процессор [Электронный ресурс]: для студентов и аспирантов всех специальностей АВТИ /А.Б.Фролов, С.Б. Гашков, А.Ю.Белова, C.Ю. Жебет, С.В.Морозов, А.В.Панкин, И.И. Щуров,.  М.: Издательский дом МЭИ, 2008.

8 Здесь и далее все измерения времени выполнения алгоритмов проводились с использованием персонального компьютера со следующими характеристиками:

Процессор: Intel pentium4 2,8 ГГц. Оперативная память: 512 МБ. Операционная система: Windows XP SP2.

В процессе измерения времени было запущено только программное обеспечение, реализующее указанные алгоритмы.

Blog

Исследование программных методов реализации операций в конечных алгебраических структурах

Содержание