Алгебраические числа
| Вид материала | Документы |
- Тема «Пифагоровы тройки. Алгебраические и трансцендентные числа» Содержание, 292.96kb.
- Обмануть Мистера Фреймана), 10633 (На редкость простая задача, 509.81kb.
- Математичні константи, 30.08kb.
- Число 10. Состав числа, 39.75kb.
- Программа междисциплинарного вступительного экзамена в магистратуру по направлению, 101.8kb.
- Исследование выпуклости функции. Точки перегиба. Асимптоты функций. Понятие об асимптотическом, 31.41kb.
- Реферат №1 Строк здачі –5-й робочий тиждень Системи числення, 45kb.
- Экскурс в историю Алгебраические софизмы, 144.92kb.
- Рабочая программа курса «Элементарная математика» для студентов II курса по специальности, 25.95kb.
- Управление по сао главного управления мчс россии, 191.06kb.
АЛГЕБРАИЧЕСКИЕ ЧИСЛА
чл.-корр. РАН Ю.В. Нестеренко
1/2 года, 3 курс
обязательный для специализации “Математические методы защиты информации”
1. Конечные расширения полей. Степень поля. Поведение степени при расширении полей.
2. Степень простого расширения. Эквивалентность конечности и конечной порожденности алгебраическими элементами.
3. Алгебраические числа. Алгебраические числовые поля. Замкнутость множества алгебраических чисел относительно арифметических операций, алгебраическая замкнутость.
4. Теорема о примитивном элементе.
5. Нормальные расширения. Группа Галуа.
6. Норма и след в алгебраическом расширении, их свойства.
7. Дискриминант совокупности чисел и его свойства. Теорема о дискриминанте линейно независимой совокупности чисел.
10. Конечные поля.
11. Целые алгебраические числа. Кольцо целых алгебраического числового поля.
12. Идеалы алгебраического числового поля. Существование конечного
базиса.13. Фундаментальный базис и дискриминант поля.
14. Простые идеалы. Свойство максимальности простых идеалов.
15. Теорема Минковского о выпуклом теле. Следствие о решениях линейных неравенств.
16. Эквивалентные идеалы. Конечность числа классов поля.
17. Теорема о разложении идеалов в произведение простых.
18. Единицы и их свойства. Теорема Дирихле о единицах.
19. Отображение группы единиц в аддитивную группу
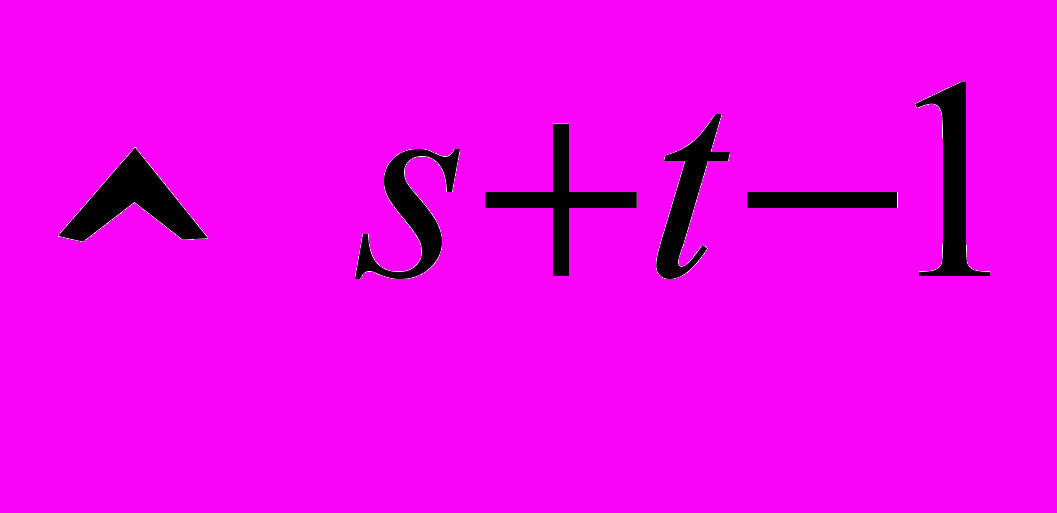. Структура ядра этого отображения. Оценка сверху ранга группы единиц.20. Существование
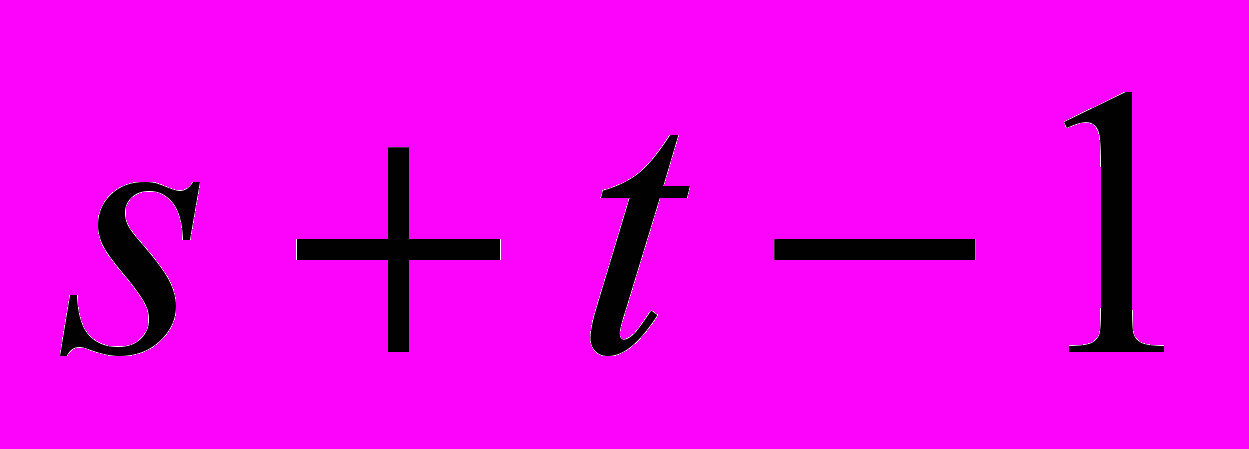независимых единиц. Завершение доказательства теоремы Дирихле.21. Норма идеала и ее свойства.
22. Теорема Куммера о разложении простых чисел в полях со степенным фундаментальным базисом.
23. Достаточные условия существования степенного фундаментального базиса.
Литература
1. Айерленд К., Роузен М. Классическое введение в современную теорию чисел. М., Мир, 1987.
2. Боревич З.И., Шафаревич И.Р. Теория чисел. М., Наука.
3. Гекке Э. Лекции по теории алгебраических чисел. Гостехиздат, 1940.
4. Ленг С. Алгебра. М., Мир, 1968.