«шаг в сторону»

Вид материала

Содержание

Подобный материал:

Урок 146, 147	13.04.
Множества и простейшие операции над ними.

1. Разбор к/р.

2. Новый материал. Прежде, чем приступить к решению неравенств, нам придется сделать «шаг в сторону», вспомнить, что мы знаем о множествах, дополнить и систематизировать эти сведения. Напомню, что множество – одно из фундаментальных понятий математики, поэтому ему нельзя дать определения, его можно только описать. Под множеством понимается совокупность любых объектов, взятых без учета их порядка. Эти объекты называют элементами множества.

Приведите примеры множеств и укажите их элементы (из алгебры, из геометрии, из «жизни»). Как записать, что объект является элементом множества? [1ÎR; АÎF]

Какими способами можно задать множества? Приведите примеры. [1) Перечисление элементов, запись: {1; 4; 5}; 2) характеристическое свойство элементов (признак, по которому составляется множество), например, множество простых чисел; множество целых чисел, кратных 5; множество домашних животных; {xÎR | x² + 3x + 2 = 0}; {(x; y) | x + y = 4} и т. д.]

Что такое пустое множество? Как оно обозначается? Приведите примеры [Æ; множество коров на Луне; множество треугольников со сторонами 1, 1 и 2; множество отрицательных чисел, больших 8; и т. д.].

Какое множество называется конечным? Приведите примеры. [Конечным называется множество, количество элементов которого можно выразить натуральным числом] Как называется непустое множество, не являющееся конечным? Приведите примеры. [Бесконечным]

Определение. Два множества называются совпадающими, если они состоят из одних и тех же элементов. В краткой форме: А º В Û "aÎA aÎB и "bÎB bÎA.

Примеры: 1) множество натуральных чисел и множество целых неотрицательных чисел; 2) {xÎR | x = 1} и {xÎZ | (x – 1)(x² – 3) = 0}, и т. д.

Основной характеристикой конечного множества является количество его элементов. Если рассмотреть два множества с одинаковым количеством элементов, то можно составить пары так, чтобы элементы не повторялись.

Например, А = {a; b; c; d}; B = {1; 2; 3; 4}. Составьте пары. Мы можем сделать это различными способами, но в любом случае каждому элементу из А будет соответствовать ровно один элемент из В, и наоборот. Такое соответствие между множествами называется взаимно однозначным. В каком случае можно установить соответствие между конечными множествами?

Если множества – бесконечны, то роль количества элементов играет характеристика, называемая мощностью множества. Говорят, что множества равномощны, если между ними можно установить взаимно однозначное соответствие.

Пример. N и {2n}. Каждому натуральному числу можно поставить в соответствие число, которое в два раза больше, и такое соответствие будет взаимно однозначным.

Все множества, равномощные N называют счетными. Примеры: {

}; Q; и т. д. Естественно, существуют множества, более мощные, чем N, например, R.

Более подробно об этом рассказывалось на кружке. Кроме того, желающие могут обратиться к литературе: ЭЮМ; Н. Я. Виленкин «Рассказы о множествах»; «Игры с бесконечностью» и пр.

3. Упражнения (самостоятельно в тетрадях с устной проверкой).

1) Запишите с помощью перечисления элементов множество

а) положительных чисел, кратных 4 и меньших 20;

б) одноцветных шахматных фигур;

в) {xÎR | x² + 5 = 6}

2) Запишите с помощью характеристического свойства множество: {7; 14; 21; 28; ...}

3) A = {xÎR | x² + * £ 0} Какими числами можно заменить знак *, чтобы множество А было:

а) пустым; б) конечным; бесконечным?

4. Новый материал. Что означает запись: АÌВ? [A – подмножество В]

Определение. АÌВ Û "аÎА аÎB. Сформулируйте. Напомню, что множество и его подмножества принято изображать с помощью кругов Эйлера (показать на доске, см. рис. 1).

Рис. 1
Устно: 1) Чем различаются записи: аÎA и {a}ÌA?

2) Верно ли, что "А а) ÆÌА; АÌА? Почему?

3) Сравните множества М и K, если МÌK и KÌM.

4) Является ли отношение «Ì» между множествами отношением эквивалентности?

Рассмотрим две основные операции алгебры множеств, которые являются аналогами операций сложения и умножения чисел соответственно.

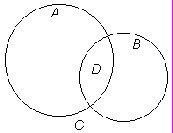
Рис. 2
Определения. 1) AÈB = C = {x | xÎA или xÎB} 2) AÇB = D = {x | xÎA и xÎB}.

Сформулируйте и изобразите (на доске и в тетрадях, см. рис. 2). Понятно, что аналогичным образом можно определить эти операции не для двух, а для любого конечного числа множеств. Для введенных операций выполняются законы, аналогичные законам сложения и умножения чисел и законам сложения векторов и умножения вектора на число.

AÈB = ВÈА	AÇB = ВÇА	переместительный закон
(AÈB)ÈС = АÈ(BÈС)	(AÇB)ÇС = АÇ(BÇС)	сочетательный закон
АÈÆ = А	АÇÆ = Æ	закон поглощения пустого множества
(AÈB)ÇС = (AÇС)È(BÇС)		распределительные
(AÇB)ÈС = (AÈС)Ç(BÈС)		законы

Как доказать эти законы? [Доказываем, что любой элемент левой части является элементом правой части и наоборот, используя определения и круги Эйлера] Докажите один из распределительных законов (устно).

Устно: Как связаны множества А и В, если: а) AÈB = А; б) AÇB = А; в) AÈB = AÇB?

[а) ВÌА; б) АÌВ; в) А º В]

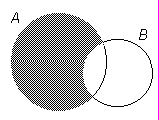
Кроме рассмотренных операций над множествами иногда применяется еще одна операция, являющаяся аналогом вычитания.

Определение. А\B = {xÎR | xÎA и xÏB} (см. рис. 3)

Рис. 3
5. Упражнения (самостоятельно в тетрадях с устной проверкой).

1) Запишите объединение и пересечение множеств:

а) А = {1; 3; 5; 7}; B = {2; 3; 5; 4}; б) натуральных и простых чисел; в) ромбов и прямоугольников.

2) Найдите: а) R\Q; б) А\Æ; в) Æ\А; г) {параллелограммов}\{вписанных четырехугольников}; д) {вписанных четырехугольников}\{параллелограммов} [г) параллелограммы, не являющиеся прямоугольниками; д) вписанные четырехугольники, не являющиеся прямоугольниками]

Домашнее задание: основные определения и законы – по тетради; Т.: п. 30 – прочитайте самостоятельно; №876; Зад.: №6.75; №6.100 (в); №6.104; №6.79. Оцените, в каких границах может быть средний по величине угол треугольника.

Blog

«шаг в сторону»

Содержание