Проект «Площади многоугольников»
| Вид материала | Документы |
- Урок геометрии в 8 классе по теме «Площади многоугольников», 52.25kb.
- Геометрия Площадь многоугольника, 23.87kb.
- Тема. Построение правильных многоугольников, 82.73kb.
- ТемЫ рефератов по мерчендайзингу, 204.9kb.
- Разработка урока по теме «Понятие площади многоугольника», 32.86kb.
- Прайс – Дизайн Проект, стоимость услуг за 1 кв м. при площади, 76.4kb.
- «Решение задач на построение сечений многоугольников», 72.88kb.
- Механика Жидкостей и Газов, 12.81kb.
- Блиц (матан и триг.) блиц (геометрия) Вопросы по планиметрии, 56.04kb.
- Городские тематические экскурсии, 85.03kb.
Проект « Площади многоугольников»
Автор проекта: учитель математики Верхнеиндырчинской основной школы Апастовского муниципального района Республики Татарстан Курмашева А.А.
Участники проекта : учащиеся 8 класса
Дидактические цели проекта:
1.Расширить знания учащихся о треугольниках, квадратах, прямоугольниках и трапециях, их элементах и их площадях как с математической точки зрения, так и с других точек зрения ( исторической, географической, в повседневной жизни)
2.Развить творческую активность учащихся, умение делать обобщения на основе данных, полученных в результате исследований.
3.Развить познавательную деятельность учащихся, которая в свою очередь, способствует развитию разносторонней личности.
4. Воспитывать у учащихся стремление к самосовершенствованию, удовлетворению познавательных потребностей.
Основными задачами проекта являются
- формирование у учащихся понятия площади многоугольников;
- развитие исследовательских навыков;
- развитие познавательного интереса для их дальнейшего самообразования;
- формирование навыков проектной работы.
Прогнозируемые результаты
В результате выполнения проекта «Площади многоугольников» учащиеся должны:
- знать определения треугольника, квадрата, прямоугольника и трапеции, формулы их площадей;
- продемонстрировать осведомленность о практическом применении площадей этих фигур;
- знать сведения вычисления площадей в древности;
- получать навыки анализа и систематизации полученных ранее знаний; навыки выполнения проектной работы;
- самостоятельно работать с дополнительной литературой.
Гипотеза
В древних египетских и вавилонских математических документах встречаются следующие виды четырехугольников : квадраты, прямоугольники, равнобедренные и прямоугольные трапеции. Потребность измерения расстояний и площадей привела к появлению зачатков геометрических знаний в глубине тысячелетий. Изучение площадей плоских фигур вызвало у учащихся большой интерес и побудило их к более глубокому изучению свойств треугольника, квадрата, прямоугольника и трапеции и их площадей, как с математической точки зрения, так и с других точек зрения ( исторической, географической, в повседневной жизни)
Рабочие группы и вопросы для исследования
Группа «Исследователи свойств многоугольников»
- Изучить свойства треугольника, квадрата, прямоугольника и трапеции.
- Найти определения треугольника, квадрата, прямоугольника и трапеции, которые были сформулированы древними учёными.
- Сравнить современные трактовки с древними.
Группа «Исследователи площадей многоугольников»
Изучить доказательства площадей треугольника, квадрата, прямоугольника и трапеции
Группа «Историки»
Найти информацию о нахождении площадей древними учёными.
Группа « Практики»
1. Найти материал, подтверждающий применение площадей в архитектуре и строительстве.
2.Найти материал, подтверждающий применение площадей в географии.
Во время отчетов рабочих групп учитель следит за их выводами и делает свои выводы, в заключении даёт оценку работе каждой группы.
Отчётные материалы
1.Создание презентации (слайды, рисунки)
2. Подготовка сообщений.
Описание проекта.
Проект посвящён свойствам и площадям треугольника, квадрата, прямоугольника и трапеции. В проекте участвовало 4 рабочих групп:
- Исследователи свойств многоугольников
- Исследователи площадей многоугольников
- Историки
- Практики
Первая группа исследователей свойств многоугольников изучала определения и свойства треугольника, квадрата, прямоугольника и выяснила следующее:
В учебнике « Геометрия 7-11» , автор Погорелов А.В.дано определение треугольника «Треугольником называется фигура , которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки». Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
Замечательные линии и точки в треугольнике.
Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника ( точка O, рис.26 ) расположен внутри треугольника, а ортоцентр тупоугольного треугольника ( точка O, рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника ( AD, BE, CF, рис.28 ) пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника ( AD, BE, CF, рис.29 ) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).
Средняя линия треугольника – это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине его основания и параллельна ему.
Параллелограмм ( ABCD, рис.32 ) – это четырёхугольник, противоположные стороны которого попарно параллельны.
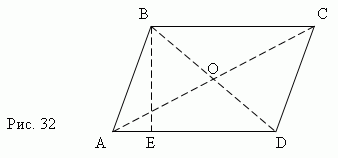
Любые две противоположные стороны параллелограмма называются его основаниями, а расстояние между ними – высотой ( BE, ).
Свойства параллелограмма.
1. Противоположные стороны параллелограмма равны ( AB = CD, AD = BC ).
2. Противоположные углы параллелограмма равны (
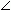 A =
A = 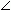 C,
C, 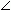 B =
B = 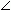 D ).
D ).3. Диагонали параллелограмма делятся в точке их пересечения пополам ( AO = OC, BO = OD ).
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон:
AC² + BD² = AB² + BC² + CD² + AD² .
Признаки параллелограмма.
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
1. Противоположные стороны попарно равны ( AB = CD, AD = BC ).
2. Противоположные углы попарно равны (
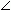 A =
A = 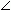 C,
C, 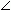 B =
B = 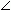 D ).
D ). 3. Две противоположные стороны равны и параллельны ( AB = CD, AB || CD ).
4. Диагонали делятся в точке их пересечения пополам ( AO = OC, BO = OD ).
Прямоугольник.
Если один из углов параллелограмма прямой, то все остальные углы также прямые . Такой параллелограмм называется прямоугольником ( рис.33 ) .
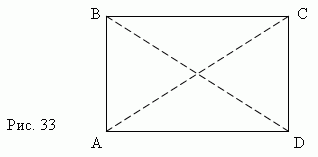
Основные свойства прямоугольника.
Стороны прямоугольника являются одновременно его высотами.
Диагонали прямоугольника равны: AC = BD.
Квадрат диагонали прямоугольника равен сумме квадратов его сторон ( см. выше теорему Пифагора ):
AC 2 = AD 2 + DC 2 .
Ромб. Если все стороны параллелограмма равны, то этот параллелограмм называется ромбом .
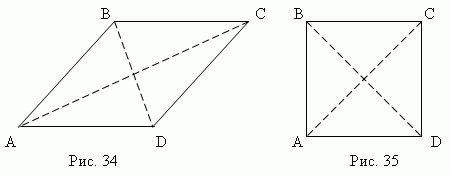
Диагонали ромба взаимно перпендикулярны ( AC
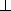 BD ) и делят их углы пополам (
BD ) и делят их углы пополам ( 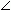 DCA =
DCA = 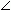 BCA,
BCA, 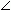 ABD =
ABD = 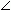 CBD и т.д. ).
CBD и т.д. ).Квадрат – это параллелограмм с прямыми углами и равными сторонами. Квадрат является частным случаем прямоугольника и ромба одновременно; поэтому он обладает всеми их вышеперечисленными свойствами.
Трапеция - это четырёхугольник, у которого две противоположные стороны параллельны .
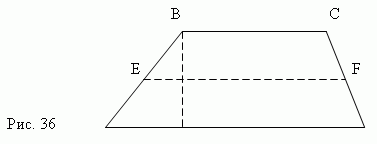
Здесь AD || BC. Параллельные стороны называются основаниями трапеции, а две другие ( AB и CD ) – боковыми сторонами. Расстояние между основаниями ( BM ) есть высота. Отрезок EF, соединяющий средние точки E и F
боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований:
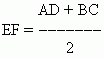
и параллельна им: EF || AD и EF || BC.
Трапеция с равными боковыми сторонами ( AB = CD ) называется равнобочной трапецией. В равнобочной трапеции углы при каждом основании равны (
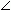 A =
A = 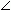 D,
D, 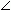 B =
B = 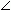 C ).
C ). Параллелограмм может рассматриваться как частный случай трапеции.
Группа исследователей площадей плоских фигур выяснила
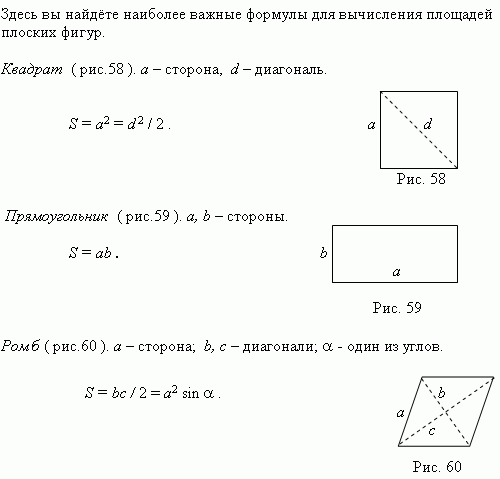

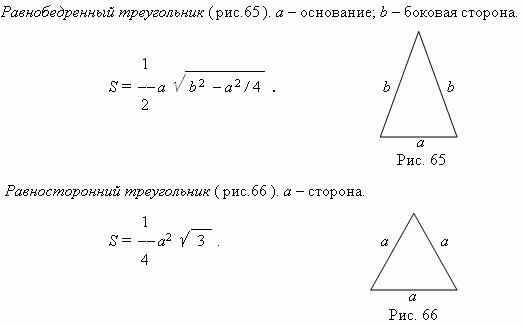
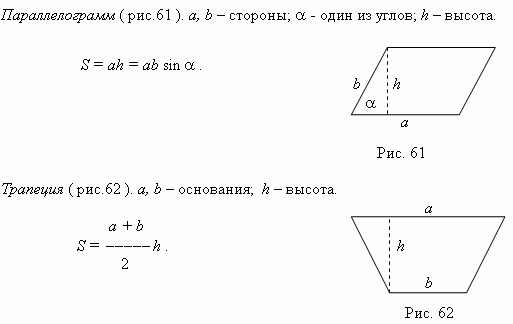

Произвольный треугольник. a, b, c – стороны; a – основание; h – высота;
A, B, C – углы, противоположные сторонам a, b, c ; p = ( a + b + c ) / 2.
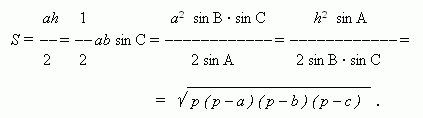
Последнее выражение называется формулой Герона.
Однако данные определения существовали не всегда. Группа историков выяснила, что возникновение геометрии уходит вглубь тысячелетий и связано, прежде всего, с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением за окружающим миром. Об этом свидетельствуют названия геометрических фигур. Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик), от которого также произошло слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус», а термин «линия» возник от латинского «линиум» (льняная нить). Одна из главных величин в геометрии - площадь. Площадь - это величина, характеризующая размер той части плоскости, которая заключена внутри плоской замкнутой фигуры. Обозначается буквой S.
Основная ее задача - измерить площадь, т.е. найти число, которое выражало бы эту величину. Другими словами необходимость установить некоторое соотношение между площадями фигур и числами, их выражающими. Чтобы измерить площадь фигуры, надо, прежде всего, выбрать единицу измерения площади. Такой единицей является квадрат, сторона которого равна некоторой единице измерения. Площади простейших фигур можно определить следующим образом: накладываем единичные квадраты на измеряемую площадь, столько раз, сколько возможно, и подсчитываем количество уместившихся квадратов. Полученное число и есть искомая площадь фигуры.
Египет.
Если не учитывать весьма малый вклад древних обитателей долины между Тигром и Евфратом, и Малой Азии, то геометрия зародилась в Древнем Египте где-то в 1700 году до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения
нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянам стали такие виды их деятельности, как возведение пирамид и изобразительное искусство. Египтяне при применении геометрических знаний всецело руководствовались интуицией и приближенными представлениями.
Греция.
Около 600 года до н.э. ионийские греки, совершившие путешествие в Египет, привезли на родину первые сведенья о геометрии. Самым известным путешественником в Египет был Фалес (ок. 640-ок.546 до н.э.). Он был преуспевающим купцом, посвятившим последние годы жизни науке и политике.
Фалес первым начал доказывать истинность геометрических соотношений, последовательно выводя их логически из некоторого набора метод дедуктивного
рассуждения, которому представало стать доминирующим в геометрии и фактически - во всей математике, сохраняя свое фундаментальное значение и в наши дни.
Группа историков разыскала
Задачи царицы Дидоны
Задачи, в которых требуется определить условия, при которых некоторая величина принимает наибольшее или наименьшее значение, принято называть задачами “на экстремум” (от лат. слова extremum – “крайний”) или задачами “на максимум и минимум” (от латинских maximum и minimum –соответственно “наибольшее” и “наименьшее”). Такие задачи очень часто встречаются в технике и естествознании, в повседневной практической деятельности людей. Из всех геометрических задач на экстремум считается самой простой и самой древней: “Какой из всех прямоугольников заданного периметра имеет наибольшую площадь?”. Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в VI книге “Начал” Евклида, где доказывается, что, если рассмотреть прямоугольник и квадрат одного и того же периметра, то площадь квадрата будет больше. Доказательство основано на сравнении площадей. Площадь прямоугольника равна
 , а площадь квадрата
, а площадь квадрата  и
и  , если
, если  . Таким образом, получили, что из всех прямоугольников с заданным периметром наибольшую площадь имеет квадрат.
. Таким образом, получили, что из всех прямоугольников с заданным периметром наибольшую площадь имеет квадрат. В решении Евклида, во-первых, указан ответ (квадрат) и, во-вторых, доказано, что по площади он превосходит все другие возможные фигуры (прямоугольники заданного периметра). Именно так понимают в математике решения задачи на экстремум: дать ответ и доказать его экстремальное свойство.
Геометрические задачи, в которых отыскивается фигура с экстремальным свойством среди других фигур с равным периметром, называются изопериметрическими. Такие задачи рассматривал древнегреческий математик Зенодор (II-I вв. до н.э.). Например, Зенодор утверждал, что:
1) из всех многоугольников с равным периметром и равным числом сторон наибольшую площадь имеет правильный многоугольник;
2) из двух правильных многоугольников с равным периметром большую площадь имеет тот, у которого число углов больше;
3) из всех плоских фигур с равным периметром наибольшую площадь имеет круг.
Строгое доказательство третьего утверждения Зенодора было доказано только в XVIII веке знаменитым математиком Л. Эйлером.
Изопериметрические задачи известны также под названием “задачи Дидоны” по имени легендарной основательницы города Карфагена и его первой царицы. Согласно легенде, вынужденная бежать из своего родного города, царица Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей место для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узенькие ремешки и, разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было бы покрыть шкурой целиком. Если учесть, что Дидона выбирала участок, примыкающий к берегу морю, то на языке математике задачу, стоящую перед Дидоной можно сформулировать так: какой формы должна быть кривая длины l, чтобы площадь фигуры, ограниченная этой кривой и заданной линией Г, была наибольшей.
Группа историков обнаружила головоломки « Танграм»
История головоломки "Танграм"
Головоломка "Танграм" - квадрат, разрезанный на 7 частей из которых составляют различные силуэты. Он появился в Китае в конце восемнадцатого века (рисунок). Первое ее изображение (1780 г.) обнаружено на ксилографии японского художника Утамаро, где две девушки складывают фигурки "чи чао ту" - так называется ташрам на его родине (в переводе - умственная головоломка из семи частей"). Название танграм возникло в Европе вероятнее всего от слова "тань" (на кантонском диалекте - китаец) и часто встречающегося греческого корня "грамма" (буква). Впрочем, авторы многих книг по занимательной математике приписывают изобретение танграма якобы жившему 4 тысячи лет назад в Китае ученому Тангу. Эта тщательно разработанная легенда от начала до конца выдумана изобретательным автором головоломок Сэмом Лойдом.
Рисунки, составленные из частей танграма
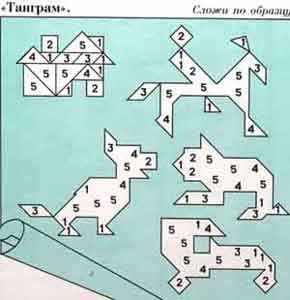
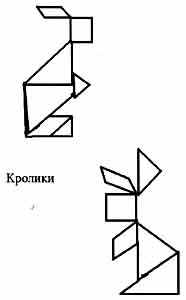
Рисунки, составленные из частей Колумбова яйца
4. Головоломка Наполеона
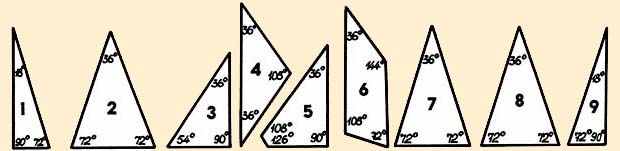
Очевидцы рассказывают, что среди прочих математических, шахматных и тактических задач по военному искусству император Наполеон любил задавать своим офицерам и эту головоломку: какие плоские геометрические фигуры можно построить из девяти предложенных в россыпь деталей?
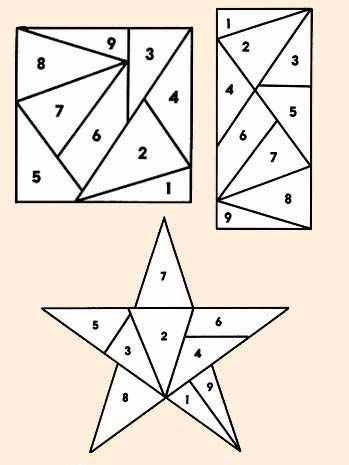
Простую с виду задачу решить удавалось не каждому. Маршал Даву, говорят, сумел собрать из предложенных деталей квадрат, а Мюрат - и квадрат, и прямоугольник. Позже нашелся полковник, построивший звезду. Но никто до сих пор не сумел построить из этих деталей треугольник, ромб или трапецию... Да и есть ли решение вообще?
Н
 о прежде чем браться за решение головоломки, обратите внимание на одну особенность углов в деталях треугольной и четырехугольной формы: 18, 36, 90, 108, 126, 144о. Заметили - они кратны цифре 18? Почему? Может, именно в этой кратности скрыта подсказка?
о прежде чем браться за решение головоломки, обратите внимание на одну особенность углов в деталях треугольной и четырехугольной формы: 18, 36, 90, 108, 126, 144о. Заметили - они кратны цифре 18? Почему? Может, именно в этой кратности скрыта подсказка? Всё вышеизложенное говорит о том, площади многоугольников интересны не только с исторической и математической точек зрения, но они представляют интерес и в повседневной жизни.
Группа «практиков» выяснила следующее.
Без знаний о площадях многоугольников невозможно представить развитие архитектуры и дизайнерского искусства. Благодаря точным расчётам площадей составляющих геометрических фигур нельзя создать шедевры с исторической точки зрения, как Исаакиевский собор.
Уместно будет высказывание выдающегося французского архитектора Ле Корбюзье :
«Человеку , сведущему в геометрии и работающему с нею, становятся доступны…все те высшие наслаждения, которые называются наслаждениями математического порядка…Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Стоит поразмыслить о прошлом, вспомнить то, что было ранее, и мы будем ошеломлены, видя, что окружающий нас мир- это мир геометрии, чистой, истинной, в наших глазах. Всё вокруг- геометрия. Никогда мы не видели так ясно таких форм, как круг, прямоугольник, угол, цилиндр, шар, выполненных так отчётливо, с такой тщательностью и так уверенно»
 Рис.
Рис.Фантазия архитектора может достигнуть и таких форм и это придает зданию весьма оригинальный вид.

Строительное производство сегодня — это механизированный процесс сборки зданий и сооружений из крупноразмерных деталей, изготовленных заводским способом. Столяр работает в строительно-монтажных организациях, на деревообрабатывающих предприятиях, в столярных мастерских. Он выполняет различные операции на станках: на круглопильных — раскрой пиломатериалов, на фуговальных — строгание, на долбежных и шипорезных — выдалбливание гнезд и нарезание шипов у заготовок.
Непосредственно на строительном объекте столяр устанавливает оконные и дверные блоки, производит настилку дощатых и паркетных полов, монтирует встроенную мебель и т. д. Выполнение такой работы невозможно без знания устройства и правил эксплуатации деревообрабатывающих станков, знания технологии и организации строительного производства, умения читать чертежи. Профессия требует объемного воображения, хорошего глазомера, знания геометрии, рисования, черчения. Это лишь одна строительная профессия, а их очень много. Во всех случаях невозможно обойтись без знаний геометрии, без расчетов площадей поверхностей пола , стены , крыши.
Группа практиков выяснила следующее, что в геодезии- науке об определении положения объектов на земной поверхности, о размерах, форме и гравитационном поле Земли и других планет также применяются знания геометрии . Это отрасль прикладной математики, тесно связанная с геометрией, математическим анализом, классической теорией потенциала, математической статистикой и вычислительной математикой. В то же время это наука об измерениях, разрабатывающая способы определения расстояний, углов и силы тяжести с помощью различных приборов.
Геодезические работы ведутся на трех уровнях. Во-первых, это плановая съемка на местности – определение положения точек на земной поверхности относительно местных опорных пунктов для составления топографических карт, используемых, например, при строительстве плотин и дорог или составлении земельного кадастра. Следующий уровень включает проведение съемок в масштабах всей страны; при этом площадь и форма поверхности определяются по отношению к глобальной опорной сети с учетом кривизны земной поверхности.
ВЫВОД.
Во время подготовки к проекту каждой группе пришлось выполнять свою работу . Каждый из них получил большой запас знаний не только из области математики, но и из области истории, геодезии, архитектуры. Все приобретённые знания помогут стать более образованными и интересными людьми.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.
6. Используемая литература.
1. «Геометрия 7 - 9 класс». Авторы –Л.С. Атанасян и др.
2. «Справочник по начальной математике» Автор - С. Лукьянченко.
3. «Справочник по высшей математике» Автор - С. Лукьянченко.
4. «Математическая энциклопедия» Авторы - М. Ю. Серебряков, Л. В. Кузнецова
5. «Школьникам о математике и математиках» Автор- М.М. Лиман.
6. «История математики в школе.VII- VIII классы».Автор- Г.И. Глейзер.
7. «Словарь-справочник по математике». Автор-Н.И. Александров , И.П. Ярандай.
8. «Математика в понятиях, определениях и терминах» Авторы- О. В. Мантуров и др.
Этапы, описание выполняемых работ.
| Сроки | Этапы | Деятельность учащихся | Деятельность учителя |
| 18.11.2006-22.11.2006 | I. Организационно - подготовительный | Обсуждение темы проекта, его целей и задач; разработка плана реализации идеи; распределение тем исследований между учащимися | Представление проблемной ситуации с помощью мультимедийных средств; формирование мотивации участников, создание инициативной группы учащихся, консультирование по выбору тематики и жанра проекта; помощь в подборке необходимых материалов, определение лишь общего направления и главных ориентиров поиска; определение критериев оценки деятельности учащихся на всех этапах |
| 23.11.2006-7.12.2006 | II.Поисковый | Сбор, анализ и систематизация необходимой информации; обсуждение ее в микрогруппах; выдвижение и проверка гипотез; оформление макета или модели проекта; самоконтроль | Регулярное консультирование по содержанию проекта, помощь в систематизации и обобщении материалов, индивидуальные и групповые консультации по правилам оформления проекта, стимулирование умственной активности учащихся, отслеживание деятельности каждого участника, оценка промежуточных результатов, мониторинг совместной деятельности |
| 8.12.2006-18.12.2006 | III. Итоговый | Оформление пакета документов по проекту и информационных стендов, схем, диаграмм; подготовка устной презентации и защита содержания проекта; рефлексия: выдвижение, прогнозирование новых проблем, вытекающих из полученных результатов | Помощь в разработке отчёта о работе, подготовка выступающих к устной защите, отработка умения отвечать на вопросы оппонентов и слушателей, выступление в качестве эксперта на защите проекта, участие в анализе проделанной работы, оценка вклада каждого из исполнителей |
Схема организации работы по проекту. Этапы реализации.
I. Подготовительный - «Мозговой штурм».
Подготовительный этап:
Представление проблемной ситуации с помощью мультимедийных средств.
Распределение по группам.
Выбор темы исследования учащимися.
Выбор творческого названия проекта.
Основной этап:
Выбор творческого названия проекта.
Разработка целей и задач.
Обсуждение с учащимися возможных источников информации, критериев оценки результата исследования.
Обсуждение предстоящих исследований
Заключительный этап:
Обсуждение индивидуальных планов работы учащихся.
Обсуждение необходимого оборудования.
II. Основной - «Консультация в группах».
Подготовительный этап:
Сбор, анализ и систематизация необходимой информации.
Советы педагога по усовершенствованию работы.
Консультации по сбору и обработки материала.
Основной этап:
Разрешение проблем, возникших в ходе самостоятельной работы.
Выдвижение и проверка гипотез.
Оценка промежуточных результатов.
Мониторинг совместной деятельности.
Заключительный этап:
Оформление макета или модели проекта.
III.Заключительный - «Конференция».
Подготовительный этап.
Подготовка оборудования к показу работ.
Подготовка сценария проведения дискуссии.
Подготовка устной презентации и защита содержания проекта.
Основной этап:
Демонстрация творческих разработок учащихся по группам.
Защита содержания проекта.
Обсуждение, оценка актуальности.
Заключительный этап:
Оценка результатов деятельности учащимися, одноклассниками, учителем.
рефлексия: выдвижение, прогнозирование новых проблем, вытекающих из полученных результатов.
ГОУ гимназия № 1567
Автор проекта: Купраш Анна Дмитриевна
Руководитель проекта:
учитель математики
Такуш Елена Валентиновна
Тема: «Площади многоугольников».
Цель проекта: Изучение площадей фигур. используя идею равновеликости.
Задачи:
- Проанализировать литературу и обобщить информацию по данной теме.
- Найти нетрадиционные доказательства теорем о площадях треугольников.
- Применить теорию равновеликости фигур для решения задач.
Работа состоит из трех частей.
В первой части работы были выведены формулы площадей некоторых многоугольников, при этом были использованы только идея равновеликости фигур и основные свойства площадей:
1) Равные многоугольники имеют равные площади;
2) Если многоугольник составлен из двух многоугольников, не имеющих внутренних точек, то его площадь равна сумме площадей этих многоугольников;
3) Площадь квадрата со стороной, равной единице длины, равна 1 (единице измерения площадей).
Во второй части работы были решены задачи о площадях с использованием тех же свойств площадей.
В третьей части работы были исследованы положения прямых, разбивающих фигуры на две равновеликие части.
В работе были рассмотрены такие задачи, как:
- На стороне параллелограмма была взята точка, была рассмотрена зависимость площади получившегося треугольника от площади параллелограмма. Также была решена аналогичная задача для точки, лежащей внутри параллелограмма;
- Исследование площадей параллелограммов с парой сторон, лежащих на параллельных прямых;
- Применение свойства медиан для решения задач;
- Задачи о разрезании фигур на две равновеликие части.
Практическая значимость работы определяется возможностью использования данного материала на уроках геометрии для расширения геометрического кругозора учащихся.
