Тезисы докладов научной конференции «математические модели сложных систем и междисциплинарные исследования»

Вид материала

Тезисы

Содержание Дополнительные доклады В.И. Голов, А.И. Поташев П.С. Краснощеков, В.В. Федоров, Ю.А. Флеров

Подобный материал:

• Тезисы докладов будут размещены на сайте конференции, 22.56kb.
• Тезисы докладов 1 Межвузовская научно -практическая конференция студентов и молодых, 100.64kb.
• Отчет о работе программы в 2010 году Институты-исполнители, 663.35kb.
• 1. Введение. Основные понятия моделирования Общая характеристика проблем моделирования., 38.29kb.
• Программа 3 информационные и вычислительные технологии в задачах поддержки принятия, 598.4kb.
• Рабочая программа наименование дисциплины Математические модели в теории, 197.61kb.
• Математическое моделирование (вопросы к экзамену), 89.87kb.
• Вопросы к экзамену в 3 учебном семестре По дисциплине «Математические методы и модели, 15.89kb.
• Программа II всероссийской молодёжной научной конференции, 133.96kb.
• I научная конференция, 34.22kb.

Дополнительные доклады

Применение методов классической томографии для характеризации мишени при сканировании естественным светом В.И. Голов, А.И. Поташев	46
0 целесообразности математического моделирования концепций народного просвещения РФ, Д.Р. Гончар	47

Декомпозиция в задачах проектирования

П.С. Краснощеков, В.В. Федоров, Ю.А. Флеров


1. Задача проектирования сложной технической системы рассматривается в следующей постановке:

найти    X* = max (X, Fε)

(1)

Здесь X — множество альтернатив проектируемой системы, X — множество максимальных элементов из X по отношению к F^ε. Бинарное отношение за X задается в виде

x'Fεx"  Wj (x')Wj (x") – ε, j = 1, …, m,

(2)

Где ε  0, W(x) = (W¹(x), …, W^m(x)) — векторный критерий эффективности, Wⁱ(x) — частные критерии.

2. Метод последовательного анализа вариантов (декомпозиция в пространстве критериев). Введем систему бинарных отношений V₁, …, V_p на множестве X, аппроксимирующих отношение F^ε «изнутри»: V^k  F^ε , k = 1, …, p, и предположим «полноту» этой системы — F^ε = 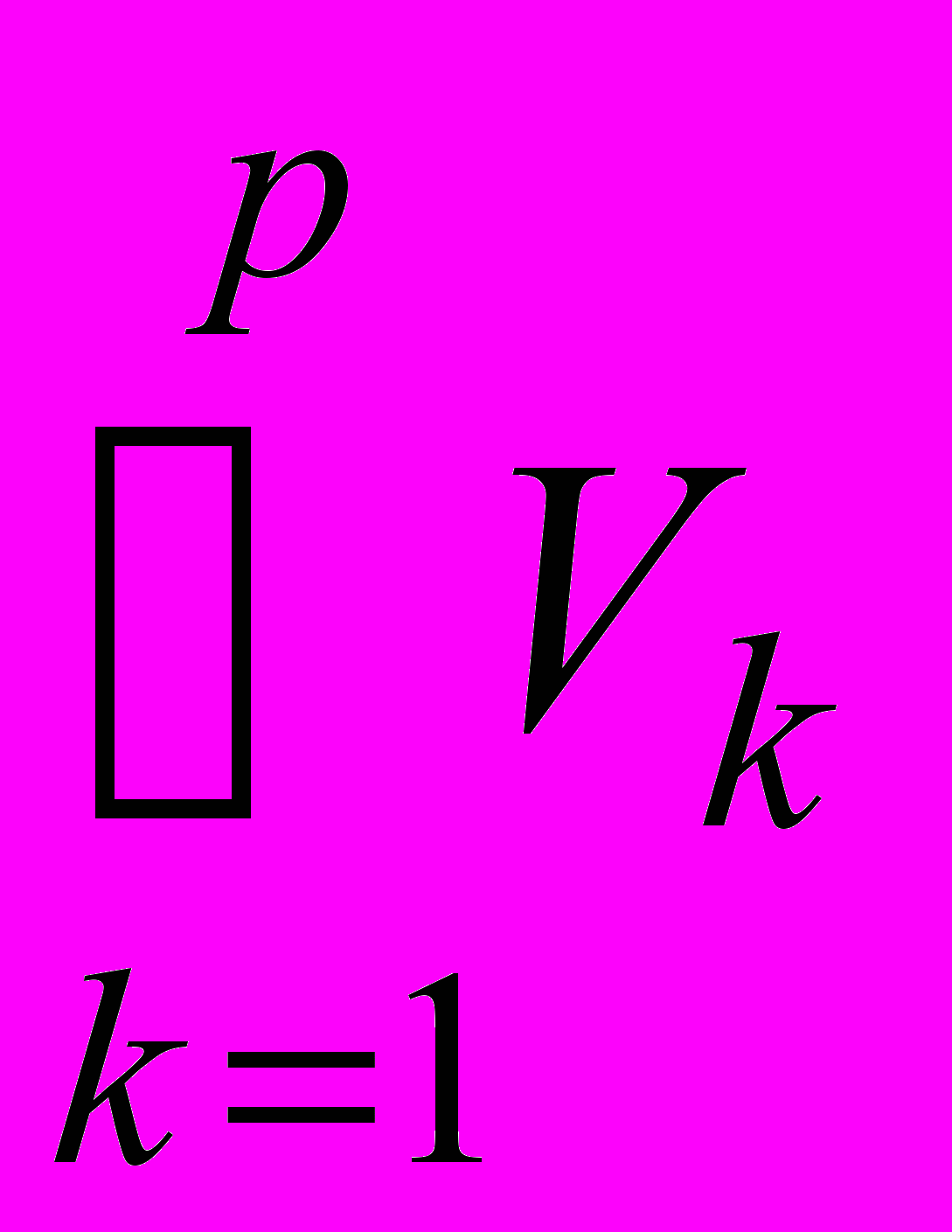. Тогда решение задачи (1) может быть получено по схеме последовательного анализа вариантов: X^*₀ = X, X^*_k = max(X^*_k–1, V_k), k = 1, …, p. Показано, что используя самую общую информацию о бинарном отношении F^ε, можно построить искомое «простое» бинарное отношение V  F^ε.

3. Декомпозиция на основе агрегирования (декомпозиция в пространстве параметров). Рассмотрим задачу проектирования сложной технической системы (1), (2), полагая ε = 0. Введем множества X_k = X, X_i = r_i(X_i+1), i = k–1, …, 1, где r_i — функция агрегирования, и определим вспомогательные бинарные отношения F_j^(j) на множествах X_i, порожденные частными критериями , которые определяются как и отношение F^ε в (2). При агрегировании предпологается, что чем меньше индекс i, тем проще устроены множества X_i, и тем легче вычисляются значения . Для решения задачи используется рекуррентная схема. Решение X^*_k совпадает с X^*, если X^* — внешне устойчиво и отношения F_j^(j) согласованы с агрегированием. Пусть заданы критерии ; i = 1, …, k; j = 1, …, q. Для построения системы согласованных отношений определяются величины _i.

Теорема. Пусть _i – _i+1  _i  i = 1, …, k–1. Тогда отношения F_j^j, отвечающие , согласованы с агрегированием.

Основные понятия
геометрической теории декомпозиции¹

Ю.Н. Павловский

Геометрическая теория декомпозиции (ГТД) [1 — 3] является языковой средой, ориентированной на изучение декомпозиций математических объектов. В основе ГТД лежат два двойственных друг другу понятия — понятие о Р-декомпозиции математического объекта и понятие о его F-декомпозиции. Упрощая и огрубляя ситуацию, можно сказать, что Р-декомпозиция есть такое семейство подобъектов данного объекта, по которому он восстанавливается единственным образом, а F-декомпозиция — обладающее аналогичным свойством семейство его фактор-объектов. Для того, чтобы воспользоваться средствами ГТД, необходимо погрузить изучаемый объект в бурбаковское исчисление родов структур с морфизмами [4].