Программа 3 информационные и вычислительные технологии в задачах поддержки принятия решений отчет

Вид материала

Программа

Содержание Координатор программы Отчеты по проектам Основные (важнейшие) результаты Влияние структуры высокочастотного (ВЧ) разряда на процесс плазмохимического травления кремния в CF Рис. 9. Распределение концентрации фтора C Г. Г. Черных, д.ф.-м.н,. г.н.с. Моделирование работы насыпного фильтра для охлаждения высокотемпературных продуктов сгорания твердотопливного газогенератора. А.Д. Рычков, д.т.н., г н.с. Общая характеристика выполненных в 2009 г. работ. Повышение разрешения изображений динамической сцены. Повышение четкости изображений, получаемых с конфокального микроскопа. Оценивание пространственно-временной динамики поведения биологических объектов. Алгоритм управления движением автономного подвижного аппарата. Исследование группы нелинейных перспектив для систем отображения визуальной информации. Общая характеристика работ, выполненных в 2009 г. Основные (важнейшие) результаты Общая характеристика выполненных в 2009 г. работ. Основные (важнейшие) результаты М(39 в-в, 67 реакт., 88 парам) Методическое, алгоритмическое и программное обеспечение для комплексной поддержки территориального управления ... Полное содержание

Подобный материал:

• Информационные технологии анализа данных используются для обобщения учетной информации,, 178.99kb.
• Системы поддержки принятия решений общие сведения о системах поддержки принятия решений, 145.37kb.
• Рабочая программа дисциплины «Системы поддержки принятия решений» Рекомендуется для, 115.78kb.
• Системы поддержки принятия решений: эволюция концепции и некоторые перспективы, 98.37kb.
• Анализ принятия управленческих решений, 54.28kb.
• Темы курсовых проектов по дисциплине «Теория принятия решений», 35.1kb.
• Программа по дисциплине "Интеллектуальные информационные системы" для подготовки специалиста, 151.52kb.
• Темы курсовых проектов по дисциплине «Теории принятия решений» Можаева, 30.34kb.
• Ложения темпоральной (временной) логики для ветвящегося времени в плане ее использования, 138.35kb.
• Рабочая программа учебной дисциплины теория принятия решений Направление подготовки, 591.05kb.

РОССИЙСКАЯ АКАДЕМИЯ НАУК

СИБИРСКОЕ ОТДЕЛЕНИЕ

Приоритетное направление 4.3.
Системы автоматизации, GALS– технологии, математические модели и методы исследования сложных управляющих систем и процессов

Программа 4.3.1.
ИНФОРМАЦИОННЫЕ И ВЫЧИСЛИТЕЛЬНЫЕ ТЕХНОЛОГИИ В ЗАДАЧАХ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ

ОТЧЕТ
о работе программы в 2009 г.


Институты-исполнители:

Институт автоматики и электрометрии СО РАН

Институт вычислительного моделирования СО РАН

Институт вычислительных технологий СО РАН

Институт систем энергетики им. Л.А. Мелентьева СО РАН

Координатор программы:


академик                        Ю.И.Шокин

Ученый секретарь программы:


д.ф.-м.н.                         Л.Б.Чубаров

Новосибирск, 2009

Отчеты по проектам

Проект 4.3.1.1. Информационно-вычислительные технологии в задачах поддержки принятия решений (Институт вычислительных технологий СО РАН)

На этапе 2009 г. предполагалось:

• Выполнить трехмерное математическое моделирование эволюции электромагнитных полей в метаматериалах.
  
• Разработать нестационарные модели течений в гидротурбинах для переходных режимов, учитывающие гидравлические удары.
  
• Провести расчеты в аксиально-симметричной постановке ВЧ - разряда во фторсордержащих газах на базе гидродинамической модели.
  
• Провести математическое моделирование спутного турбулентного течения с варьируемым значением суммарного избыточного импульса в линейно стратифицированной среде с целью изучения тонкой микроструктуры гидрофизических полей.
  
• Численно исследовать процесс охлаждения высокотемпературных продуктов сгорания твердотопливных газогенераторов с помощью насыпных фильтров в системах быстрого наддува эластичных оболочек.
  
• Провести численное моделирование сверхзвуковых течений в воздухозаборниках летательных аппаратов с возникновением режимов выбитой ударной волны, приводящей к запиранию потока.
  

Основные (важнейшие) результаты

Разработка эффективных параллельных вычислительных алгоритмов для моделирования задач нанофотоники

Исполнители

Федорук М.П., д.ф.-м.н., зам. дир.;

Лебедев А.С., к.ф.-м.н., с.н.с.;

Штырина О.В., к.ф.-м.н., н.с.;

Чубаров Д.Л., м.н.с.;

Прокопьева Л.Ю., м.н.с.;

Витковский В.Э., асп.

Разработан алгоритм метода конечных объемов для решения трехмерных нестационарных уравнений Максвелла в средах с переменными значениями диэлектрической и магнитной проницаемостей, позволяющий эффективно моделировать распространение электромагнитного излучения в сложных наноструктурированных материалах. Реализована параллельная версия этого алгоритма. Расчеты на высокопроизводительных вычислительных многопроцессорных комплексах продемонстрировали практически линейное ускорение для двумерного и одномерного случаев (, ).



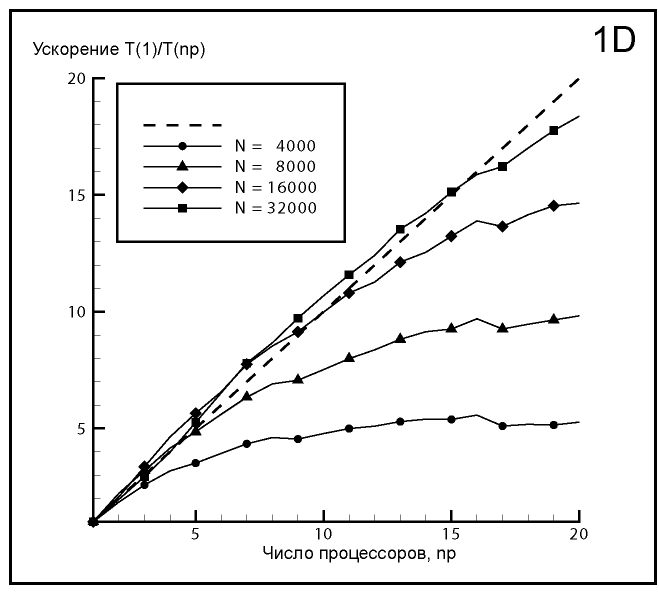
Рис. 1. Ускорение параллельной версии конечно-объемного алгоритма в одномерном случае, – число вычислительных узлов сетки.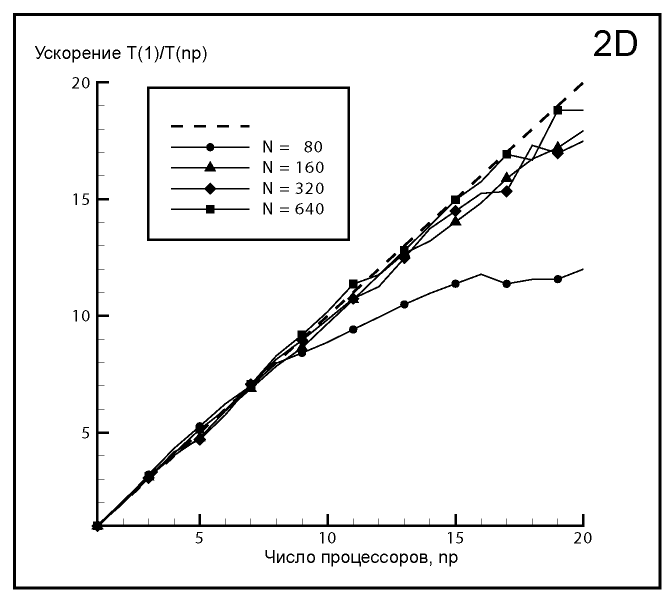



Рис. 2. Ускорение параллельной версии конечно-объемного алгоритма в двухмерном случаях, – число вычислительных ребер на стороне квадрата

Эффективность предложенного алгоритма продемонстрирована на примере расчета цилиндрической гиперлинзы (Рис. 3 – Рис. 6).

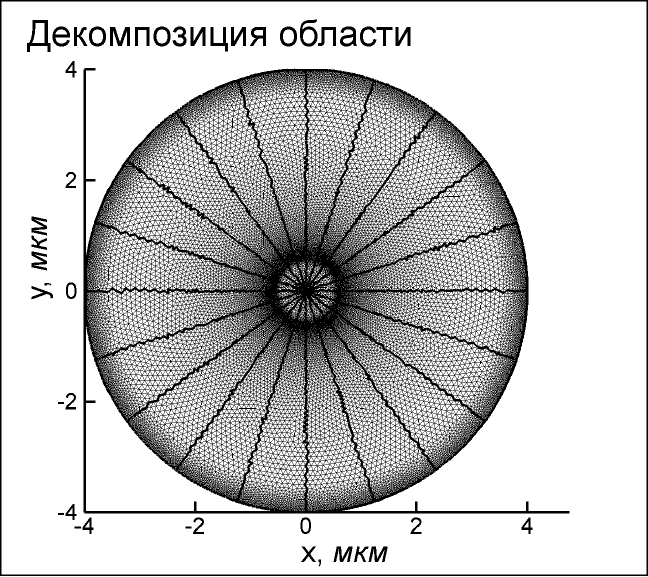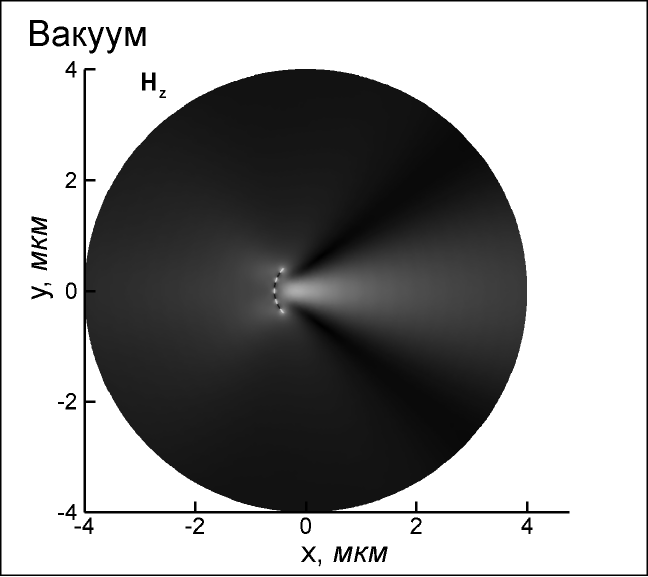Рис. 3. Декомпозицая расчетной области для проведения параллельных расчетов	Рис. 4. Источники в вакууме, амплитуда поля
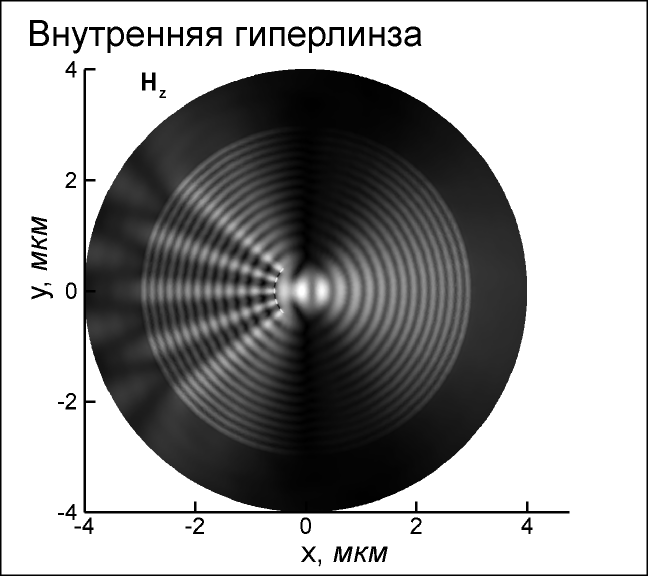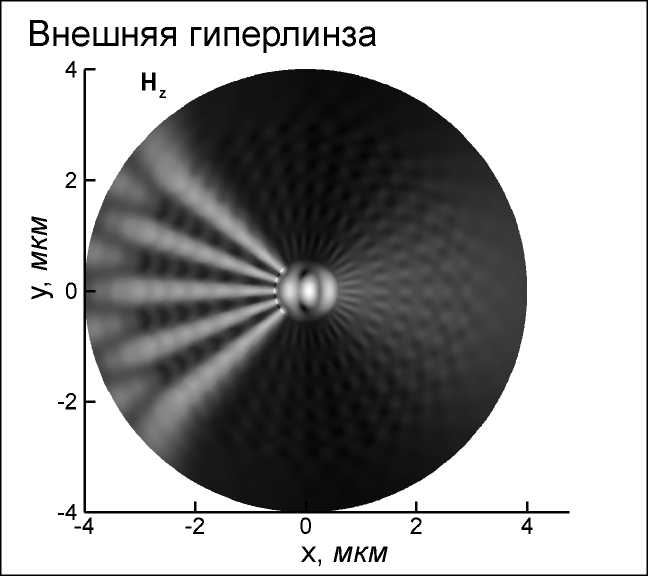Рис. 5. Внутренняя линза, амплитуда магнитного поля	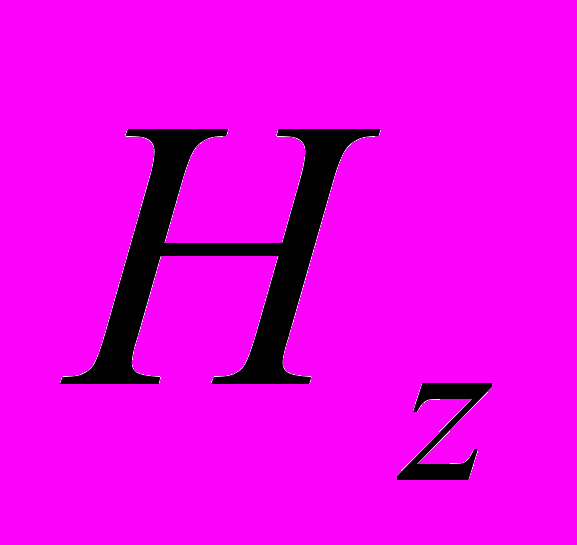Рис. 6. Внешняя линза, амплитуда магнитного поля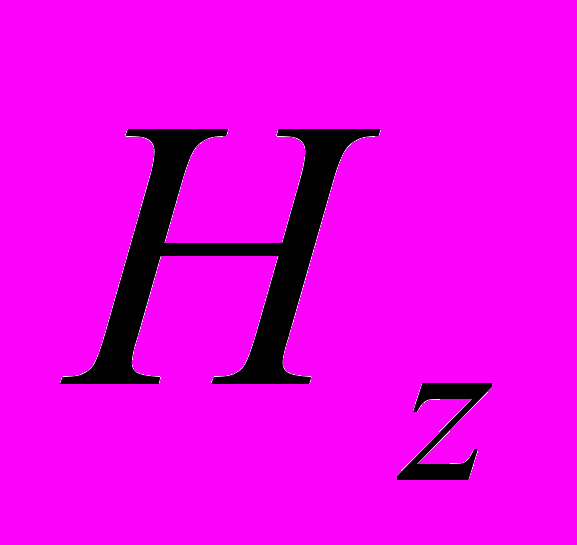

Разработан вычислительный алгоритм и выполнена его параллельная реализация для моделирования процесса записи объемных микро - и наноструктур путем воздействия фемтосекундных лазерных импульсов на оптические световоды. Для моделирования процесса записи используется система нелинейных уравнений, которая описывает эволюцию медленной огибающей электрического поля и динамику плотности плазменных электронов .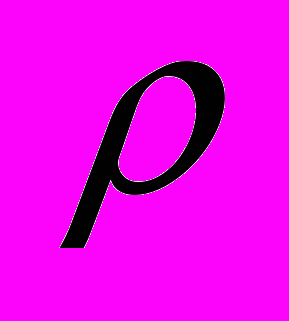

Алгоритм реализации этой системы уравнений основан на методе расщепления по физическим процессам, параллельном алгоритме прогонки для решения линейной части первого уравнения и декомпозиции по радиальной переменной 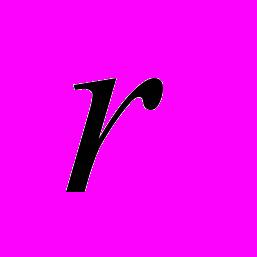для решения второго уравнения. На рисунках (Рис. 7, Рис. 8) представлены результаты расчетов.

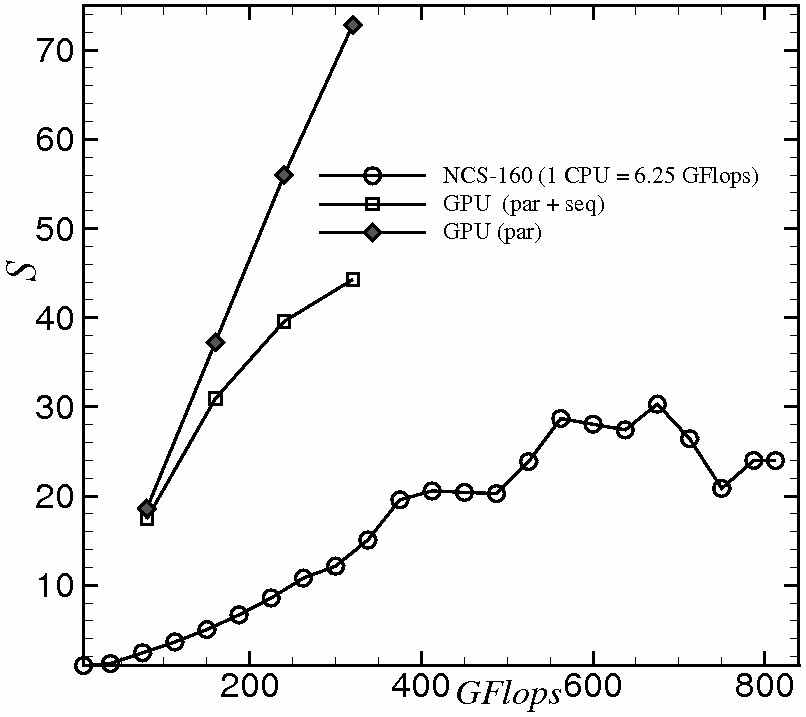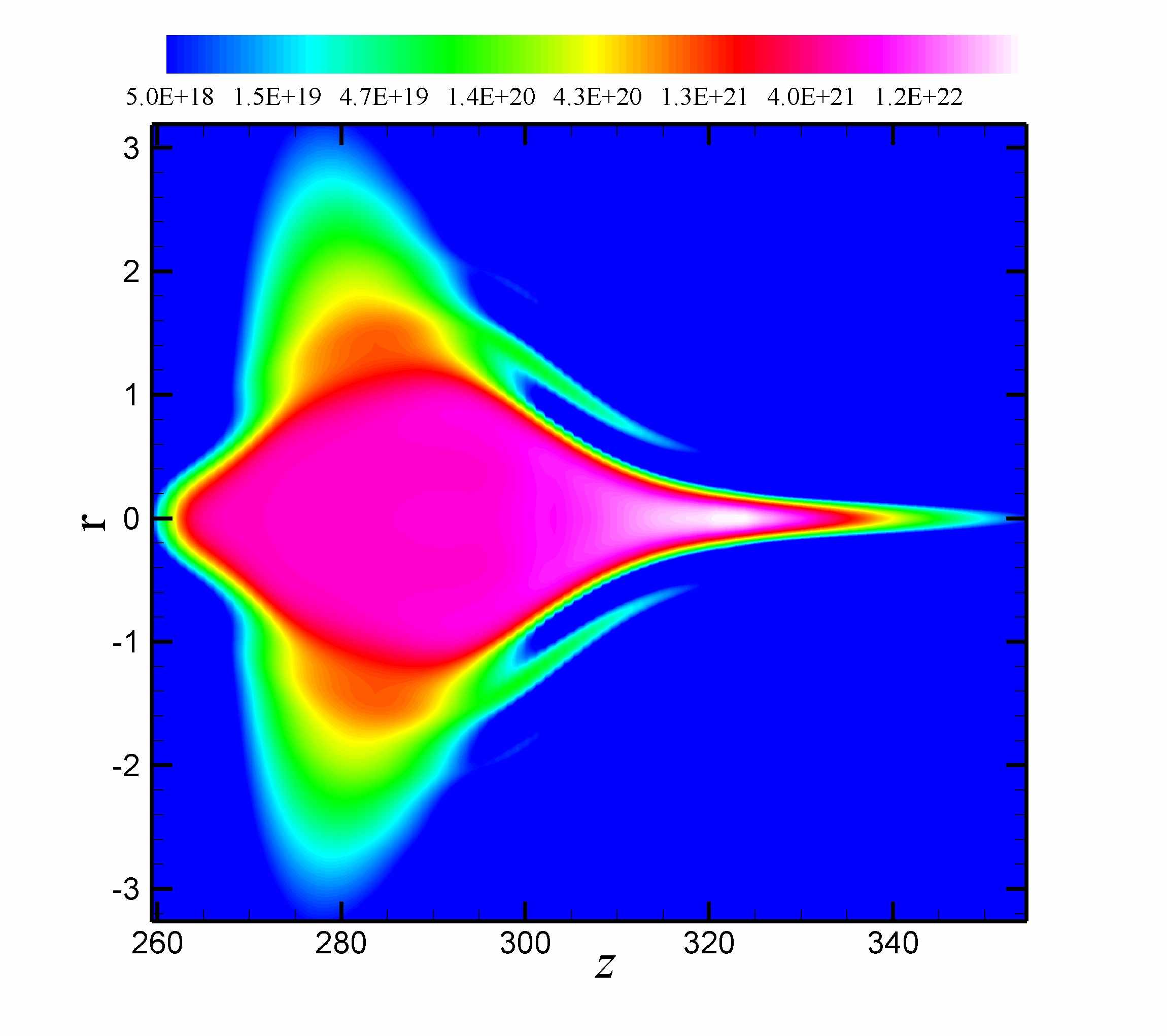Рис. 7. Ускорение параллельного алгоритма относительно для кластера (Itanium 2) и универсального графического ускорителя (Tesla C1060)	Рис. 8. Распределение плотности электронов плазмы при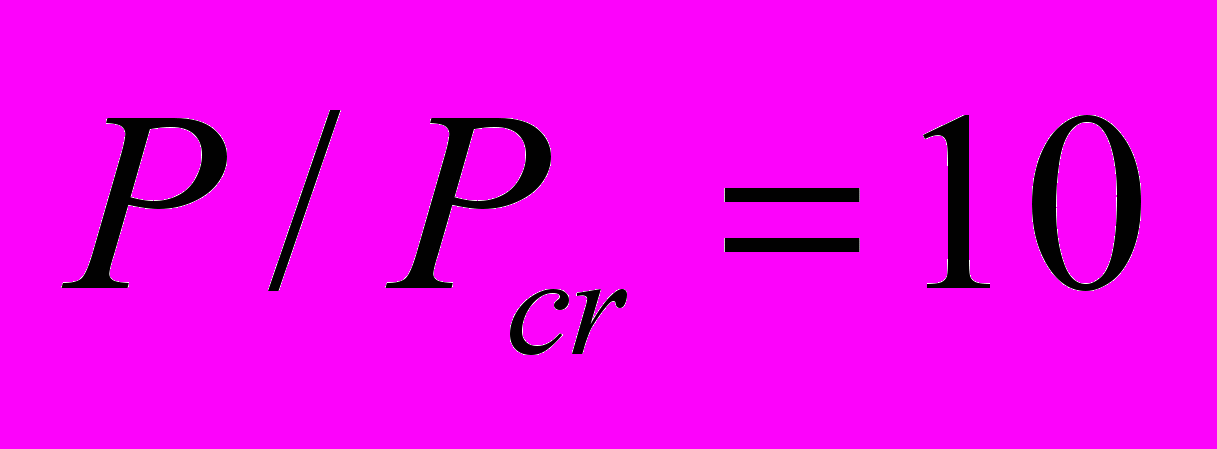

Разработка нестационарных моделей течения в гидротурбинах для переходных режимов, учитывающих гидравлические удары.

Исполнители раздела

1. Лапин В Н., к.ф.-м.н., н.с.;
   
2. Черных Г.Г., д.ф.-м.н., г.н.с.;
   
3. Чирков Д В., к.ф.-м.н., н.с.;
   
4. Банников Д.В., асп.;
   
5. Есипов Д В., асп.;
   
6. Ешкунова И Ф., асп.;
   
7. Авдюшенко А Ю., асп.;
   
8. Астракова А С., маг.;
   
9. Панов Л В., маг.;
   
10. Жамбалова Д.Б., маг.
    

Разработаны математическая модель и методика расчета переходных процессов в гидравлических турбинах, возникающих при переходе из одного режима работы в другой, учитывающая явление гидравлического удара. Модель основана на совместном решении осредненных по Рейнольдсу нестационарных 3D уравнений Навье-Стокса в проточном тракте гидротурбины, уравнения вращения рабочего колеса как твердого целого и 1D уравнений «упругого» гидравлического удара в напорном водоводе. В большинстве случаев переходные режимы связаны с открытием/закрытием направляющего аппарата. Поэтому для описания изменения геометрии проточной части со временем базовый алгоритм расчета течения жидкости адаптирован к использованию подвижной сетки. Разработаны новые граничные условия, позволяющие задавать на входном сечении не расход жидкости, а полную энергию потока, что позволило решить широкий класс задач, как стационарных, так и нестационарных, где расход заранее неизвестен.

Выполнено моделирование одного из переходных процессов – начального этапа выхода в разгонный режим работы при фиксированном положении лопаток направляющего аппарата. При мгновенном снятии нагрузки с генератора частота вращения рабочего колеса (РК) начинает быстро увеличиваться, подчиняясь закону вращения РК как твердого целого.

Влияние структуры высокочастотного (ВЧ) разряда на процесс плазмохимического травления кремния в CF₄/O₂.

Исполнители

1. Ю.Н. Григорьев, д.ф.-м.н., г.н.с.;
   
2. А.Г. Горобчук, к.ф.-м., н.с.
   

На основе неизотермической модели плазмохимического реактора травления исследовано влияние неоднородной структуры ВЧ-разряда на основные характеристики процесса плазменного травления. Внутренние характеристики плазмы ВЧ-разряда рассчитывались в диффузионно-дрейфовом приближении для фторсодержащих газовых смесей. Выполнено численное моделирование радиального плазмохимического реактора с неоднородным ВЧ-разрядом и многокомпонентной плазменной кинетикой. Определено влияние структуры ВЧ-разряда на массообмен, скорость и однородность травления кремниевых образцов в зависимости от концентрации кислорода. Показано, что однородность травления образцов существенно зависит от изменения электронной плотности в радиальном направлении, которым часто пренебрегают, рассчитывая разряд в одномерной постановке. На рисунке (Рис. 9) показано распределение концентрации фтора CF (Моль/см3) в радиальном плазмохимическом реакторе.



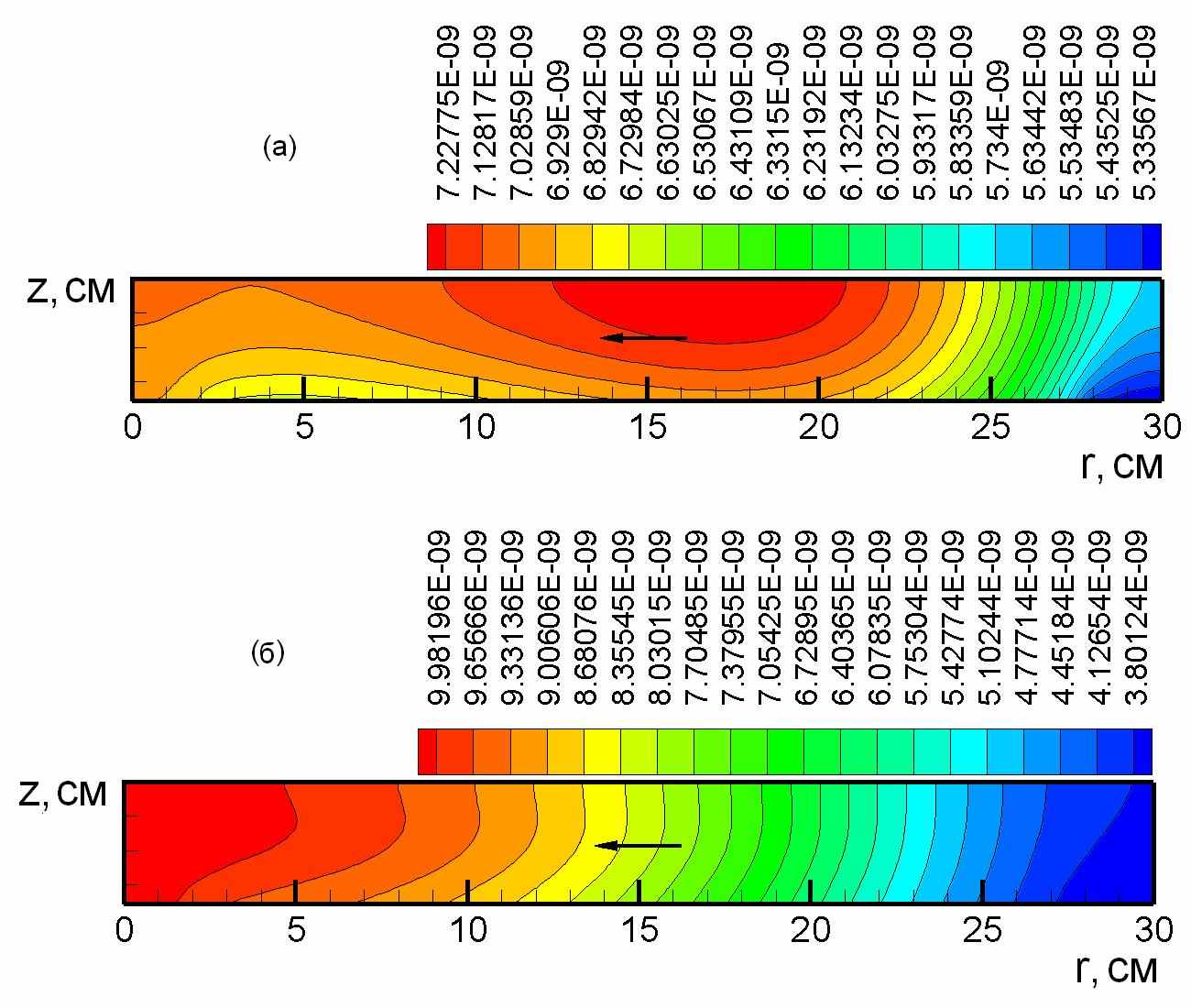
Рис. 9. Распределение концентрации фтора C_F (Моль/см³) в радиальном плазмохимическом реакторе: а - однородное распределение электронной плотности, б - распределение электронной плотности, имеющее радиальную зависимость в виде функции Бесселя. Параметры: p = 0.5 тор, Q = 200 см³/мин, T_w = 300 K, 30% содержание O₂ в CF₄/O₂. Направление подачи газа - к центру реактора.

Математическое моделирование спутного турбулентного течения в устойчиво стратифицированной среде.

Исполнители:

1. Г. Г. Черных, д.ф.-м.н,. г.н.с.;
   
2. О.Ф. Воропаева, д.ф.-м.н, с.н.с.
   

Построены усовершенствованные численные модели динамики турбулентного следа в устойчиво стратифицированной среде. Для детального описания тонкой структуры течения в дальнем следе с нулевым избыточным импульсом построена численная модель, основанная на дифференциальных уравнениях переноса тройных корреляций турбулентных флуктуаций поля скорости, записанных с учетом вклада кумулянтов четвертого порядка, и на модифицированных алгебраических аппроксимациях тройных совместных корреляций турбулентных флуктуаций полей скорости и плотности. Результаты расчетов хорошо согласуются с известными экспериментальными данными об анизотропном вырождении следа.

Для описания динамики турбулентного следа за буксируемым телом в линейно стратифицированной среде построена иерархия математических моделей турбулентности второго порядка. Наиболее сложная математическая модель включает в себя наряду с дифференциальными уравнениями переноса компонент тензора рейнольдсовых напряжений уравнение переноса тройной корреляции турбулентных флуктуаций вертикальной компоненты скорости. Показано, что, как и в случае однородной жидкости, суммарный избыточный импульс порядка 5-10 % от суммарного избыточного импульса за буксируемым телом слабо влияет на вырождение энергии турбулентности. Основное влияние малого суммарного избыточного импульса сказывается на вырождении дефекта осредненной продольной компоненты скорости. Турбулентные следы с малым суммарным избыточным импульсом генерируют внутренние волны, слабо отличающиеся от внутренних волн, генерируемых безымпульсным турбулентным следом.

Моделирование работы насыпного фильтра для охлаждения высокотемпературных продуктов сгорания твердотопливного газогенератора.

Исполнители:

1. А.Д. Рычков, д.т.н., г н.с.
   

Разработана математическая модель и реализующий ее численный алгоритм для моделирования процесса охлаждения высокотемпературных продуктов сгорания твердотопливных газогенераторов в фильтрах активного охлаждения. Результаты численного моделирования показали более высокую эффективность охлаждения продуктов сгорания газогенератора при использовании активных фильтров по сравнению с пассивными.

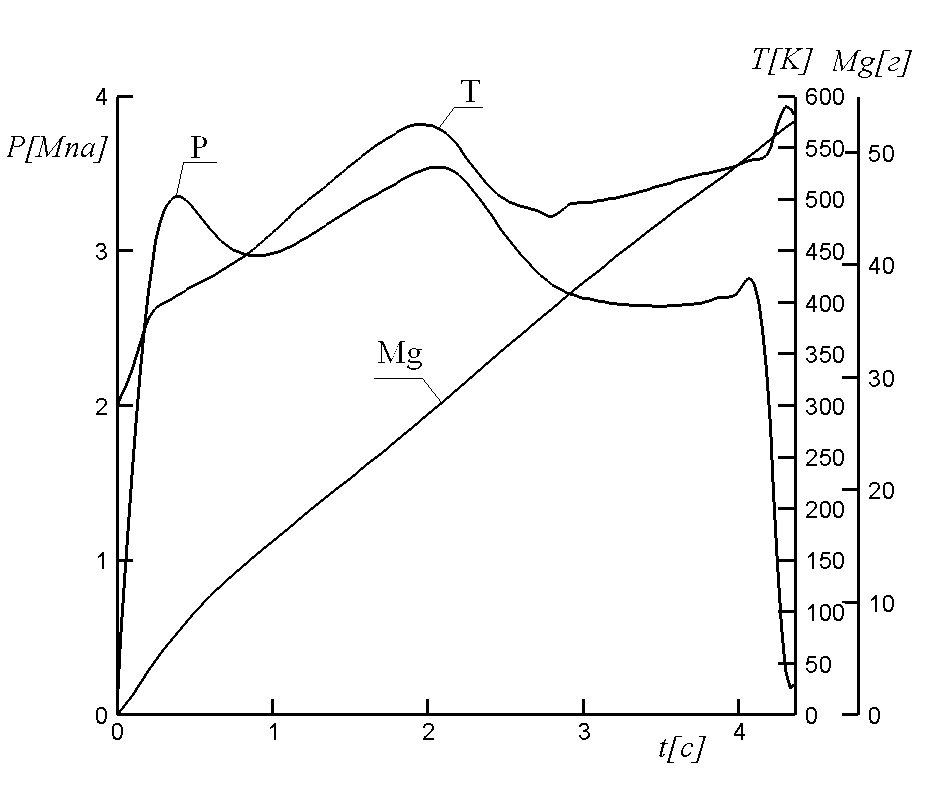Рис. 10. Изменение давления в камере охлаждения при x = 0 для активного (1) и пассивного (2) фильтров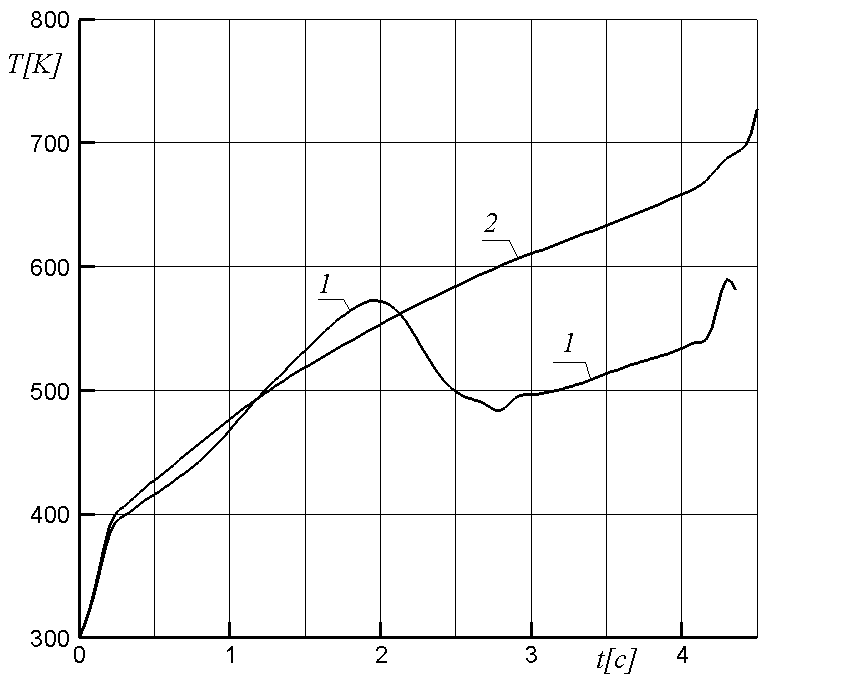

Рис. 11. Изменение температуры на выходе из камеры охлаждения для активного (1) и пассивного (2) фильтров

Численное моделирование сверхзвуковых течений в воздухозаборниках летательных аппаратов с возникновением режимов выбитой ударной волны, приводящей к запиранию потока.

Исполнители:

1. В.М. Ковеня, д.ф.-м.н., г.н.с;.
   
2. А.В.Базовкин, аспирант;
   
3. А.Ю. Слюняев, аспирант.
   

Проведена модификация численного алгоритма решения уравнений Навье-Стокса сжимаемого теплопроводного газа, позволившая повысить точность расчетов за счет применения неравномерных адаптивных сеток, сгущающихся в областях больших градиентов. Проведены расчеты сверхзвукового обтекания модельной конфигурации гиперзвукового летательного аппарата (ГЛА) в продольной плоскости сечения в двумерном приближении в широком диапазоне чисел Маха, Рейнольдса и углов атаки. Получены основные закономерности течений около несущей поверхности аппарата, в воздухозаборнике и в окрестности тела за ним при различных краевых условиях для температуры поверхности стенок. Численно подтверждено явление выбитой ударной волны – отхода ударной волны от носка воздухозаборника с увеличением угла атаки, имеющее место в режимах течений, близких к запиранию канала. При углах атаки до 9 градусов ударная волна присоединена к кромке, а при больших углах атаки отходит от тела. Иллюстрацией этого явления служит рисунок (Рис. 12), где приведены поля скоростей при 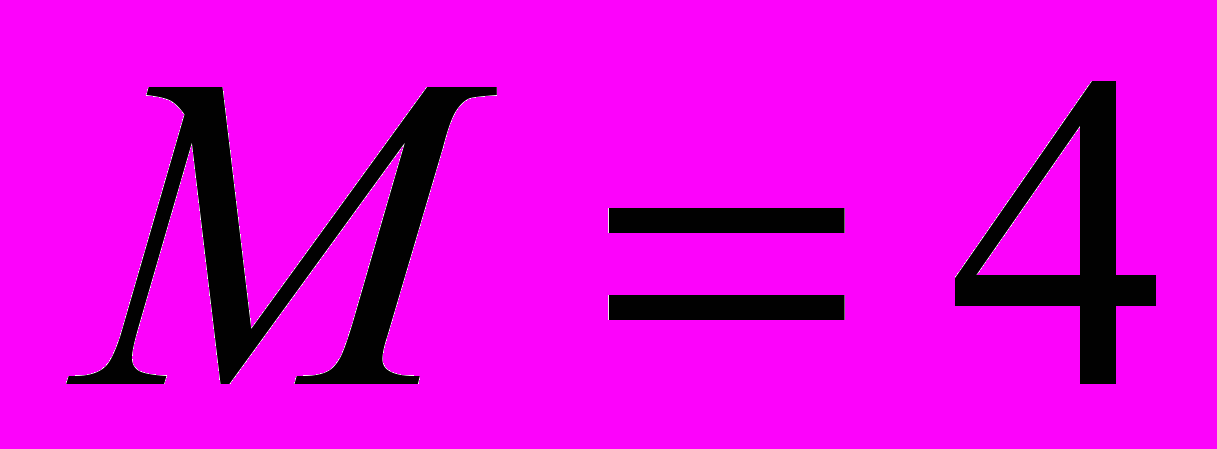для углов атаки 3 и 15 градусов.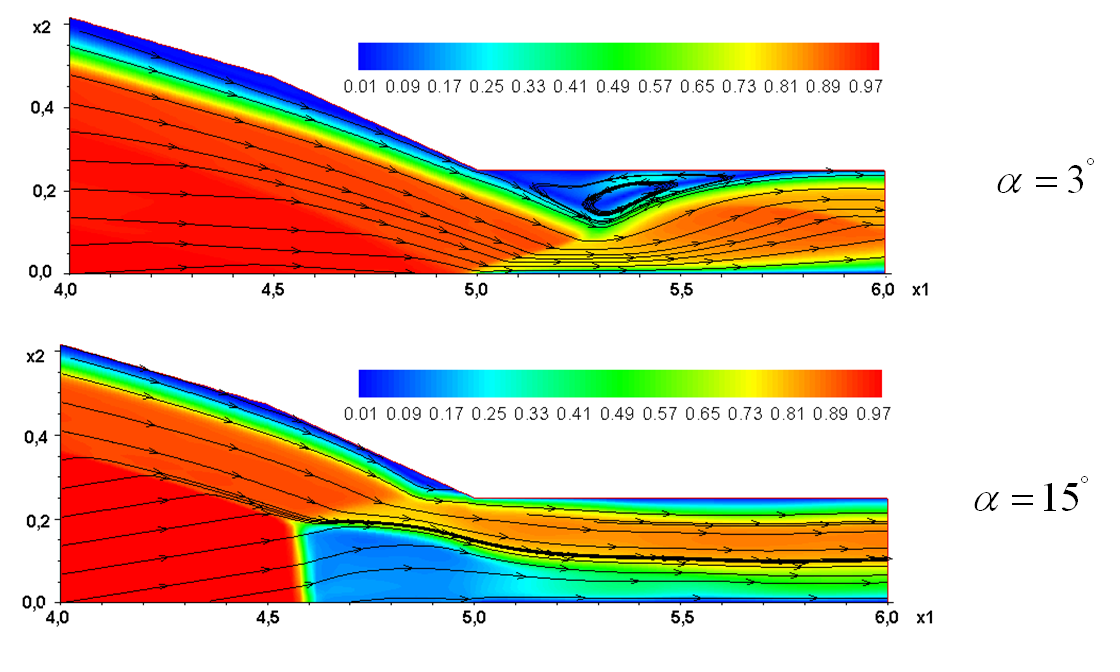



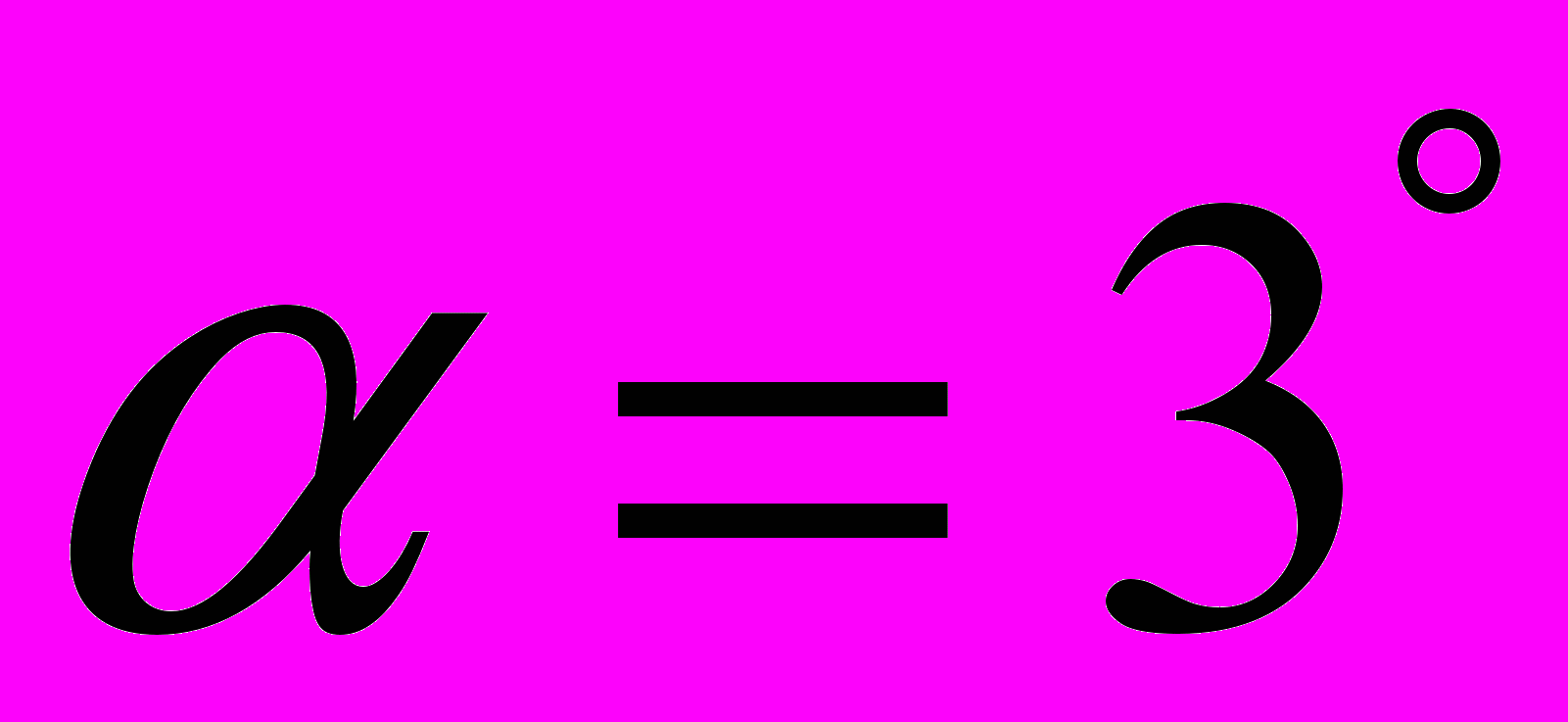
Рис. 12. Распределения полей скорости газа в области входа в канал воздухозаборника