Geum.ru

Типовая учебная программа для высших учебных заведений по специальности: 1-31 03 01 Математика (по направлениям)

Вид материалаПрограмма

Содержание


Рекомендована к утверждению в качестве типовой
Пояснительная записка
Примерный тематический план
Количество часов
Всего аудиторных часов
Векторы и координаты
Прямая на плоскости. Плоскость и прямая в пространстве
Фигуры второго порядка на плоскости
Фигуры второго порядка в пространстве
Подобный материал:



Министерство образования Республики Беларусь

Учебно-методическое объединение вузов Республики Беларусь

по естественнонаучному образованию


УТВЕРЖДАЮ

Первый заместитель Министра образования

Республики Беларусь

________________ А.И. Жук

«___» __________2008 г.

Регистрационный № ТД-______/тип.


Аналитическая геометрия


Типовая учебная программа

для высших учебных заведений по специальности:

1-31 03 01 – Математика (по направлениям)



СОГЛАСОВАНО

Председатель УМО вузов Республики Беларусь по естественнонаучному образованию

_____________ В.В. Самохвал


«___» __________ 2008 г.
СОГЛАСОВАНО

Начальник Управления высшего и среднего специального образования

________________ Ю.И. Миксюк

«___» __________ 2008 г.


Первый проректор Государственного учреждения образования «Республиканский институт высшей школы»

________________ И.В. Казакова

«___» __________ 2008 г.


Эксперт-нормоконтролер

________________

«___» __________ 2008 г.


Минск 2008


Составители:


Кононов С.Г., доцент кафедры геометрии, топологии и методики преподавания математики Белорусского государственного университета, кандидат физико-математических наук, доцент;


Суворов В.В., доцент кафедры геометрии, топологии и методики преподавания математики Белорусского государственного университета, кандидат физико-математических наук, доцент;


Филиппович К.С., ст. преподаватель кафедры геометрии, топологии и методики преподавания математики Белорусского государственного университета.


Рецензенты:

Кафедра алгебры и геометрии учреждение образования "Белорусский государственный педагогический университет им. М. Танка";

И.В. Белько, заведующий кафедрой прикладной математики и экономической кибернетики учреждения образования "Белорусский государственный экономический университет", доктор физико-математических наук, профессор.


РЕКОМЕНДОВАНА К УТВЕРЖДЕНИЮ В КАЧЕСТВЕ ТИПОВОЙ:

Кафедрой геометрии, топологии и методики преподавания математики механико-математического факультета Белорусского государственного университета (протокол № 11 от 18 марта 2008 г.);

Научно-методическим советом Белорусского государственного университета

(протокол № 3 от 27 марта 2008 г.);


Научно-методическим советом по математике и механике Учебно-методического объединения вузов по естественнонаучному образованию

(протокол № 3 от 10 апреля 2008 г.).


Ответственный за выпуск: С.Г. Кононов


Пояснительная записка

Аналитическая геометрия является одной из основных дисциплин, которые читаются студентам-математикам в течение первого года обучения. Главными целями курса аналитической геометрии являются:
  • освоение новых по сравнению с элементарной геометрией пространств:
    многомерных евклидовых, аффинных, проективных и изучение типичных фигур
    в этих пространствах;
  • овладение основным методом исследования в аналитической геометрии – методом координат;
      • приобретение студентами достаточного объема знаний, навыков и умений в области аналитической геометрии для их использования при изучении других математических дисциплин.

Для достижения этих целей решаются следующие задачи.

В начале первого семестра с целью сохранения преемственности со школьной геометрией рассмотрение ограничивается трехмерным евклидовым пространством 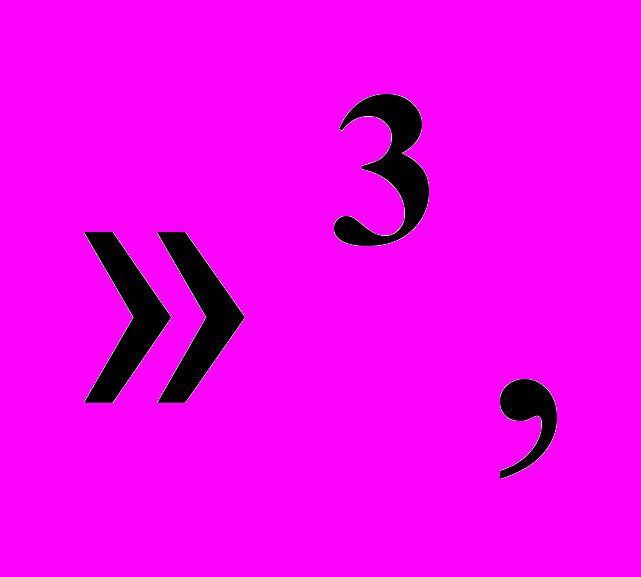при этом векторы в трехмерном евклидовом пространстве 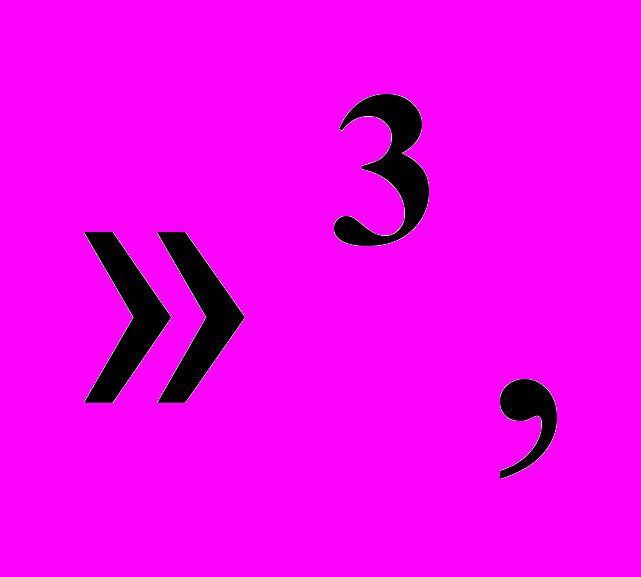прямые на евклидовой плоскости 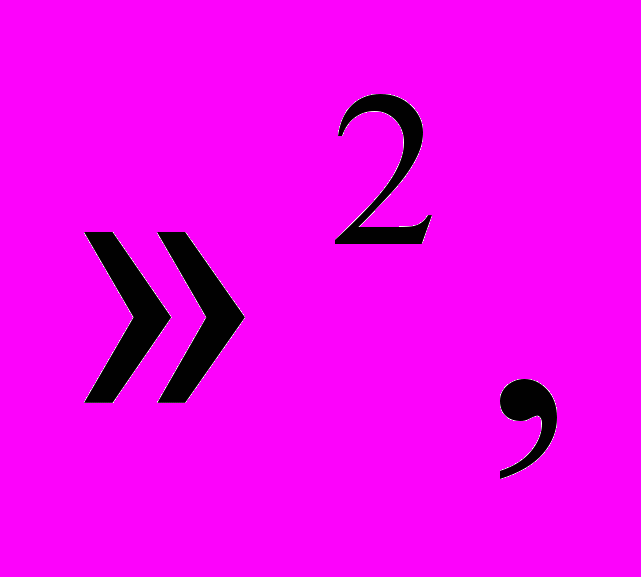плоскости и прямые в пространстве изучаются всесторонне с точки зрения высшей математики. Далее рассматриваются фигуры второго порядка на плоскости 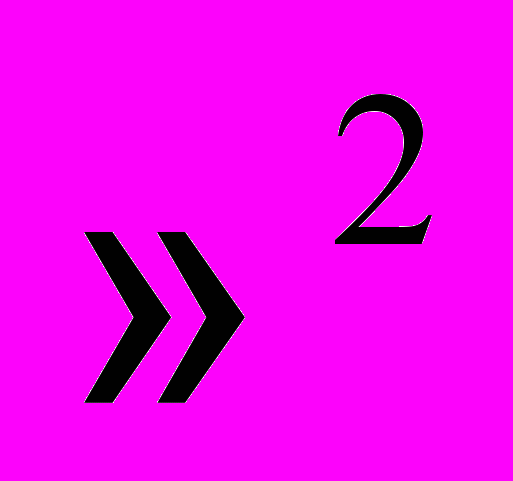и в пространстве 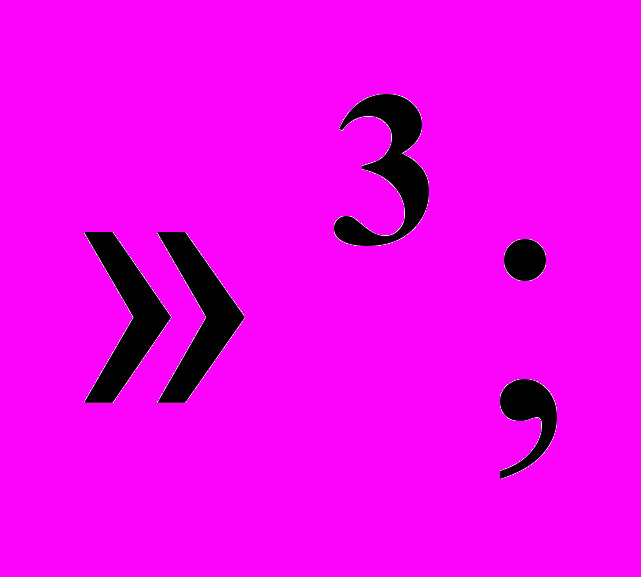вводится принципиально новое понятие проективной плоскости и аналогов рассмотренных ранее фигур на проективной плоскости.

Во втором семестре основное внимание уделяется геометрии многомерных пространств: аффинных, евклидовых и проективных. Определяются и изучаются фигуры первого и второго порядков в вещественных аффинных и евклидовых пространствах; аффинные преобразования и движения; аффинная и евклидова геометрия; элементы проективной геометрии.

В течение всего процесса обучения происходит систематическое изучение геометрических преобразований, проведение теоретико-группового взгляда на геометрию.

В соответствии с образовательным стандартом в результате изучения дисциплины обучаемый должен:

знать:

– векторы в 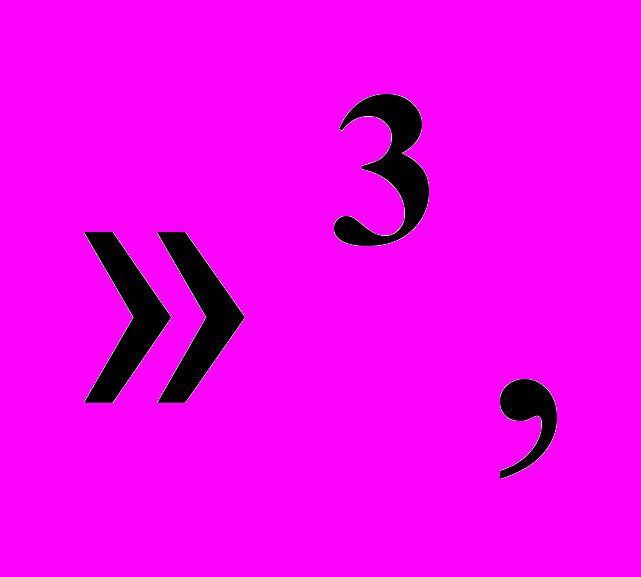операции над векторами;

– эллипс, гиперболу, параболу, эллипсоиды, гиперболоиды, параболоиды: их канонические уравнения и свойства;

– понятия аффинного, евклидова и проективного пространств; реперы и координаты точек; 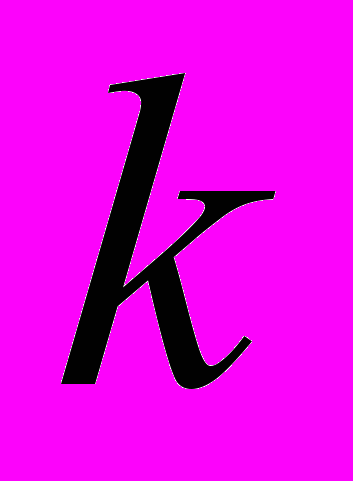-мерные плоскости и фигуры второго порядка; группы геометрических преобразований.

уметь:

– выполнять операции над векторами; записывать общие и параметрические уравнения плоскостей в различных пространствах, определять их взаимное расположение;

– по общему уравнению фигуры второго порядка 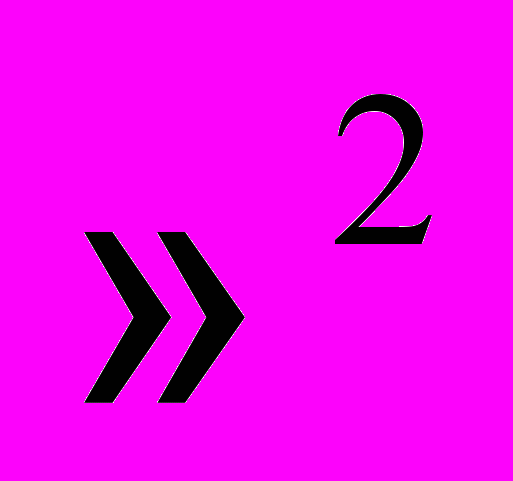в и в 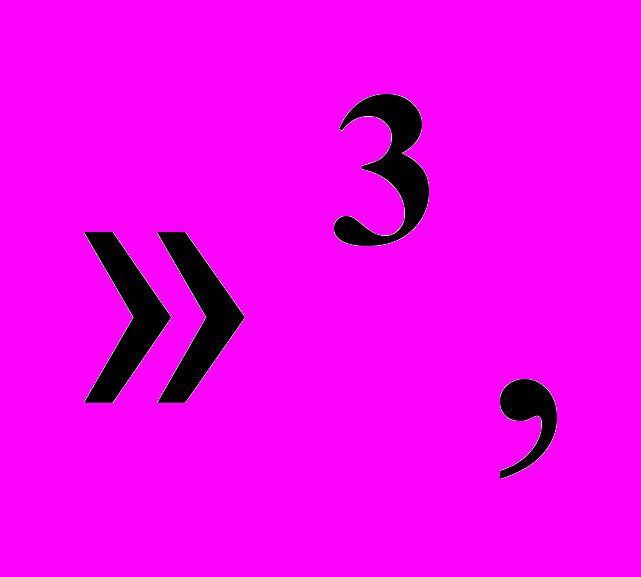определять ее тип, размеры, расположение относительно системы координат; приводить общее уравнение фигуры второго порядка в аффинном пространстве к нормальному виду.

Аналитическая геометрия играет важную роль в математическом образовании, так как ее конструкции, идеи и методы исследований широко используются в других математических дисциплинах. В свою очередь, для успешного изучение аналитической геометрии требуется знания ряда разделов высшей алгебры, что требует достаточно тесного согласования изучаемой дисциплины с параллельно читаемой дисциплиной «Алгебра и теория чисел».

Всего на изучение аналитической геометрии согласно типового учебного плана отводится 292 часа, из них аудиторных – 136. Примерное распределение аудиторных часов приведено в тематическом плане дисциплины.

Примерный тематический план





№ п/п


Наименование темы

Наименование Наименованиетемы

Количество часов


Лекции
Лабораторные и практические занятия

1.
Введение
1



2.
Векторы и координаты
10
10

3.
Прямая на плоскости. Плоскость и прямая в пространстве

11
12

4.
Фигуры второго порядка на плоскости

8
10

5.
Фигуры второго порядка в пространстве

6
6

6.
Аффинное 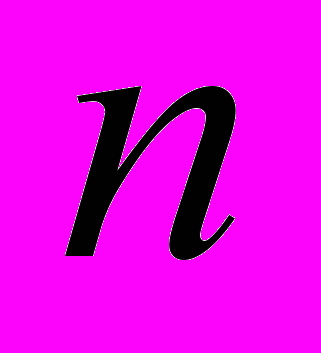-мерное пространство

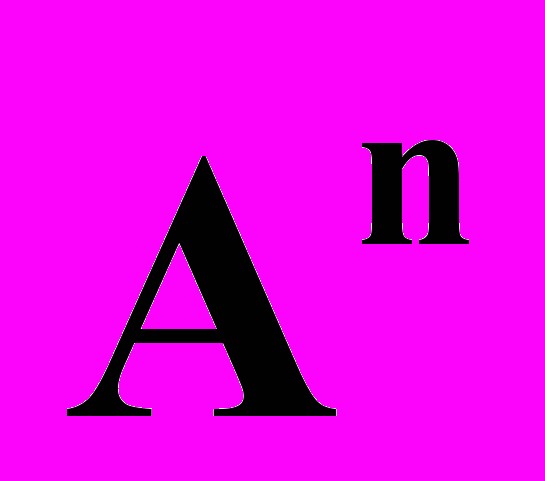8
8

7.
Точечное 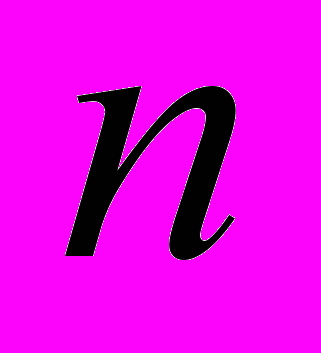-мерное пространство

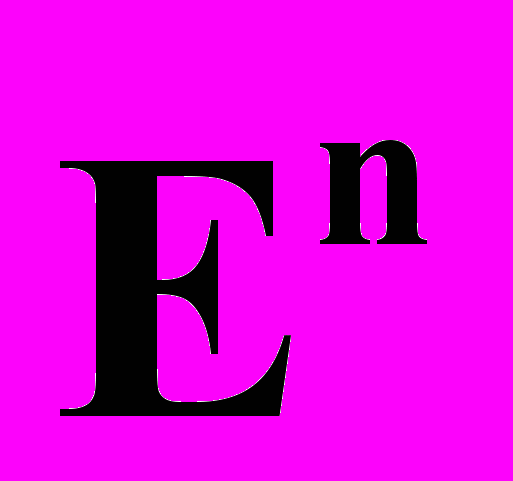6
6

8.
Квадрики в аффинном пространстве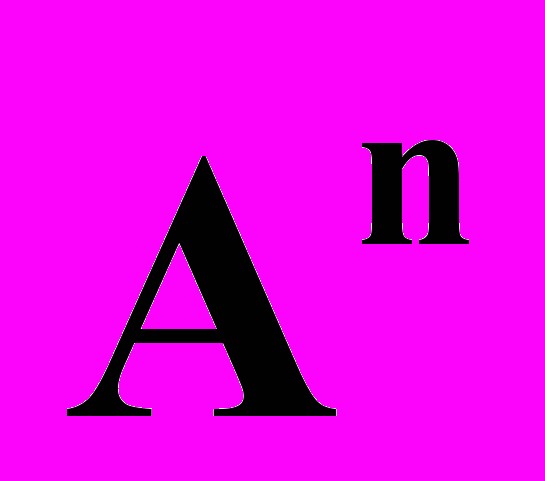

8
6

9.
Квадрики в евклидовом пространстве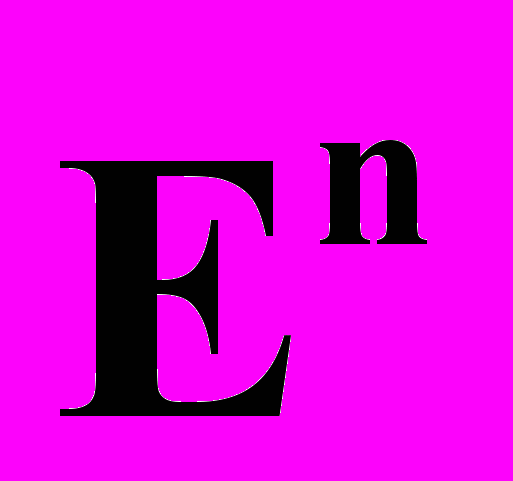

4
6

10.
Проективная плоскость 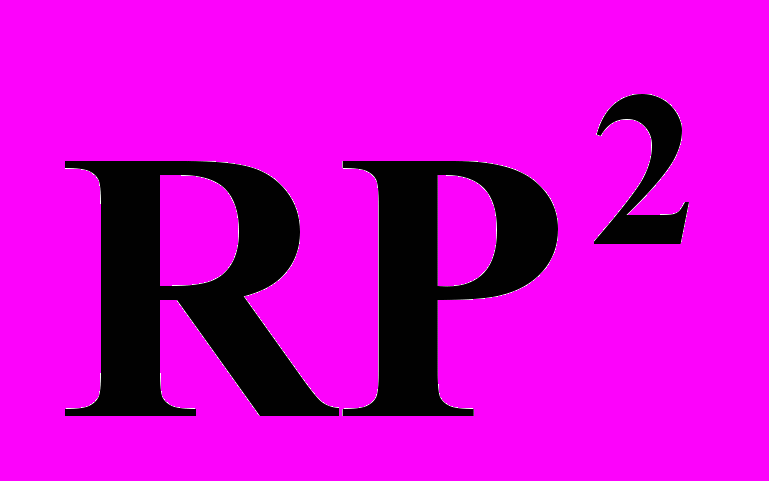и проективное пространство

6
4

Всего аудиторных часов
68
68

ИТОГО:

136

68

Содержание дисциплины "Аналитическая геометрия"

Введение


Роль геометрии в математике и ее приложениях. Предмет и методы аналитической геометрии.

Векторы и координаты

Направленные отрезки. Векторы как классы эквивалентных направленных отрезков. Сложение векторов, умножение вектора на число, откладывание вектора от точки. Проекции. Деление отрезка в данном отношении. Линейная зависимость и независимость векторов, коллинеарность и компланарность. Базисы и реперы. Аффинная и прямоугольная системы координат. Полярные, сферические и цилиндрические координаты. Преобразование координат. Фигуры и их уравнения. Скалярное произведение векторов. Векторное произведение векторов. Ориентация плоскости и пространства. Смешанное произведение трех векторов.

Прямая на плоскости. Плоскость и прямая в пространстве

Различные виды уравнений прямой на плоскости. Взаимное расположение двух прямых на плоскости. Пучок прямых. Различные виды уравнений плоскости в пространстве. Взаимное расположение двух плоскостей. Различные виды уравнений прямой в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Связка прямых и плоскостей. Формулы расстояний от точки до прямой и от точки до плоскости. Геометрический смысл неравенств с двумя и тремя переменными.

Фигуры второго порядка на плоскости

Эллипс – различные определения, каноническое уравнение, фокусы, эксцентриситет. Гипербола – определение, каноническое уравнение, фокусы, эксцентриситет, асимптоты. Директрисы эллипса и гиперболы. Парабола – определение, каноническое уравнение, фокус и директриса. Параметрические уравнения эллипса и гиперболы. Уравнение эллипса, гиперболы и параболы в полярных координатах. Общее уравнение фигуры второго порядка на плоскости, приведение его к каноническому виду. Классификация фигур второго порядка на плоскости.

Фигуры второго порядка в пространстве

Понятие фигуры второго порядка в пространстве, ее исследование с помощью сечений. Фигуры вращения второго порядка, переход к общим фигурам второго порядка.

Сфера. Эллипсоид вращения, трехосный эллипсоид. Параболоид вращения. Эллиптический параболоид. Однополостный гиперболоид вращения. Однополостный гиперболоид общего вида, его прямолинейные образующие. Двуполостный гиперболоид вращения. Двуполостный гиперболоид общего вида. Гиперболический параболоид, его прямолинейные образующие. Цилиндры второго порядка –эллиптический, параболический, гиперболический. Конус второго порядка, конические сечения.

Аффинное 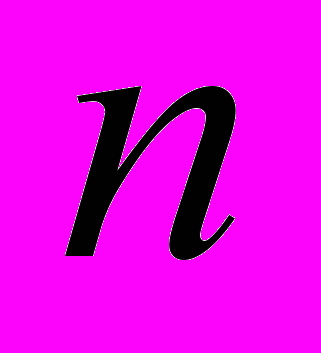-мерное пространство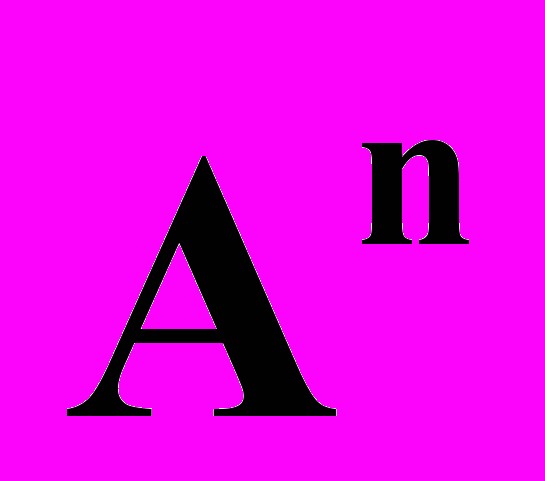

Понятие аффинного пространства. Координаты в 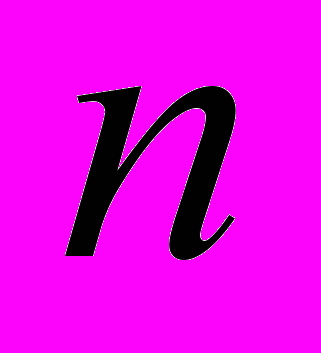-мерном аффинном пространстве 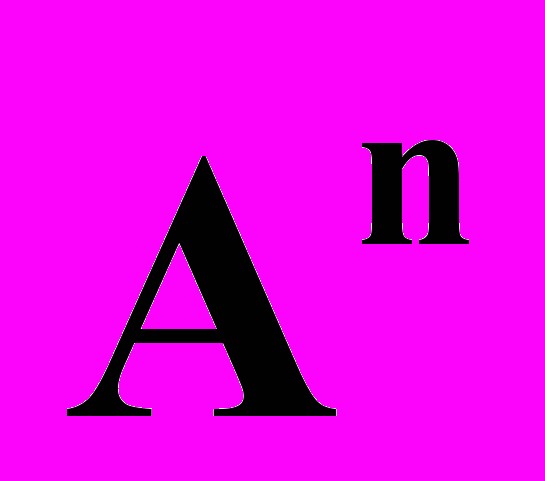. 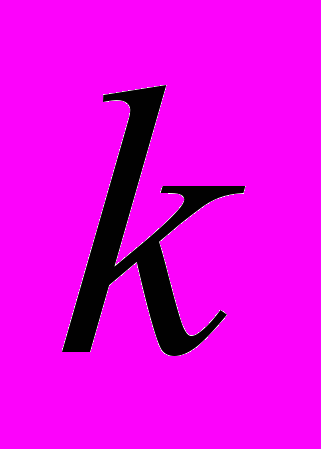-мерные плоскости в пространстве 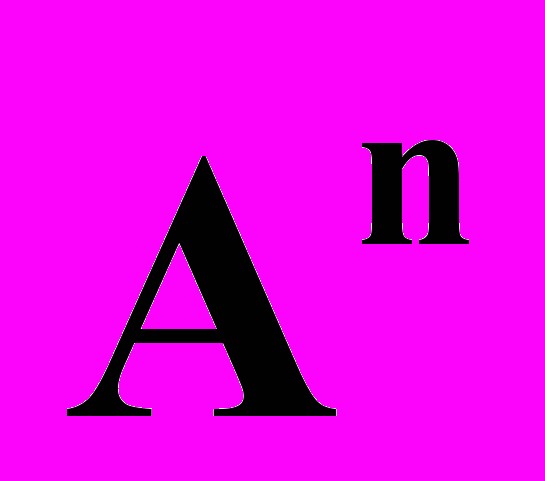, аффинная оболочка фигуры, системы точек общего положения. Общие и параметрические уравнения плоскостей в пространстве 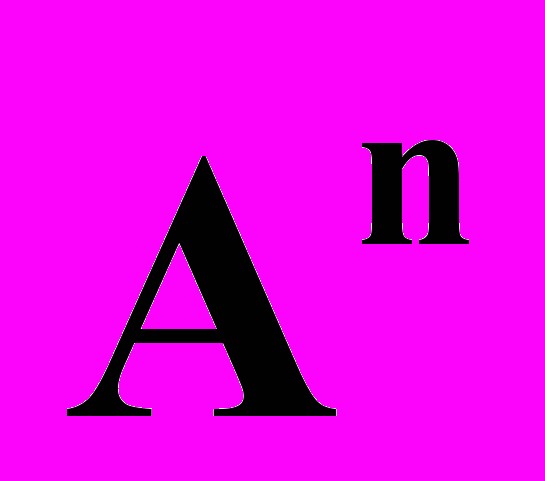. Взаимное расположение двух плоскостей. Барицентрические координаты. Понятие выпуклой фигуры. Аффинные отображения. Изоморфизм аффинных пространств. Аффинные преобразования. Геометрия аффинной группы.

Точечное 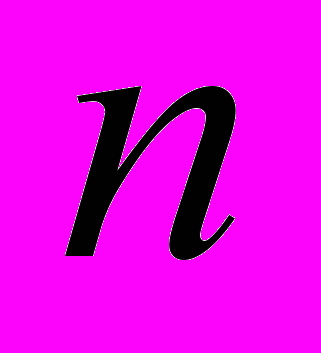-мерное евклидово пространство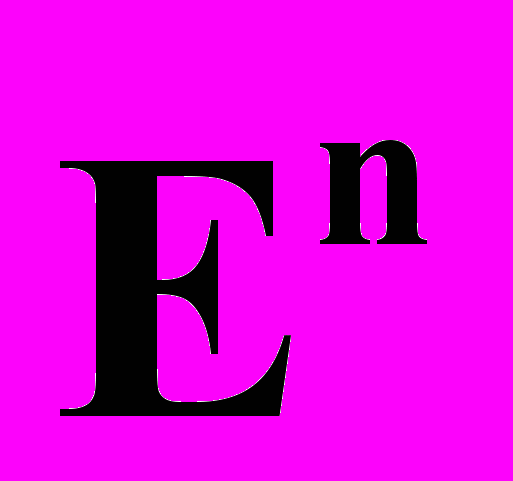

Понятие 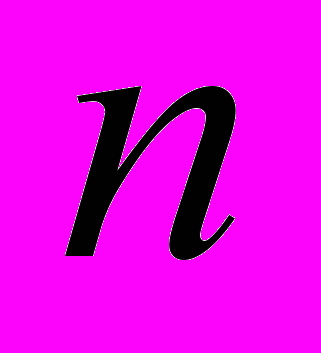-мерного евклидова пространства 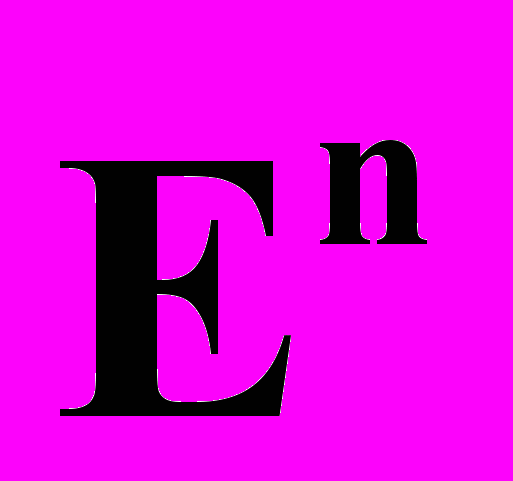. Координаты в пространстве 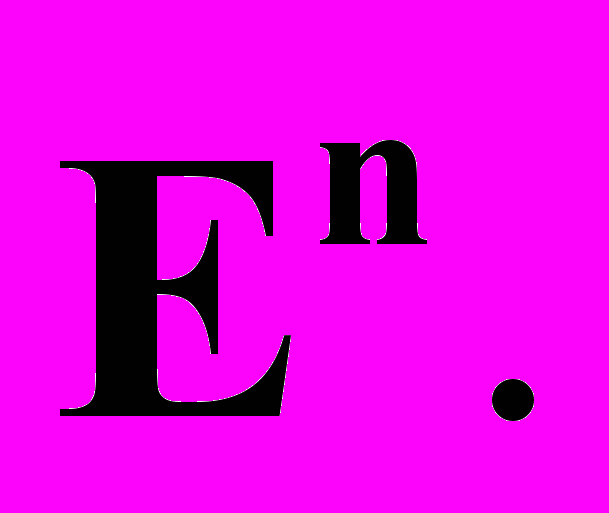Плоскости в пространстве 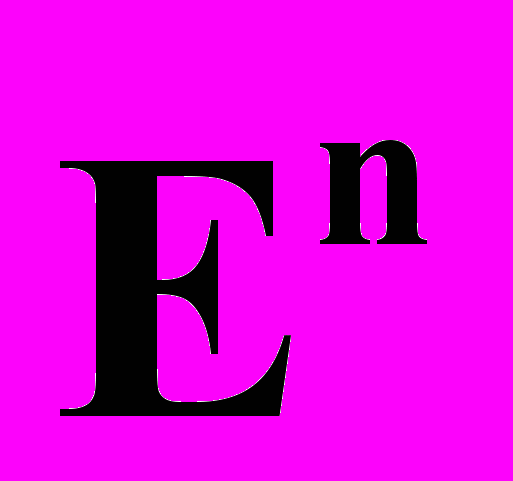, ортогональность плоскостей. Шары, сферы, симплексы, параллелепипеды. Расстояние от точки до гиперплоскости. Объем параллелепипеда.

Движения пространства 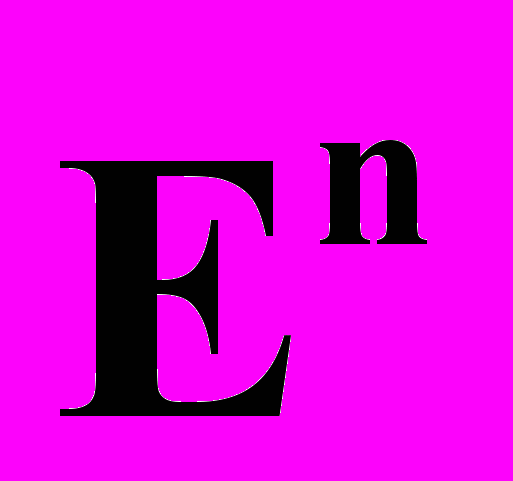. Классификация движений плоскости и пространства Аффинные преобразования пространства .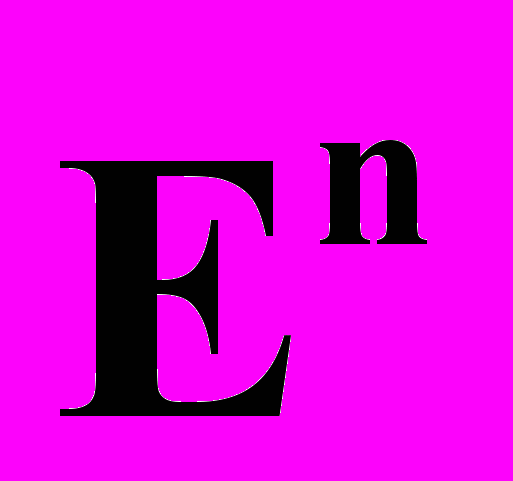

Квадрики в аффинном пространстве

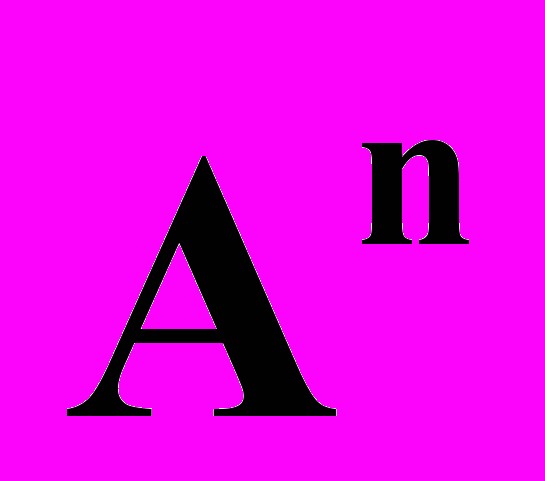
Понятие вещественно-комплексного 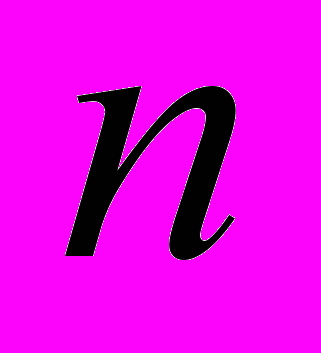-мерного аффинного пространства 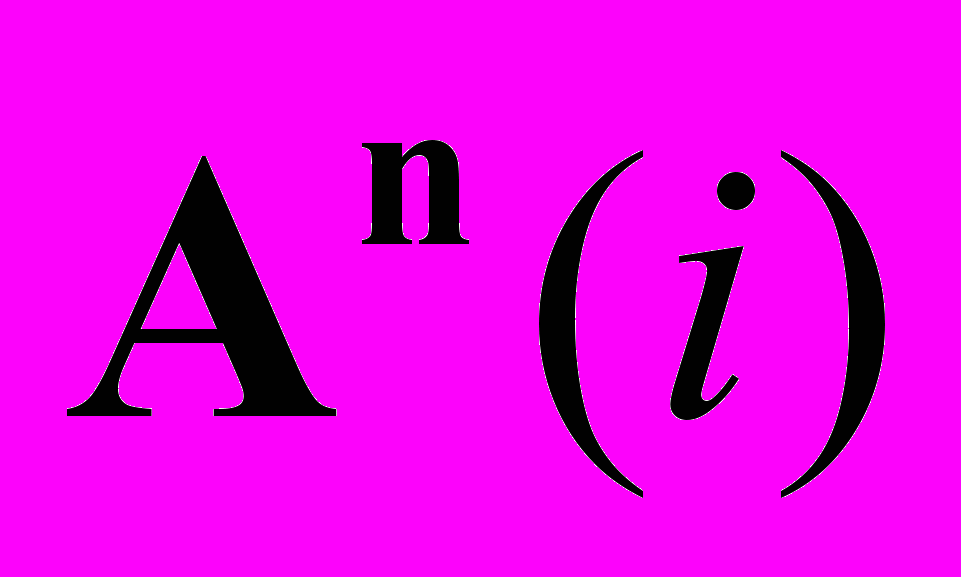. Понятие алгебраической линии и поверхности. Квадрики в пространстве 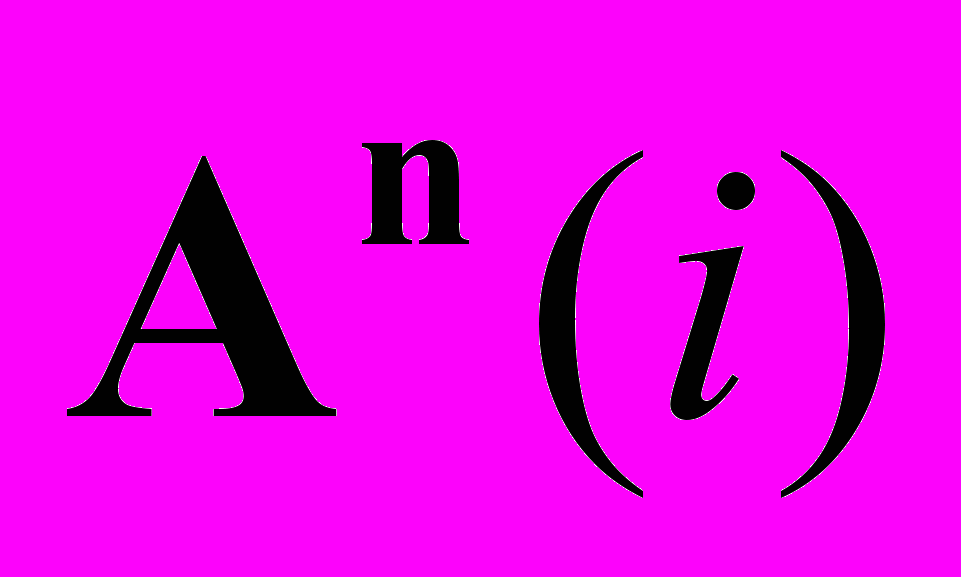. Пересечение квадрики с прямой. Асимптотические направления. Линии эллиптического, гиперболического, параболического типов на плоскости . Центры квадрик. Диаметральные плоскости квадрики. Диаметры линий второго порядка. Приведение уравнений квадрики к нормальному виду с помощью преобразования координат. Аффинная классификация квадрик в пространстве 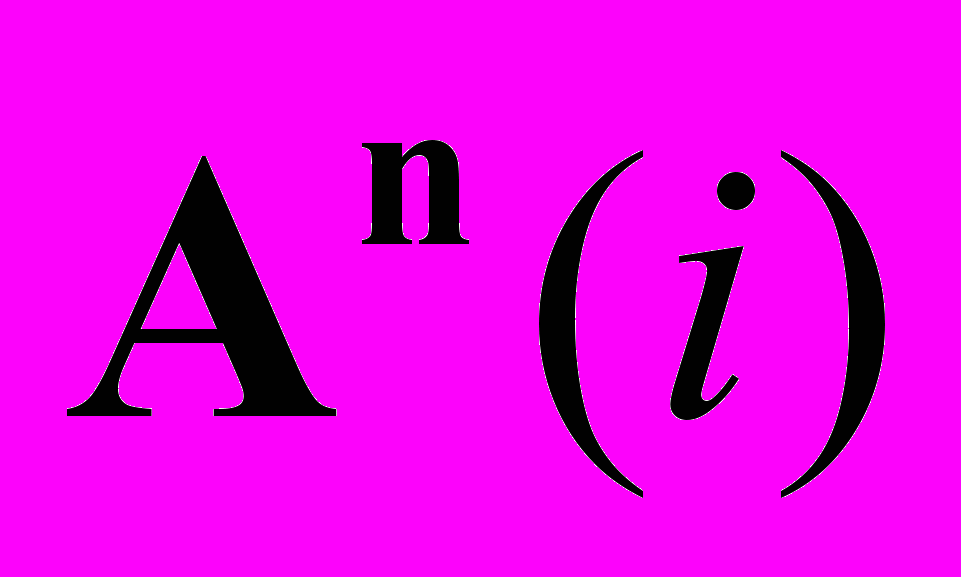. Аффинная классификация линий второго порядка. Аффинная классификация поверхностей второго порядка.

Квадрики в евклидовом пространстве

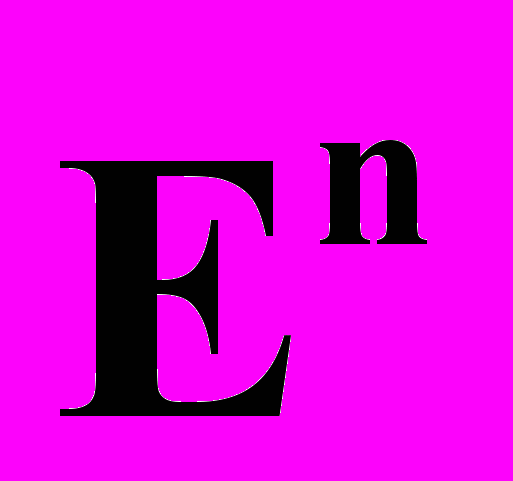
Понятие вещественно-комплексного 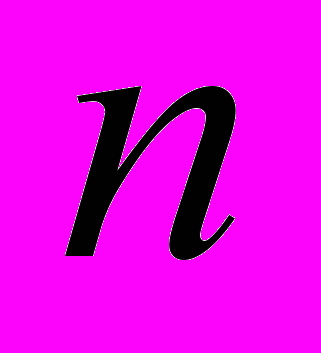-мерного евклидова пространства . Приведение уравнения квадрики в пространстве к каноническому виду. Исследование поверхности второго порядка в пространстве по общему уравнению.

Проективная плоскость 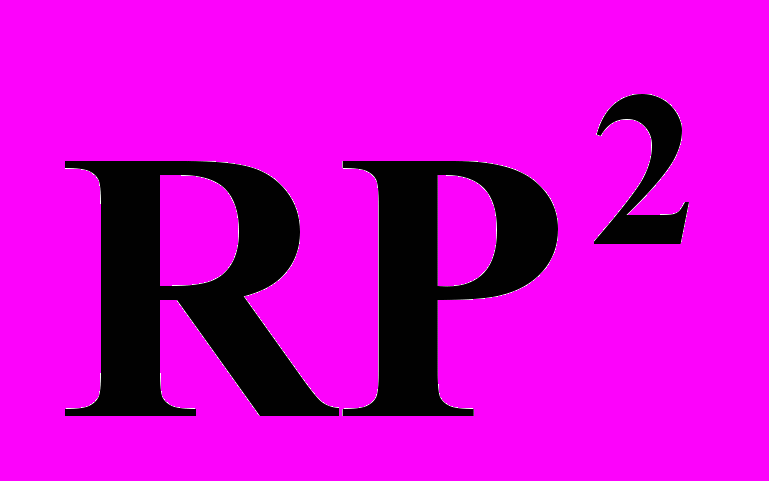и проективное пространство

Две модели вещественной проективной плоскости 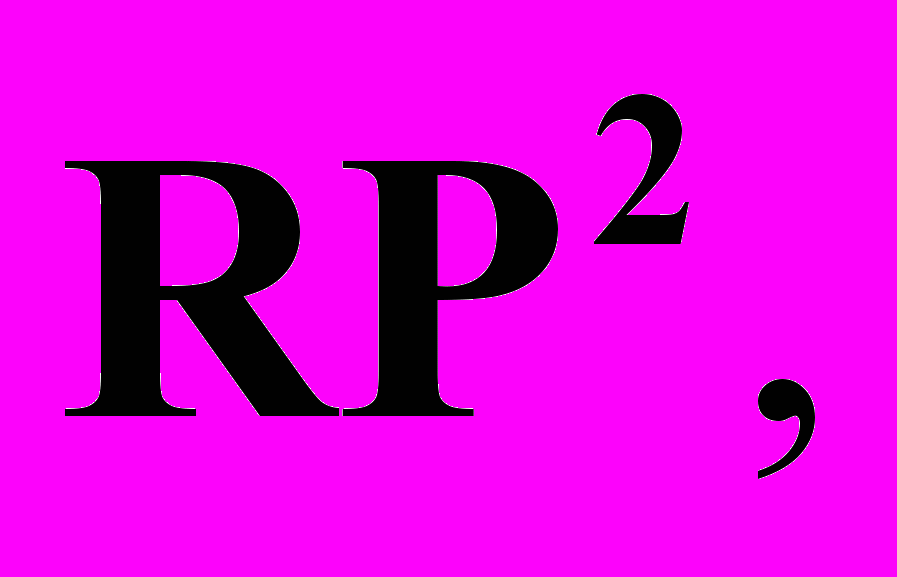однородные и неоднородные координаты. Принцип двойственности для проективной плоскости. Проективные преобразования плоскости 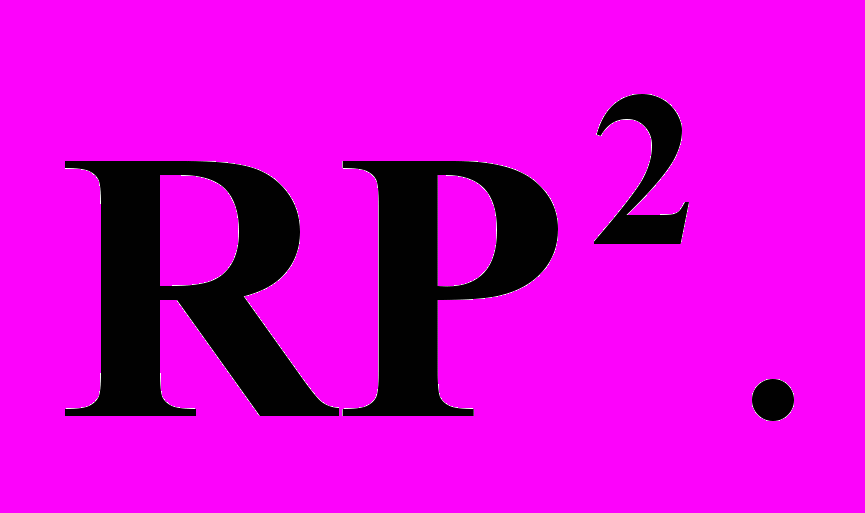Кривые второго порядка на проективной плоскости 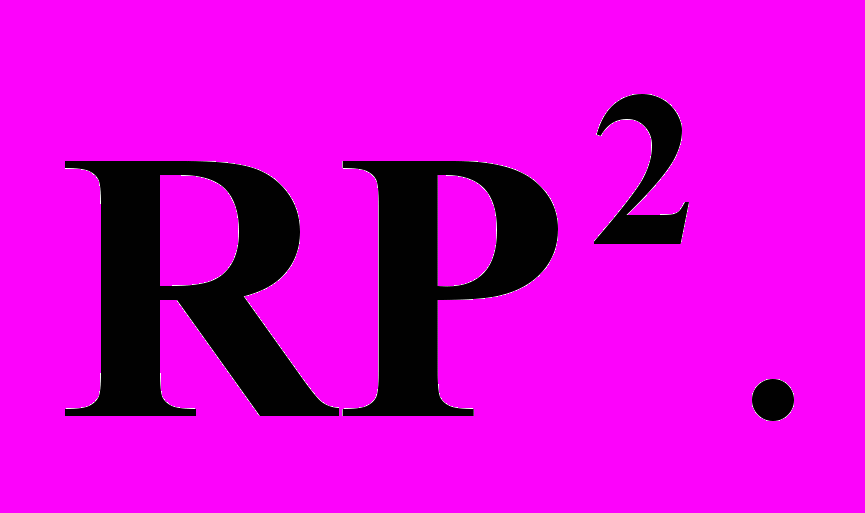Понятие 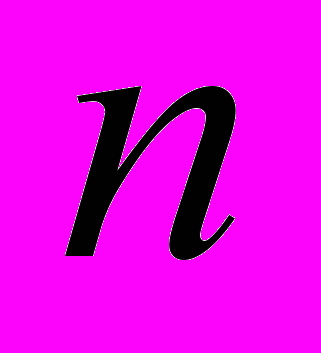-мерного проективного пространства . Аффинная карта проективного пространства . Координаты и плоскости в пространстве . Проективные преобразования. Сложное отношение четырех точек. Геометрия проективной группы. Квадрики в вещественно-комплексном проективном пространстве 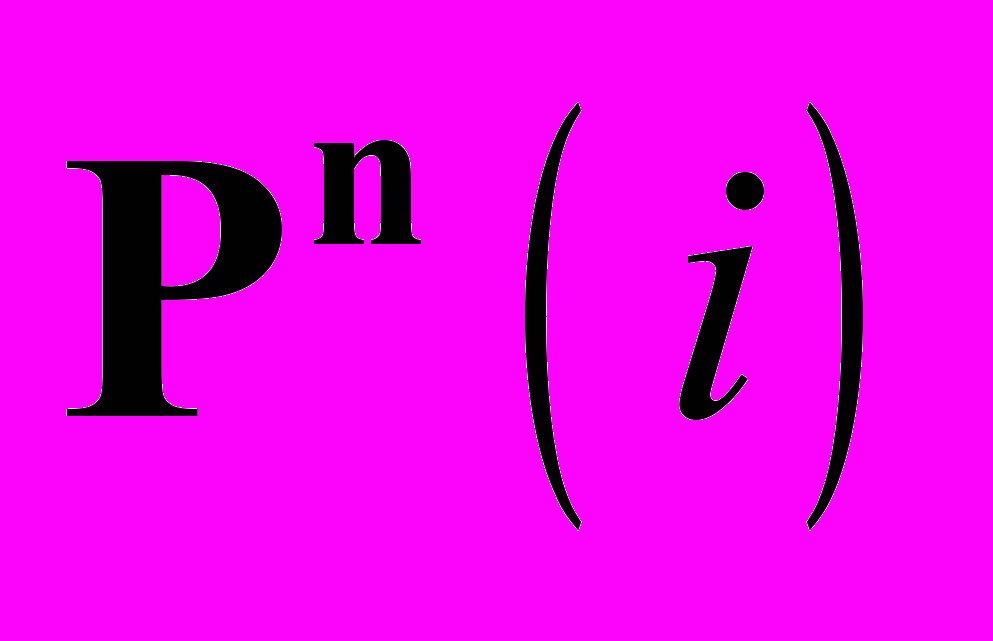. Аксиоматика проективной геометрии. Теорема Дезарга.


Основная литература

1. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия, часть 1. Минск: «Вышэйшая школа»,1984.

2. Милованов М.В., Толкачев М.М., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия, часть 2. Минск: «Вышэйшая школа»,1987.

3. Александров П.С. Курс аналитической геометрии и линейной алгебры. Москва: «Наука», 1979.

4. Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. Москва: «Наука», 1976.

5. Бурдун А.А., Мурашко Е.А., Феденко А.С. Сборник задач по алгебре и аналитической геометрии. Минск: «Унiверсiтэтскае»,1999.


Дополнительная литература


1. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. Москва: «Наука», 1986.

2. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. Москва: «Наука», 1974.

3. Постников М.М. Аналитическая геометрия. Москва, «Наука», 1973.

4. Постников М.М. Лекции по геометрии. Семестр I. Аналитическая геометрия. Москва: «Наука», 1979.


РЕЦЕНЗИЯ


типовой учебной программы дисциплины

«Аналитическая геометрия»

по специальности 1-31 03 01 «Математика»

(авторы: Кононов С.Г., Суворов В.В., Филиппович К.С.)


«Аналитическая геометрия» является, наряду с алгеброй и математическим анализом, одной из фундаментальных дисциплин, лежащих в основе классической университетской подготовки математиков. Рецензируемая учебная программа соответствует годовому курсу, включающему два часа лекций и два часа практических занятий в неделю, при этом двадцать процентов часов отводится на контролируемую самостоятельную работу студентов.

Как следует из тематического плана, по содержанию весь материал дисциплины делится на две части: аналитическую геометрию в евклидовом трехмерном пространстве и многомерную аналитическую геометрию. Первая половина базируется на школьном курсе элементарной геометрии. В ней изучаются фигуры первого порядка (прямые и плоскости) и фигуры второго порядка (эллипсы, гиперболы, параболы, эллипсоиды, гиперболоиды, параболоиды, цилиндры и конусы). Кроме того, вначале подробно рассматривается важное понятие вектора и операции над векторами.

При изложении второй половины дисциплины существенно используются понятия и результаты раздела линейной алгебры университетского курса алгебры и теории чисел. Основной упор делается на идее многомерного пространства, при этом четко различаются понятия и теоремы, носящие аффинный характер, и те, которые вытекают из наличия скалярного произведения в пространстве векторов.

Достаточное внимание в программе уделено главному методу аналитической геометрии – методу координат, а также изучению геометрических преобразований. В заключительной части курса предполагается изложение основ проективной геометрии.

Таким образом, рецензируемая программа полностью охватывает материал, относящийся к университетскому курсу аналитической геометрии для математиков, содержащийся в образовательном стандарте по специальности 1-31 03 01 «Математика». Представляется вполне обоснованным порядок изложения материала и почасовая разбивка. В программе учтено необходимое согласование с параллельно читаемыми курсами согласно типовому учебному плану. Рецензируемая программа может служить типовой учебной программой по дисциплине «Аналитическая геометрия» по специальности 1-31 03 01 «Математика».


Рецензент – заведующий кафедрой

алгебры и геометрии

Белорусского государственного педагогического университета

им. Максима Танка

доктор педагогических наук,

профессор Шлыков В.В.


Рецензия утверждена на заседании кафедры алгебры и геометрии БГПУ, протокол № от 200 г.


Зав. кафедрой профессор Шлыков В.В.


РЕЦЕНЗИЯ


типовой учебной программы дисциплины «Аналитическая геометрия»

для студентов специальности 1- 31 03 01 «Математика»

(авторы: Кононов С.Г., Суворов В.В., Филиппович К.С.)


«Аналитическая геометрия» является одним из основных математических курсов, которые читаются студентам университетов специальности 1 - 31 03 01 «Математика» в течение первых лет обучения.

Согласно рецензируемой учебной программе весь курс делится на две части: маломерную аналитическую геометрию (геометрию евклидовой плоскости и евклидова пространства , которая читается в первом семестре, и многомерную аналитическую геометрию (геометрию 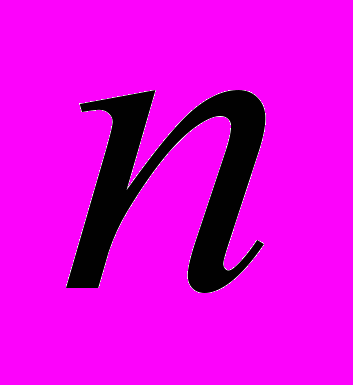-мерного аффинного пространства и 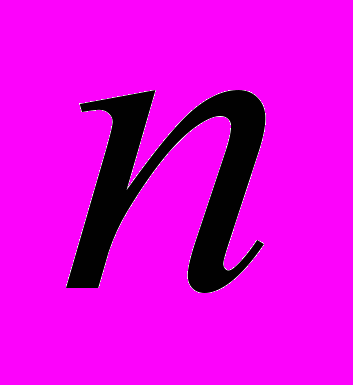-мерного евклидова пространства 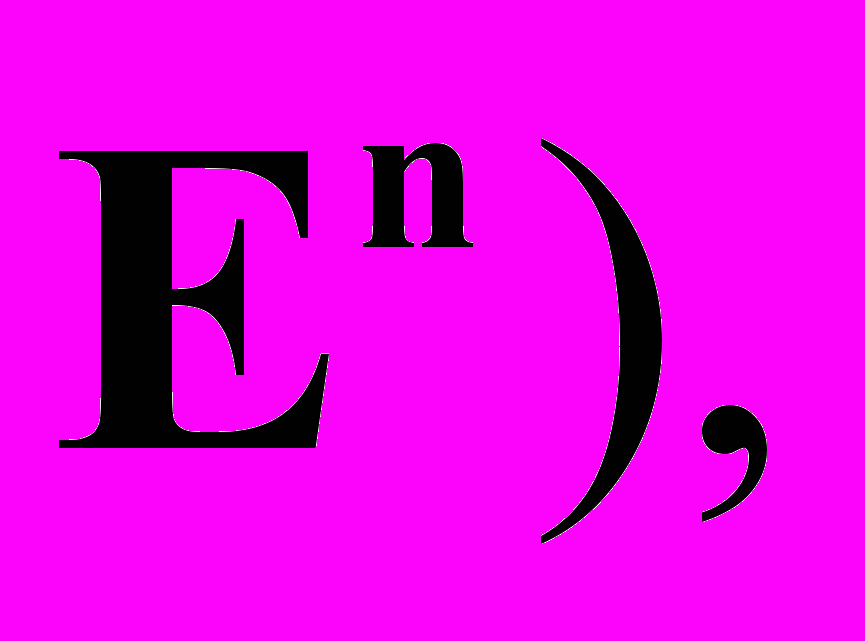которая читается во втором семестре.

Первая часть базируется в основном на элементарной геометрии и включает в себя материал, относящийся к фигурам первого порядка (прямым и плоскостям) и второго порядка (эллипсам, гиперболам, параболам, эллипсоидам, гиперболоидам, параболоидам). Кроме того, подробно изучаются векторы и операции над ними.

Вторая часть во многом опирается на линейную алгебру, которая излагается параллельно в курсе алгебры и теории чисел. Здесь рассматриваются 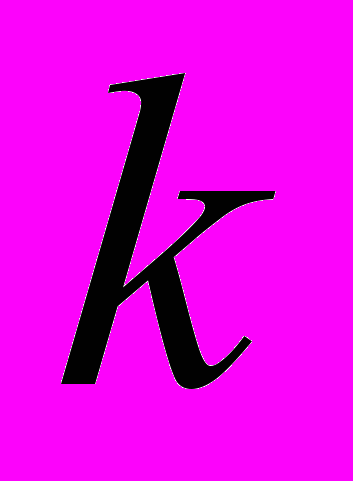-мерные плоскости в 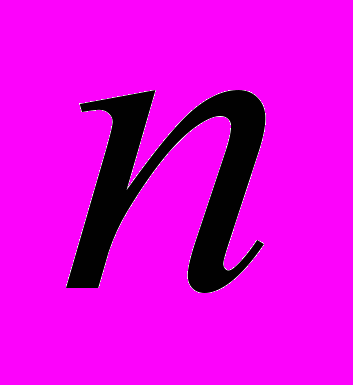-мерном пространстве, а также квадрики – многомерное обобщение кривых и поверхностей второго порядка. Изучаются также морфизмы аффинных и евклидовых пространств, в частности, группы аффинных преобразований и движений. Дается введение в проективную геометрию.

Рецензируемая программа полностью покрывает материал университетского курса аналитической геометрии для математиков, содержащийся в образовательном стандарте по специальности 1-31 03 01 «Математика». Студенты, усвоившие материал лекционного курса, и прошедшие практические и лабораторные занятия согласно прилагаемого тематического плана, получают знания и умения, достаточные для успешного применения геометрических идей в других математических дисциплинах. Почасовая разбивка учебного лекционного материала и практических занятий представляется обоснованной и доступной для студентов. Для изложения аналитической геометрии во втором семестре требуется тесное согласование с параллельно читаемым курсом алгебры и теории чисел.

Рецензируемая программа может быть принята в качестве типовой учебной программы дисциплины «Аналитическая геометрия» по специальности 1- 31 03 01 «Математика».


Рецензент:

заведующий кафедрой

прикладной математики и экономической кибернетики БГЭУ

доктор физико-математических наук,

профессор /И.В. Белько /