Geum.ru

Ямщиков Денис Викторович 11 класс, гимназия №587, Санкт-Петербург Целью данного реферат

Вид материалаРеферат

Содержание


Из истории
Геометрический смысл комплексного числа
Применение комплексных чисел для решения некоторых задач
Подобный материал:
Теория комплексных чисел

Ямщиков Денис Викторович

11 класс, гимназия №587, Санкт-Петербург

Целью данного реферата является изучение истории возникновения комплексных чисел, а также рассмотрение алгебраической, тригонометрической и показательной формы комплексных чисел.

Решение многих задач по физике и математике приводит к уравнениям, не имеющим решения в области действительных чисел. Но нельзя с уверенностью заявить, что решений у той или иной задачи нет, потому что в квадратном уравнении получился отрицательный дискриминант. Решение есть, но оно уже относится к области комплексных чисел. Сегодня сложно представить себе ряд наук без применения комплексных чисел. Комплексные числа нашли свое применение в теории электротехники, электромеханике, радиотехнике, самолетостроение и в других науках.

Из истории

В XVI в. в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Получалось, что путь к этим трем корням уравнения ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Чтобы объяснить получившийся парадокс, итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой породы. Он показал, что система уравнений x + y = 10, xy = 40, не имеющая решений в множестве действительных чисел, имеет решения вида x = 5±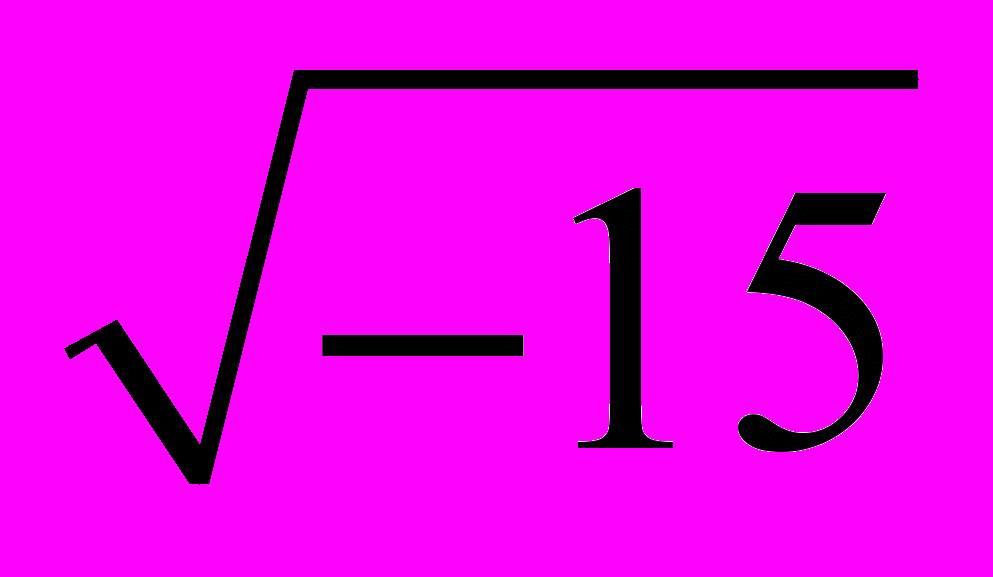, y = 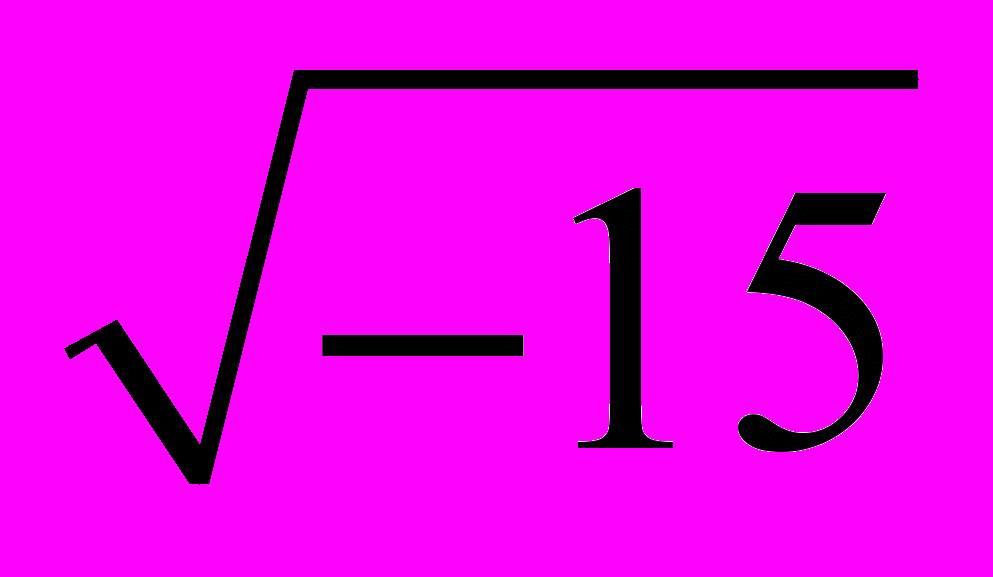, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать, что = 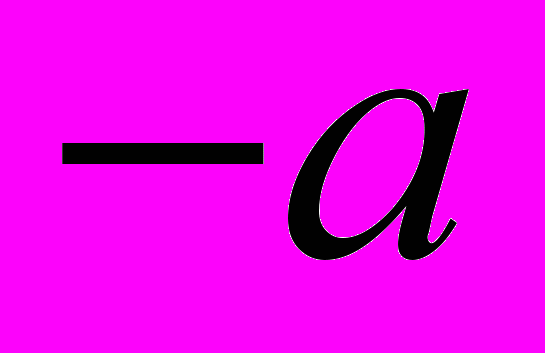. Кардано называл такие величины «чисто отрицательными» и даже «софистически отрицательными», считал их бесполезными и стремился не применять их. Название «мнимые числа» ввел в 1637 г. французский математик и философ Р. Декарт, а в 1777 г. один из крупнейших математиков XVIII в. — Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа 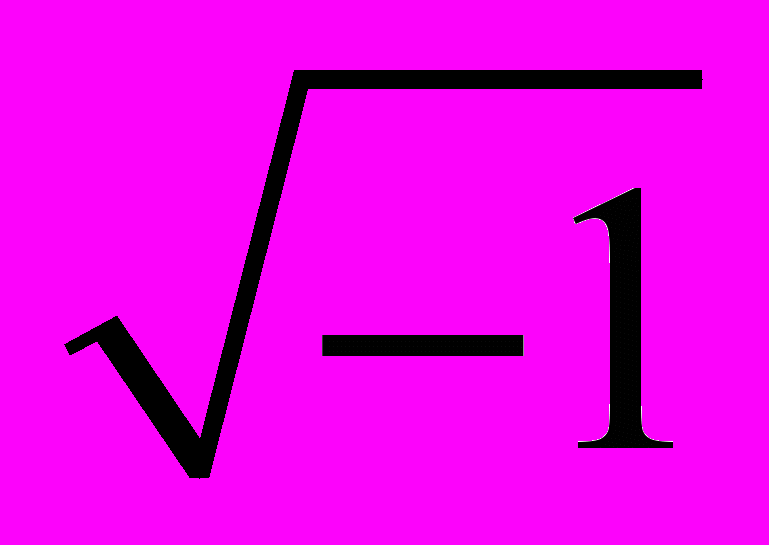(«мнимой» единицы); этот символ вошел во всеобщее употребление благодаря К. Гауссу (1831).

Понятия

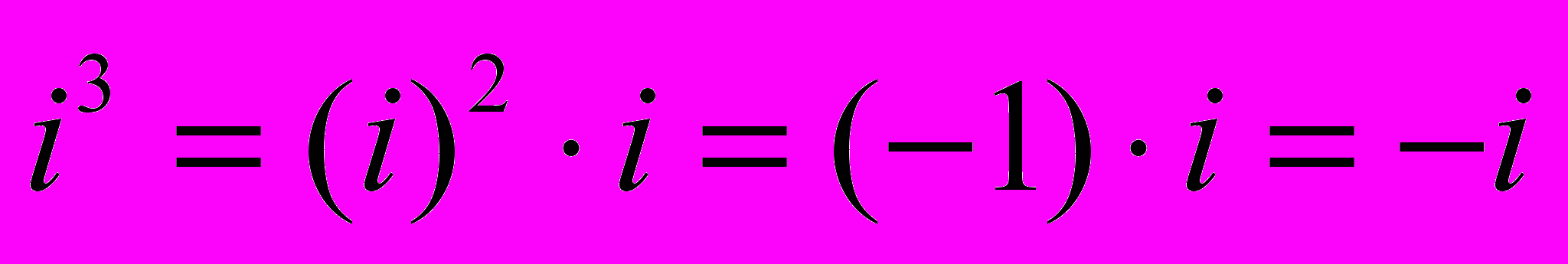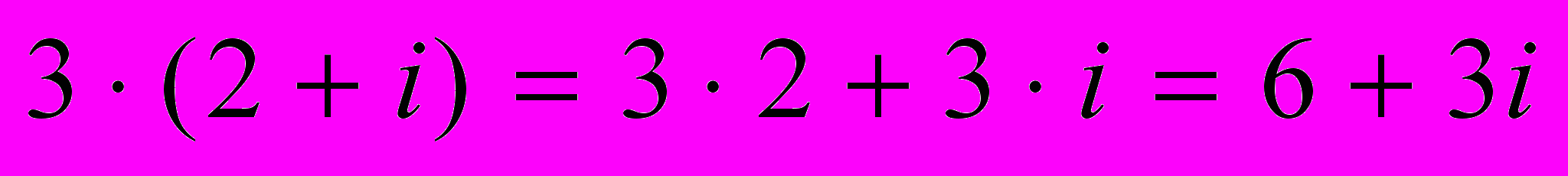Число называется мнимой единицей. Можно рассматривать мнимую единицу как формальный объект, который имеет следующее свойство: Примеры вычислений с мнимой единицей: 1) ; 2) ; 3) 4) .

Комплексные числа — это пара действительных чисел с заданными определенным образом операциями умножения и сложения. Комплексное число записывают как

Число называется действительной частью числа , а число i - мнимой частью числа.

Геометрический смысл комплексного числа

Комплексное число z = x + iy можно изображать вектором с началом в точке 0 и концом в точке z. Этот вектор обозначается той же буквой z. Из рисунка (см. выше) или из формулы |z| = (x2 + y2)1/2 видно, что длина вектора z равна |z| и справедливы следующие нестрогие неравенства |x| ≤ |z| и |y| ≤ |z|, т.е. |Re z| ≤ |z| и |Re z| ≤ |z|.
     С помощью векторной интерпретации наглядно иллюстрируются сумма и разность комплексных чисел. Число z1 + z2 изображается вектором, построенным по правилу сложения векторов z1 и z2, а вектор z1 - z2 можно построить как сумму векторов z1 и -z2. Видно, что расстояние между точками z1 и z2 равно длине вектора z1 - z2, т.е. равно |z1 - z2|. Это же утверждение следует из равенства |z1 - z2| = [(x1 - x2)2 + (y1 - y2)2]1/2 .

Тригонометрическое представление

Комплексное число z = a + bi однозначно определяется своим модулем (расстоянием до точки O) и углом между Oz и действительной осью — этот угол называется аргументом комплексного числа и обозначается так: .

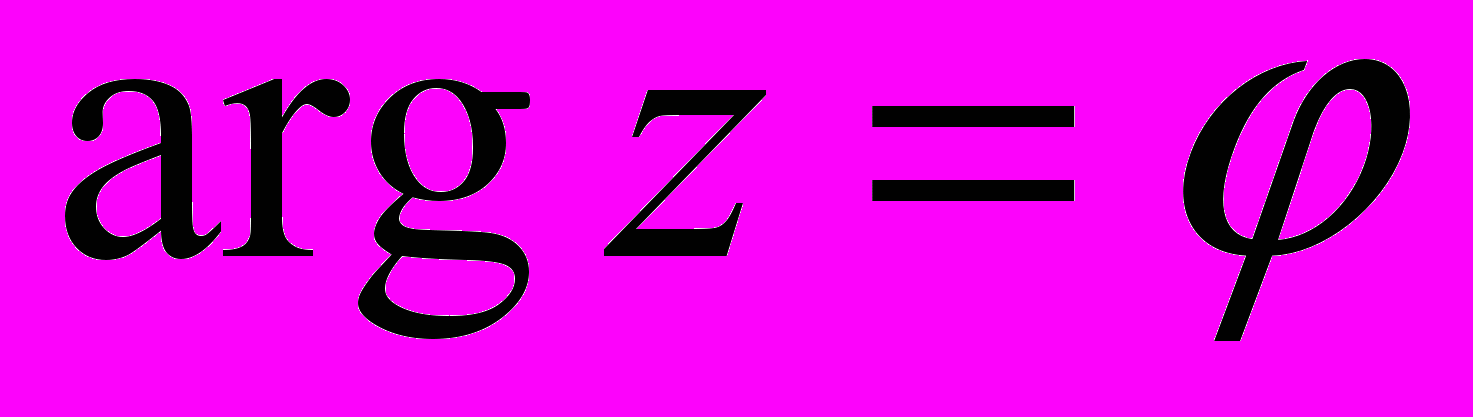Так как a = |z|cos, b = |z|sin, то в тригонометрической форме комплексное число имеет следующий вид: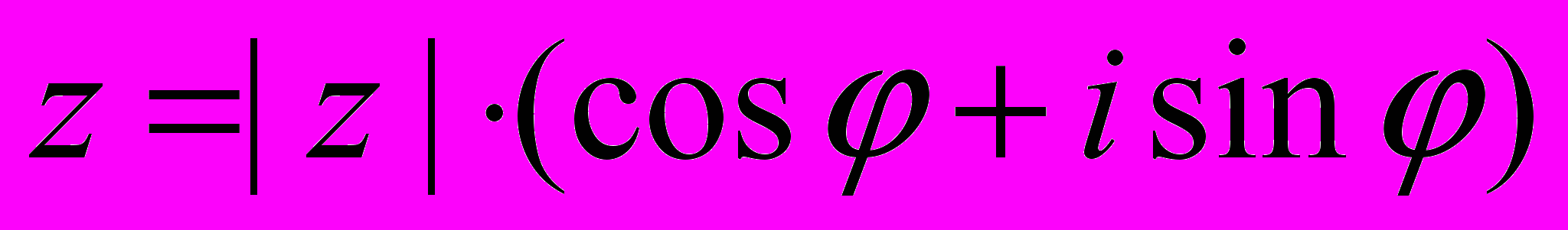

Умножение одного комплексного числа на другое происходит следующим образом:

, так как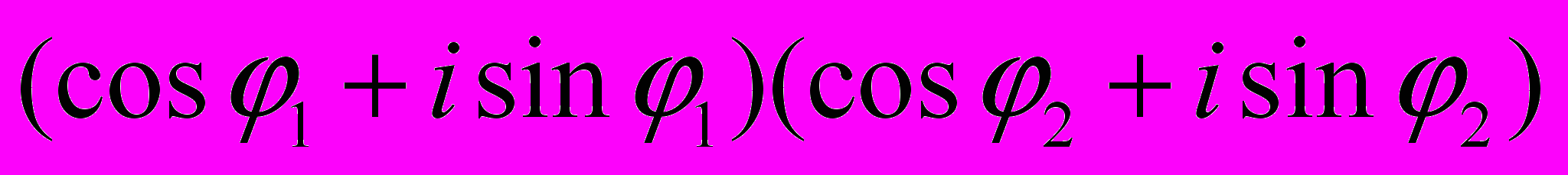

=

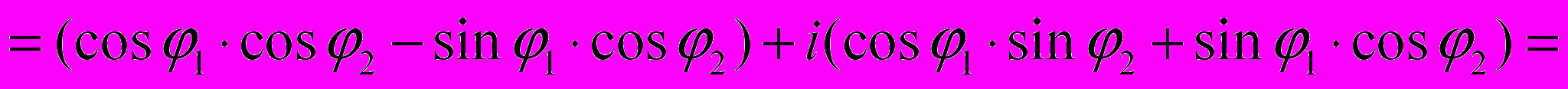
Например, возведение в степень происходит на основе формулы Муавра -

Для n = 2 (для комплексного числа длиной в единицу), она выводится следующим образом:

так как



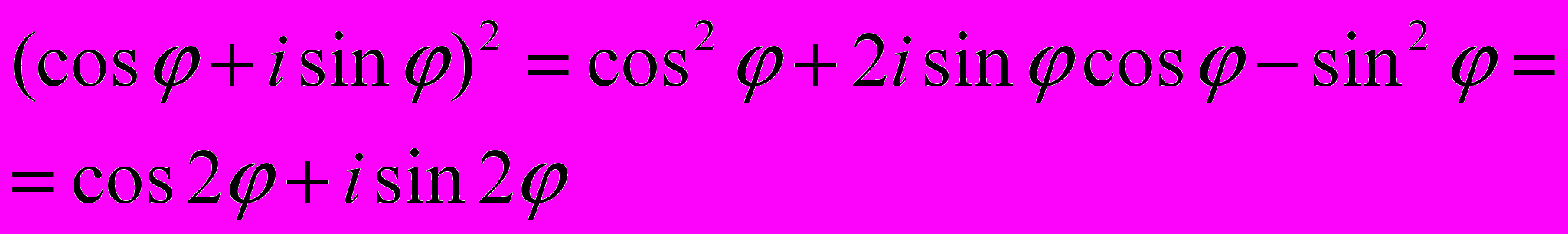
то

Для n = 3 (для комплексного числа длиной в единицу), она выводится следующим образом:

используя предыдущий пример, мы получаем, что



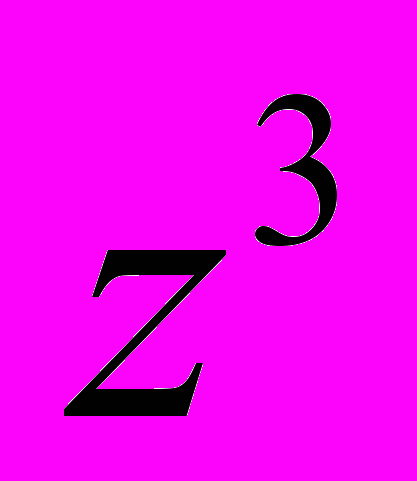
то есть 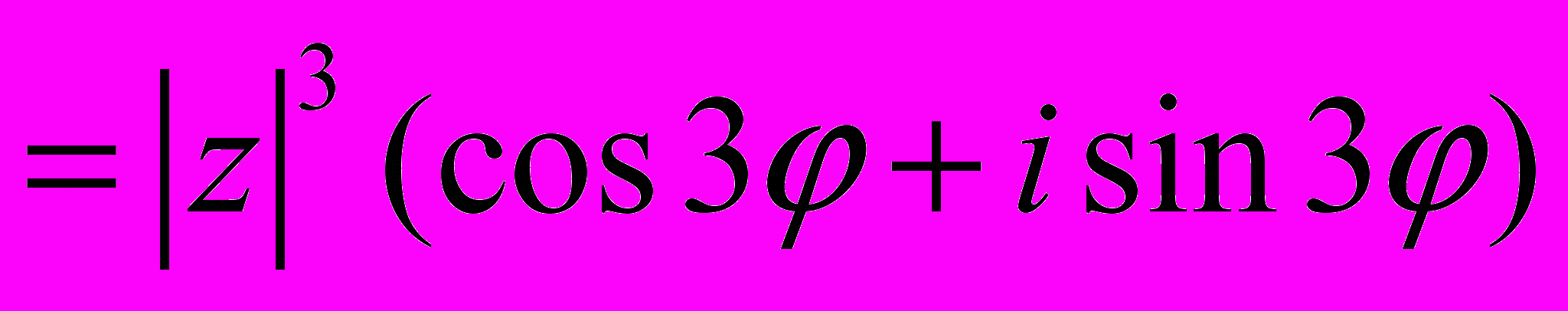, то есть в соответствии с формулой Муавра.

Показательная форма комплексного числа

Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой 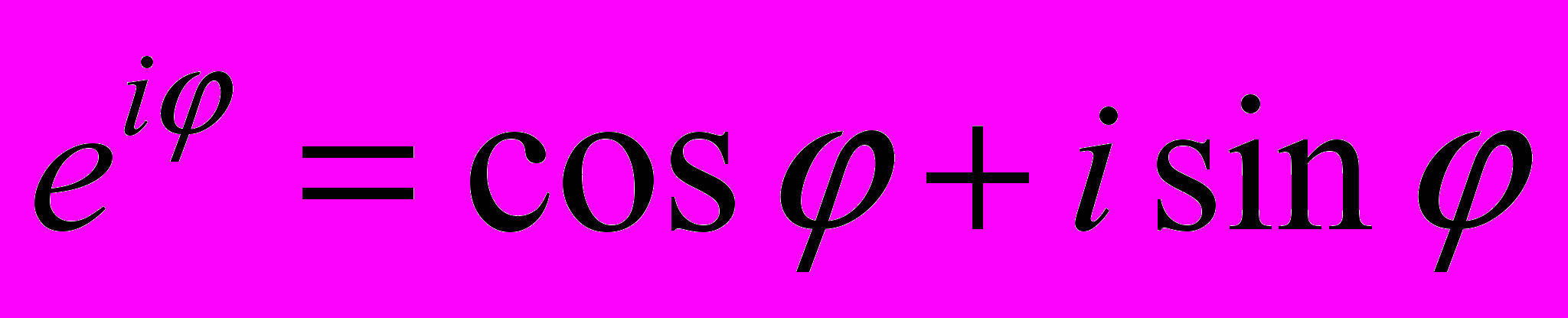которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа. Пусть комплексное число в тригонометрической форме имеет вид . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим . Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь ,.

Применение комплексных чисел для решения некоторых задач


Использование тригонометрической формы комплексного числа допускает простое решение некоторых тригонометрических задач, в том числе и тригонометрических систем. Далее рассматривается три примера, одним из которых является тригонометрическая система, а другой представлен ниже:

Пример: Выразить sin 3x и cos 3x в виде некоторой функции от sin x и cos x

- по формуле Муавра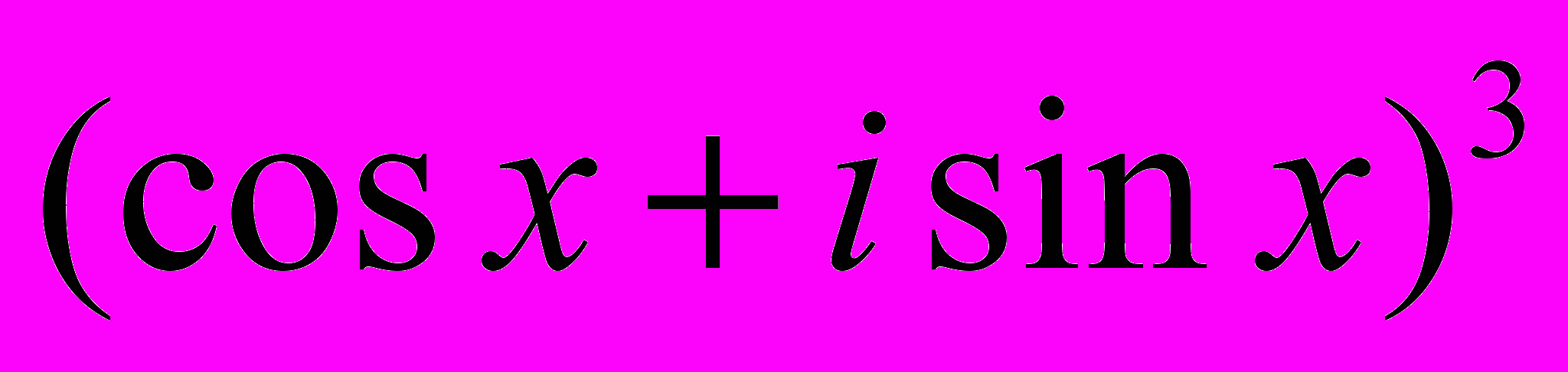





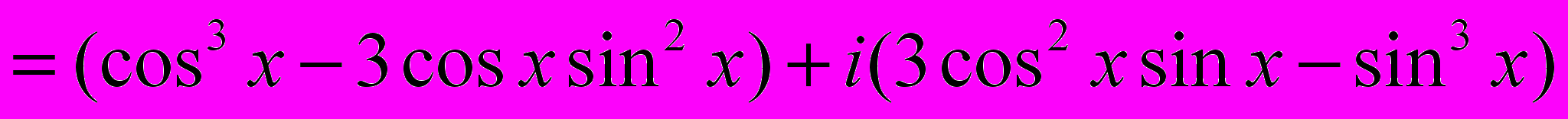
Из равенства двух комплексных чисел следует, что их действительные и мнимые части равны:





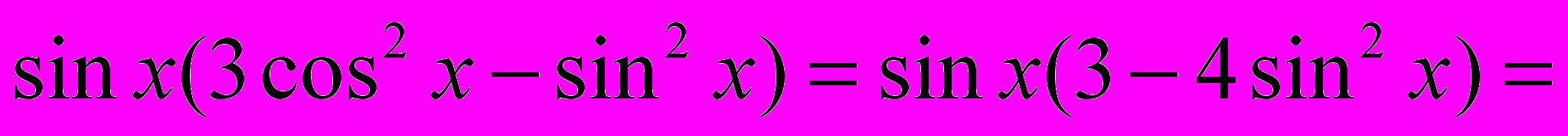
Как уже было упомянуто в начале, сложно представить себе ряд наук без применения комплексных чисел. Комплексные числа успешно прижились в электронике, где благодаря их применению с восхитительной простотой описывается поведение сложных электроцепей. Они также весьма эффективны в описании механики небесных тел, в частности для решения систем уравнений, которые помогают астрономам рассчитывать орбиты планет, спутников и астероидов. А не так давно они нашли широкое применение в компьютерной графике, во многом благодаря их популяризации.