Декілька сторінок з історії розвитку логіки
| Вид материала | Закон |
- Тема Екскурс в історію логіки, 463.37kb.
- Панель інструментів Обычные кнопки, 167.53kb.
- Змістовно-діяльнісна структура модулів навчальної дисципліни «Логіка (загальна та юридична)», 77.47kb.
- Реферат з логіки на тему:, 80.53kb.
- Навчання історії у профільних класах: теорія І практика, 136.83kb.
- Яковенко В. Повсякденне життя житомирян в умовах окупації, 103.76kb.
- Програма розрахована на 70 годин (35 годин 10 кл.; 35 годин 11кл). 10-й клас, 112.63kb.
- Реферат на тему, 189.78kb.
- З ім'ям М. Кропивницького пов'язані створення українського професіонального театру, 740.79kb.
- Литвинко алла степанівна, 485.85kb.
Розділ другий
ДЕКІЛЬКА СТОРІНОК З ІСТОРІЇ РОЗВИТКУ ЛОГІКИ
Логіка як наука про мислення та його закономірності сформувалась ще у Стародавній Індії, а потім перекочувала у Стародавню Грецію, Вавілон, Стародавній Єгипет, Стародавній Рим. До того ж, логіка в країнах Близького Сходу і в Європі формувалась в кожній окремо, незалежно одна від одної. Традиції розвитку знань логіки в Індії сприймались мислителями Китаю, Тибету, Монголії, Кореї, Японії, Індонезії. Вчення про мислення впливали на розвиток логіки у Візантії, Вірменії, Грузії, Україні, Росії. Отже знання логіки виникають і розвиваються тоді, коли процеси людського мислення стають предметом власного дослідження. Розвиваючись у лоні філософських знань, логіка завжди виступала як складова частина філософії і тільки згодом поступово відокремлювалась, так би мовити, на правах автономії. Розвитку знань логіки сприяла безліч причин, в основному розвиток різних наук, що ґрунтувалися на теоретичному мисленні, яке вимагало коректних умовиводів і доведень, а також розвиток ораторського мистецтва.
За тисячоліття історія логіки пережила три великих періоди: антична логіка (V - III ст. до н.е.); схоластична логіка (середина XIII - середина XIV століть); сучасна логіка (із середини XIX ст. до сучасності). Вперше поняття логічне для формування критеріїв істини і правил пізнання ввів до наукового обігу видатний філософ-матеріаліст Демокріт (близько 460 - 370 до н.е.), який назвав свій твір про критерії і правила пізнання "Про логічне, або Про канони". Трактат Демокріта, як і багато інших творів, до сучасності не дійшли.
Правда, деякі дослідники вказують, що логіка Давньої Індії, яка, звичайно, розвивалась у надрах філософського знання, зароджується ще у ХІІ-VII ст. до н.е. У найдавнішіх пам’ятниках індійської культури, якими вважаються чотири збірники релігійних гімнів – Вед, не тільки викладені релігійні уявлення про дійсність, а й містилися філософські погляди на світ, на людину та її мислення. В одному з розділів Упанішад – релігійно-філософських коментарів до ведичних гімнів – йдеться про індивідуальні думки та їхній зв’язок зі словами, про можливість пізнання, а також про типи інтелектуальної і психічної діяльності.
Давньоіндійський філософ Дармакирті (VII ст. до н.е.) у своїй праці “Крапля логіки” розглядав питання побудови суджень та умовиводів. Давньоіндійському епосу також притаманна логіко-філософська спрямованість. У ньому розкрито три джерела пізнання: сприйняття, висновок, або умовивід, і свідоцтва святого письма або авторитетної особи. Пізніше (III-V ст. до н.е.) логічні школи вайшеншика та ньяя здійснили істотний вплив на розвиток буддійської логіки, створили теорію умовиводу, розробили теорію умовиводу за аналогією. Досягнення цієї логіки поширювались разом з релігією буддизму.
Логіка Стародавнього Китаю розвивалась у вченнях багатьох авторитетних мислителів. Наприклад, Конфуцій виступав за чіткість суджень, образність висловлювань, логічну обгрунтованість думок. Мо-цзи та його послідовники розробляли логіку і теорію пізнання. Вони висунули категорію “бянь” (судження) як основний логічний метод. За її допомогою визначалися істина і хибність, законна і незаконна дія; встановлювалися тотожність і відмінність; з’ясовувались співвідношення між іменами (поняттями) і дійсністю, усувалися сумніви. Пізніше на основі цієї категорії було розроблено класифікацію імен, досліджувались логічні відношення між іменами, розглядалися стверджувальні й заперечні судження.
Давньокитайська логіка набула серйозного розвитку. Так, прихильники логіки Мо-цзи вже вважали, що два протилежних судження не можуть бути істинними або хибними одночасно, оскільки лише одне з них є істинним, тоді як інше – хибне. Вони досліджували й розробляли питання створення логічних систем, впритул підійшли до розуміння змісту закону тотожності, основного принципу закону виключеного третього.
Послідовники Мо-цзи запропонували сім методів міркування або висунення гіпотез. Ними вони вважали: 1) “хуо”, тобто ймовірність, 2) “цзя”, або уявлення, 3) ”сяо”, або наслідування певного зразка, 4) “бі”, тобто зіставлення, 5) “моу”, або порівняння, 6) “юань”, або посилання на думку опонента, 7) “гуй”, або поширення судження на інші об’єкти.
Характерною рисою давньокитайської логіки був істотний вплив на її розвиток різних політичних доктрин і морально-етичних концепцій. Слід підкреслити, що логічні концепції Стародавнього Китаю сформувалися раніше, ніж у стародавній Греції. Однак після раннього періоду династії Цинь вони припинили свій подальший розвиток. Це було зумовлено тим, що з цього періоду й до недавнього часу в країні офіційно визнавалось лише конфуціанство і безпідставно відкидались вчення інших представників багатої філософської культури, в тому числі логічні, етичні, естетичні та інші концепції.
Філософи-ідеалісти Стародавньої Греції також досліджували проблеми логіки. Так, Сократ висловлював свої міркування про сутність і значення логічних методів індукції та дедукції. Відомий філософ Платон, послідовник Сократа, з’ясовує визначення і поділ понять, аналізує логічну форму судження, яку він вважав основним елементом мислення і впритул наблизився до відкриття основних законів логіки.
На виникнення логіки як науки значний вплив здійснили давньогрецькі софісти – це перші професійні вчителі "мудрості" і красномовства (Протагор, Гіппій та інші). Софісти бралися доводити істинність і хибність будь-якого положення, вдаючись до прийомів, що отримали назву софістичних, тобто цілком свідомо спотворюючи і порушуючи правила побудови думок. Цих "учителів" Аристотель справедливо називав учителями "уявної мудрості".
Істинним засновником логіки став видатний давньогрецький мислитель Аристотель. Створену і детально розроблену ним науку Аристотель називав не логікою, а аналітикою, своєму головному твору з логіки він дав назву "Аналітика". У ньому Аристотель детально аналізує силогізм як особливу форму умовиводу, розкриває сутність доведення, прийоми визначення і поділу понять та їхнє значення в науці. Крім цієї праці, до логічних творів Аристотеля відносяться також "Топіка", "Категорії", "Про софістичні спростування", "Про тлумачення". Пізніше (у І ст. до н.е.) послідовники Аристотеля об'єднали всі його логічні трактати під загальною назвою "Органон" (від грецьк. – знаряддя, інструмент, засіб пізнання, дослідження). Ціла низка важливих логічних проблем розглянута Аристотелем в його головній філософській праці, яка згодом одержала назву "Метафізика". Саме тут ним було викладено три основних закони формальної логіки – закон тотожності, закон суперечності і закон виключеного третього.
Важливо засвоїти, що Аристотель вважав зв'язок думок, виражений у законах і правилах логіки, не довільним, а обумовленим зв'язком самих речей. Це значить, що він, на відміну від ідеалістів Сократа і Платона, відстоював матеріалістичну лінію Демокрита у філософських питаннях логіки, хоча ця позиція була в нього не до кінця послідовною. Наприклад, при аналізі загальних філософських категорій він виявляв коливання між матеріалізмом і ідеалізмом або інколи висловлювався в дусі ідеалізму.
Аристотель не перший, хто вживав терміну "логіка". Уперше це поняття вводиться у науковий обіг у ІІІ - ІІ столітті до н.е. стоїками. Представники цієї школи – Зенон, Хрізіпп, Сенека – розглядали логіку як частину філософії. Розвиваючи логічне вчення Аристотеля, стоїки не обмежувалися дослідженням категоричного силогізму, а займалися переважно тими умовиводами, до складу яких входили умовні й розділові судження. Вони досліджували сукупність категорій, що входять до складу сучасної математичної логіки, таких як імплікація, диз'юнкція, кон'юнкція та інші.
У період християнського Середньовіччя (із середини XII ст.) відбулося своєрідне "друге відкриття" Аристотеля через арабські джерела. Однією з перших робіт, де були відновлені логічні дослідження і став використовуватися термін "логіка", була "Діалектика" П'єра Абеляра. Саме схоласти додали Аристотелевій логіці роль необхідного знання, і вона як пропедевтика наук міцно увійшла до структури освіти, стала Schullogik (шкільною логікою). Античну і схоластичну логіку сьогодні прийнято поєднувати під назвою "традиційної" або "формальної" логіки, змістом якої ми й будемо займатися в межах відведеного нам навчальною програмою часу.
Подальший розвиток логіки пов'язаний з виникненням і поступовим розвитком у надрах феодалізму капіталістичних суспільних відносин, розвитком дослідно-експериментального знання. Нова реальність вже не укладалася в межі схем дедуктивних побудов і не отримувала адекватного пояснення за їх допомогою. Виникла необхідність створення нової логіки. Велику роль у розробці нової логіки зіграли видатні мислителі: англійський філософ і натураліст Френсіс Бекон, французький філософ і математик Рене Декарт, німецький філософ і математик Готтфрід Лейбніц.
Родоначальник англійського матеріалізму Ф. Бекон пристрасно виступав проти середньовічної схоластики як головної перешкоди на шляху вивчення природи. Він критикував дедуктивний метод Аристотеля як безплідний і на противагу йому свій головний філософський здобуток назвав "Новий Органон". У цьому творі він виклав основи індуктивної логіки. Перевагу, силу своєї логіки він вбачав саме в індуктивному методі, який протиставлявся дедукції, силогістиці Аристотеля. Вважаючи, що безпосереднім завданням пізнання є розкриття причинних зв'язків між предметами і явищами дійсності, Ф. Бекон розробив методи визначення причинних зв'язків між явищами. Подальша розробка цих методів була плідно продовжена потім Гершелем, Уевеллем і Дж Ст. Міллем.
Справедливості заради треба сказати, що необхідність індуктивної логіки була ясно усвідомлена і висловлена ще в XIII ст., дійсним засновником її був францисканський чернець Роджер Бекон, а не його більш знаменитий однофамілець Френсіс Бекон, лорд Веруламський. Захищаючи дослідне знання, Р. Бекон стверджував, що "є два способи пізнання: за допомогою доведення і за допомогою досвіду. Доведення дає розв’язання питання, але не дає нам впевненості в його коректності, доки істинність отриманого розв’язку не буде підтверджена досвідом".
"Погоджуй свої думки одну з одною", – вимагали в часи Аристотеля. "Погоджуй свої думки з авторитетом", – таким було гасло середньовічних часів. "Погоджуй їх з фактами", – ось що стало основною вимогою до коректності мислення збоку логіків нової доби. У відповідь на нові запити часу і було створено те, що звичайно, хоча й не особливо вдало називають "індуктивною логікою".
Як з'ясувалося пізніше, Ф. Бекон зовсім неправомірно протиставляв індукцію дедукції, перебільшив пізнавальне значення першої і зменшив значення другої. У XIX ст. англійський філософ і логік Джон Стюарт Мілль систематизував результати досліджень Ф. Бекона в галузі індуктивних методів причинного зв'язку явищ, створивши індуктивну логіку як логіку спостереження і пояснення явищ. Його "Система логіки силогістичної і індуктивної" стала новою прибудовою до старого будинку. Пізніше з'ясувалося, що немає ніякої суперечності між цими двома методами логіки (дедуктивним і індуктивним), що один доповнює інший і через цей інший тільки й може повноцінно функціонувати, проявляючи свою пізнавальну сутність.
Рене Декарт у своїй праці "Міркування про метод...", критикуючи середньовічну схоластичну логіку, слідом за Беконом розробляв принципи філософії і логіки, які слугували нагальним потребам суспільної практики, посилювали можливість панування людини над природою. Метою для Декарта було створення наукового методу. Але якщо Бекон висував ідею всеосяжності й універсальності методу індукції, то Декарт, посилаючись на строгість математичних доведень, віддавав перевагу дедукції. "Користуйтеся дедукцією, і ви відкриєте будь-які двері", – стверджував Декарт.
Послідовники Р. Декарта з монастиря в Пор-Роялі Антуан Арно і П’єр Ніколь у 1662 р. написали підручник логіки "Логіка, чи Мистецтво мислити", відомий під назвою "Логіка Пор-Рояля". Одне із завдань авторів полягало в тому, щоб звільнити логіку Аристотеля від схоластичних перекручень. Але вони так захопилися боротьбою зі схоластичними догмами, що непомітно перейшли кордони традиційної логіки і фактично потужно взялися за створення методології наукового пізнання, за створення своєрідних правил логіки відкриттів. Тому логіка в них розглядалась як пізнавальний універсальний інструментарій для різноманітних галузей наукового дослідження.
Реформаторство в логіці продовжив Г. Лейбніц. Він обґрунтовував ідею числення розуму, подібного до математичного числення, яке базується на універсальній логічній мові, що відрізняється від природних мов точністю і однозначністю висловлювань. Зокрема, він запропонував використання методів математики в логіці, тобто описувати закони людського мислення точною і строгою математичною мовою, щоб зробити їх дійовим інструментарієм наукового дослідження. Тому німецького математика і філософа Г.Лейбніца можна вважати одним з фундаторів математичної логіки. Ідея числення, яку він вважав найефективнішим методом досягнення будь-якої істини, знайшла втілення тільки через 200 років у роботах англійського математика і логіка Дж. Буля, який написав дві фундаментальні роботи: «Математичний аналіз логіки» і «Закони мислення».
Слід зазначити, що Лейбніц сформулював четвертий основний закон логіки: закон достатньої основи (підстави). Він поклав початок розробці принципів побудови дедуктивних теорій. По суті, позначені Лейбніцем основні розділи математичної логіки – класична логіка висловлень і логіка предикатів, – є сучасною базою дедуктивної логіки. Вони виходять за межі нашого курсу і не будуть тут розглядатися.
Традиційну логіку вперше назвав "формальною" великий німецький філософ Іммануіл Кант. Формальну логіку він розглядав як науку про чисті форми мислення, ніяк не пов'язані зі змістом мислення і незалежні від нього. Логічні форми і закони мислення Кант оголосив апріорними (до всякого досвіду заданими) формами людського розсудку, даними нам у готовому вигляді. Кант вважав, що логіка з часів Аристотеля не зробила жодного кроку вперед і має зовсім замкнутий, закінчений характер.
Георг-Вільгєльм-Фрідріх Гегель створив діалектичну логіку, методологію якої Карл Маркс успішно застосував при дослідженні економічних процесів капіталізму й при написанні всесвітньовідомої праці «Капітал», надавши їй (діалектичній логіці) матеріалістичну інтерпретацію.
У другій половині XIX ст., а тим більше в XX ст. на людство чекала ціла злива відкриттів у різноманітних галузях науки і техніки, завдяки яким логіка трансформувалась в низку цікавих теоретичних ідей. Назвемо лише деяких видатних учених, які внесли значний доробок у розвиток новітньої логіки.
Джордж Буль— один із засновників математичної логіки. В основу створюваної ним логічної теорії він поклав гіпотезу про тісні зв'язки між алгеброю і логікою, завдяки яким за певних умов формули і прийоми алгебри можуть бути успішно перенесені в логіку, і навпаки. Він розробив відповідне логічне числення, в якому застосував закони й операції математики (додавання класів, множення тощо). Логіко-алгебраїчний метод дав можливість виявити нові типи висновків, які не враховувались у традиційній силогістиці. Дж. Буль детально проаналізував закони комутативності, асоціативності, дистрибутивності. Ідеї Дж.Буля знайшли підтримку і дальший розвиток в роботі відомого російського математика і логіка П.С.Порецького «Про способи розв'язання логічних рівнянь і про зворотний спосіб математичної логіки».
Сучасна символічна (математична) логіка являє собою подальший розвиток традиційної формальної логіки. Саме успіхи математичної логіки перетворили стару формальну логіку на струнку науку з точними поняттями і послідовними доведеннями. Для математичної логіки характерним є вивчення законів і форм мислення за допомогою методів математики і використання «мови символів» (знаків), що дає можливість зробити логіку точною наукою, а думку, виражену в символах математичної логіки, – чіткою і однозначною. Мова символів, певною мірою застосовувана ще Арістотелем, на сучасному етапі набула значного поширення, в зв'язку з чим термін «символічна логіка» використовується тепер як синонім математичної логіки.
Огастес де Морган – засновник логічного аналізу взаємодій. Він сформулював основні принципи логіки висловлювань і логіки класів. У математичній логіці Морган сформулював закони, які мають його ім'я – «закони де Моргана».Один з цих законів виражається так – заперечення кон’юнкції еквівалентне диз’юнкції заперечення. Наприклад: “Невірно, що завтра буде холодно і завтра буде дощити, тоді і тільки тоді, коли завтра не буде холодно або завтра не буде дощити”.
Готліб Фреге вважається фундатором основ логічної семантики. У своїй фундаментальній праці «Основні закони арифметики» він побудував систему формалізованої арифметики на основі розробленого ним розширеного числення предикатів з метою обґрунтування ідеї про зведення математики до логіки. Слід зазначити, що всім визначенням числа, запропонованим до Фреге, була притаманна елементарна логічна помилка. Склалася така звичка серед математиків і філософів “число” ототожнювати з “множиною”. Але конкретний приклад “числа” – це певне число, скажімо 3, а конкретний приклад 3 – це певна трійка. Трійка і є множиною, а клас усіх трійок, котрий Фреге ототожнює з числом 3, є множина множин, а число взагалі, частковим випадком котрого виступає 3, є множиною множин множинності. Елементарна граматична помилка, яка полягала у змішуванні числа взагалі з простою множиною даної трійки, зробила всю філософію числа до Фреге переплетенням абсурду в строгому розумінні слова. З робіт Фреге випливає, що арифметика і чиста математика взагалі є не що інше, як продовження дедуктивної логіки. Він сформулював низку ідей і понять, розробка яких багато в чому визначила розвиток логіки у двадцятому столітті. Зокрема, Фреге ввів у науковий обіг поняття логічної функції; уперше сформулював і став використовувати квантори; включив до системи понять “істинність значення” та ін. Г.Фреге систематично досліджував відношення між мовними виразами і предметами, які позначаються цими виразами; розкрив відмінність між значенням і смислом мовних виразів. Тому його праці розцінюються як початок нового етапу розвитку математичної (символічної) логіки.
Чарлз-Сандерс Пірс – відомий американський філософ і логік. Спочатку він заявив про себе роботами у галузі хімії, фізики, математики та астрономії, а пізніше присвятив себе філософії та логіці. У логіці йому, разом з Фреге, належить винахід кванторів. Він по праву вважається основоположником семіотики – загальної теорії знаків. Він, зокрема, класифікував знаки на: іконічні, індекси та символи (залежно від того, чи несе відношення знака до об’єкта характер подібності, послідовності або умовний характер). У своєму численні він використовував як строгу, так і нестрогу диз'юнкції. Ч. Пірс сформулював закони матеріальної імплікації. Шкода, що протягом тривалого часу його праці не були відомі широкій науковій громадськості. Безумовно, ця обставина значно загальмувала стрімкий розвиток семіотики.
Давид Гільберт (1862-1943) – видатний німецький математик і логік, сформулював систему основоположних принципів аксіоматики геометрії, арифметики й фізики, через які намагався довести незалежність і несуперечність, що лежать в основі аксіом. Він досяг значних успіхів у застосуванні методу формалізації в тлумаченні логічних умовиводів, у розробці числення висловлювань і предикатів, у дослідженні аксіоматизації знань. Він здійснив строго аксіоматичну побудову геометрії Евкліда, що наперед визначило подальший розвиток досліджень з аксіоматизації наукового знання, запропонував розгорнутий план обґрунтування математики шляхом її повної формалізації. Щоправда, ця програма виявилась нездійсненною, проте її ідеї сприяли виникненню і розвитку метаматематики (теорії доведень).
На початку ХХ ст. нідерландський математик Л.Е.Я. Брауер (1881-1966) висловив сумнів у тому, що закони класичної логіки мають абсолютну істинність. У зв’язку з цим він запропонував інноваційну програму, спрямовану на повернення математикам впевненості, яку похитноло відкриття парадоксів теорії множин. Вона дістала назву інтуїціонізму. Брауер вважав, що основу математики становлять не логічні конструкції, які так підносив Гільберт, а інтуїція, завдяки якій математичні поняття та висновки набувають безпосередньої ясності. За Брауером, математичні твердження, згідно з якими об’єкт, котрий має дану властивість, існує, означають, що відомим є метод, який дає змогу хоча б у принципі побудувати такий математичний об’єкт. Значний внесок у розвиток конструктивної математики й логіки належить А.А. Маркову (1903-1979). Він, як і Брауер, критично ставився до теорії множин і не визнавав її як основу для побудови математики, вважаючи, що будувати її необхідно конструктивно. Ці ідеї стали згодом основою для побудови конструтивної логіки.
У ХХ ст. радянський математик П.С. Новиков (1901-1975) зазначав, що конструктивна логіка з’явилась у зв’язку зі спробами звільнити математичне мислення від неефективних методів. Типовим прикладом вияву неефективності в класичній математиці вважалось доведення існування математичних об’єктів із заданими властивостями, які не дають змоги здійснити конструктивну побудову індивідуального об’єкта з цими самими властивостями. Тому, за Новиковим, конструктивний підхід диктує інше, ніж у класичній математиці, осмислення логічних понять.
Альфред-Норт Уайтхед – англо-американський філософ і математик. Спочатку він займався логічними і математичними дослідженнями, які знайшли своє відображення в його роботах “Універсальна алгебра” і “Про математичні поняття матеріального світу”; у співавторстві з Б. Расселом написав тритомну працю “Принципи математики”, яка стала значним внеском у розвиток математичної логіки. Захоплюючі роздуми Уайтхеда про науку привели його до вивчення філософських основ природи, де він намагався примирити світ чуттєвого сприйняття і світ науки.
Бертран Рассел– британський математик, логік, соціолог, філософ, Нобелевський лауреат з літератури, має великі заслуги у сфері розробки мови сучасної логічної символіки. Логіку він тлумачить як універсальну математику в розумінні реляціоналізму. Він систематично виклав теорію числення висловлювань і теорію класів. У книзі “Математичні принципи” розвинув математичну логіку способом аксіоматизації і формалізації числень висловлювань, класів і предикатів, а також теорію типів як способу переборення парадоксів. Філософія, вважає Рассел, запозичує свої проблеми з природознавства, вона прокладає йому шлях і повинна логічно аналізувати і тлумачити принципи й поняття природничих наук. Світ, підкреслює він, складається з чуттєвих даних, логічно пов’язаних один з одним.
Видатний німецький математик Георг Кантор (1845-1918) розробив сучасну теорію множин і досліджував нескінченні множини, які знайшли плідні застосування в математиці й логіці. Зіставлення операцій Буля над висловленнями з операціями Кантора над множинами показало, що вони мають такі спільні властивості, як комутативність (тобто переміщення:
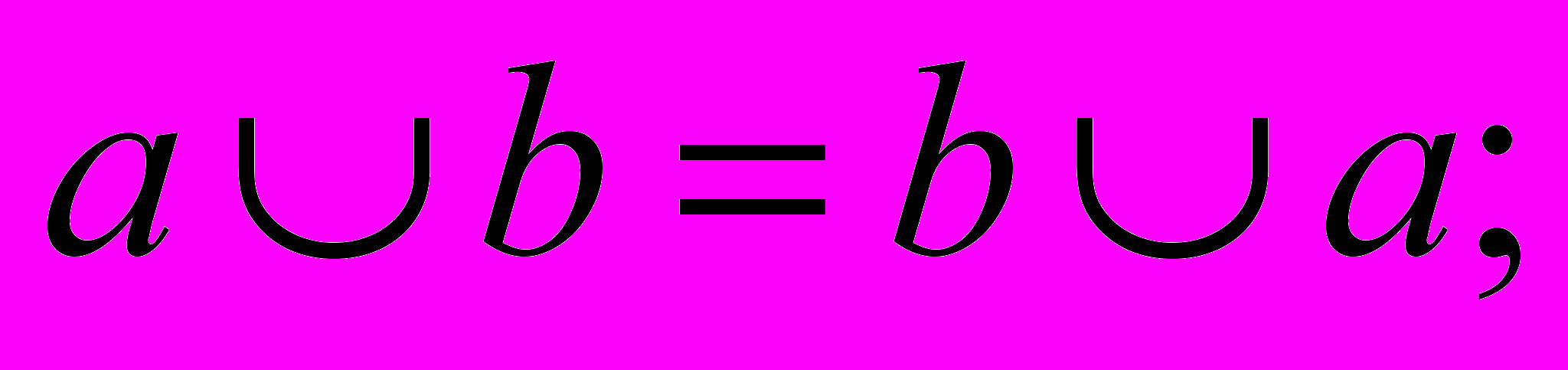
), асоціативність (тобто сполучення: 
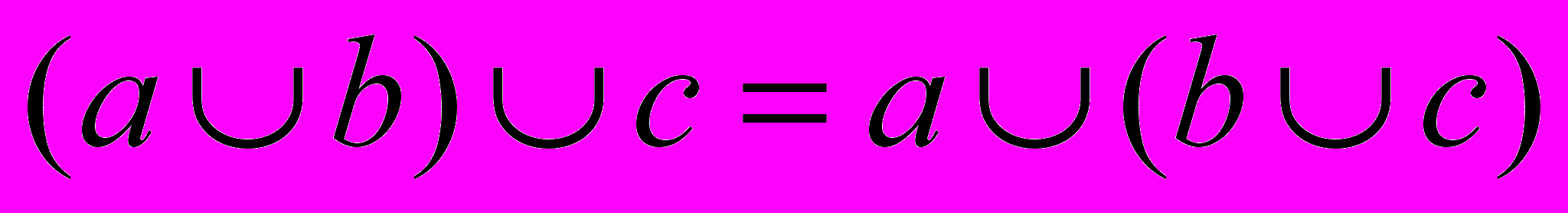та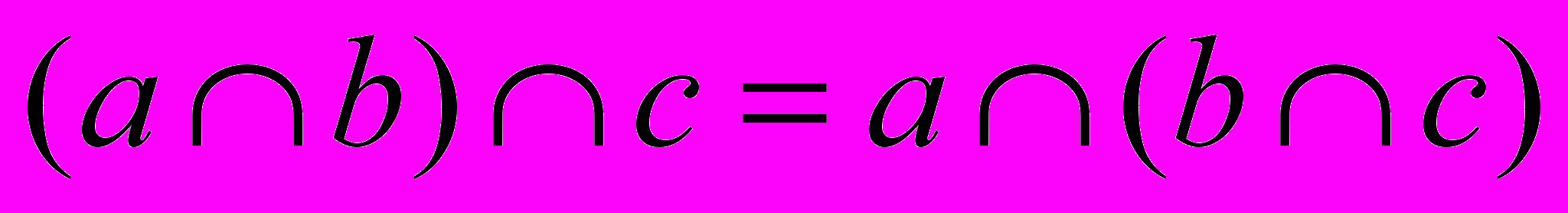 
), дистрибутивність (іншими словами, розподілення: 
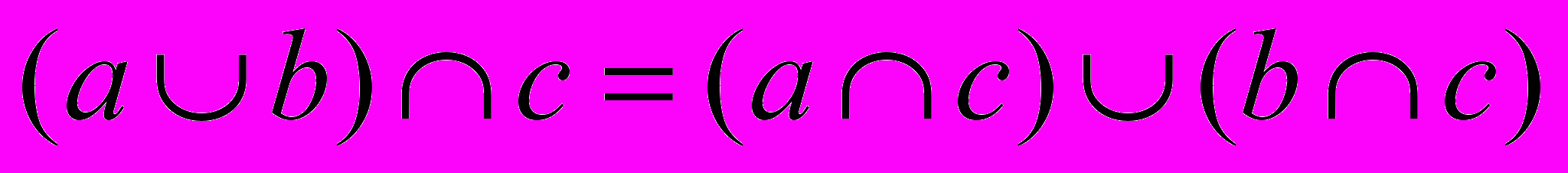та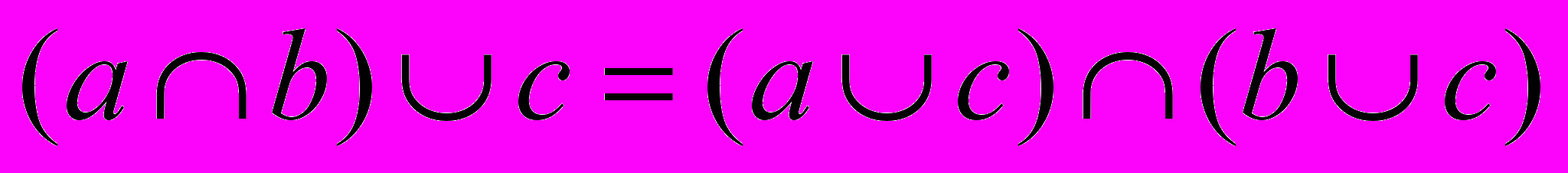 
). При цьому такі властивості відрізняються від звичних властивостей операцій над числами.Джузеппе Пеано (1858—1932) запропонував ідеї, завдяки яким було здійснено перехід від старої алгебри логіки до математичної логіки в її сучасному вигляді. Він ввів прийняті в сучасній математичній логіці символи (— знак входження елемента до тієї чи іншої множини; — знак включення множини; — знак об'єднання множин; — знак перетину множин), сформулював систему аксіом для арифметики натурального ряду.
Платон Порецький - російський логік, астроном і математик – першим у Росії розробив і читав курс математичної логіки. Формальні методи в логіці, згідно з переконанням Порецького, можуть бути обґрунтовані тільки аналізом змістовними підставами, основами; логічні числення не відміняють змістовність формальної логіки, а припускають її. Він вважав, що математична логіка за своїм предметом є логіка, а за методом – математика. Порецьким були отримані вагомі результати, які збагатили скарбницю алгебри логіки. Він розвинув і удосконалив методи розв’язання логічних рівнянь, запропонованих Дж. Булем, У.-С. Джевонсом, Е. Шредером. Найголовніший результат Порецького полягає у находженні в алгебрі логіки оригінального алгоритму, який дозволяє ефективно отримувати всі наслідки (певного виду) з даних засновків, всі гіпотези, з яких може слідувати даний висновок, всі різноманітні еквівалентні форми, в яких можуть бути наведені дані висловлювання – засновки і висновки. Значуще місце в його працях посідала «теорія наслідків». Порецький узагальнив теорію силогістики традиційної логіки, проаналізував деякі несилогістичні міркування тощо.
Отже математична логіка виникла як результат взаємодії двох наук – математики і логіки, спільність яких полягала в тому, що символічна логіка абстрагується від конкретного змісту висловлювань, розкриває більш загальні закономірності мислення і на цьому підгрунті дає можливість не тільки констатувати те, чого вже досягло мислення у своєму розвитку, а й виявити його перспективні можливості. У цьому плані слушним є зауваження німецького логіка Г. Клауса про те, що основні закони традиційної логіки – закон тотожності, закон суперечності, закон виключеного третього та закон достатньої підстави – не вичерпують усієї множини логічних законів і тому не охоплюють всіх можливостей мислення. Це справді так. Кожна наука в міру свого розвитку нагромаджує фактичний матеріал, який для свого осмислення потребує більш досконалих методів. У логіці такими є, зокрема, методи математики. Саме метод формалізації дає змогу перевести дослідження процесів мислення на строгу мову символів, здійснити необхідні узагальнення, встановити нові закономірності, без яких логіка не може розвиватися далі.
Розвиток логіки значною мірою пов’язаний з потребами її практичного застосування, з проблемами науки і техніки, які потребують нових підходів і методів для свого розв’язання. Так, поява і широке використання релейних пристроїв зумовили необхідність вивчення закономірностей функціонування і оптимізації їхньої структури. Зручним апаратом для розв’язання таких задач стали логіко-математичні методи, важливий внесок у розробку яких належить американському вченому Клоду Шеннону (1916-2001). Він побудував логіко-математичне числення, яке грунтується на основних ідеях загальної теорії релейних кіл, а також показав, що це числення випливає з деяких елементарних логічних положень.
Значним є внесок у розвиток сучасної логіки і деяких інших учених, зокрема представників львівсько-варшавської школи, до якої належали К. Твардовський, Я. Лукасевич, С. Лесьневський, А. Тарський, Т. Котарбіньський, К. Айдукевич та інші.
Так, Альфред Тарський – логік і математик, один з найвідоміших представників львівсько-варшавської школи. Йому належить вагомий внесок у розробку методів вирішення проблеми розв’язання, у теорію моделей, у теорію визначності понять, у розвиток алгебраїчних методів вивчення числення предикатів, у теорію логік з формулами нескінченої довжини, у багатозначну логіку та інші розділи математичної логіки й основ математики. Він став засновником формальної семантики. У роботі «Поняття істини у формалізованих мовах» Тарський дав класичне визначення поняття істини для великої групи формалізованих мов. Йому належить ряд досліджень в галузі методології дедуктивних наук. Роботи Тарського з семантики й металогіки помітно вплинули на розвиток семіотики й послужили зразком застосування формальних методів для аналізу змістовних проблем і теорій.
Ян Лукасевич – польський логік, вів інтенсивно дослідницьку роботу у форматі математичної логіки. Йому належать основні роботи в галузі багатозначної логіки, а також ряд досліджень з побудови та аксіоматизації систем пропозиціональної логіки, модальної логіки, з розробки оригінальної логічної символіки (без дужок). Низку праць Лукасевич присвятив історії логіки (логічні ідеї ранніх стоїків, силогістика Аристотеля, які він описав у вигляді формалізованої системи тощо). Результати досліджень в галузі логіки він використав для обґрунтування раціоналістичної позиції на противагу ірраціоналізму в науці й філософії.
Казимеж Айдукевич – польський логік, також належав до львівсько-варшавської школи логіків. Розробляв логіко-семантичну концепцію значення, згідно з якою значення і зміст терміну визначаються способом його вживання у певній концептуальній системі. Ототожнивши наукову теорію із замкненою в логіко-семантичному відношенні системою понять, він прийшов до так званого радикального конвенціоналізму. Айдукевич вважав, що вихідні принципи й поняття мови науки, а також правила логічного висновку та емпіричної інтерпретації наукових пропозицій грунтуються на конвенціях, тобто певних домовленостях. Теорія, яка зображує “картину реальності”, на його думку, цілком залежить від системи понять і змінюється при переході від однієї системи до іншої.
Отже львівсько-варшавська школа – це група польських логіків і філософів, які працювали у Варшаві й Львові в період між двома світовими війнами. Саме представники цієї школи поклали початок семіотичним та логіко-методологічним дослідженням у Польщі. Школі було притаманне негативне, заперечне відношення до ірраціоналізму, прагнення до зближення філософських і наукових. досліджень, використання засобів логічного аналізу для зміцнення та обґрунтування раціоналістичних позицій, для підвищення точності й однозначності мови науки і філософії. Представники цієї школи зробили вагомий внесок у логічну семантику, теорію множин, модальну й багатозначну логіку, в математичну логіку, у металогіку і методологічні дослідження (теорія індукції, побудова і функції наукової теорії, розробка аксіоматичного методу, теорія ймовірностей) та інші галузі наукового знання.
Істотний внесок у розвиток математики й логіки, викликаний як прагненням зблизити актуальну і потенційну нескінченності, так і потребами практики, належить відомому американському вченому Л.А. Заде, який став основоположником нечіткої логіки. Стосовно некласичних підмножин класичних множин він зробив базовими поняттями “нечіткість”, “неясність”, “правдоподібність”, “випадковість”, “можливість”. Як зазначає відомий французький математик А. Кофман, у самому поєднанні термінів “нечіткий” і “логіка” криється щось незвичне. Однак застосування апарату нечіткої логіки вже дало змогу успішно розв’язувати цілий клас важливих практичних завдань.
Реальне життя дає широкі можливості досить часто зустрічатися з ситуаціями і проблемами, в яких просто необхідно враховувати неясність і неточність інформації про явища і процеси навколишнього світу, і тут теорія Заде дозволяє дати хоча б схематичний начерк розв’язання таких проблем. Заде протиставляє двозначній і навіть многозначній логіці логіку з нечіткою істинністю, нечіткими зв’язками і нечіткими висновками. На його переконання, саме така логіка, ще не досить вивчена, відіграє основну роль у здатності людського мислення вибирати з широкого інформаційного потоку лише ті відомості, які мають хоча б посереднє відношення до розв’язуваної проблеми. У першу чергу це стосується здатності людини вибирати корисну інформацію з повідомлень, сформульованих за допомогою природної мови.
Відносно новим напрямком стала і так звана модальна логіка. Під модальністю прийнято розуміти спосіб ставлення суб’єкта, що висловлюється, до предмета висловлення. Свого часу ще І. Кант відносив до модальних такі види суджень: асерторичні (які констатують факти дійсності, не виражаючи їх незаперечної логічної необхідності), проблематичні (які виражають можливість) і аподиктичні (які виражають необхідний зв’язок між предметами), хоча вони й не вичерпують всієї множини можливих відношень модальності. Протягом певного часу модальність не притягувала увагу логіків і вважалась ними скоріше предметом психологічного вивчення. І тільки у ХХ ст. ставлення логіків до модальності істотно змінилось. Вона стала об’єктом всебічного, глибокого і системного логіко-філософського аналізу. Вагомий внесок у його здійснення належить американському логіку К.І. Льюїсу, який у публікаціях 1916 і 1932 рр., виходячи з досягнень сучасної йому символічної логіки, запропонував формалізовану систему класичних модальностей і спробував побудувати теорію строгої імплікації.
При цьому основна ідея Льюїса полягала у проведенні розрізнення між зв’язками, які виступають вираженням логічної необхідності, та зв’язками, які її не виражають. У результаті йому вдалося виразно позначити розмежування матеріальної (або інтуїтивно-змістовної) і строгої (або необхідної) імплікації. Пізніше цю систему назвали численням алетичних модельностей, які дають змогу досліджувати проблеми логічного слідування, яке, на думку Льюїса, тісно пов’язане з поняттями необхідності й можливості. Сьогодні модальна логіка є досить розвиненою галуззю формальної логіки.
За радянських часів формальну логіку протягом певного періоду ігнорували, а то й критикували її як підвалин у метафізичного методу. Але починаючи з другої половини 40-х років вона посідає належне місце як навчальний предмет у вищих навчальних закладах і навіть в деяких середніх школах. Сучасну ж логіку, зокрема логіку висловлювань і логіку предикатів, зневажливо називали логістикою. Вагомий внесок у розвиток сучасної логіки внесли російські філософи Є.К. Войшвілло, В.Ф. Асмус, Д.П. Горський, О.А. Зінов’єв, М.І.Кондаков.
Логіко-філософська думка в Україні також активно розвивалася. Такі філософи, як В. Іванов, В. Шинкарук, А. Яценко широко досліджували ціннісні форми свідомості. Проблеми логіки філософського і наукового знання вивчались Т. Ойзерманом, В. Шинкаруком, М. Поповичем і С.Б. Кримським. Ці вчені та їх учні С.А. Васильєв, А.Є. Конверський, В.Д. Титов та інші зробили певний внесок у розвиток символічної логіки, логічної семантики й семіотики і пробудили інтерес до цієї цікавої і конче необхідної галузі знань як важливого засобу пізнання об’єктивної дійсності.
Контрольні запитання та вправи
- Якими є характерні риси абстрактного мислення?
- Яку роль відіграє мова в абстрактному мисленні?
- Які основні форми мислення вивчає логіка?
- Що таке логічна постійна і логічна змінна? Покажіть це на прикладах.
- Яка думка називається істинною, а яка хибною?
- Яке міркування називається логічно коректним, а яке неправильним?
- В якому зв'язку з іншими науками перебуває логіка?
- Що таке математична (символічна) логіка?
- Яке теоретичне і практичне значення має логіка в житті людини?