Лекция №15 Математические модели в управлении производством

Вид материала

Лекция

Содержание Задача о коммивояжере Задача о назначениях Задача о перевозках с промежуточными пунктами Задача о рюкзаке Задача о складе

Подобный материал:

• Методика получения математических моделей элементов. Математические модели, используемые, 28.81kb.
• Учебная программа по дисциплине Математические методы и модели в управлении для специальности, 79.82kb.
• Программа дисциплины Математические модели приятия решения в управлении банком для, 124.82kb.
• Рабочей программы учебной дисциплины математические методы и модели в экономике уровень, 37.32kb.
• Тематика курсовых работ Математические модели в демографии. Математические модели, 3.05kb.
• Лекция 5  математические модели теории надежности. Статистическая обработка результатов, 74.69kb.
• Программа дисциплины «математические модели в экономике» Для направления, 156.79kb.
• Программа дисциплины «Дискретные математические модели», 224.89kb.
• Методические указания по выполнению реферата по учебной дисциплине экономико-математические, 275.52kb.
• Методические указания по выполнению реферата по учебной дисциплине экономико-математические, 281.81kb.

Лекция № 15

Математические модели в управлении производством


Математическая модель производства – это математическое описание взаимосвязей процесса производства, на основании которого можно изучать закономерности его развития и давать прогноз на будущее. В общем виде модель процесса производства можно представить следующим образом (рис.1).


Технологич.

способы

Интенсив. испол.




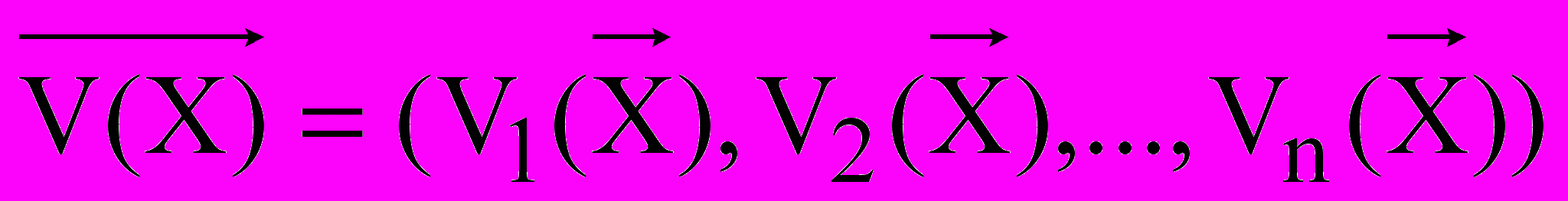
n – количество видов продуктов


1

2

.

.

.

l

x₁

x₂

.

.

.

x_l
















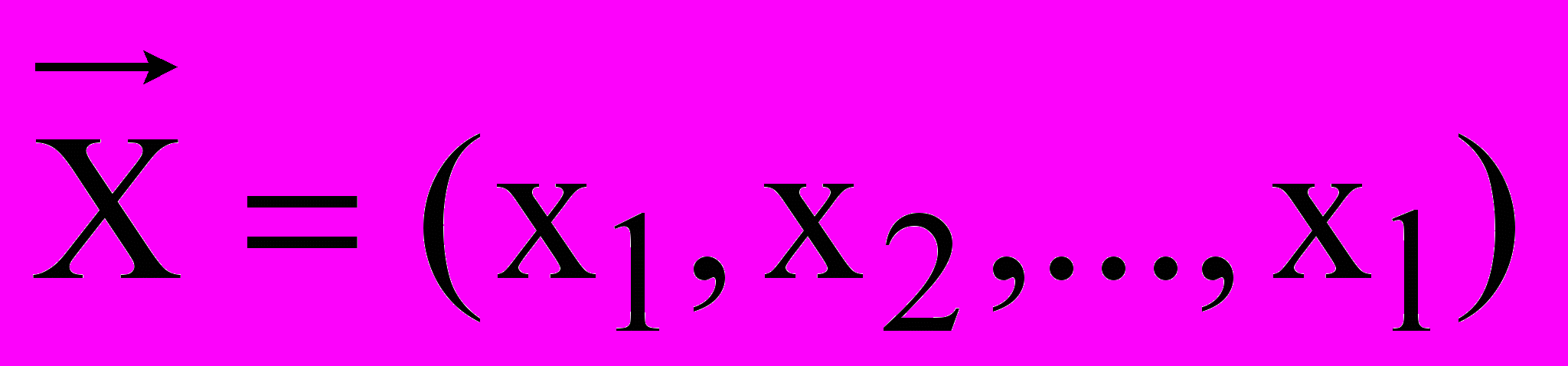
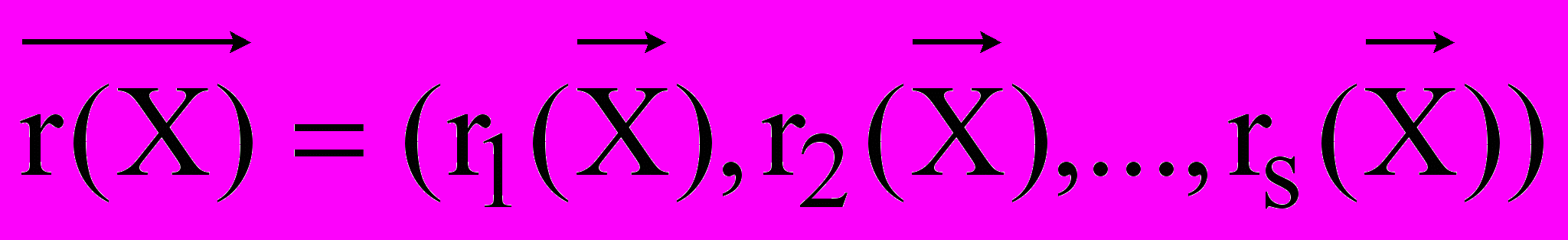
s – количество используемых ресурсов






Рисунок 1 – Формальная модель процесса производства.


Пусть возможности производства характеризуются конечным множеством базисных технологических способов k=1,2,…,l, каждому из которых соответствует интенсивность его использования x_k. Предположим, что для производства n продуктов используется s ресурсов (труд, производственные мощности, природные ресурсы). Интенсивность рассматриваемой экономической системы можно представить l-мерным вектором X=(x₁,x₂,…,x_l), компоненты которого неотрицательны и характеризуют интенсивность использования соответствующих базисных способов. Для характеристики системы с технологической стороны следует указать также векторные функции –

и ,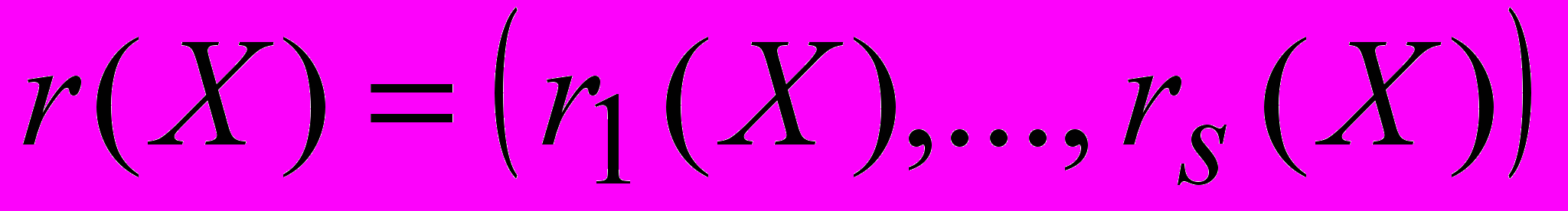

где V(X) – вектор объемов производства продукции при поддержании системы на уровне интенсивность X, r(X) – вектор затрат ресурсов, необходимых для функционирования системы с интенсивностью X. Тогда, с точки зрения производства, рассматриваемая экономическая система полностью характеризуется векторами X, V(X), r(X) и R- вектором наличных ресурсов.

Пусть критерий эффективности системы определяется объемом выпускаемой продукции и выражается соотношением –

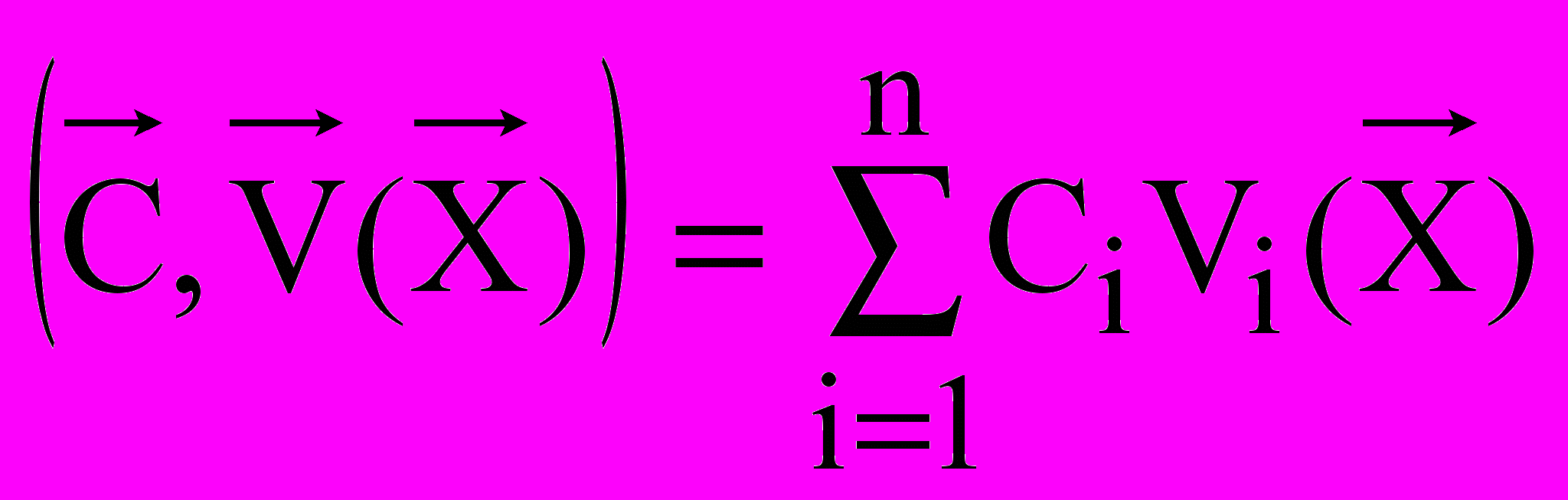, (1)

где С – вектор коэффициентов критерия эффективности.

Тогда задача управления производством состоит в отыскании уровня интенсивностей X=(x₁,x₂,…,x_n), доставляющего экстремум функционалу (1) –

, (2)

при ограничениях ,

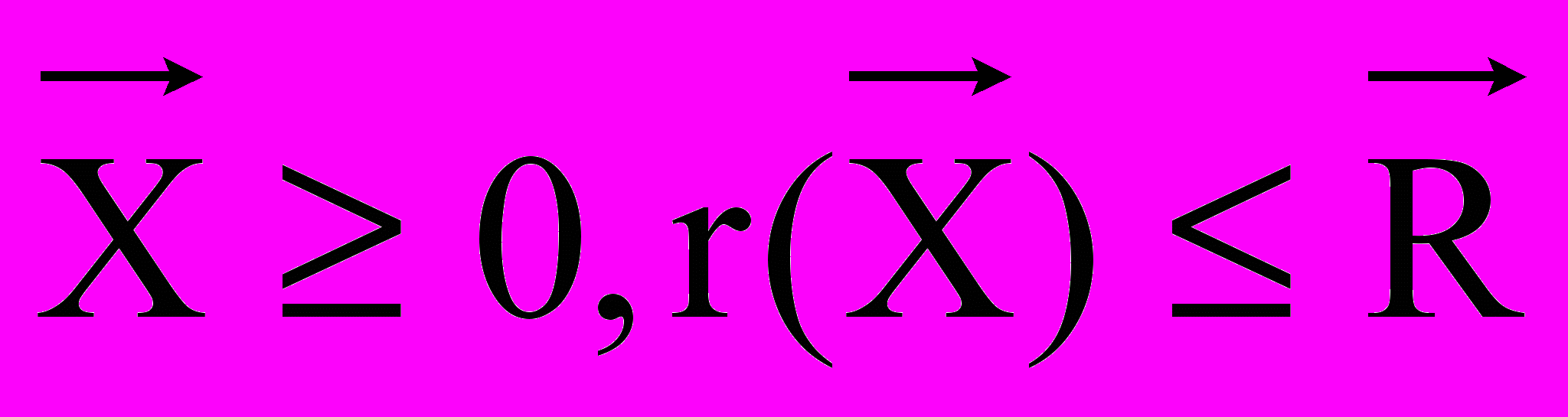где 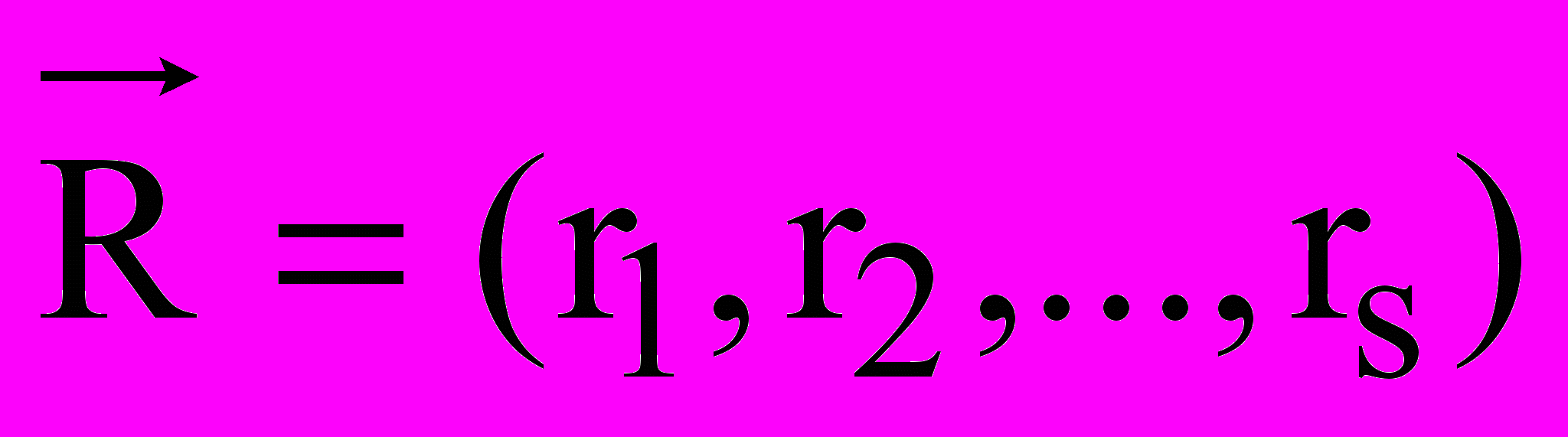- вектор начальных ресурсов.

Сформулированная в таком виде модель производства является задачей нелинейного


Для выработки решений по оптимальному размещению распределенного производства используют модели размещения производства. Данные модели делят на модели размещения однопродуктовых и многопродуктовых производств. Первые применяют для определения мощностей и пунктов размещения предприятий (их элементов), выпускающих однородную продукцию. Математическая формализация задачи размещения однопродуктовых производств заключается в следующем. Имеется m пунктов производства и n пунктов потребления однородной продукции. Годовой выпуск продукции на i-м предприятии (i=1,…,m) составляет , где r - вариант развития данного предприятия (r=1,…,w_i), а потребность j-го пункта потребления (j=1,…,n) составляет b_j. Производственные затраты на единицу продукции на i-м предприятии при r-м варианте его развития составляют 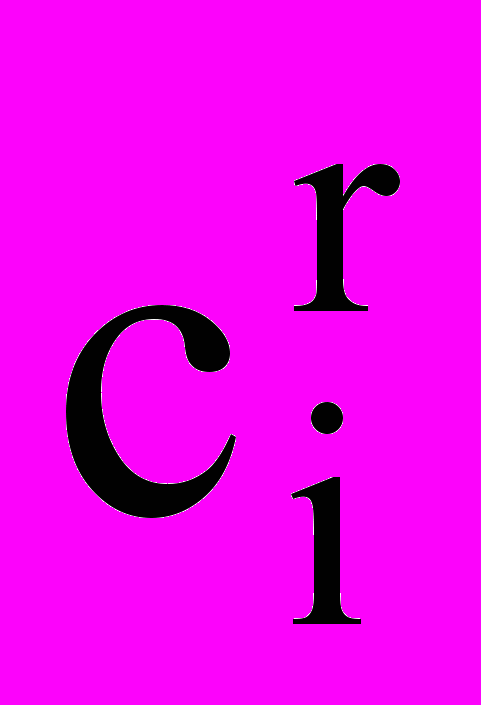, транспортные расходы на перевозку единицы продукции от i-го предприятия в j-й пункт потребления – s_ij, а удельные капиталовложения на расширение, реконструкцию или новое строительство i-го предприятия при r-м варианте его развития - 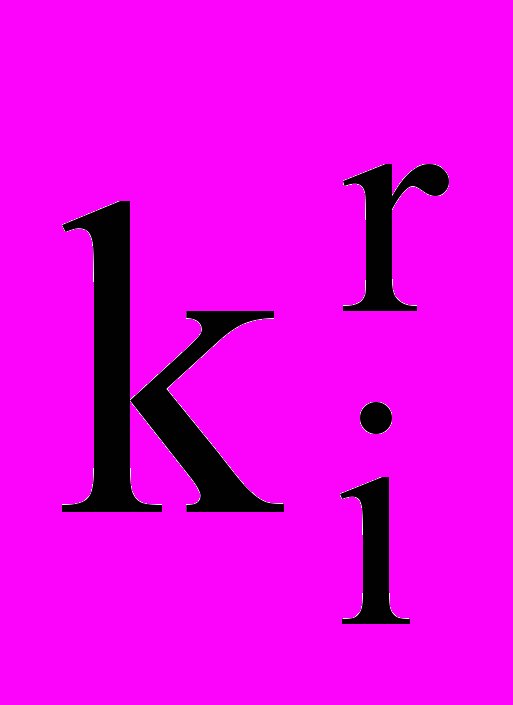. Выбранные объемы поставок с i-го предприятия при r-м варианте его развития в j-й пункт потребления 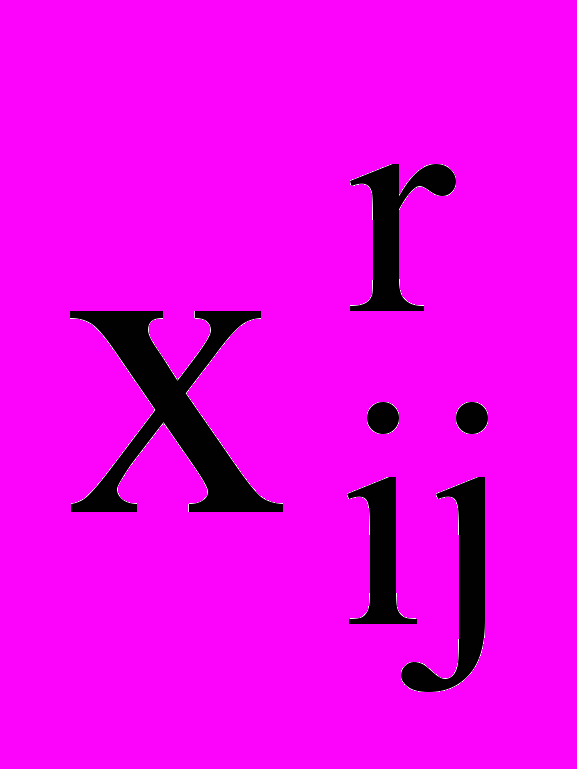не должны быть отрицательными, то есть - .

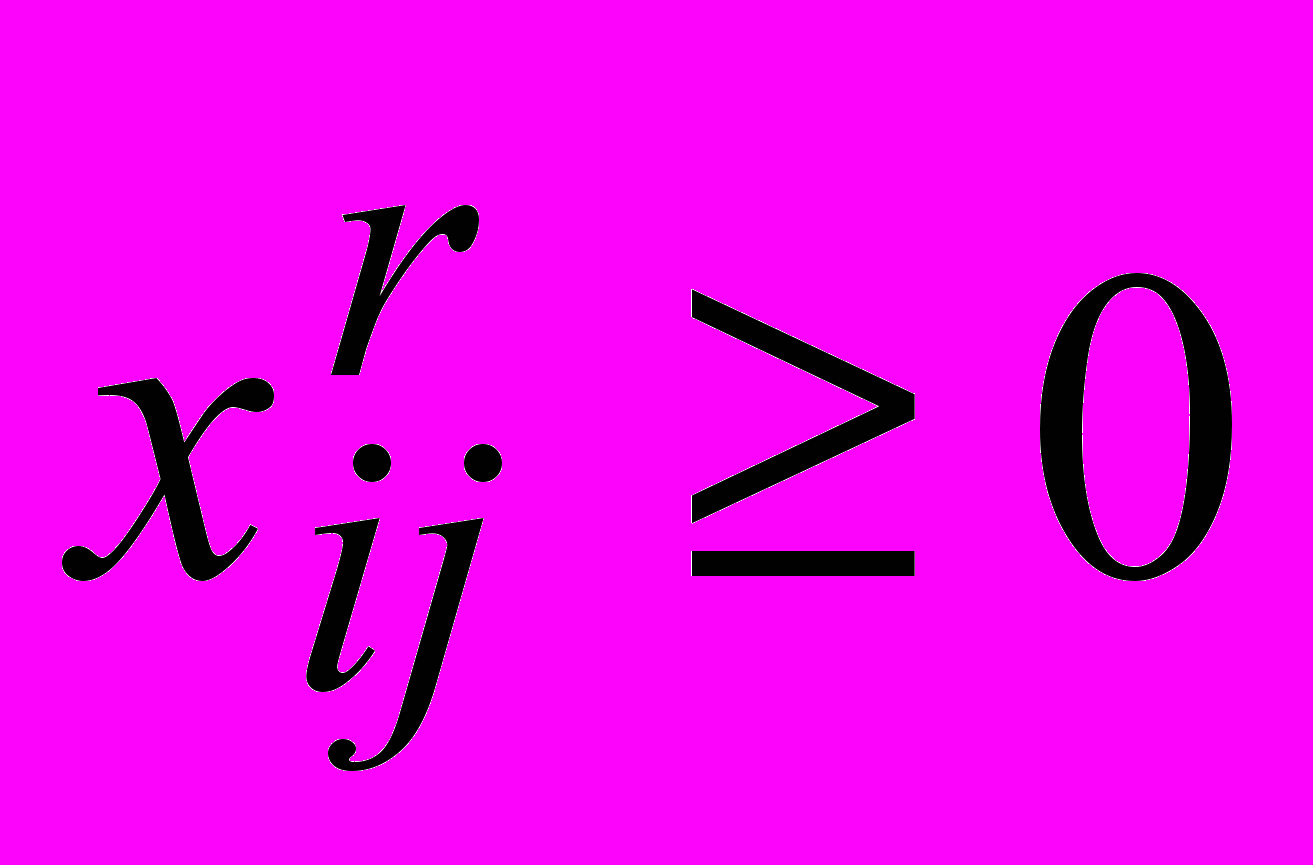Общее количество отобранных вариантов развития предприятий должно быть равно числу предприятий, если все предприятия входят в оптимальный план, либо быть меньше этого числа, если не на всех предприятиях из числа заданных экономически целесообразно выпускать продукцию. Если - интенсивность использования в плане r-го варианта развития i-го предприятия-поставщика, то .

Суммарное производство продукции всеми предприятиями отрасли должно быть равно или больше общей потребности всех пунктов ее потребления –



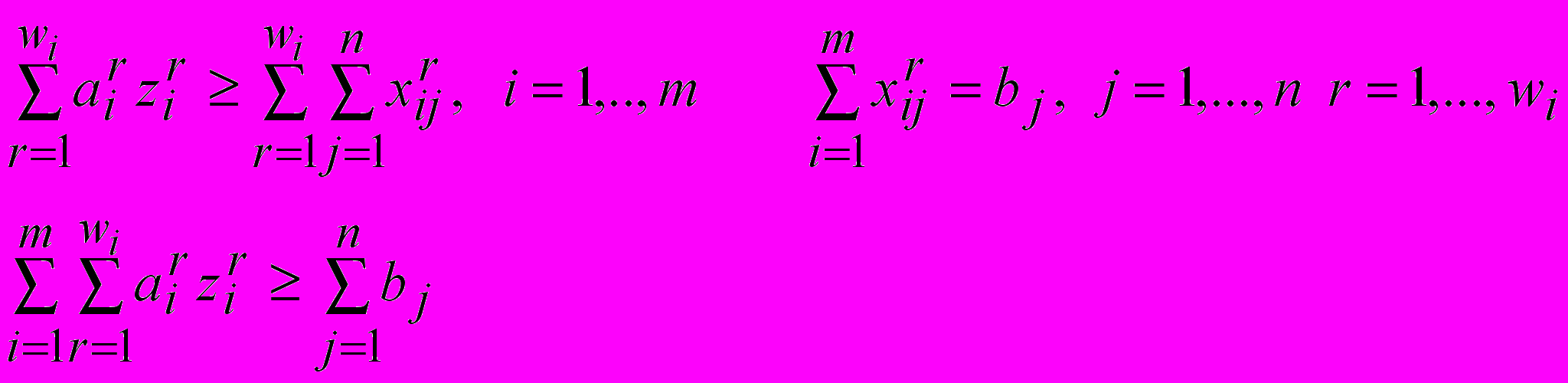
Целевая функция задачи (функция суммы производственных затрат, затрат на транспортировку всей продукции от предприятий-поставщиков до потребителей и удельных капитальных вложений на реконструкцию, расширение или новое строительство) должна достигать минимума –

,

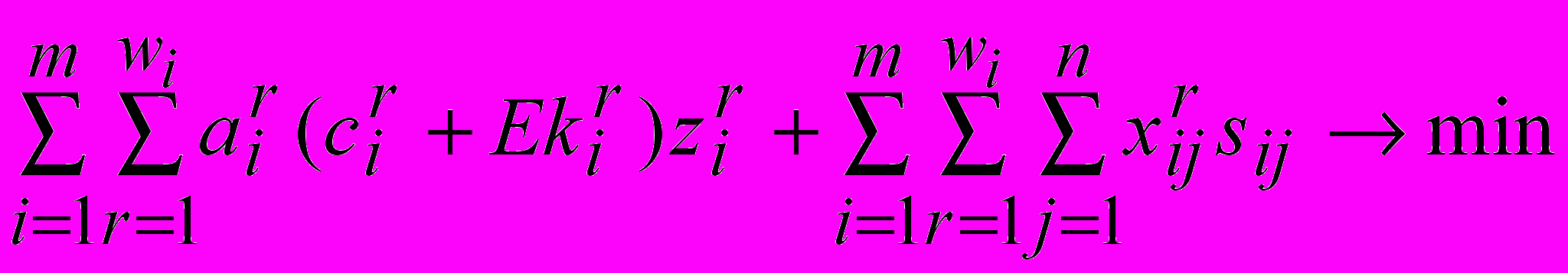где Е – нормативный коэффициент капитальных вложений.

Данные задачи решаются различными методами математического программирования в зависимости от вида и характера целевой функции и ограничений.

Размещения многопродуктовых производств предназначены для оптимального планирования размещения сети предприятий, их размеров, специализации, кооперирования при выработке двух и более видов продукции. Рассмотрим пример построения такой модели. Заданными величинами являются:

варианты объемов производства различных изделий в возможных пунктах размещения производства 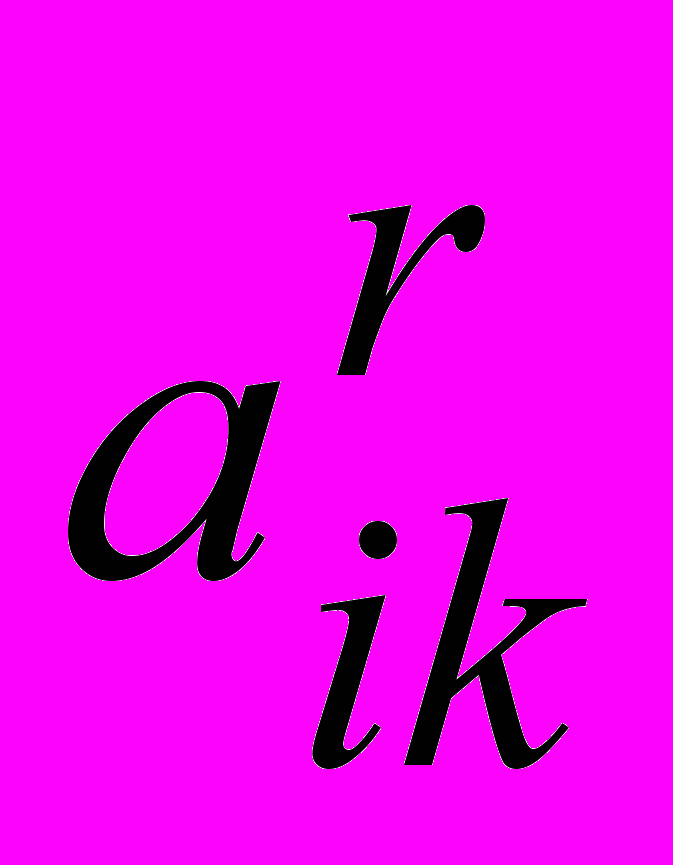, где i – пункт размещения предприятия, r – вариант предприятия, k – вид продукции. Сущность ограничений на целочисленность состоит в том, что по данному конкретному изделию может быть выбран только один целый вариант объема выпуска продукции предприятием. Кроме того, вместе с каждым вариантом задаются 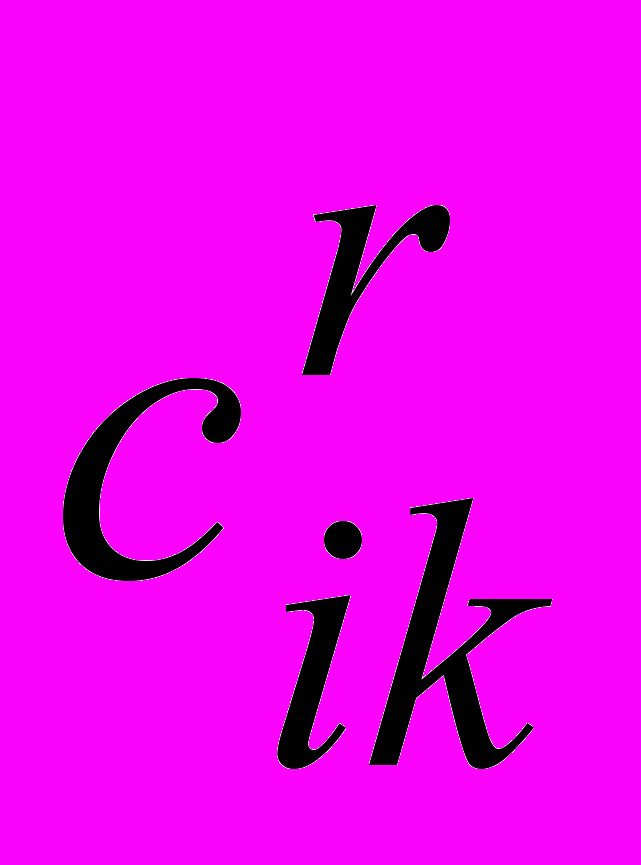- величины производственных затрат на единицу продукции. Природа их может быть различна в зависимости от конкретной задачи. Это может быть либо приведенные затраты, включающие помимо себестоимости удельные капитальные вложения, взятые при определенной норме эффективности. Задаются удельный расход дефицитных ресурсов 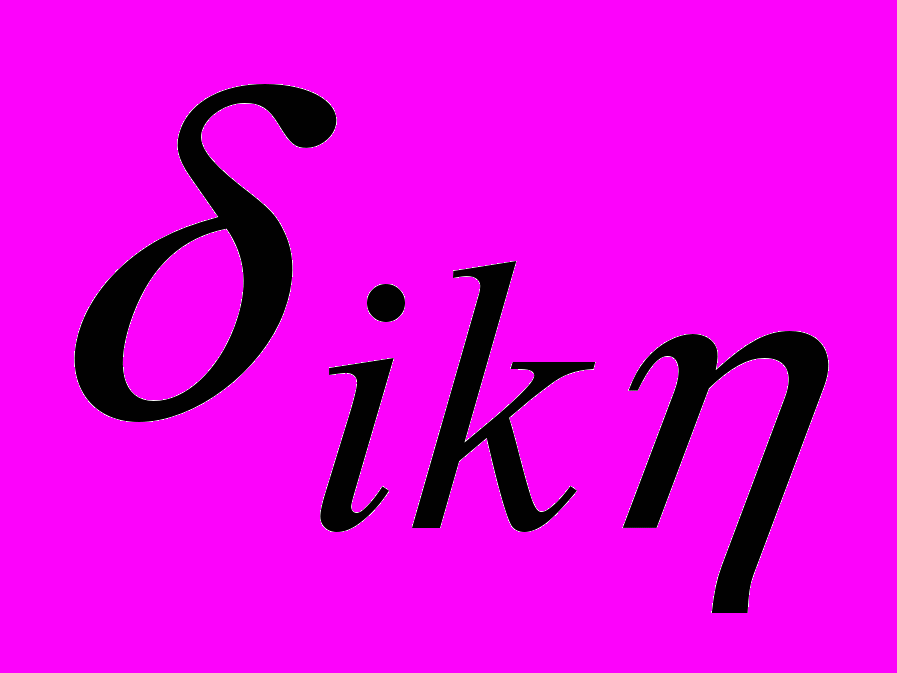и лимит, установленный по этим ресурсам для отрасли ( 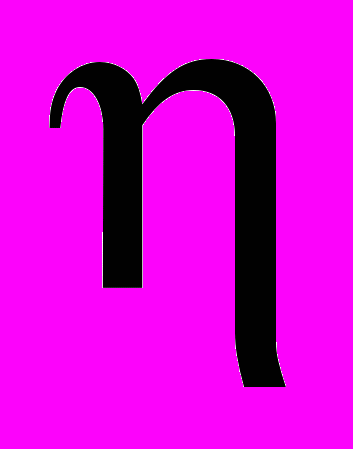- индекс дефицитного ресурса); территориальное распределение потребности в различных видах продукции 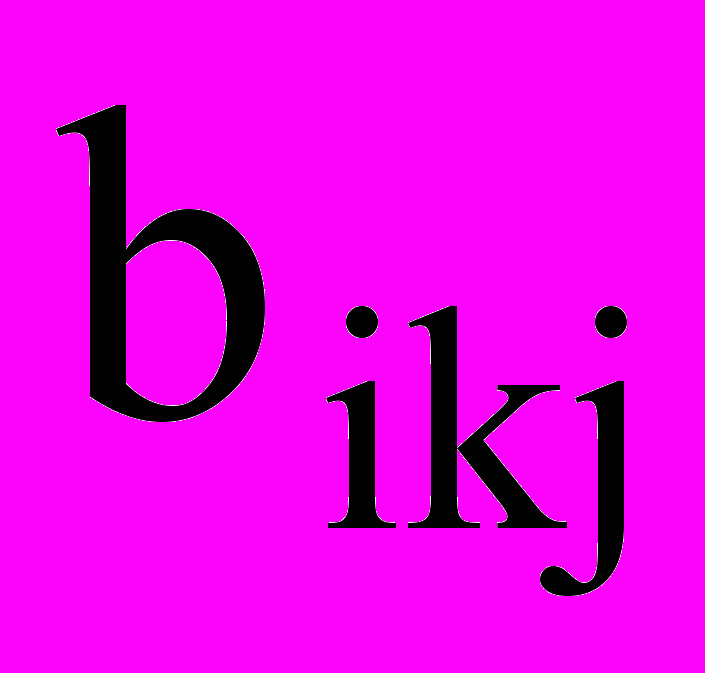(j – индекс района потребления); затраты по перевозке различных изделий в расчете на принятую единицу измерения . Задача размещения математически сводится к отысканию неотрицательных значений неизвестных 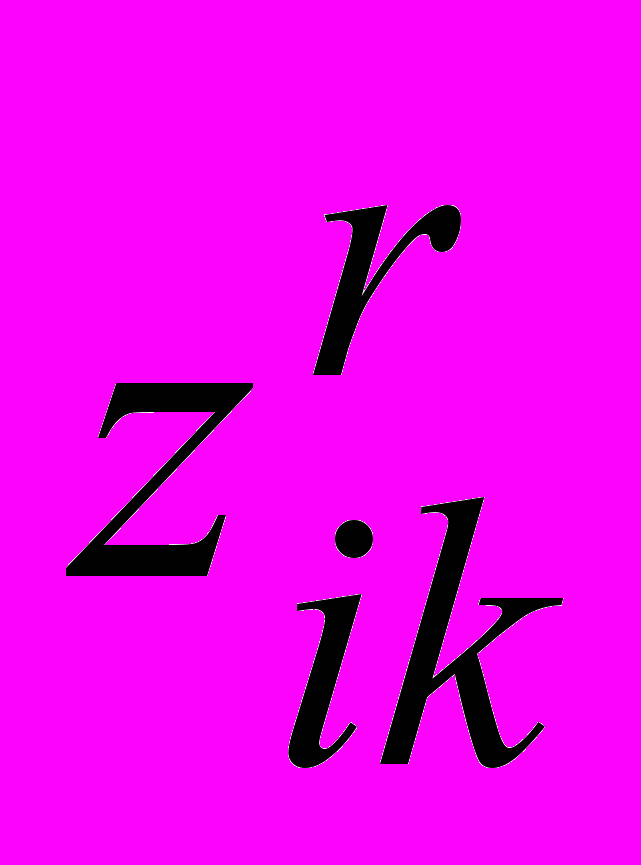и 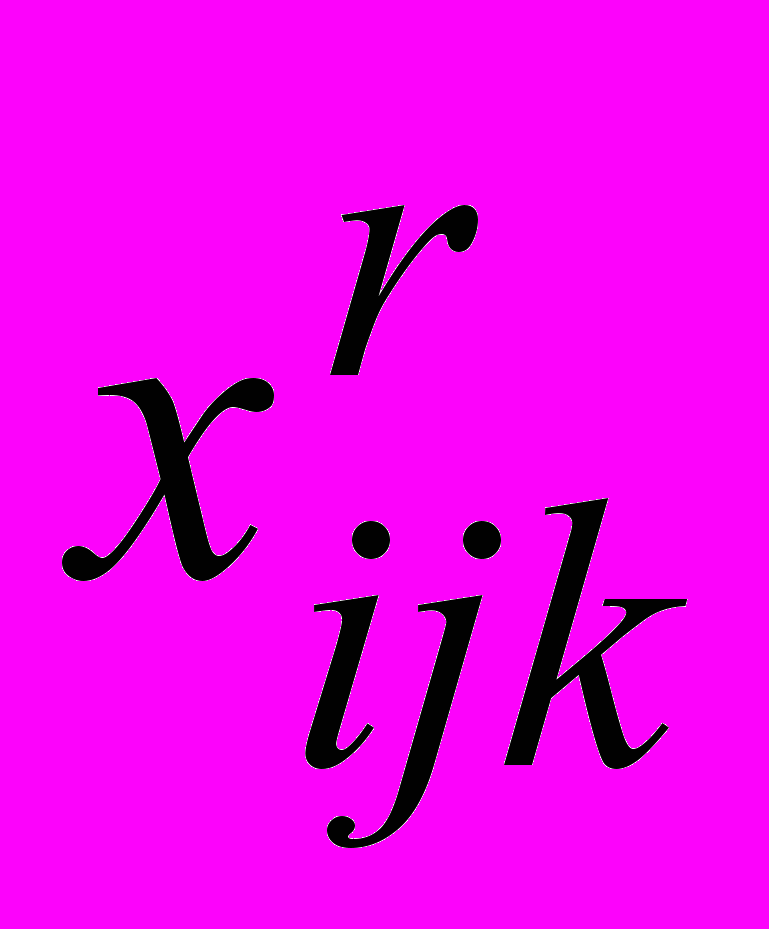, удовлетворяющих условиям –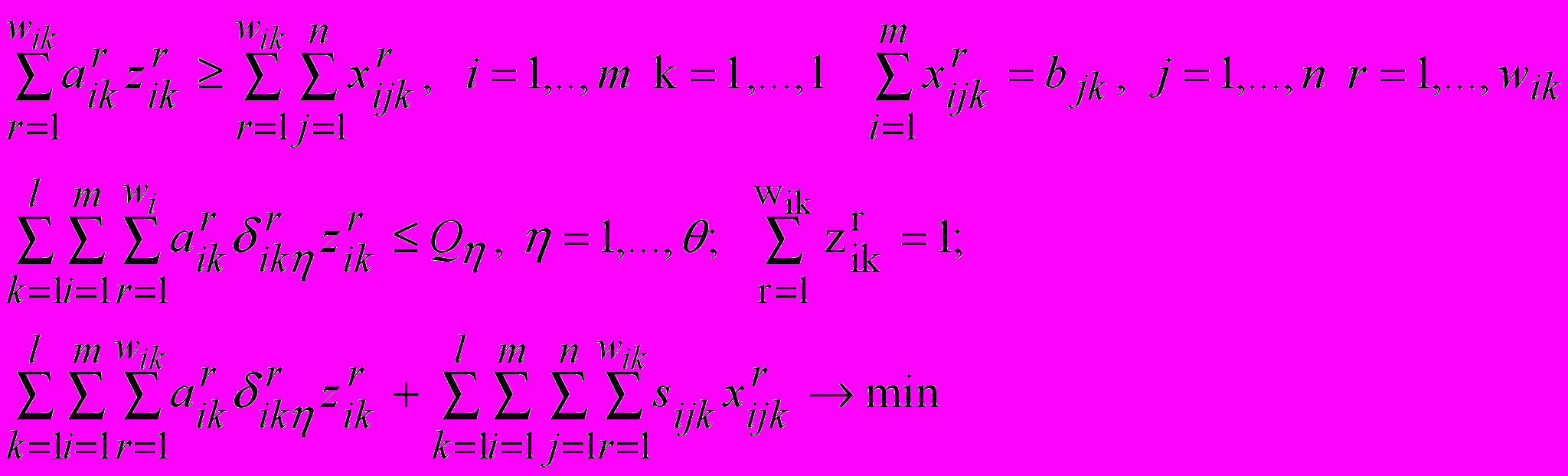



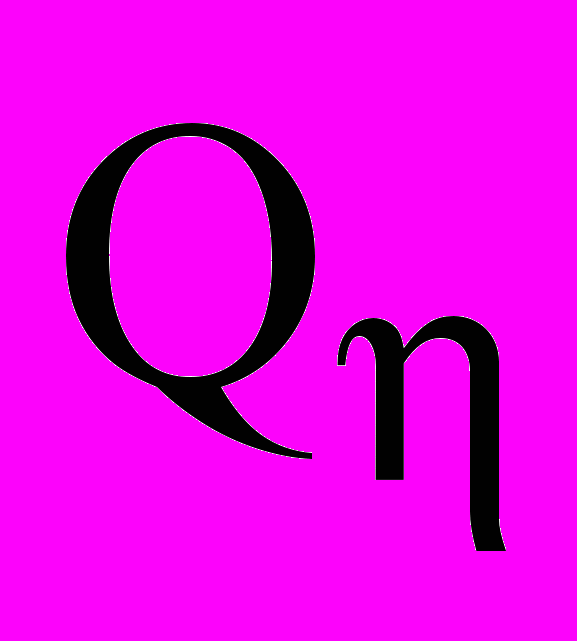- лимит ресурсов по отрасли.


В условиях, когда транспортный фактор оказывает существенное влияние на величину затрат задачи размещения производства являются задачами распределительного типа, получившими название транспортных задач. В противном случае задачи размещения производства могут быть сведены к задачам производственного планирования. Рассмотрим примеры типовых задач указанных типов.

К задачам транспортного типа относятся задача о коммивояжере, задача о назначениях, задача о перевозках с промежуточными пунктами и задача о распределении поставок.

Задача о коммивояжере

Общая формулировка задачи о коммивояжере – торговец, выезжающий из некоторого города, должен посетить каждый из (n-1) других городов только один раз и вернуться в исходный город. Матрица расстояний 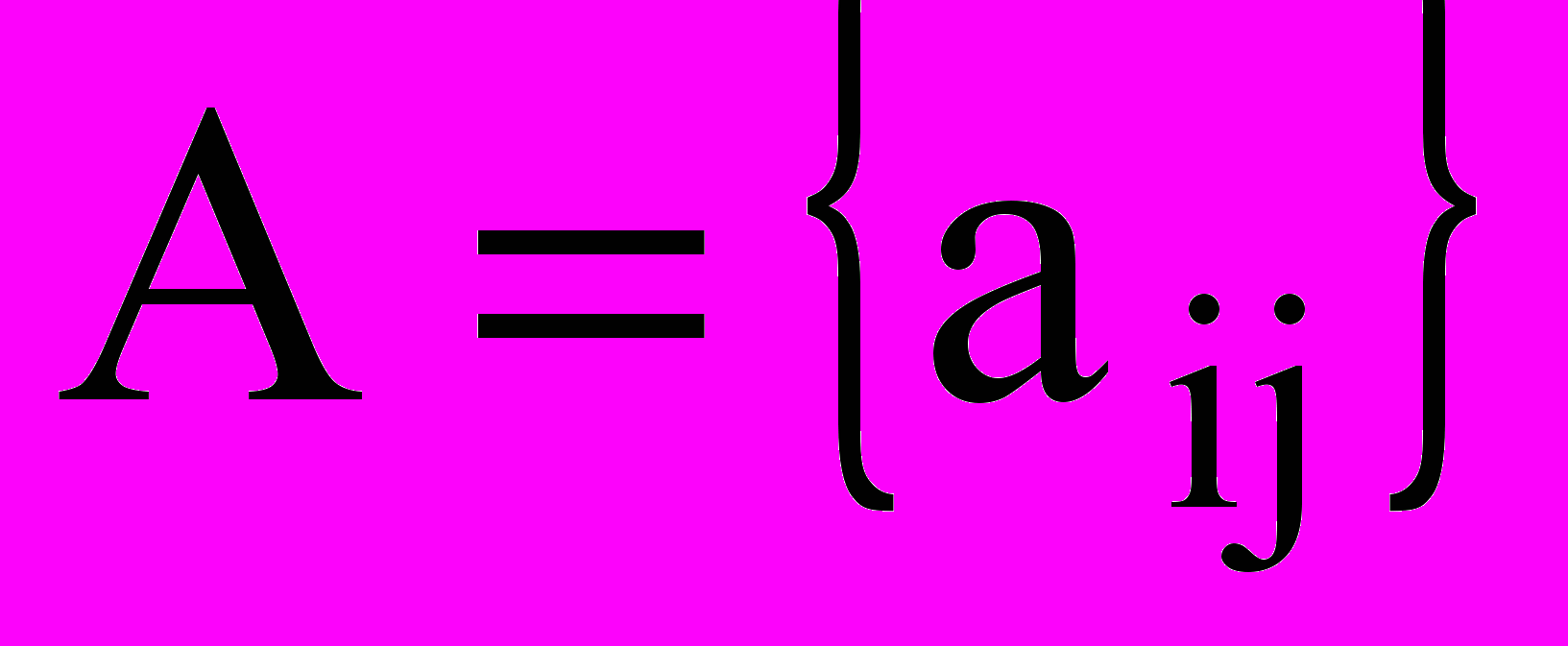известна. Требуется определить, в каком порядке торговец должен посещать города, чтобы общее пройденное расстояние было минимальным. Если рассматривать как время, издержки или другой показатель, то к задаче о коммивояжере сведется ряд прикладных задач, связанных с обходом ряда пунктов, проведением коммуникаций между ними, составлением расписания выполнения работ, оптимизацией программ для ЭВМ и др. Решение задачи о коммивояжере может быть найдено путем перебора (n-1)! возможных маршрутов. Однако с ростом n число вариантов быстро достигает астрономических цифр, что вынуждает отказаться от прямого их перебора. Один из способов решения задачи о коммивояжере состоит в сведении ее к задаче целочисленного линейного программирования, состоящей в минимизации линейной формы затрат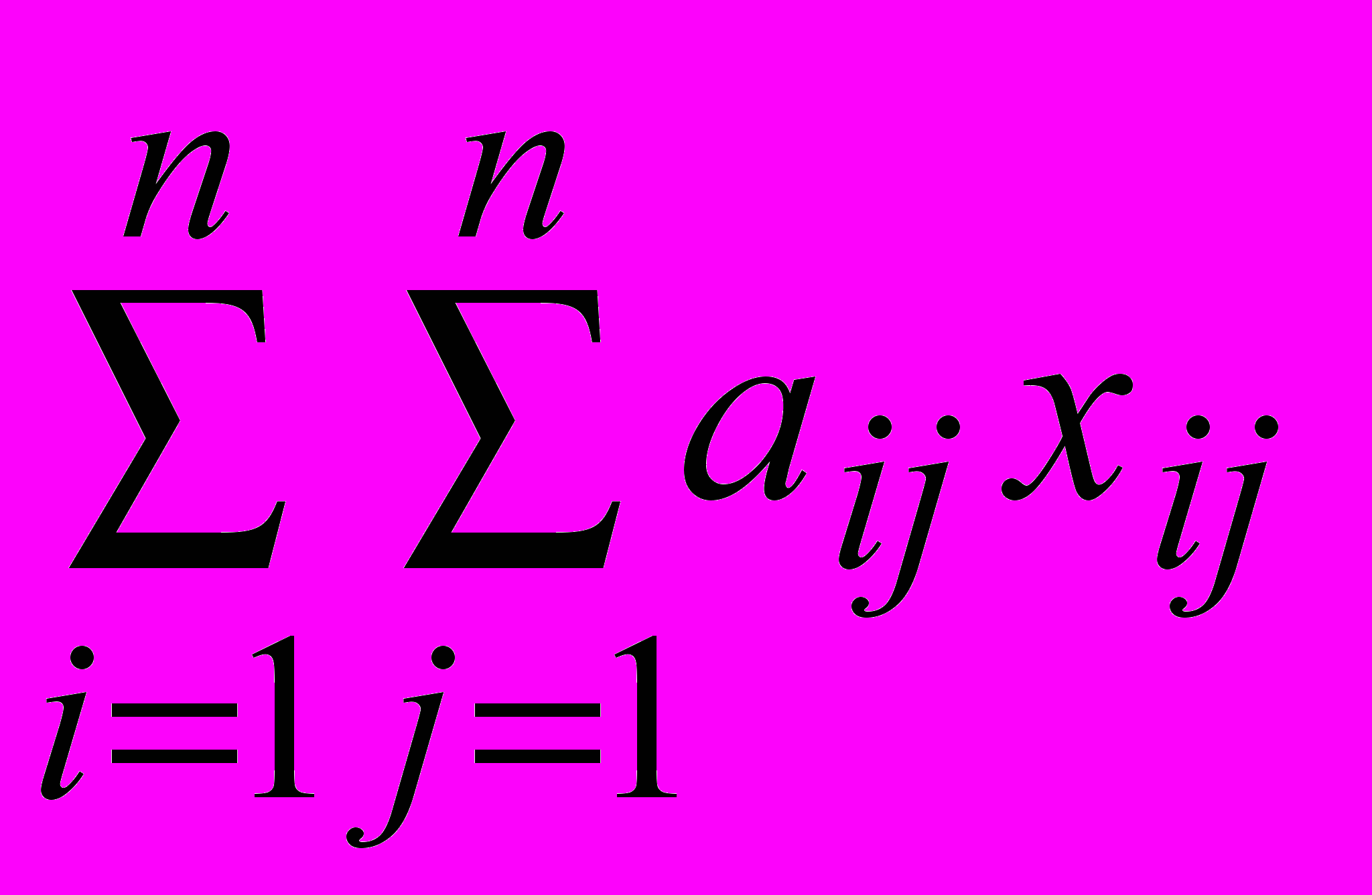

при ограничениях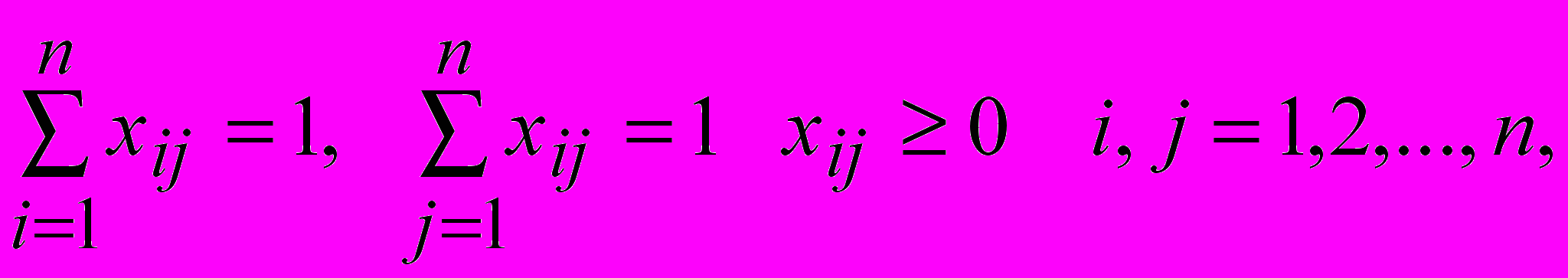



,

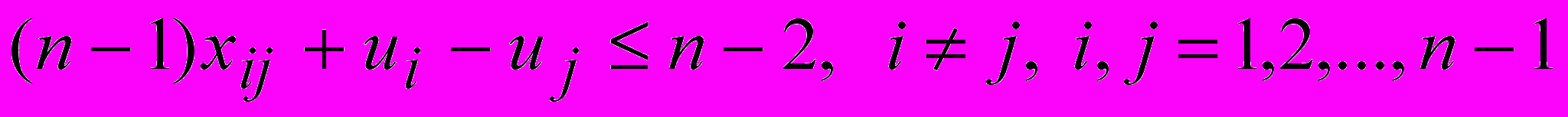где u_i, u_j – некоторые специально подобранные вспомогательные целые числа.

Приведенные ограничения выражают однократность посещения городов, неотрицательность переменных и односвязность маршрута.

Наиболее эффективным из известных способов получения точного решения задачи о коммивояжере считается метод ветвей и границ.


Задача о назначениях

Задача о назначениях – задача о наилучшем распределении n работ между n исполнителями в предположении, что каждый исполнитель назначается только на одну работу и каждая работа предназначается только для одного исполнителя. Исполнители различаются по своим способностям выполнять ту или иную работу. Пусть - производительность i-го исполнителя на j-й работе. Наилучшим считается распределение работ, максимизирующее эффективность, измеряемую суммой производительностей всех n исполнителей. Обозначим через 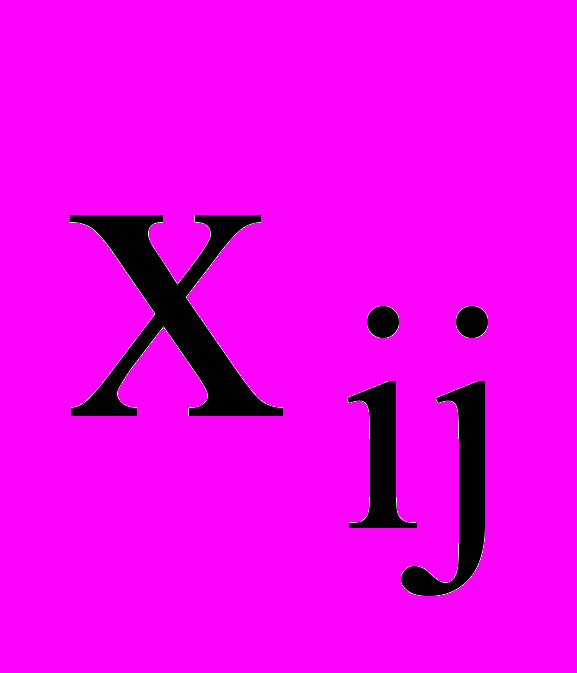переменную, равную единице, если i-й исполнитель назначен на j-ю работу, и нулю, если для j-й работы выбран другой исполнитель. Задача сводится к задаче линейного программирования, заключающейся в нахождении 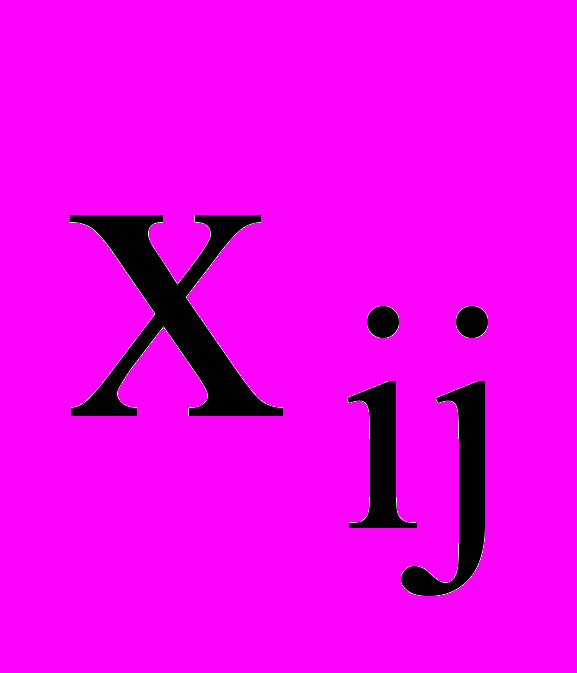, которые максимизируют 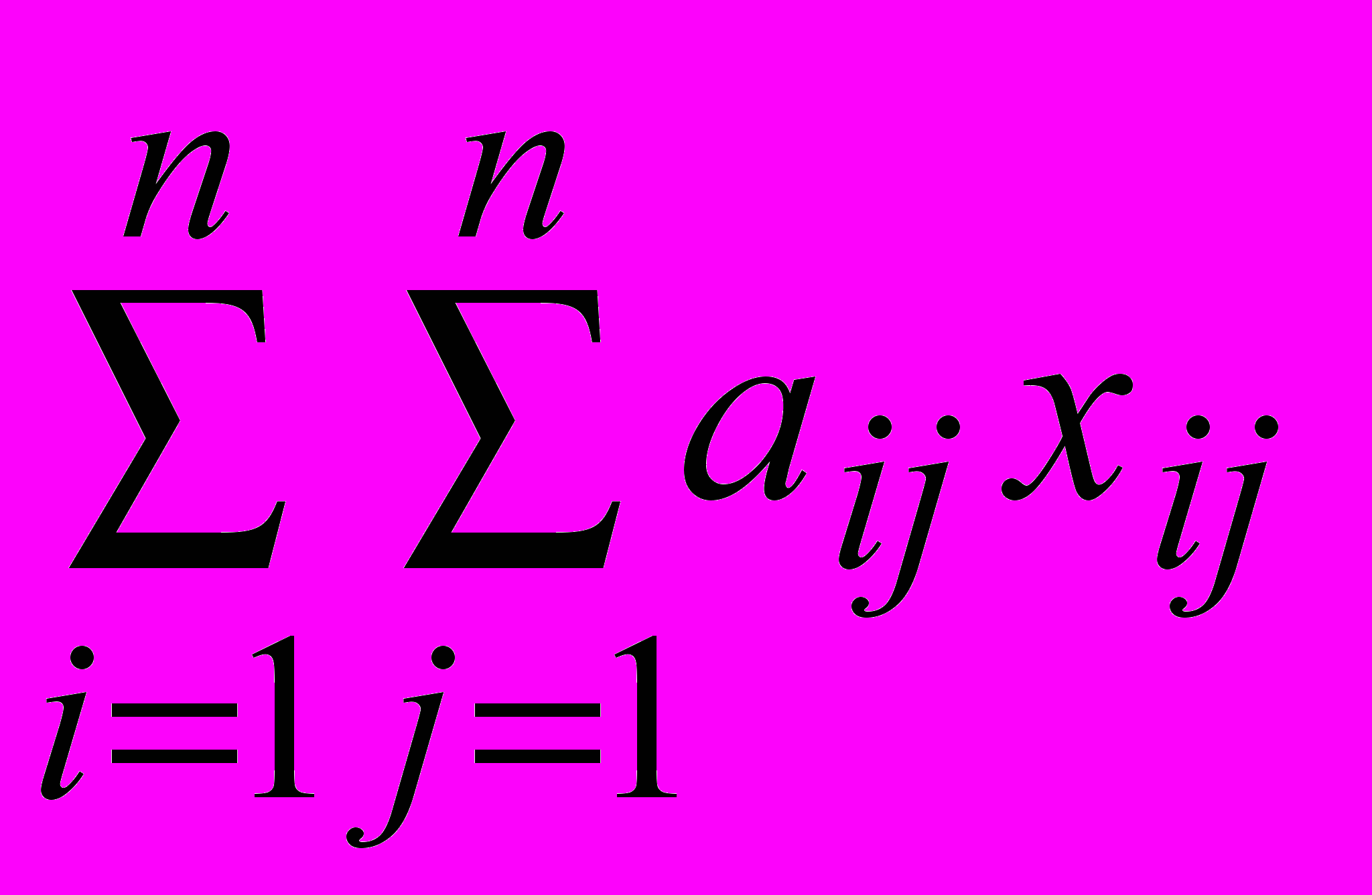при условиях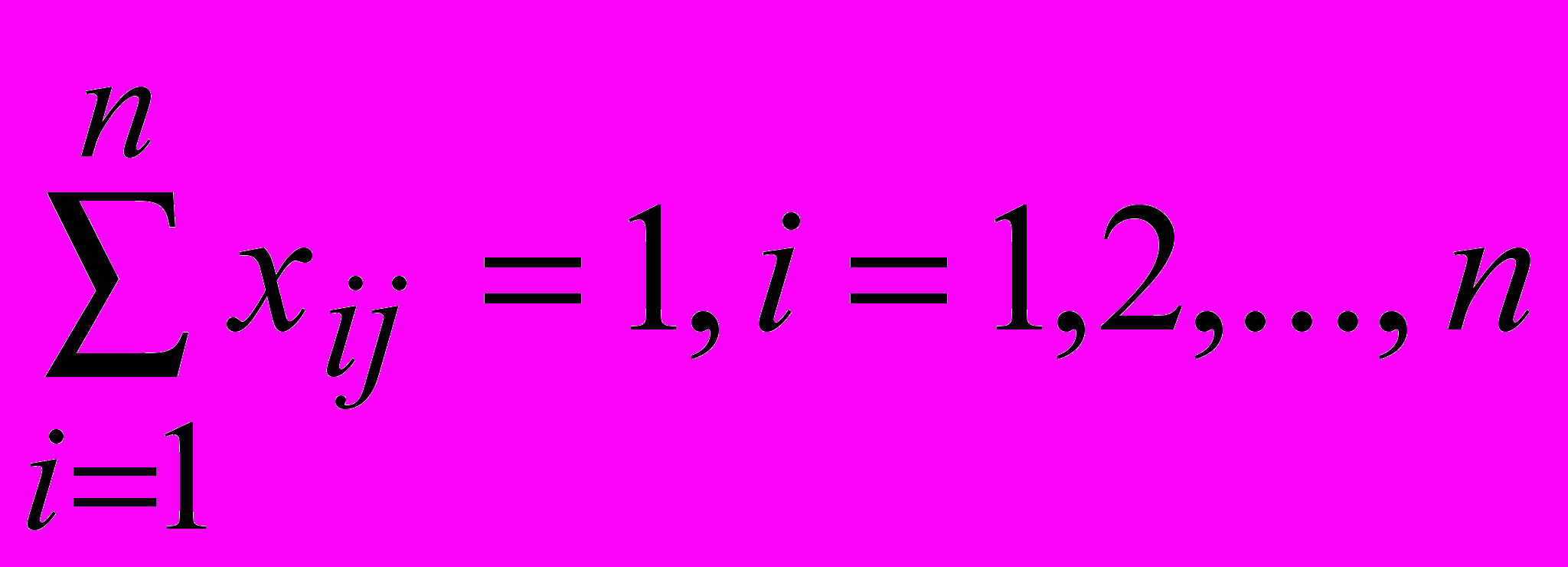

.

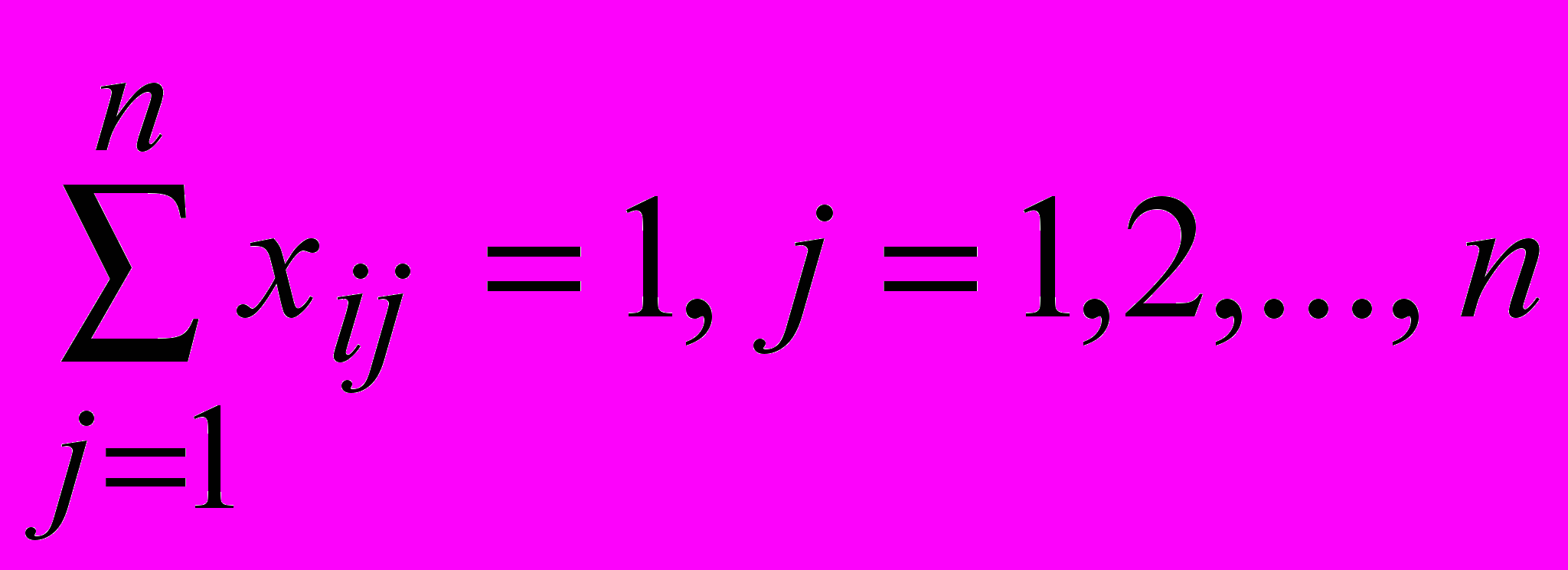
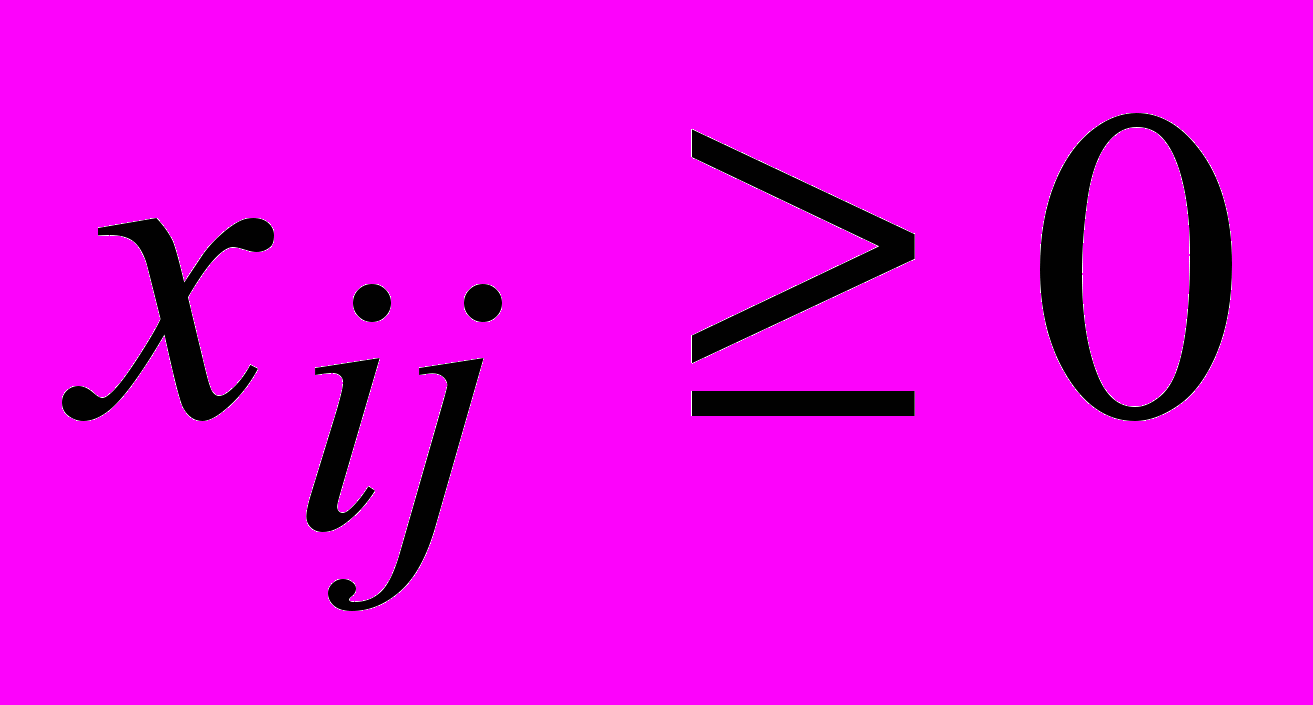Сформулированная задача всегда имеет целочисленное решение, поэтому каждое 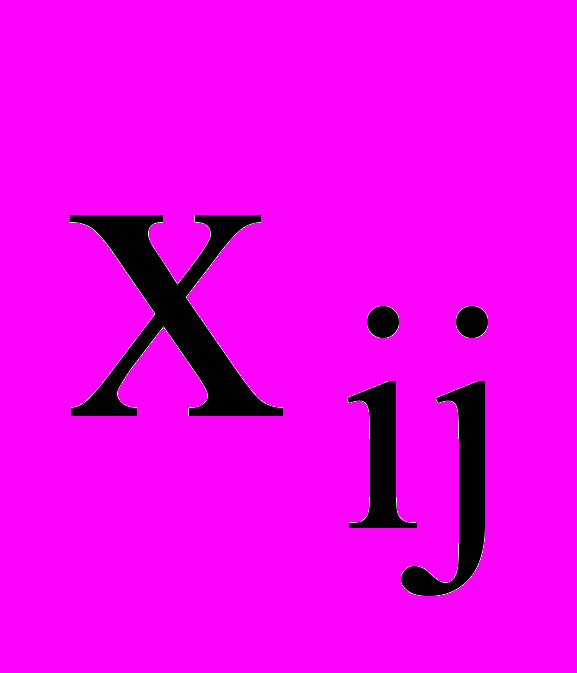всегда будет 0 или 1. Наиболее эффективным методом решения данной задачи является венгерский метод.

Задача о перевозках с промежуточными пунктами

Задача о перевозках с промежуточными пунктами – это обобщенная транспортная задача, когда для каждого пункта потребления составляется уравнение материального баланса. Это уравнение отражает тот факт, что для каждого пункта объем вывезенного продукта минус количество завезенного продукта равен чистому объему продукта, произведенного в этом пункте (если разность положительна), или чистому объему потребляемого в нем продукта (если разность отрицательна).

Уравнение материального баланса для каждого пункта имеет вид –



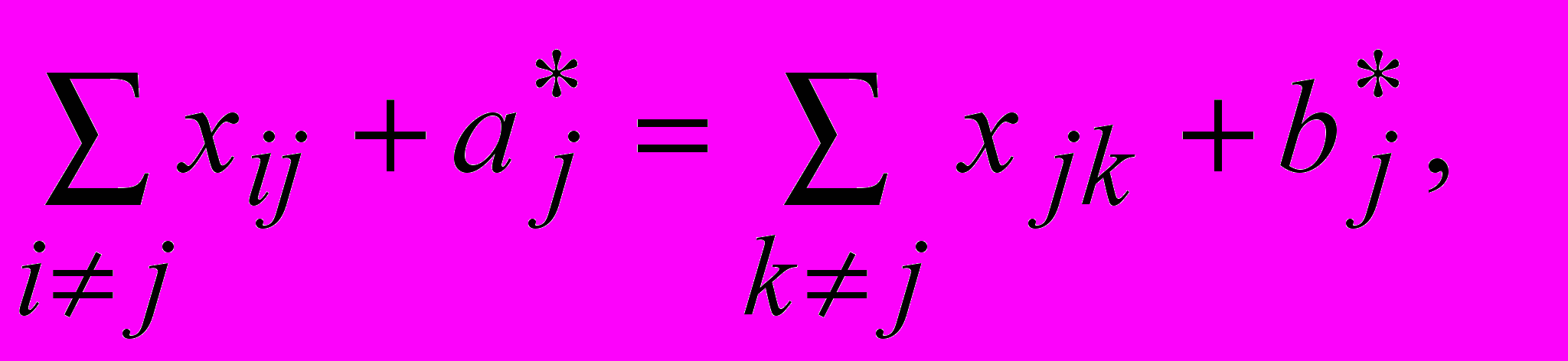
где - объем завезенного продукта из i в j, ; - объем вывезенного продукта из j в k, ; - объем производства в пункте j; 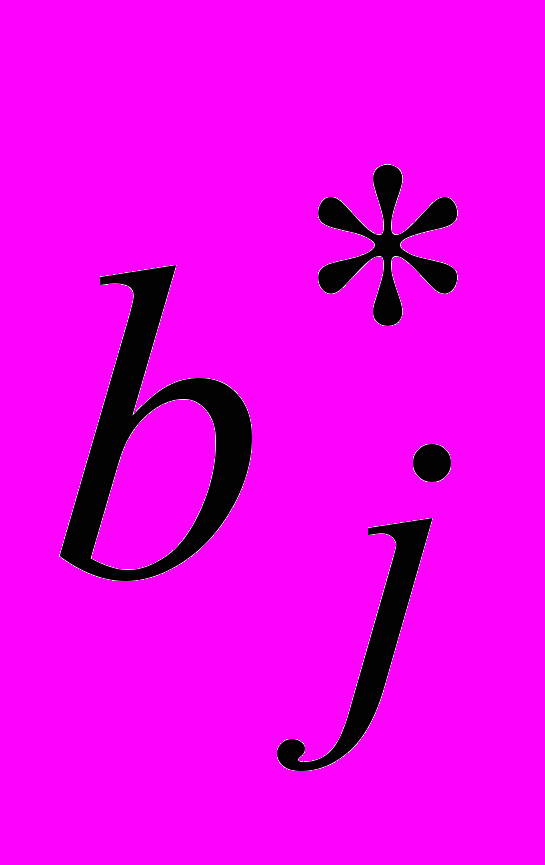- объем потребления в пункте j.

Задача о перевозках с промежуточными пунктами заключается в нахождении чисел 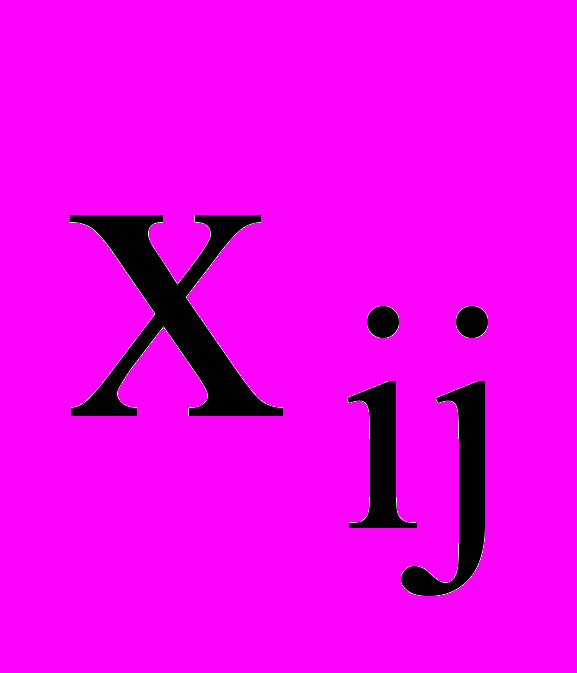(i,j=1,2,…,n), удовлетворяющих уравнению материального баланса и минимизирующих целевую функцию - ,

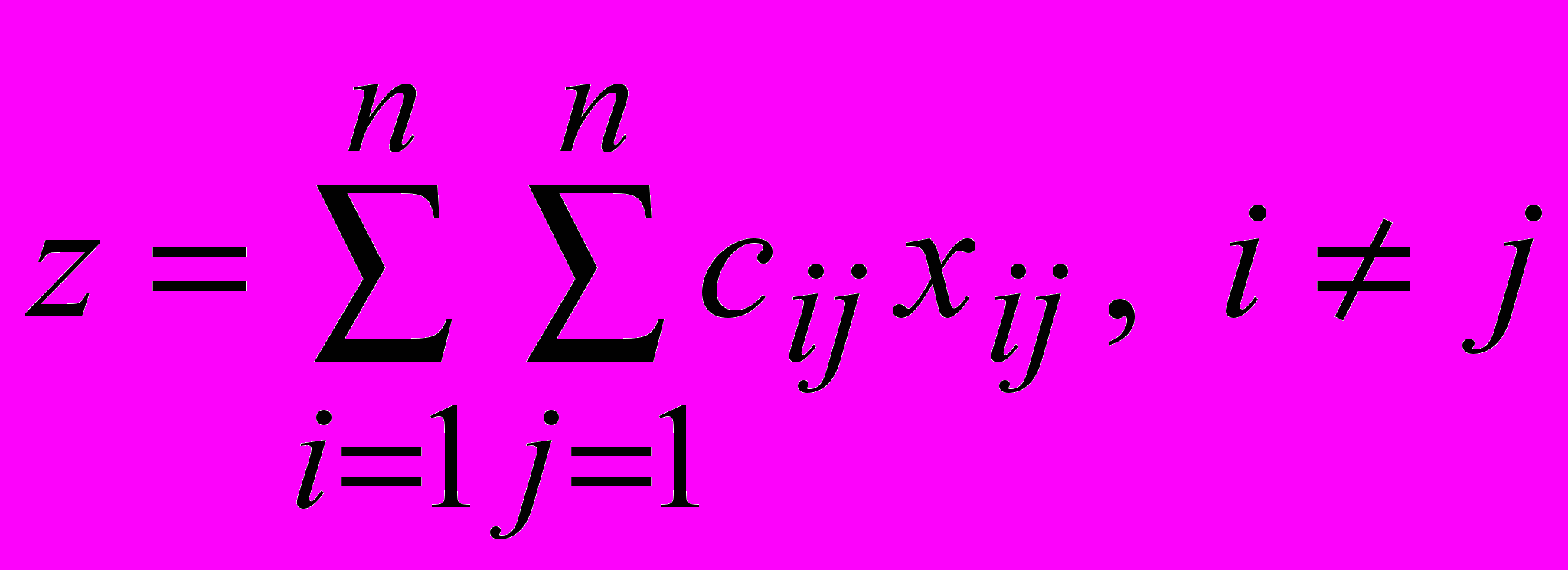где c_ij – затраты на транспортировку единицы продукта из пункта i в пункт j.

Данная задача является задачей линейного программирования. Для ее решения применяются симплекс-метод, методы теории графов.


К задачам производственного планирования относятся задача о рюкзаке и задача о складе.

Задача о рюкзаке

Задача о рюкзаке – задача о наилучшем выборе предметов из общего числа предметов n таким образом, чтобы суммарный вес (объем, габариты и прочее) выбранных предметов не превышал заданного предела b, а их суммарная полезность была максимальной. Каждый из предметов имеет вес a_j и характеризуется коэффициентом полезности c_j. Пусть x_j равно единице, если j-й предмет принимается к укладке в рюкзак, и x_j равно нулю в противном случае. Тогда задача представляет собой задачу целочисленного линейного программирования, заключающуюся в нахождении целых x_j , которые максимизируют 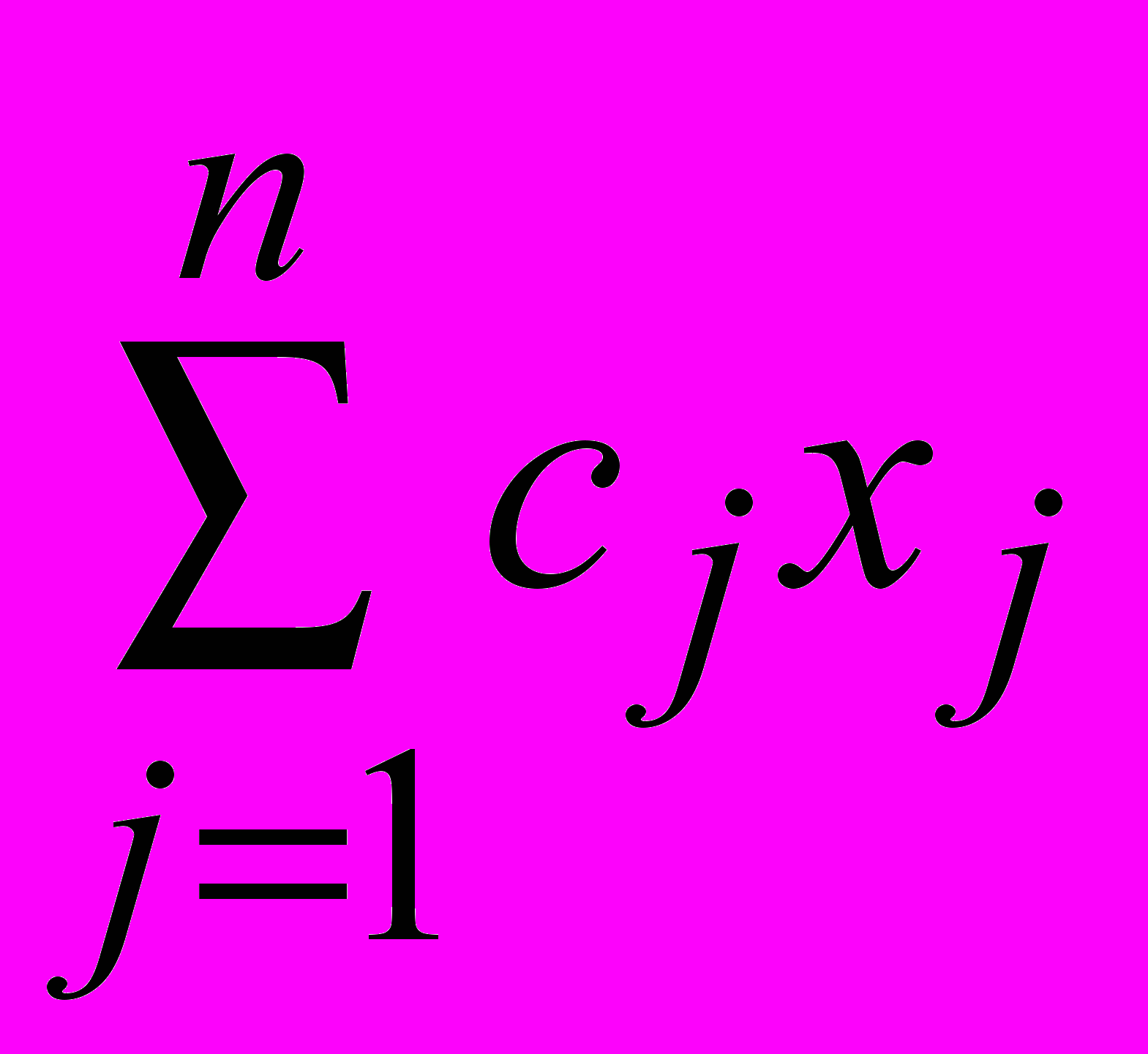при условиях

.

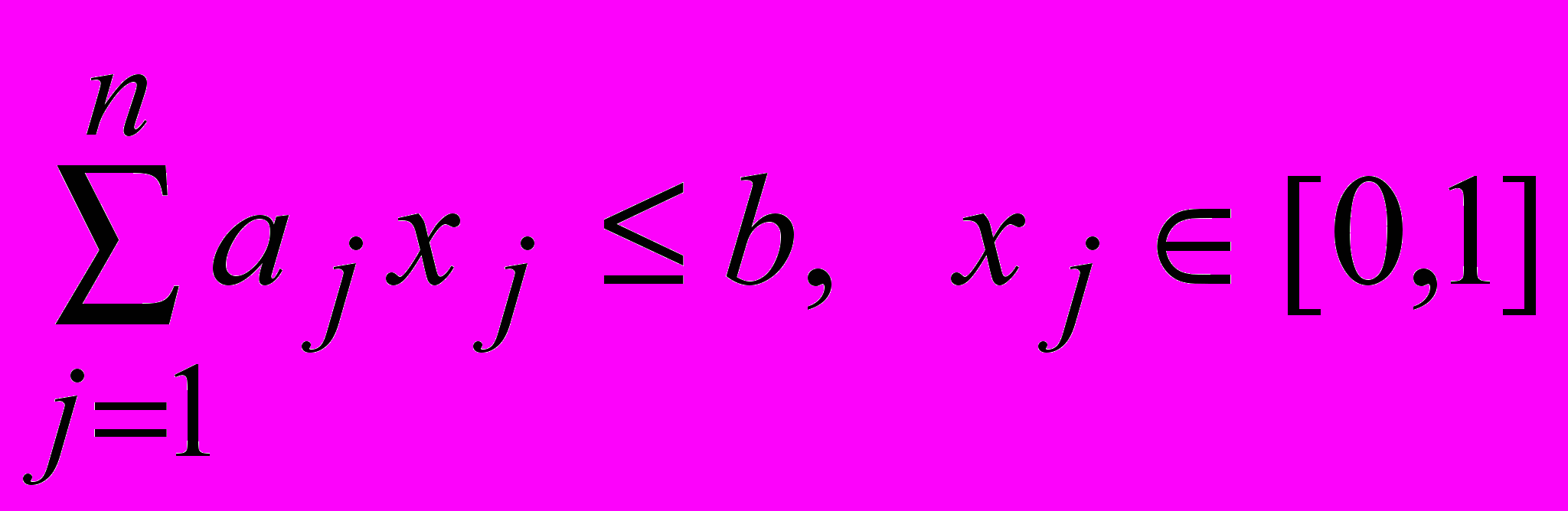К задаче о рюкзаке сводятся многие задачи размещения оборудования в различных помещениях. В каждой конкретной задаче коэффициент полезности может описывать различные качества предметов – стоимость, калорийность и другое. Соответственно и ограничения могут носить разный физический смысл. Наиболее эффективными методами решения задачи о рюкзаке являются метод Гомори и метод ветвей и границ.

Задача о складе

Задача о складе – одна из задач оптимального планирования в системах, связанных с закупками и сбытом однородного продукта. Задача о складе является прикладной задачей линейного программирования. Пусть в начальный момент времени на складе, вместимость которого k единиц продукта, имеется в наличии k₀ таких единиц. В каждый из n дискретных моментов времени (1,2,…,n) производится закупка и продажа некоторого количества единиц продукта. В момент времени n наличный запас его должен оказаться равным k₁. Общее количество продукта, которое может быть закуплено за все n единиц времени равно R. Исходными данными служат следующие величины: стоимость p_i продажи единицы продукта, реализованного в момент времени i, затраты q_i на покупку единицы продукта, закупленного в момент времени i, затраты c_i на хранение единицы продукта в течении промежутка времени (i-1,i), i=1,2,…,n. Обозначим через 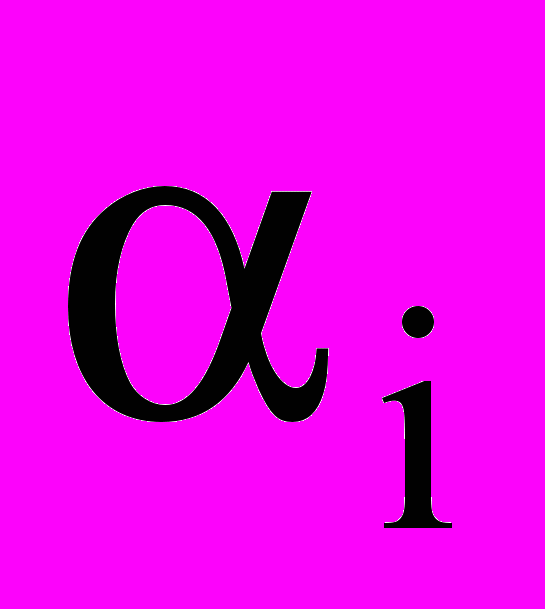количество продукта, реализованное в момент времени i, - количество продукта, закупленное в момент времени i, 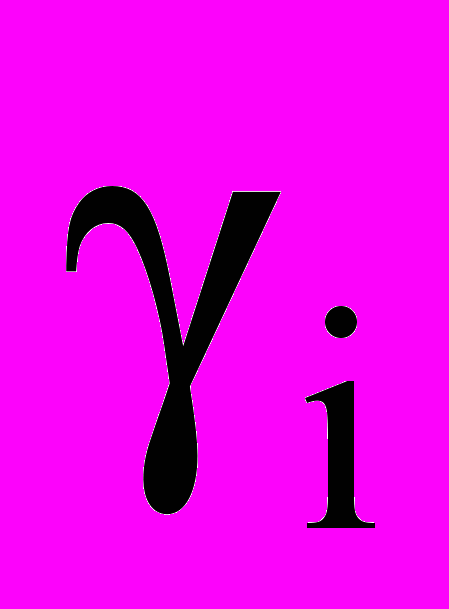- остаток продукта, хранившегося на складе в промежутке (i-1,i) и нереализованного в момент времени i, 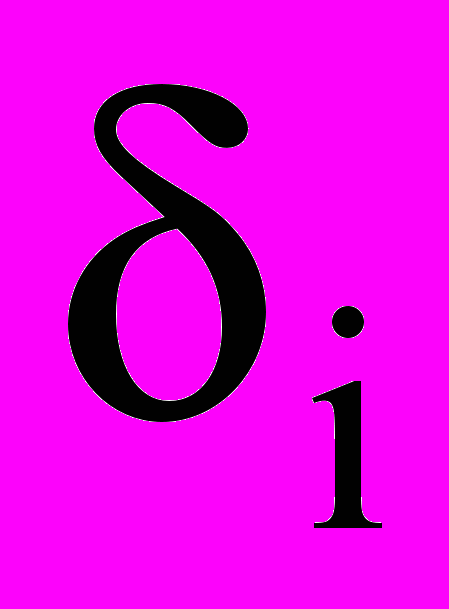- общее количество продукта на складе после закупок в момент времени i. В результате решения задачи должны быть получены такие значения 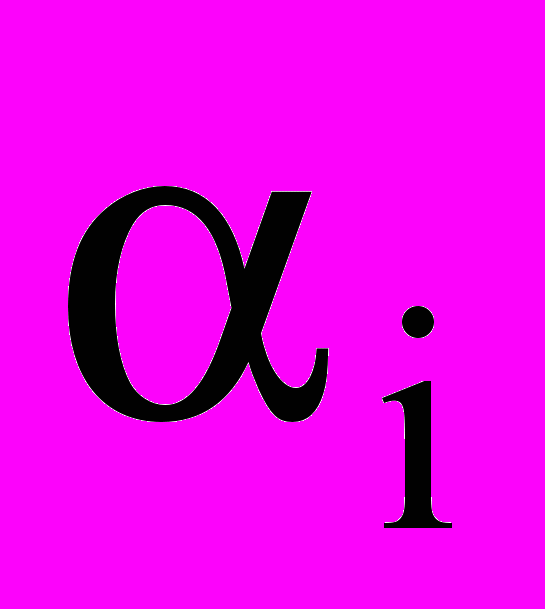и , при которых общая прибыль 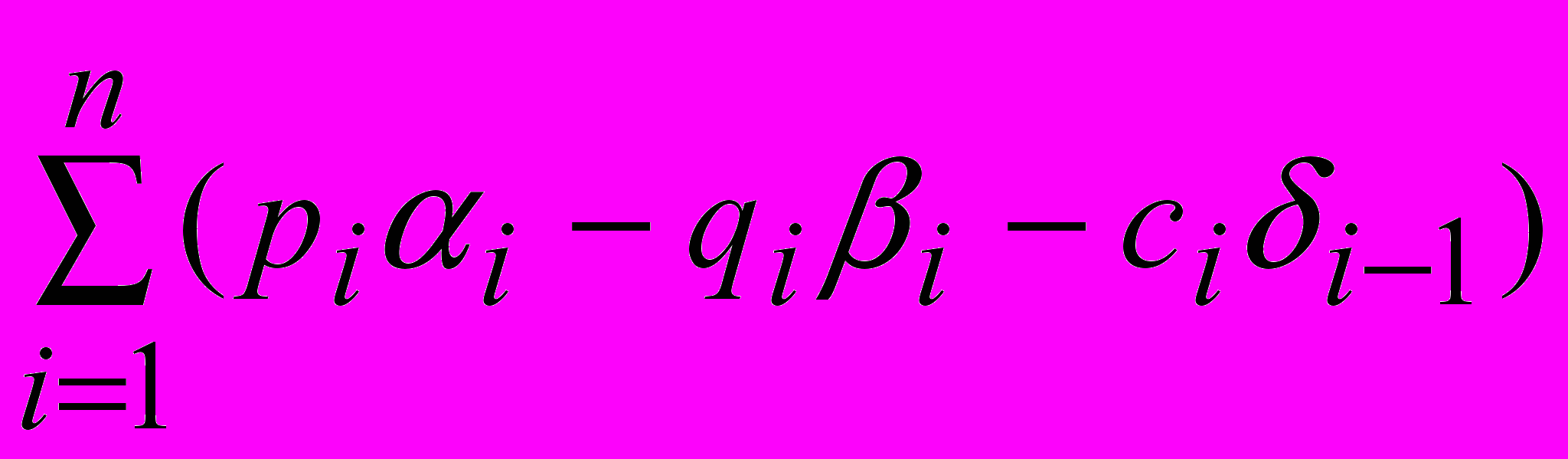оказывается максимальной при ограничениях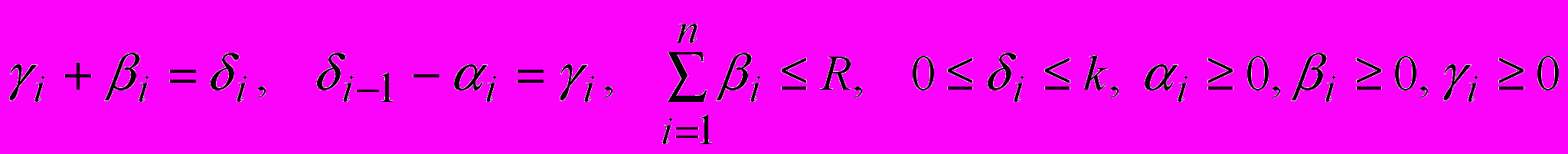





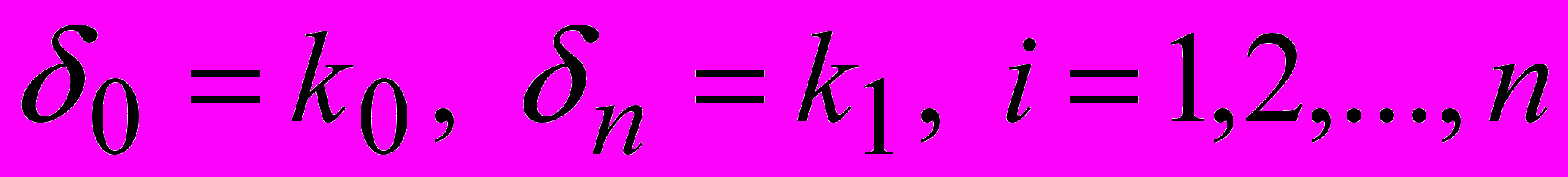
Решение задачи сводится к определению оптимального однородного потока в сети.