Кафедра физики и технологии электротехнических материалов и компонентов (фтэмк)

Вид материала

Документы

Содержание Зависимость диэлектрической проницаемости от температуры, давления, влажности, напряжения Диэлектрическая проницаемость смесей

Подобный материал:

• Аннотация научно-образовательного материала, 44.22kb.
• Совершенствование электрогидравлического регулятора мощности дуговой печи постоянного, 176.56kb.
• Моделирование старения кабелей и проводов в условиях тропического климата, 215.85kb.
• Рабочая учебная программа дисциплины технология конструкционных материалов деталей, 175.41kb.
• Кафедра «Физическое материаловедение и технология новых материалов» (фмтм), 59.94kb.
• Н. Ю. Использование компонентов медиаобразования при изучении квантовой физики. Автореф, 310.43kb.
• Составила Л. Шевченко лекция, 66.47kb.
• Информационное сообщение – 1 международная научно-техническая конференция, 194.89kb.
• Описание проекта/технологии, 171.34kb.
• Предисловие Курс «Электротехническое материаловедение», 948.12kb.

Зависимость диэлектрической проницаемости от температуры, давления, влажности, напряжения

Характер температурной зависимости диэлектрической проницаемости диэлектриков с различными видами поляризаций часто определяют с помощью температурного коэффициента диэлектрической проницаемости:

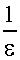
Т_к = 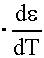K^-1. (19)

Влияние давления на диэлектрическую проницаемость учитывается барическим коэфициентом диэлектрической проницаемости:

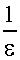
Б_к = 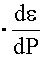Па^-1. (20)

Для линейных диэлектриков Б_к, как правило, положителен, т.к. при всестороннем сжатии диэлектрика увеличивается число способных поляризоваться молекул в единице объема. В некоторых полярных жидкостях в зависимости диэлектрической проницаемости от давления наблюдается максимум.

Увлажнение заметно увеличивает гигроскопических диэлектриков, что, в первую очередь, можно объяснить высокими значениями диэлектрической проницаемости воды ( = 81 ). Вместе с тем, при увлажнении уменьшается удельное сопротивление, увеличивается угол диэлектрических потерь и уменьшается электрическая прочность диэлектрика.

Для линейных диэлектриков, используемых главным образом в качестве электрическо изоляции и диэлектрика конденсаторов, диэлектрическая проницаемость в большинстве случаев может считаться практически независящей от напряжения. Сильно выраженная зависимость диэлектрической проницаемости от напряжения, приложенного к диэлектрику, характерна для сегнетоэлектриков.

	Линейные диэлектрики
	Сегнетоэлектрики

Диэлектрическая проницаемость смесей

На практике часто используются неоднородные композиционные диэлектрики, представляющие собой смеси двух или более различных веществ - компонентов смеси. К таким материалам относятся многие пластические массы, состоящие из связующего и наполнителей, керамические, волокнистые, пропитанные и непропитанные пористые материалы и т.п.

Для расчета эффективной диэлектрической проницаемости смеси предполагается, что ее отдельные компоненты не вступают друг с другом в химические реакции, т.е. смесь является физической.

Простейшим неоднородным диэлектриком является плоский конденсатор, который можно рассматривать как два параллельно (а) или последовательно (б) соединенных конденсатора с однородными диэлектриками.

Обозначая через y₁ и y₂ доли объемного содержания (объемные концентрации) первого и второго компонента для рассмотренного случая будем иметь для параллельного соединения:

^* = ₁ y₁ + ₂ y₂ ; (21)

для последовательного соединения:

^* = _{1 2}/( y_{1 1} + y_{2 2}) ; (22)

Для более общего случая смеси, состоящей из m компонентов для параллельного соединения:

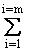^* = y_ii ; (23)

для последовательного соединения:

1/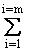^* = (y_i/_i) ;(24)

Для расчета статистической смеси (хаотической, неупорядоченной в пространстве) предложено большое число формул, из которых широкое применение имеет формула Лихтенеккера. Эта формула, носящая название логарифмического закона смещения, для смеси двух компонентов имеет вид:

lg^* = y₁lg₁ + y₂lg₂ ; (25) а для m компонентов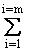: lg^* = y_i lg_i; (26)

Для "вспененных" материалов (пенопластов, пенокерамики и др.), заполненных большим количеством мелких пор, из последней формулы (считая, что для газов =1, а плотность равна нулю) получается уравнение

lg^*= D^*/D_т lg_т ; (27)

где _т и D_т - диэлектрическая проницаемость и плотность сплошного, твердого диэлектрика,

a ^* и D^* - диэлектрическая проницаемость и плотность вспененного материала.