Задание модели системы в пространстве состояний, построение оптимального наблюдателя и получение оценки вектора состояния на основе вектора измерений, построение оптимального регулятора с использованием оценки вектора состояния

Вид материала

Документы

Подобный материал:

• 1 Линии напряженности. Поток вектора напряженности, 73.42kb.
• Эконометрика (Николенко) перечень вопросов к экзамену по всему курсу, 37.83kb.
• Системный анализ параметров вектора состояния организма человека, проживающего в условиях, 694.75kb.
• Системный анализ параметров вектора состояния организма женщин репродуктивного возраста, 689.14kb.
• Лекция №… Поляризация света, 149.95kb.
• Решение задачи формирования оптимального портфеля основано на двух группах предположений:, 31.2kb.
• Вопросы к экзамену по высшей математике, 73.71kb.
• Кнлу 2009/2010 навч рік Екзаменаційні питання з курсу “Вища математика” Розділ І. Аналітична, 47.8kb.
• Федеральная служба по надзору в сфере образования и науки сборник «Построение Общероссийской, 1565.91kb.
• Лекция 11-2011 Последовательность эколого-геохимической оценки состояния окружающей, 178.79kb.

Позняк Е.В., МЭИ (ТУ)


НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ МАТЕРИАЛ


ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

ЛИНЕЙНЫМИ НЕПРЕРЫВНЫМИ СИСТЕМАМИ


В научно-образовательном материале приведена классификация задач оптимального управления, изложены основные подходы к определению оптимального управления, подробно рассмотрены вопросы, связанные с синтезом и анализом оптимальных линейных непрерывных систем на примере системы с оптимальным линейно-квадратичным регулятором. Большое внимание уделяется задаче о синтезе оптимального наблюдателя, на примере механической системы с 4 степенями свободы поэтапно рассмотрена процедура определения оптимального управления:

• задание модели системы в пространстве состояний,
  
• построение оптимального наблюдателя и получение оценки вектора состояния на основе вектора измерений,
  
• построение оптимального регулятора с использованием оценки вектора состояния,
  
• замыкание обратной связью системы с оптимальным регулятором.
  

Восстановление состояния динамической системы по результатам измерений выполняется с помощью фильтра Калмана. Представлены результаты моделирования для различных вариантов СКО входных случайных процессов – шумов измерений и шумов процесса.

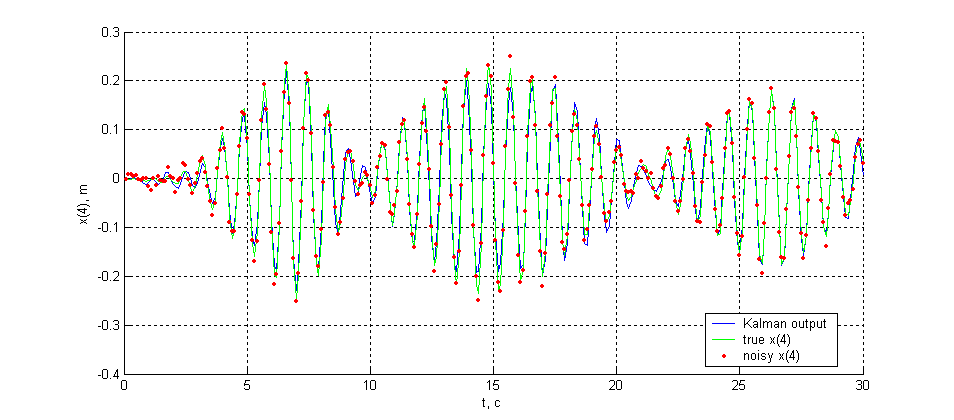Рис. 1 Перемещение четвертой массы (восстановлены по перемещениям m3), СКО измерительного шума 0.01 м, СКО шума процесса 0.01 м.

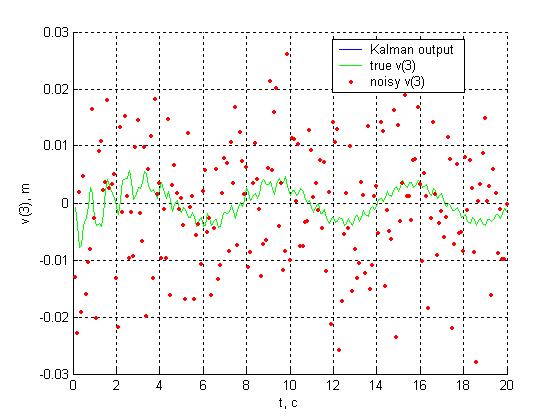Рис. 2 Скорость третьей массы (точка установки датчика перемещений), СКО измерительного шума 0.01 м, шум процесса отсутствует.