Исследование фрактальных характеристик развития трещиноватости горных пород под действием поверхностно-активных веществ
| Вид материала | Исследование |
- Определение свойств горных пород и оценка сопротивляемости горных пород разрушению, 79.2kb.
- Тема «земная кора. Горные породы», 40.42kb.
- Внеклассное мероприятие: «Вудивительном мире камня» (экскурсия знакомство с минералами, 69.88kb.
- Методика экспериментального определения скорости всплытия пузыря. Обсуждение результатов, 163.1kb.
- Тема: Минералы и горные породы, 19.13kb.
- Экспериментальное обоснование прочности и разрушения насыщенных осадочных горных пород, 554.01kb.
- Прогнозирование прочности и устойчивости горных пород по фрактальной размерности линии, 305.61kb.
- Исследование взаимосвязи параметров электромагнитных молотов с физико-механическими, 195.5kb.
- Особенности окисления фосфолипидов и неионных поверхностно-активных веществ 02. 00., 343.11kb.
- Учебно-наглядный комплекс : Коллекция минералов и горных пород, презентация. Ход урока, 14.55kb.
На правах рукописи
ОСИПОВ Игорь Сергеевич
ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ХАРАКТЕРИСТИК РАЗВИТИЯ ТРЕЩИНОВАТОСТИ ГОРНЫХ ПОРОД ПОД ДЕЙСТВИЕМ
ПОВЕРХНОСТНО-АКТИВНЫХ ВЕЩЕСТВ
Специальность 25.00.20 – «Геомеханика, разрушение горных пород,
рудничная аэрогазодинамика и горная теплофизика»
Автореферат диссертации
на соискание ученой степени кандидата технических наук
Екатеринбург – 2008
Работа выполнена в ГОУ ВПО
«Уральский государственный горный университет»
Научный руководитель - | доктор технических наук, профессор Латышев Олег Георгиевич |
| Официальные оппоненты: | доктор технических наук, доцент Ермолаев Александр Иванович кандидат технических наук Берсенев Геннадий Порфирьевич |
| Ведущая организация - | Институт горного дела УрО РАН |
Защита состоится « 4 » декабря 2008 г. в 12.00 часов на заседании диссертационного совета Д 212.280.02 при Уральском государственном горном университете по адресу: 620144, г. Екатеринбург, ул. Куйбышева, 30, ауд. 2142
С диссертацией можно ознакомиться в научной библиотеке
Уральского государственного горного университета
Автореферат диссертации разослан «___» октября 2008 г.
Ученый секретарьдиссертационного совета | Багазеев В. К. |

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Эффективность технологии горного производства определяется свойствами и состоянием разрабатываемых пород. В первую очередь это относится к процессам их разрушения. До настоящего времени единой работоспособной теории разрушения твердых тел не создано, и в этом направлении ведутся интенсивные научные исследования. При всем различии в исходных физических предпосылках все современные теории и концепции прочности горных пород связывают процесс разрушения с образованием новых поверхностей в ходе зарождения и развития трещин.
Перспективным средством интенсификации трещинообразования и, следовательно, разрушения горных пород является использование поверхностно-активных веществ (ПАВ), действие которых основано на адсорбционном понижении поверхностной энергии тел (эффект Ребиндера). Поверхностно-активные вещества давно и успешно используются в самых различных областях науки и практики. Однако, несмотря на очевидную эффективность их применения, широкого распространения в горной практике они не получили из-за слабой разработанности теоретической и методической основ. Известны лишь немногочисленные работы в этом направлении, наметившие основные подходы к решению данного вопроса, которые нуждаются в дальнейшем развитии. Одним из таких направлений является изучение роли эффекта Ребиндера в развитии трещиноватости горных пород.
Известные методы изучения трещиноватости пород обычно рассматривают трещины как линейные структуры, что не соответствует их природе. Учесть реальную геометрию трещин позволяет активно развивающийся в настоящее время инструментарий фрактальной геометрии. При этом, ее использование позволяет не только определить конфигурацию трещин, но и в более широком смысле оценить фрактальность, т. е. самоподобие, как фундаментальное свойство природы.
Все вышеизложенное определяет актуальность данной темы исследований.
Объект исследования – скальные горные породы как природные гетерогенные структуры с развитой системой трещин.
Предмет исследования – закономерности изменения фрактальных характеристик трещиноватости горных пород под воздействием внешних нагрузок и поверхностно-активной среды.
Цель работы – разработка системы прогнозных оценок эффективности использования поверхностно-активных веществ в процессах разрушения горных пород.
Идея работы – использование фрактальных характеристик трещиноватости для прогнозирования эффективности использования поверхностно-активных веществ в процессах разрушения горных пород.
Основные задачи исследования:
1. Разработка методики, аппаратурного и компьютерного обеспечения люминесцентной дефектоскопии применительно к изучению фрактальных характеристик трещиноватости горных пород.
2. Исследование закономерностей образования и развития трещин в горных породах под действием внешних нагрузок и поверхностно-активной среды на основе лабораторных испытаний.
3. Определение влияния поверхностно-активных веществ на характеристики разрушаемости горных пород.
4. Разработка компьютерных процедур моделирования развития трещин в горных породах.
5. Разработка системы прогнозных оценок эффективности использования ПАВ в процессах разрушения горных пород ударом и взрывом, а также невзрывчатыми разрушающими средствами (НРС).
Методы исследований: лабораторное определение свойств горных пород по стандартным методикам; люминесцентный способ изучения трещин под микроскопом; изучение фрактальных характеристик трещиноватости горных пород; компьютерное моделирование распределения и динамики трещин; определение характеристик гранулометрического состава горных пород, разрушенных единичным ударом; статистическая проверка надежности и достоверности результатов экспериментальных исследований; аналитические исследования разрушаемости горных пород с учетом фундаментальных законов физики твердого тела (горных пород) и фрактальной геометрии.
Защищаемые научные положения:
1. Степень нарушенности и удельная поверхностная энергия горных пород определяются фрактальными характеристиками их трещиноватости, которые измеряются для различных условий нагружения с помощью разработанной методики фиксации координат трещин способом люминесцентной дефектоскопии.
2. Развитие под действием ПАВ существующих в горной породе трещин и зарождение новых микротрещин описываются разными по характеру распределениями, имеют различную природу и определяются уравнениями теории Гриффитса и кинетической концепции прочности, параметры которых учитывают фрактальную размерность трещин.
3. Эффективность использования ПАВ при динамическом разрушении пород оценивается ростом концентрации активируемых нарушений, которая определяется разработанной методикой моделирования процесса на ударном копре. Установленные параметры экспоненциального распределения фрактальных размеров трещин (уравнения Коши) используются для прогнозирования вероятности разрушения пород при различном уровне напряжений.
Достоверность научных положений, выводов и результатов работы обеспечивается использованием апробированных методов фрактальной геометрии, достаточным с точки зрения статистических критериев объемом экспериментальных исследований, удовлетворительной сходимостью результатов аналитических расчетов и реализации компьютерных моделей с наблюдаемыми значениями трещиноватости и свойств изученных пород (расхождение не превышает естественную вариацию данных характеристик), непротиворечивостью полученных результатов фундаментальным положениям физики разрушения твердого тела (горных пород).
Научная новизна результатов исследования заключается в следующем:
- на основе метода люминесцентной дефектоскопии установлена процедура определения фрактальных характеристик трещиноватости горных пород и разработана новая компьютерная имитационная модель динамики трещин на основе системы итерационных функций фрактального броуновского движения, в которой впервые учитываются закономерности роста трещин в горной породе под действием поверхностно-активных веществ.
- впервые установлено различие в законах распределения фрактальных характеристик трещин разного класса и определены параметры аппроксимирующих уравнений (логарифмически линейного и Вейбулла).
- получены новые соотношения для оценки прочностных и деформационных свойств горных пород на основе классических уравнений Гриффитса и кинетической концепции прочности с учетом фрактальных характеристик развития трещиноватости горных пород под действием ПАВ.
- разработана новая методика оценки активируемых ударом и взрывом нарушений в горной породе на основе установленной взаимосвязи концентрации этих нарушений с параметрами гранулометрического состава продуктов дробления, учитывающая действие поверхностно-активных веществ.
Практическая значимость работы заключается:
- в разработке комплексной методики изучения трещин и оценки их фрактальных характеристик, которая является эффективным инструментом анализа при проведении научных исследований в области физики разрушения твердых тел;
- в обосновании методики прогнозирования свойств и состояния горных пород при воздействии на них поверхностно-активными веществами;
- в создании методики оценки концентрации активируемых ударом и взрывом нарушений, позволяющей проектировать параметры БВР, обеспечивающие требуемое качество дробления горных пород с заданной надежностью.
Личный вклад автора состоит: в прямом его участии в экспериментальных исследованиях; отработке методики люминесцентного способа изучения фрактальных характеристик трещиноватости горных пород; аналитических исследованиях влияния трещиноватости на свойства и состояние горных пород; получении основных выводов и рекомендаций работы.
Реализация результатов работы. Методика изучения трещиноватости горных пород способом люминесцентной дефектоскопии и сопровождающие ее компьютерные программы и модели, а также методика оценки концентрации активируемых нарушений в горных породах, обработанных растворами ПАВ, переданы для использования Институту горного дела УрО РАН, Уральскому филиалу ВНИМИ и ГОУ ВПО «Магнитогорскому государственному техническому университету».
Теоретические и экспериментальные результаты исследований по направленному изменению трещиноватости, свойств и состояния горных пород поверхностно-активными веществами используются при чтении лекций и проведении лабораторных занятий по курсам: «Физика разрушения горных пород при бурении и взрывании», «Методы и средства изучения быстропротекающих процессов». Автор участвует в проведении данных занятий и их методическом обеспечении.
Основные материалы, полученные в диссертации, будут включены в готовящуюся к изданию монографию «Исследование фрактальных свойств и теоретические основы прогноза образования и развития трещин в процессах разрушения горных пород».
Апробация работы. Основные результаты работы докладывались и обсуждались: на Всероссийской конференции-конкурсе студентов выпускного курса – СПбГГИ (ТУ), г. Санкт-Петербург, 2005 г. (автором получен Диплом второй степени); на научно-технических конференциях: «Теория и практика добычи, обработки и применения природного камня» – МГТУ, г. Магнитогорск, 2005, 2008 гг.; на II Международной конференции «Проектирование, строительство и эксплуатация комплексов подземных сооружений» – УГГУ, г. Екатеринбург, 2007 г.; на пятой Международной научной конференции "Физические проблемы разрушения горных пород" – СПбГГИ (ТУ), г. Санкт-Петербург, 2006 г.; на международной научной конференции «Неделя горняка» - МГГУ, г. Москва, 2008 г.; на ежегодных молодежных научно-практических конференциях Уральского государственного горного университета (2003 – 2008 гг.).
Публикации. Основные положения диссертации опубликованы в 14 печатных работах, включая одну монографию.
Объем и структура работы. Объем диссертации составляет 168 страниц машинописного текста, включая 51 рисунок и 11 таблиц. Диссертация состоит из введения, четырех глав, заключения, библиографического списка из 123 наименований.
Работа выполнена в рамках исследований по следующей тематике: «Управление свойствами и состоянием скальных горных пород поверхностно-активными веществами и проектирование оптимальных параметров их разработки в меняющихся горно-геологических условиях» (грант Минобразования РФ ТО2-04.4-3154, 2003-2004 гг.); «Изучение последствий и теоретические основы прогноза изменения геологической среды при подземных техногенных воздействиях» (задание Федерального агентства по образованию 1.13.05, 2005-2007 гг.); «Исследование фрактальных свойств и теоретические основы прогноза образования и развития трещин в процессах разрушения горных пород» (задание Федерального агентства по образованию, 2008-2010 гг.).
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Анализ современных концепций прочности твердых тел (А. А. Гриффитс, Т. Екобори, С. Н. Журков, Дж. Ирвин, Е. Орован, Г. П. Черепанов и др.) показывает, что главный механизм разрушения связан с динамикой зарождения и развития трещин, а критерием прочности является удельная поверхностная энергия горной породы и геометрия трещин.
Для изучения характеристик трещиноватости горных пород нами усовершенствован метод люминесцентной дефектоскопии, широко применяемый в металлургии для контроля качества выпускаемых изделий. Создана лабораторная установка, включающая микроскоп МБС-10 с микрофотоустройством МФУ, цифровой фотоаппарат Sony DSC-W200 и ультрафиолетовый облучатель Line 506. Разработана и апробирована процедура экспериментальных исследований с фотофиксацией картины трещин.
По современным представлениям полезная энергия разрушения горных пород расходуется на образование новых поверхностей трещин. Поэтому для количественной оценки данного процесса требуется экспериментальное определение геометрии трещин. Однако используемые до настоящего времени способы анализа картины трещин основаны на решении задачи Бюффона («метод палетки»), когда трещина принимается как линейное образование, что не соответствует действительности.
Для точного измерения геометрии трещин топологической размерности недостаточно. Впервые с этим фактом столкнулся Д. Ричардсон. При измерении длины береговой линии Великобритании на картах разного масштаба он заметил, что чем меньше раствор циркуля δ, тем все большие подробности входят в измеряемую длину и результаты измерения непрерывно увеличиваются. Он установил, что рост измеряемой длины L подчиняется степенному закону (закон Ричардсона):
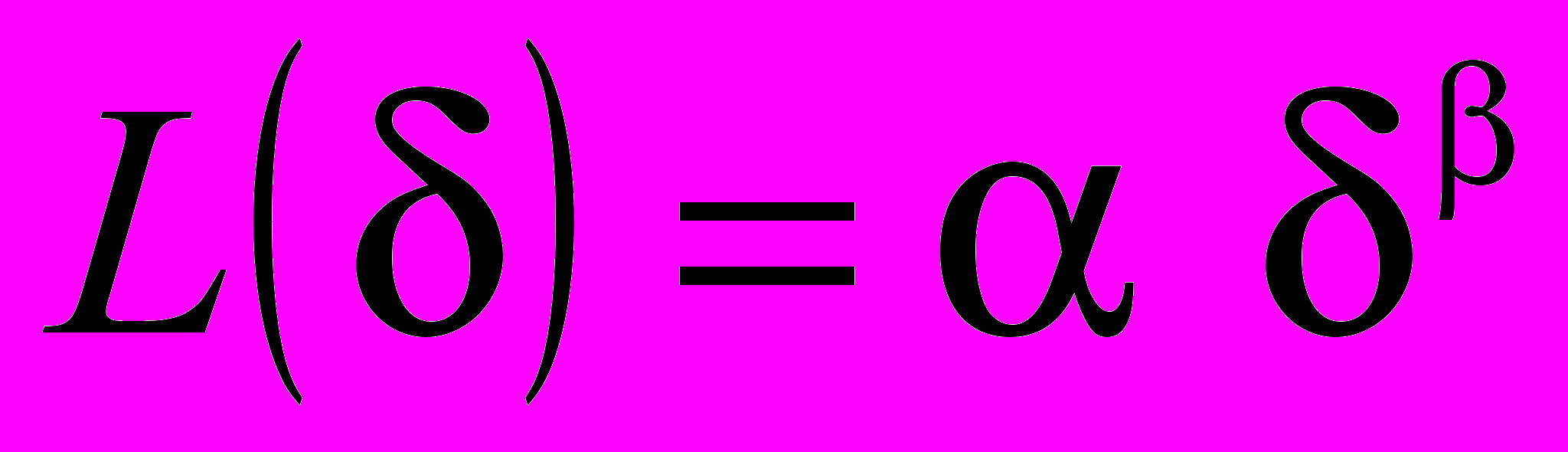 , (1)
, (1)где α – некоторая константа; β – отрицательный показатель степени.
Таким образом, измеряемый размер трещины зависит от масштаба измерения и может не соответствовать ее топологической размерности. Впервые понятие дробной размерности dH ввел Ф. Хаусдорф (1919 г.). Он показал, что в законе Ричардсона β – 1 = - dH. В 1975 г. Б. Мандельброт назвал объекты с дробной размерностью фракталами. Появилась новая отрасль знаний - фрактальная геометрия, теория и прикладные аспекты которой в настоящее время успешно развиваются (О. Е. Акимов, Р. Кроновер, С. С. Крылов, Б. Мандельброт, А. А. Потапов, В. В. Шитов и др.). В различных задачах определяются разные виды фрактальной размерности: размерность подобия, Хаусдорфа, емкостная размерность Колмогорова, размерность Минковского. Для изучения таких природных объектов, как трещины, наиболее подходящим является метод покрытия, при котором исследуемое множество покрывается различными по форме правильными геометрическими фигурами.
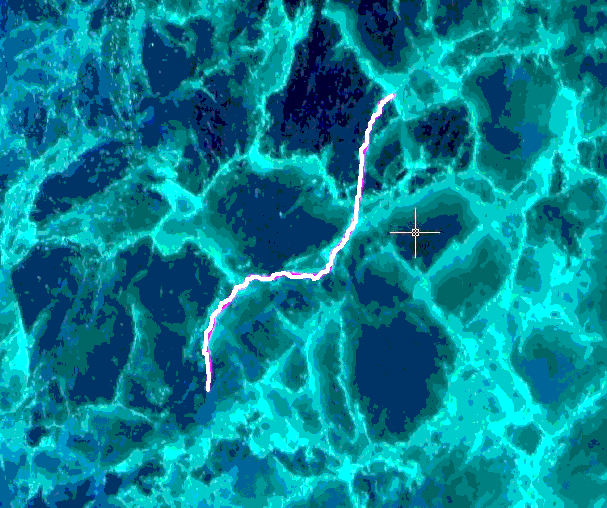
В соответствии с разработанной методикой для оценки фрактальных характеристик трещиноватости образцы горных пород подвергались статической нагрузке (25 МПа) и на описанной выше лабораторной установке осуществлялась фотофиксация картины трещин на шлифованных гранях образцов, параллельных линии нагружения. Полученные фотографии поверхности образцов переносились в систему AutoCAD, где каждая трещина покрывалась ломаной линией, максимально четко повторяющей ее трек (рис. 1, а).
В результате для каждой трещины была получена модель, в которой определены координаты всех характерных точек (вершин, изломов, разветвлений и т.п.) трещины при данном увеличении. Кроме того, определялись линейные и реальные (для заданного увеличения) размеры трещин.
Для отработки методики определения фрактальной размерности трещин произведено сравнение двух методов.
Метод «циркуля» заключается в многократном измерении линии (трещины) со все уменьшающимся раствором циркуля δi, и при каждом измерении вычисляется длина трещины: L(δi) = δiN(δi), где N(δi) – число отрезков длиной i, покрывающих всю линию. Из закона Ричардсона следует:
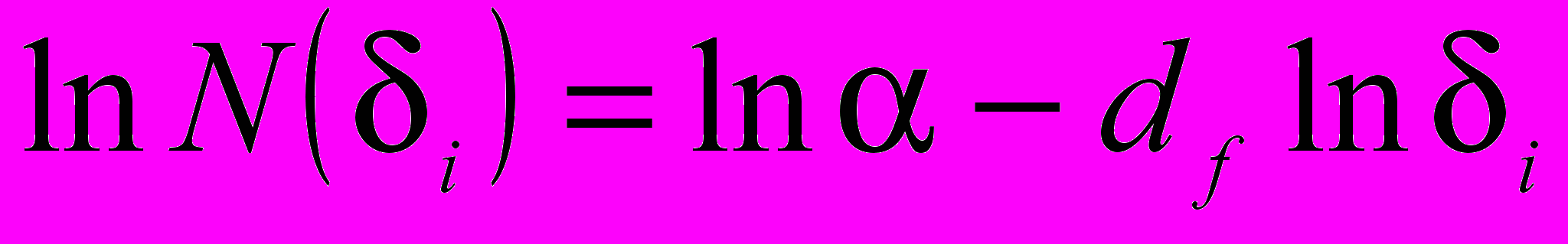 . (2)
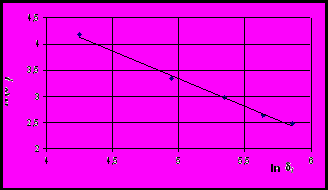
. (2)По полученным парам значений δi - N(δi) для каждой трещины производится построение графика зависимости (2) (рис. 1, б) и методом «наименьших квадратов» определяется фрактальная размерность df.

а б
Рис. 1. Определение фрактальной размерности методом «циркуля»:
а – модель трещины в системе AutoCAD; б – график зависимости уравнения (2)
Сущность метода «покрытия» заключается в нанесении на модель трещины квадратной сетки при размере ячейки ri с одновременным подсчетом минимального числа клеток N(ri), покрывающих фрактал (трещину) (рис. 2, а). По установленной зависимости
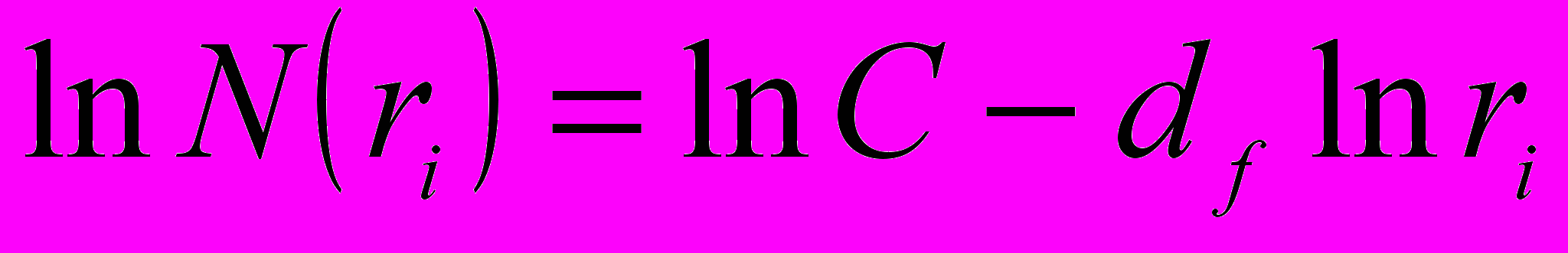 (3)
(3)производится построение графика (рис. 2, б) и методом «наименьших квадратов» определяется фрактальная размерность df.
Сравнение результатов определения df методами «циркуля» и «покрытия» показало хорошее соответствие (различие статистически незначимо и определяется только естественной погрешностью измерений). Таким образом, оба метода дают сопоставимые результаты. Учитывая, что метод покрытия более универсален (может быть реализован в компьютерной программе) и используется для оценки других характеристик трещиноватости, он был принят нами в качестве основного.
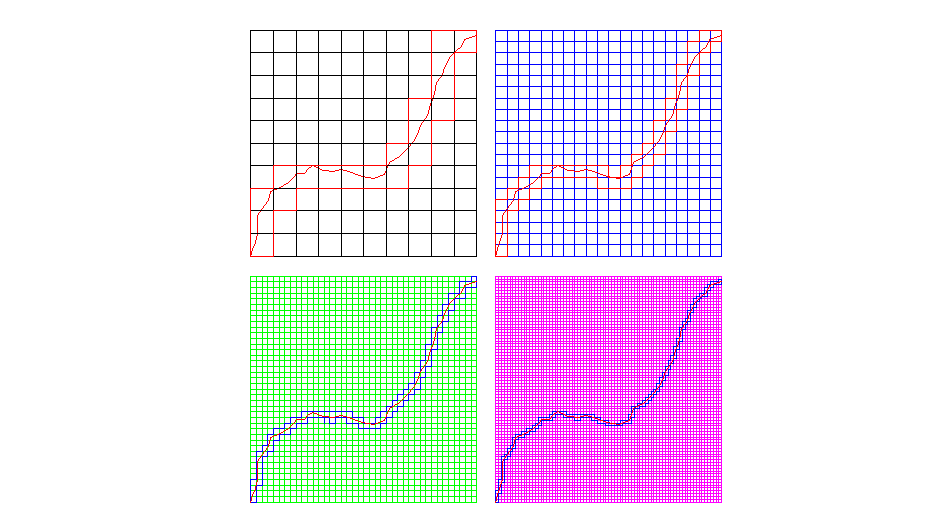
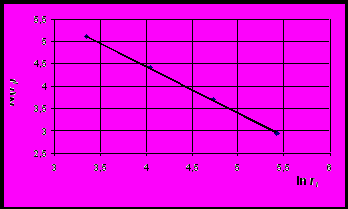
а б
Рис. 2. Определение фрактальной размерности методом «покрытия»:
а – реализация метода в системе AutoCАD; б – график зависимости уравнения (3)
Описанная классическая процедура определения фрактальной размерности трещин основана на ручном счете. Это неизбежно связано с возможностью возникновения ошибки вследствие субъективности восприятия объекта (трещины) и огромными затратами времени, если учесть, что на каждом образце требуется обмерить сотни трещин. Поэтому нами поставлена и решена задача автоматизации вычислений с помощью компьютерной программы. В основу положено доказательство Р. Кроновера об адекватности траектории трещины одномерной реализации фрактального броуновского движения (ФБД) с нулевым математическим ожиданием и дисперсией
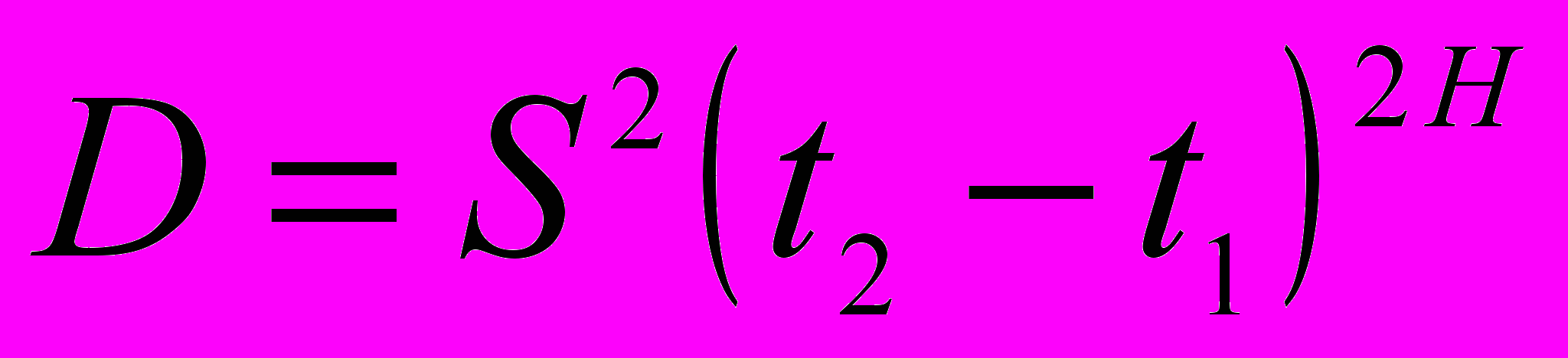 , где S – некоторая положительная константа, определяющая масштаб отклонений координат трещины от оси t; Н – характеристический параметр ФБД (0 < Н < 1).
, где S – некоторая положительная константа, определяющая масштаб отклонений координат трещины от оси t; Н – характеристический параметр ФБД (0 < Н < 1).Алгоритм компьютерной программы вычисления фрактальной размерности трещины можно представить следующим образом.
1. На вход программы подается матрица координат трещины (xi - yi).
2. Линия, соединяющая вершины трещины, принимается за ось абсцисс t, т. е. все координаты трещины пересчитываются на новую систему координат (t –ΔX). Расчетные формулы:
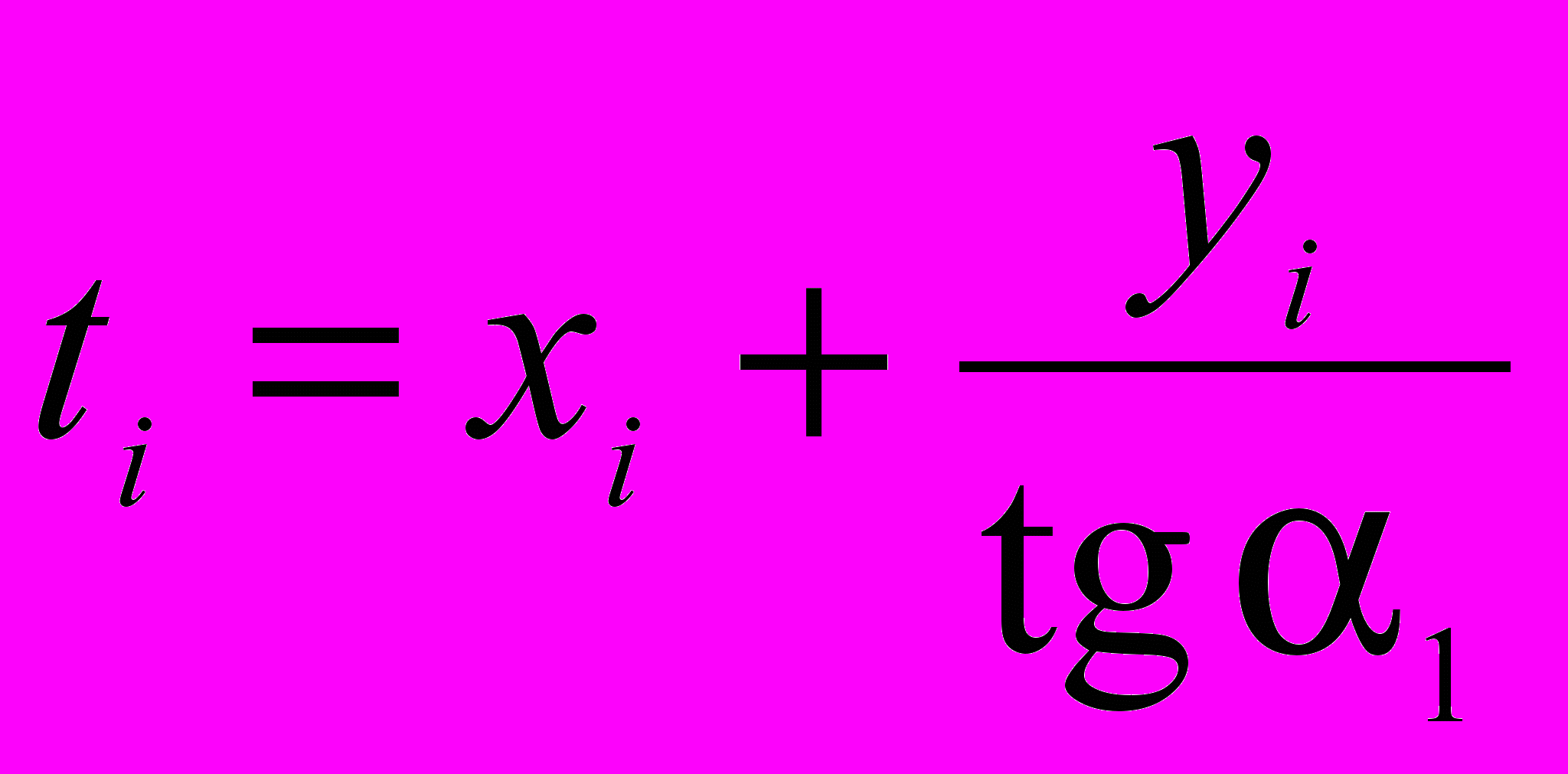 , (4)
, (4)где α1 = (π/2 – β);
β = arctg (yк/хк) – угол наклона линии, соединяющей вершины трещины;
(х0 = y0 = 0) и (хк, yк) – координаты второй вершины трещины;
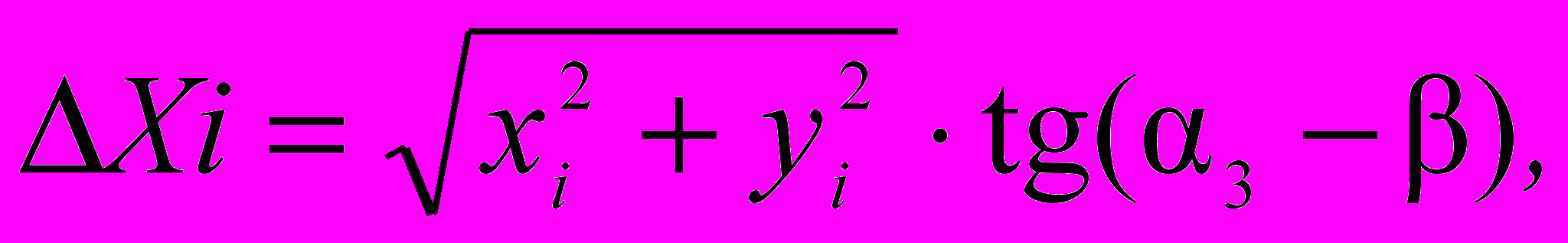 (5)
(5)где α3 = arctg (yi/xi) – угол наклона прямой, соединяющей данную точку с началом координат.
3. Ось t, т. е. линейная длина трещины L0, разбивается на n частей (в программе минимальный шаг принят как L0/100).
4. С каждым значением ti сопоставляется величина приращения ΔXi.
5. Формируется матрица (ti – ΔXi).
6. При разных значениях шага Δt (в программе принято 10 равномерно увеличивающихся значений Δt) просчитывается сумма квадратов отклонений приращений S(ΔX).
7. Производится построение графика уравнения
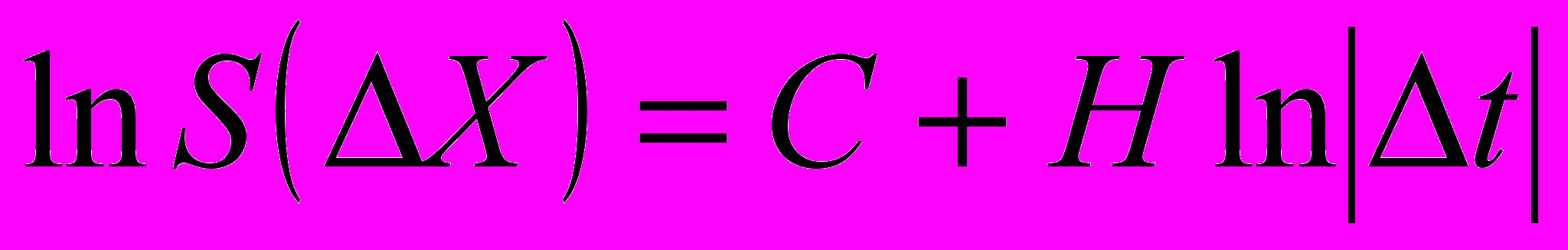 , (6)
, (6)методом «наименьших квадратов» определяется величина Н и фрактальная размерность трещины df = 2 - Н.
На рис. 3 представлен пример реализации компьютерной программы.
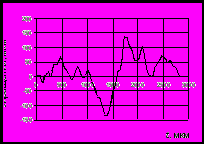
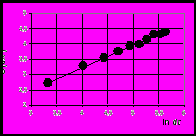
а б в
Рис. 3. Стадии реализации программы: а – координаты трещины; б – график приращений трещины; в – график зависимости уравнения (6)
Для рассмотренной трещины Н = 0,722 и ее фрактальная размерность
df = 1,288. При этом коэффициент корреляции r = 0,99. Наряду с указанными действиями программа автоматически определяет среднее арифметическое значение модуля отклонений трещины от линии, соединяющей ее вершины ΔХср, коэффициент вариации Квар и доверительный интервал δх. Для рассмотренной трещины: ΔХср = 47,5 мкм; Квар = 82,4 %; δх. = 7,7 мкм.
Помимо фрактальной размерности конкретных трещин важным является их пространственное распределение по поверхности или объему горной породы. Оценкой такого распределения может служить корреляционная размерность d2, которая оценивается по расстоянию между точками множества на фрактале (С. С. Крылов, Н. Ю. Бобров). Разработанный нами алгоритм и компьютерная программа определения корреляционной размерности основаны на вычислении корреляционного интеграла
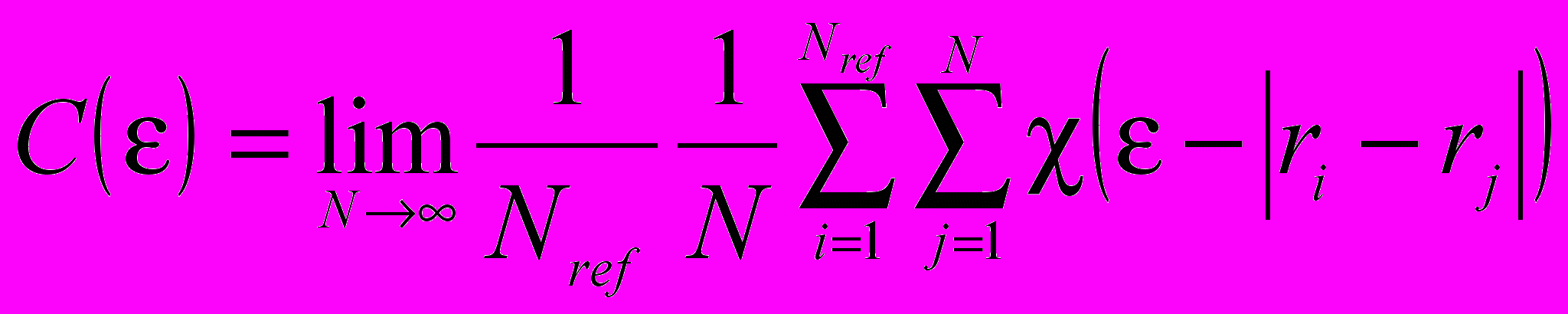 , (7)
, (7)представляющего собой сумму значений функции Хевисайда χ(εj – ׀ri - rj׀). Последовательность реализации процедуры заключается в следующем. На изображении поверхности образца с выделенной системой трещин выбираются несколько (не менее 3-4) референтных точек Nref(i). Задаются радиусы εj окружностей (сфер – для трехмерного случая) с логарифмическим шагом увеличения. Для каждой вершины трещины с координатами хj – yj вычисляется ее расстояние до данной референтной точки rij и сравнивается с соответствующим радиусом окружности (сферы) εj Если rij < εj, функция Хевисайда приобретает значение 1, в противном случае – 0. Данная процедура производится для каждой референтной точки и путем суммирования значений функции Хевисайда для каждой сферы радиусом εj всех референтных точек определяется корреляционный интеграл С(εj). Затем по полученным парам значений
С(εj) - εj производится построение графика функции log C(εj) = f(log εj) и способом наименьших квадратов вычисляется корреляционная размерность d2.
Изложенные выше процедуры позволили определить фрактальные характеристики трещиноватости изученных образцов горных пород. По результатам анализа более 1080 трещин можно сделать следующие обобщения.
Истинная длина трещины определяется ее фрактальной размерностью df в соответствии с уравнением
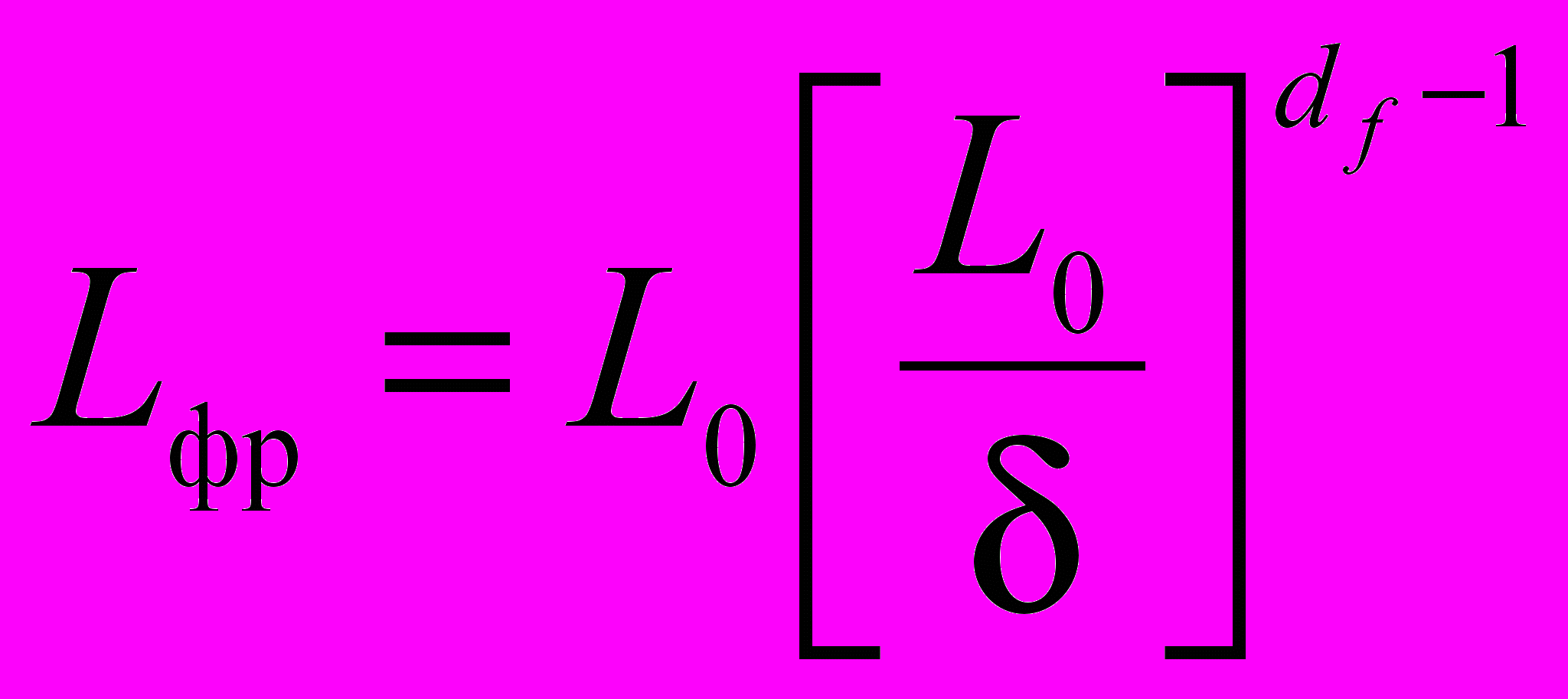 , (8)
, (8)где L0 – расстояние между вершинами трещины, мкм;
δ – принятый шаг измерений трещины, мкм.
Установлено, что величина фрактальной размерности df логарифмически возрастает с увеличением L0 (коэффициент детерминации R2 = 0,9603):
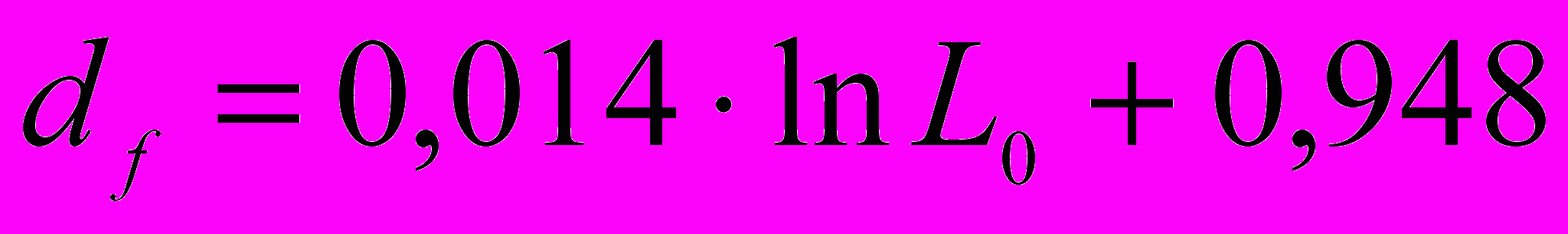 . (9)
. (9)Указанное явление роста величины df с ростом L0 можно объяснить тем, что процесс роста трещины происходит в неоднородной среде, характеризуемой величиной зернистости. Поскольку локальное нарушение развивается, в первую очередь, на контактах зерен, слагающих породу, то, начиная с определенной длины (сравнимой с размером зерна), трещина приобретает большую степень изломанности по сравнению с той, которая определяется только квантовыми скачками распространения.
Распределение углов отклонения трещин от линии действия нагрузки не противоречит нормальному (распределению Гаусса) с параметрами среднего арифметического, моды и медианы, близкими к 450 при величине стандартного отклонения порядка 200. Преобладающие углы α = 450 соответствуют площадкам с наибольшими касательными напряжениями.
Процесс зарождения и развития трещин в горных породах при их нагружении определяется множеством случайных независимых факторов, учесть которые в единой детерминированной модели не представляется возможным. В таком процессе в зависимости от сочетания различных случайных факторов природа сама реализует одну из бесконечного множества вероятных возможностей. Свидетельство тому – разнообразие конфигурации трещин и их распределение в пространстве, зафиксированное нами в опытах, проводившихся в одинаковых условиях. В такой ситуации общепризнанным и эффективным средством научного познания является статистическое имитационное моделирование процесса (метод Монте-Карло). При этом главным условием является адекватность модели реальному процессу трещинообразования в горной породе. Это обеспечивается использованием в компьютерной программе установленных нами фрактальных характеристик реальной трещиноватости пород.
На вход разработанной нами компьютерной имитационной модели подаются ее параметры, зависящие от условий нагружения: распределение трещин по длине или вероятность их нахождения в заданном интервале размеров; распределение трещин в пространстве (в простейшем случае – на плоскости образца); распределение углов отклонения развития трещин по отношению к линии действия нагрузки. На выходе модели имеем заданное число вариантов (розыгрышей) общей картины трещиноватости горной породы с определением координат каждой трещины и ее фрактальной размерности.
Математические процедуры, заложенные в основу имитационной модели, в зависимости от задач исследования позволяют реализовать два различных подхода, идеи которых приведены в работах Р. Кроновера. В первом случае используется рандомизированный алгоритм аффинных преобразований на основе графической реализации «L - системы», состоящей из инициатора, т.е. набора переменных начального состояния фрактала (трещины), и порождающих правил, учитывающих, как должна изменяться трещина от итерации до итерации. В свою очередь, порождающие правила определяются задаваемыми в программе параметрами фрактального броуновского движения.
Второй подход основан на реализации метода «случайных срединных смещений» и применяется при известных (или заданных в ходе моделирования) координатах вершин трещины, ее характерных точек (например, мест перегиба, разветвления и т.п.). Идея метода состоит в вычислении случайного смещения точки, находящейся посередине отрезка прямой, соединяющей две характерные точки (вершины) трещины. Ход реализации метода ясен из рис. 4.
Реализация имитационной программы позволяет получить множество различных вариантов распределения трещин при заданных условиях опыта. Выбор окончательного результата может осуществляться двумя путями – сравнением с реальной, полученной в опыте картиной трещин или усреднением множества реализаций с вычислением статистических характеристик процесса.
а б в
Рис. 4. Реализация метода «случайных срединных смещений» (а – после первого шага;
б – после второго шага; в – после седьмого шага)
Таким образом, методика изучения трещин, включающая люминесцентный микроскопический способ фиксации их координат, вычисление фрактальных характеристик и имитационную компьютерную модель, позволяет оценивать реальную геометрию трещин, степень нарушенности и удельную поверхностную энергию горных пород.
Эффективным средством направленного изменения свойств и состояния горных пород является использование поверхностно-активных веществ (ПАВ), действие которых заключается в адсорбционном понижении поверхностной энергии тел (эффект Ребиндера). Теоретические и экспериментальные исследования (Ю. В. Горюнов, Ф. Д. Овчаренко, Н. В. Перцов, П. А. Ребиндер, Е. Д. Щукин и др.) показывают, что адсорбция активных молекул из раствора происходит на свободных поверхностях, прежде всего на поверхности трещин. Поэтому эффективность действия ПАВ напрямую связана с геометрией трещин, и в то же время поверхностно-активные вещества сами влияют на процесс трещинообразования. Это определяет перспективность применения ПАВ для управления свойствами и состоянием пород в процессах горного производства (А. Д. Алексеев, Г. Я. Воронков, И. И. Круглицкий, Н. Ф. Кусов, О. Г. Латышев, Г. И. Марцинкевич, О. А. Эдельштейн и др.).
Анализ данных исследований показывает, что действие ПАВ приводит к существенному снижению прочности и упругости горных пород, сопровождается их пластифицированием и активизацией реологических процессов. Наши исследования принятых к изучению горных пород показали, что, несмотря на различный темп снижения прочности, в финальной стадии, т. е. при полном насыщении образцов оптимально подобранными активными растворами, относительное снижение прочности пород отличается мало и в среднем составляет около 50 % (в 2 раза). Также действие ПАВ сопровождается снижением в 1,8÷2,3 раза предела упругости и на 25÷43 % модуля упругости. Наблюдается общий рост деформаций при уменьшении их упругой составляющей, т. е. происходит значительное пластифицирование горных пород, когда более половины общей энергоемкости разрушения приходится на необратимые (пластические) изменения в породе. Установлено, что введение в горные породы растворов ПАВ увеличивает интенсивность их пластифицирования до 35 %.
В основе такого изменения свойств лежит увеличение дефектности (трещиноватости) горных пород. Для изучения данного вопроса кафедрой шахтного строительства УГГУ (О. Г. Латышев) в содружестве с кафедрой коллоидной химии Московского государственного университета (Н. И. Иванова) были выполнены комплексные исследования влияния ПАВ на характеристики трещиноватости горных пород. Образцы выдерживались при постоянной одноосной нагрузке 25 МПа в течение 480 часов в воздушно-сухом состоянии и в растворе ПАВ - додецилсульфата натрия R-O-SO3Na (ДС). Нагрузка соответствовала горному давлению на глубине 800÷1000 м для условий СУБРа. Однако на тот период (1988 г.) под микроскопом определялись только линейные размеры трещин. Для изучения трещин с учетом их фрактальных характеристик нами выполнены аналогичные эксперименты с теми же горными породами (андезитовые туфы пироксен-плагиоклазового состава Североуральских месторождений) по разработанной нами методике.
Реализация описанных выше процедур позволила смоделировать фрактальные характеристики трещин в ранее выполненных исследованиях и получить новую информацию. Обобщение полученных результатов (рис. 5,
см. таблицу) позволяет сделать следующие выводы.
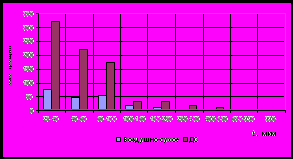
Анализ данных показывает, что даже при малых нагрузках, порядка 20 % от разрушающих, действие поверхностно-активных веществ почти в 4 раза увеличивает концентрацию трещин и их удельную поверхность и почти в 8 раз – степень нарушенности горной породы. Учет фрактальной размерности позволил определить истинную геометрию трещин и их характеристики, которые существенно превышают эти показатели для трещин в случае их линейного представления (см. рис. 5, б).


Интервал трещиноватости, мкм

Интервал трещиноватости , мкм

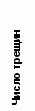
а б
Рис. 5. Результаты изучения трещиноватости (а - распределение трещин по длине;
б - прирост длин трещин для образца, нагружавшегося в растворе ДС)
| Среда | Общее число трещин | Средняя длина трещин lср10-6, м | Концентрация трещин N1010, 1/м3 | Удельная поверхность Sуд, м2/м3 | Нарушенность |
| Воздух | 218 | 78,0 | 2,86 | 234,1 | 0,0056 |
| Раствор ПАВ | 815 | 83,8 | 11,11 | 927,9 | 0,0444 |
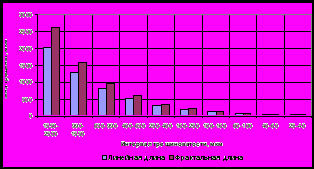
Г
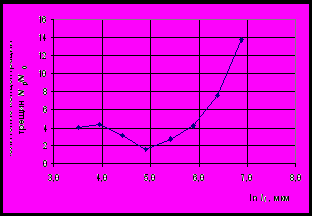
Рис. 6. Относительное приращение
концентрации трещин в ПАВ
рафик изменения концентрации трещин различных размеров при нагружении пород в присутствии активной среды (рис. 6) имеет явно выраженный нелинейный характер. Наличие экстремума на графике свидетельствует о том, что действие ПАВ приводит к развитию ранее существовавших в породе трещин (что сопровождается снижением концентрации трещин средних размеров) и зарождению новых микротрещин (левая ветвь графика).
Концентрация указанных трещин описывается разными законами распределения, что свидетельствует о разном механизме их образования. Трещины больших размеров (более 80 мкм) распределены по логарифмически-линейному закону (коэффициент вариации Квар = 7,0%; критерий Пирсона χн2 = 0,06 > χкр2 = 7,81)
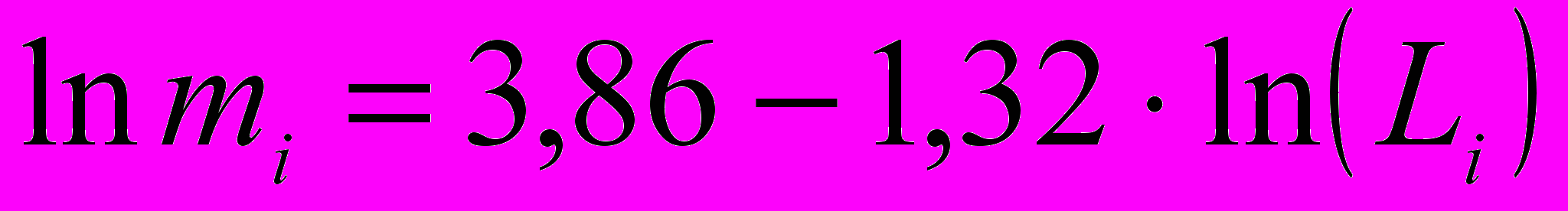 . (10)
. (10)Зарождающиеся микротрещины описываются распределением Вейбулла (Квар = 16,9%; χн2 = 0,0052):
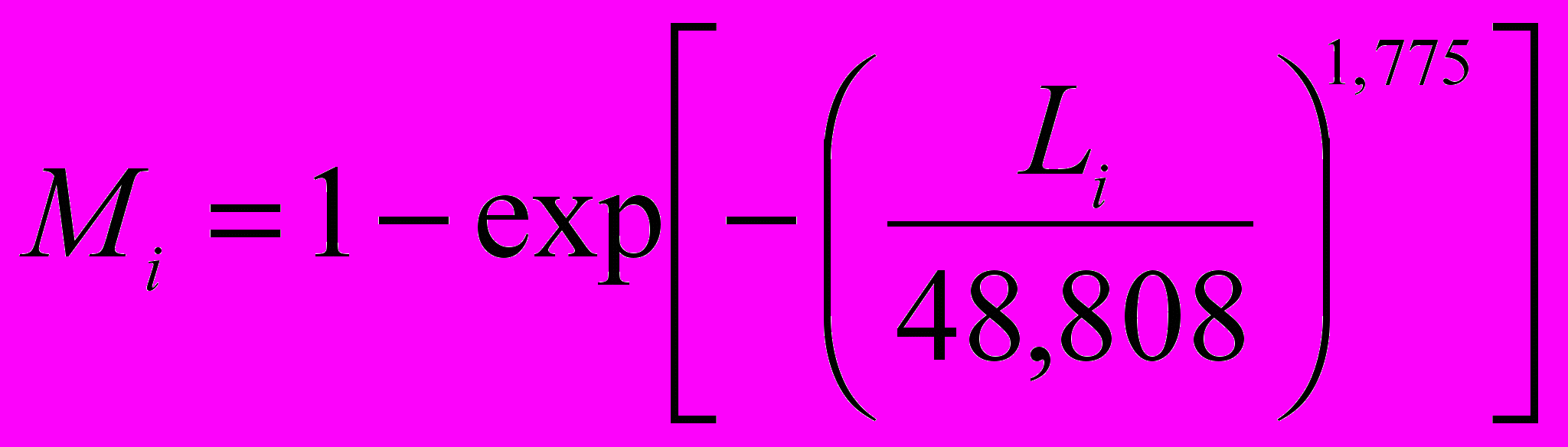 . (11)
. (11)Аналитическая оценка действия ПАВ с позиций теории трещин Гриффитса и кинетической концепции прочности позволила получить соотношения, являющиеся основой прогнозирования свойств и состояния горных пород, их удельной поверхностной энергии и трещиностойкости с учетом фрактальных свойств трещиноватой горной породы как природной самоподобной структуры. В основу этих соотношений положена подстановка в классическое уравнение Гриффитса истинной длины трещины с учетом ее фрактальной размерности
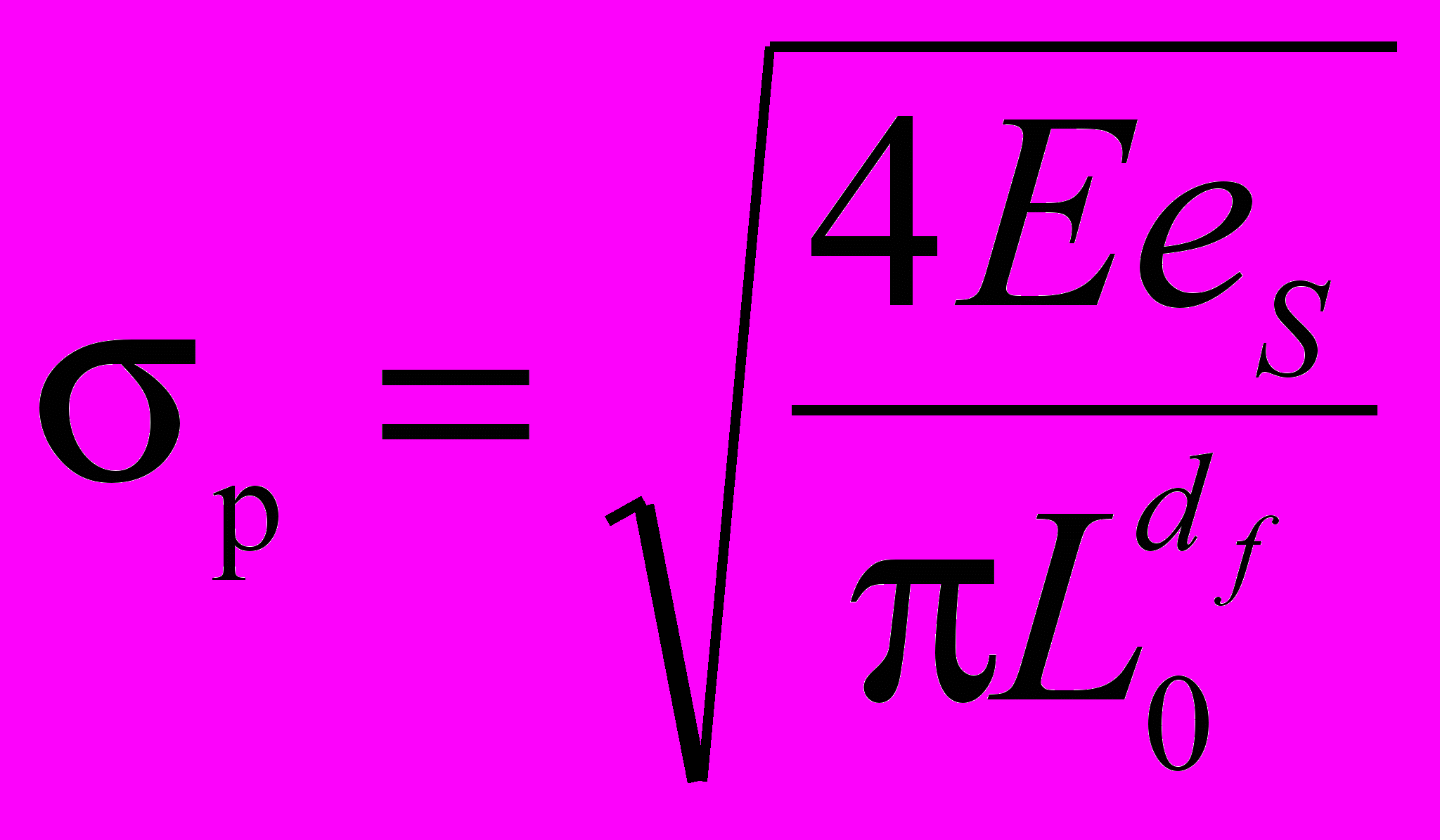 , (12)
, (12)где σр – критическое напряжение на разрыв, Па; Е – модуль упругости, Па;
еs – удельная поверхностная энергия породы, Дж/м2; L0 – расстояние между вершинами трещины, м; df – фрактальная размерность трещины.
Из данного уравнения можно определить совокупную поверхностную энергию горной породы с учетом поправки Орована – удельной энергии пластических деформаций ep:
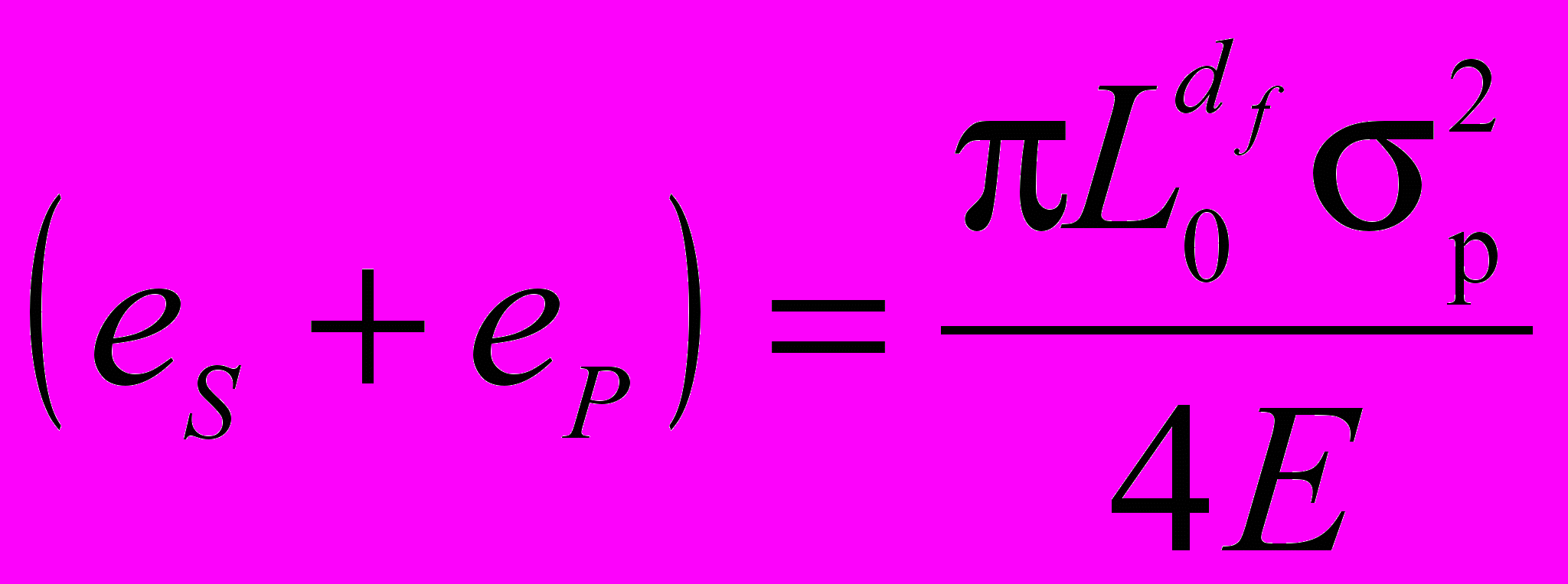 . (13)
. (13)Расчет, выполненный для андезитового туфа, показал, что под воздействием ПАВ совокупная поверхностная энергия породы возрастает с (es+ep) =
= 101,8 Дж/м2 до (es+ep) = 123,1 Дж/м2, т.е. наряду с уменьшением еs происходит увеличение удельной энергии пластических деформаций ep. Приняв, что при разрушении исходного туфа зона пластической деформации в вершине трещины отсутствует (т.е. Е = const), можно определить величину ep при воздействии ПАВ на породу. Для туфа ep = 64,5 Дж/м2.
Ослабление под влиянием активных молекул межатомного взаимодействия приводит к локальным перенапряжениям в горной породе. Это определяет увеличение активационного объема, что в соответствии с кинетической концепцией прочности (С. Н. Журков) сопровождается активизацией процессов движения и размножения дислокаций, их группированием и зарождением микротрещин. Для андезитового туфа концентрация микротрещин под действием ПАВ увеличивается в 3,98 раза по сравнению с исходной породой, следовательно, в такой же пропорции увеличивается активационный объем.
При динамическом нагружении горных пород имеющиеся в породе дефекты структуры (макро- и микротрещины) не успевают включиться в процесс деформирования, что приводит к возрастанию динамической прочности и упругости пород. Полученные экспериментальные соотношения позволяют прогнозировать динамические характеристики горных пород и являются основой методики определения разрушаемости пород ударом и взрывом.
Таким образом, развитие под действием ПАВ существующих в горной породе трещин и зарождение новых микротрещин описываются разными по характеру распределениями, имеют различную природу и определяются уравнениями теории Гриффитса и кинетической концепции прочности, параметры которых учитывают фрактальную размерность трещин.
Полученные результаты позволяют прогнозировать эффективность использования ПАВ в процессах разрушения горных пород. Анализ технологии добычи каменных блоков с помощью невзрывчатых разрушающих составов (НРС) показывает (Г. Д. Першин, Е. Г. Пшеничная), что эффективность отбойки определяется двумя факторами – образованием зародышевой трещины на стенке шпура и ее прорастанием до соседнего шпура в ряду. Использование ПАВ активизирует каждую из сторон процесса. Установлено, что безотносительно к условиям реального массива и применяемого НРС межшпуровое расстояние в строчке шпуров обратно пропорционально прочности пород при растяжении Lшп ~ 1/σр.
Расчеты, выполненные по результатам изучения фрактальных характеристик трещиноватости гранита Мансуровского месторождения, показывают, что применение поверхностно-активных веществ в технологии отбойки пород НРС позволяет на 16 % увеличить межшпуровое расстояние и, следовательно, в такой же пропорции уменьшить число шпуров.
На кафедре шахтного строительства УГГУ (В. А. Безматерных,
Г. П. Берсенев, В. Г. Симанов) разработана и апробирована методика расчета параметров БВР, основанная на оценке концентрации активируемых нарушений, которая, в свою очередь, зависит от характеристик исходной трещиноватости горных пород. Согласно данной методике, л.н.с. W и расстояние между зарядами в ряду а зависят от линейной плотности дефектов γ0, параметра λ функции надежности, массовой скорости и0 на границе зарядной полости, скорости поперечной волны Сs в породе, требуемого максимального размера куска Rк, радиуса заряда r0 и прочности породы на растяжение σр и сжатие σсж. Основные расчетные соотношения:
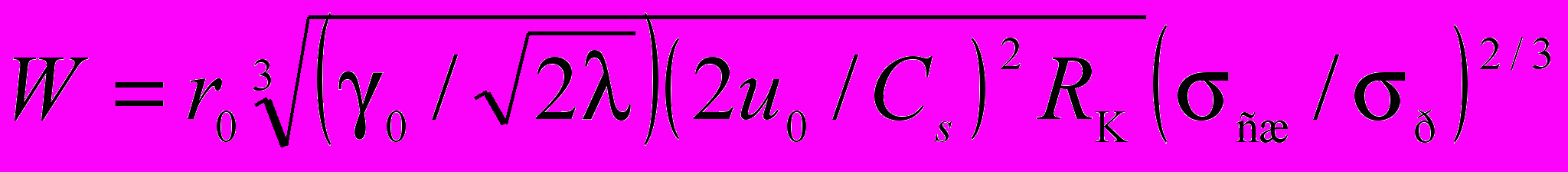 ;
; 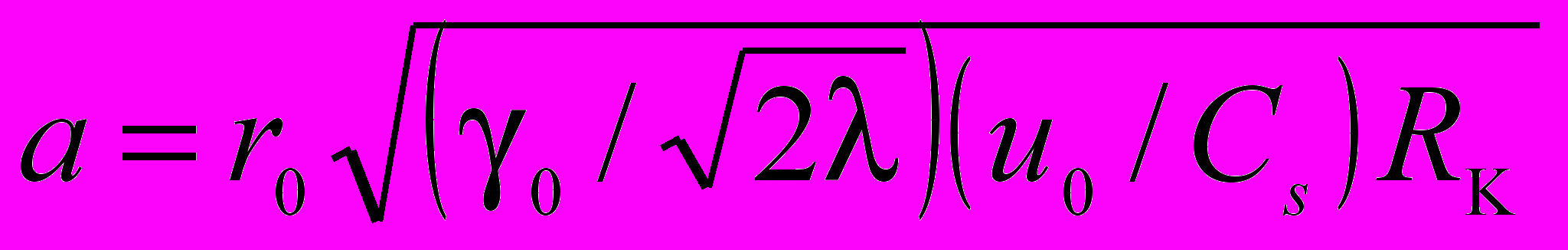 ;
; Наряду с этим линейная концентрация активируемых взрывом нарушений γl зависит также от плотности ВВ ρВВ, скорости детонации D, плотности породы ρ, скорости продольной волны См в породе и линейного размера разрушаемой породы R. Для плоского и цилиндрического заряда
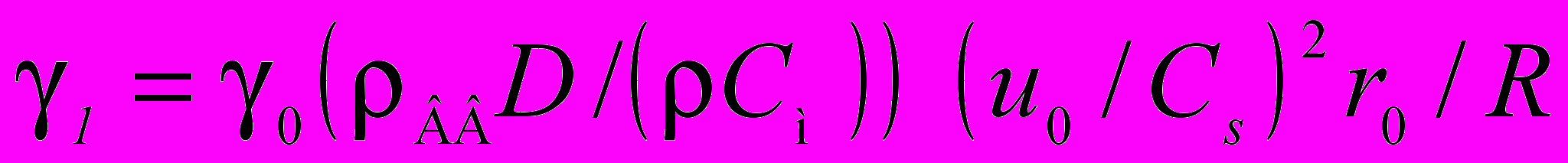 ;
; 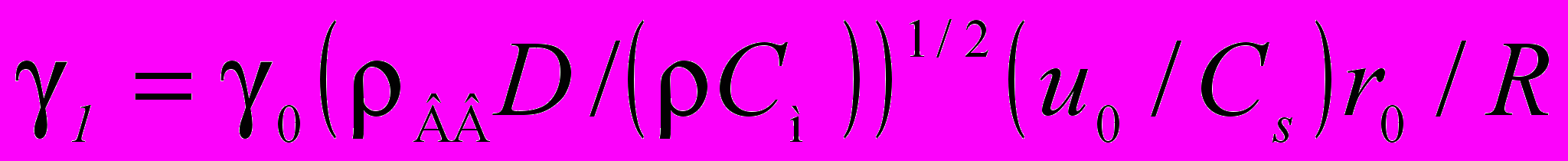 .
. Значения величин γ0, γL для различных пород определяются путем опытного взрывания, что требует наличия взрывной камеры и связано со значительной трудоемкостью определений. На основе предложенной ранее и апробированной процедуры моделирования результатов взрыва на ударном копре (О. Г. Латышев, А. С. Жилин) нами разработана методика определения концентрации активируемых нарушений путем анализа гранулометрического состава продуктов дробления. Получено уравнение, связывающее число нарушений с энергией удара (индекс корреляции R2 = 0,933):
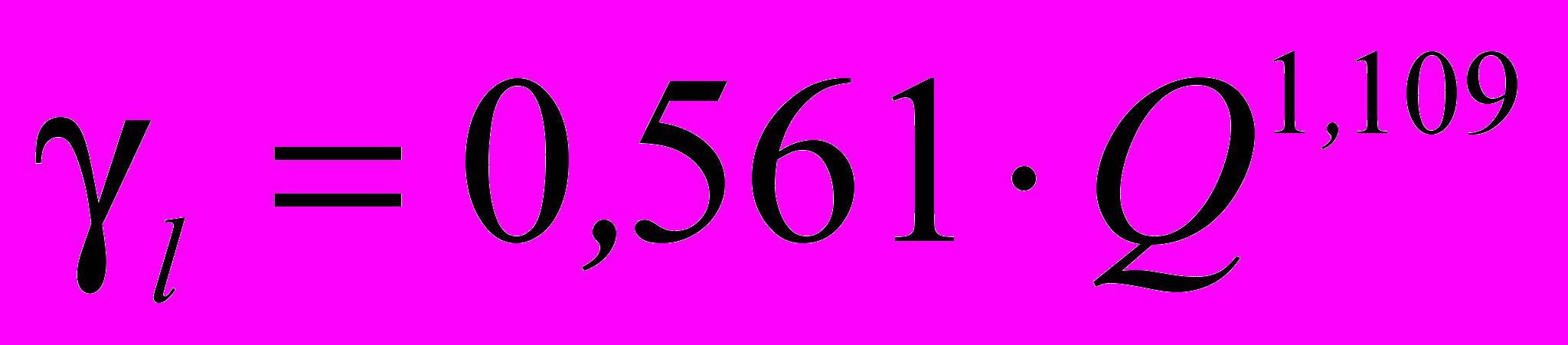 , (14)
, (14)где γL – линейная концентрация активируемых нарушений.
Экспериментальные исследования исходных горных пород Североуральских бокситовых месторождений и обработанных растворами ПАВ показали хорошее соответствие ранее полученным для этих пород в опытных взрывах значениям концентраций активируемых нарушений. В частности, было установлено, что при обработке известняков СУБРа 0,1 %-м раствором MgCl2 плотность активируемых нарушений увеличилась с γl = 191 1/м до γl = = 269 1/м, т.е. в 1,41 раза.
Прогнозирование концентрации активируемых нарушений позволяет оценивать качество дробления горных пород взрывом с заданной степенью надежности (Г. П. Берсенев). Расчеты, произведенные для эффузивов Североуральских бокситовых месторождений, показывают, что использование поверхностно-активных веществ приводит к существенному возрастанию ЛНС при том же уровне надежности и качестве дробления горных пород. Так, при взрывании шпурами л.н.с. изменяется от W = 1,06 м (для исходной породы) до W = 1,29 м (для породы, обработанной ПАВ). При взрывании скважинами данные величины составляют соответственно W = 5,58 м и W = 6,21 м.
Характеристики трещиноватых горных пород и их изменение при их динамическом разрушении имеют вероятностную природу. Ввиду того, что число трещин в горной породе велико и они распределены независимо и случайно, плотность распределения трещин по размерам можно описать уравнением Коши. Тогда вероятность разрушения горной породы при данном напряжении составит
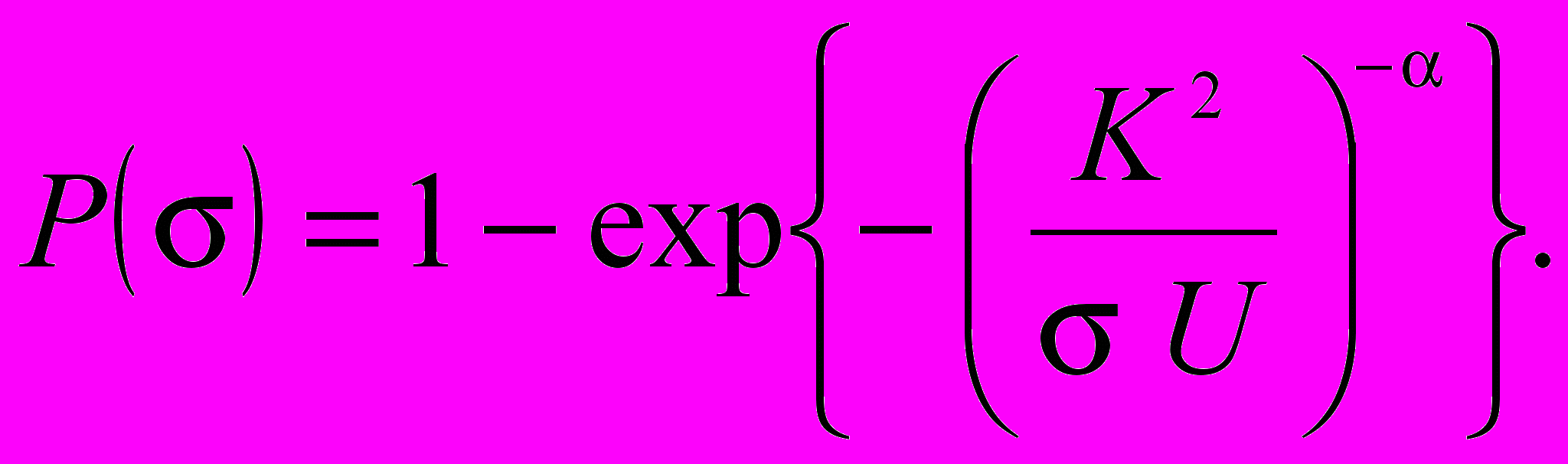 (15)
(15)Параметры данного уравнения U и α были установлены экспериментально для исходной породы и после обработки ПАВ (для исходных пород, нагружавшихся в воздушной среде, параметры распределения: 1/U = 1,1∙10-3 мкм, α = 1,83; для пород, нагружавшихся в растворе ДС: 1/U = 0,81∙10-3 мкм, α = 1,96). При этом показатель К является константой, характеризующей модуль упругости горной породы и величину ее удельной поверхностной энергии.
Расчет для пород, нагружавшихся в воздушно-сухом состоянии и обработанных в ПАВ, для напряжений в диапазоне 0÷1500 МПа дал следующие результаты (рис. 7).
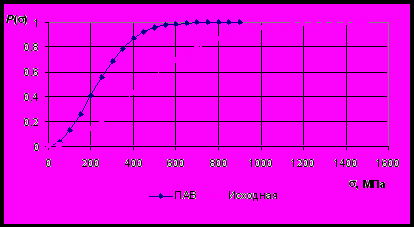
Рис. 7. Вероятность разрушения горной породы при данном напряжении
Анализ полученных данных свидетельствует о росте вероятности разрушения породы при заданном напряжении, если порода предварительно обработана активным раствором.
Таким образом, методика оценки концентрации активируемых нарушений в скальных породах позволяет оценить эффективность использования ПАВ при динамическом разрушении пород. Установленные параметры экспоненциального распределения фрактальных размеров трещин (уравнения Коши) используются для прогнозирования вероятности разрушения пород при различном уровне напряжений.
Одной из основных особенностей эффекта Ребиндера является избирательность действия ПАВ. В этой связи важнейшей задачей является выбор для конкретных условий применения эффективных растворов ПАВ в их оптимальной концентрации. В качестве экспрессной оценки эффективности ПАВ используется величина контактной прочности горных пород. Для более точной оценки нами предлагается новый критерий, основанный на оценке удельной поверхности трещин, образующихся под действием ПАВ, что напрямую соответствует физико-химическому механизму эффекта Ребиндера.
Для реализации указанных выше эффектов действия ПАВ необходимо обеспечить доставку активных растворов в разрушаемые горные породы и контроль данного процесса. С этой целью на кафедре шахтного строительства УГГУ (О. Г. Латышев, В. В. Сынбулатов) изучена кинетика насыщения горных пород растворами ПАВ, проработана технология и методы контроля процесса. Доставка активных растворов в породный массив возможна и без предварительного их нагнетания, что связано с остановкой забоя. Установлено, что уже в ходе бурения шпуров и скважин с добавкой в промывочную жидкость нужного количества поверхностно-активных веществ породный массив насыщается активным раствором на 30÷70 % в зависимости от характера пород и технологии бурения.
ЗАКЛЮЧЕНИЕ
В диссертации на основании выполненных теоретических исследований и лабораторных испытаний дается решение научной задачи прогнозирования эффективности направленного изменения свойств и состояния горных пород поверхностно-активными веществами. Данная задача решена на основе установленных закономерностей изменения фрактальных характеристик зарождения и развития трещин и имеет существенное значение для теории процессов разрушения горных пород.
Основные научные результаты, выводы и рекомендации работы заключаются в следующем.
1. Усовершенствован люминесцентный микроскопический метод дефектоскопии, адаптированный к особенностям горных пород, создана и апробирована лабораторная установка, подобран оптимальный состав люминофора и разработана процедура фотофиксации трещин с компьютерной программой определения их координат.
2. Разработанные алгоритмы и компьютерные программы позволяют надежно определять реальную геометрию трещин путем оценки их фрактальной размерности. Определение корреляционной размерности трещиноватой горной породы дает комплексную характеристику ее нарушенности. Совокупность проведенных исследований позволила установить зависимость фрактальной размерности от линейной длины трещин, параметры нормального распределения углов ориентировки трещин по отношению к линии действия нагрузки и характеристики пространственного расположения трещин.
3. Установленные закономерности являются базой имитационного моделирования трещинообразования в горных породах, в основу которого положены методы срединного смещения и фрактального броуновского движения. Реализация модели позволяет получать комплексную информацию о динамике развития трещин.
4. Адсорбция активных молекул на поверхности трещин приводит к понижению поверхностной энергии горных пород, что сопровождается общим ростом трещиноватости пород под нагрузкой: концентрации трещин – в 3,88 раза; их удельной поверхности – в 3,96 раза ; степени нарушенности породы – в 7,93 раза. Все это приводит к изменению их свойств и состояния: прочность изученных пород снижается на 20÷80 %; модуль упругости – в среднем в 1,3÷1,6 раза.
5. Увеличение общей трещиноватости пород, насыщенных раствором ПАВ, обусловлено двумя факторами – ростом уже существующих трещин и зарождением новых микротрещин. Концентрация указанных трещин описывается разными законами распределения (логарифмически линейным и распределением Вейбулла), что свидетельствует о различии в физических механизмах данных процессах.
6. Аналитическая оценка действия ПАВ с позиций теории трещин Гриффитса и кинетической концепции прочности позволила получить соотношения, являющиеся основой прогнозирования свойств и состояния горных пород, их удельной поверхностной энергии и трещиностойкости с учетом фрактальных свойств трещиноватой горной породы как природной самоподобной структуры.
7. Технология добычи каменных блоков с помощью невзрывчатых разрушающих составов (НРС) определяется двумя факторами – образованием зародышевой трещины на стенке шпура и ее прорастанием до соседнего шпура в ряду. Использование ПАВ сопровождается активизацией каждого из сторон процесса. Расчеты показывают, что применение поверхностно-активных веществ в технологии отбойки пород НРС позволяет на 16 % увеличить межшпуровое расстояние и, следовательно, в такой же пропорции уменьшить число шпуров.
8. Методика оценки концентрации активируемых нарушений в скальных породах позволяет оценить эффективность использования поверхностно-активных веществ при динамическом разрушении пород. Установленные параметры экспоненциального распределения фрактальных размеров трещин (уравнения Коши) используются для прогнозирования вероятности разрушения горных пород при различных уровнях напряжений.
9. Обоснованные в работе методики, теоретические и практические результаты используются в учебном процессе. Экологическая проработка и полученные рекомендации переданы лаборатории разрушения горных пород взрывом Института горного дела УрО РАН и ГОУ ВПО «Магнитогорскому государственному техническому университету».
Основные положения диссертации опубликованы в следующих работах:
В монографии:
1. Теоретические основы прогноза и управления свойствами геологической среды при подземных техногенных воздействиях / Латышев О. Г. Корнилков М. В., Осипов И. С., Сынбулатов В. В.; под ред. О. Г. Латышева. – Екатеринбург: Изд-во УГГУ, 2007. – 216 с.
В ведущих рецензируемых изданиях, определенных ВАК России:
2. Выбор поверхностно-активной среды для управления свойствами пород в горной технологии / Латышев О. Г., А. С. Жилин, И. С. Осипов, В. В. Сынбулатов // Изв. вузов. Горный журнал. –2004. -№ 6. – С. 117-121.
3. Латышев О. Г. К обоснованию методики определения характеристик дробимости горных пород ударом и взрывом / О. Г. Латышев, А. С. Жилин, И. С. Осипов // Известия вузов. Горный журнал. – 2005. – №1. – С. 103-107.
4. Осипов И. С. К оценке трещиноватости горных пород как критерия их дробимости / И. С. Осипов, А. С. Жилин, О. Г. Латышев // Известия вузов. Горный журнал. – 2005. – №4. – С. 96-101.
5. Латышев О. Г. Кинетика насыщения породного массива растворами поверхностно-активных веществ при бурении шпуров и скважин / О. Г. Латышев, В. В. Сынбулатов, И. С. Осипов // Известия вузов. Горный журнал. – 2008. – №3. – С. 123-129.
В научных сборниках, журналах и материалах конференций:
6. Анохина О. О. Взаимосвязь статического и динамического модулей упругости горных пород Гайского месторождения / О. О. Анохина, И. С. Осипов // Известия УГГГА. Специальный выпуск. Материалы Уральской горнопромышленной декады, 10 20 апреля 2003 г. – Екатеринбург: Изд-во УГГГА, 2003. – С. 186-189.
7. Латышев О. Г. Пути повышения качества дробления горных пород ударом и взрывом / О. Г. Латышев, А. С. Жилин, И. С. Осипов // Известия УГГУ. Выпуск 21. Серия: Горное дело. – 2005. – С. 69-72.
8. Латышев О. Г. Управление процессом зарождения и развития трещин при добыче природного камня невзрывчатыми разрушающими веществами / О. Г. Латышев, И. С. Осипов // Добыча, обработка и применение природного камня: сб. науч. тр. – Магнитогорск, 2005. – С. 81-88.
9. Осипов И. С. К методике оценки активируемых нарушений при взрывном дроблении горных пород // Полезные ископаемые России и их освоение / Санкт-Петербургский государственный горный институт (технический университет). – СПб, 2006. – 356 с. (Записки Горного института. – Т.167. Ч.2). – С. 113-115.
10. Осипов И. С. К методике оценки трещиноватости горной породы люминесцентным способом // Известия УГГУ. Материалы Уральской горнопромышленной декады, 3 13 апреля 2006 г. – Екатеринбург, 2006. – С. 24-25.
11. Осипов И. С. Анализ методов оценки трещиноватости горных пород // Проектирование, строительство и эксплуатация комплексов подземных сооружений: Труды II Международной конф., г. Екатеринбург, 22-24 мая 2007 г. – Екатеринбург: Изд-во УГГУ, 2007. – С. 170-172.
12. Осипов И.С. Исследование характеристик распределения трещин в образцах горных пород способом люминесцентной дефектоскопии // Добыча, обработка и применение природного камня: сб. науч. тр. – Магнитогорск: МГТУ, 2008. – С. 228-232.
13. Латышев О. Г. Методика изучения фрактальных характеристик трещиноватости горных пород / О. Г. Латышев, В. В. Сынбулатов, И. С. Осипов // Добыча, обработка и применение природного камня: сб. науч. тр. – Магнитогорск: МГТУ, 2008. – С. 217-227.
14. Осипов И. С. Определение фрактальных размерностей трещин применительно к горным породам Североуральских бокситовых месторождений // Известия УГГУ. Материалы Уральской горнопромышленной декады, 14 23 апреля 2008 г. – Екатеринбург, 2008 – С. 109-110.

| Подписано в печать 15.10.2008 Бумага писчая Печ. л. 1,0. Тираж 100 экз. Заказ | Формат 60х80 1/16 Печать на ризографе |
Отпечатано в лаборатории множительной техники УГГУ
620144, г. Екатеринбург, ул. Куйбышева, 30
Уральский государственный горный университет
