«исследование зависимости периода и частоты механических колебаний от параметров колебательной системы»
| Вид материала | Исследование |
- Лабораторная работа №21, 85.92kb.
- Исследование устройства пространства параметров в зависимости от коэффициентов связи, 225.9kb.
- 1 исследование затухающих колебаний, 65.22kb.
- Колебания и волны (3 часа), 13.22kb.
- Алгоритмы и устройства обнаружения и оценки параметров сигналов сО скачкообразным изменением, 259.41kb.
- Решение дифференциального уравнения затухающих колебаний, график затухающих колебаний,, 68.04kb.
- Рассматривается напряженно-деформированное состояние в кварцекристаллическом чувствительном, 9.28kb.
- Оценка влияния переменности инерционных характеристик силового агрегата на параметры, 234.19kb.
- Экзаменационные вопросы по дисциплине «Акушерство», 24.86kb.
- Курсовая работа по электронике «lc -генератор с обратной связью», 106.97kb.
Муниципальное образовательное учреждение
«МОРОЗОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
РЕФЕРАТ ПО ФИЗИКЕ
на тему
«ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА И ЧАСТОТЫ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ ОТ ПАРАМЕТРОВ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ»
(ГОСУДАРСТВЕННАЯ (ИТОГОВАЯ) АТТЕСТАЦИЯ)
Ученицы 9 класса
КОШЕЛЬ АНАСТАСИИ ЮРЬЕВНЫ
Руководитель Н.А. Баландина
С. Морозово, 2010 год
ОГЛАВЛЕНИЕ
- Введение. 3 стр.
- Основная часть. 4 стр.
1. Теоретическое обоснование работы. 4 стр.
- Исследование зависимости периода и частоты
колебаний математического маятника от его параметров. 8 стр.
3. Исследование зависимости периода и частоты
колебаний пружинного маятника от его параметров. 9 стр.
4. Исследование зависимости периода и частоты
колебаний физического маятника от его параметров. 10 стр.
5. Исследование зависимости периода и частоты
колебаний оборотного маятника от его параметров. 11 стр.
6. Некоторые применения колебательных систем. 13 стр.
III. Заключение. 16 стр.
IV. Литература. 17 стр.
V. Приложения. 18 стр.
I. ВВЕДЕНИЕ
Я выбрала данную тему для исследования, так как в школьном курсе физики она рассматривается довольно кратко, а встречаются колебания в жизни широко. Мне было интересно познакомиться не только с теми колебательными системами, которые рассмотрены в школьном учебнике, но и с другими. Кроме того, эксперимент по данной теме не предполагает каких-то сложных приборов, колебательные системы можно изготовить самостоятельно.
Предмет исследования – зависимость периода и частоты колебаний от параметров колебательной системы.
Объект исследования – различные колебательные системы: математический маятник, пружинный маятник, физический маятник, оборотный маятник.
Цели исследования:
1) Подготовка к государственной итоговой аттестации за курс основной школы.
2) Углубление и расширение знаний по теме «Механические колебания».
Задачи исследования:
1) Определить период и частоту колебаний пружинного, математического, физического, оборотного маятников.
2) Выяснить зависимость периода и частоты колебаний указанных колебательных систем от их характеристик.
3) Совершенствовать навыки физического эксперимента.
4) Расширить знания о применении колебательных систем.
II. ОСНОВНАЯ ЧАСТЬ
1. Теоретическое обоснование работы.
Механические колебания – это периодически повторяющиеся движения тела в двух противоположных направлениях около положения равновесия.
Виды колебаний
Свободные колебания
Вынужденные колебания
Авто-колебания
Свободные колебания – колебания, происходящие под действием внутренних сил. Для того чтобы в системе могли возникнуть свободные колебания, трение в системе должно быть мало.
Вынужденные колебания – колебания, происходящие под действием внешних сил.
Система, в которой генерируются незатухающие колебания за счет поступления энергии от источника внутри системы, называется автоколебательной. Незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил, называются автоколебаниями.
Колебательная система – система тел, которая способна совершать свободные колебания.
Примеры колебательных систем: математический маятник, пружинный маятник, физический маятник, оборотный маятник.
Математический маятник – это материальная точка, подвешенная на длинной, невесомой, нерастяжимой нити. В реальных условиях математическим маятником можно считать шар, подвешенный на нити при условии, что размеры шара много меньше длины нити, масса нити много меньше массы шара, растяжение нити шаром настолько мало, что им можно пренебречь (рис. 1).
П
араметрами математического маятника можно считать длину нити маятника (L, м) и массу шарика (m, кг).Рис. 1
С
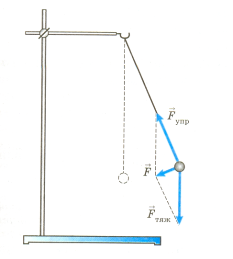илой, возвращающей математический маятник к положению равновесия, является равнодействующая сил тяжести и упругости нити (рис. 2). Под действием этих сил шарик движется к положению равновесия, при этом равнодействующая уменьшается, а скорость шарика увеличивается. В положении равновесия равнодействующая сил тяжести и упругости нити равна нулю, скорость шарика достигает максимального значения, поэтому он по инерции движется дальше. Снова появляется возвращающая сила, которая будет направлена к Рис. 2
положению равновесия, скорость шарика уменьшается до нуля. Затем все повторяется.
Пружинный маятник – груз, подвешенный на пружине (рис. 3). Параметрами пружинного маятника будем считать жесткость пружины (k, Н/м) и массу груза (m, кг).
Рис. 3
Возвращающей силой в пружинном маятнике является равнодействующая силы тяжести и силы упругости пружины.
Ф
изическим маятником называется тело произвольной формы, которое может вращаться вокруг горизонтальной оси, не проходящей через центр тяжести тела. Маятник находится в устойчивом равновесии, если его центр тяжести находится ниже оси вращения. Выведенный из положения равновесия маятник совершает колебания под действием момента силы тяжести. В данной работе в качестве физического маятника использовался деревянный параллелепипед, в котором проделано отверстие для горизонтальной оси (рис. 4).Рис. 4
Параметры физического маятника – его масса (m, кг) и расстояние от оси вращения до центра тяжести (l, м). Центром тяжести называется точка, к которой приложена сила тяжести, действующая на тело (рис. 5)
N О – ось вращения физического маятника.
S – центр тяжестиO
O 
- сила реакции подвеса
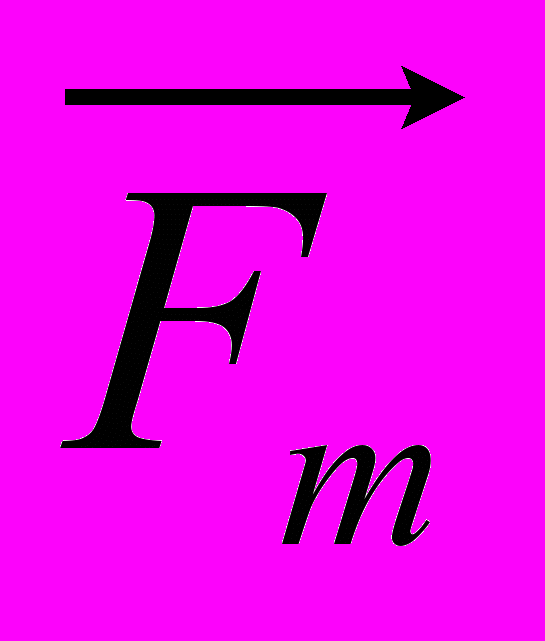- сила тяжестиS
Рис. 5
Fт
О
боротный маятник является частным случаем физического маятника и состоит из стального стержня, на котором укреплены два шарика. Стержень подвешен на вертикальной проволоке (рис. 6). Параметры оборотного маятника – длина подвеса (L, м), длина горизонтального стержня (l, м), масса шаров на горизонтальном стержне (m, кг).
Рис. 6
Колебания, происходящие по закону синуса или косинуса, называются гармоническими. Гармонические колебания описываются следующими характеристиками: период колебаний, частота колебаний, амплитуда колебаний, фаза колебаний.
Амплитуда колебаний – максимальное отклонение колеблющегося тела от положения равновесия. Амплитуда обозначается буквой А, измеряется в метрах (м).
Период колебаний – время, в течение которого тело совершает одно полное колебание. Период обозначается буквой Т, измеряется в секундах (с).
Частота колебаний – число колебаний, совершенных телом за 1 секунду. Частота обозначается буквой ν, измеряется в герцах (Гц). 1 герц – частота колебаний, при которой за 1 с тело совершает одно полное колебание. Период и частота колебаний – величины, обратные друг другу, то есть Т=
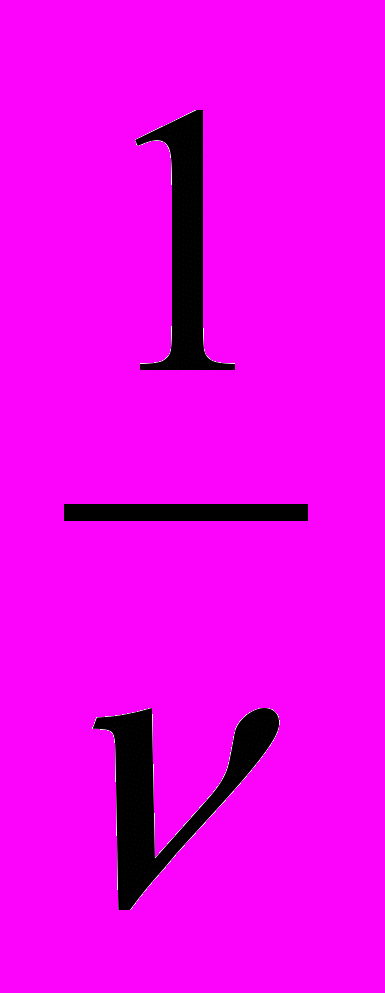или ν=
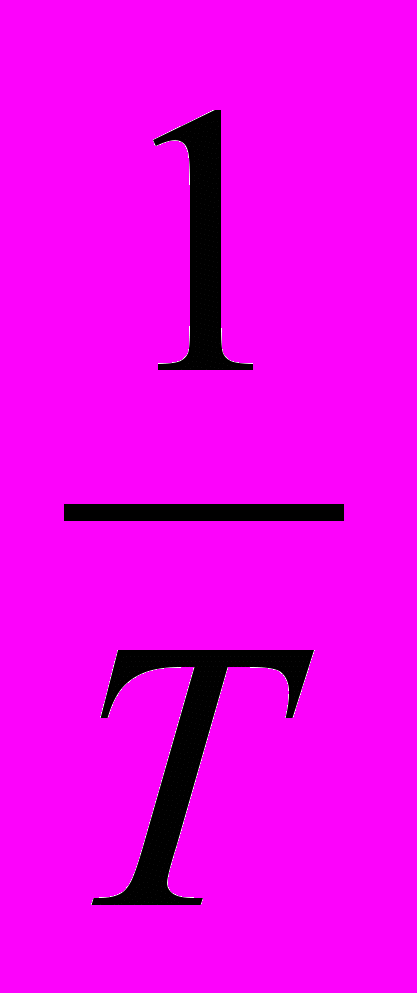.Т
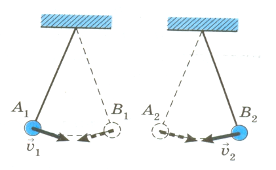еперь рассмотрим колебания двух одинаковых маятников (рис. 7). В один и тот же момент времени левый маятник из крайнего левого положения начинает движение вправо, а правый маятник из крайнего правого положения движется влево. Оба маятника колеблются с одной и той же частотой и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости маятников направлены в противоположные стороны, это значит, что они колеблются в разных (противоположных) фазах. Рис. 7
Гармонические колебания описываются следующими уравнениями:
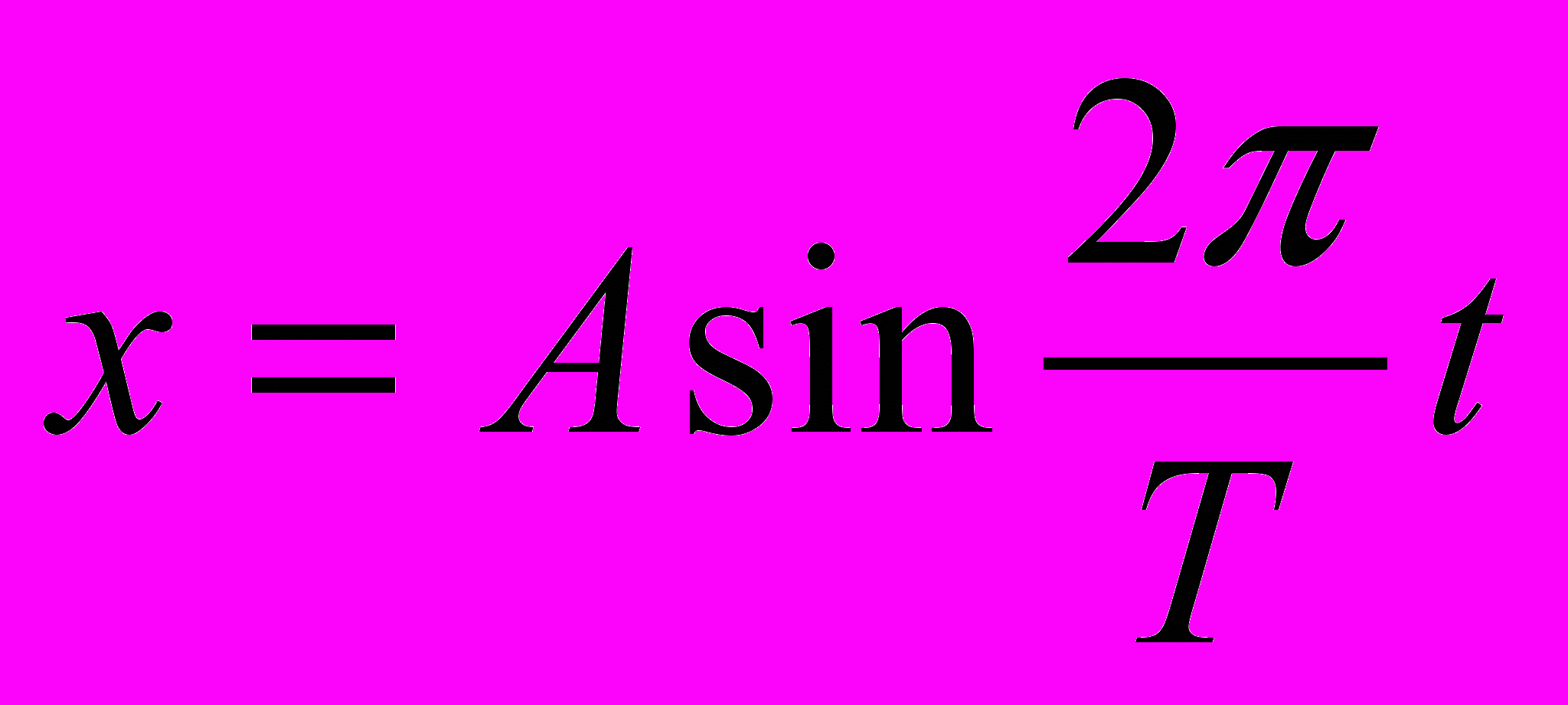или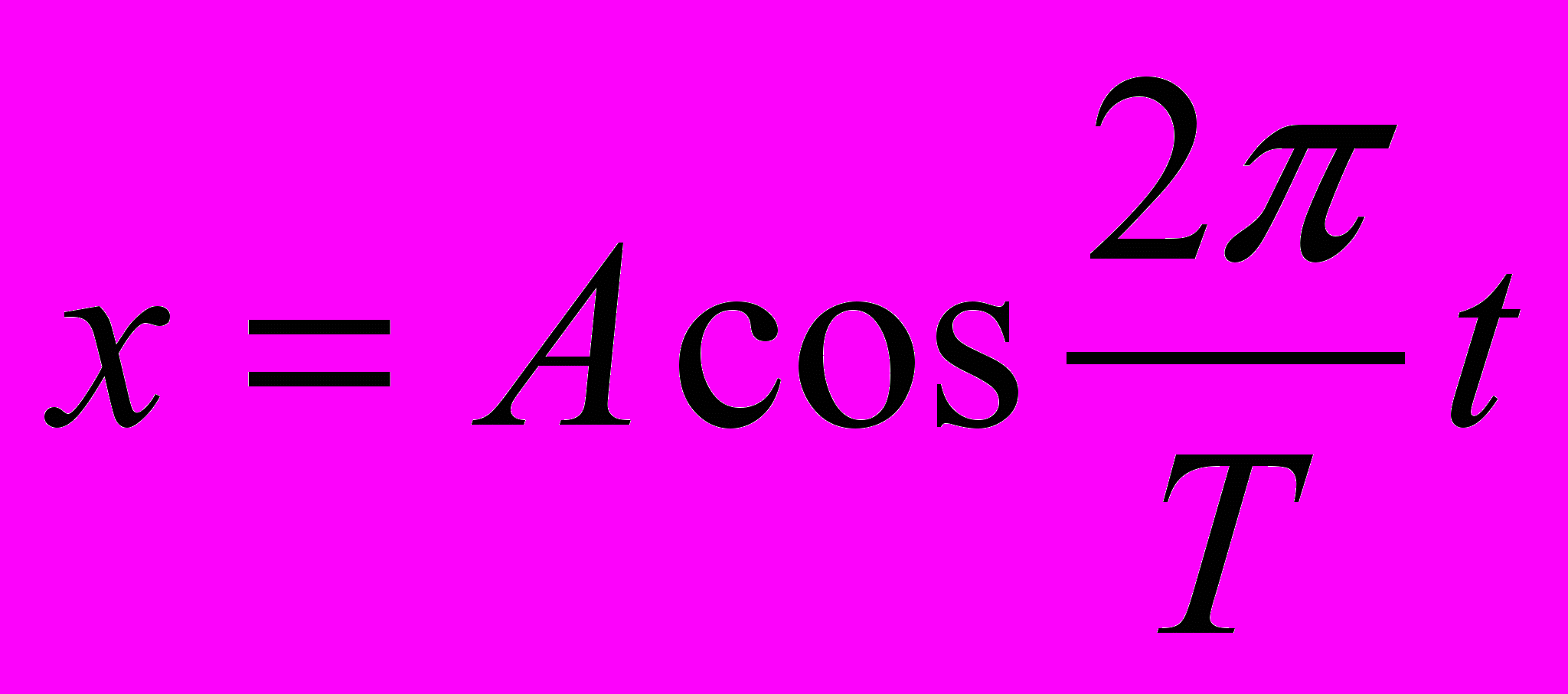 
.При малых амплитудах колебания всех перечисленных выше колебательных систем можно считать гармоническими.
- Исследование зависимости периода и частоты колебаний
математического маятника от его параметров.
Оборудование: штатив с муфтой и лапкой, шарик на нити длиной около 1,3 м, лента измерительная, секундомер, груз массой 100 г, весы с разновесами.
Гипотеза № 1 - период и частота колебаний математического маятника зависят от длины нити: чем больше длина нити маятника, тем больше период колебаний и меньше частота колебаний.
N – количество колебаний, сделанных маятником за время t.
Т=
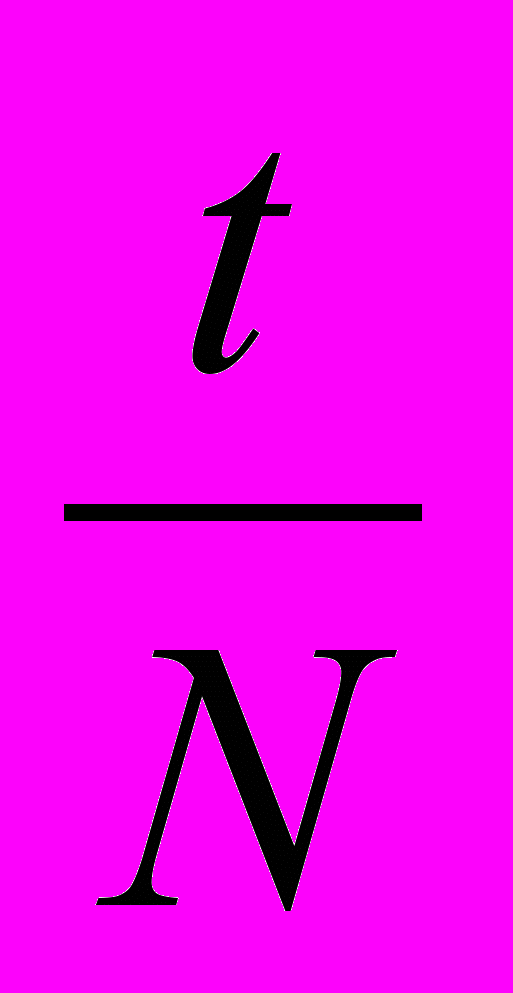, ν =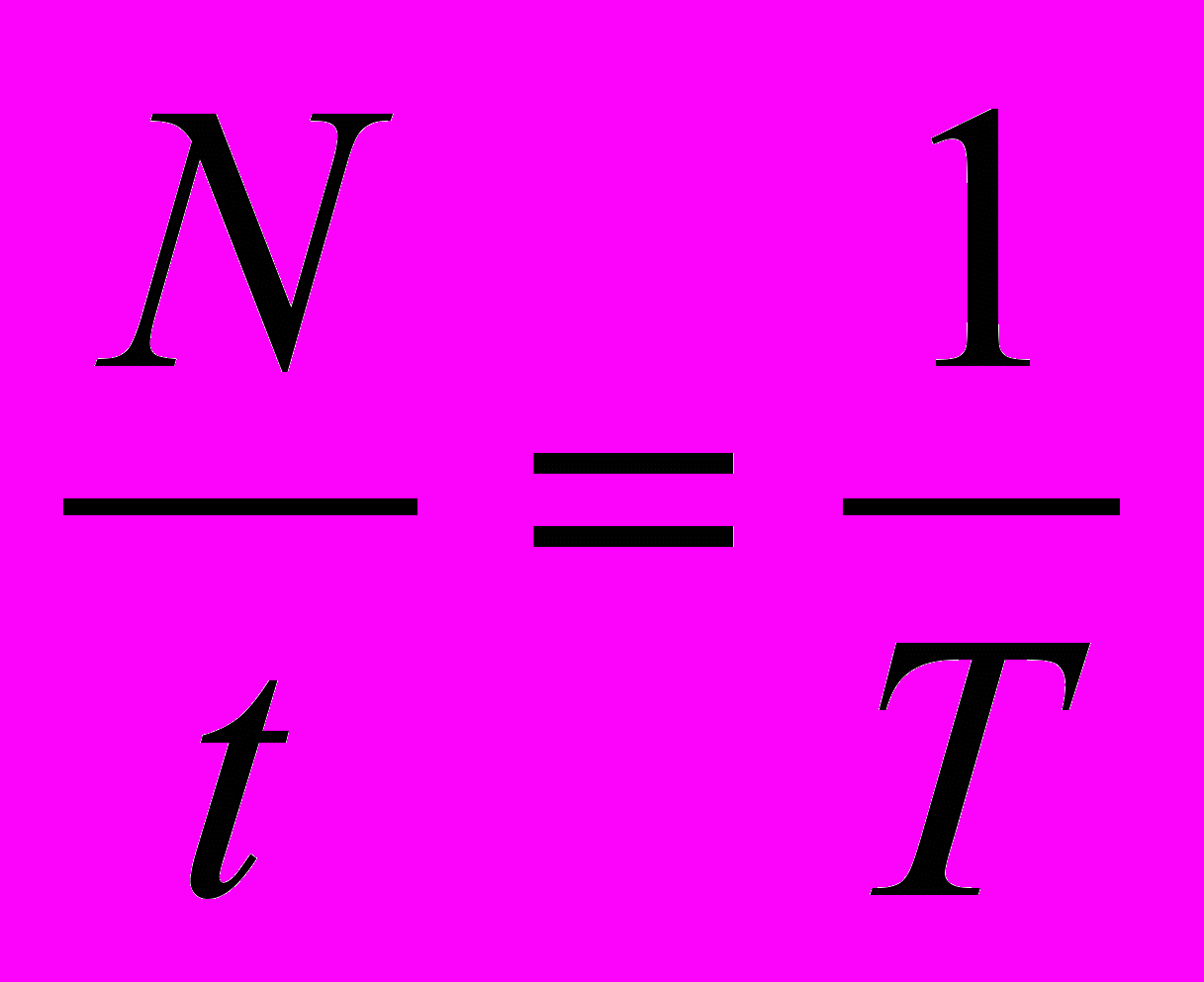
Таблица 1
| № опыта | 1 | 2 | 3 | 4 |
| L, м | 0,2 | 0,45 | 0,8 | 1,25 |
| N | 30 | 30 | 30 | 30 |
| t, с | 27,43 | 40,38 | 54,13 | 67,26 |
| T, с | 0,91 | 1,35 | 1,8 | 2,24 |
| ν, Гц | 1,1 | 0,74 | 0,56 | 0,45 |
Вывод: при увеличении длины нити математического маятника период его колебаний увеличивается, а частота колебаний уменьшается (гипотеза № 1 подтвердилась).
Сравним следующие отношения:
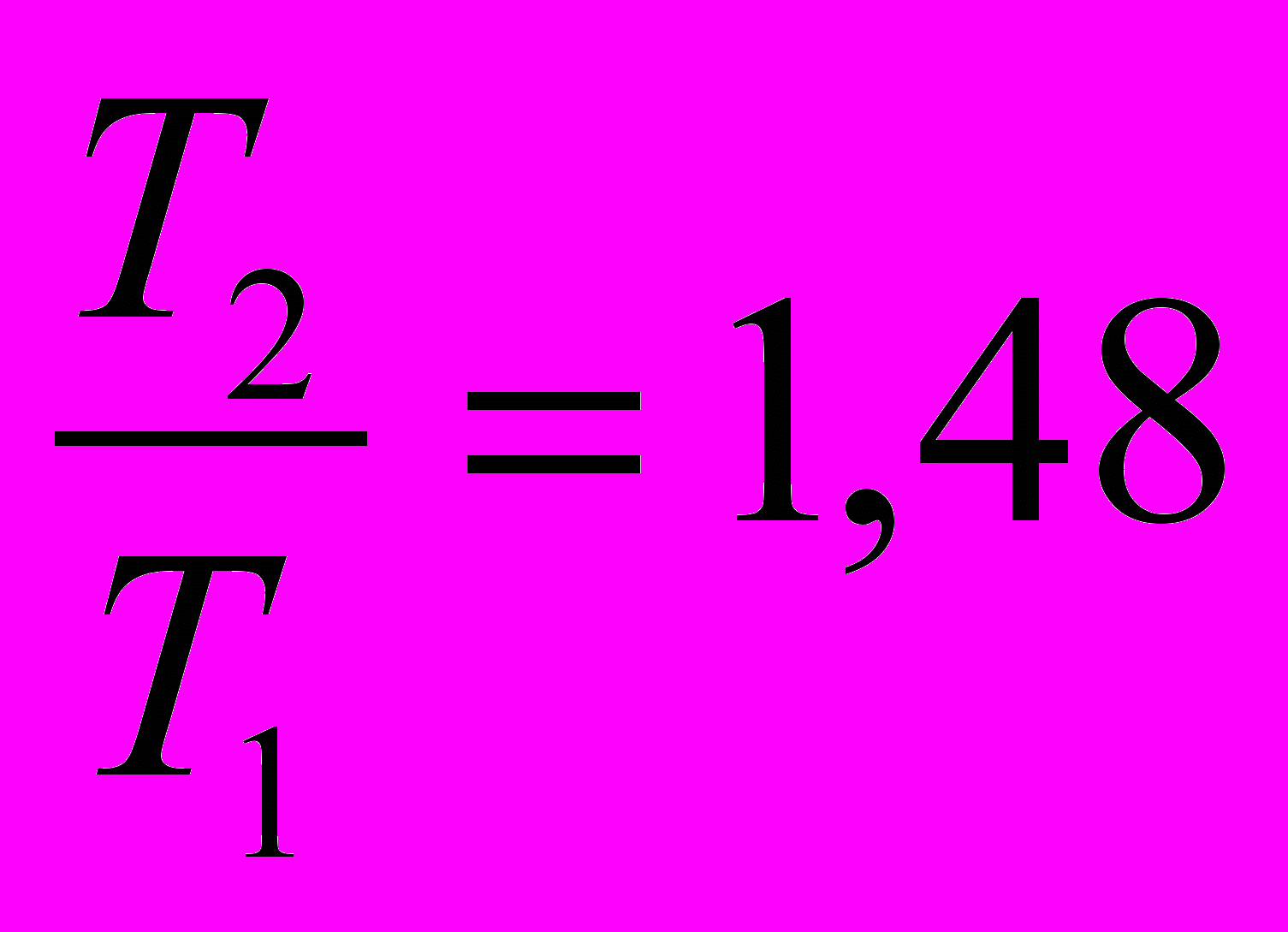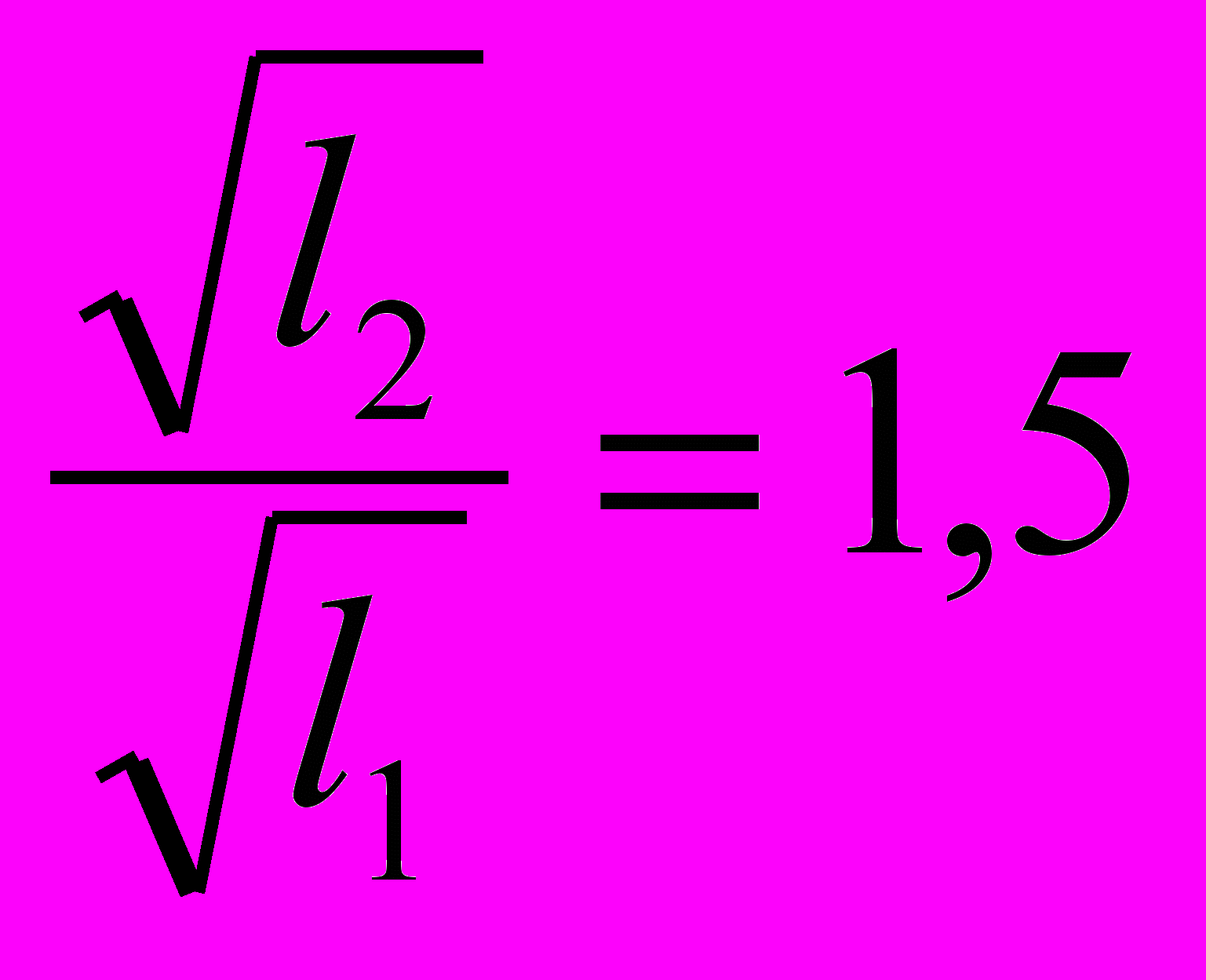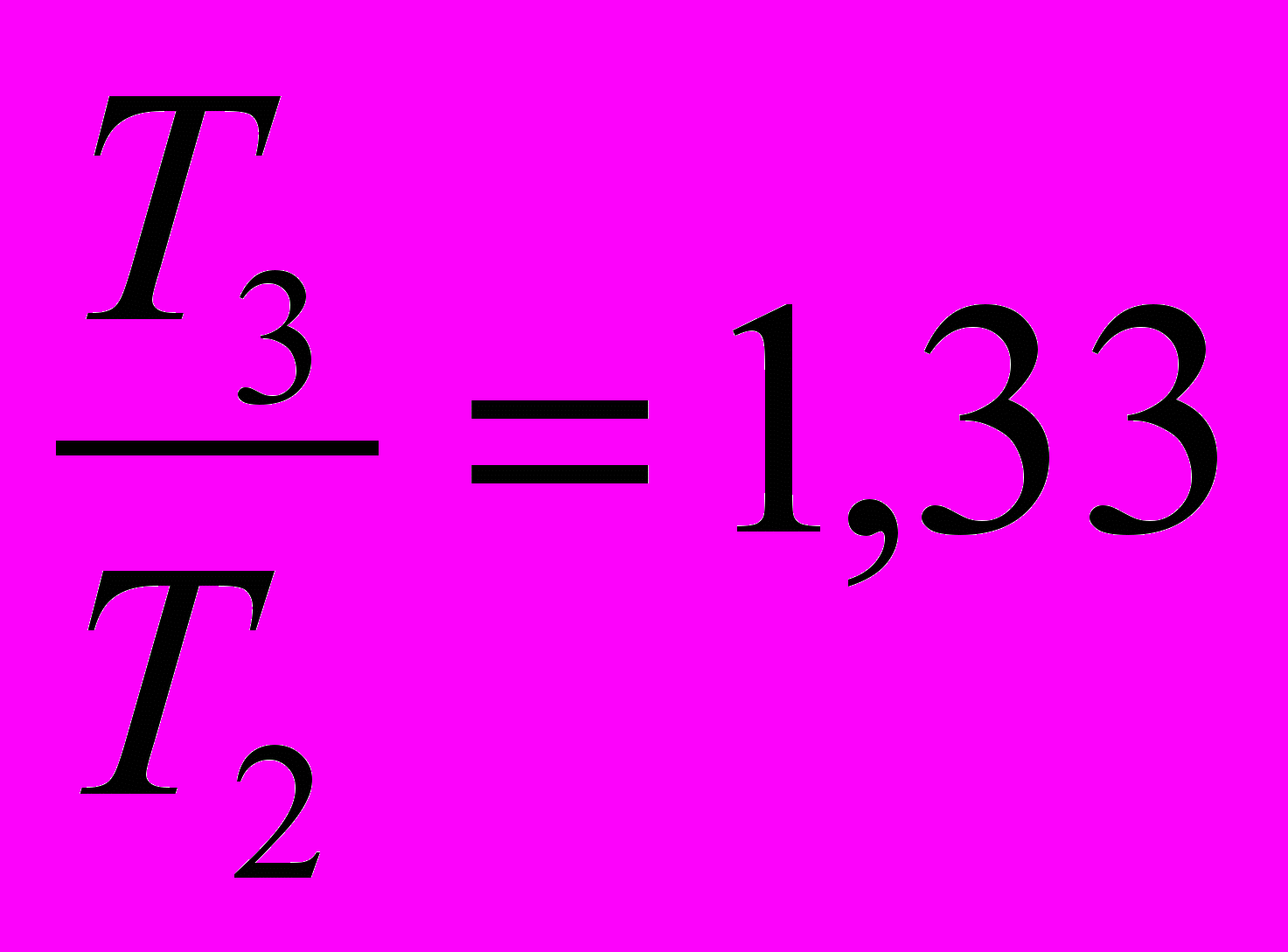и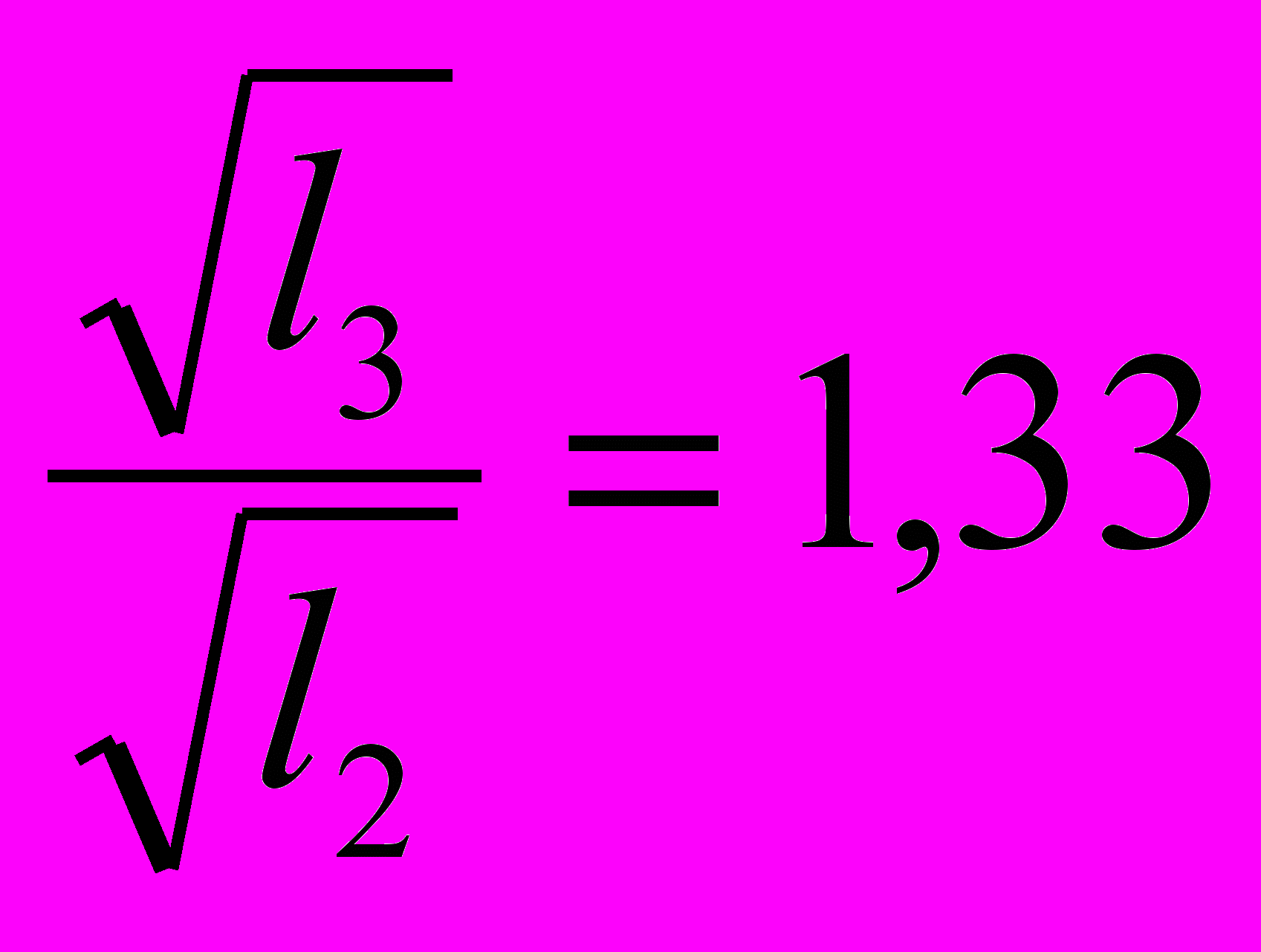 
; 
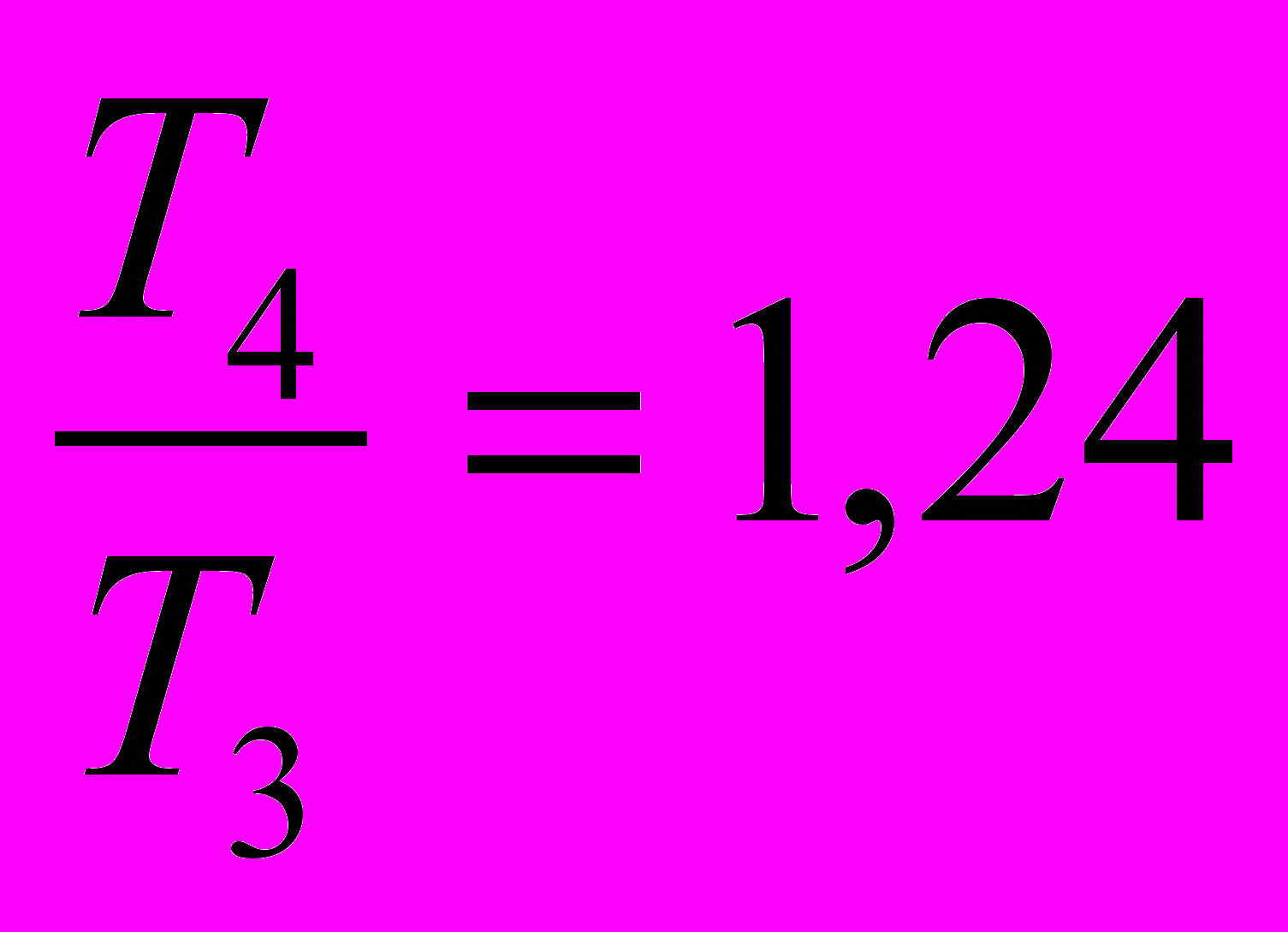и 
; 
и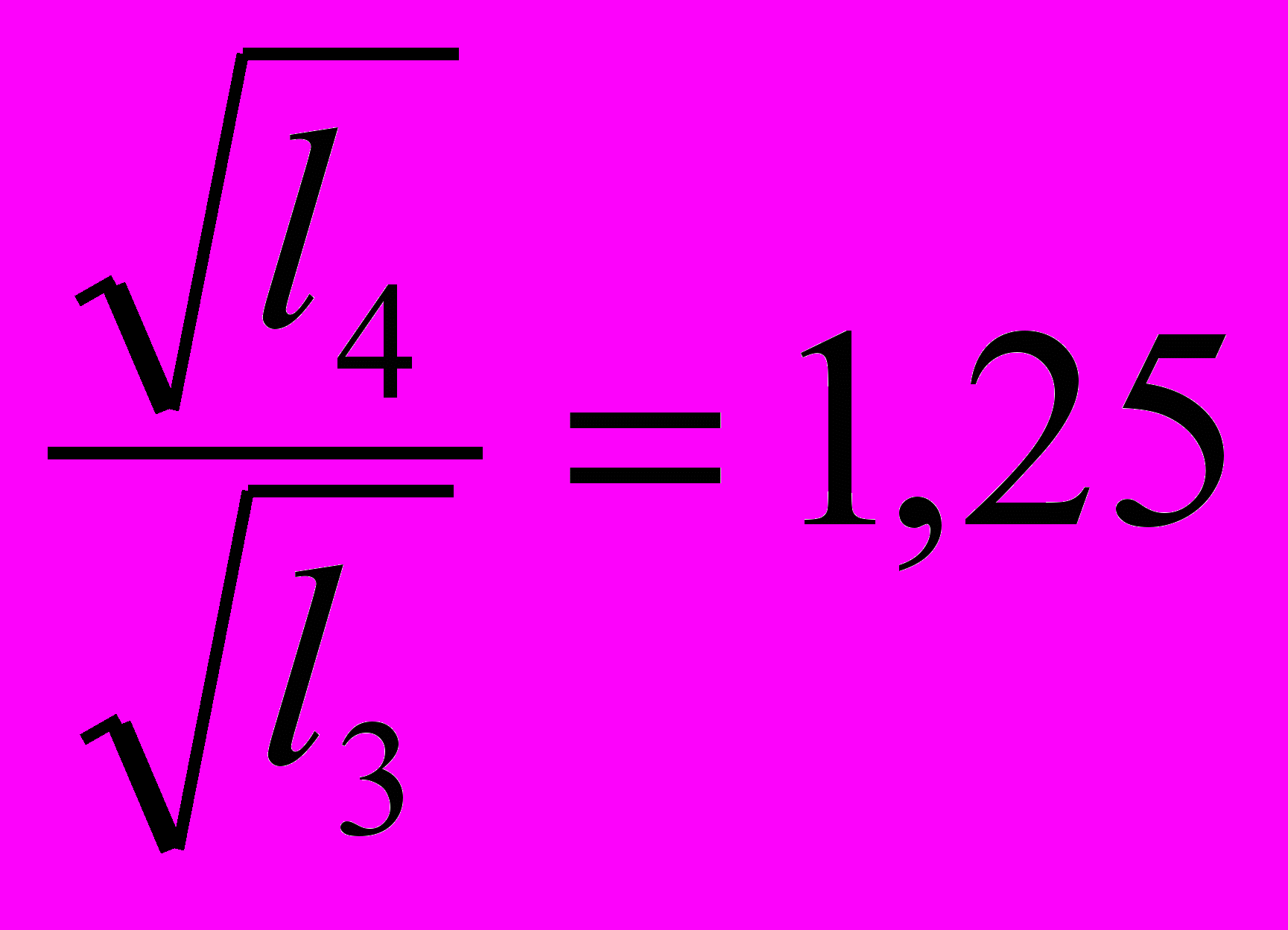 
Можно видеть, что период колебаний математического маятника пропорционален корню квадратному из длины нити маятника, а частота колебаний, соответственно, обратно пропорциональна корню квадратному из длины нити маятника: Т~
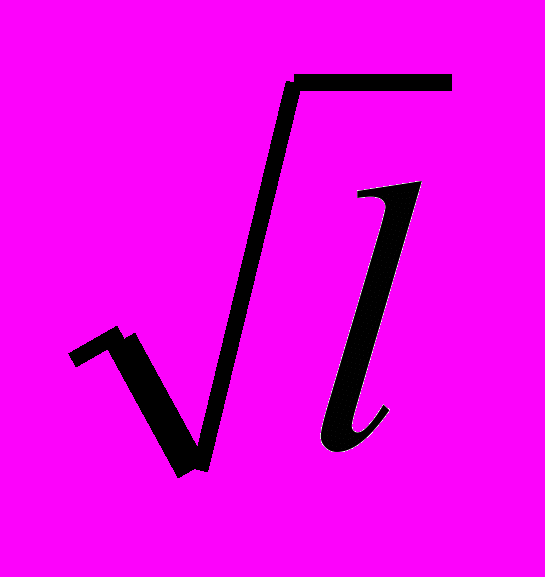; ν~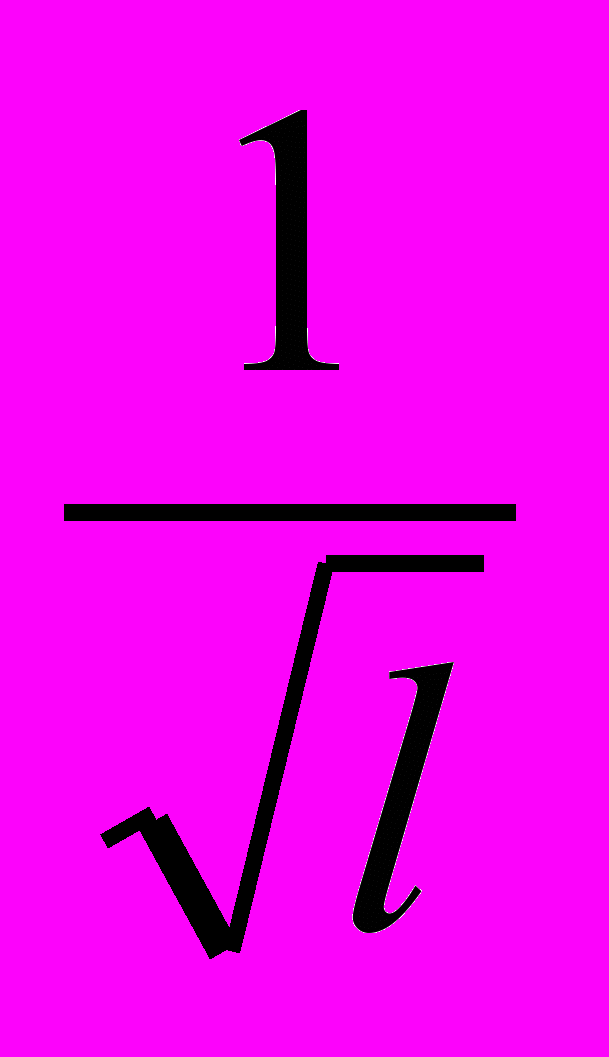
.Гипотеза № 2 – период и частота колебаний математического маятника зависят от амплитуды колебаний: чем больше амплитуда, тем больше частота колебаний и меньше период колебаний.
Таблица 2
| № опыта | N | L, м | A, м | t, c | Т, с | ν, Гц |
| 1 | 30 | 0,52 | 0,05 | 41,2 | 1,4 | 0,7 |
| 2 | 30 | 0,52 | 0,1 | 41,6 | 1,4 | 0,7 |
| 3 | 30 | 0,52 | 0,15 | 42 | 1,4 | 0,7 |
Вывод: период и частота колебаний математического маятника не зависят от амплитуды колебаний (гипотеза № 2 не подтвердилась).
Гипотеза № 3 – период и частота колебаний математического маятника зависят от массы груза: чем больше масса груза, тем больше частота колебаний и меньше период колебаний.
В первом опыте на нити подвешен один шарик, а во втором опыте к шарику добавлен груз массой 100 г.
Таблица 3
| № опыта | m, кг | N | L, м | t, c | Т, с | ν, Гц |
| 1 | 0,63 | 30 | 0,52 | 42 | 1,4 | 0,7 |
| 2 | 1,63 | 30 | 0,52 | 43 | 1,4 | 0,7 |
Вывод: Период и частота колебаний математического маятника не зависят от массы груза (гипотеза № 3 не подтвердилась).
- Исследование зависимости периода и частоты колебаний
пружинного маятника от его параметров.
Оборудование: штатив с муфтой и держателем для пружины – 3 шт., пружины разной жесткости – 3 шт., весы с разновесами, набор грузов по 100 г, секундомер, линейка.
Сначала определим жесткости пружин. Если груз, подвешенный к пружине, будет покоиться, то действующие на него силы тяжести и упругости будут друг друга уравновешивать (рис. 8)
Fу=Fт; По закону Гука Fу=kx, значит, kx=mg, отсюдаF
у 
k=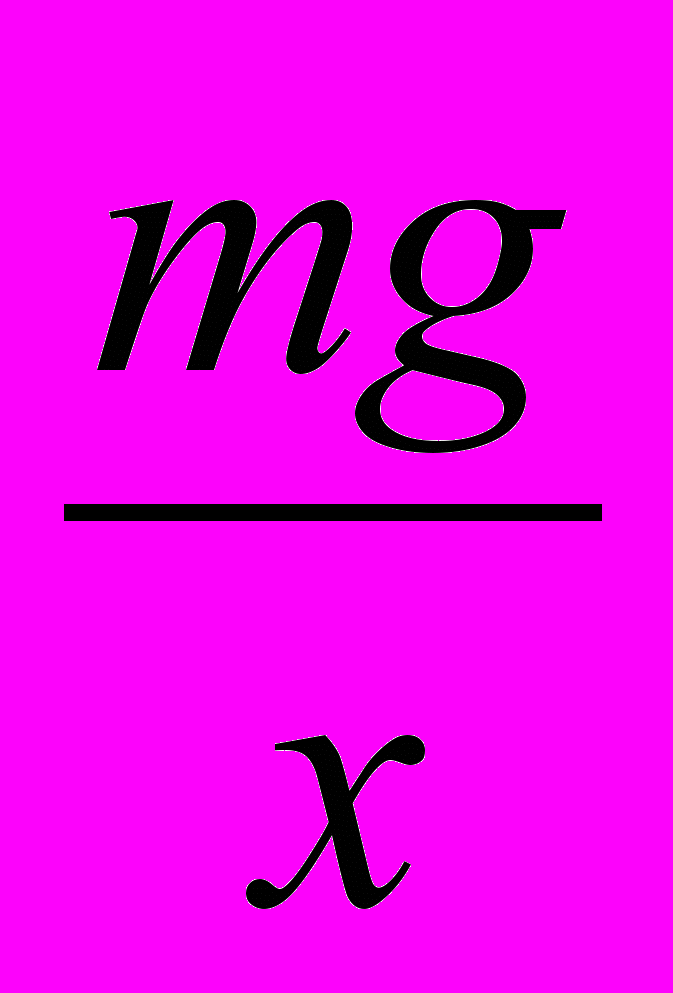
, где х – растяжение пружины под действием грузамассой m.
Fт Рис. 8
Расчет жесткости пружин Таблица № 4
| № опыта | m, кг | х, м | k, Н/м |
| 1 | 0,3 | 0,055 | 55 |
| 2 | 0,3 | 0,12 | 25 |
| 3 | 0,1 | 0,43 | 2,3 |
Гипотеза № 4 – период и частота колебаний пружинного маятника зависят от массы груза: чем больше масса груза, тем больше период колебаний и меньше частота колебаний.
Таблица 5
| № опыта | k, Н/м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 55 | 0,2 | 20 | 12 | 0,6 | 1,7 |
| 2 | 55 | 0,3 | 20 | 15 | 0,75 | 1,3 |
| 3 | 55 | 0,4 | 20 | 18 | 0,9 | 1,1 |
Вывод: период и частота колебаний пружинного маятника зависят от массы груза: чем больше масса груза, тем больше период колебаний и меньше частота колебаний (гипотеза № 4 подтвердилась).
Сравним отношения:
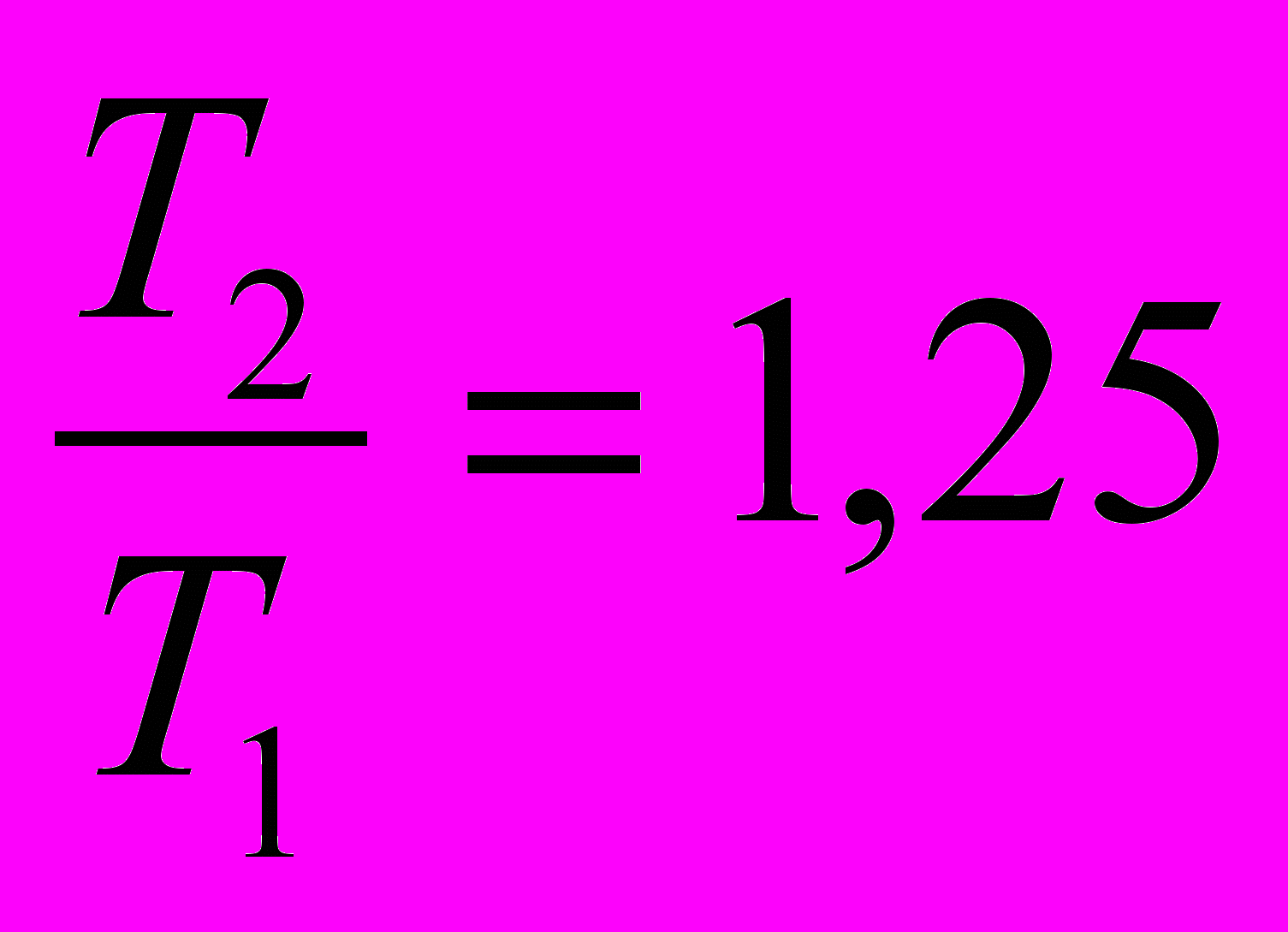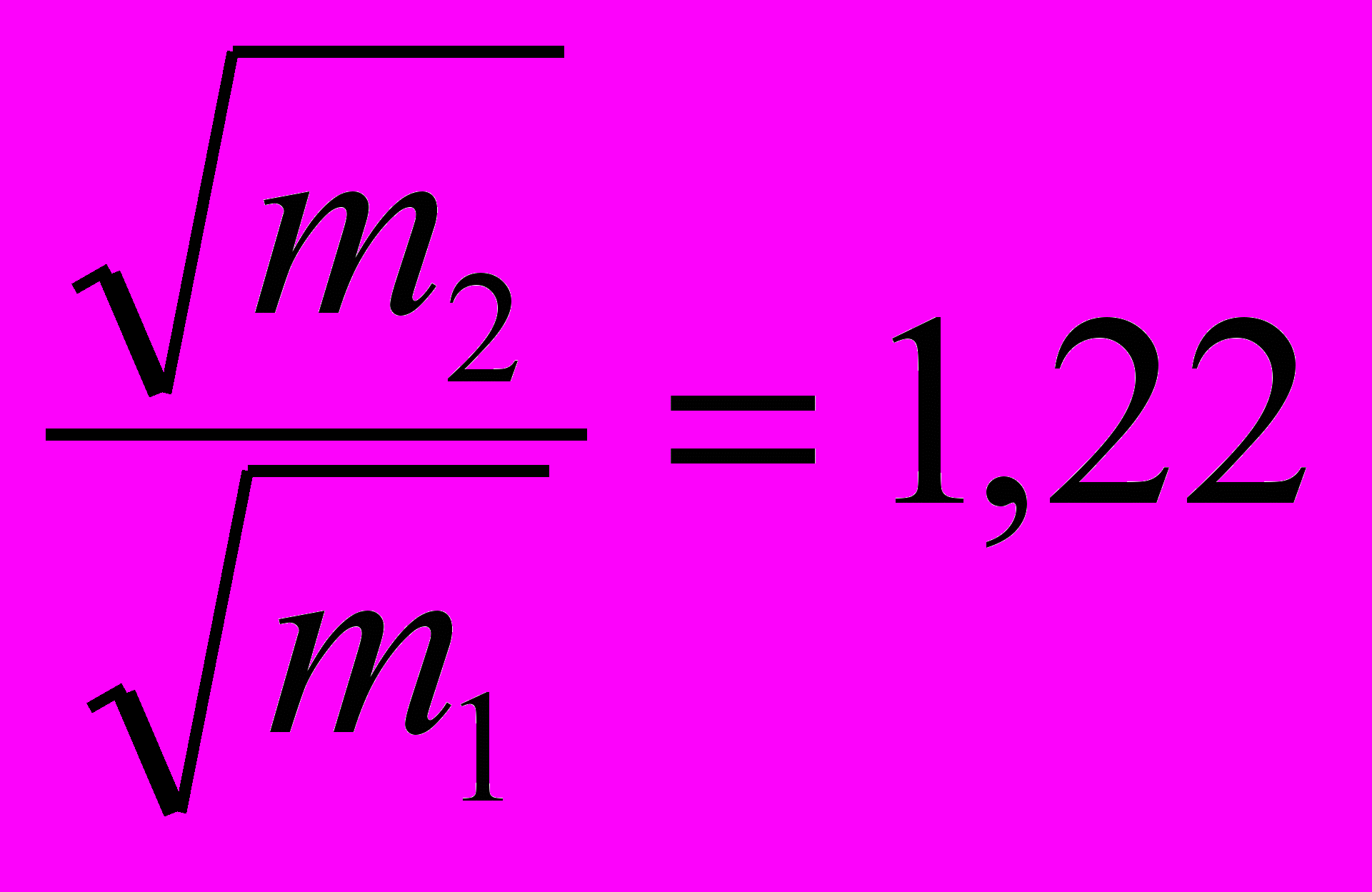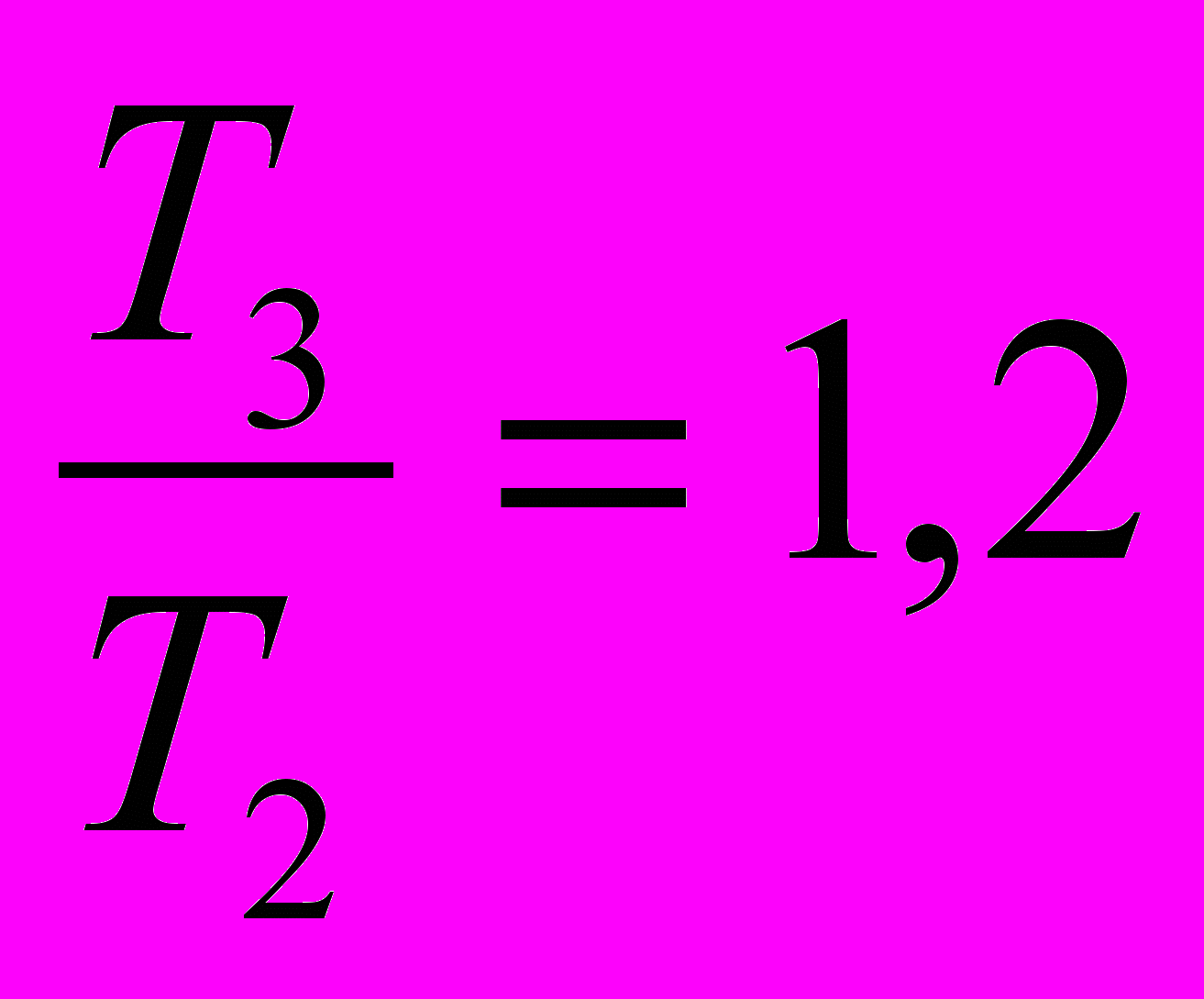и 
; 
и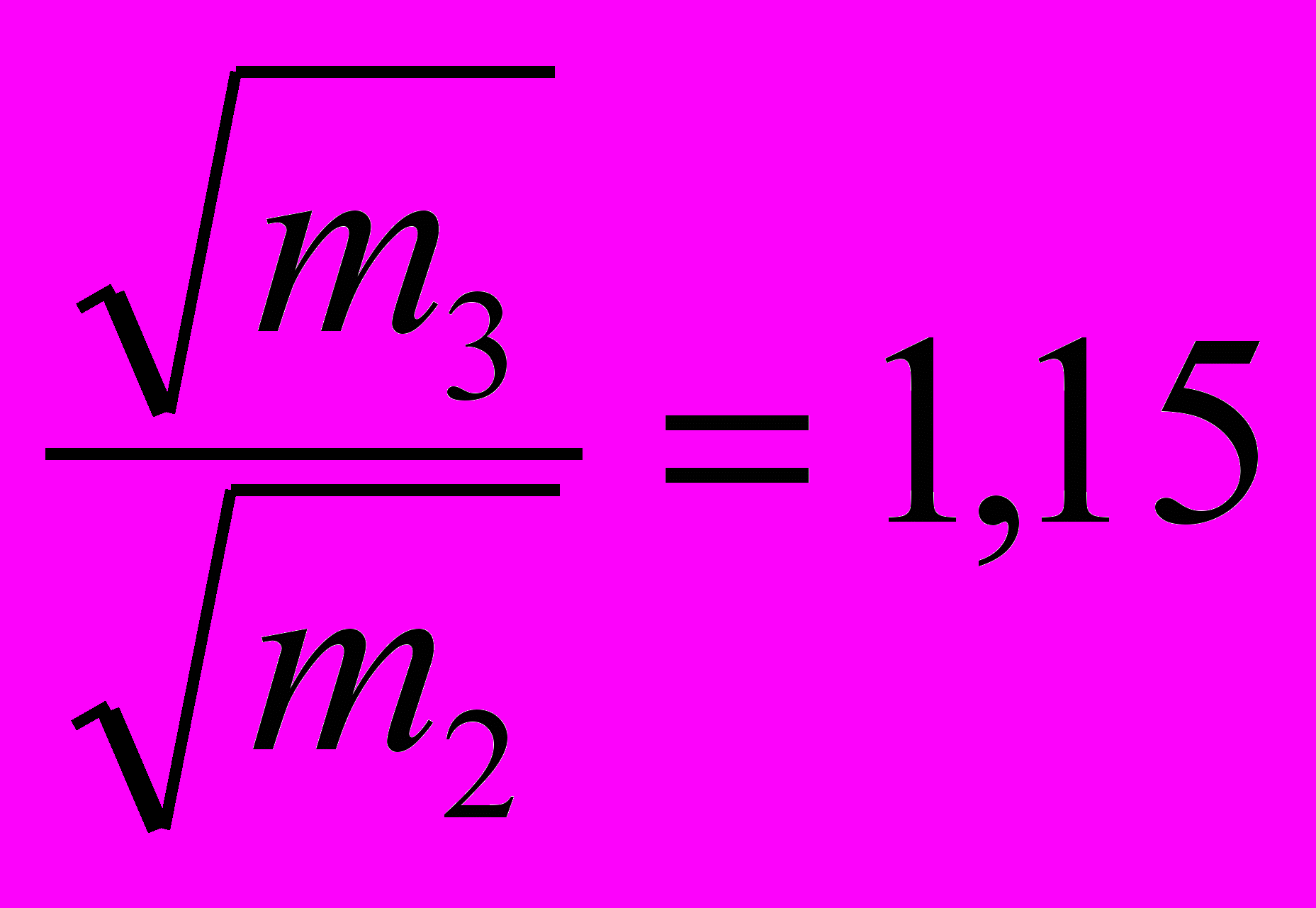 
Можно видеть, что период колебаний пружинного маятника зависит пропорционально от корня квадратного из массы груза, а частота колебаний, соответственно, обратно пропорциональна корню квадратному из массы груза: Т~
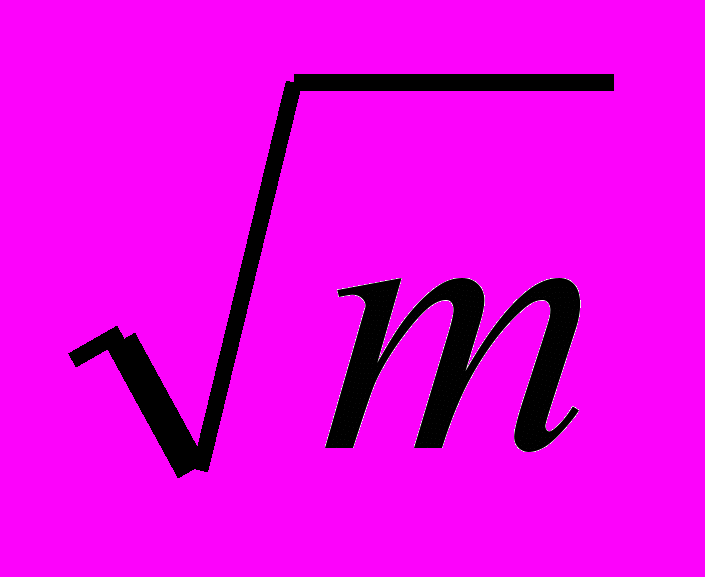; ν~
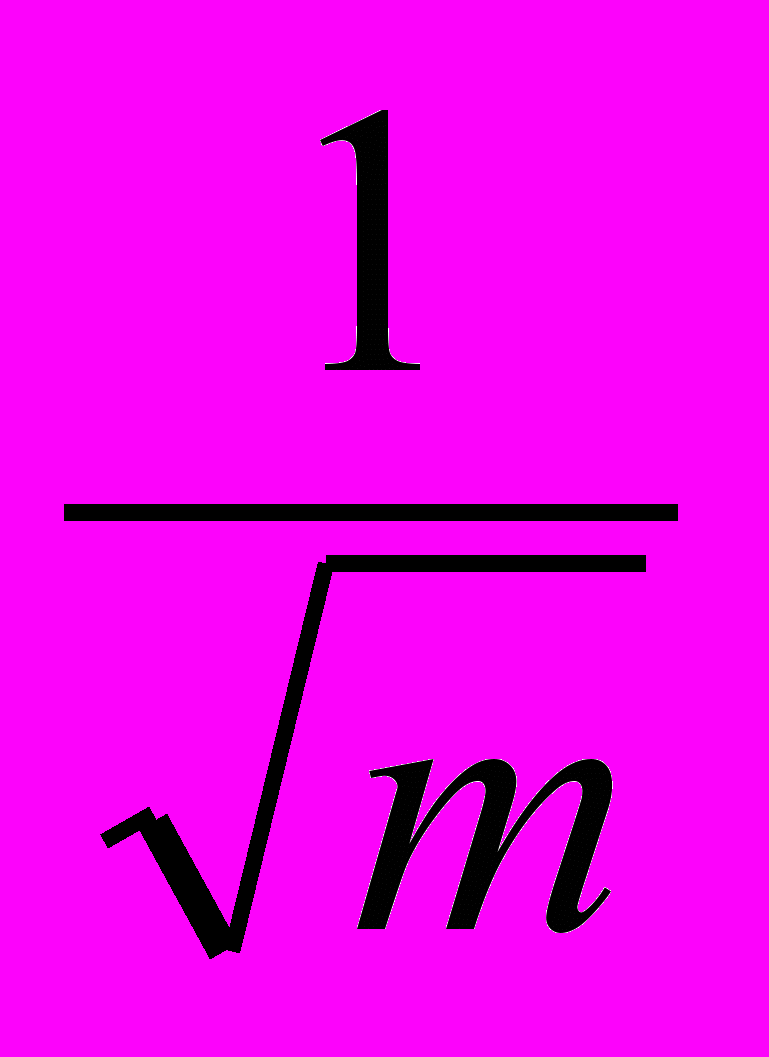.Гипотеза № 5 – период и частота пружинного маятника зависят от амплитуды колебаний: чем больше амплитуда колебаний, тем больше период колебаний и меньше частота.
Таблица 6
| № опыта | k, Н/м | m, кг | А, м | N | t, c | Т, с | ν, Гц |
| 1 | 25 | 0,2 | 0,16 | 20 | 12 | 0,6 | 1,7 |
| 2 | 25 | 0,2 | 0,11 | 20 | 12 | 0,6 | 1,7 |
Вывод: период и частота колебаний пружинного маятника не зависят от амплитуды колебаний (гипотеза № 5 не подтвердилась).
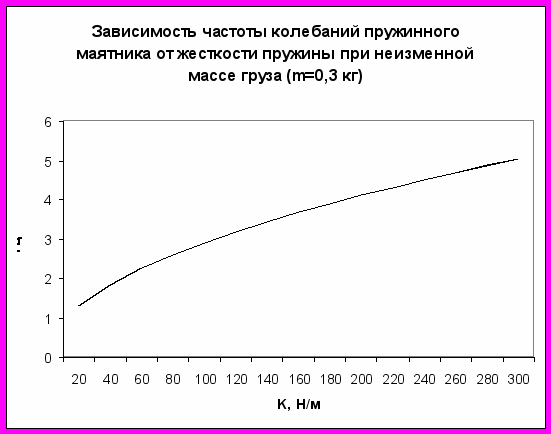
Гипотеза № 6 – период и частота колебаний пружинного маятника зависят от жесткости пружины: чем больше жесткость пружины, тем меньше период колебаний и больше частота колебаний.
Таблица 7
| № опыта | k, Н/м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 2,3 | 0,2 | 20 | 39 | 1,95 | 0,51 |
| 2 | 25 | 0,2 | 20 | 12 | 0,6 | 1,67 |
| 3 | 55 | 0,2 | 20 | 8,6 | 0,43 | 2,33 |
Вывод: период и частота пружинного маятника зависят от жесткости пружины: чем больше жесткость пружины, тем меньше период колебаний и больше частота колебаний (гипотеза № 6 подтвердилась).
Сравним отношения:
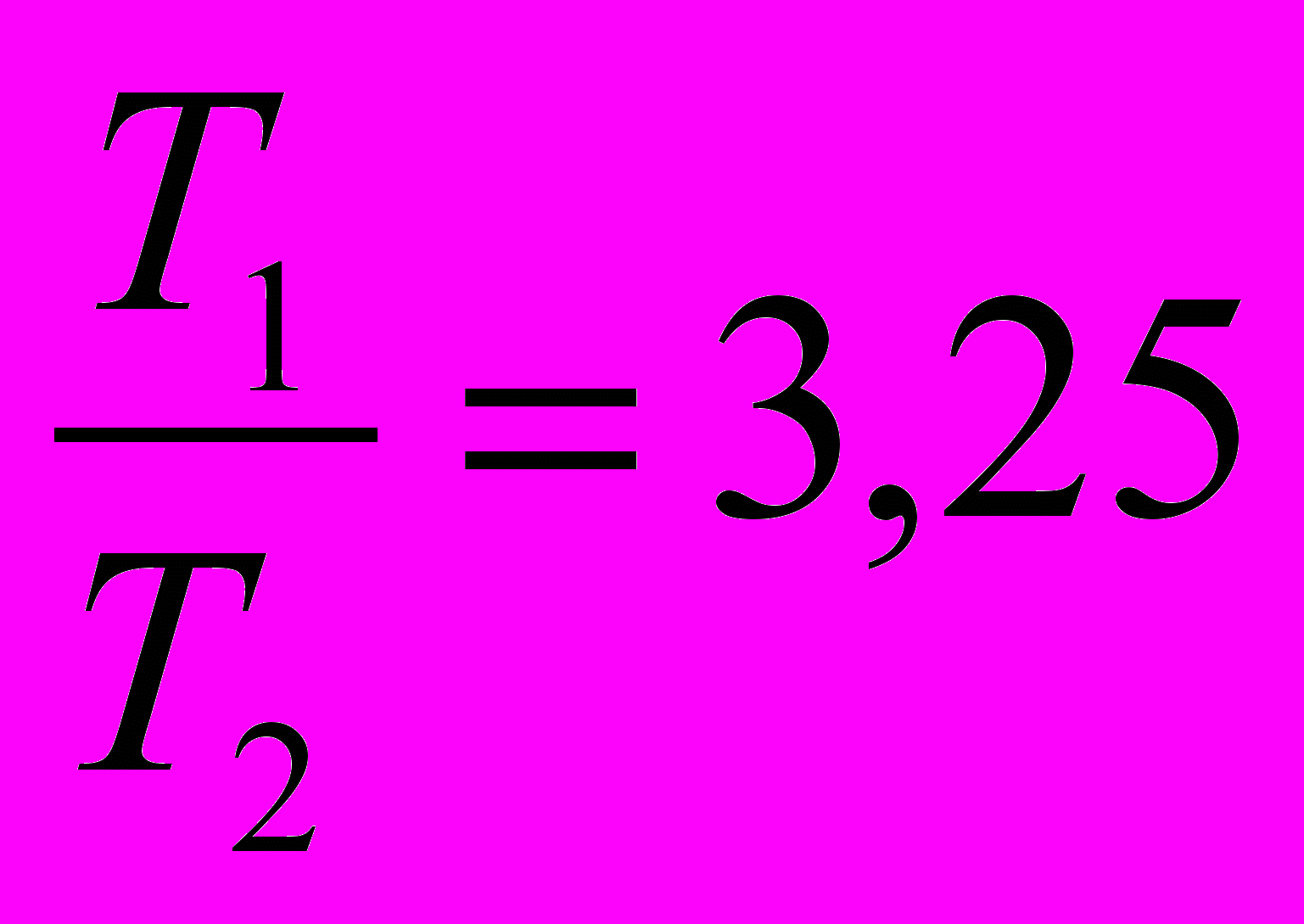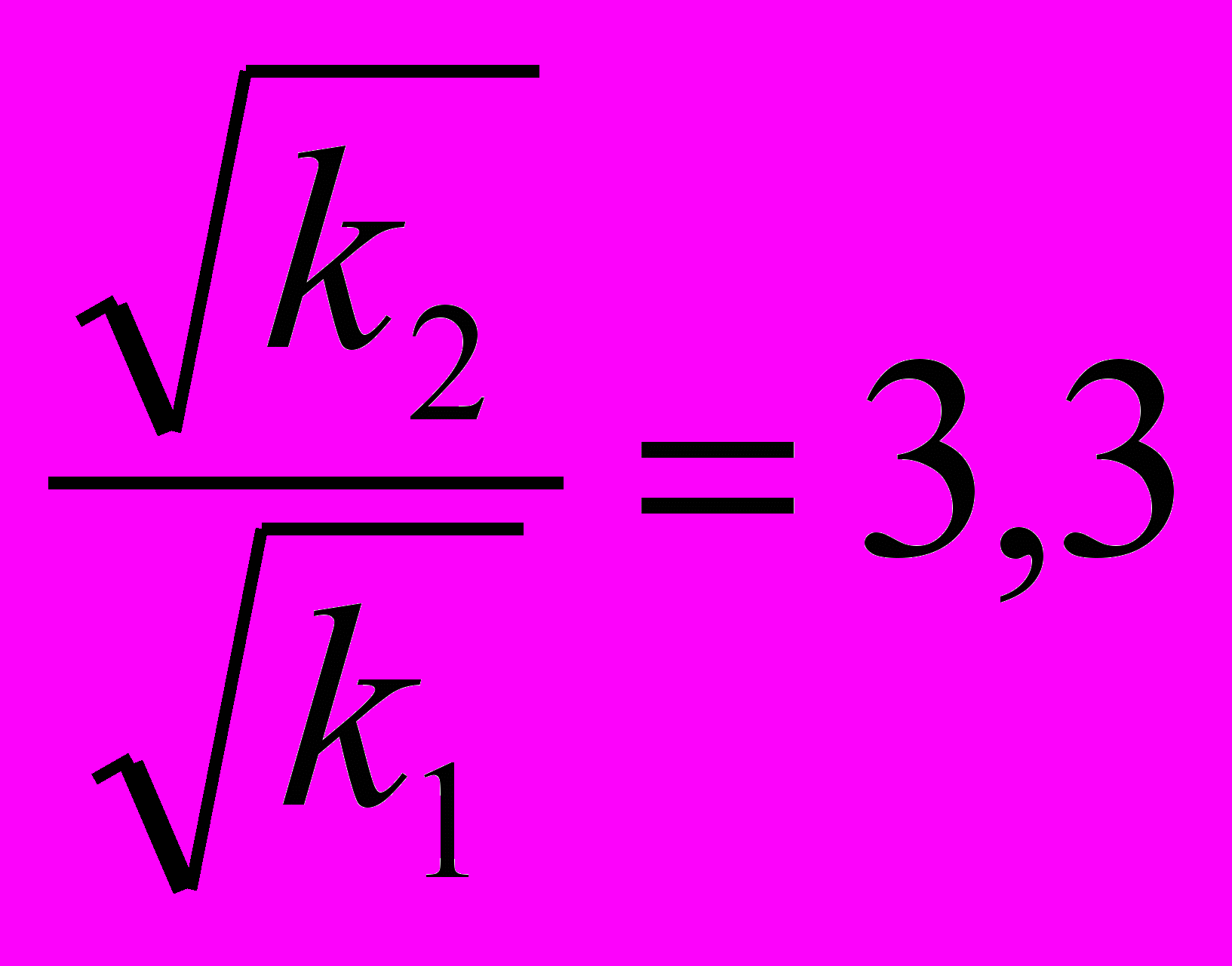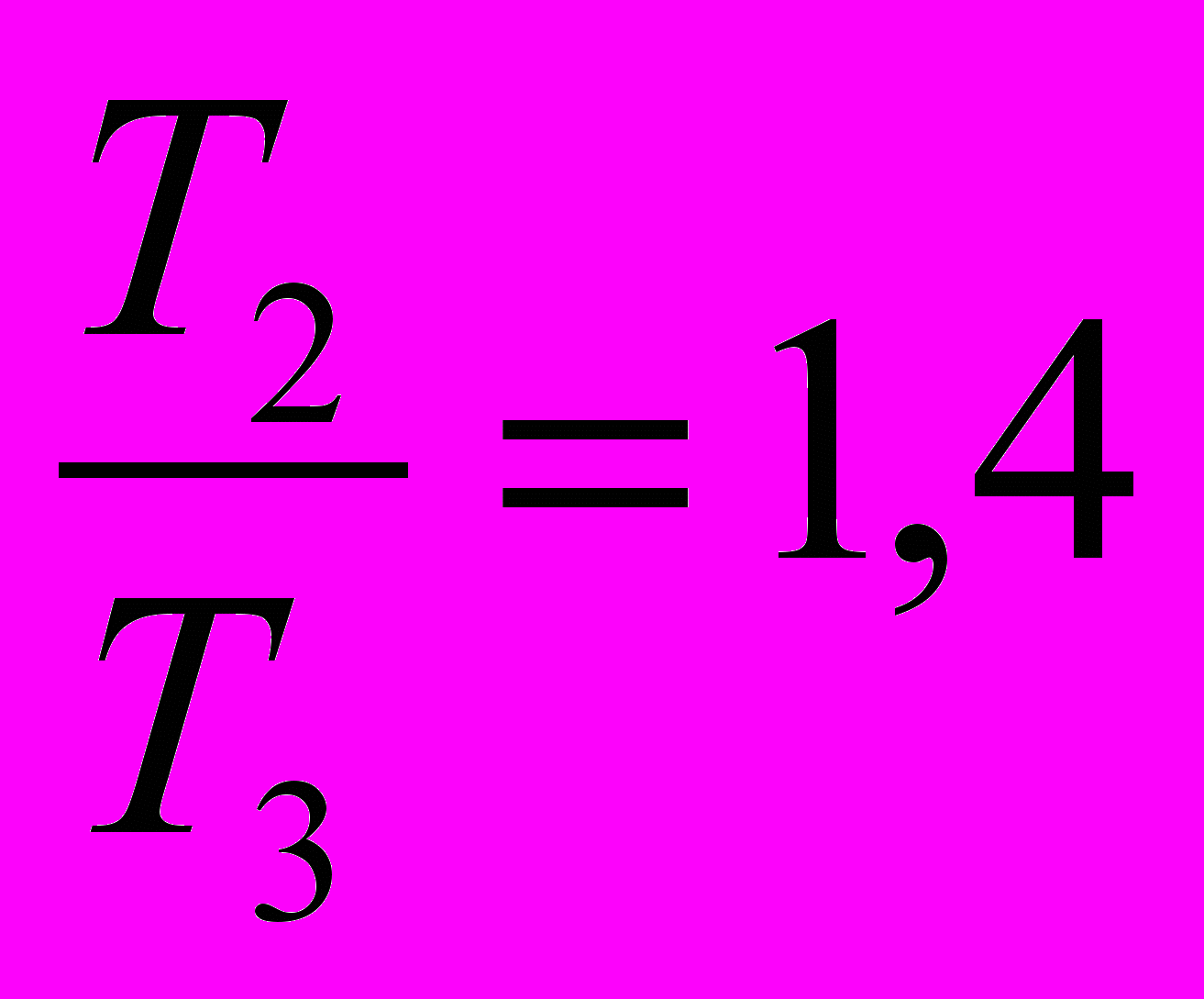и 
; 
и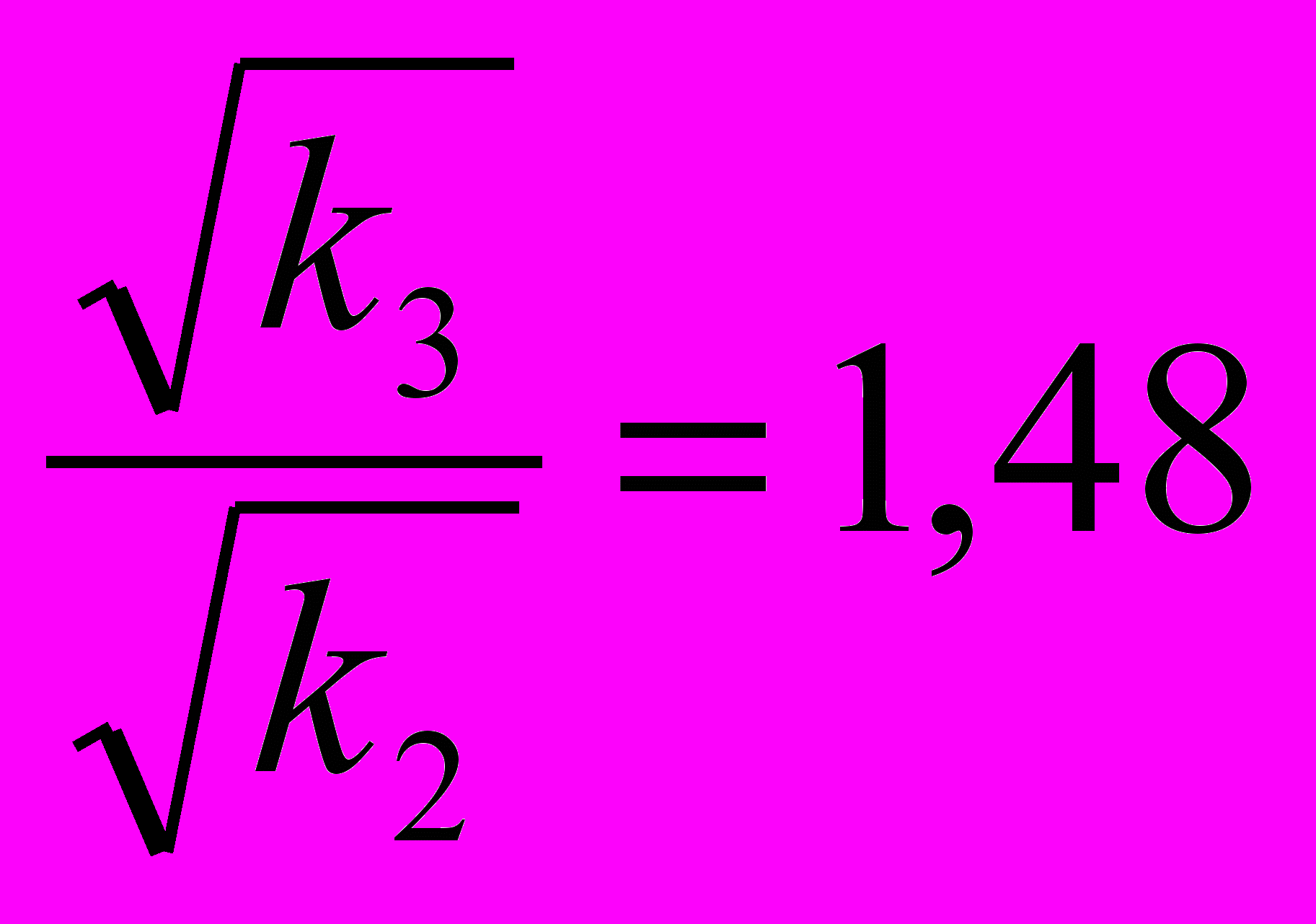 
Можно видеть, что период колебаний пружинного маятника зависит обратно пропорционально от корня квадратного из жесткости пружины, а частота колебаний, соответственно, пропорциональна корню квадратному из жесткости пружины: Т~
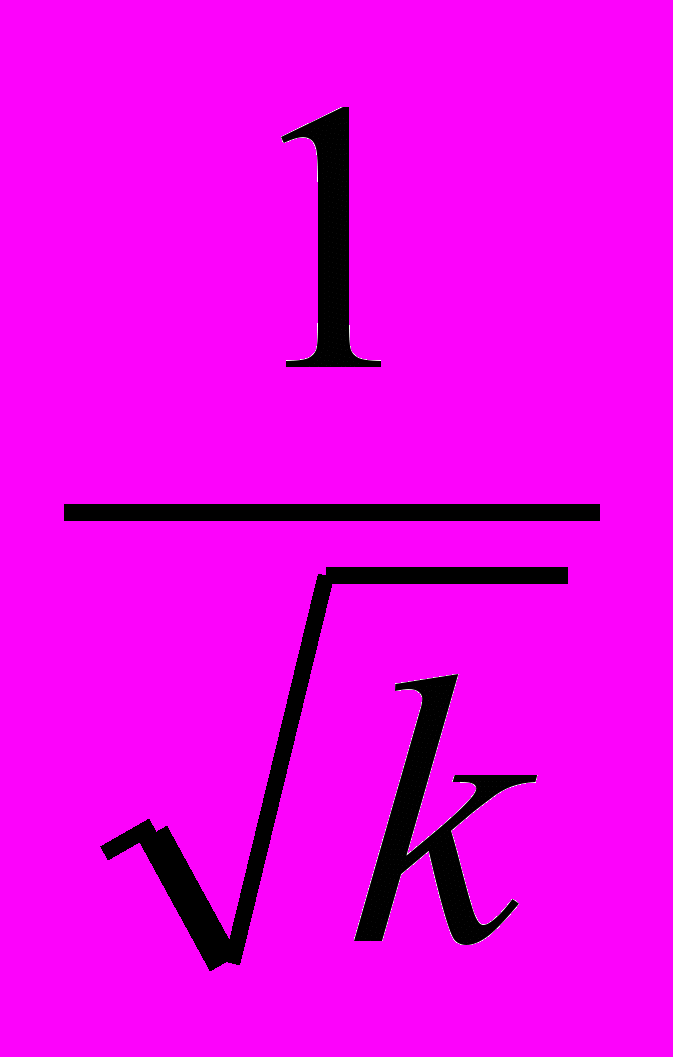; ν ~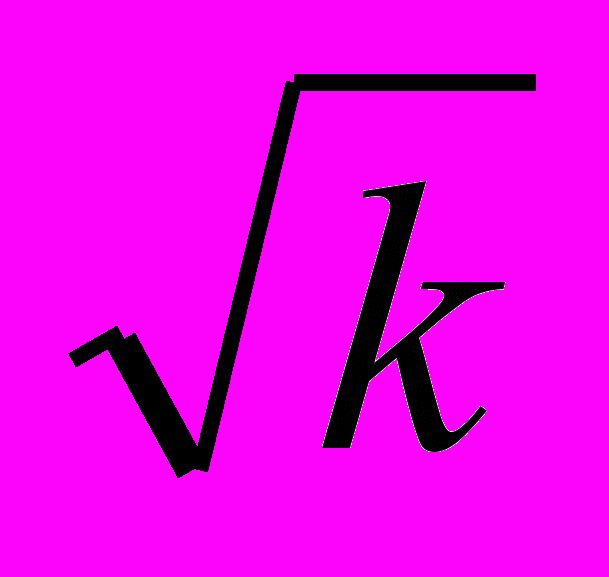
.- Исследование зависимости периода и частоты колебаний физического маятника от его параметров.
Оборудование: физические маятники в виде параллелепипеда разной длины и массы, весы с разновесами, секундомер, линейка измерительная, штатив с муфтой, металлический стержень диаметром около 5 мм.
Гипотеза № 7 – период и частота колебаний физического маятника зависят от его массы: чем больше масса физического маятника, тем больше период его колебаний и меньше частота.
Таблица 8
| № опыта | L, м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 0,5 | 0,063 | 20 | 22 | 1,1 | 0,9 |
| 2 | 0,5 | 0,186 | 20 | 22 | 1,1 | 0,9 |
| 3 | 0,5 | 0,321 | 20 | 22 | 1,1 | 0,9 |
L – длина физического маятника.
Вывод: период и частота колебаний физического маятника не зависят от его массы (гипотеза № 7 не подтвердилась).
Гипотеза № 8 – период и частота физического маятника зависят от расстояния от оси вращения маятника до его центра тяжести: чем больше это расстояние, тем больше период и меньше частота колебаний физического маятника.
Таблица 9
| № опыта | l, м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 0,4 | 0,195 | 10 | 15 | 1,5 | 0,7 |
| 2 | 0,3 | 0,195 | 10 | 15 | 1,5 | 0,7 |
| 3 | 0,2 | 0,195 | 10 | 15 | 1,5 | 0,7 |
Вывод: период и частота физического маятника не зависят от расстояния от оси вращения до центра тяжести маятника (гипотеза № 8 не подтвердилась). Можно предположить, что период и частота колебаний физического маятника зависят, видимо, от его формы.
- Исследование зависимости периода и частоты колебаний оборотного маятника от его параметров.
Оборудование: оборотный маятник, шарики разной массы, надетые на стержни разной длины, секундомер, весы с разновесами, линейка.
Гипотеза № 9 – период и частота оборотного маятника зависят от длины горизонтального стержня: чем больше длина горизонтального стержня, тем больше период колебаний и меньше частота колебаний.
Таблица № 10
| № опыта | L, м | l, м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 0,52 | 0,13 | 0,087 | 10 | 30 | 2,1 | 0,48 |
| 2 | 0,52 | 0,19 | 0,087 | 10 | 21 | 3 | 0,33 |
Вывод: период и частота оборотного маятника зависят от длины горизонтального стержня: чем больше длина горизонтального стержня, тем больше период колебаний и меньше частота колебаний (гипотеза № 9 подтвердилась).
Сравним отношения:
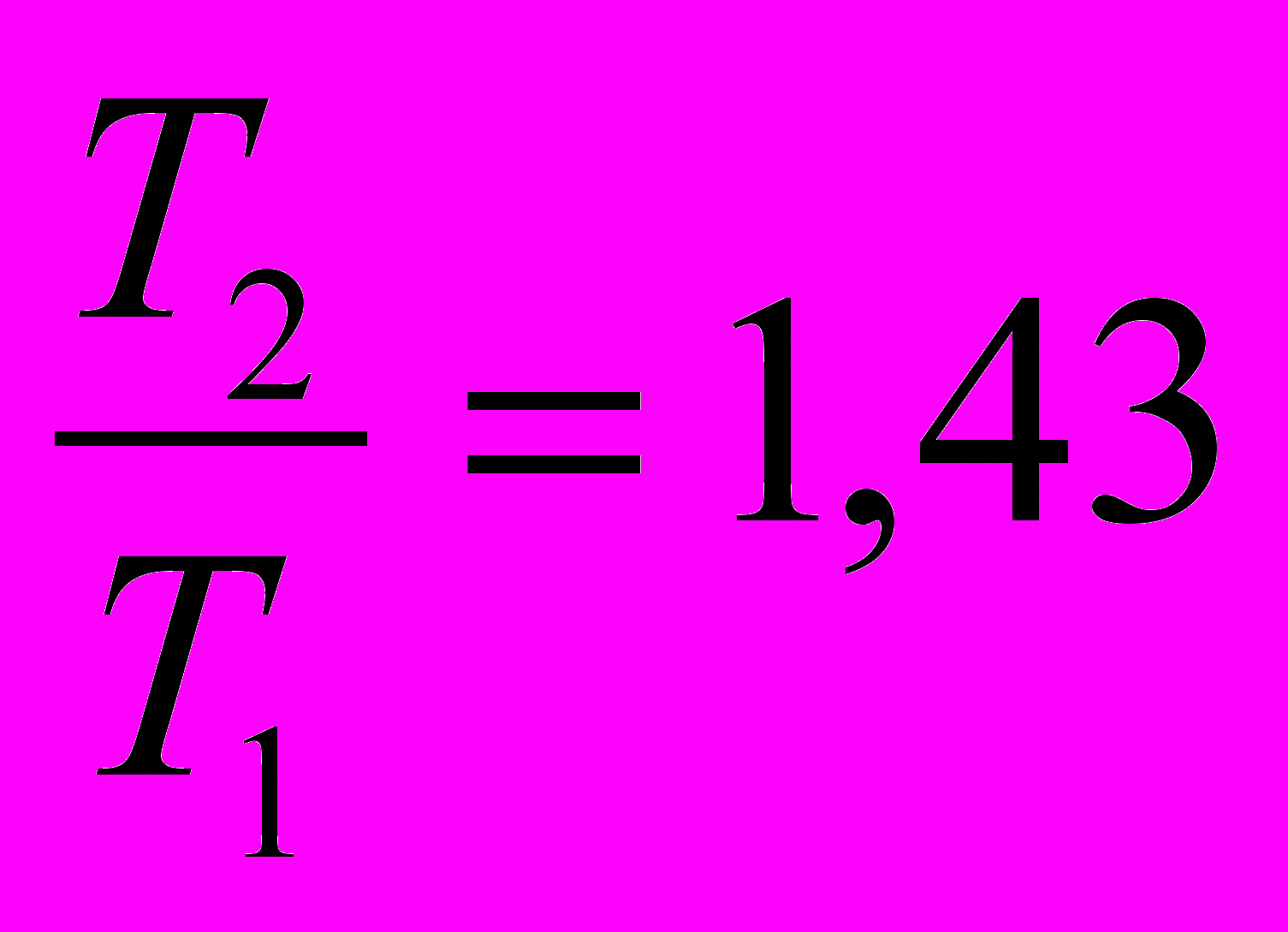и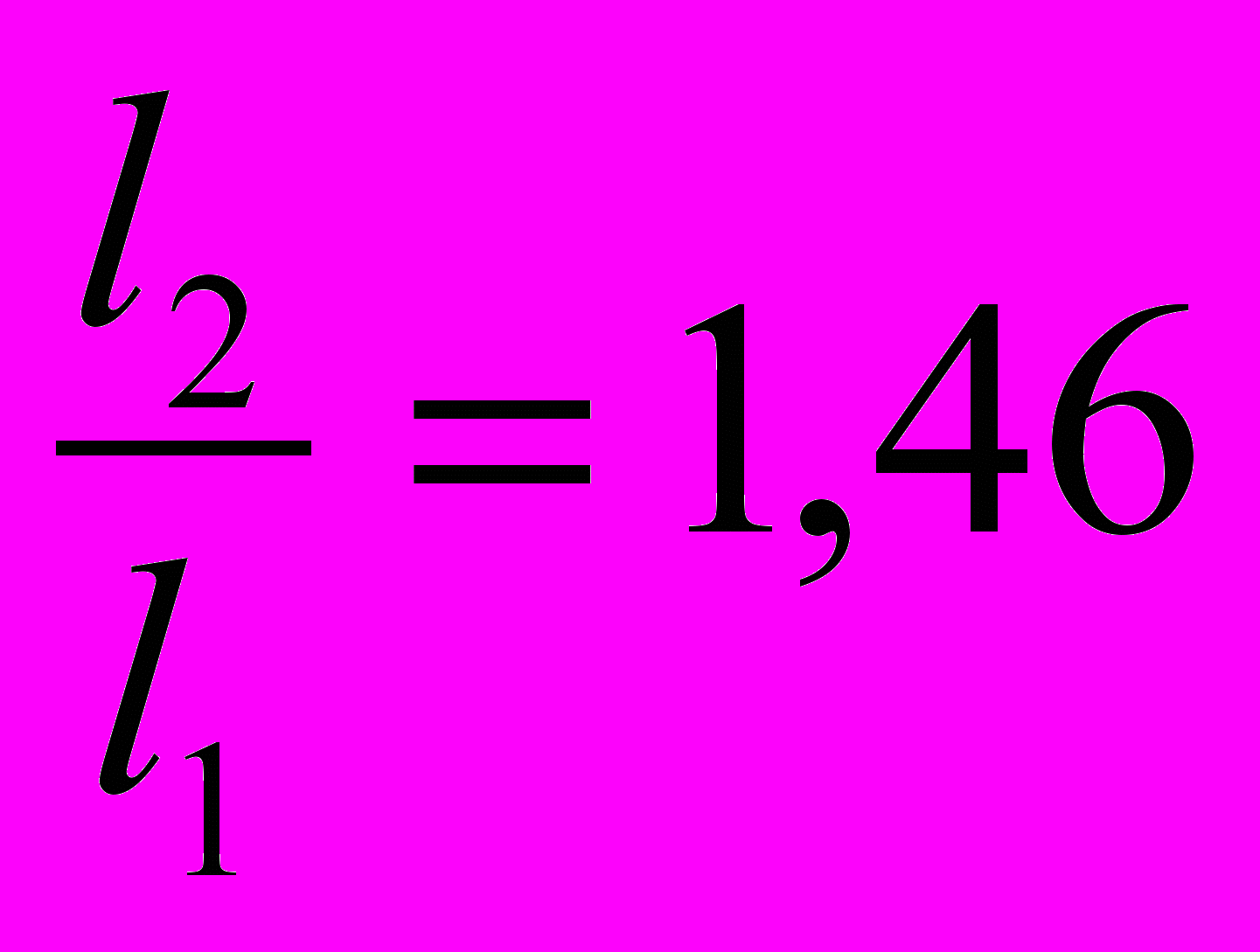 
. Можно предположить, что период колебаний оборотного маятника прямо пропорционален (частота колебаний обратно пропорциональна) длине горизонтального стержня: Т~l.Гипотеза № 10 – период и частота оборотного маятника зависят от массы шаров: чем больше масса шаров, тем больше период и меньше частота колебаний.
Таблица № 11
| № опыта | L, м | l, м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 0,52 | 0,19 | 0,087 | 10 | 30 | 3 | 0,33 |
| 2 | 0,52 | 0,19 | 0,014 | 10 | 19 | 1,9 | 0,53 |
Вывод: период и частота оборотного маятника зависят от массы шаров: чем больше масса шаров, тем больше период и меньше частота колебаний (гипотеза № 10 подтвердилась). Зависимость периода и частоты колебаний оборотного маятника от массы шаров, видимо, более сложная и определить её на основании двух опытов невозможно.
Гипотеза № 11 – период и частота колебаний оборотного маятника зависят от длины его подвеса: чем меньше длина подвеса, тем меньше период и больше частота колебаний оборотного маятника.
Таблица № 12
| № опыта | L, м | l, м | m, кг | N | t, c | Т, с | ν, Гц |
| 1 | 0,52 | 0,19 | 0,087 | 10 | 30 | 3 | 0,33 |
| 2 | 0,37 | 0,19 | 0,087 | 10 | 28 | 2,8 | 0,36 |
| 3 | 0,22 | 0,19 | 0,087 | 10 | 23 | 2,3 | 0,43 |
Вывод: период и частота колебаний оборотного маятника зависят от длины его подвеса: чем меньше длина подвеса, тем меньше период и больше частота колебаний оборотного маятника (гипотеза № 11 подтвердилась).
Сравним отношения:
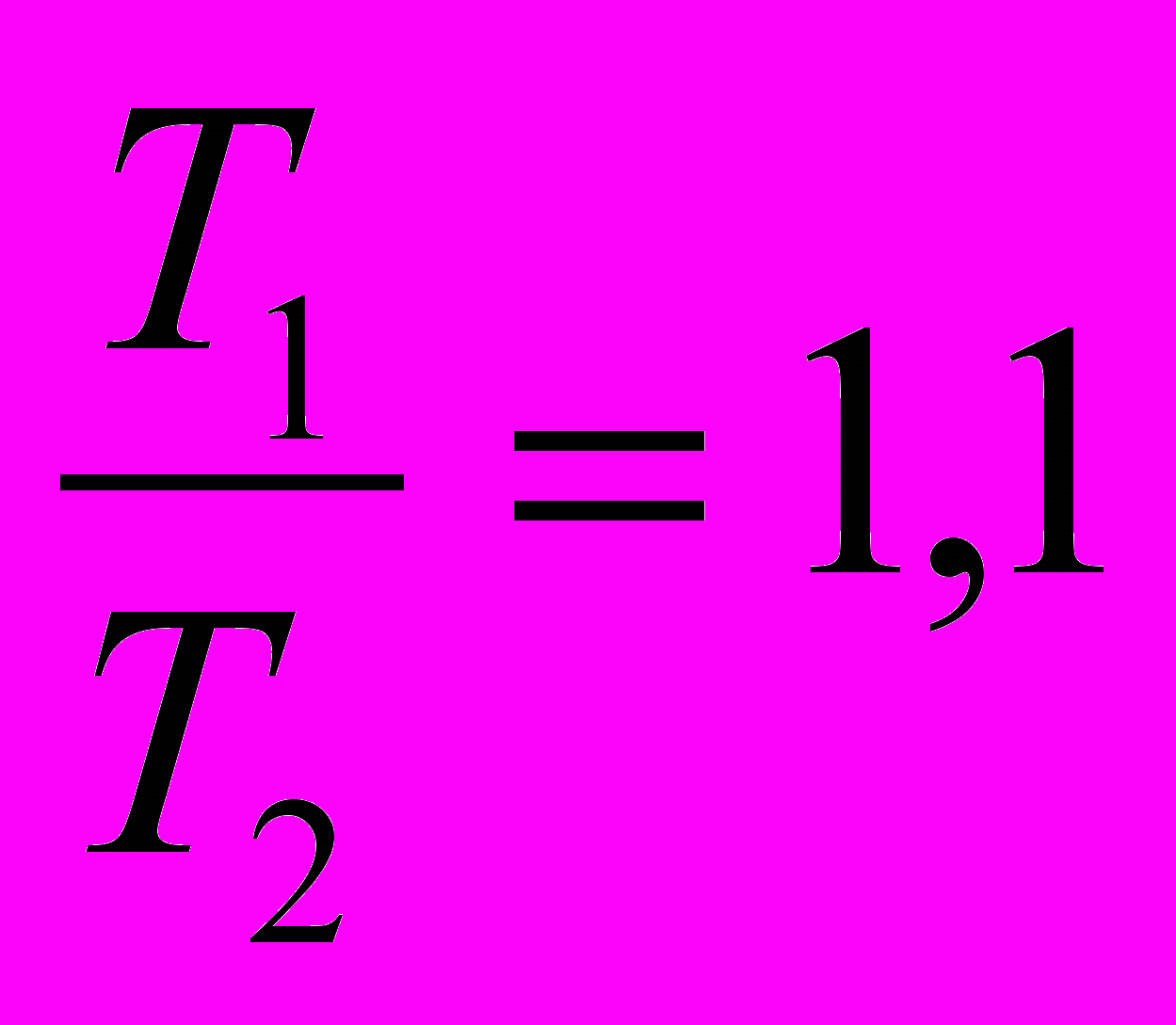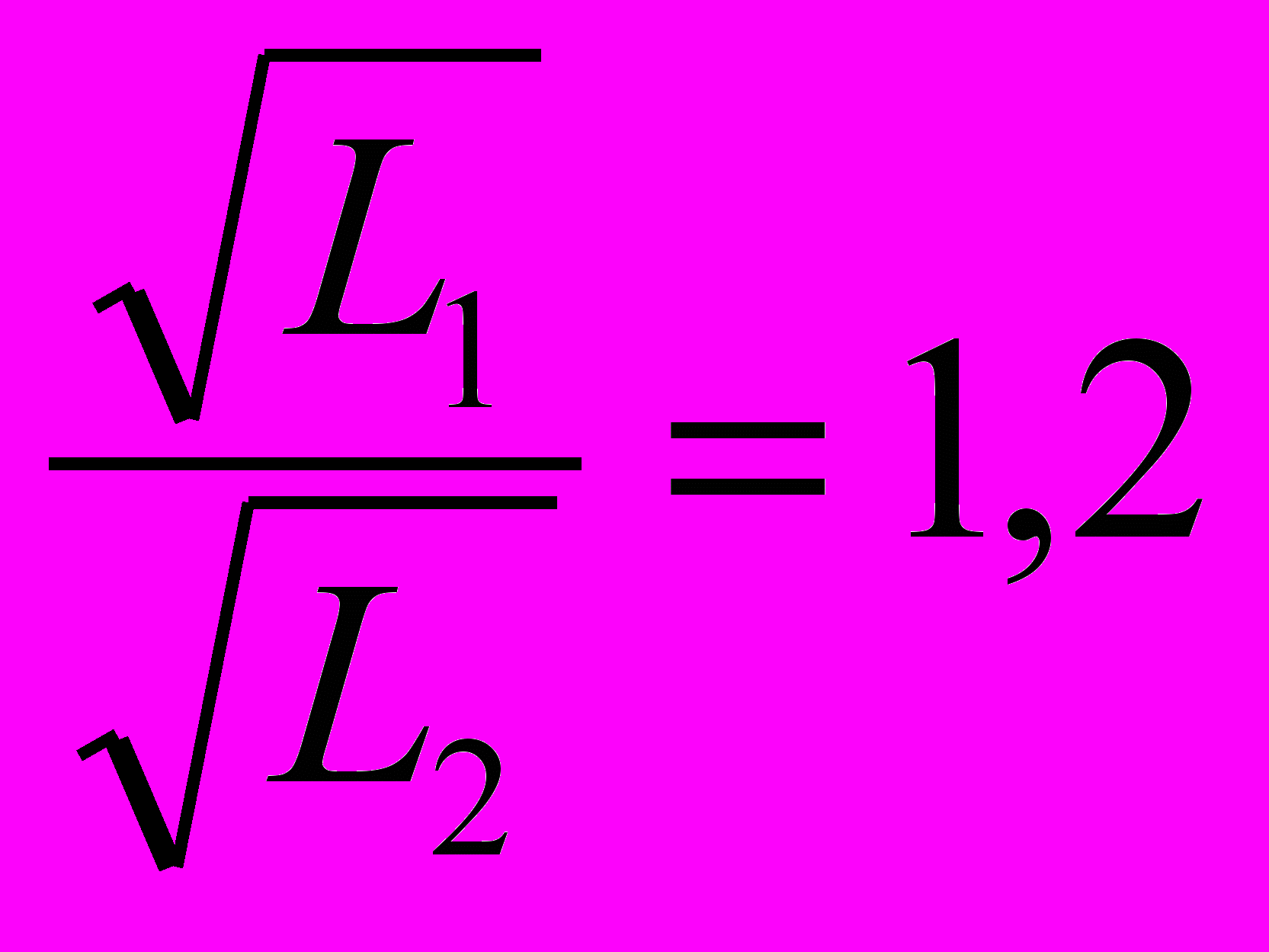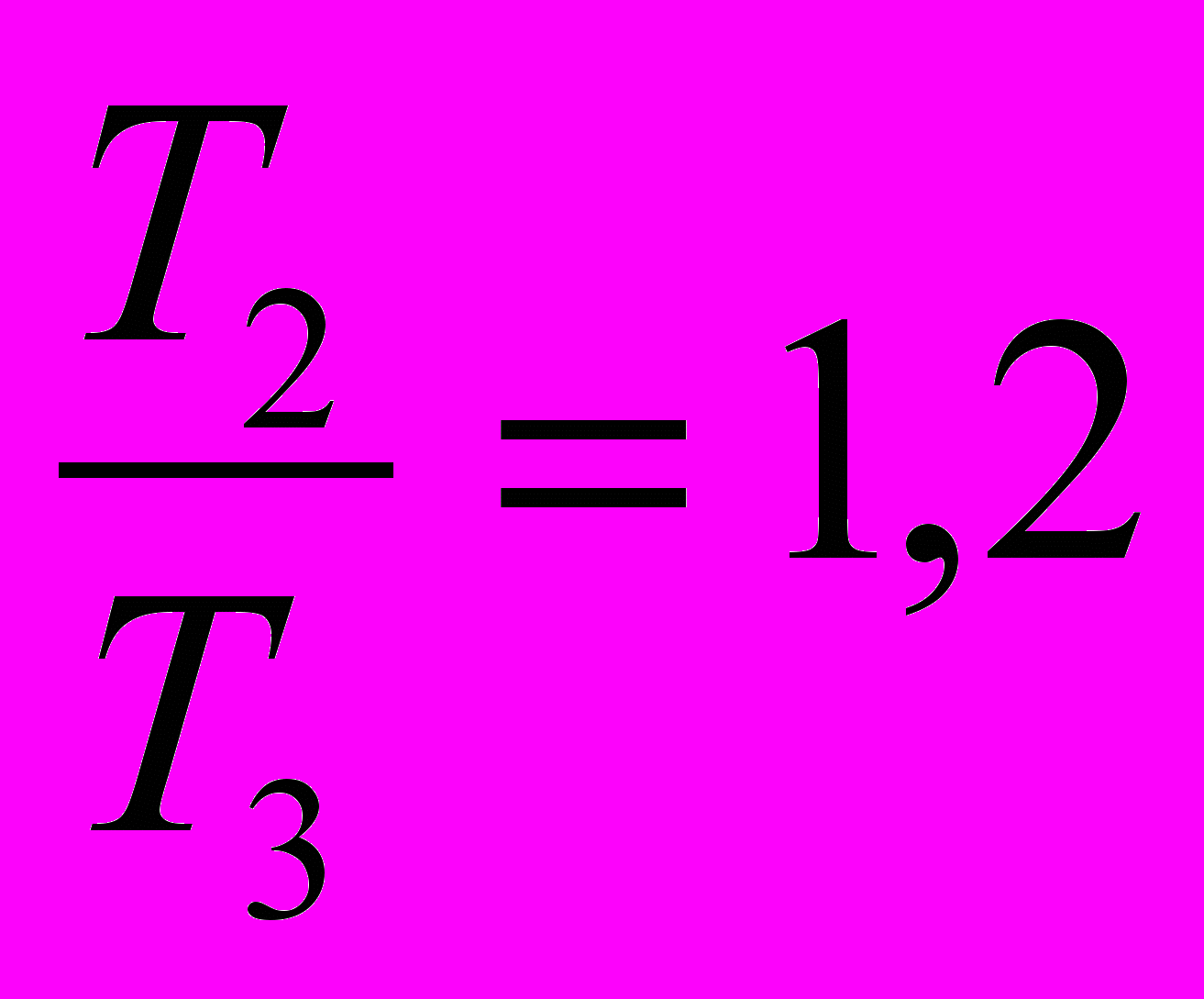и 
; 
и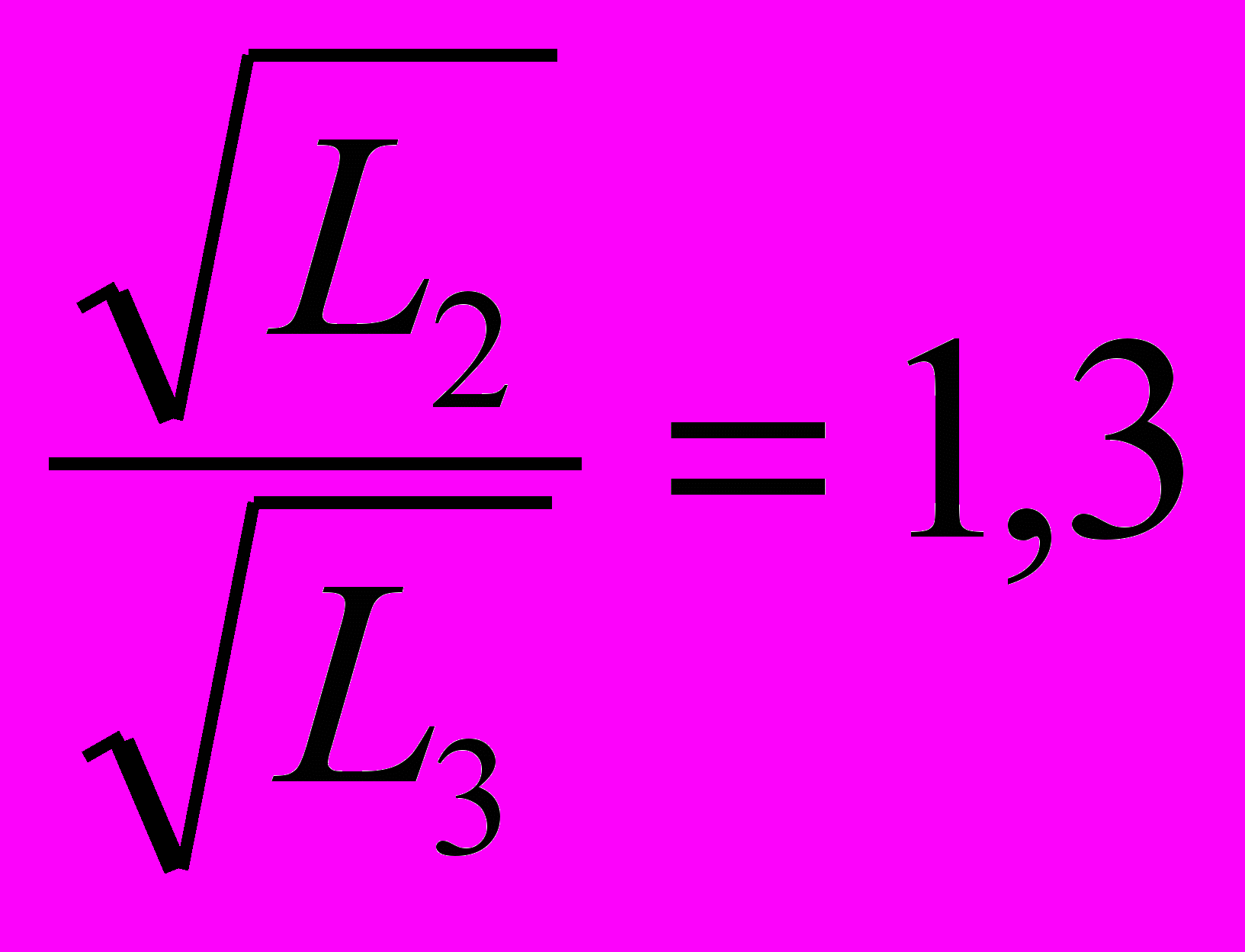 
. Можно предположить, что период колебаний оборотного маятника прямо пропорционален (а частота колебаний обратно пропорциональна) корню квадратному из длины подвеса маятника: Т~
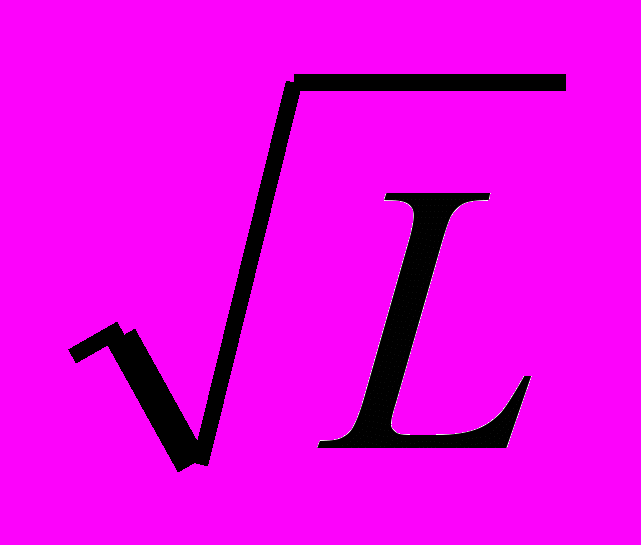; ν~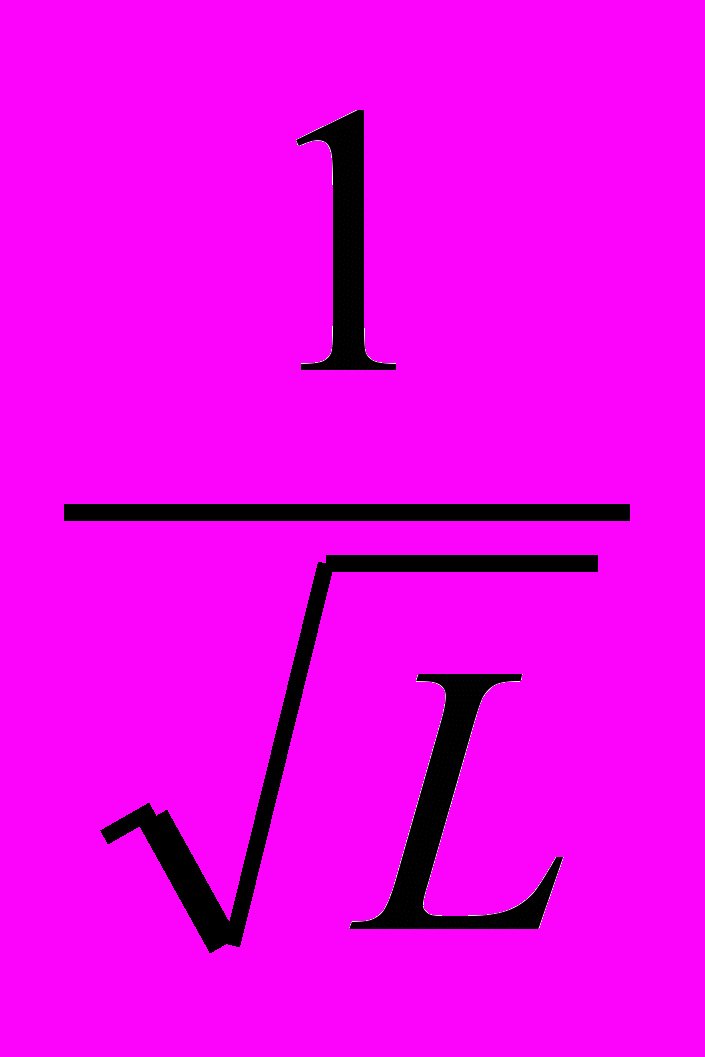
.- Некоторые применения колебательных систем.
Р
ис. 96.1. Маятник Фуко (рис.9).
3 января 1851 года января Жан Бернар Леон Фуко провёл успешный опыт с маятником, впоследствии получившим его имя. Для опыта был выбран Парижский Пантеон, в нем можно было укрепить нить маятника длиной 67 метров. На конце нити из стальной проволоки был укреплён чугунный шар массой 28 килограммов. Перед пуском шар отводился в сторону и привязывался тонкой бечёвкой, опоясывающей шар по экватору. Под маятником был сделан круглый помост, по краю которого насыпан валик песка. Одно полное колебание маятника длилось 16 сек, и при каждом размахе прикреплённое под шаром маятника остриё прочерчивало новую черту на песке, наглядно показывая вращение под ним помоста, а, следовательно, и всей Земли.
В основе опыта лежит свойство маятника сохранять плоскость колебаний независимо от вращения опоры, к которой маятник подвешен. Наблюдатель, вращающийся вместе с Землёй, видит постепенное изменение направления качаний маятника относительно окружающий земных предметов.
При практическом осуществлении опыта с маятником Фуко важно устранить причины, нарушающие его свободное качание. Для этого его и делают очень длинным, с тяжелым и симметричным грузом на конце. Маятник должен иметь одинаковую возможность качаться во всех направлениях, быть хорошо защищённым от ветра. Укрепляют маятник либо на карданном шарнире, либо на горизонтальном шарикоподшипнике, поворачивающемся вместе с плоскостью качания маятника. Большое значение для результатов опыта имеет пуск маятника без бокового толчка.
На первой публичной демонстрации опыта Фуко в Пантеоне именно для этого маятник и привязали бечёвкой. Когда маятник после привязывания пришел в состояние полного покоя, веревку пережгли, и он пришел в движение.
Так как маятник в Пантеоне совершал одно полное колебание за 16,4 с, вскоре стало видно, что плоскость качания маятника поворачивается по часовой стрелке относительно пола. При каждом следующем качании металлическое острие сметало песок примерно в 3 мм, от предыдущего места. Плоскость качания маятника за 32 ч совершила полный оборот и вернулась в прежнее положение.
Самая длинная нить - 98 метров – была у маятника Фуко, расположенного в Исаакиевском соборе в г. Санкт-Петербурге. Маятник снят в 1992 году, как не соответствующий назначению здания.
Теперь на Северо-Западе России есть лишь один маятник Фуко – в Санкт-Петербургском Планетарии. Длина его нити невелика – около 8 метров, но от этого степень наглядности не уменьшается. Этот экспонат Планетария вызывает неизменный интерес у посетителей всех возрастов.
М
аятник Фуко, размещающийся в настоящее время в вестибюле для посетителей здания Генеральной Ассамблеи Организации Объединённых Наций в Нью-Йорке, является даром правительства Нидерландов.Этот маятник представляет собой 200-фунтовый позолоченный шар диаметром 12 дюймов, частично наполненный медью и подвешенный на проволоке из нержавеющей стали под потолком над церемониальной лестницей в 75 футах от пола. Верхний конец проволоки закреплен с помощью универсального шарнира, что позволяет маятнику свободно качаться в любой вертикальной плоскости. При каждом колебании шар проходит над рельефным металлическим кольцом с электромагнитом, в результате чего в меди внутри шара наводится электрический ток. Это взаимодействие дает необходимую энергию для преодоления трения и сопротивления воздуха и обеспечивает равномерность качания маятника.
- Камертон (рис.10).
Применяется для точной настройки музыкальных инструментов.
Рис. 10
- Качели.
Рис. 11 
Рис.12Качели (рис. 10, рис. 11) — сооружение для качания как для забавы или развлечения. Устанавливаются на детских площадках, местах отдыха и т. д.
Виды качелей:
- сиденье, подвешенное между столбами. Подвес может быть как жёстким, так и нежёстким (используются верёвки/цепи);
- доска на подставке;
- тарзанка.
6.4. Рессора.
Рессо́ра - вид устройства, упругий элемент подвески транспортного средства. Рессора передаёт нагрузку с рамы или кузова на ходовую часть (колеса, опорные катки гусеницы и т. д.) и смягчает удары и толчки при прохождении по неровностям пути.
В
иды рессор:- листовая рессора (рис.12). Листовая рессора представляет собой пакет листов различной длины, изготовленных из закаленной стали и соединённых хомутами. В наиболее распространённом варианте рессорной подвески средняя часть пакета закреплена на ходовой части машины и опирается на неё, а концы закреплены на кузове с помощью подвижных соединений; Рис.12
- торсионная рессора. Основным рабочим элементом торсионной рессоры является торсион — упругий стержень, работающий на скручивание. Торсионные рессоры применяются, в основном, для подвесок бронемашин;
-
пружинная рессора (рис.13). В пружинной рессоре в качестве рабочего упругого элемента используется пружина. Могут использоваться цилиндрические, конические, параболоидные или тарельчатые пружины.Рис. 13
III. ЗАКЛЮЧЕНИЕ
Я выбрала для более глубокого изучения и исследования тему «Механические колебания», так как хотела расширить свои знания в этой области. В процессе выполнения исследований я убедилась в том, что некоторые гипотезы, сформулированные мной, подтвердились (гипотезы №№ 1, 4, 6, 9, 10, 11), а некоторые (гипотезы №№ 2, 3, 5, 7, 8) не подтвердились.
В итоге оказалось, что период и частота колебаний математического маятника зависят от длины нити; период и частота колебаний пружинного маятника зависят от массы груза и жесткости пружины; период и частота колебаний физического маятника зависят, видимо, от его формы; период и частота колебаний выбранного мной оборотного маятника зависят от массы шаров, от длины горизонтального стержня и от длины подвеса.
Мне было очень интересно узнать, что маятник Фуко просто и доступно объясняет тот факт, что Земля вращается вокруг своей оси, а плоскость качания маятника остается постоянной. Я узнала, что помимо всем известных качелей, колебательные системы используются для настройки музыкальных инструментов и даже для смягчения ударов и толчков в транспортных средствах. Для этого существуют рессоры.
Я думаю, что мне удалось достичь поставленной цели и выполнить сформулированные задачи.
IV. ЛИТЕРАТУРА
- Блудов М.И. Беседы по физике, часть 1// М.: «Просвещение», 1984.
- Верин А. Опыт Фуко// Л. – М., 1934.
- Гуревич А.Е. Физика-9. Учебник для общеобразовательных учебных заведений// М.: ДРОФА, 2001.
- Ландау Л.Д., Китайгородский А.И. Физика для всех// М.: издательство «Наука», 1974.
- Перышкин А.В., Гутник Е.М. Физика-9. Учебник для общеобразовательных учреждений// М.: ДРОФА, 2003.
- Роджерс Эрик Физика для любознательных, том 1//М.: издательство «Мир», 1970.
- Саенко П.Г. Физика-9. Учебник для 9 класса средней школы// М.: «Просвещение», 1992.
8. Электронная энциклопедия krugosvet.ru
9. Электронная энциклопедия Википедия.
- ПРИЛОЖЕНИЯ
Графики зависимости периода и частоты колебаний математического и пружинного маятника от параметров колебательной системы.
График 1
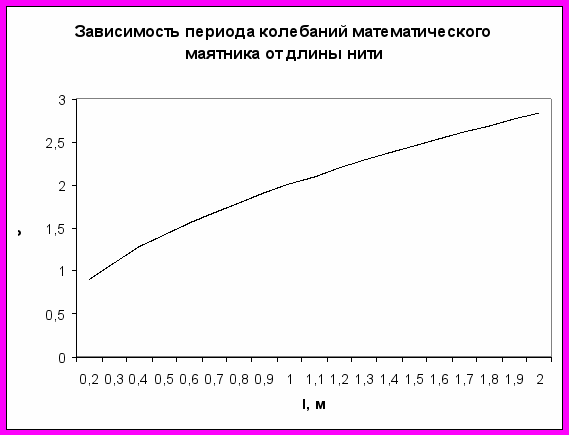
График 2
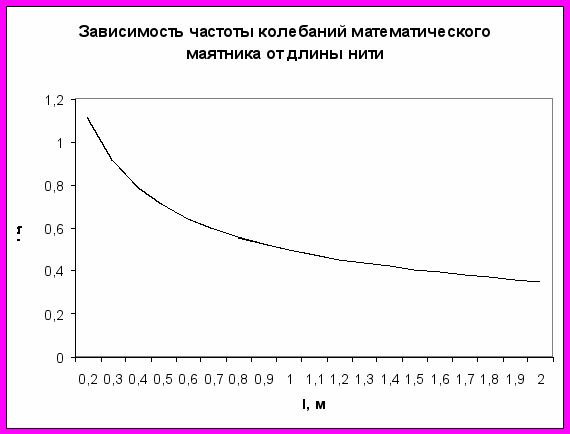
График 3
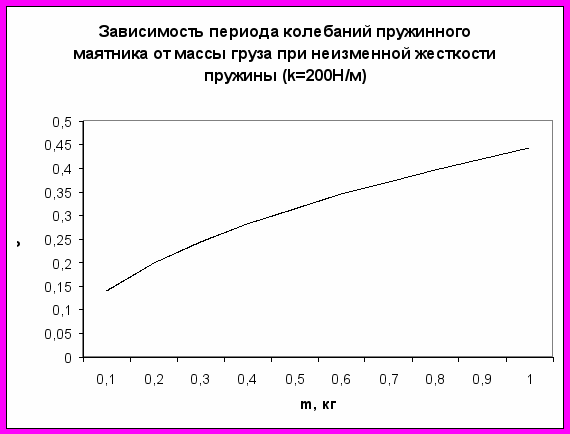
График 4
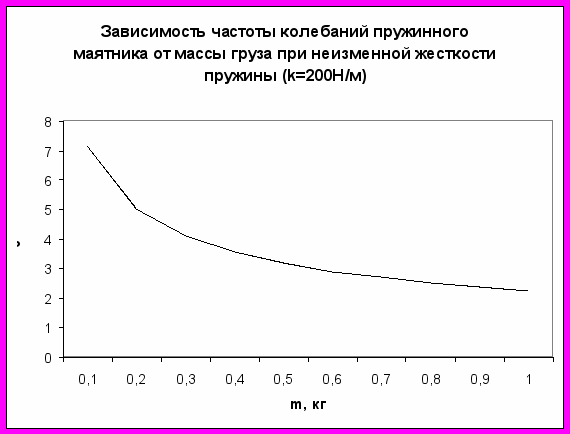
График 5
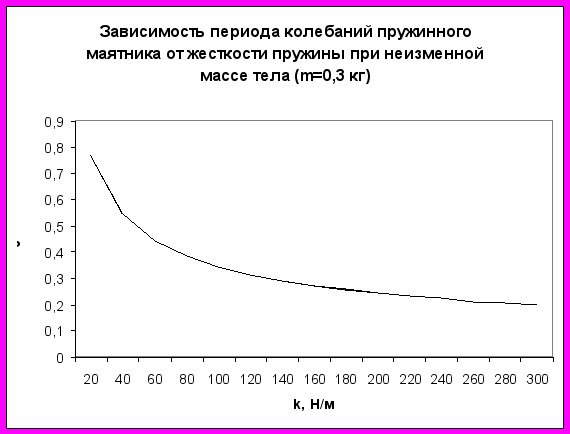
График 6
