Михаилом Васильевичем Ломоносовым, когда он издал первый в России учебник
| Вид материала | Учебник |
- Михаилом Васильевичем Ломоносовым, когда он издал первый в России учебник, 60.16kb.
- На районный конкурс сочинений, посвящённый 300- летию со дня рождения М. В. Ломоносова, 50.98kb.
- Урок в 6А классе по теме: «Великий сын России М. В. Ломоносов», 152.75kb.
- Первый почетный гражданин города в. А. Меньшиков, 53.56kb.
- Стенограмма прямой телефонной линии с ректором Ижгту иваном Васильевичем Абрамовым, 170.13kb.
- Какое пособие для обучения грамоте было написано Ломоносовым и в каком году? 15. Развитие, 135.11kb.
- Учебник является единым комплексом программ, который, 38.85kb.
- План-конспект занятия в объединении «Глиняная игрушка» на тему: «Творческая встреча, 61kb.
- Н. С. Тимофеев Муниципальное право России: учебник, 8003.95kb.
- Первый русско-корейский словарь М. Пуцилло, 65.2kb.
Лекция 1.
Введение.
Термин «физика» впервые появился в сочинениях одного из величайших мыслителей древности — Аристотеля, жившего в IV веке до нашей эры. Физика была тесно связана с философией, первоначально даже термины «физика» и «философия» были синонимами, поскольку обе дисциплины пытаются объяснить законы функционирования Вселенной.
Филосо́фия (др.-греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω — люблю и σοφία — мудрость) — дисциплина, изучающая наиболее общие существенные характеристики и фундаментальные принципы бытия и познания, бытия человека, отношения человека и мира.
Фи́зика (от др.-греч. φύσις «природа») — наука, изучающая наиболее общие и фундаментальные закономерности, определяющие структуру и эволюцию материального мира.
В результате научной революции1 XVI века физика выделилась в отдельное научное направление.
В русский язык слово «физика» было введено Михаилом Васильевичем Ломоносовым, когда он издал первый в России учебник физики в переводе с немецкого языка.
В современном мире значение физики чрезвычайно велико. Всё то, чем отличается современное общество от общества прошлых веков, появилось в результате применения на практике физических открытий. Так, исследования в области электромагнетизма привели к появлению телефонов, открытия в термодинамике позволили создать автомобиль, развитие электроники привело к появлению компьютеров.
Несмотря на огромный объём накопленных знаний, современная физика ещё очень далека от того, чтобы объяснить все явления природы.

Рисунок 1. Схема развития физического знания
Процесс познания в физике начинается либо с наблюдения некоторого (обычно – повторяющегося) явления в естественных условиях, либо со специально поставленных опытов-экспериментов. На основе накопленного экспериментального материала путем обобщения строится некоторое предварительное предположение – гипотеза. Гипотезы, выдерживающие проверку, превращаются в законы. Физические законы — устойчивые повторяющиеся объективные закономерности, существующие в природе. Физические теории, как правило, базируются на нескольких физических законах, и способны не только удовлетворительно объяснять известные явления, но и могут предсказывать новые явления и закономерности.
Появление достоверного опыта, не согласующегося с существующей теорией, является побудительным толчком к созданию новой, более совершенной теории или к уточнению существующей. Как правило, «хорошие» теории не отвергаются полностью, а входят как составная часть или предельный случай существующей (пример – классическая и релятивистская механика). Реализуется известный принцип развития вверх по спирали, что можно прокомментировать схемой рис.1.
Исторически физика подразделяется на несколько взаимосвязанных частей (рис.2). В нашем курсе рассматриваются только некоторые из них.
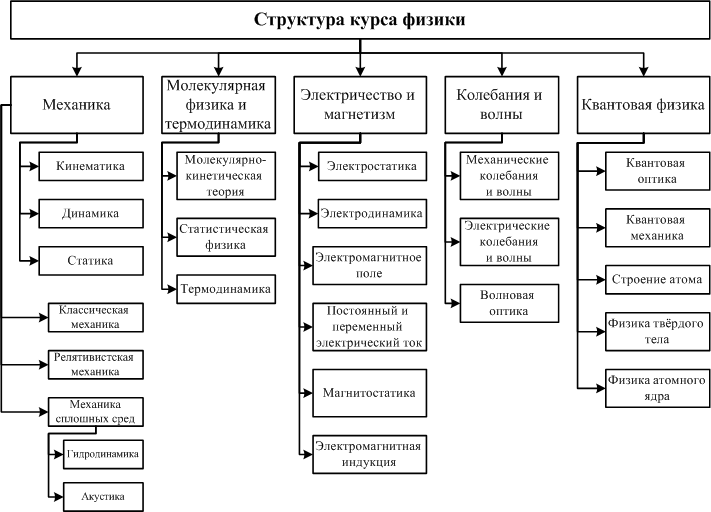
Рисунок 2. Структура курса физики
Часто, говоря о структуре физики, разделяют макроскопическую и микроскопическую физику:
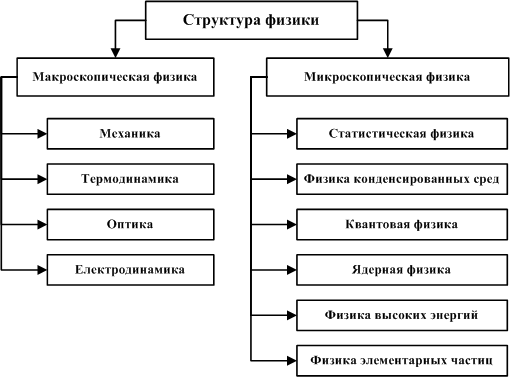
Рисунок 3. Структура физики
Изучая физику, мы будем иметь дело с физическими величинами. Необходимо ясно представлять себе, что такое физическая величина, чем она отличается от математической иди от величин, рассматриваемых в других науках. Физическую величину с помощью специальных средств измеряют для нахождения её значения в принятых единицах. Если единицы физических величин выбирать произвольно, возникнут трудности при их сравнении. Поэтому применяют стандартные системы единиц. В настоящее время обязательной к применению является СИ - Система Интернациональная, которая строится на семи основных единицах — метр, килограмм, секунда, ампер, кельвин, моль, кандела — и двух дополнительных — радиан и стерадиан.
Метр (м) —длина пути, проходимого светом в вакууме за 1/299792458 с.
Килограмм (кг) — масса, равная массе международного прототипа килограмма (платиноиридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре, близ Парижа).
Секунда (с) — время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Ампер (А) — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создает между этими проводниками силу, равную 2∙10-7 Н на каждый метр длины.
Кельвин (К) — 1/273,16 часть термодинамической температуры тройной точки воды2.
Моль (моль) — количество вещества системы, содержащей столько же структурных элементов, сколько атомов содержится в нуклиде 12С массой 0,012 кг.
Кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540∙1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср. (Раньше это определение исходило из люмена, кандела – сила света точечного источника в направлениях, где он испускает световой поток 1 лм, одинаково распределённый в телесном угле 1 ср).
Радиан (рад) — угол между двумя радиусами окружности, длина дуги между которыми равна радиусу.
Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
Для установления производных единиц используют физические законы, связывающие их с основными единицами. Например, из формулы равномерного прямолинейного движения v = s/t (s - пройденный путь, t - время) производная единица скорости получается равной 1 м/с.
-
Физические основы механики
Окружающий нас мир, всё существующее вокруг нас и обнаруживаемое нами посредством ощущений представляет собой материю. В настоящее время известны два вида неживой материи – вещество и поле. Неотъемлемым свойством материи и формой её существования является движение. Движение в широком смысле слова — это всевозможные изменения материи — от простого перемещения до сложнейших процессов мышления. Движение несотворимо и неуничтожимо, как и сама материя. Материя существует и движется в пространстве и во времени, которые являются формами бытия материи.
Механическое движение — это изменение в пространстве с течением времени взаимного расположения тел или их частей.
Механика — часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.
Механика делится на три раздела: 1) кинематику; 2) динамику; 3) статику.
Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают.
Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение.
Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.
Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед (287—212 до н. э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564—1642) и окончательно сформулированы английским ученым И. Ньютоном (1643—1727).
Механика Галилея — Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью с, изучаются релятивистской механикой, основанной на специальной теории относительности, сформулированной А.Эйнштейном (1879—1955). Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики неприменимы — они заменяются законами квантовой механики.
-
Кинематика. Основные понятия кинематики
Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчёта. Оно считается неподвижным (для данной задачи).
Положение тела в пространстве описывается с помощью системы координат. Реальное пространство трёхмерно, и положение материальной точки в любой момент времени полностью определяется тремя числами — её координатами в выбранной системе отсчета.
Как правило, используют прямоугольную, или декартову, систему координат3. Для описания движения точки, кроме тела отсчёта и системы координат, необходимо ещё иметь часы – устройство, с помощью которого можно измерять различные отрезки времени.
Тело отсчёта, система координат и связанные с ней часы образуют систему отсчета.
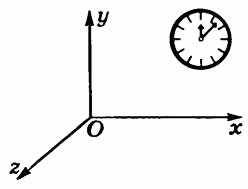
Рисунок 4. Система отсчёта
OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Возьмем какую-нибудь точку в пространстве, М (x, y, z). Здесь x, y, z – координаты точки М в данной системе координат. Проведем из начала координат к точке М вектор
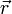 . Этот вектор называется радиус–вектором точки М.
. Этот вектор называется радиус–вектором точки М.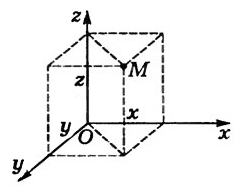
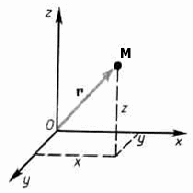
Рисунок 5. Точка и её координаты
Положение точки M в данный момент времени в выбранной системе отсчёта характеризуется тремя координатами х, у и z или радиус-вектором
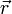 , проведенным из начала системы координат в данную точку (рис. 5).
, проведенным из начала системы координат в данную точку (рис. 5).Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.
Единичный вектор, направленный вдоль оси x,обозначается
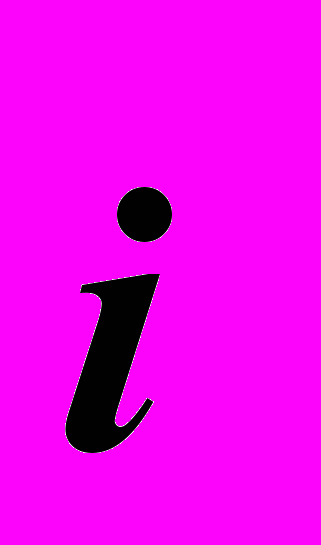 . Единичный вектор, направленный вдоль оси y, обозначается
. Единичный вектор, направленный вдоль оси y, обозначается 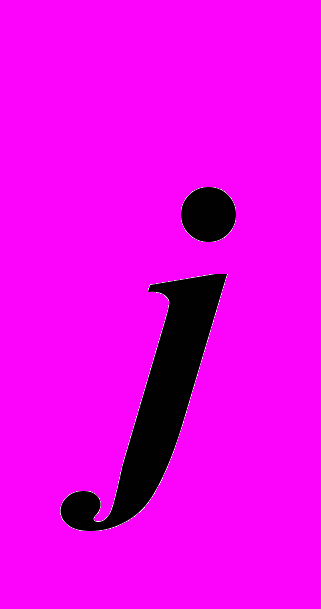 . Единичный вектор, направленный вдоль оси z, обозначается
. Единичный вектор, направленный вдоль оси z, обозначается  .
. Вектора
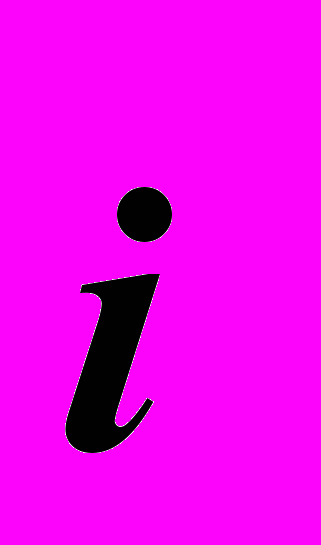 ,
, 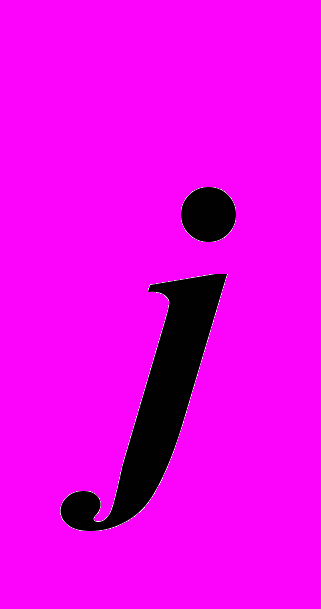 ,
,  называются координатными векторами. Радиус-вектор точки М можно представить в виде суммы произведений ортов на соответствующие координаты точки М:
называются координатными векторами. Радиус-вектор точки М можно представить в виде суммы произведений ортов на соответствующие координаты точки М: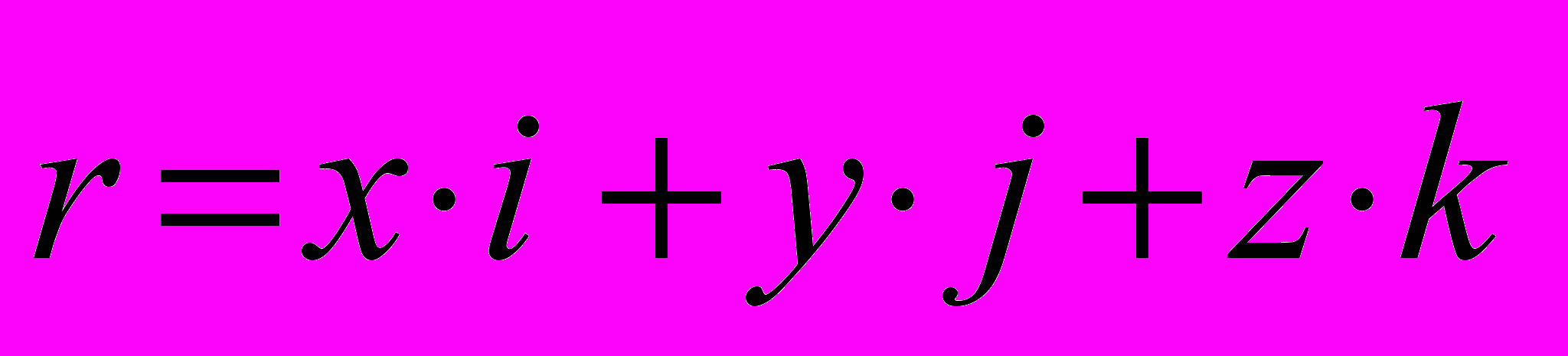
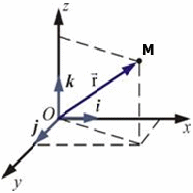
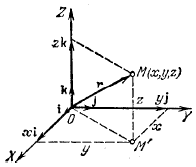
Рисунок 6. Орты и радиус-вектор точки.
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.
Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.
Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным.
Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (y = f(x) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
В зависимости от скорости различают равномерное (скорость не изменяется) и неравномерное (ускоренное, равноускоренное, прерывистое) движение.
Схематично это можно представить так:
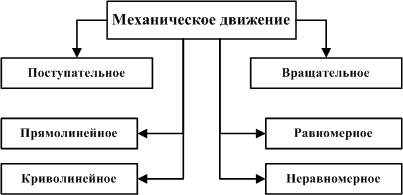
Рисунок 7. Механическое движение
Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s > 0.
Перемещение
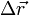 тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M0) и конечное (точка М) положение тела (см. рис. 8):
тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M0) и конечное (точка М) положение тела (см. рис. 8):
где
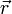 и
и 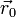 — радиус-векторы тела в эти моменты времени.
— радиус-векторы тела в эти моменты времени.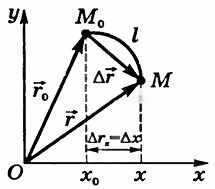
Рисунок 8. Путь и перемещение
Проекция перемещения на ось Ox:
 , где x0 и x — координаты тела в начальный и конечный моменты времени.
, где x0 и x — координаты тела в начальный и конечный моменты времени.Модуль перемещения не может быть больше пути:
 .
.Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
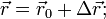
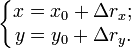
Если бы мы рассматривали движение тела в пространстве, добавилось бы третье уравнение:
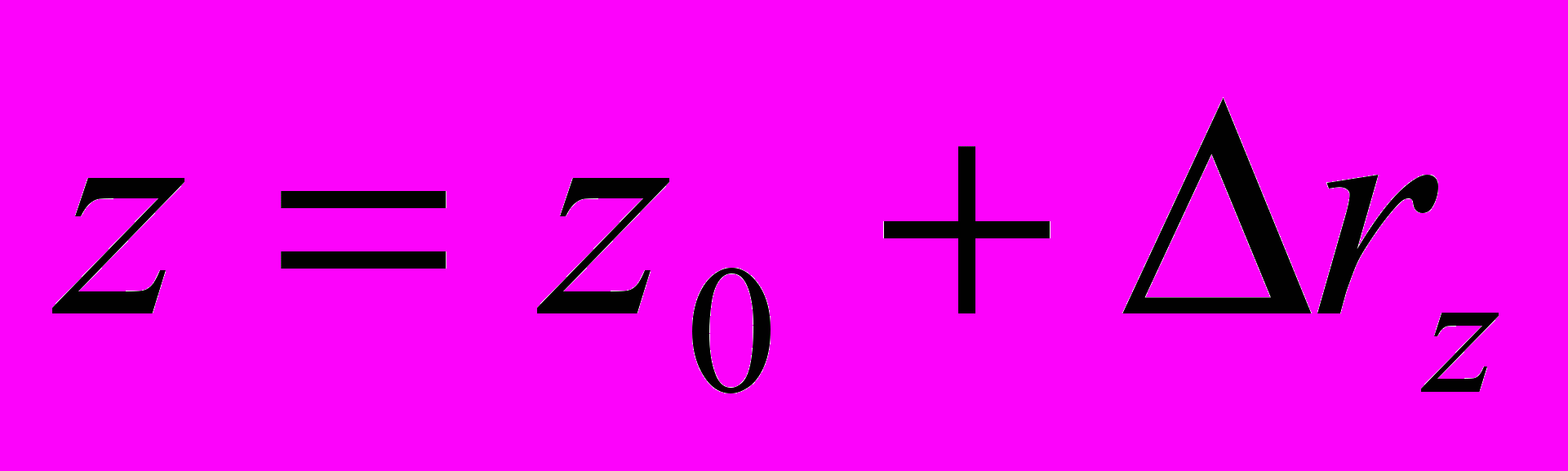 ,
,Таким образом, изменения радиус-вектора описываются функцией координат и времени:
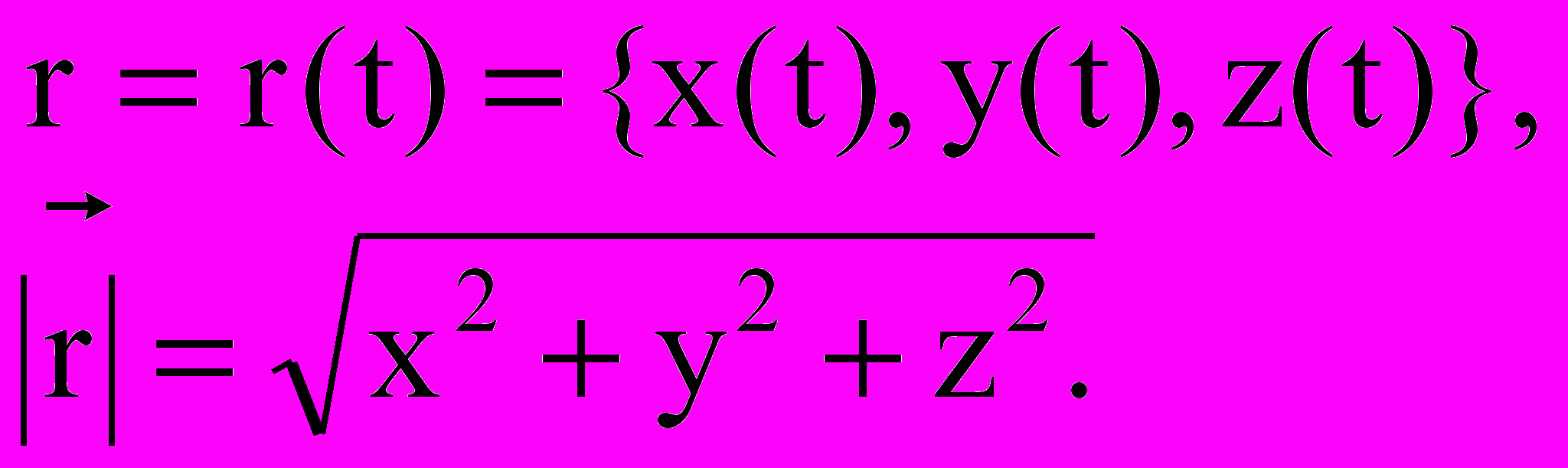
Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.
Часто бывают важны усреднённые значения физических величин. Для их обозначения используется знак ¯ или < >.
Средняя скорость
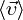 — векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 7):
— векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 7):
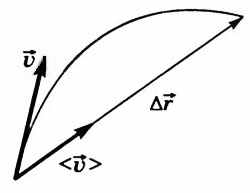
Рисунок 9. Скорость
В СИ единицей скорости является метр в секунду (м/с).
Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.
Иногда пользуются средней скоростью пути:
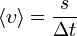 , где s — путь, пройденный за промежуток времени Δt. Средняя скорость пути — это скалярная величина.
, где s — путь, пройденный за промежуток времени Δt. Средняя скорость пути — это скалярная величина.Мгновенная скорость
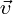 тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени
тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени 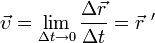 . Здесь
. Здесь 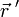 — производная от радиус-вектора по времени.
— производная от радиус-вектора по времени.Мгновенная скорость
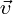 , таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени.
, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени.В проекции на ось Ох:
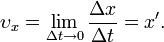
Аналогичные формулы можно записать для проекций вектора скорости на другие оси.
Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 9).
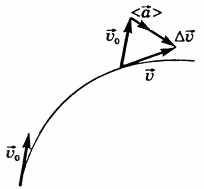
Рисунок 10
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.
Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:

Вектор
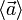 направлен параллельно вектору изменения скорости
направлен параллельно вектору изменения скорости 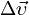 (
( ) в сторону вогнутости траектории (рис. 8).
) в сторону вогнутости траектории (рис. 8).Мгновенное ускорение:
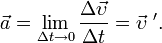
В СИ единицей ускорения является метр на секунду в квадрате (м/с2).
В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.
При прямолинейном движении с возрастающей по модулю скоростью (рис. 9, а) векторы
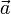 и
и 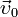 сонаправлены (
сонаправлены (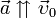 ) и проекция ускорения на направление движения положительна.
) и проекция ускорения на направление движения положительна.При прямолинейном движении с убывающей по модулю скоростью (рис. 9, б) направления векторов
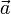 и
и 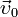 противоположны (
противоположны (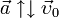 ) и проекция ускорения на направление движения отрицательна.
) и проекция ускорения на направление движения отрицательна.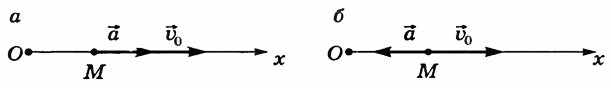
Рисунок 11
Вектор
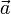 при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости
при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости 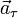 и перпендикулярно скорости
и перпендикулярно скорости 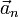 (рис. 10),
(рис. 10), 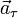 — тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении,
— тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, 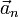 — нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении. Модуль ускорения
— нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении. Модуль ускорения 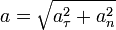 .
.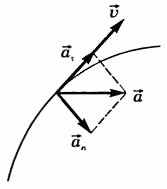
Рисунок 12
Длина пути, пройденного точкой за промежуток времени от t1 до t2, определяется интегралом
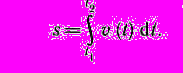
В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда это выражение примет вид
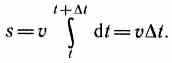
1 Революция в науке — период развития науки, во время которого старые научные представления замещаются частично или полностью новыми, несовместимыми со старыми представлениями. Так, отрезок времени примерно от даты публикации работы Николая Коперника «Об обращениях небесных сфер» (De Revolutionibus), то есть с 1543 г., до деятельности Исаака Ньютона, сочинение которого «Математические начала натуральной философии» было опубликовано в 1687 г., обычно называют периодом «научной революции»
2 Тройна́я то́чка воды́ — строго определенные значения температуры и давления, при которых вода может одновременно и равновесно существовать в виде трёх фаз — в твердом, жидком и газообразном состояниях. Тройная точка воды — температура 273,16 К и давление 611,73 Па.
3 Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
