Диссипативные структуры и нестационарные процессы в межфазной гидродинамике 01. 02. 05 Механика жидкости, газа и плазмы
| Вид материала | Автореферат диссертации |
- Паспорт специальности 01. 02. 05 Механика жидкости, газа и плазмы Шифр специальности:, 20.82kb.
- Аэродинамика сверхзвукового пространственного обтекания затупленных тел при наличии, 340.26kb.
- Ровенская Ольга Игоревна Применение кинетических и Навье-Стокса уравнений для описания, 851.64kb.
- Назначение приборов для расхода и количества жидкости, газа и пара, 171.6kb.
- Программа-минимум кандидатского экзамена по специальности 01. 02. 05 «Механика жидкостей,, 69.43kb.
- Рабочая программа учебной дисциплины механика жидкости и газа Кафедра-разработчик, 13.38kb.
- Примерная программа дисциплины гидравлика (механика жидкости и газа) Рекомендуется, 377.85kb.
- Подсекция: Механика жидкости и газа, 203.35kb.
- К рабочей программе учебной дисциплины, 21.38kb.
- Аннотация примерной программы учебной дисциплины «Механика жидкости и газа» Цели, 60.08kb.
На правах рукописи
Макарихин Игорь Юрьевич
ДИССИПАТИВНЫЕ СТРУКТУРЫ
И НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ
В МЕЖФАЗНОЙ ГИДРОДИНАМИКЕ
01.02.05 – Механика жидкости, газа и плазмы
Автореферат
диссертации на соискание ученой степени
доктора физико-математических наук
Пермь - 2010
Диссертационная работа выполнена на кафедре общей физики Пермского государственного университета
| Официальные оппоненты: | доктор физико-математических наук, профессор Кузнецов Владимир Васильевич | |
| | | |
| | доктор физико-математических наук, профессор Селезнев Владимир Дмитриевич | |
| | | |
| | доктор физико-математических наук, профессор Любимова Татьяна Петровна | |
| | | |
| | | |
| Ведущая организация: | Институт проблем механики РАН, Москва | |
| | | |
| | ||
| Защита состоится 6 мая 2010 г. в 14 часов на заседании диссертационного совета Д 004.012.01 в Институте механики сплошных сред УрО РАН по адресу: 614013, г. Пермь, ул. Академика Королева, 1, Институт механики сплошных сред УрО РАН. Сайт ru. | ||
| | ||
| С диссертацией можно ознакомиться в библиотеке Института механики сплошных сред УрО РАН | ||
| | ||
| | ||
| Автореферат разослан "_____"____________________ 2010 г. | ||
| | ||
| Ученый секретарь диссертационного совета |  И.К. Березин | |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Диссертация охватывает широкий круг вопросов, объединенных стержневой проблемой: равновесие, движение и устойчивость различных диссипативных систем, в которых поверхностные (капиллярные) силы являются определяющими факторами изучаемых процессов. Данную проблематику традиционно относят к межфазной гидродинамике – науке, теоретический фундамент которой заложил более ста лет назад Дж. В. Гиббс своей работой «О равновесии гетерогенных веществ». Развитие идей Гиббса привело к созданию физико-химической гидродинамики, из которой выделилась более узкая область – гидродинамика межфазных поверхностей, лежащая на пересечении традиционной гидродинамики с коллоидной химией и другими физико-химическими науками.
В последнее время межфазная гидродинамика развивается особенно бурно. Причин тому несколько. Во-первых, главной причиной является использование возможностей, которые открылись с появлением компьютеров. Стали доступными эксперименты и расчёты, ранее немыслимые из-за сложности; значительно расширился арсенал математических средств.
Во-вторых, научно-техническая революция, бурное развитие техники ставят перед исследователями всё более сложные задачи. Гетерогенные системы – едва ли не основные объекты современной техники. Потребности экологии, металлургической, нефтяной, химической отраслей промышленности вынуждают физиков переходить к изучению сложных систем в самых разнообразных условиях. Особое внимание к исследованиям по данной тематике обусловлено разработками в области космических технологий и систем обеспечения орбитальных станций. В биологии капиллярные эффекты изучаются в связи с движением бактерий и клеточных микрообъектов; в медицине – в контексте проблем распространения сурфактантов при легочных заболеваниях и заболеваниях крови; в математике ветвление равновесных форм и конвективная неустойчивость, вызванная капиллярными эффектами, дают новые примеры для синергетики. В общем плане следует исходить из того, что человечество по мере расходования полезных ископаемых и совершенствования техники все интенсивнее должно переходить к микро - и нанотехнологиям, когда поверхностная энергия полезного материала становится важнейшим фактором.
В-третьих, изучение взаимодействия различных по физической природе сил определяется логикой развития самих естественных наук. Изучаемые в работе структуры относятся к открытым системам. Больцман был в своё время первым и почти единственным, кто понял, что изучение неравновесных процессов в открытых физических системах является одной из важнейших задач естествознания. Принципиально новым шагом в этом направлении была развитая Эйнштейном, Смолуховским и Ланжевеном теория броуновского движения, которая стала рабочим инструментом при рассмотрении многих физических явлений.
Благодаря сложности открытых систем в них возможно образование различного рода структур, для самоорганизации или деградации которых необходимо наличие диссипации. Чтобы подчеркнуть это обстоятельство, И. Пригожин ввёл термин «диссипативные структуры». Среди них, однако, к настоящему времени хорошо изученными можно считать только автоколебания в генераторах, ячейки Бенара и автоволны на поверхности жидкости – соответственно временные, пространственные и пространственно-временные диссипативные структуры.
Цель работы – экспериментальное и теоретическое исследование гидродинамических эффектов в задачах межфазной конвекции с точки зрения возникновения диссипативных структур, а также их качественное и количественное объяснение при помощи соответствующих математических моделей.
Научная новизна. В работе впервые рассмотрены малоизученные или неизвестные ранее диссипативные структуры, в которых конкуренция поверхностных и объёмных сил различной физической природы приводит к появлению новых структур. Показано, что конечным этапом их эволюции может стать как самоорганизация, так и наступление физического или динамического хаоса. Для этой цели впервые:
- теоретически и экспериментально исследованы процессы слияния капель в невесомости (техника Плато) и капель, плавающих на горизонтальной поверхности жидкости;
- выполнены эксперименты по изучению явления кумуляции при ударе капли о свободную поверхность другой или той же самой жидкости, заполняющей неглубокую кювету с наклонным к горизонту дном, построена математическая модель явления;
- для определения условий, в которых линейное натяжение превалирует над поверхностным, проведена серия экспериментов с каплями насыщенного водой четырёххлористого углерода, удерживаемого капиллярными силами на поверхности воды, предварительно насыщенной CCl4;
- проведены экспериментальные и теоретические исследования разрушения пузырей, изучена зависимость от времени средних размеров плёнки, остающейся от пузыря непосредственно перед завершением процесса;
- проведены эксперименты по изучению явления неслияния соприкасающихся капель, которые доказывают, что причиной эффекта является втягивание воздуха в зазор между ними;
- изучены типичные неустановившиеся и стационарные течения во вращающихся жидкостях. Теоретически исследовано влияние вращения на конвективные движения индивидуальных жидкостей и растворов, заполняющих сферическую полость в неоднородно нагретом твёрдом массиве, в котором на бесконечности поддерживается постоянный градиент температуры;
- экспериментально и теоретически изучен дрейф шаров во вращающихся жидкостях. Получены экспериментальные данные зависимости скорости дрейфа шаров от числа Рейнольдса, определённого по угловой скорости вращения и радиусу шара;
- результаты проведенных экспериментов по неустойчивости стекающих струй к меандрированию проанализированы с помощью метода, предложенного Ланжевеном для анализа движения броуновской частицы. Показано, что единственным параметром, формирующим режим, может служить отношение параметра Ланжевена D (коэффициент диффузии в пространстве скоростей) к диссипативному фактору . Экспериментально и аналитически методом преобразования Лапласа определена функция распределения, которая позволяет предсказывать вероятности меандрирования стекающей струи любой длины;
- в группе задач по изучению пространственно-временных диссипативных структур решена задача о термокапиллярной конвекции от линейного источника тепла и проведено исследование полученного решения на устойчивость по отношению к разного рода возмущениям.
Достоверность результатов диссертационной работы обеспечивается количественным совпадением полученных в работе теоретических зависимостей с результатами экспериментов, специально поставленных автором диссертации, так и с данными других исследователей; применением стандартных аналитических, асимптотических и численных методов; совпадением асимптотических и численных результатов; использованием различных геометрических и физических моделей исследуемых процессов и состояний и сравнением результатов с известными теориями.
Научная и практическая значимость результатов диссертационной работы заключается в том, что в ней решены многочисленные и разнообразные по физическому содержанию задачи, интересные как в плане поиска новых примеров ветвления равновесных состояний или конвективной неустойчивости, так и в чисто практическом применении результатов в межфазной тензиометрии, наземных и космических технологиях. Разработанная методика и результаты используются в научно-исследовательской работе в Пермском государственном университете, в Пермском педагогическом университете, Институте механики сплошных сред и Институте экологии и генетики микроорганизмов УрО РАН, в Ивановском государственном университете, в Мадридском политехническом университете (Испания), в университетах городов Лавборо и Эдинбург (Великобритания), а также в учебном процессе в Пермском государственном университете в лекциях, лабораторных практикумах, а также включены в учебные пособия по курсам «Межфазная гидродинамика», «Гидромеханика невесомости» и «Динамика жидкостей с особыми свойствами».
Диссертационная работа выполнялась в рамках разрабатываемой кафедрой общей физики Пермского государственного университета темы «Конвекция и теплообмен в ламинарном, переходном и турбулентном режимах; влияние осложняющих факторов на конвективную и гидродинамическую устойчивость». Исследования являются также составной частью Государственной программы поддержки ведущих научных школ (гранты № 96-15-96084 и № 00-15-00112), Международного научно-технического проекта «Конвективные явления и процессы тепломассопереноса в условиях невесомости и микрогравитации», Федеральной целевой программы «Интеграция» (грант № 98-06), программы «Университеты России» (направление II, «Неравновесные процессы в макроскопических системах»), проектов «Гидродинамическая неустойчивость и дрейф жидких деформируемых включений в макрогетерогенных системах» Минобразования РФ (1999, 2001 гг.). Работы выполнялись при финансовой поддержке грантов РФФИ 96-01-01738, 98-010-00507, 06-01-72031, 06-08-00752, 07-01-96040 и 09-01-00846, грантов INTAS-94-529 и INTAS-99-01505, гранта CRDF PE-009-0.
Апробация работы. Результаты исследований докладывались на IX Школе-семинаре «Нелинейные задачи теории гидродинамической устойчивости" (Москва, 1993), II International Conference on Nonlinear Mechanics (Beijing, China, 1993), на третьей международной конференции «Современные проблемы электрогидродинамики и электрофизики жидких диэлектриков» (Санкт-Петербург, 1994), International Workshop «Non-gravitational Mechanisms of Convection and Heat/mass Transfer» (Zvenigorod, 1994), IX European Symposium «Gravity-depended Phenomena in Physical Sciences» (Berlin, Germany, 1995), на XII и XVI зимних школах по механике сплошных сред (Пермь, 1999, 2009), на XIII International Conference on Dielectric Liquids (Nara, Japan, 1999), II International Workshop “Two-Phase Systems for Ground and Space Applications” (Kyoto, Japan, 2007), III International Symposium on Physical Sciences in Space (Nara, Japan, 2007), на Пермском городском гидродинамическом семинаре им. Г.З. Гершуни и Е.М. Жуховицкого, научном семинаре Института механики сплошных сред УрО РАН (рук. акад. РАН В.П. Матвеенко), семинаре по прикладной механике сплошных сред Института проблем механики РАН.
Публикации. Основные результаты диссертации опубликованы в 22 работах, в том числе монографии.
Личный вклад автора. Работы [1, 2, 5, 7, 18, 21] выполнены автором лично, В работе [3] автору принадлежит математическая модель наблюдаемых явлений, аналитические и численные расчеты, физическая интерпретация результатов; в работах [4, 9-13] – постановка задачи, аналитические и численные расчеты, интерпретация результатов, в работе [6] – участие в измерениях, обработке экспериментальных результатов, в работе [8] – участие в постановке задачи, измерения, обработка результатов, в работах [14, 16, 17, 19, 20, 22] – экспериментальные и теоретические результаты, участие в обработке результатов, их интерпретация.
Структура и объём работы. Диссертация состоит из введения (первая глава), четырех глав с изложением результатов, шести приложений, заключения и списка цитированной литературы, включающего 179 наименований. Общий объем диссертации 435 страниц, включая 121 рисунок и 4 таблицы.
Автор благодарен Ю.К. Братухину и С.О. Макарову за постоянное внимание к работе, полезные обсуждения и ценные советы.
СОДЕРЖАНИЕ ДИССЕРТАЦИИ
В первой главе дана общая характеристика диссертационной работы, обоснована ее актуальность, сформулирована цель исследования, отмечены новизна, практическая и научная ценность полученных результатов, их достоверность.
Вторая глава диссертации посвящена экспериментальному и теоретическому исследованию процессов слияния капель жидкости, происходящих в различных внешних условиях. В п. 2.1 приведен обзор литературы, в п. 2.2 – изложено состояние проблемы на сегодняшний день. В разделе 2.3 изучены начальные стадии слияния капель с учётом их деформации в пренебрежении вязкостью на основе принципов Гиббса. В п. 2.4 содержится теория слияния капель на конечных стадиях процесса в полной гидродинамической постановке с использованием уравнений Навье-Стокса и непрерывности. Здесь форма капель аппроксимирована эллипсоидом с малым эксцентриситетом.
Выводы теории проверены в специально поставленных экспериментах, которые описаны в п. 2.5. Основная экспериментальная установка состояла из двух прозрачных, вставленных одна в другую кубических полостей, стенки которых были изготовлены из плексигласа. Пространство между полостями заполнялось термостатированной водой. Во внутреннюю полость заливалась рабочая жидкость – водный раствор спирта, в который с помощью шприца помещались две капли силиконового масла объемом V = 2.5-5 см3. Подбором степени плотности водного раствора и температуры добивалось равенство плотностей обеих жидкостей (техника Плато). Поскольку капельки силиконового масла при соприкосновении друг с другом не сливались и вели себя как упругие тела (сходное явление упругого отражения соударяющихся капель исследовано в п. 2.7 диссертации), приходилось протыкать их иглой диаметра 0.13 мм. Наблюдение за характером слияния сфер производилось визуально и с помощью съёмки на видеокамеру с дальнейшей покадровой обработкой. Типичная последовательность кадров приведена на рис. 1. По измеренным расстояниям между крайними точками сливающихся капель были построены графики зависимости размеров капли от времени (рис. 2), где квадратиками отмечены экспериментальные точки, сплошная линия – теория.
 |
| Рис. 1 |
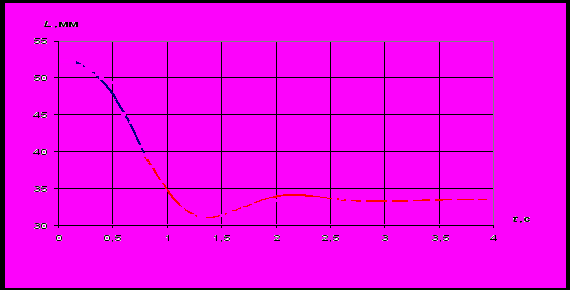 |
| Рис. 2 |
В разделе 2.6 представлены результаты экспериментального изучения слияния двух одинаковых капель четыреххлористого углерода, плавающих на поверхности дистиллированной воды. Методика эксперимента не отличалась от изложенной в п. 2.5. Приведены графики зависимости расстояния между крайними точками сливающихся капель от времени, построенные по результатам экспериментов и предложенной теории. Констатируется количественное согласие теоретических и экспериментальных результатов.
В п. 2.7 изучен эффект неслияния прижатых друг к другу капель с помощью специально разработанного для этой цели нового метода контакта свободной капли с периодически движущейся поверхностью. В данном методе основной объем жидкости приводится в периодическое вертикальное колебательное движение, в результате которого на свободной поверхности жидкости возникает стоячая волна. Капля жидкости помещается на эту поверхность. При достаточно больших скоростях движения поверхности капля не коагулирует с основным объемом жидкости из-за значительной разности в скоростях движения. Имеется возможность определять скорость, при которой исчезает коагуляция двух объемов жидкости, менять геометрические параметры капли, задавать силовые характеристики взаимодействия. Таким образом, появляется возможность более детально исследовать явление исчезновения коагуляции пары объемов жидкости.
