Диссипативные структуры и нестационарные процессы в межфазной гидродинамике 01. 02. 05 Механика жидкости, газа и плазмы

Вид материала

Автореферат диссертации

Содержание В четвертой главе исследовано образование пространственно-временных диссипативных структур в различных конвективных задачах. Пятая глава

Подобный материал:

• Паспорт специальности 01. 02. 05 Механика жидкости, газа и плазмы Шифр специальности:, 20.82kb.
• Аэродинамика сверхзвукового пространственного обтекания затупленных тел при наличии, 340.26kb.
• Ровенская Ольга Игоревна Применение кинетических и Навье-Стокса уравнений для описания, 851.64kb.
• Назначение приборов для расхода и количе­ства жидкости, газа и пара, 171.6kb.
• Программа-минимум кандидатского экзамена по специальности 01. 02. 05 «Механика жидкостей,, 69.43kb.
• Рабочая программа учебной дисциплины механика жидкости и газа Кафедра-разработчик, 13.38kb.
• Примерная программа дисциплины гидравлика (механика жидкости и газа) Рекомендуется, 377.85kb.
• Подсекция: Механика жидкости и газа, 203.35kb.
• К рабочей программе учебной дисциплины, 21.38kb.
• Аннотация примерной программы учебной дисциплины «Механика жидкости и газа» Цели, 60.08kb.

В четвертой главе исследовано образование пространственно-временных диссипативных структур в различных конвективных задачах.

В п. 4.1 представлены результаты изучения электроконвективной неустойчивости слабопроводящей жидкости в вертикальном конденсаторе. Раздел 4.1.1 содержит подробный обзор работ по устойчивости течений в слое между двумя вертикальными параллельными плоскостями, нагретыми до разных температур и классификацию типов неустойчивости, п. 4.1.2 посвящён изложению работ по электроконвекции. Даётся классификация механизмов электризации жидких диэлектриков и их влияние на электроконвекцию.

В п. 4.1.3 изложено численное решение задачи о электроконвекции в плоском вертикальном слое слабопроводящей жидкости при следующих допущениях: величина тока, протекающего по жидкости, мала, что позволяет не учитывать джоулево тепловыделение при определении поля температур и пренебречь влиянием возникающих магнитных полей; электризация жидкости создается токами проводимости, и, следовательно, возникающие в объёме жидкости силы обусловленные неоднородной поляризацией, значительно меньше сил Кулона; свободные заряды возникают только вследствие неоднородности электропроводности, вызванной неизотермичностью жидкости. Влияние механизма инжекционного зарядообразования считается пренебрежимо малым; жидкость механически несжимаема, течение ламинарное, нестационарное, плоское; уравнение свободной конвекции записано в приближении Буссинеска; все термодинамические параметры жидкости постоянны, кроме проводимости, линейно изменяющейся с температурой.

В этих условиях известная система уравнений электроконвекции имеет следующий вид:




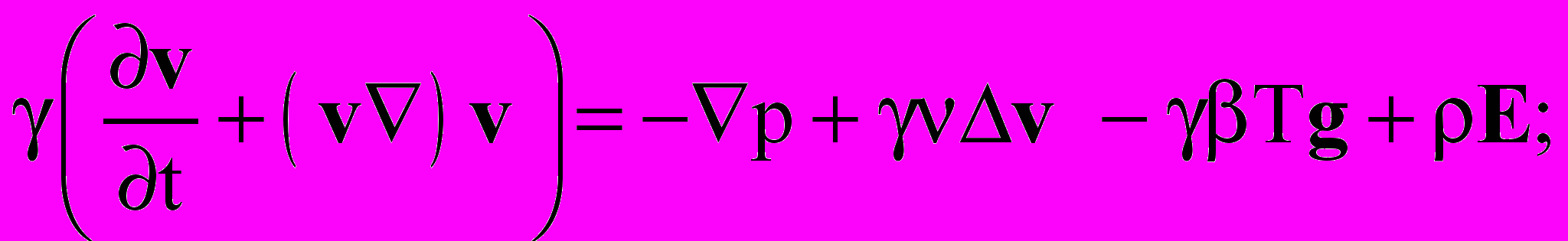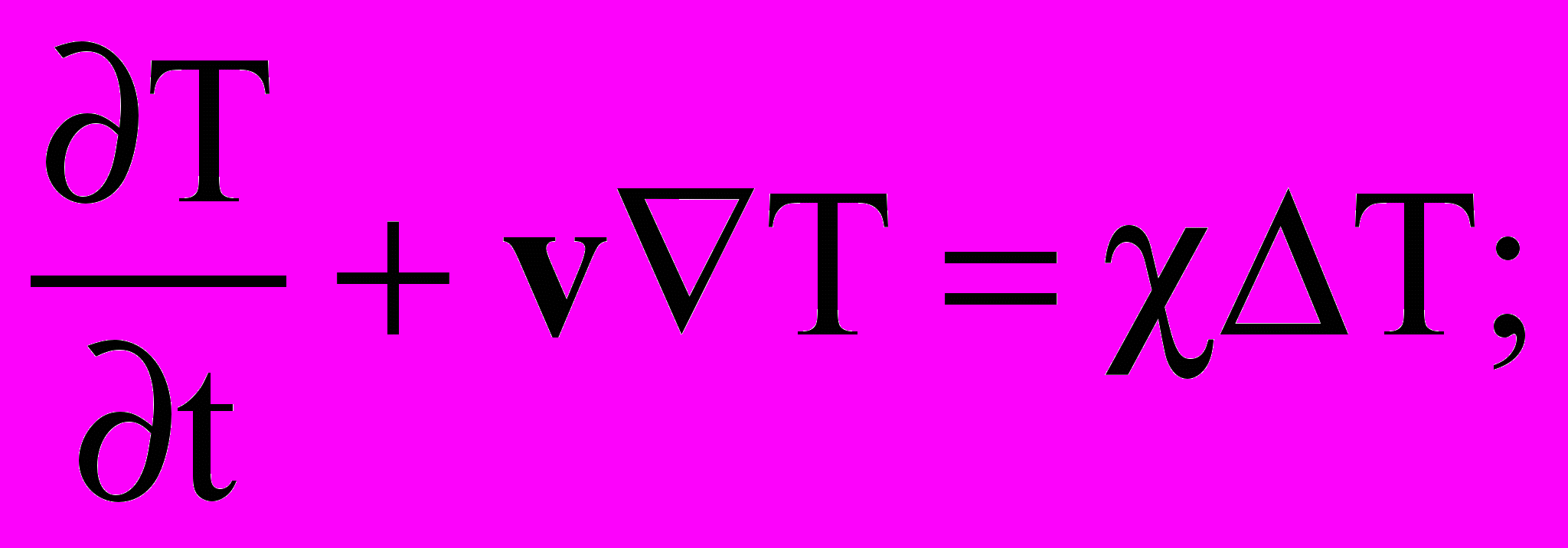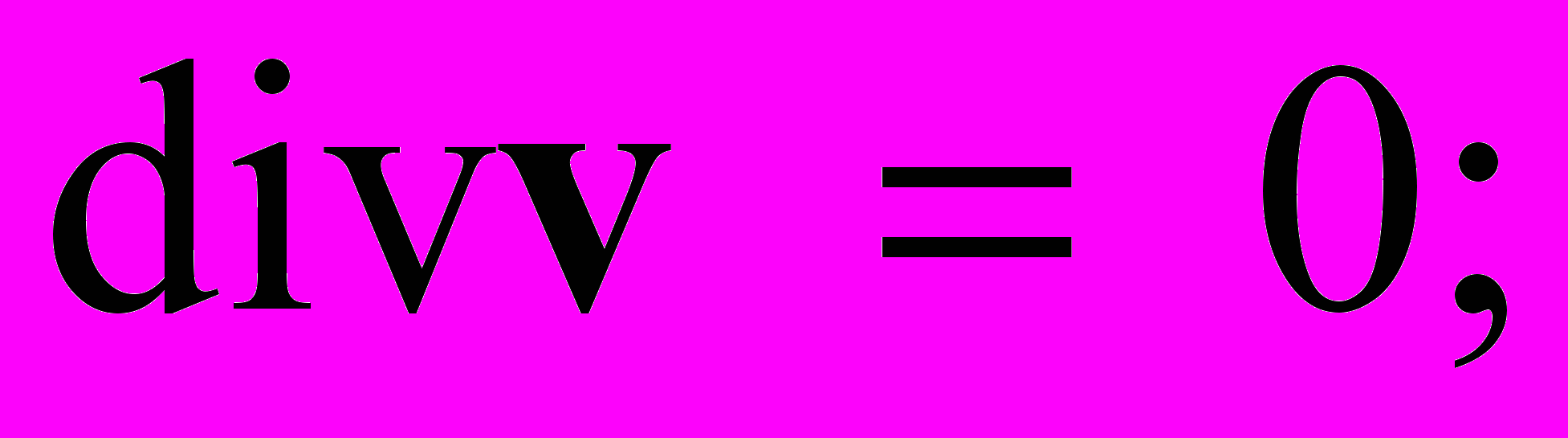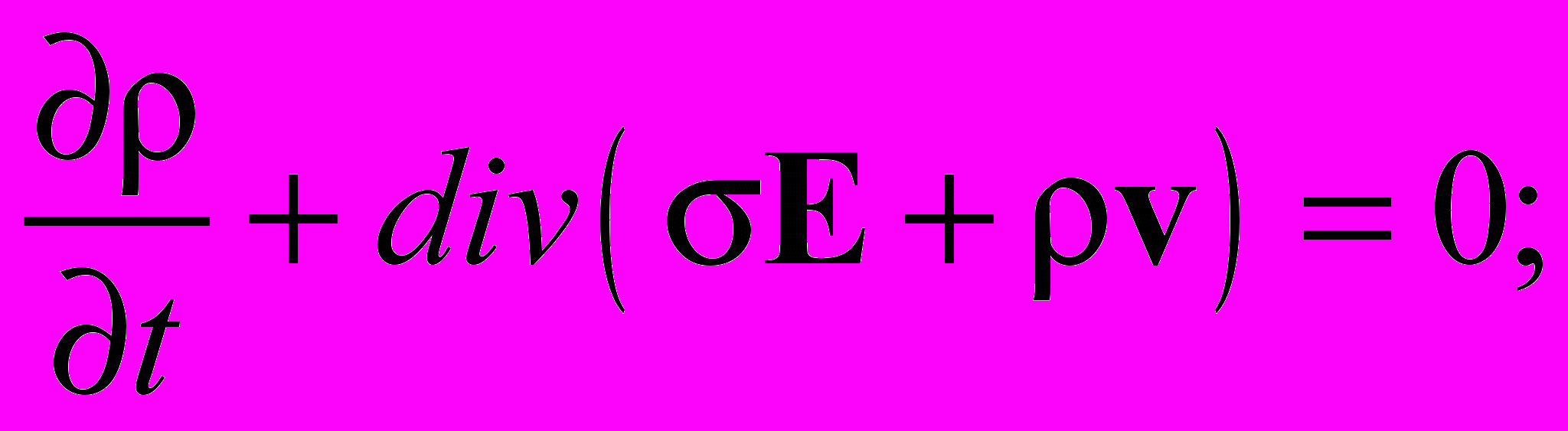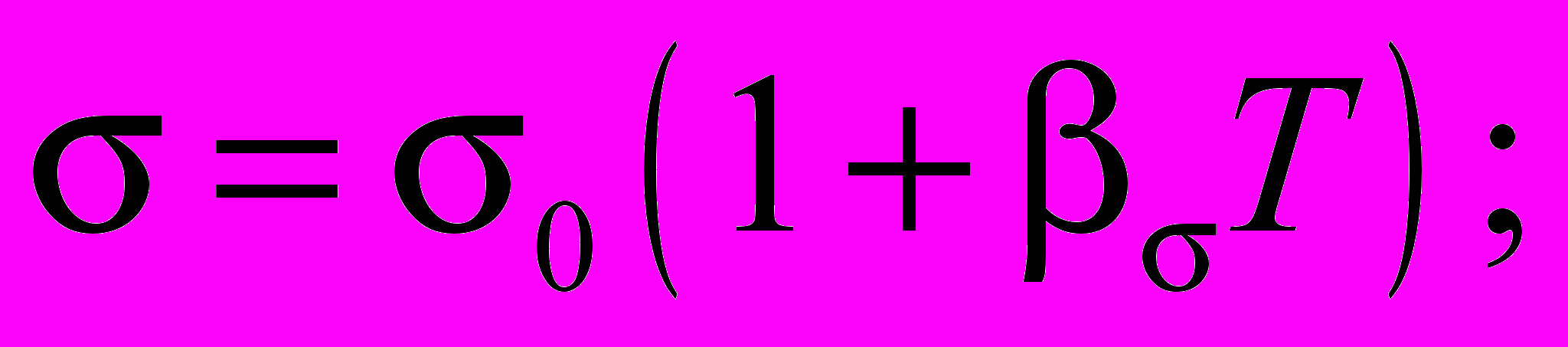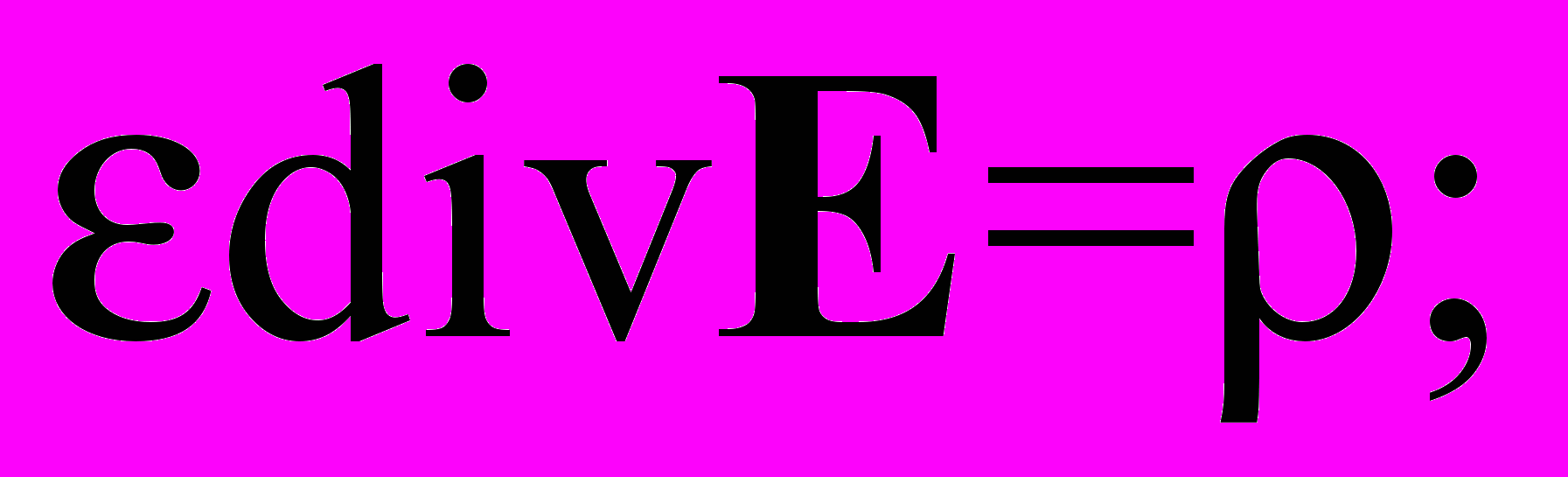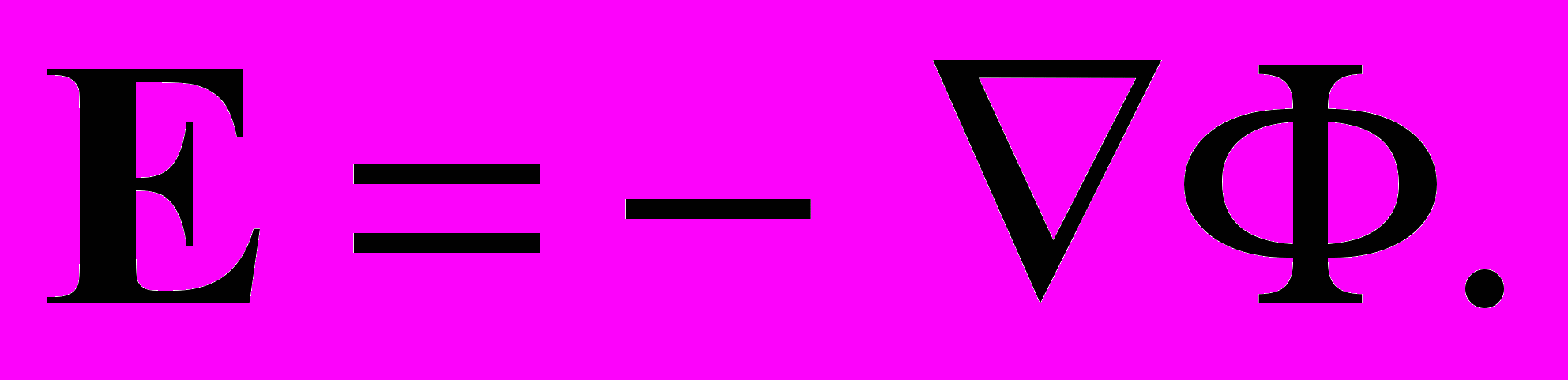Здесь , , , , ₀  соответственно плотность, вязкость, температуропроводность, диэлектрическая проницаемость и средняя электропроводность жидкости,  и _  коэффициенты температурной зависимости массовой плотности и плотности заряда,   плотность заряда, E и Ф  напряженность и потенциал электрического поля, v, T, p – скорость, температура и давление жидкости. Слой жидкого диэлектрика заключен между вертикальными, твердыми, идеально тепло- и электропроводящими стенками (теплообменниками-электродами), находящимися на расстоянии 2h друг от друга. В системе координат с вертикально расположенной осью z, осью y – горизонтально вдоль слоя и осью x горизонтально поперек слоя с границами слоя совпадающими с плоскостями x =  h и условиями на них v = 0, T =  , Ф =  U, где h  полуширина слоя жидкости,  и U – половина разности температур и потенциалов между границами слоя, найденное основное стационарное решение исследовано на устойчивость. Как известно, для стационарного конвективного течения между вертикальными параллельными плоскостями наиболее опасными являются плоские возмущения, при которых отсутствуют продольная горизонтальная компонента v_y скорости и зависимость от продольной горизонтальной координаты y. В работе рассмотрены именно такие возмущения.

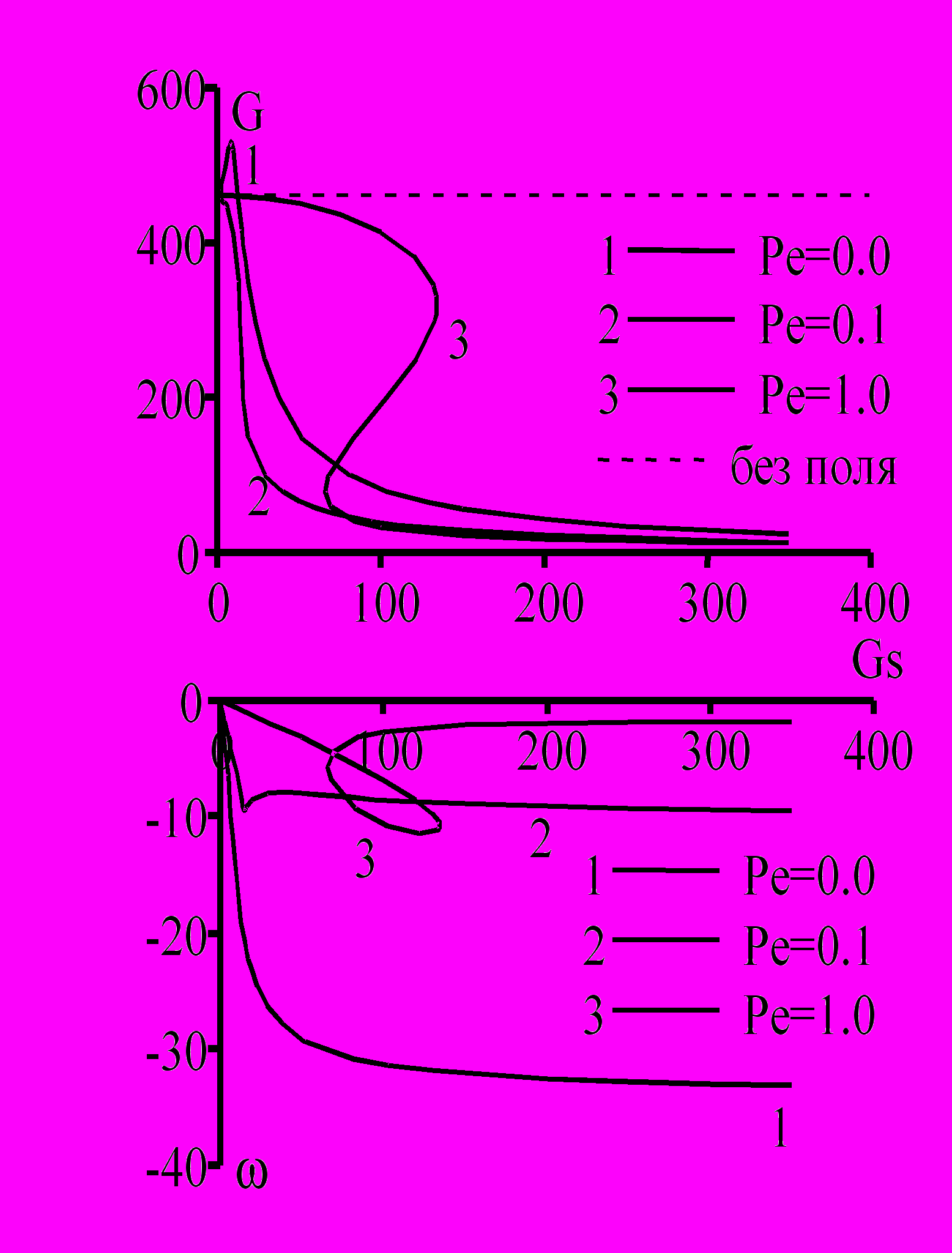
Результаты численного расчёта представлены в виде зависимости числа Грасгофа G = gh³/² от числа Gs = U²_/gh³. Такой способ представления результатов удобен для сравнения с экспериментальными данными, поскольку число G зависит от перепада температур, а число Gs зависит от напряжения. Это означает совпадение с точностью до масштабных множителей графика зависимости критической температуры от квадрата напряжения с графиком зависимости G от Gs. Для выяснения влияния поля на волновое число k исследовалась форма нейтральных кривых для разных значений электрических параметров.

Для изучения были выбраны различные комбинации чисел Прандтля P =  и Pe = /₀h², позволяющие устанавливать произвольные соотношения для времен релаксации скорости, температуры и заряда. На рис. 10 представлен случай P = 0,1, когда характерное гидродинамическое время (время релаксации скорости) много больше характерного теплового времени (времени релаксации температуры); такие возмущения условно считают "изотермическими". Штриховая линия показывает критическое число Грасгофа в отсутствии электрического поля. При Pe = 0 (кривая 1, случай, когда характерное тепловое время много больше времени релаксации заряда), с ростом Gs поначалу наблюдается стабилизация стационарного течения, сменяющаяся затем дестабилизацией при больших значениях Gs.

Рис. 10

Если тепловое время сравнимо с электрическим (Pe = P = 0.1, кривая 2), то начальной стабилизации уже не наблюдается; электрическое поле монотонно уменьшает устойчивость течения при своем возрастании. При электрическом времени, существенно превосходящем гидродинамическое (Pe = 1, кривая 3) также существует дестабилизация, но уже не монотонно усиливающаяся, а имеющая более сложный вид. В средней части графика наблюдается S-образный изгиб, означающий возможность трехкратного перехода границы устойчивости одной и той же моды при фиксированном Gs (в диапазоне значении от 66 до 134) и плавно возрастающим от нуля G. При минимизации параметрической зависимости по волновому числу k ширина изгиба уменьшается (с 68 до 21 по Gs), но возможность неоднократного перехода между областями устойчивости и неустойчивости сохраняется (под термином «ширина» подразумевается расстояние между крайними левым и правым выступами изгиба). С ростом числа Pe изгиб расширяется и перемещается в область больших Gs, причем величина сдвига гораздо больше увеличения ширины. Это приводит к расширению участка слабой изменяемости G в области малых Gs.

Во всех случаях неустойчивость приобретает колебательный характер, причем при малых Gs частота  зависит от значения Gs линейно.

В работе, кроме того, приведены несколько десятков графиков нейтральных кривых для различных комбинаций значений чисел Gs, P и Pe; зависимости числа Грасгофа G и частоты  колебательной моды от числа Gs при различных значениях Р и Pe; зависимости критического числа Грасгофа от числа Прандтля при значениях электрического числа Грасгофа Gs = 0; области чисел Прандтля P и электрического Прандтля Pe, в которой существует дополнительная стабилизация за счет электрического поля и т.д.

Раздел 4.1.4 «Экспериментальное исследование устойчивости течения неоднородно нагретой слабопроводящей жидкости в вертикальном конденсаторе» содержит подробное описание экспериментальной установки, методик измерения и полученных результатов.

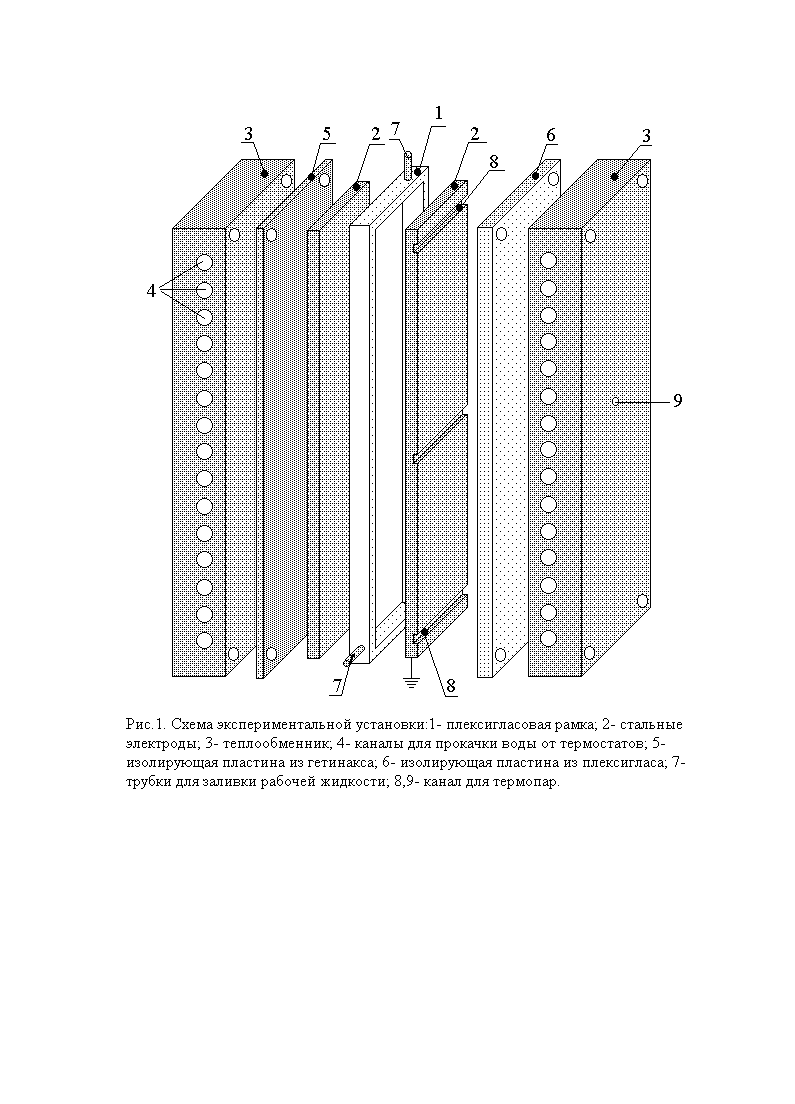
Экспериментальная ячейка, в которой проводились исследования ЭТК-неустойчивости течения представлена на рис. 11. Ячейка представляла собой вертикальный конденсатор, образованный прозрачной плексигласовой рамкой 1 и электродами 2 размерами 43×10×0,3 см. Толщина рамки определяла расстояние между электродами конденсатора и в разных сериях опытов была равна 8,0, 5,0 и 3,5 мм. Толщина вертикального слоя изменялась с целью исследования ЭТК-неустойчивости в более широком интервале электрического и обычного чисел Грасгофа. Градиент температуры в слое задавался теплообменниками 3, представляющими массивные алюминиевые блоки 45×14×5,5 см с цилиндрическими каналами 4 в каждом. По каналам прокачивалась вода от двух термостатов UTU-2. Такая массивная конструкция позволяла поддерживать температуру каждого теплообменника с точностью до 0,1 ⁰С при неравномерности температуры вдоль его поверхности не более 0,02 ⁰С. Между теплообменниками и электродами устанавливались тонкие электроизолирующие пластины: 5 – из гетинакса толщиной 0,10 см и 6 – из плексигласа толщиной 0,38 см. Плексигласовая прокладка 6 служила образцовой пластинкой постоянной теплопроводности в методе Шмидта Мильвертона исследования устойчивости равновесия жидкости.

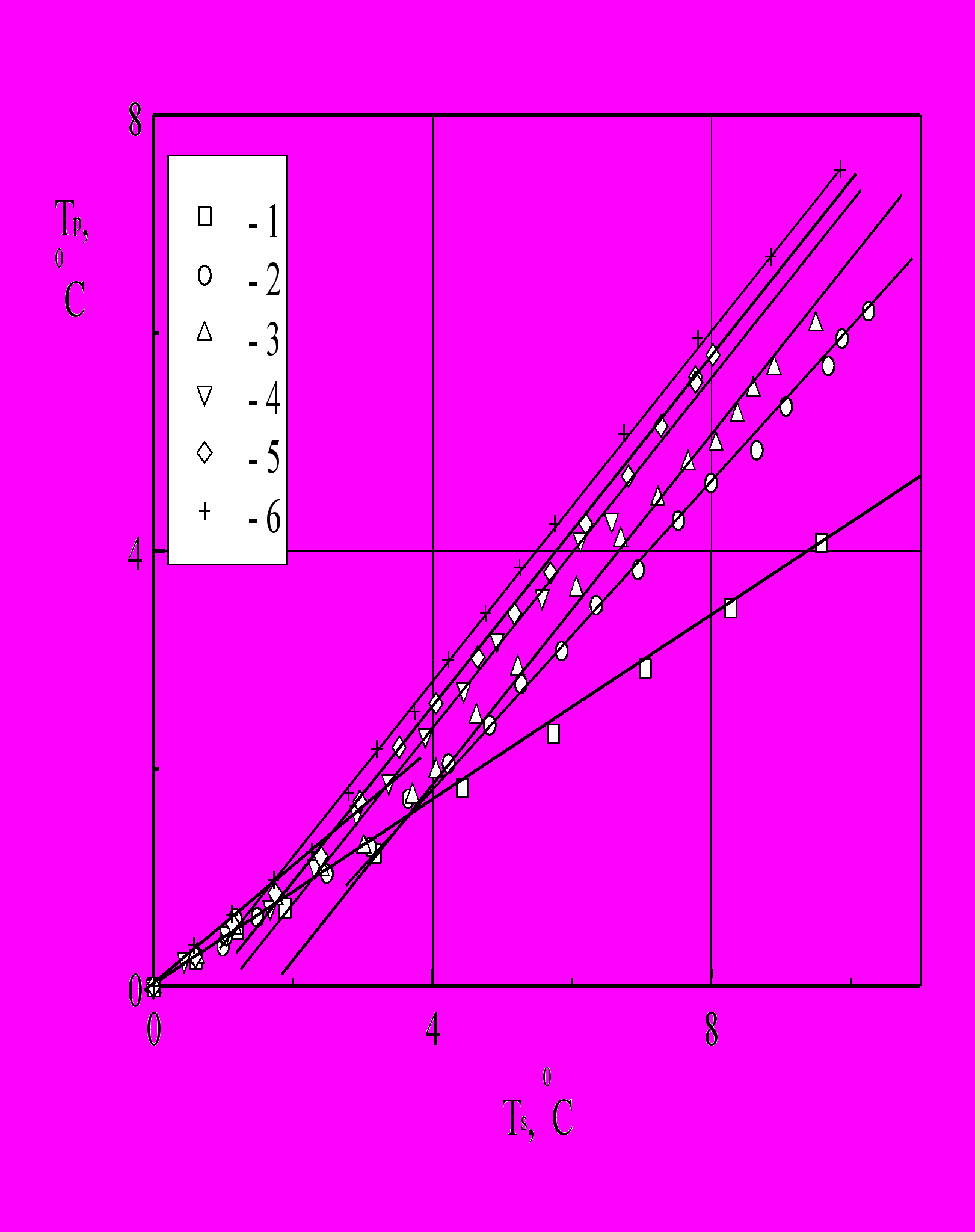
Методика эксперимента заключалась в сравнении теплового сопротивления жидкого слоя и изолирующей прокладки путем измерения перепадов температуры на слое жидкости ΔT_s и на изолирующей прокладке ΔT_p. Если электрическое поле не влияет на основное термогравитационное течение и теплоперенос определяется только молекулярной теплопроводностью, то отношение падения температуры на слое жидкости T_s к падению температуры на образце ΔT_p есть постоянная величина при различных перепадах температуры между теплообменниками.

Рис. 11

При возникновении ЭК эффективная теплопроводность жидкости увеличивается, а отношение падений температур уменьшается. По построенной зависимости ΔT_p от ΔT_s определялось критическое значение разности температуры на слое жидкости ΔT^*, при котором начинается ЭК. Вплоть до этого значения зависимость представляет собой прямую линию, выходящую из начала координат. После кризиса угол наклона прямой изменяется, что свидетельствует о возникновении ЭК.

Рис. 12

Характерные зависимости перепада температуры на датчике теплового потока от перепада температуры на слое жидкости для нескольких фиксированных значений напряжения на электродах (от 0 до 3500 В) представлены на рис. 12. Видно, что для нулевого напряжения (1) зависимость представляет собой прямую, проходящую через начало координат. Такая зависимость характеризует молекулярный режим теплопередачи, потому что основное термогравитационное течение не переносит тепла поперек слоя. Зависимость ΔT_p - ΔТ_s в присутствии поля при малых значениях перепадов температуры на слое жидкости совпадает с соответствующей для U = 0 В, что соответствует отсутствию ЭК. Однако при дальнейшем увеличении перепада температуры зависимость терпит излом и перепад температуры на прослойке увеличивается быстрее, чем перепад на слое жидкости. Это свидетельствует о том, что в модели возникает ЭК, которая увеличивает тепловой поток и, соответственно, уменьшает перепад температуры на слое жидкости.

Рис. 13

Таким образом, для каждого фиксированного значения напряжения на электродах были найдены критические значения перепадов на слое жидкости ΔT^*, соответствующие точке излома характеристик теплопередачи ΔT_p - ΔT_s. По измеренным параметрам рабочей жидкости и полученным критическим перепадам температур была построена карта устойчивости термогравитационного течения (рис. 13) в безразмерных координатах электрическое Gs и традиционное G числа Грасгофа. Безразмерные параметры вычислялись в соответствии с формулами и 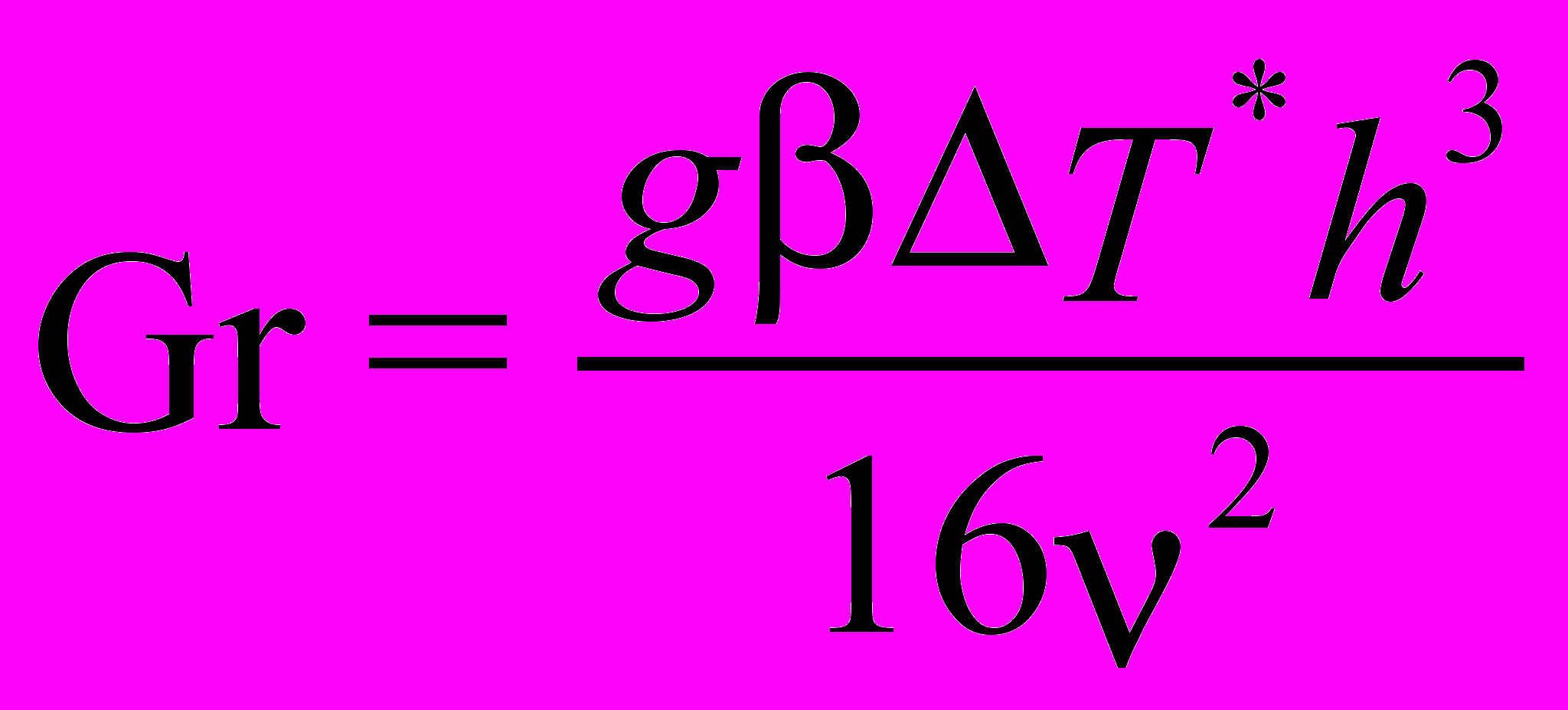. На рисунке приведены данные теоретических расчетов для соответствующих данным сериям экспериментов электрическому и обычному числам Прандтля. Видно, что результаты экспериментов согласуются с расчетами.

Раздел 4.2 посвящен исследованию обнаруженного эффекта возникновения звуковых автоколебаний в акустическом резонаторе. Показано, что процесс образования пространственно-временных диссипативных структур в парогазовых генераторах может быть объяснен, в отличие от предыдущих исследований, без привлечения дополнительных подгоночных параметров.

Раздел 4.3 «Термокапиллярное течение от линейного источника тепла» содержит три подраздела. В п.4.3.1 поставлена и решена стационарная задача о термокапиллярной конвекции от линейного источника тепла постоянной мощности, расположенного на горизонтальной поверхности вязкой несжимаемой жидкости. Полученное аналитическое выражение для погранслойного приближения слишком громоздко, поэтому для определения параметров задачи используется модифицированный метод Кармана-Польгаузена, который в комбинации с методом Галеркина позволил найти выражения для составляющих скорости как функций поперечной координаты.

В разделе 4.3.2 исследована устойчивость найденного погранслойного течения от линейного источника тепла, расположенного на свободной поверхности жидкости, по отношению к плоским возмущениям: на основное стационарное течение и стационарное поле температуры наложены возмущения поверхности, зависящие от продольной координаты x и времени t. С помощью метода разделения переменных задача сведена к системе обыкновенных дифференциальных уравнений для амплитуд возмущений, которые решены методом Галёркина. В качестве иллюстрации полученных результатов приведены нейтральные кривые устойчивости для воды (рис. 14). На рис. 14а и 14б представлены нейтральная кривая гидродинамической моды для воды и соответствующие частоты колебаний. В линейной задаче декремент предполагался чисто мнимым   i, а волновое число – комплексным k = k_r+ik_i. Нейтральный режим определялся условием k_i = 0 и на рис. 14 представлены нейтральные кривые в координатах (k, Ма) и (k, ).

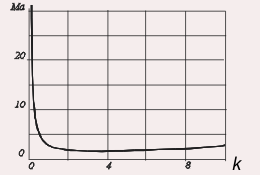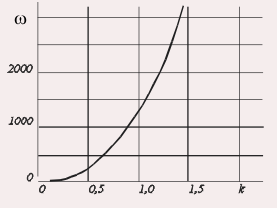Рис. 14а	Рис. 14б

В п. 4.3.3 исследована устойчивость найденного в п. 4.3.1 погранслойного течения от линейного источника тепла, расположенного на свободной поверхности жидкости, по отношению к возмущениям в плоскости yz в той же постановке, что и в п. 4.3.2. Численные расчёты показали, однако, что при всех числах Марангони движение по отношению к данному возмущению устойчиво: условие совместности системы уравнений оказывается невозможно выполнить ни при каких значениях Ма.

Пятая глава диссертации содержит результаты экспериментального и теоретического исследования меандрирования струй, стекающих по наклонной плоскости. В разделе 5.1 приведен обзор работ по изучаемой теме, в разделе 5.2 излагаются результаты тестовых экспериментов и проведённых теоретических исследований неустойчивости стекающих струй к меандрированию, на основании которых констатируется, что меандрирование струек происходит вследствие неконтролируемых в эксперименте самых разнородных случайных причин. Поэтому результаты опытов предлагается анализировать, используя метод, предложенный Ланжевеном для анализа движения броуновской частицы.

В следующем разделе 5.3 «Стекание струйки как броуновское движение гармонического осциллятора» описываются эксперименты и способ обработки результатов, при котором вся струя сопоставляется одной броуновской частице. В качестве случайного события рассматривается получение в заданных контролируемых условиях видеокадра струи воды, снятой в течение трёх минут. Условиями, которые фиксировались в экспериментах, были углы наклона подложки, мощности струй, постоянная в течение всех опытов температура и одинаковая по условиям очистки перед съёмкой каждого видеокадра поверхность подложки (плоское стекло площадью 50150 см² и доска 90120 см², покрытая пластиком). Каждый из видеокадров разбивался на 180 фотокадров, соответствующих последовательным моментам времени (временной интервал  менялся в ходе экспериментов и составлял от 0.08 до 1.0 с). Затем на каждой фотографии в случайной декартовой системе координат измерялись в условных единицах координаты 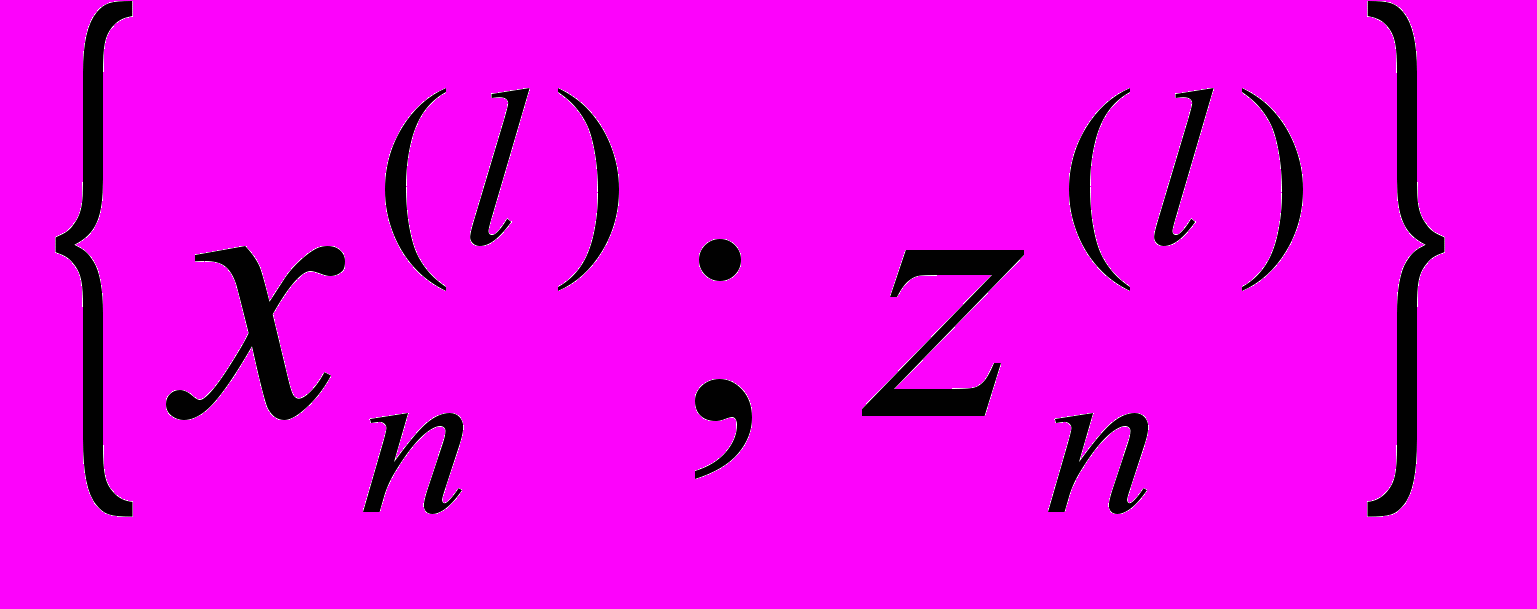, (n менялось от 5 до 20) точек струи, отделённых друг от друга фиксированным расстоянием z вдоль струи (интервал z составлял в разных опытах от одного до пяти сантиметров для различных используемых подложек). По измеренным точкам определялся методом наименьших квадратов линейный трэнд 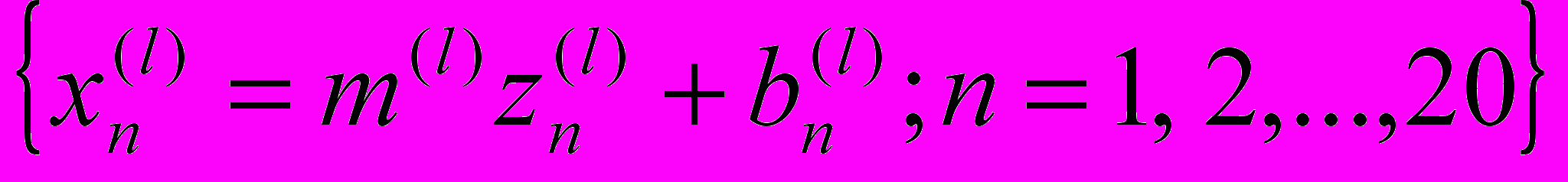. Средний тангенс угла m^(l) отклонения струи вбок рассматривался как одномерная координата 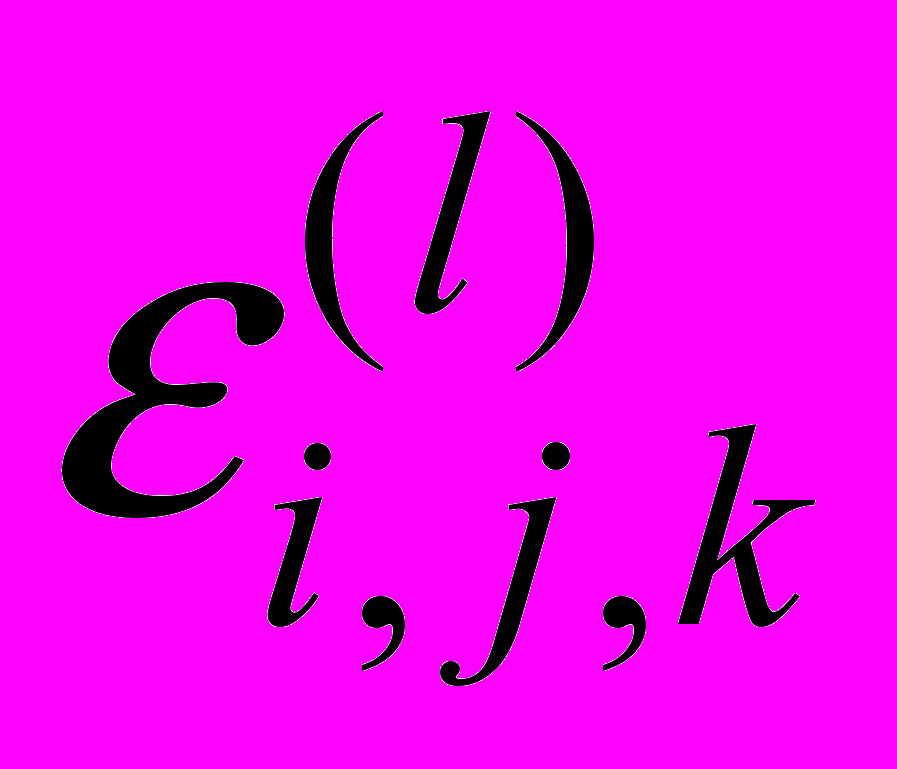«броуновской частицы», задающая случайное положение струи: m^(l)  Полученные таким образом выборки 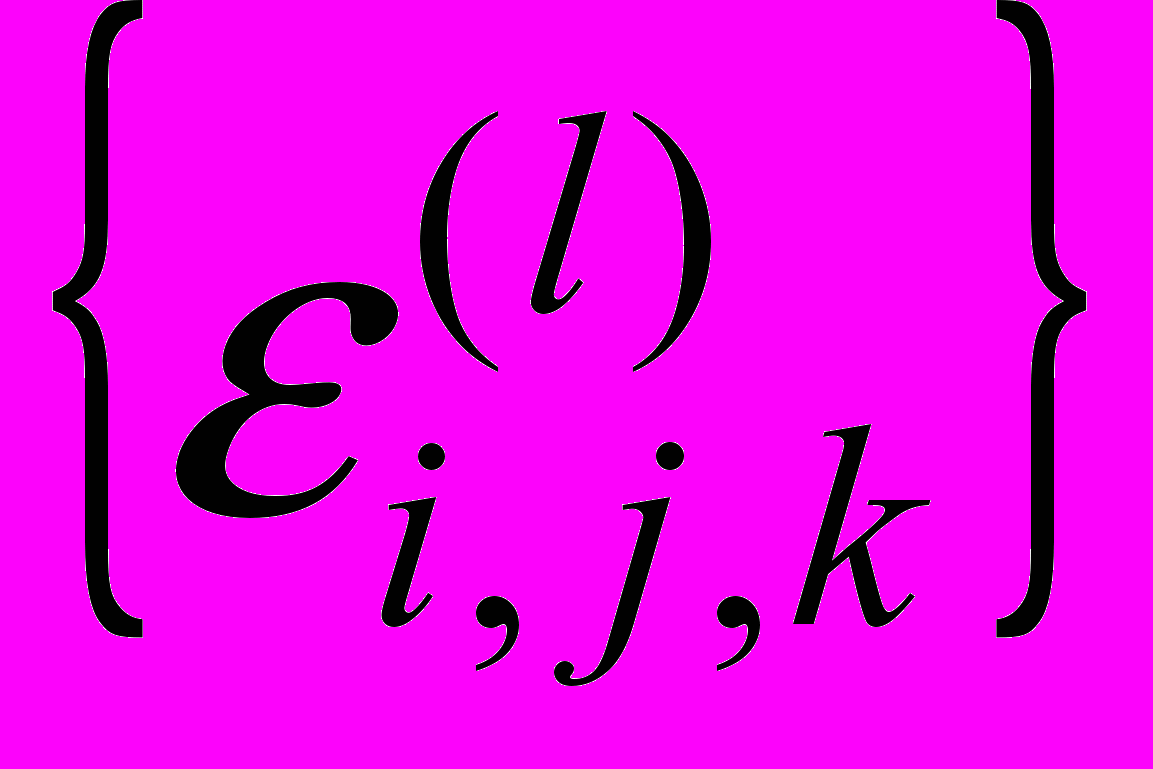для каждого k-того видеокадра, снятого для выбранного угла наклона i и заданного напора струи j, рассматривались как элемент теоретически бесконечной генеральной совокупности {с^(l)} с некоторой плотностью вероятности {с(t)} реализации каждого значения с^(l). В экспериментах число элементов выборок менялось от 180 до 4000.

При статистическом описании процесса меандрирования струи использовалось уравнение Эйлера для виртуальной «броуновской частицы» в вязкой среде при наличии действующей на неё упругой силы и ланжевеновского источника в следующей форме:

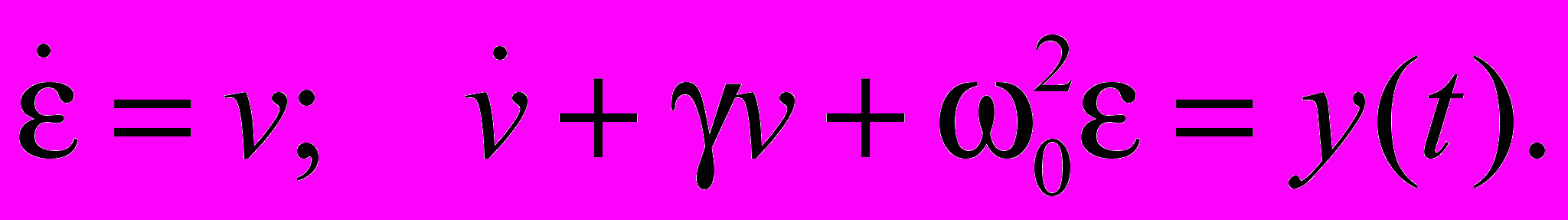
Функция  зависит от времени в общем случае случайным образом и соответствует одномерному отклонению от положения равновесия «броуновской частицы», с которой отождествляется вся струя, а диссипативный фактор  и ланжевеновский источник y(t) являются различными, хотя и «родственными по происхождению» характеристиками подложки. И тот и другой определяются взаимодействием струи с поверхностью:  – характеризует, кроме вязкости, силу сцепления струи с подложкой, а y(t) – силу случайных толчков, вызванных хаотически распределёнными по поверхности подложки микроскопическими неровностями. Поэтому окончательный результат анализа оказался зависящим от единого комплекса, содержащего оба параметра на паритетных началах. Упругая сила ² возникает из-за наличия в системе возвращающих сил: гравитационные и капиллярные силы стремятся выпрямить изогнувшуюся струю. Параллельно был проведён анализ броуновского движения струек методом Эйнштейна (п. 5.4).

Объединённые результаты всех экспериментов представлены на рис. 15 в виде карты режимов стекания струек для различных расходов в интервале от 0.5 до 5.0 см³/с и углов наклона 24.6⁰ (), 33.4⁰ (), 37.5⁰ (), 49.6⁰ (), 60.3⁰ (ж). Как и ожидалось, единственным параметром, формирующим режим, может служить отношение параметра Ланжевена к диссипативному фактору: D/. (D – коэффициент диффузии в пространстве скоростей). Среднее отклонение а русла струи от прямой линии при монотонном (прямоточном или меандрированном) не превышает в выбранных условных единицах 0.5. Выше расположена широкая горизонтальная полоса, в которую не попала ни одна экспериментальная точка. При D/ 2 струи начинают метаться из стороны в сторону, а амплитуда а испытывает резкий скачок, увеличиваясь сразу на порядок. Таким образом, переход от стационарного течения к динамическому происходит при D/  2 скачком, при резком, на порядок, увеличении средней амплитуды колебаний струи. Все процессы, и стационарные, и динамические, характеризуются характерным для броуновских движений стопроцентным разбросом экспериментальных данных с пренебрежимо малой корреляцией всех измеряемых величин.

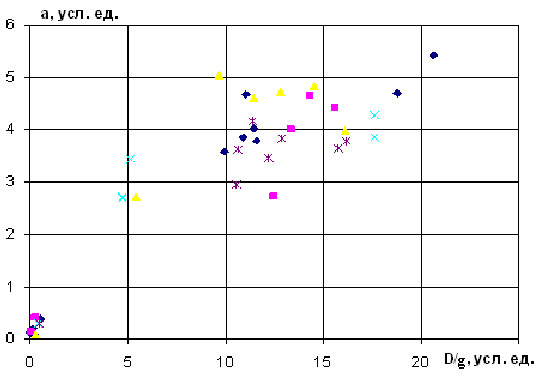Рис. 15

В разделе 5.5 анализ течения струек проводится методами физической кинетики. Струя, стекающая по наклонной плоскости вниз, вдоль оси z, под действием силы тяжести из-за различных не контролируемых в эксперименте причин (непредсказуемое изменение в ходе процесса формы поперечного сечения струи и углов натекания и оттекания, обычно неизвестное качество обработки подложки и т.д.) отклоняется в сторону от первоначального направления. Это отклонение (имеется в виду отклонение конечной точки z струи поперёк движения на x) при заданном угле наклона плоскости к горизонту  и определённой мощности струи Q см³/с непостоянно из-за вероятности заметных флуктуаций. Обозначим неизвестную функцию распределения через f(, Q, z, x). Нормированная на единицу функция f(z, x), (аргументы , Q далее не будем указывать) представляет собой вероятность того, что конец струи длиной z отклонится в сторону на величину x, лежащую между x и x + dx. Заметим, что вероятности для струй повернуть по и против часовой стрелки одинаковы из-за зеркальной симметрии задачи, поэтому далее будем регистрировать сам факт меандрирования, отмечая поворот в любую сторону на x как «благоприятное событие». 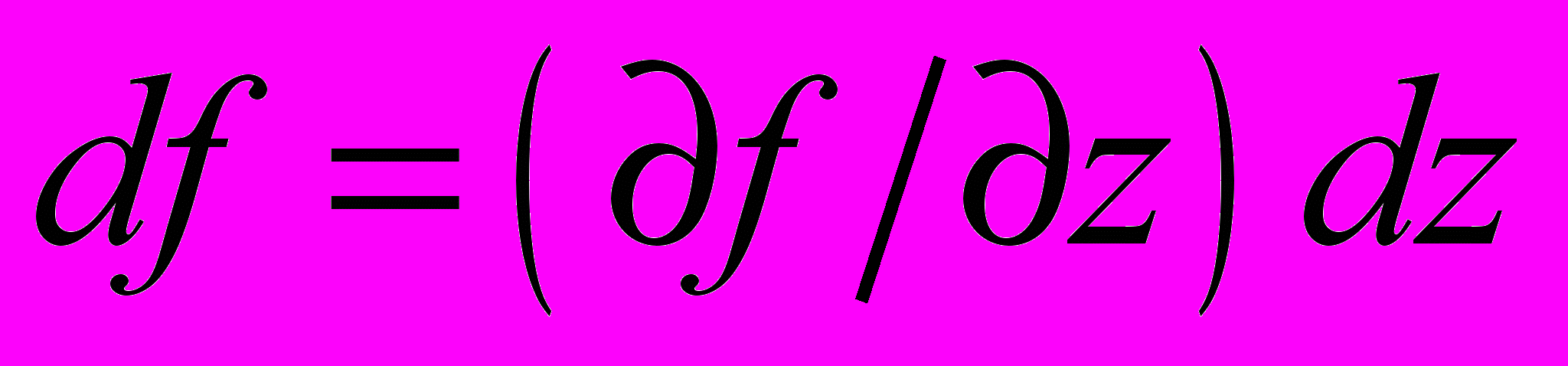Кинетическое уравнение можно получить, приравняв изменение функции на расстоянии dz «интегралу столкновений», который определяется разностью между количеством струй, повернувших на , и числом струй, выпавших из этого множества:

.

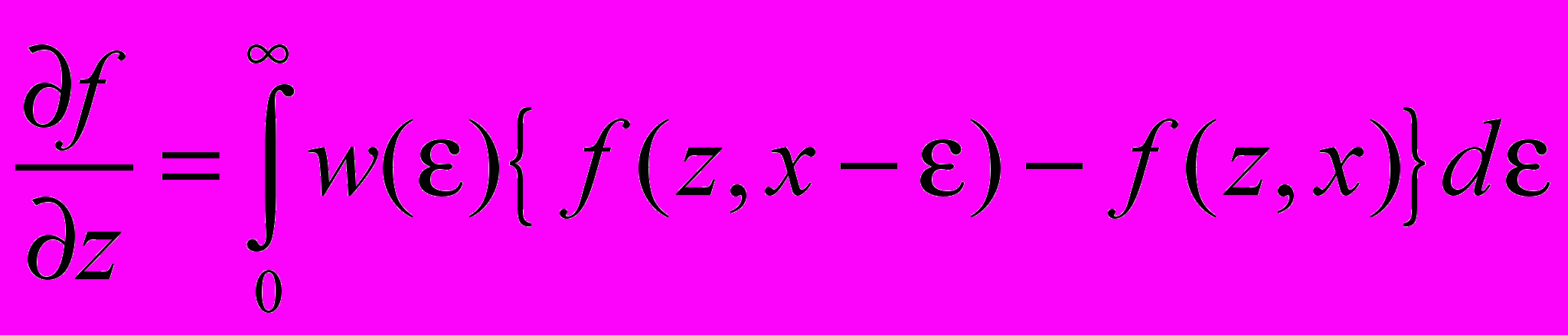Здесь w() – плотность вероятности того, что струя на единице длины пути отклонится в сторону на . Далее будем писать w(), хотя аргументами вероятности w являются, естественно, все параметры задачи. Полученное уравнение Фредгольма решается путём преобразований Лапласа по координате x. Используя далее обратное преобразование Лапласа и теорему запаздывания, определим функцию распределения в общем случае:

.

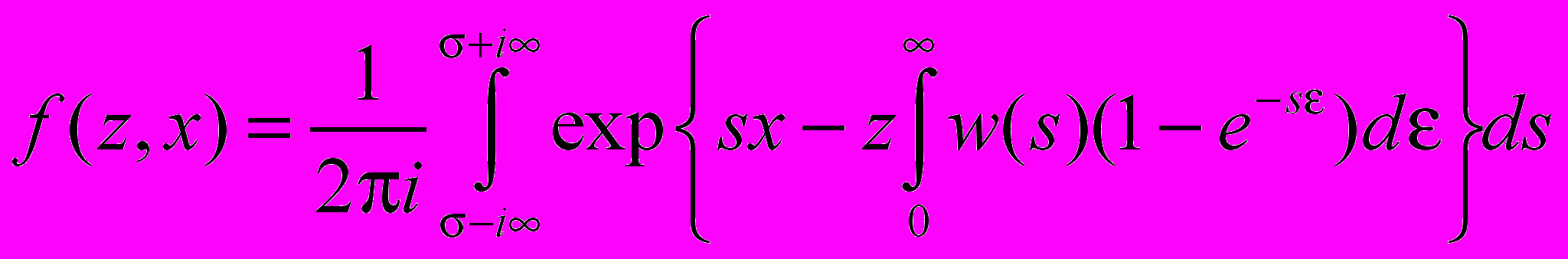Для возможности её применения нужно экспериментально определить функцию w(), зависящую от всего комплекса физико-химических параметров задачи. В предварительных экспериментах было установлено, что при угле наклона, больше 10^о наблюдалось течение струйки со случайными смещениями в сторону. Поэтому изучалось стекание струйки воды под действием силы тяжести при заданном расходе Q по плоской подложке с углом наклона от 10^о до 80^о. Основные эксперименты проводились по следующей схеме. Проточная вода фиксированной температуры под строго выдерживаемым давлением, который обеспечивал намеченный расход, подавалась на инжектор, установленный вдоль продольной оси подложки. Струя воды, стекающая из инжектора по пластине в течение получаса от начала пуска, фиксировалась затем каждые четверть минуты цифровым фотоаппаратом. Вытекающая вода периодически, каждые 30 минут, собиралась в мензурку для определения постоянства расхода. Затем поверхность плексигласа промывалась, высушивалась и опыт повторялся 5 раз при том же расходе и угле наклона подложки. Меандрирование струек происходит вследствие неконтролируемых в эксперименте самых разнородных случайных причин, что приводит к большому разбросу экспериментальных данных. Это вынуждало использовать для определения функции w(a, Q, e) стандартными методами большой объём выборок. В соответствии с этим обработка экспериментов сводилась к определению формы струек по координатам шести выделенных на ней точек при определённых и постоянных для всех серий экспериментов значений z_i. На рис. 16 эти шесть точек являлись точками пересечений струёй горизонтальных линий, разделённых интервалом Dz = 10 см. Видно, что струя в первой горизонтальной полосе «помнит» об импульсе, заданном инжектором. Течение струи на второй полосе соответствует переходному режиму от детерминированного к хаотическому. Течение струй на последних трёх полосах полностью хаотическое.

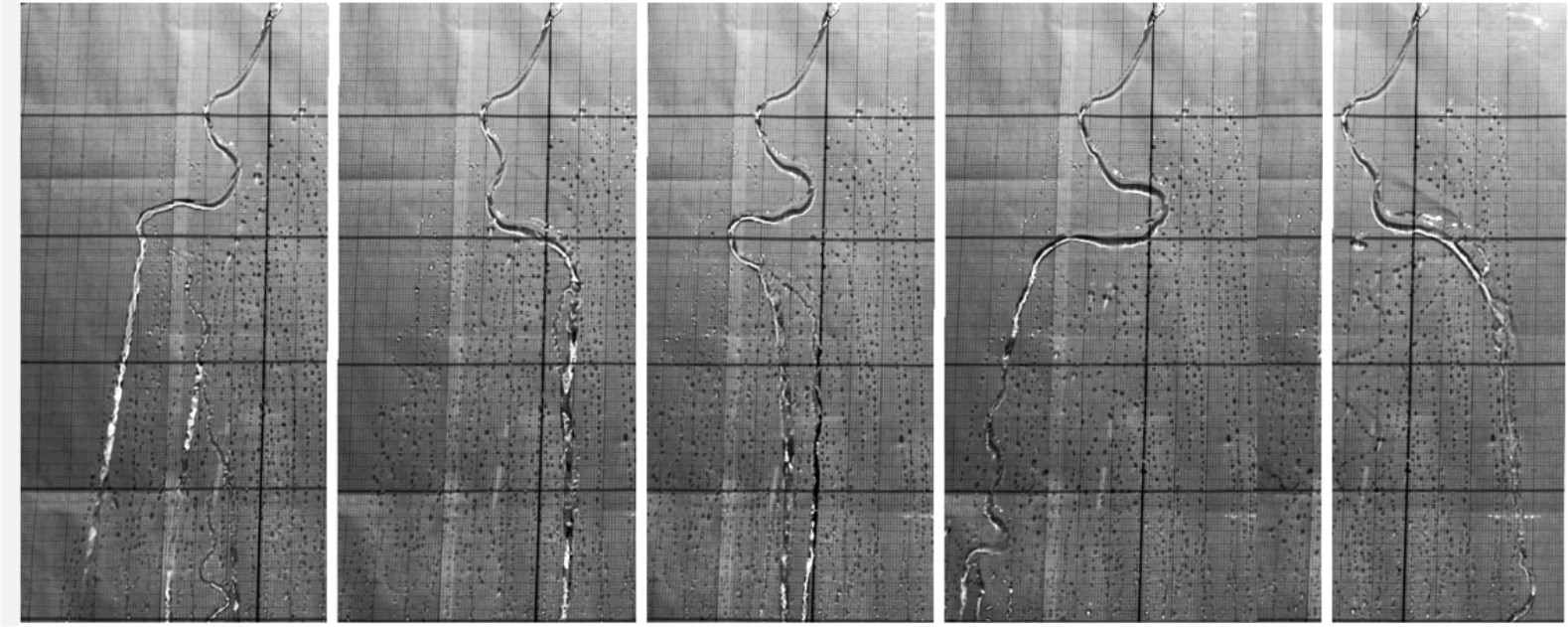Рис. 16

Для каждого из пяти углов наклона плоскости к горизонту и каждого из пяти идентичных получасовых экспериментов фиксировались отклонения x_n струи в пяти заданных точках на расстояниях nz_n (n = 1,..., 5; z_n = 10 см). В результате для каждой серии получена информация о средних отклонениях на каждой из пяти полос. При дальнейшей обработке учитывались отклонения e только на последних трёх полосах. Соответствующие результаты представлены одним из графиков на рис. 17, на котором показано число попаданий из 2500 реализаций в пятипроцентный интервал отклонений e, нормированных на единицу. Точки соответствуют одному из экспериментов по стеканию струи мощностью струи 0,1 л/мин по плоскости, наклоненной к горизонту на угол 64^о. Кривая представляет из себя ненормированную функцию N() = 300 exp(–5.5).

Рис. 17	Рис. 18

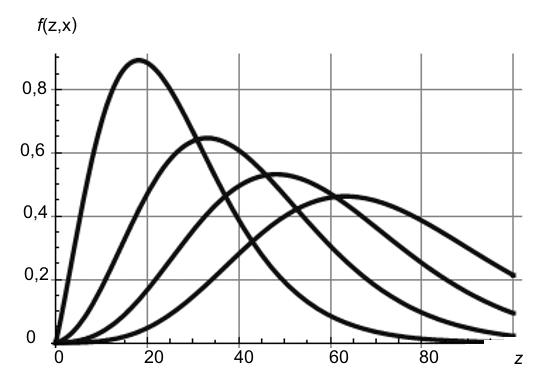
С помощью полученных экспериментальных результатов методом наименьших квадратов определена функция w(e) = 300 exp(–5.5e). После нормирования и подстановки w(e) в выражение для функции изображения, получаем выражение для оригинала f(z, x) (рис. 18) для четырех значений безразмерного x = 0,5; 1,0; 1,5; 2,0 (единица длины 10 см). Форма кривых напоминает известные распределения Максвелла молекул газа по скоростям. Как и у функции распределения Максвелла, кривые f(z, x) имеют максимумы, которые смещаются вправо и становятся ниже с ростом x. Максимальный и самый острый экстремум из числа приведённых здесь относится к безразмерному x = 0.5. На такое расстояние, вероятнее всего, отклонится в сторону струя вблизи точки z  19. Как и следовало ожидать, при больших значениях z все функции распределения асимптотически стремятся к нулю: как очень малые, так и очень большие значения x в этих областях одинаковы и маловероятны.

Приложения содержат подробные аналитические выкладки и программы расчетов для пакета Mathematica.