Geum.ru

Диссипативные структуры и нестационарные процессы в межфазной гидродинамике 01. 02. 05 Механика жидкости, газа и плазмы

Вид материалаАвтореферат диссертации
Третья глава
Подобный материал:
1   2   3   4

В подразделах 2.7.1 и 2.7.2 подробно описаны экспериментальные установки и методика экспериментов. Волновой рельеф на поверхности жидкости создавался за счет колебаний жидкости в рабочей кювете, помещенной на столик вибростенда, установленного на металлической виброизолированной плите размером 200300 см2 и генерирующего периодические колебания вдоль вертикальной оси. Частота и амплитуда вибраций вибростенда регулировались при помощи стандартного лабораторного генератора, диапазон воспроизводимых частот которого лежит в пределе от 20 Гц до 200 кГц. Для контроля подводимого напряжения к генератору последовательно подключался универсальный вольтметр В7-78, который обеспечивал измерение переменного напряжения в диапазоне частот от 3 Гц до 300 кГц. Частота вибраций измерялась с точностью до четвертого знака при помощи цифрового частотомера марки DAGATRON-8023, подключенного параллельно с вибростендом к генератору колебаний. Рабочая кювета с исследуемой жидкостью внутри, помещались на поверхность вибростенда, после чего на поверхности жидкости возбуждались капиллярные волны. Кювета представляла собой круг из органического стекла, диаметром 13,7 см, толщиной 1,6 см, с тремя выемками в форме окружностей с диаметрами 12,8; 9,8; 6,8 см, глубиной 0,8 см и шириной 1 см. В качестве исследуемой жидкости был выбран технически чистый изопропиловый спирт C3H8O. Температура внешней среды поддерживалась постоянной.


Количественные измерения амплитуды волн производились при помощи лазерно-оптического датчика перемещений «OMRON» модели ZX-LD30V, соединенного при помощи интерфейсного блока с COM портом персонального компьютера. Оптический датчик перемещений располагался на высоте 2,5-3,5 см над волновой поверхностью жидкости на стальной пластине, прикрепленной к двухкоординатному столику, который позволял перемещать датчик в двух перпендикулярных направлениях горизонтальной плоскости, и фиксировать положение датчика с точностью до 10 микрон. Для опроса датчика использовалось программное обеспечение «SmartMonitor»; возможности программы позволяли опрашивать датчик с частотой 100 Гц, что позволило получить полную информацию о поведении любой точки волнового фронта жидкости. Явление неслияния для последующего анализа фиксировалось видеокамерой и цифровым фотоаппаратом.

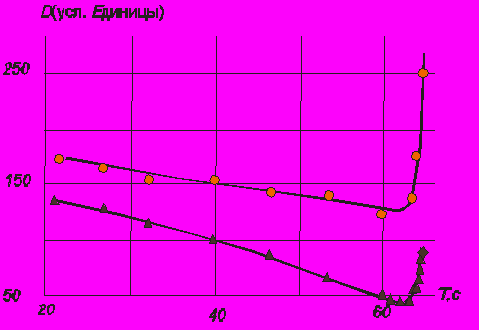
Эксперимент происходил следующим образом: после установления на вольтметре эмпирически подобранного оптимального для работы напряжения, равного 32,29 В, в среднюю дорожку кюветы при помощи шприца наливалось 18 см3 изопропилового спирта. При помощи двухкоординатного столика лазерно-оптический датчик устанавливали так, что его падающий сканирующий луч попадал в один из двух максимумов (находящийся на расстоянии 2,5 мм от внутренней стенки кюветы) волнового профиля. Далее, с помощью программного обеспечения, в течение 20 секунд происходил опрос датчика. За это время в компьютер поступало 2000 значений амплитуды. Обрабатывая данные, получали единственное значение амплитуды волн в максимуме для данной частоты вибраций. Затем частоту генератора изменяли, и измерения повторялись вновь. Ввиду частичного испарения изопропилового спирта необходимо было контролировать толщину слоя. В результате были получены амплитуды капиллярных волн как функции частоты генератора для диапазона частот от 19 до 50 Гц, с шагом 10 Гц, и для диапазона частот от 22 до 22,6 Гц, с шагом 0,1 Гц. Основная часть экспериментов была направлена на регистрацию критического напряжения подаваемого сигнала, при котором капля не коагулировала с общим объемом жидкости. Также были поставлены задачи исследования зависимости частоты вращения и размера капли от времени существования, и исследования поведения капли на волновой поверхности в зависимости от объема наливаемой жидкости.

Анализ результатов проведенных экспериментов содержит вывод, что одной из причин неслияния капли с жидкостью кюветы может быть всасывание воздуха в зазор между ними. Найден также критический диаметр капли, равный 3,9 мм, при котором происходит эффект коагуляции капли с общим объемом жидкости.

Раздел 2.8 посвящен результатам экспериментального и теоретического исследования эффекта кумуляции при ударе капли о воду. В п. 2.8.1 содержится обзор литературы, а в п. 2.8.2 описаны эксперименты по изучению взаимодействия падающей капли со свободной поверхностью другой или той же самой жидкости, заполняющей неглубокую кювету с наклонным к горизонту дном. Экспериментальная кювета представляла собой склеенный из стеклянных пластинок куб с длиной ребра 7,5 см. Кювета заполнялась исследуемой жидкостью заподлицо с краями. В процессе опытов в жидкость вставлялась укреплённая сбоку на шарнире стеклянная пластинка, которая позволяла менять угол наклона «дна» и «глубину» кюветы.




Рис. 3
Эксперимент проходил следующим образом. Высокоскоростная видеокамера настраивалась на скорость съёмки в 1000 кадров за секунду и фокусировалась на область подготовленной заранее капли. Затем, к моменту выдавливания капли, включались прожектор и видеокамера. Весь эксперимент продолжался не более 5 секунд. Из полученного фильма вырезались около сотни фотокадров, на которых зафиксировано столкновение капли с жидкостью и выброс струйки (рис. 3). Для выяснения вопроса, отдаёт ли капля при ударе часть своей массы внешней жидкости, были поставлены специальные эксперименты с подкрашенными жидкостями. Опыты показали, что обмена не происходит: при падении подкрашенной капли воды на чистую воду возникает подкрашенные «султан» и капелька-лидер, а жидкость в кювете остаётся прозрачной; наоборот, выброшенная вверх из подкрашенной воды в кювете чистая капелька остаётся прозрачной.

Разделы 2.8.3 и 2.8.4 посвящены теоретическому исследованию явления кумуляции, в частности объяснению эффекта наклона струи в сторону «берега». При ударе о свободную поверхность жидкости капля прогибает её, что приводит к увеличению поверхностной энергии. В соответствии с принципом Гиббса система сразу начинает восстанавливать своё равновесное состояние с минимальной энергией и схлопывает образовавшуюся полость, выбрасывая каплю вместе с «султаном» вверх. Если при этом будет сказываться влияние наклонного дна, то образовавшаяся при ударе капли полость будет несимметричной. В более мелкой области падающая капля «расчистит» себе более плоское ложе, чем в более глубокой. В воздушной прослойке образуется градиент давлений, направленный в сторону глубоких слоёв жидкости в кювете. Давления сформируют наклонную к вертикали силу, которая и вытолкнет каплю в сторону уменьшения глубины слоя.

В тех же разделах определено последовательное изменение формы капли в начальные моменты времени и сила сопротивления движению капли. Задача решена методом разложения в ряды по предполагаемому малым числу Рейнольдса в полной гидродинамической постановке с учётом вязкости капли, внешней жидкости и прослойки воздуха между ними. Решение доведено до третьего порядка, что позволило определить максимальную силу сопротивления капле, её форму и форму образующейся полости во внешней жидкости. Констатируется количественное и качественное совпадение результатов исследований для частного случая капель воды, падающих на воду.



Рис. 4
В п. 2.9 исследуется влияние линейного натяжения на устойчивость плавающих капель. Для проверки приведённой в п. 2.9.1 гипотезы об определяющей роли линейного натяжения для малых капель, была проведена серия экспериментов (п. 2.9.2) с каплями насыщенного водой четырёххлористого углерода, удерживаемого капиллярными силами на поверхности воды, предварительно насыщенной CCl4. Капля четырёххлористого углерода выдавливалась из шприца на поверхность воды, налитой в чашечку Петри. Затем, через несколько минут, в течение которых капля, испаряясь, превращалась в шайбочку примерно миллиметрового диаметра D, включалась цифровая видеокамера и производилась съёмка коллапса капли. По результатам построен график D(t), (рис. 4), имеющий резко выраженный минимум вблизи момента, когда капля перед тем, как полностью испариться, взрывообразно расползается по поверхности воды тончайшей плёнкой. В том же разделе показано с помощью предложенной симметричной модели системы и принципов Гиббса, что обнаруженный в эксперименте сценарий процесса растекания капли летучей жидкости по другой жидкости может свидетельствовать об определяющей роли линейного натяжения в удержании на поверхности жидкости капиллярными силами крайне малых тяжёлых капель. Для таких капель роль силы тяжести (энергия системы, обусловленная силами тяжести, пропорциональна кубу линейных размеров капли) и поверхностного натяжения (поверхностная энергия пропорциональна квадрату линейных размеров) становится ничтожной по сравнению с линейными капиллярными эффектами, которые и распрямляют каплю, превращая её в плёнку.

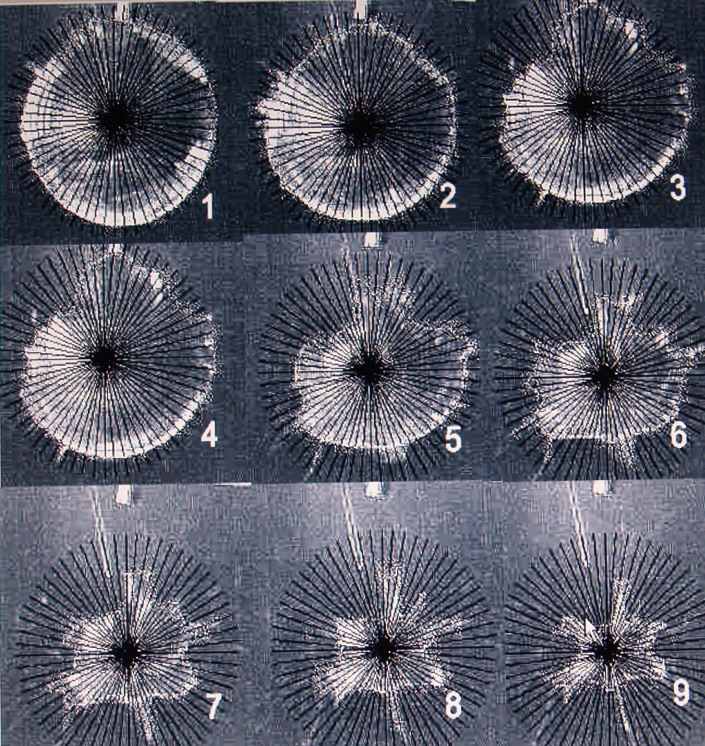
В разделе 2.10 экспериментально и теоретически исследуется морфологическая неустойчивость тонких пленок на примере процесса разрушения мыльных пузырей. В описанных в п. 2.10.1 экспериментах для получения пузырей использовалась жидкость Fairy®, разбавленная дистиллированной водой до концентрации по объёму 1/3. Разрушение оболочки с помощью нагретого стержня фиксировалось с помощью высокоскоростной камеры, которая настраивалась на скорость съёмки 1000 кадров в секунду (рис. 5).







Рис. 5
Раздел 2.10.2 содержит разложение формы отверстия в пузыре рядами Фурье. Для этого определялся центр отверстия 0 по отмеченным координатам двухсот точек периметра. Затем из точки 0 были проведены равноотстоящие друг от друга 100 лучей (рис. 5). Точки пересечения лучей с периметром изображения отверстия заносились в таблицу, что позволяло определить расстояние Rn(t) каждой точки периметра отверстия до его центра 0 для всех десяти моментов времени. Полученные на этом пути результаты нанесены на график «амплитуда an моды как функция соответствующей длины волны » (рис. 6).




Рис. 6
На графике точками отмечены усреднённые по выборке нормированные на единицу по максимальному значению амплитуды гармоник в рядах Фурье, которыми аппроксимировались контуры плёнки. Для наглядности вокруг ромбиков нарисованы контуры окружностей, деформированные соответствующими модами. Фиктивная мода с  = 2, которая всегда присутствует в разложении Фурье благодаря принятой методике обработки результатов, на графике не указана. На основании проведённых расчётов можно утверждать, что схлопывающаяся плёнка, остающаяся от пузыря на последних этапах коллапса представляет собой грубой формы овал, модулированный по периметру пяти-, реже шестиконечными звёздноподобными фигурами (рис. 5).

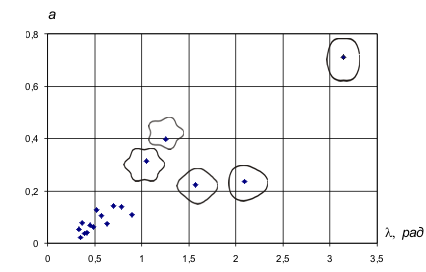
В п. 2.10.3 промоделированы завершающие моменты схлопывания пузыря на этапе «часового стекла». С помощью первой теоремы Грина и вычисленной функции Лагранжа получено уравнение Лагранжа, решение которого позволило определить средний радиус плёнки как функцию квадрата времени.

Третья глава «Образование пространственных диссипативных структур во вращающихся жидкостях» разделена на несколько параграфов. В п. 3.1 отмечаются особенности течений Праудмена и Тейлора, обсуждаются причины, побуждающие изучать конвективные движения и дрейф шаров и капель во вращающихся жидкостях при числах Рейнольдса от единицы до нескольких десятков.

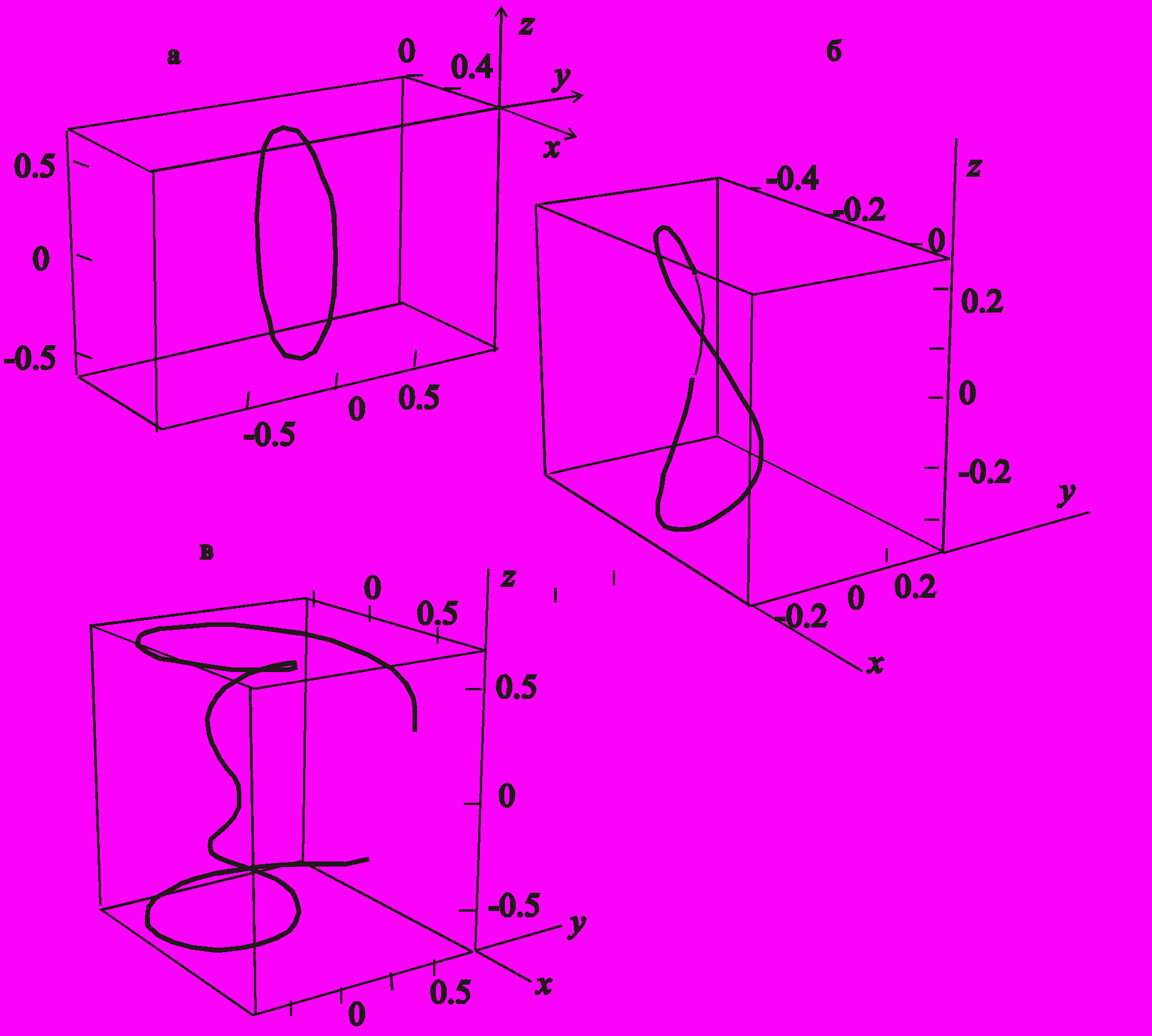
В п. 3.2 аналитически решена задача о конвективной устойчивости жидкости, заполняющей сферическую полость, выфрезерованную в однородном твёрдом массиве, в котором на бесконечности поддерживается постоянный градиент температуры ÑТ¥ = Аеz и который вращается с постоянной угловой скоростью   ez, направленной против ускорения силы тяжести g = –gez. Проведена аналогия различных аспектов процесса с классическими результаты Сильвестона и других авторов по определению кризиса теплового потока через горизонтальный и почти горизонтальный слой, подогреваемый снизу (так называемая «задача Рэлея»).



Рис. 7
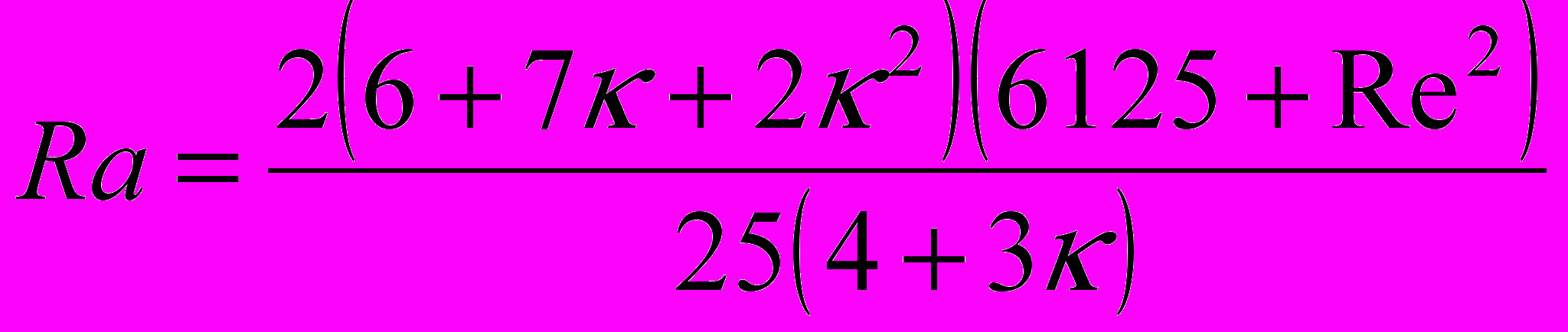Решение задачи в приближении Буссинеска с учётом несжимаемости и вязкости жидкости выполнено методом Галёркина с минимальным числом функций, которое позволяет проследить влияние на процессы вращения полости. Результаты представлены формулой (Ra – критическое число Рэлея, при котором начинается лавинообразное перемешивание жидкости, Re – числo Рейнольдса, определённого по угловой скорости вращения полости,  – отношение теплопроводностей жидкости и массива) и в виде линий тока в аксонометрической проекции для трёх значений числа Рейнольдса (рис. 7). Из графиков видно, что в не вращающейся жидкости линии тока расположены в меридиональных плоскостях полости, при медленном вращении жидкости кориолисова сила разворачивает струйки вбок, закручивая их в спираль при дальнейшем увеличении Re.




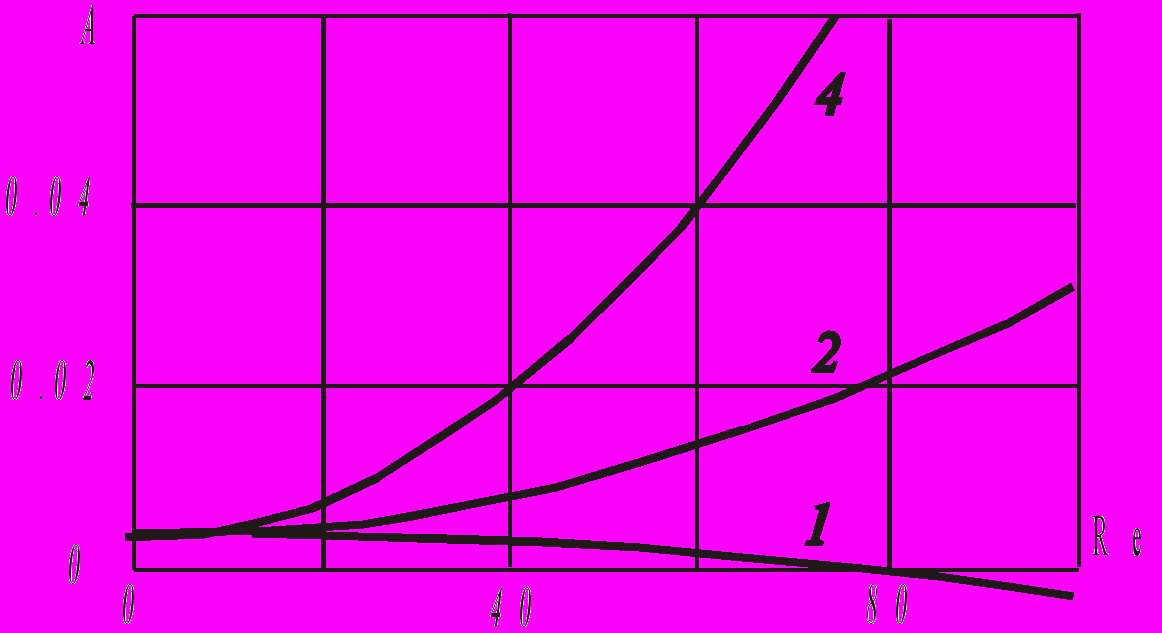Рис. 8
В п. 3.3 исследовано влияние вращения на конвективное движение жидкой смеси, заполняющей сферическую полость в неоднородно нагретом твёрдом массиве, вращающемся с постоянной угловой скоростью , направленной против ускорения силы тяжести. Задача решается в полной постановке с учётом несжимаемости, вязкости и термодиффузии в приближении Буссинеска методом разложения в степенные ряды по числу Рейнольдса, определённому по скорости вращения полости. Решение доведено до функций третьего порядка. Результаты представлены в виде графика зависимости безразмерной амплитуды скорости в центре шара как функции числа Рейнольдса Re для трёх значений чисел Рэлея 1, 2, 4 (рис. 8). Видно, что до чисел Re порядка 10 конвективное движение в полости практически незаметно. При числах Ra  1 скорость в центре шара с увеличением Re меняет знак, что соответствует движению жидкости по оси вращения сверху вниз. Этот результат можно связать с действием центробежной силы, которая разбрасывает в стороны более холодные слои жидкости. При малых скоростях вращения силы Архимеда заставляют эти тяжёлые слои опускаться вдоль стенок к нагретому дну полости, где они, нагреваясь, поднимаются вверх вдоль оси вращения. Ситуация меняется при увеличении чисел Re. В этом случае при относительно малых мощностях подогрева, то есть малых числах Ra, силы Архимеда уже не могут противостоять центробежным. Результатом такого положения оказывается ситуация, когда в центре полости, где центробежные силы малы, скапливаются холодные слои, которые под действием сил Архимеда погружаются, давая начало новому направлению конвективного движения.

В разделе 3.4 экспериментально и теоретически изучен эффект подавления дрейфа шаров и процесс образования областей вихревого движения жидкости за шаром или перед ним (Тэйлоровские колонны). Определена физическая причина эффекта – появление вихревых обтекающих шар потоков, формирующих в приполярных областях застойные зоны, образующие своеобразные присоединённые к шару массы. Таким образом, в задачах обтекания тел во вращающихся жидкостях возникает конкурентная борьба между двумя факторами, определяющими скорость дрейфа. С одной стороны – это действующая на шар внешняя сила, с другой – сила Кориолиса, формирующая застойные области. Приведённый качественный анализ задачи подкреплён экспериментом и аналитическим расчётом, результаты которых находятся в количественном согласии.

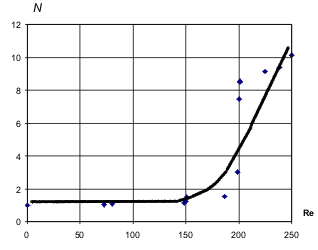Рис. 9
Наблюдение дрейфа шаров осуществлялось на установке, собранной на основе центрифуги, скорость вращения которой менялась от нуля до 30 об/мин. В качестве экспериментальной кюветы использовался прозрачный плексигласовый цилиндрический сосуд квадратного сечения со стороной 10 см и высотой 40 см, заполненный водой. Шарами служили различные по плотности и материалу шары. Для визуализации течения вблизи шаров использовалась подкрашенная перманганатом калия вода, две-три капли которой с помощью тонкой стеклянной трубочки выдавливались перед дрейфующим шаром. По другой методике шары дрейфовали через слой подкрашенной перманганатом калия воды. Движение шара записывалось как видеоролик на персональный компьютер с помощью цифровой видеокамеры, установленной на вращающейся вместе с кюветой платформе. Скорость дрейфа измерялась в средней части кюветы при условии осевого движения шара. Длина рабочего участка 36 см. Время движения измерялось с точностью до 0,04 с. Результаты экспериментов и теоретических расчётов с помощью метода Галёркина и разложения по степеням Re представлены на рис. 9 в виде графика зависимости числа N (отношения скоростей дрейфа в неподвижной и вращающейся жидкости) от числа Рейнольдса.